SỞ GD VÀ ĐT HẢI DƯƠNG
ĐỀ THI KHẢO SÁT CHẤT LƯỢNG LẦN 1
TRƯỜNG THPT ĐOÀN THƯỢNG NĂM HỌC 2017 - 2018 MÔN THI: TOÁN 10 ĐỀ CHÍNH THỨC
Thời gian làm bài: 120 phút, không kể thời gian phát đề
Câu 1 (1,5 điểm)
a) Cho hai tập hợp A  1;3;4;5;6; 
7 và B  0;2;4;6; 
8 . Tìm tập hợp C  A \ B ?
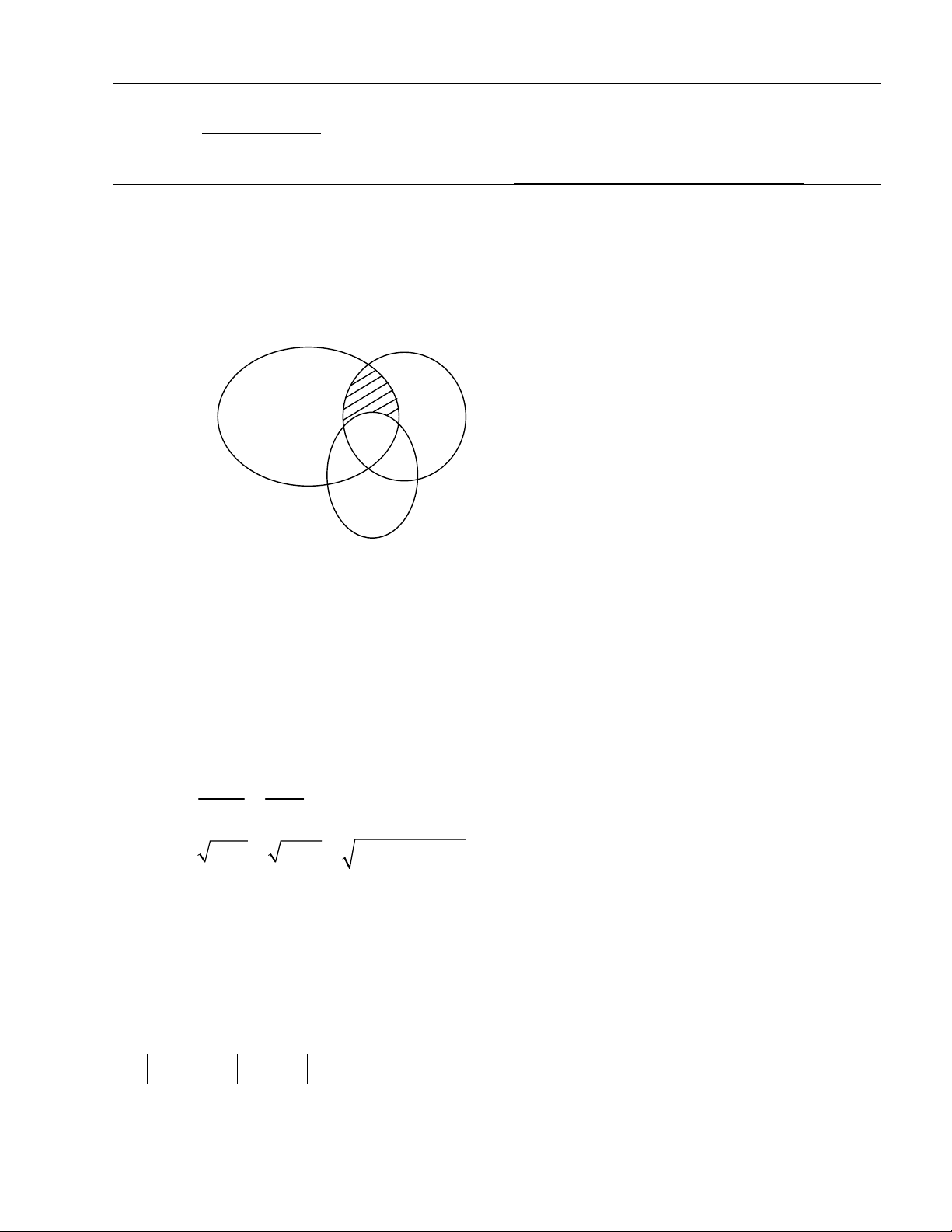
b) Cho A , B , C là các tập hợp bất kì, có biểu đồ Ven mô tả như hình vẽ dưới đây.
Tìm tập hợp mô tả phần gạch sọc trong biểu đồ Ven trên? A B C
Câu 2 (1,5 điểm). Cho hàm số 2 2
y  x  2mx  m  m 1   1 .
a) Lập bảng biến thiên của hàm số khi m  2 .
b) Tìm các giá trị của m để đồ thị hàm số  
1 cắt trục hoành tại hai điểm có hoành độ
x , x sao cho tổng 2 2
S  x  x đạt giá trị nhỏ nhất. 1 2 1 2
Câu 3 (2,5 điểm). Giải các phương trình sau: a) 2
x  4  2x  3 x  2. x  5 3 b)  . 2 x 1 x 1
c) x  1  4  x   x   1 4  x  5 2
x  3xy  3 
x  y  0
Câu 4 (0,5 điểm). Giải hệ phương trình:  4 x  9y 
 2x  y 2  5x  0
Câu 5 (0,5 điểm). Cho 4 điểm bất kỳ ,
A B,C,O . Đẳng thức nào sau đây là đúng?
  
  
  
  
A. OA  OB  B .
A B. AB  AC  B .
C C. AB  OBO .
A D. OACA . CO
Câu 6 (0,5 điểm). Cho đoạn thẳng AB có độ dài bằng .
a Một điểm M di động sao cho    
MA  MB  MA  MB . Gọi H là hình chiếu của M lên AB . Tính độ dài lớn nhất của MH ?
Câu 7 (1,0 điểm). Trong mặt phẳng toạ độ Oxy , cho hai điểm A2;4 và B1;2 . Tính độ  dài véc tơ A . B
Câu 8 (0,5 điểm). Cho hình chữ nhật ABCD có AB  3 , AD  4 . Gọi M là điểm thoả  
mãn điều kiện AM  k.AB . Xác định k để hai đường thẳng AC và DM vuông góc nhau? 4
Câu 9 (0,5 điểm). Rút gọn biểu thức: 2 2 0 0 2 2 0
P  4a sin 30  2abcos180  b sin 60 . Với 3 a,b   . sin  2cos
Câu 10 (0,5 điểm). Cho cot  2 . Tính giá trị biểu thức: Q  . sin  cos
Câu 11 (0,5 điểm). Cho phương trình: 4 3 2
x  4x  x  6x  m  2  0 ( m là tham số). Tìm
tất cả các giá trị m để phương trình trên có 3 nghiệm phân biệt.
---------------------------------Hết---------------------------------
Họ và tên : ………………………..…………………….; Số báo dạnh : ………….
HƯỚNG DẪN CHẤM ĐIỂM Câu Nội dung Điểm 1a
Tập C  1;3;5;  7 . 1,0 1,0 điểm 1b
Là tập hợp  A  B \ C 0,5 0,5 điểm Khi m  2 ta có 2
y  x  4x  3 . Tập xác định D  R 2a 0,25
Tọa độ đỉnh : I (2; 1  )
1,0 điểm Hàm số nghịch biến trên  ;
 2 và đồng biến trên 2; 0,25 Vẽ bảng biến thiên : x  2  y   0,5 1 
Phương trình hoành độ giao điểm 2 2
x  2mx  m  m 1  0   1 2b
Để đồ thị hàm số cắt Ox tại 2 điểm thì  '  m 1  0  m  1 0,5 điểm
x  x  2m Theo Viet: 1 2  2
x .x  m  m 1  0,25 1 2
S  x  x   x  x 2 2 2 2
 2x x  2m  2m  2 1 2 1 2 1 2
Lập BBT của hs f m 2
 2m  2m  2 trên 1;
Tìm được GTNN của S bằng 2 đạt được tại m  1. 0,25 3a 2
x  4  2x  3 x  2   x  2 x  2  2x  3 x  2 1,0 điểm 0,5   
x   x   x 2 2 1  0   0,5 x  1  3b ĐK: x  1  0,25 1,0 điểm
PT  x  5  3 x   1 0,25  2x  2   x  1  0,25
Kết hợp đk suy ra pt vô nghiệm 0,25 3c ĐK: 1  x  4
0,5 điểm Đặt t  x 1  4  x; t  0   
x    x 2 t 5 1 4  2 0,25 2 t  5 PT trở thành: 2 t 
 5  t  2t 15  0 2
t  3 tm  t  5  L 0,25 x 
t  3   x   1 4  x 0 2
 2  x  3x  0   tm x  3 4 2
x  3xy  3  x  y 2  0
x  3y  3x  3xy   1 0,5 điểm     x  9y 
x  y5x  0 x 3y  2 4 2 2 2 2 2
 5x  3x y 2 0,25
Thế (1) vào (2) ta được: 2 x  2
9y 15y  4  0  x  0  1   y   3  4  y   3
x  0  y  0 0,25 1
y   x  1 3 4 2
y   x  x  4  0 VN  3   
KL: Hệ pt có 2 nghiệm:    1 0;0 , 1;     3 
   5
D. OACA . CO 0,5 0,5 điểm    6
Gọi O là trung điểm AB . Khi đó MA  MB  2MO . 0,5 điểm      
Ta có MA MB  MA MB  2MO  BA hay MO  AB .
Suy ra MO  OA  OB 0,25
Do đó M nằm trên đường tròn tâm O đường kính AB . AB a
MH lớn nhất khi H trùng với tâm O hay max MH  MO   . 2 2 0,25 7 
AB      AB   2   2 1; 2 1 2  5 1,0 1,0 điểm 8 Ta có:      
       
0,5 điểm AC.DM  BC  BA.AM  AD  BC.AM  BC.AD  B .AAM  B .AAD. 0,25  16   9k   16
Khi đó AC  DM  AC.DM  0  k  . 0,25 9
Cách 2: Chọn hệ tọa độ Oxy sao cho A là gốc tọa độ, canh AB nằm
trên trục tung, AD nằm trên trục hoành (theo chiều dương), khi đó 0,25
A0;0, B0;3, D4;0,C 4;3 . Giả sử M  ; x y  
AM  k.AB  M 0;3k   
AC 4;3, DM 4;3k    16 0,25
AC  DM  AC.DM  0  9k 16  0  k   9 9 2 2  1  4  3  0,5 điểm 2 P  4a  2ab     2 1  b   0,25  2  3 2  
P  a  ab  b  a  b2 2 2 2 0,25 10
Do cot  2  sin  0 . Chia cả tử số và mẫu số cho sin ta 0,5 điểm 1 2cot 0,25 được Q  1 cot 1 2 2 Q 
 1 2 2 2   1  3 2  5 0,25 1 2 11 2 Pt   2
x  x   2 2
3 x  2x  m  2  0   1 0,5 điểm Đặt 2
t  x  2x . Đk của t để tồn tại x là t  1 (1) trở thành: 2
t  3t  m  2  0 2 0,25
Với t  1 cho một giá trị x .
Với mỗi t  1 cho hai giá trị x t   1
(1) có ba nghiệm phân biệt  2 có hai nghiệm t ,t t/m 1 1 2 t  1  2
g/s (2) có nghiệm t  1  m  6  .
Thử lai: với m  6
 phương trình (2) có hai nghiệm t  1;t  4 0,25 1 2 (tm ycbt) KL: m  6 