Đề KSCL Toán 11 tháng 5 năm 2020 trường THPT Nguyễn Thị Giang – Vĩnh Phúc

Giới thiệu đến quý thầy, cô giáo và các em học sinh đề KSCL Toán 11 tháng 5 năm 2020 trường THPT Nguyễn Thị Giang – Vĩnh Phúc, đề thi có mã đề 132 gồm 05 trang với 40 câu trắc nghiệm, học sinh có 90 phút để làm bài thi, đề thi có đáp án.

39 20 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 11

Môn: Toán 11

Thông tin:

27 trang 8 tháng trước

Tác giả:

Profile Kim Oanh
Trang 1/6 - Mã đề thi 132
SỞ GD & ĐT VĨNH PHÚC
TRƯỜNG THPT NGUYỄN THỊ GIANG
Mã đề: 132
ĐỀ KSCL THÁNG 5 NĂM HỌC 2019 - 2020
Môn: Toán; Lớp 11
Thời gian làm bài 60 phút, không kể giao đề
(Đề gồm 05 trang)
Câu 1: Cho hai điểm
A
,
B
thuộc đồ thị hàm số
sinyx
trên đoạn
0; .
Các điểm
C
,
D
thuộc trục
Ox
thỏa mãn
là hình chữ nhật và
3
CD
. Độ dài cạnh
BC
bằng
A.
1
. B.
3
2
. C.
1
2
. D.
2
2
.
Câu 2: Gọi S là tập hợp tất cả các giá trị của tham số m sao cho giá trị lớn nhất của hàm số
2
2y x x m
trên đoạn
0;3
bằng 5. Tổng tất cả các phần tử của S là
A.
8
. B.
12
. C.
2
. D.
2
.
Câu 3: Cho đồ thị hàm số
y f x
như hình vẽ.
Xét các khẳng định sau
i)
1
lim
x
fx


. ii)
1
lim
x
fx


.
iii)
lim 1
x
fx

. iv)
lim
x
fx


.
Hỏi có bao nhiêu khẳng định đúng?
A. 3. B. 1. C. 2. D. 4.
Câu 4: Cho hình chóp S.ABCD, đáy ABCD là hình vuông cạnh bằng a, tam giác SAB đều. Gọi M là điểm
trên cạnh AD sao cho
, 0;AM x x a
. Mặt phẳng
qua M và song song với (SAB) lần lượt cắt các
cạnh CB, CS, SD tại N, P, Q. Khi diện tích tứ giác MNPQ bằng
2
23
9
a
thì x bằng bao nhiêu?
A.
2
a
. B.
2
3
a
. C.
3
a
. D.
4
a
.
Câu 5: Cho cấp số cộng
n
u
với
1
2u
và
2020
2020u
. Công sai của cấp số cộng đã cho bằng
A.
2017
2018
. B.
2018
2019
. C.
1
. D.
2019
2020
.
Câu 6: Cho hình lập phương
.ABCD EFGH
. Góc giữa hai đường thẳng
,AB EH
là
A.
90
. B.
0
. C.
45
. D.
60
.
O
x
y
D
C
A
B
Trang 2/6 - Mã đề thi 132
Câu 7: Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
a
, mặt bên
SAB
là tam giác đều nằm trong
mặt phẳng vuông góc với đáy. Tính khoảng cách giữa hai đường thẳng
,SA BC
.
A.
2a
. B.
a
. C.
5
2
a
D.
3
2
a
.
Câu 8: Sau đợt nghỉ dịch Covid-19, từ ngày 04 tháng 5 năm 2020, học sinh trường THPT Nguyễn Thị
Giang đi học trở lại. Nhà trường yêu cầu tất cả học sinh đều phải đeo khẩu trang. Qua khảo sát, lớp 11A
có 16 học sinh nữ và 24 học sinh nam, trong đó chỉ có một nửa số học sinh nữ và một nửa số học sinh
nam đeo khẩu trang theo quy định. Nếu chọn ngẫu nhiên một học sinh của lớp 11A để kiểm tra, hãy tính
xác suất để chọn được học sinh nữ hoặc học sinh đeo khẩu trang.
A.
9
10
. B.
7
10
. C.
2
3
. D.
1
2
.
Câu 9: Cho hình chóp
.S ABC
có đáy
ABC
là tam giác vuông cân tại
B
,
,AB a SA AB
,
,2SC BC SB a
. Gọi
,MN
lần lượt là trung điểm
,SA BC
và
là góc giữa
MN
và
ABC
. Giá trị
cos
bằng
A.
3
2
B.
2 11
11
. C.
26
5
. D.
6
3
.
Câu 10: Tất cả các nghiệm của phương trình
cos2 0x
là
A.
2
2
x k k
. B.
4
x k k
.
C.
42
x k k

D.
2
x k k
.
Câu 11: Có 6 chiếc ghế được kê thành một hàng ngang. Xếp ngẫu nhiên 6 học sinh, gồm 3 học sinh lớp
A, 2 học sinh lớp B, 1 học sinh lớp C, ngồi vào hàng ghế đó, sao cho mỗi ghế có đúng một em học sinh.
Xác suất để học sinh lớp C chỉ ngồi cạnh học sinh lớp B là
A.
3
20
. B.
1
6
. C.
2
15
. D.
1
5
.
Câu 12: Đạo hàm của hàm số
sin2yx
là
A.
2cosx
. B.
2cos2x
. C.
2sin2x
. D.
2cos2x
.
Câu 13: Cho cấp số nhân
n
u
với
1
2u
và
2
1u
. Công bội của cấp số nhân đã cho bằng
A.
1
2
B.
1
. C.
2
. D.
1
.
Câu 14: Cho tứ diện đều
có cạnh
AB a
. Tích vô hướng
.ABCD
bằng
A.
2
2
a
. B.
2
2
a
. C.
2
a
. D.
0
.
Câu 15: Cho hai đường thẳng
a
và
b
chéo nhau. Có bao nhiêu mặt phẳng chứa
a
và song song với
b
?
A.
0
. B.
1
. C. Vô số. D.
2
.
Câu 16: Một vật chuyển động thẳng xác định bởi phương trình
32
1
21
2
S t t t
(
t
là thời gian tính
bằng giây, S là đường đi tính bằng mét). Tính vận tốc
/ms
của vật tại thời điểm
0
2ts
?
A.
14 /ms
. B.
9/ms
. C.
12 /ms
. D.
6/ms
.
Trang 3/6 - Mã đề thi 132
Câu 17: Cho tam thức bậc hai
y f x
có đồ thị như hình vẽ bên dưới. Tìm số nghiệm của phương
trình
sin 2fx
với
3
;
2
x




.
6
4
2
2
4
6
10
5
5
10
-3
3
-1
O
A.
4
. B.
2
. C.
3
. D.
1
.
Câu 18: Hàm số
21
1
x
y
x
có đạo hàm là
A.
2
3
( 1)

y
x
. B.
2
1
( 1)
y
x
. C.
2
1
( 1)

y
x
. D.
2
y
.
Câu 19: Tam giác mà ba đỉnh của nó là ba trung điểm của ba cạnh tam giác
ABC
được gọi là tam giác
trung bình của tam giác
ABC
. Ta xây dựng dãy tam giác
1 1 1 2 2 2 3 3 3
, , , ...ABC A B C A B C
sao cho
1 1 1
A BC
là
một tam giác đều cạnh bằng 3 và với mỗi số nguyên dương
2n
, tam giác
n n n
A B C
là tam giác trung
bình của tam giác
1 1 1n n n
A B C
. Với mỗi số nguyên dương
n
đặt
n
S
là diện tích hình tròn ngoại tiếp tam
giác
n n n
A B C
. Tính
12
... ...
n
S S S
A.
15
4
. B.
5
. C.
9
2
. D.
4
.
Câu 20: Cho hàm số
cosf x x x
. Tính giá trị
'
2
f



.
A.
0
. B.
1
. C.
2
. D.
2
.
Câu 21: Có bao nhiêu giá trị nguyên dương của
m
để phương trình
3sin 4cos 0x x m
có nghiệm?
A.
11
. B.
5
. C.
6
. D.
10
.
Câu 22: Cho hình chóp
S.ABCD
có đáy
là hình thoi tâm
O
. Biết
SA SC
và
SB SD
. Khẳng
định nào sau đây sai?
A.
AC SDB
. B.
CD SBD
. C.
BD SAC
. D.
SO ABCD
.
Câu 23: Với k là số nguyên dương, c là hằng số, giới hạn
lim
k
x
c
x

bằng
A.
0
. B.

. C.

. D.
k
x
.
Câu 24: Tìm
a
sao cho
2
32
, khi x 1
1
2ax 1 , khi x 1
xx
fx
x

liên tục tại
1
o
x
.
A.
2a
. B.
0a
. C.
1a
. D.
1a 
.
S
A
B
C
D
O
Trang 4/6 - Mã đề thi 132
Câu 25: Số cách chọn ra 5 bạn từ một tổ có 10 bạn là
A.
10
5
C
. B.
5
10
C
. C.
10
5
. D.
5
10
A
.
Câu 26: Cho tứ diện
. Điểm
M
thuộc đoạn
AC
(
M
khác
A
,
M
khác
C
). Mặt phẳng
đi
qua
M
song song với
AB
và
AD
, cắt tứ diện đã cho theo giao tuyến là
A. Hình vuông. B. Hình bình hành. C. Hình chữ nhật. D. Hình tam giác.
Câu 27: Cho cấp số nhân
n
u
có số hạng đầu
1
u
, công bội
q
. Tính số hạng thứ
n
.
A.
1
1
n
n
u u q
. B.
1
1
n
u u n q
.
C.
1
1
n
u u n q
. D.
1
n
n
u u q
.
Câu 28: Với
k
,
n
là hai số nguyên dương tùy ý thỏa mãn
kn
, mệnh đề nào dưới đây đúng?
A.
!!
!
k
n
k n k
C
n
. B.
!
!
k
n
n
A
nk
. C.
!
!
k
n
n
C
nk
. D.
!
!
k
n
n
A
k
.
Câu 29: Hàm số
2
21
43
x
fx
xx

liên tục trên khoảng nào sau đây?
A.
1;1
. B.
0;2
. C.
2;4
. D.
1
;3
2



.
Câu 30: Biết giới hạn
2
33
lim ,
2
x
x m a
xb

m là số thực, a, b là số nguyên và
a
b
tối giản. Tính
2ab
.
A.
1
. B.
1
. C.
0
. D.
1
2
.
Câu 31: Cho hàm số
32
11
32
f x x x x
. Tập nghiệm của bất phương trình
'0fx
là
A. . B.
1
. C.
. D.
.
Câu 32: Cho hàm số
y f x
xác định và có đạo hàm trên tập số thực. Biết
' 1 5; 1 6ff
. Tìm
giới hạn
2
1
30
lim
1
x
f x f x
x

.
A.
29
. B.
0
. C.
110
. D.

.
Câu 33: Tính
1
lim
1
x
x
x
bằng
A.
0
. B.

. C.

. D.
1
.
Câu 34: Hình chóp tứ giác có tất cả số mặt là
A.
4
. B.
6
. C.
7
. D.
5
.
Câu 35: Cho hình chóp S.ABC có G là trọng tâm của tam giác ABC. Tính
,d G SBC
khi biết
,3d A SBC
(đơn vị dài).
A.
2
3
. B.
3
. C.
1
. D.
1
3
.
Câu 36: Giới hạn
1
lim
2020n
bằng
A.
0
. B.
1
3
. C.
1
2
. D.

.
Câu 37: Cho
3
cos , ;0
42
xx



. Tính
tan x
.
A.
7
3
. B.
7
3
. C.
7
4
. D.
7
9
.
Trang 5/6 - Mã đề thi 132
Câu 38: Tìm khẳng định đúng trong các khẳng định sau:
A. Nếu hai mặt phẳng cùng song song với mặt phẳng thứ ba thì chúng song song với nhau.
B. Nếu ba mặt phẳng phân biệt cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến đó phải đồng
quy.
C. Trong không gian, hai đường thẳng cùng vuông góc với đường thẳng thứ ba thì hai đường thẳng đó
song song với nhau.
D. Nếu một đường thẳng song song với một mặt phẳng thì nó song song với một đường thẳng nào đó
trong mặt phẳng đó.
Câu 39: Có bao nhiêu tiếp tuyến của đồ thị hàm số
3
1yx
song song với đường thẳng
3 1 0xy
?
A.
3
. B.
2
. C.
0
. D.
1
.
Câu 40: Số cách xếp 4 bạn A, B, C, D đứng thành hàng ngang sao cho A và B luôn cạnh nhau là
A.
12
. B.
24
. C.
6
. D.
48
.
----- Hết -----
Họ và tên thí sinh:......................................................... Số báo danh:...............................................
Cán bộ coi thi không giải thích gì thêm. Học sinh không được sử dụng tài liệu.
Trang 6/6 - Mã đề thi 132
made
Cautron
dapan
132
1
B
132
2
C
132
3
A
132
4
C
132
5
B
132
6
A
132
7
D
132
8
B
132
9
D
132
10
C
132
11
D
132
12
D
132
13
A
132
14
D
132
15
B
132
16
C
132
17
C
132
18
A
132
19
D
132
20
C
132
21
B
132
22
B
132
23
A
132
24
C
132
25
B
132
26
D
132
27
A
132
28
B
132
29
A
132
30
C
132
31
B
132
32
C
132
33
B
132
34
D
132
35
C
132
36
A
132
37
A
132
38
D
132
39
D
132
40
A
ĐÁP ÁN CHI TIẾT
Câu 1. Cho hai điểm
,AB
thuộc đồ thị hàm số
sin
yx=
trên đoạn
[ ]
0;
π
. Các điểm
,CD
thuộc trục
Ox
thỏa mãn
ABCD
là hình chữ nhật và
3
CD
π
=
.
Độ dài cạnh
BC
bằng
A.
1
. B.
3
2
. C.
1
2
. D.
2
2
.
Lời giải
Chọn B
Giả sử
( )
;0Da
với
0 a
π
<<
.
ABCD
là hình chữ nhật;
(
)
;sin
Aa a
;
;sin
33
Ba a
ππ


⇒+ +




Do
ABCD
là hình chữ nhật
sin sin
33
aa a
ππ

= + ⇒=


vì
0 a
π
<<
Độ dài cạnh
3
2
BC =
.
Câu 2. Gọi
S
là tập hợp tất cả các giá trị của tham số
m
sao cho giá trị lớn nhất của hàm số
2
2y x xm=−+
trên đoạn
[ ]
0;3
bằng
5
.
Tổng tất cả các phần tử của
S
là
A.
8
. B.
12
−
. C.
2−
. D.
2
.
Lời giải
Chọn C
Xét hàm số
( )
2
2fx x x m=−+
trên đoạn
[ ]
0;3
.
Có
( )
22fx x
′
= −
;
( )
01fx x
′
=⇔=
.
Ta có
( )
0fm=
,
( )
11fm= −
,
( )
33fm= +
.
Khi đó
[ ]
0;3
max 3ym= +
hoặc
[ ]
0;3
max 1
ym= −
.
Ta xét các Trường hợp sau:
TH1:
[
]
0;3
max 3 5 2ym m
= +=⇒ =
.
Thử lại với
2m =
.
Khi đó
[
]
22
22 22, 0;3yxx xx x=−+=−+∀∈
nên
[
]
0;3
max 5y
=
.
Do đó
2m =
(thỏa mãn).
TH2:
[
]
0;3
max 1 5 4ym m
=−=⇒=−
.
Thử lại với
4m
= −
.
Khi đó
2
24yx x
=−−
nên
[ ]
0;3
max 5y =
.
Do đó
4
m
= −
(thỏa mãn).
Vậy có hai giá trị thỏa mãn là
2; 4mm= = −
.
Tổng tất cả các phần tử của
S
là
2 4 2.
−=−
Câu 3. Cho đồ thị hàm số
( )
y fx=
như hình vẽ.
Xét các khẳng định sau
i)
( )
1
lim
x
fx
+
→−
= +∞
. ii)
( )
1
lim
x
fx
−
→−
= +∞
.
iii)
( )
lim 1
x
fx
→−∞
=
. iv)
( )
lim
x
fx
→+∞
= +∞
.
Hỏi có bao nhiêu khẳng định đúng?
A. 3. B. 1. C. 2. D. 4.
Lời giải
Chọn A
Qua đồ thị hàm số
( )
y fx=
ta có:
(
)
1
lim
x
fx
+
→−
= +∞
;
( )
1
lim
x
fx
−
→−
= +∞
;
(
)
lim 1
x
fx
→−∞
=
.
Vậy chon đáp án A.
Câu 4. Cho hình chóp
.S ABCD
, đáy
ABCD
là hình vuông cạnh bằng
a
, tam giác
SAB
đều. Gọi
M
là điểm trên cạnh
AD
sao cho
( )
, 0;AM x x a= ∈
. Mặt phẳng
( )
α
qua
M
và song song với
( )
SAB
lần lượt cắt các cạnh
,,CB CS SD
tại
,,.N PQ
Khi diện tích tứ giác
MNPQ
bằng
2
23
9
a
thì
x
bằng bao nhiêu?
A.
2
a
. B.
2
3
a
. C.
3
a
. D.
4
a
.
Lời giải
Chọn C
Kẻ đường thẳng qua
M
và song song với
AB
, cắt
BC
tại
N
.
Kẻ đường thẳng qua
N
và song song với
SB
, cắt
SC
tại
P
.
Kẻ đường thẳng qua
M
và song song với
SA
, cắt
SD
tại
Q
.
Suy ra tứ giác
MNPQ
là thiết diện của hình chóp
.S ABCD
cắt bởi
( )
α
.
Có
( ) ( )
( ) ( )
( ) ( )
SCD PQ
SCD ABCD CD
ABCD MN
α
α
∩=
∩=
∩=
,,PQ CD MN⇒
hoặc đôi một song song, hoặc đồng quy.
Mà
( )
//MN // .CD PQ CD PQ CD⇒<
(1)
Gọi
H
là hình chiếu vuông góc của
S
lên
( )
ABCD
.
Ta có:
SA SB HA HB=⇒=
. Suy ra
H
thuộc đường trung trực đoạn
AB
.
( )
HC HD SC SD SBC SAD c c c⇒ = ⇒ = ⇒∆ =∆ − −
( )
PCN QDM PCN QDM c g c PN QM⇒ = ⇒∆ =∆ − − ⇒ =
(2)
Từ (1) và (2) ta có tứ giác
MNPQ
là hình thang cân.
Ta có:
PQ SQ AM
PQ AM x
CD SD AD
== ⇒= =
.
Gọi
E PN QM ENM= ∩ ⇒∆
cân tại
.E
Mà
( )
(
)
, , 60
o
PN NM SB AB
= =
ENM⇒∆
là tam giác đều cạnh
a
và
EPQ∆
là tam giác đều cạnh
x
.
22
33
44
MNPQ EMN EPQ
ax
S SS
∆∆
⇒ = −= −
Ta có:
2222
23 3 323
9 44 9 3
MNPQ
a ax a a
Sx
= ⇔ − = ⇔=
.
Câu 5. Cho cấp số cộng
( )
n
u
với
1
2
=u
và
2020
2020
=u
. Công sai của cấp số cộng đã cho bằng
A.
2017
2018
. B.
2018
2019
. C.
1
. D.
2019
2020
.
Lời giải
Chọn B
Gọi
d
là công sai của cấp số cộng
( )
n
u
.
Khi đó
2020 1
2019= +uu d
.
Hay .
Câu 6. Cho hình lập phương
.ABCD EFGH
. Góc giữa hai đường thẳng
AB
,
EH
là
A.
0
90
. B.
0
0
. C.
0
45
. D.
0
60
.
Lời giải
2018
2020 2 2019
2019
=+ ⇔=dd
Chọn A
Vì
AD
song song với
EH
nên góc giữa hai đường thẳng
AB
,
EH
bằng góc giữa hai đường thẳng
AB
,
AD
. Đó là góc
BAD
.
Do
ABCD
là hình vuông nên góc
0
90=BAD
.
Vậy góc giữa hai đường thẳng
AB
,
EH
bằng
0
90
.
Câu 7. Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
a
, mặt bên
SAB
là tam giác đều nằm trong
mặt phẳng vuông góc với đáy. Tính khoảng cách giữa hai đường thẳng
,SA BC
.
A.
2a
. B.
a
. C.
5
2
a
. D.
3
2
a
.
Lời giải
Chọn D
D
A
C
G
E
H
F
B
I
C
A
D
B
S
H
Gọi
I
là trung điểm của
AB
. Do
SAB
là tam giác đều nằm trong mặt phẳng vuông góc với
đáy nên
( )
SI ABCD⊥
.
Ta có
//AD BC
( )
//BC SAD⇒
nên
( )
;d BC SA
( )
( )
;d BC S AD=
( )
( )
;d B SAD=
( )
( )
2;d I SAD=
Trong mp
( )
SAI
kẻ
IH SA⊥
tại
H
, mà
AD IH⊥
nên
(
)
IH SAD
⊥
( )
( )
;IH d I SAD⇒=
( )
;d BC SA
( )
( )
2;d I SAD=
2IH=
22
.
2.
SI IA
SI IA
=
+
22
3
.
22
2.
3
44
aa
aa
=
+
3
2
a
=
Vậy
( )
3
;
2
a
d BC SA =
.
Câu 8. Sau đợt nghỉ dịch Covid-19, từ ngày 04 tháng 5 năm 2020, học sinh trường THPT Nguyễn Thị
Giang đi học trở lại. Nhà trường yêu cầu tất cả các học sinh đều phải mang khẩu trang. Qua khảo
sát, lớp 11A có 16 học sinh nữ và 24 học sinh nam, trong đó chỉ có một nửa số học sinh nữ và
một nửa số học sinh nam đeo khẩu trang theo quy định. Nếu chọn ngẫu nhiên một học sinh của
lớp 11A để kiểm tra, hãy tính xác suất để chọn được học sinh nữ hoặc hoặc học sinh đeo khẩu
trang.
A.
9
10
. B.
7
10
. C.
2
3
. D.
1
2
.
Lời giải
Chọn B
Số phần tử không gian mẫu :
(
)
40n
Ω=
.
Gọi
A
là biến cố chọn được học sinh nữ hoặc học sinh đeo khẩu trang.
Ta có
( )
nA=
16 12+
28=
Vậy
( )
PA=
( )
( )
nA
n
=
Ω
28
40
=
7
10
=
Câu 9. Cho hình chóp
.S ABC
có đáy là tam giác vuông cân tại
B
,
AB a=
,
SA AB⊥
,
SC BC⊥
,
2SB a=
. Gọi
,MN
lần lượt là trung điểm của
,SA BC
và
α
là góc giữa
MN
và
( )
ABC
. Giá
trị
cos
α
bằng
A.
3
2
. B.
2 11
11
. C.
26
5
. D.
6
3
.
Lời giải
Chọn D
Vẽ
( )
SD ABC⊥
Khi đó ta có
AB SA
AB SD
⊥
⊥
AB AD⇒⊥
BC SC
BC SD
⊥
⊥
BC CD⇒⊥
Suy ra
ABCD
là hình vuông
Gọi
H
là trung điểm của
AD
khi đó
MH SD
( )
MH ABC⇒⊥
MNH
α
⇒=
(
α
là góc giữa
MN
và
( )
ABC
).
SD
22
SB BD= −
( )
( )
2
2
22aa= −
2a=
.
12
22
a
MH SD
= =
,
HN a=
,
22
6
2
MN MH HN= +=
Vậy
cos
α
HN
MN
=
6
2
a
a
=
6
3
=
.
Câu 10. Tất cả các nghiệm của phương trình
cos 2 0x =
là
A.
( )
2
2
x kk
π
π
=+∈
. B.
( )
4
x kk
π
π
=+∈
.
C.
( )
42
x kk
ππ
=+∈
. D.
(
)
2
x kk
π
π
=+∈
.
Lời giải
Chọn C
cos 2 0x =
(
)
2
2
x kk
π
π
⇔=+ ∈
(
)
42
x kk
ππ
⇔= + ∈
.
Câu 11. Có
6
chiếc ghế được kê thành một hàng ngang. Xếp ngẫu nhiên
6
học sinh, gồm
3
học sinh lớp
A
,
2
học sinh lớp
B
,
1
học sinh lớp
C
vào hàng ghế đó, sao cho mỗi ghế có đúng một em
học sinh. Xác suất để học sinh lớp
C
chỉ ngồi cạnh học sinh lớp
B
là
A.
3
20
. B.
1
6
. C.
2
15
. D.
1
5
.
Lời giải
Chọn D
Ta có
( )
6! 720n Ω= =
.
Gọi
X
là biến cố cần tìm. Khi đó:
Trường hợp 1: Học sinh lớp
C
ngồi đầu dãy hoặc cuối dãy.
+ Xếp học sinh lớp
C
ngồi đầu dãy hoặc cuối dãy có 2 cách.
+ Chọn 1 học sinh trong
2
học sinh lớp
B
và xếp cạnh học sinh lớp
C
có 2 cách.
+ Xếp 4 học sinh còn lại vào 4 vị trí có
4! 24=
cách.
Khi đó số cách xếp là:
2.2.24 96=
cách.
Trường hợp 2: Học sinh lớp C không ngồi đầu dãy.
+ Số cách xếp học sinh lớp
C
ngồi giữa hai học sinh lớp
B
là
2
cách (ta xem nhóm
3
học
sinh này như một học sinh
D
)
+ Số cách xếp
3
học sinh lớp
A
và học sinh
D
vào
4
vị trí là
4! 24
=
cách.
Khi đó số cách xếp là
2.24 48=
cách.
Từ
2
trường hợp, suy ra số phần tử của biến cố
X
là
(
)
96 48 144nX =+=
cách.
Vậy xác suất của biến cố cần tìm là
( )
(
)
( )
144 1
720 5
nX
PX
n
= = =
Ω
.
Câu 12. Đạo hàm của hàm số
2
y sin x=
là
A.
2cosx
. B.
22
cos x−
. C.
22sin x
. D.
22cos x
.
Lời giải
Chọn D
Ta có
( )
' 2 '. 2 2 2y x cos x cos x
= =
.
Câu 13. Cho cấp số nhân
(
)
n
u
với
1
2u
=
và
2
1u =
. Công bội của cấp số nhân đã cho bằng?
A.
1
2
. B.
1
−
. C.
2
. D.
1
.
Lời giải
Chọn A
Gọi
q
là công bội của cấp số nhân
Ta có:
2
1
1
2
u
q
u
= =
.
Câu 14. Cho tứ diện đều
ABCD
có cạnh
AB a=
. Tích vô hướng
.AB CD
 
bằng
A.
2
2
a
. B.
2
2
a−
. C.
2
a
. D.
0
.
Lời giải
Chọn D
Cách 1:
.AB CD =
 
(
)
.CB CA CD
−
  
..CB CD CA CD= −
   
00
. .cos60 . .cos60CB CD CACD
= −
0=
.
Cách 2:
Gọi
M
là trung điểm của CD.
Do:
( )
CD AM
CD MAB CD AB
CD BM
⊥
⇒⊥ ⇒⊥
⊥
Vậy:
.0AB CD
=
 
.
Câu 15. Cho hai đường thẳng
a
và
b
chéo nhau. Có bao nhiêu mặt phẳng chứa
a
và song song với
b
?
A.
0
. B.
1
. C. Vô số. D.
2
.
Lời giải
Chọn B
Theo định lý 3 bài đường thẳng song song với mặt phẳng của sách giáo khoa, chọn B.
Câu 16. Một vật chuyển động thẳng xác định bởi phương trình
32
1
21
2
St t t=− +−
(
t
là thời gian tính
bằng giây,
S
là đường đi tính bằng mét). Tính vận tốc
( /)ms
của vật tại thời điểm
0
2( )ts=
?
A
C
B
D
A.
14( / )
ms
. B.
9( / )ms
.
C.
12( / )
ms
. D.
6( / )
ms
.
Lời giải
Chọn C
Ta có:
2
( ) ( ) 3 2 (2) 12vt S t t t v
′
= = −+ ⇒ =
.
Câu 17. Cho tam thức bậc hai
( )
y fx
=
có đồ thị như hình vẽ bên dưới. Tìm số nghiệm của phương
trình
( )
sin 2fx= −
với
3
;
2
x
π
π

∈−


.
A.
4
. B.
2
. C.
3
. D.
1
.
Lời giải
Chọn C
Giả sử
( )
2
f x ax bx c= ++
. Vì đồ thị hàm số đi qua các điểm
( )
1; 0−
,
( )
3; 0
và
( )
0; 3−
nên ta
có hệ
( ) ( )
2
2
2
.1 .1 0
01
.3 .3 0 9 3 0 2
33
.0 .0 3
a bc
abc a
a b c a bc b
cc
a bc
− + −+=
−+= =


+ += ⇔ + +=⇔ =−


=−=−
+ +=−

.
Ta được
( )
2
23fx x x=−−
.
Ta có
(
)
22
sin 1 2
sin 2 sin 2sin 3 2 sin 2sin 1 0
sin 1 2
x
fx xx xx
x
= +
=−⇔ − −=−⇔ − −= ⇔
= −
sin 1 2 0.414x
⇔ = − ≈−
Ta có bảng biến thiên của hàm số
sinyx=
trên
3
;
2
π
π

−


.
Từ bảng biến thiên suy ra phương trình
sin 1 2x = −
có 3 nghiệm thuộc khoảng
3
;
2
π
π

−


.
Do đó, phương trình
( )
sin 2fx= −
có 3 nghiệm thuộc khoảng
3
;
2
π
π

−


.
Câu 18. Hàm số
21
1
x
y
x
+
=
−
có đạo hàm là
A.
( )
2
3
'
1
y
x
= −
−
. B.
( )
2
1
'
1
y
x
=
−
. C.
( )
2
1
'
1
y
x
= −
−
. D.
'2
y =
.
Lời giải
Chọn A
Ta có:
( ) (
) ( )
(
)
(
)
( )
(
)
2 22
2 1. 1 1.2 1
2 22 1 3
'
1 11
xx x x
xx
y
x xx
′′
+ −− − +
−− −
= = = −
− −−
.
Câu 19. Tam giác mà ba đỉnh của nó là ba trung điểm của ba cạnh tam giác ABC được gọi là tam giác
trung bình của tam giác ABC. Ta xây dựng dãy tam giác
111 2 2 2 3 3 3
, , ,...ABC A BC ABC
sao cho
111
ABC
là một tam giác đều cạnh bằng 3 và với mỗi số nguyên dương
2,n ≥
tam giác
nnn
ABC
là
tam giác trung bình của tam giác
111
.
nnn
ABC
−−−
Với mỗi số nguyên dương
n
đặt
n
S
là diện tích
hình tròn ngoại tiếp tam giác
.
nnn
ABC
Tính
12
... ...
n
SS S+ ++ +
A.
15
.
4
π
B.
5.
π
C.
9
.
2
π
D.
4.
π
Lời giải
Chọn D
Xét tam giác đều
ABC
có
,,ABC
′′′
lần lượt là trung điểm của
,,.BC CA AB
Khi đó
ABC
′′′
∆
là tam giác trung bình của
.ABC∆
Bán kính đường tròn ngoại tiếp tam giác
:ABC
3
.
3
R AB=
Bán kính đường tròn ngoại tiếp tam giác
3
:
3
ABC R AB
′′′ ′ ′′
=
Suy ra
1
.
2
R AB
R AB
′ ′′
= =
Gọi
S
là diện tích hình tròn ngoại tiếp tam giác
ABC
và
S
′
là diện tích hình tròn ngoại tiếp
,ABC
′′′
∆
khi đó
2
2
1
4
SR
SR
′′
= =
Do đó dãy số
( )
n
S
là một cấp số nhân có công bội
1
4
q =
và
1
S
là diện tích hình tròn ngoại tiếp
tam giác
111
ABC
có cạnh bằng 3 nên
2
2
1 1 11
3
. . 3.
3
S R AB
ππ π

= = =



Vậy
12 1
11
... ... . 3 . 4 .
1
1
1
4
n
SS S S
q
ππ
+ ++ += = =
−
−
Câu 20. Cho hàm số
( )
cos .fx x x=
Tính giá trị
.
2
f
π

′
−


A.
0.
B.
1.
C.
.
2
π
−
D.
.
2
π
Lời giải
Chọn C
Ta có:
( ) ( ) ( )
cos cos . cos cos sinfxxxxxxxxx
′′
′
==+=−
Do đó
cos .sin .
2 2 2 22
f
π π π ππ
 
′
−= −−− −=−
 
 
Câu 21. Có bao nhiêu giá trị nguyên dương của
m
để phương trình
3sin 4 cos 0x xm− −=
có nghiệm
A.
11
. B.
5
. C.
6
. D.
10
.
Lời giải
Chọn B
Ta có
3sin 4 cos 0 3sin 4 cosxxm xxm− −=⇔ − =
.
Điều kiện cần và đủ để phương trình trên có nghiệm là
( )
2
22
34 5mm+− ≥ ⇔ ≤
Vì
m
nguyên dương nên
{ }
1;2;3; 4;5m ∈
Câu 22. Cho hình chóp
.S AB CD
có đáy
ABCD
là hình thoi tâm
O
. Biết
SA SC=
và
SB SD=
. Khẳng
định nào sau đây sai?
A.
( )
⊥AC SDB
. B.
( )
⊥CD SBD
. C.
( )
⊥BD SAC
. D.
( )
⊥SO ABCD
.
Lời giải
Chọn B
Cách 1: Giả sử
( )
⊥CD SBD
, suy ra
CD BD⊥
(Vô lý). Vậy đáp án B sai.
Cách 2: Vì
ABCD
là hình thoi tâm
O
nên
( )
1AC BD⊥
.
Vì
SA SC=
nên tam giác
SAC
cân tại
S
, suy ra
( )
2SO AC⊥
.
Vì
SB SD=
nên tam giác
SBD
cân tại
S
, suy ra
( )
3
SO BD⊥
.
O
D
S
A
B
C
Từ (1) và (2) suy ra
( )
⊥AC SDB
. Từ (1) và (3) suy ra
( )
⊥BD SAC
.
Từ (2) và (3) suy ra
(
)
⊥
SO ABCD
.
Vậy các đáp án A, C, D đúng và đáp án B sai.
Câu 23. Với
k
là số nguyên dương,
c
là hằng số, giới hạn
lim
k
x
c
x
→+∞
bằng
A.
c
. B.
0
. C.
−∞
. D.
+∞
.
Lời giải
Chọn B
Ta có
lim
x
cc
→+∞
=
và
lim
k
x
x
→+∞
= +∞
nên
lim 0
k
x
c
x
→+∞
=
.
Câu 24. Tìm
a
sao cho hàm số
( )
2
32
1
1
21 1
xx
khi x
fx
x
ax khi x
−+ −
≠
=
−
−=
liên tục tại
0
1x =
.
A.
0
. B.
1
. C.
2
. D.
1−
.
Lời giải
Chọn B
Ta có:
(
)
( )( )
( )
2
11 1 1
12
32
lim lim lim lim 2 1
11
xx x x
xx
xx
fx x
xx
→→ → →
− −+
−+ −
= = = −+ =
−−
.
(
)
121fa= −
.
Hàm số đã cho liên tục tại
0
1x =
( ) ( )
1
lim 1 1 2 1 1
x
fx f a a
→
⇔ = ⇔= −⇔ =
.
Câu 25. Số cách chọn ra 5 bạn từ tổ có 10 bạn là
A.
10
5
.C
B.
5
10
.C
C.
10
5.
D.
5
10
.A
Lời giải
Chọn B
Số cách chọn ra 5 bạn từ tổ có 10 bạn là
5
10
.C
Câu 26. Cho tứ diện
.ABCD
Điểm
M
thuộc đoạn
AC
(
M
khác
,A
M
khác
C
). Mặt phẳng
()
α
đi qua
M
song song với
AB
và
,CD
cắt tứ diện đã cho theo giao tuyến là
A. Hình vuông. B . Hình bình hành. C. Hình chữ nhật. D. Tam giác.
Lời giải
Chọn B
Ta có
+)
|| ( )
() ()() || ( ).
() ( )
AB
AB ABC ABC MN AB N BC
M ABC
α
α
α
⊂ ⇒ ∩= ∈
∈∩
+)
|| ( )
() ()() || ( ).
() ( )
CD
CD BCD BCD NP CD P BD
N BCD
α
α
α
⊂ ⇒ ∩= ∈
∈∩
+)
|| ( )
() ()() || ( ).
() ( )
AB
AB ABD ABD PQ AB Q AD
P ABD
α
α
α
⊂ ⇒ ∩= ∈
∈∩
Theo cách dựng thì thiết diện
MNPQ
là hình bình hành.
Câu 27. Cho cấp số nhân
( )
n
u
có số hạng đầu
1
u
, công bội
q
. Tính số hạng thứ
n
.
A.
1
1
.
n
n
u uq
−
=
. B.
( )
1
1
n
u un q= −
. C.
( )
1
1
n
u un q= +
. D.
1
.
n
n
u uq=
.
Lời giải
Chọn A
Câu hỏi lý thuyết.
Công thức tính số hạng tổng quát của một cấp số nhân:
1
1
.
n
n
u uq
−
=
.
Q
P
N
D
C
B
M
A
Câu 28. Với
, kn
là hai số nguyên dương tùy ý thỏa mãn
kn≤
, mệnh đề nào dưới đây đúng ?
A.
( )
!!
!
k
n
knk
C
n
−
=
. B.
( )
!
!
k
n
n
A
nk
=
−
. C.
( )
!
!
k
n
k
C
nk
=
−
. D.
!
!
k
n
n
A
k
=
.
Lời giải
Chọn B
Câu hỏi lý thuyết.
Số chỉnh hợp chập
k
của
n
( )
, , kn k n
+
∈≤
được tính bởi công thức
( )
!
!
k
n
n
A
nk
=
−
.
Câu 29. Hàm số
2
21
()
43
−
=
−+
x
fx
xx
liên tục trên khoảng nào sau đây?
A.
( 1;1)−
B.
(0; 2)
C.
(2;4)
D.
1
;3
2



Lời giải
Chọn A
Hàm số là hàm phân thức hữu tỉ, có tập xác định
{ }
\ 1; 3D =
nên liên tục trên từng khoảng
( ) (
)
;1 , 1; 3
−∞
và
(
)
3; +∞
.
Câu 30. Biết giới hạn
2
33
lim ,
2
→
+−
=
−
x
x ma
m
xb
là số thực,
,ab
là số nguyên và
a
b
tối giản. Tính
2 −ab
.
A.
1
B.
1−
C.
0
D.
1
2
Lời giải
Chọn C
Để
2
33
lim ,
2
→
+−
=
−
x
x ma
xb
với
,ab
là số nguyên thì điều kiện cần là phương trình
33 0xm+− =
phải có nghiệm
2x =
, suy ra
3m =
.
Khi đó ta được:
( )
( )
( )
22 2
32
3 33 3 1
lim lim lim
22
2 3 33
3 33
xx x
x
x
x
x
x
x
→→ →
−
+−
= =
+
−
+
=
− ++
.
Suy ra
1, 2 2 0a b ab= =⇒ −=
.
Câu 31. Cho hàm số
( )
32
11
.
32
fx x x x= − ++
Tập nghiệm của bất phương trình
( )
'0fx≤
là
A.
.
B.
{ }
1.
C.
.∅
D.
(
)
;1 .−∞
Lời giải
Chọn B
Ta có
( ) ( )
2
2
' 21 1 0fx x x x= − += − ≥
.
Vậy
( )
' 0 10 1fx x x≤ ⇔ −= ⇔ =
.
Câu 32. Cho hàm số
( )
y fx=
xác định và có đạo hàm trên tập số thực. Biết
( )
15f
′
=
;
(
)
16
f
=
. Tìm giới
hạn
( ) ( )
2
1
30
lim
1
x
f x fx
x
→
−−
−
.
A.
29−
. B.
0
. C.
110
. D.
+∞
.
Lời giải
Chọn C
Vì
1x −
xác định khi
0
x
≥
và
( )
y fx=
xác định và có đạo hàm trên tập số thực nên
( ) ( )
2
30
1
f x fx
x
−−
−
xác định và có đạo hàm khi
0
1
x
x
>
≠
.
Áp dụng quy tắc L’Hospital ta có
( ) ( )
( ) ( ) ( )
2
11
30 2
lim lim
1
1
2
xx
f x fx fxf x f x
x
x
→→
′′
−− −
=
−
( ) ( ) ( )
1
lim 2 2
x
x fxfx fx
→
′′
= −

(
) ( ) ( )
22 1 1 1ff f
′′
= −

( )
2. 2.5.6 5 110= −=
.
Câu 33. Tính
1
lim
1
x
x
x
−
→
−
bằng
A.
0
. B.
−∞
. C.
+∞
. D.
1
.
Lời giải
Chọn B
Ta có:
( )
1
lim 1 0, 1 0
x
xx
−
→
− = −<
với mọi
1x <
và
( )
1
lim 1 0
x
x
−
→
= >
Do đó:
1
lim
1
x
x
x
−
→
= −∞
−
.
Câu 34. Hình chóp tứ giác có tất cả số mặt là
A.
4
. B.
6
. C.
7
. D.
5
.
Lời giải
Chọn D
Dễ thấy hình chóp tứ giác có tất cả số mặt là: 5.
Câu 35. Cho hình chóp
.S ABC
có
G
là trọng tâm của tam giác
ABC
. Tính
( )
( )
,d G SBC
khi biết
( )
( )
,3d A SBC =
(đơn vị dài).
A.
2
3
. B.
3
. C.
1
. D.
1
3
.
Lời giải
Chọn C
Gọi
I
là trung điểm
BC
AG⇒
cắt
( )
SBC
tại
I
.
Ta có
( )
( )
( )
( )
( )
( )
( )
( )
,
1 11
, ,1
3 33
,
d G SBC
GI
d G SBC d A SBC
AI
d A SBC
=⇒ =⇒= =
.
Câu 36. Giới hạn
1
lim
2020n +
bằng
A.
0
. B.
1
3
. C.
1
2
. D.
+∞
.
A
B
C
D
S
Lời giải
Chọn A
Ta có
1
10
lim lim 0.
2020
2020 1
1
n
n
n
= = =
+
+
Câu 37. Cho
3
cos , ;0
42
xx
π

= ∈−


. Tính
tan x
.
A.
7
3
−
. B.
7
3
. C.
7
4
. D.
7
9
.
Lời giải
Chọn B
Ta có:
2
2
22
1 1 17
1 tan tan 1 1
cos cos 3
3
4
xx
xx
+ = ⇒ =± −=± −=±



Vì
;0
2
x
π

∈−


nên
cos 0x
>
7
cos
3
x⇒=
. Vậy đáp án B đúng.
Câu 38. Tìm khẳng định đúng trong các khẳng định sau:
A. Nếu hai mặt phẳng cùng song song với mặt phẳng thứ ba thì chúng song song với nhau.
B. Nếu ba mặt phẳng phân biệt cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến đó phải
đồng quy.
C. Trong không gian, hai đường thẳng cùng vuông góc với đường thẳng thứ ba thì hai đường
thẳng đó song song với nhau.
D. Nếu một đường thẳng song song với một mặt phẳng thì nó song song với một đường thẳng
nào đó trong mặt phẳng.
Lời giải
+ Nếu hai mặt phẳng cùng song song với mặt phẳng thứ ba thì chúng song song với nhau
Sai vì chúng có thể trung nhau
+ Nếu ba mặt phẳng phân biệt cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến đó phải
đồng quy.
Sai vì chúng có thể song song
+ Trong không gian, hai đường thẳng cùng vuông góc với đường thẳng thứ ba thì hai đường
thẳng đó song song với nhau.
Sai vì hai đường thẳng chéo nhau vẫn có thể cùng vuông góc với một đường thẳng thứ 3.
Chọn D
Câu 39. Có bao nhiêu tiếp tuyến của đồ thị hàm số
3
1yx= −
song song với đường thẳng
3 10
xy
− +=
A.
3
. B.
2
. C.
0
. D.
1
.
Lời giải
Chọn D
Ta có
2
'3yx=
;
3 10 3 1xy y x− += ⇒ = +
Vì tiếp tuyến song song với đường thẳng
31
yx
= +
Nên
2
3 3 { - 1; 1}xx=⇒∈
Phương trình tiếp tuyến có dạng:
( )(
)
0 00
'y yx xx y
= −+
Với
( )
1 '3 1 03 3x yx x=⇒ = − += −
, nhận
1x =
.
Với
( )
1 '3 1 23 1x yx x=−⇒ = + − = +
, nên
1
x = −
không thỏa.
Câu 40. Số cách sắp xếp
4
bạn
,,,
ABC D
đứng thành hàng ngang sao cho
A
và
B
luôn đứng cạnh
nhau là
A.
12
. B.
24
. C.
6
. D.
48
.
Lời giải
Chọn A
+
,AB
đứng cạnh nhau coi như một người, đỏi chỗ ba người này có
3!
cách
Hai người
,AB
đứng cạnh nhau đổi chỗ cho nhau có
2!
cách.
Vậy số cách sắp xếp là
3!.2! 12=
cách.
-------------------- HẾT ---------------- ----
| 1/27
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GD & ĐT VĨNH PHÚC
ĐỀ KSCL THÁNG 5 NĂM HỌC 2019 - 2020
TRƯỜNG THPT NGUYỄN THỊ GIANG Môn: Toán; Lớp 11
Thời gian làm bài 60 phút, không kể giao đề Mã đề: 132 (Đề gồm 05 trang)
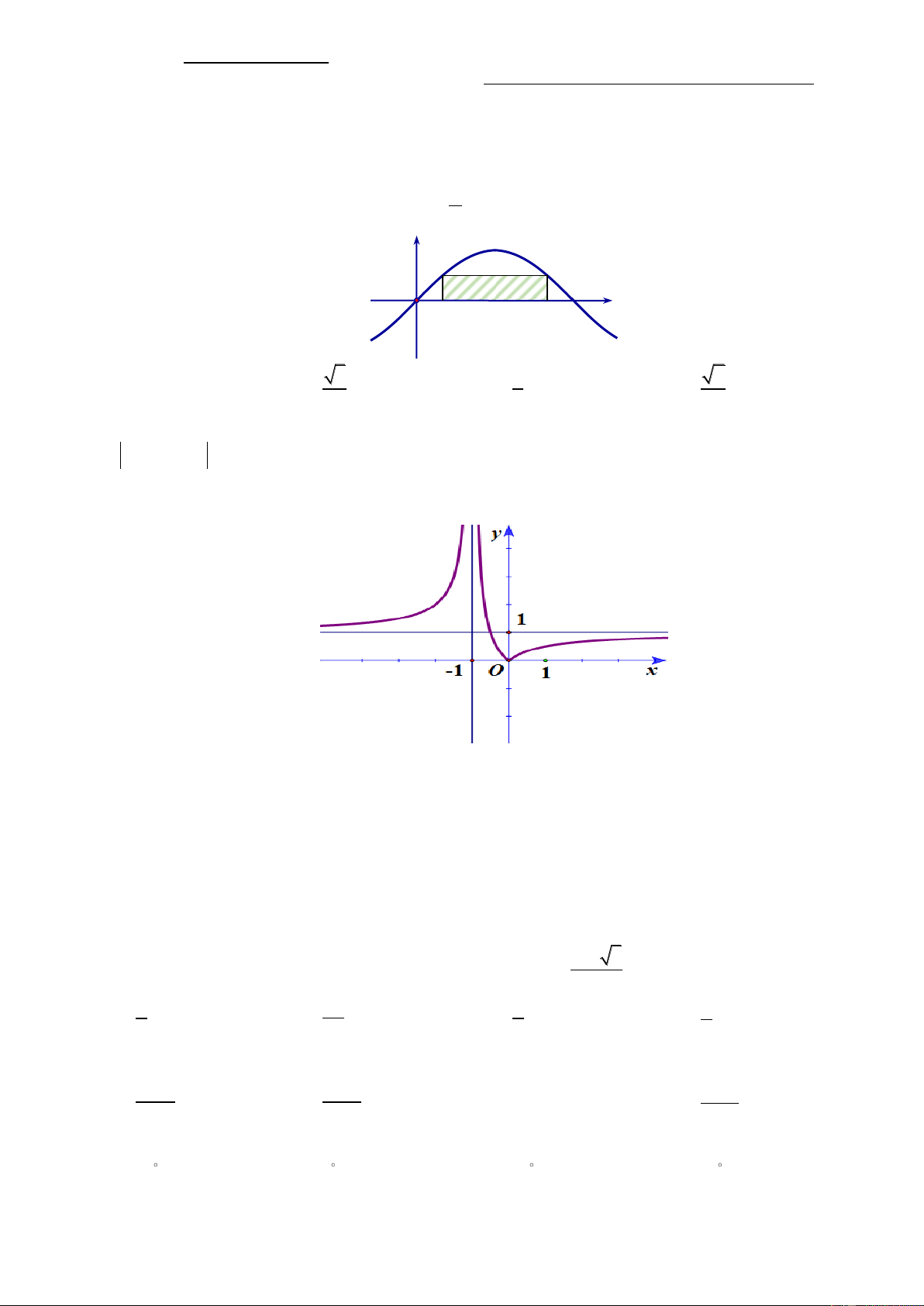
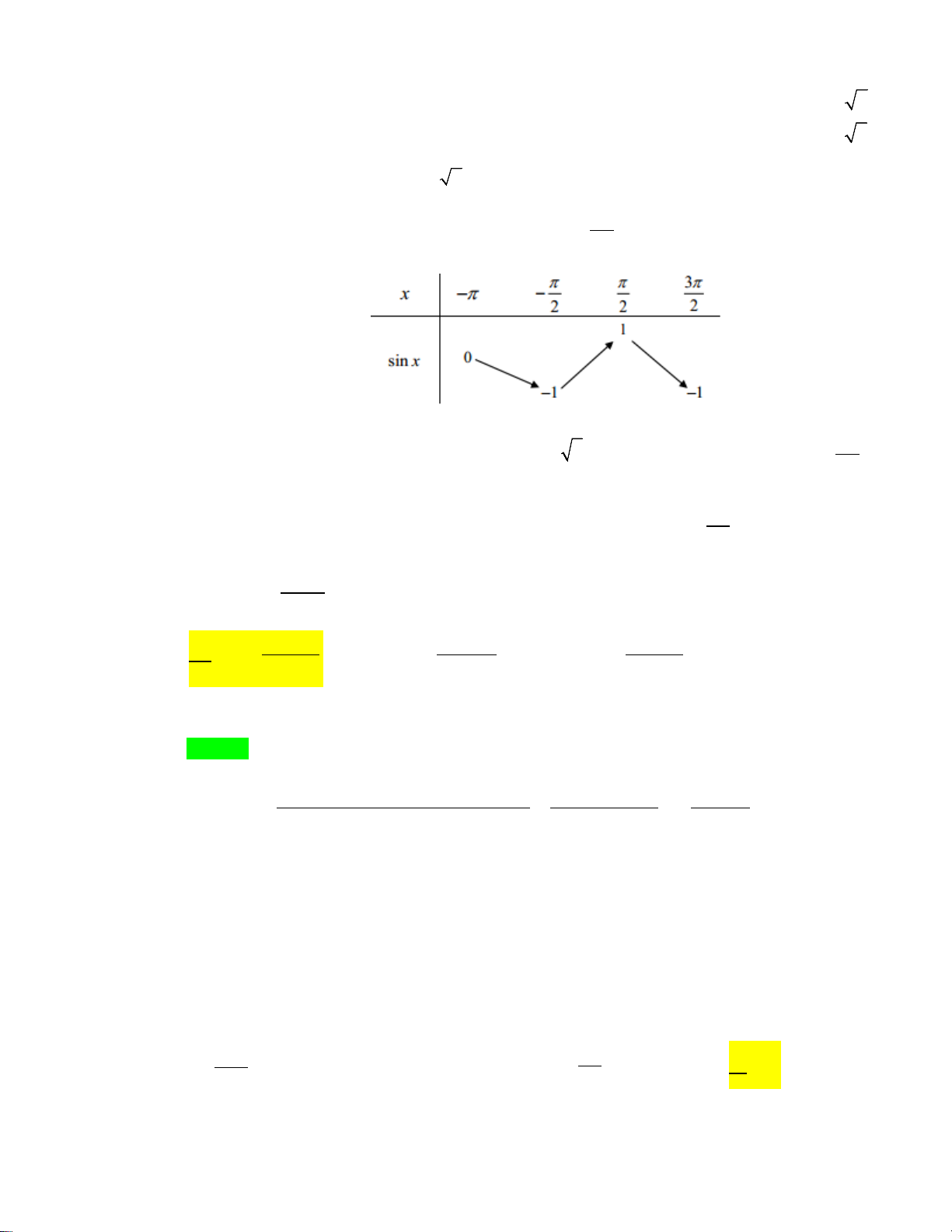
Câu 1: Cho hai điểm A , B thuộc đồ thị hàm số y  sin x trên đoạn 0; . Các điểm C , D thuộc trục 
Ox thỏa mãn ABCD là hình chữ nhật và CD
. Độ dài cạnh BC bằng 3 y A B O D C x 3 1 2 A. 1. B. . C. . D. . 2 2 2
Câu 2: Gọi S là tập hợp tất cả các giá trị của tham số m sao cho giá trị lớn nhất của hàm số 2
y x  2x m trên đoạn 0; 
3 bằng 5. Tổng tất cả các phần tử của S là A. 8 . B. 12  . C. 2  . D. 2 .
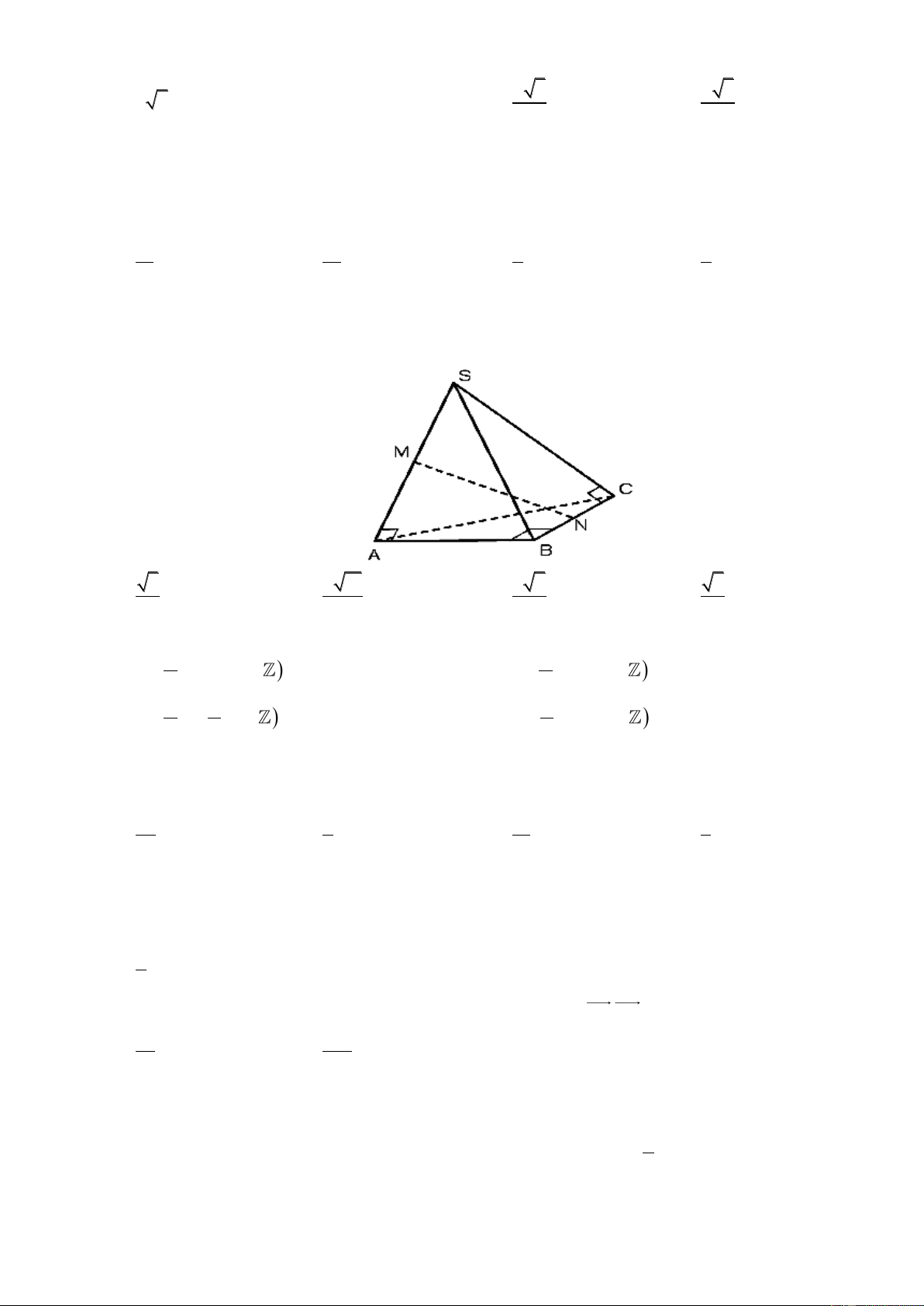
Câu 3: Cho đồ thị hàm số y f x như hình vẽ. Xét các khẳng định sau
i) lim f x   . ii) lim f x   .   x 1  x 1 
iii) lim f x  1 . iv) lim f x   . x x
Hỏi có bao nhiêu khẳng định đúng? A. 3. B. 1. C. 2. D. 4.
Câu 4: Cho hình chóp S.ABCD, đáy ABCD là hình vuông cạnh bằng a, tam giác SAB đều. Gọi M là điểm
trên cạnh AD sao cho AM  ,
x x 0;a . Mặt phẳng   qua M và song song với (SAB) lần lượt cắt các 2 cạnh 2a 3
CB, CS, SD tại N, P, Q. Khi diện tích tứ giác MNPQ bằng
thì x bằng bao nhiêu? 9 a 2a a a A. . B. . C. . D. . 2 3 3 4
Câu 5: Cho cấp số cộng u với u  2 và u
 2020 . Công sai của cấp số cộng đã cho bằng n  1 2020 2017 2018 2019 A. . B. . C. 1. D. . 2018 2019 2020
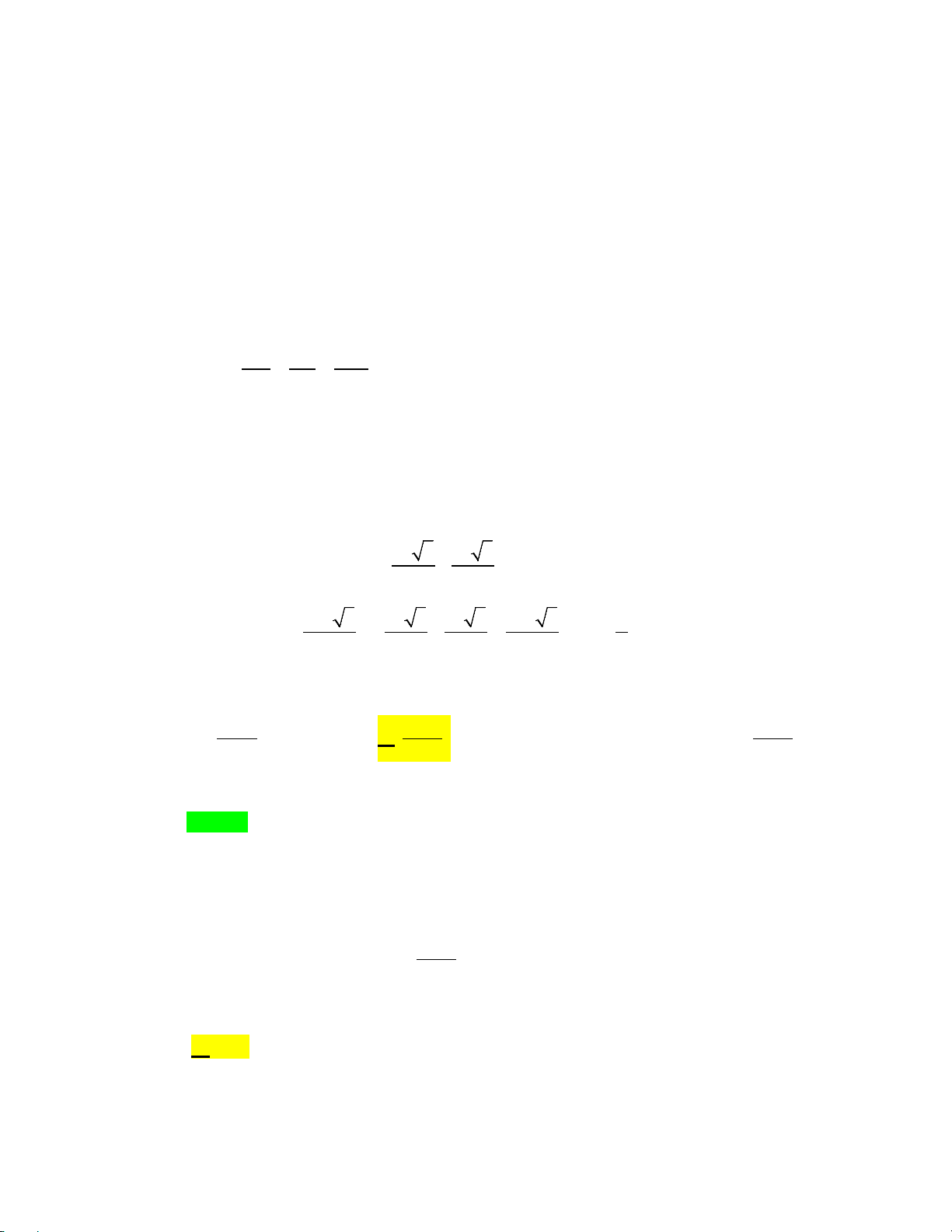
Câu 6: Cho hình lập phương ABC .
D EFGH . Góc giữa hai đường thẳng A , B EH là A. 90 . B. 0 . C. 45 . D. 60 .
Trang 1/6 - Mã đề thi 132
Câu 7: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a , mặt bên SAB là tam giác đều nằm trong
mặt phẳng vuông góc với đáy. Tính khoảng cách giữa hai đường thẳng S , A BC . a 5 a 3 A. a 2 . B. a . C. D. . 2 2
Câu 8: Sau đợt nghỉ dịch Covid-19, từ ngày 04 tháng 5 năm 2020, học sinh trường THPT Nguyễn Thị
Giang đi học trở lại. Nhà trường yêu cầu tất cả học sinh đều phải đeo khẩu trang. Qua khảo sát, lớp 11A
có 16 học sinh nữ và 24 học sinh nam, trong đó chỉ có một nửa số học sinh nữ và một nửa số học sinh
nam đeo khẩu trang theo quy định. Nếu chọn ngẫu nhiên một học sinh của lớp 11A để kiểm tra, hãy tính
xác suất để chọn được học sinh nữ hoặc học sinh đeo khẩu trang. 9 7 2 1 A. . B. . C. . D. . 10 10 3 2
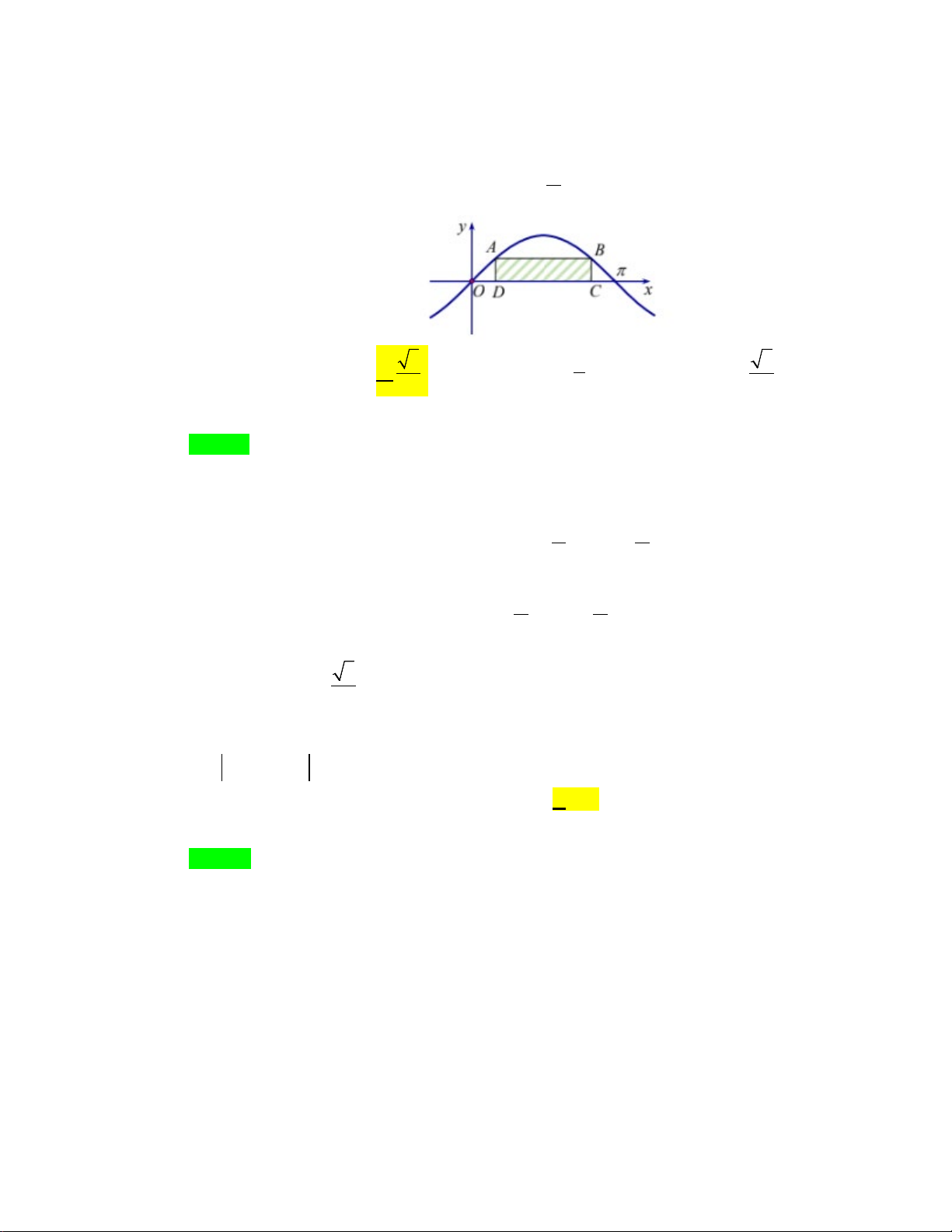
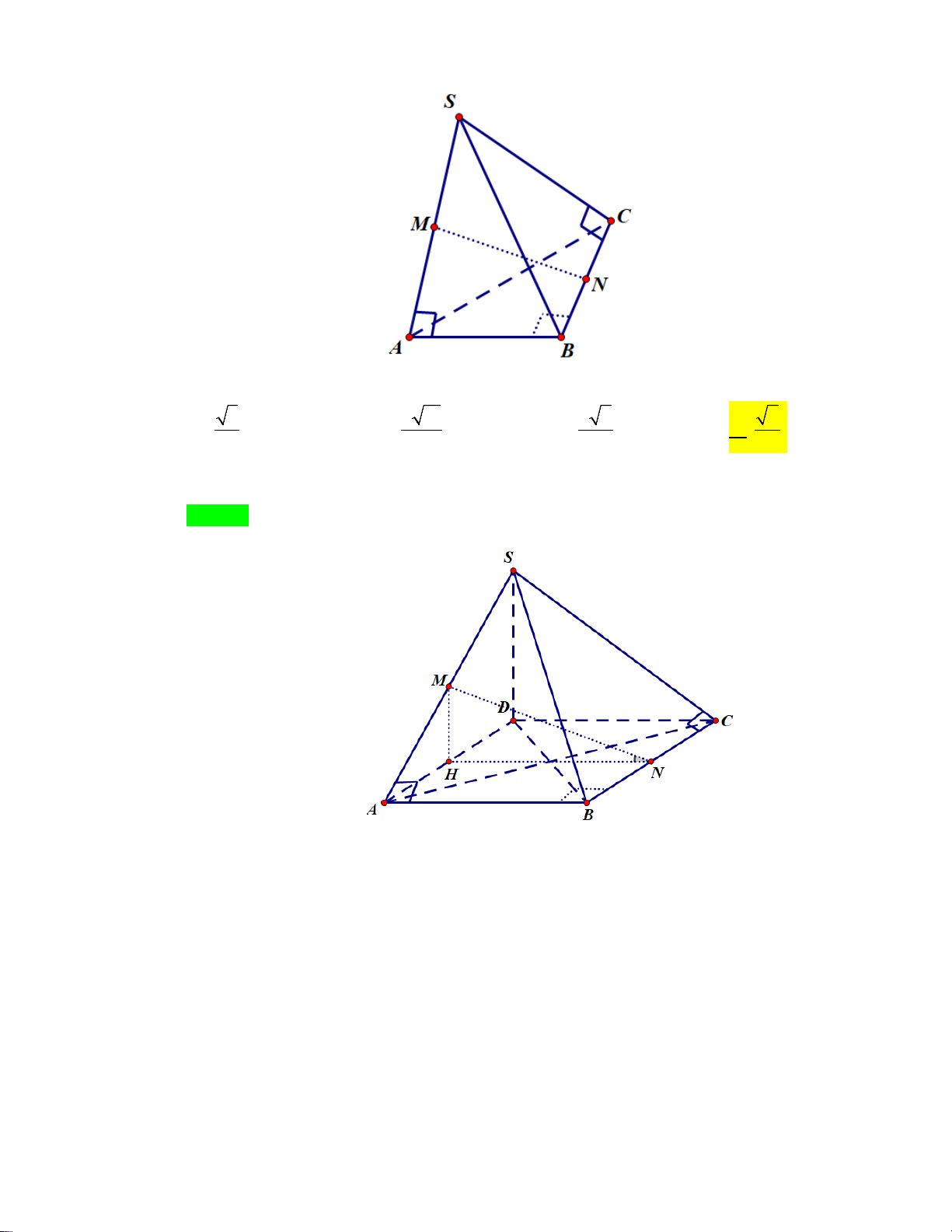
Câu 9: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B , AB  , a SA AB ,
SC BC, SB  2a . Gọi M , N lần lượt là trung điểm S ,
A BC và  là góc giữa MN và  ABC . Giá trị cos bằng 3 2 11 2 6 6 A. B. . C. . D. . 2 11 5 3
Câu 10: Tất cả các nghiệm của phương trình cos 2x  0 là   A. x
k2 k   . B. x
k k   . 2 4    C. x
k k   D. x
k k   . 4 2 2
Câu 11: Có 6 chiếc ghế được kê thành một hàng ngang. Xếp ngẫu nhiên 6 học sinh, gồm 3 học sinh lớp
A, 2 học sinh lớp B, 1 học sinh lớp C, ngồi vào hàng ghế đó, sao cho mỗi ghế có đúng một em học sinh.
Xác suất để học sinh lớp C chỉ ngồi cạnh học sinh lớp B là 3 1 2 1 A. . B. . C. . D. . 20 6 15 5
Câu 12: Đạo hàm của hàm số y  sin 2x là A. 2cos x . B. 2  cos2x . C. 2sin 2x . D. 2cos 2x .
Câu 13: Cho cấp số nhân u với u  2 và u  1. Công bội của cấp số nhân đã cho bằng n  1 2 1 A. B. 1  . C. 2 . D. 1. 2
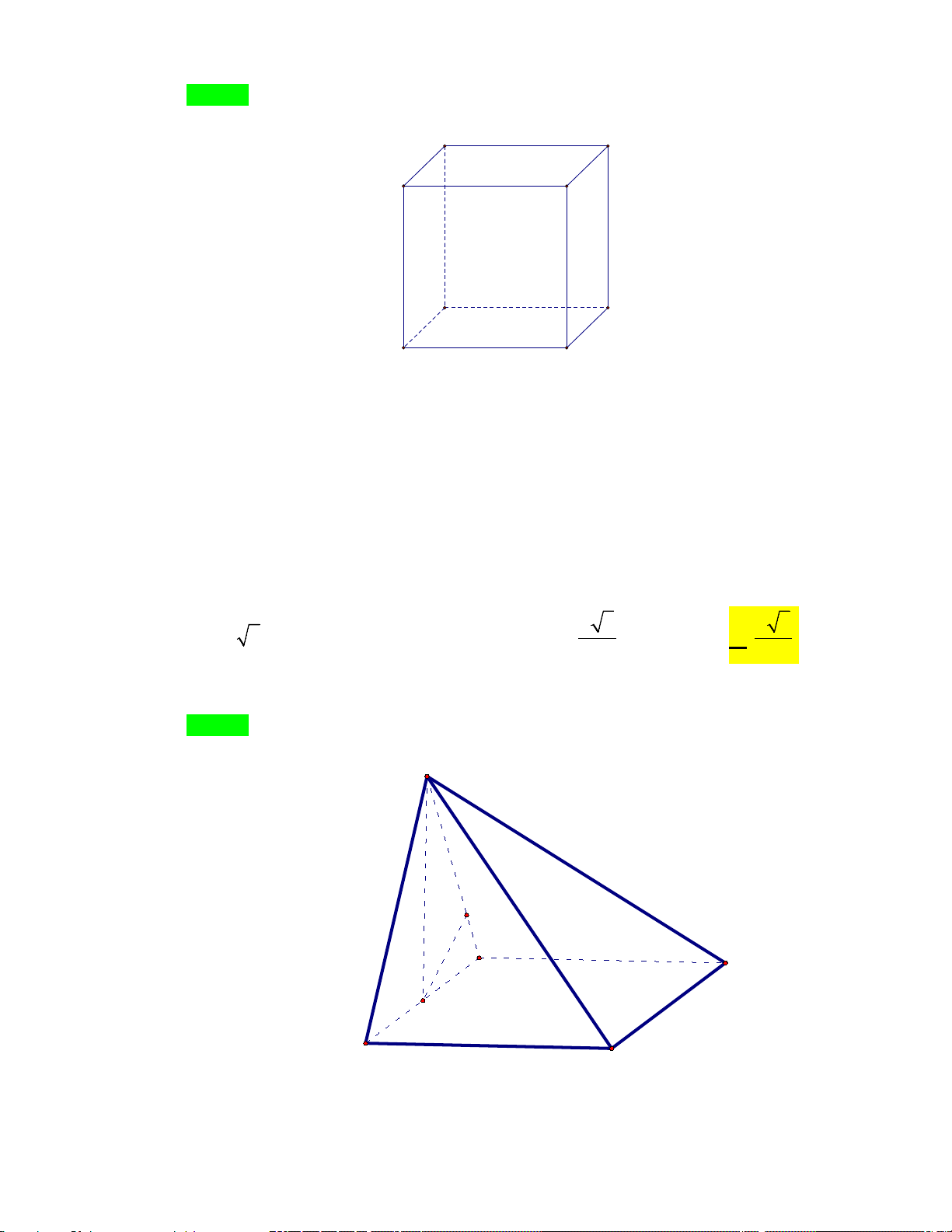
Câu 14: Cho tứ diện đều ABCD có cạnh AB a . Tích vô hướng A . B CD bằng 2 a 2 a A. . B. . C. 2 a . D. 0 . 2 2
Câu 15: Cho hai đường thẳng a và b chéo nhau. Có bao nhiêu mặt phẳng chứa a và song song với b ? A. 0 . B. 1. C. Vô số. D. 2 . 1
Câu 16: Một vật chuyển động thẳng xác định bởi phương trình 3 2 S t
t  2t 1 ( t là thời gian tính 2
bằng giây, S là đường đi tính bằng mét). Tính vận tốc m / s của vật tại thời điểm t  2 s ? 0  
A. 14m / s .
B. 9m / s .
C. 12m / s .
D. 6m / s .
Trang 2/6 - Mã đề thi 132
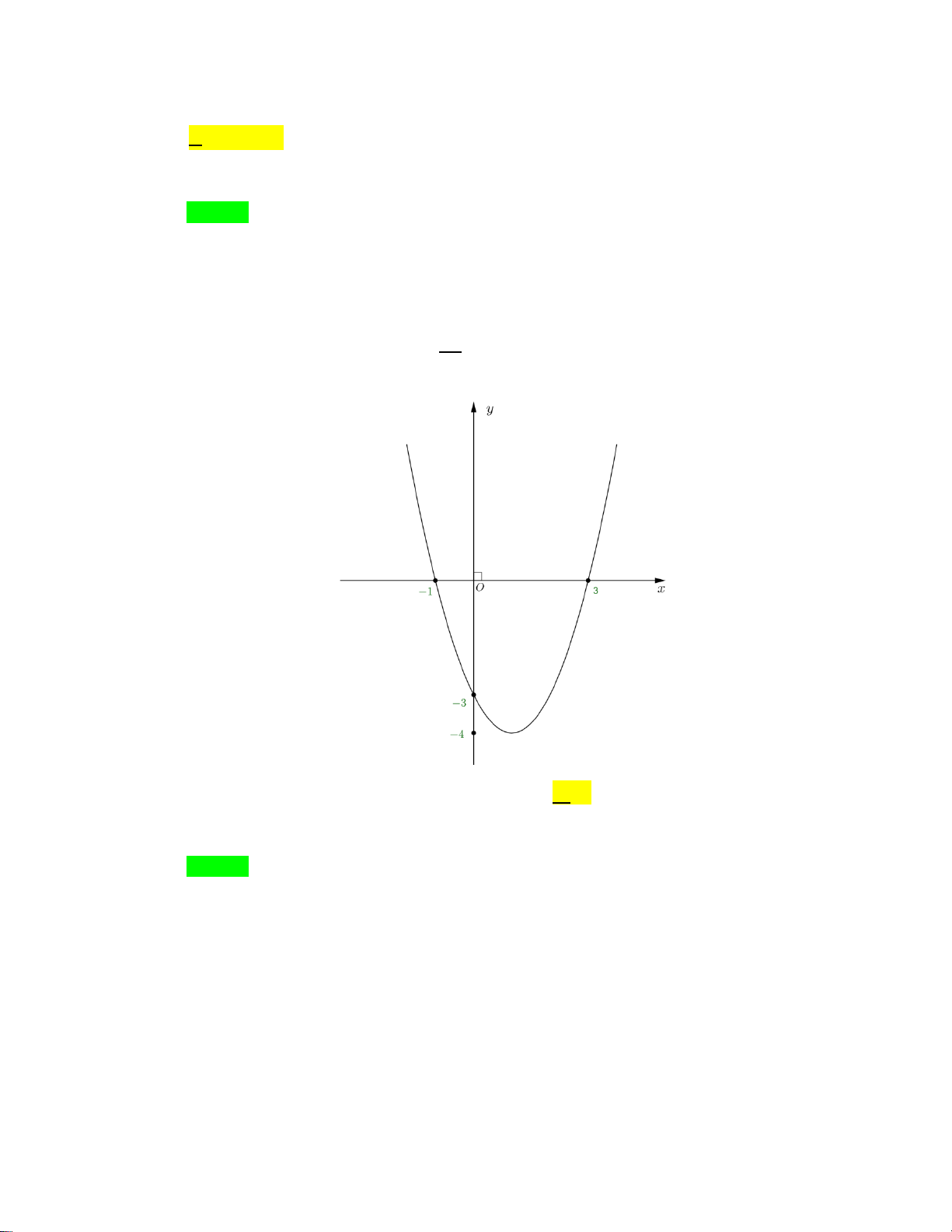
Câu 17: Cho tam thức bậc hai y f x có đồ thị như hình vẽ bên dưới. Tìm số nghiệm của phương   
trình f sin x  2  với 3 x    ;   .  2  6 4 2 10 5 5 10 -1 O 3 2 -3 4 6 A. 4 . B. 2 . C. 3 . D. 1. x Câu 18: Hàm số 2 1 y  có đạo hàm là x 1 3 1 1 A. y   . B. y  . C. y   . D. y  2 . 2 (x 1) 2 (x 1) 2 (x 1)
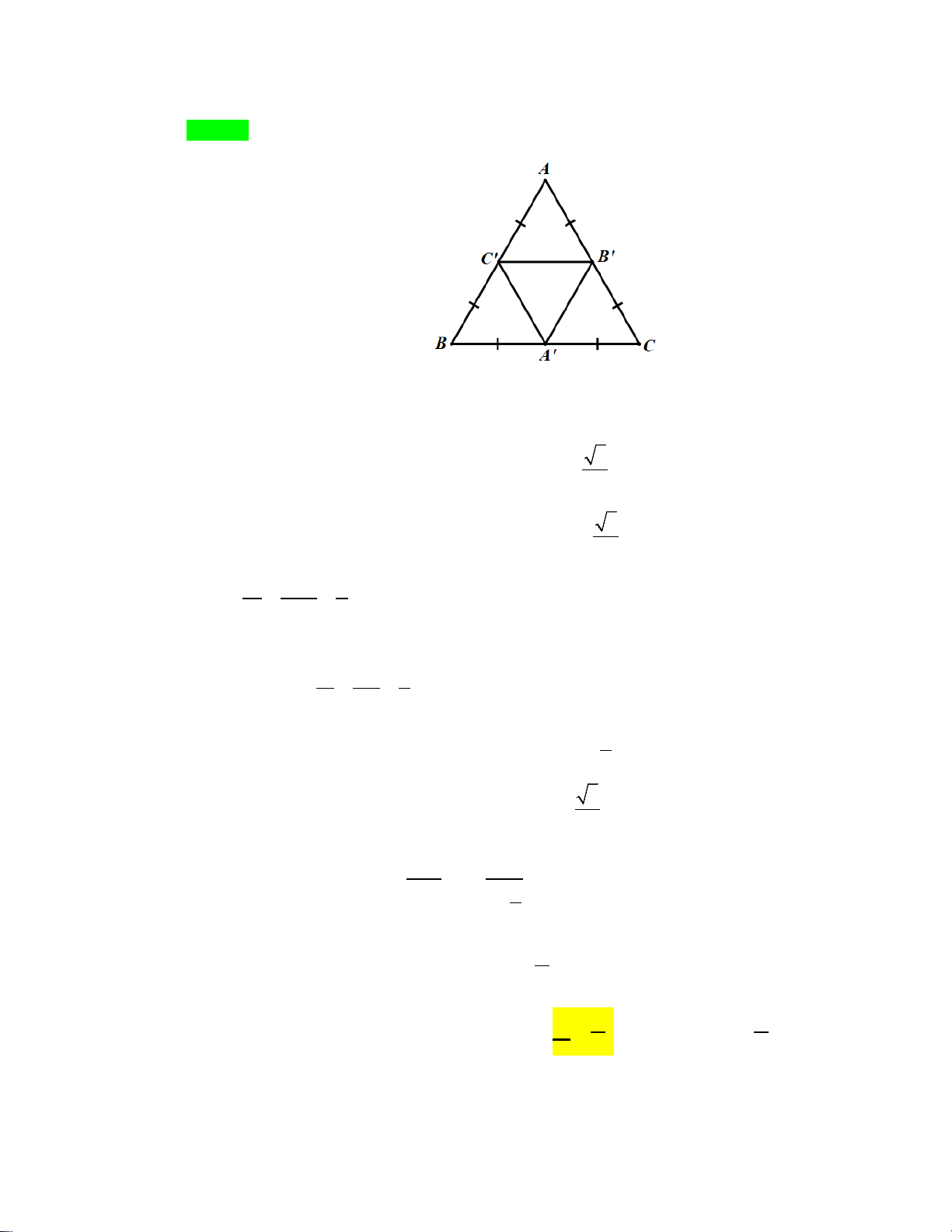
Câu 19: Tam giác mà ba đỉnh của nó là ba trung điểm của ba cạnh tam giác ABC được gọi là tam giác
trung bình của tam giác ABC . Ta xây dựng dãy tam giác A B C , A B C , A B C , ... sao cho A B C là 1 1 1 2 2 2 3 3 3 1 1 1
một tam giác đều cạnh bằng 3 và với mỗi số nguyên dương n  2 , tam giác A B C là tam giác trung n n n
bình của tam giác A B C . Với mỗi số nguyên dương n đặt S là diện tích hình tròn ngoại tiếp tam n 1  n 1  n 1  n
giác A B C . Tính S S  ...  S  ... n n n 1 2 n 15 9 A. . B. 5 . C. . D. 4 . 4 2   
Câu 20: Cho hàm số f x  x cos x . Tính giá trị f '    .  2   A. 0 . B. 1. C.  . D. . 2 2
Câu 21: Có bao nhiêu giá trị nguyên dương của m để phương trình 3sin x  4cos x m  0 có nghiệm? A. 11. B. 5 . C. 6 . D. 10 .
Câu 22: Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O . Biết SA SC và SB SD . Khẳng
định nào sau đây sai? S A D O B C
A. AC  SDB .
B. CD  SBD .
C. BD  SAC .
D. SO   ABCD . c
Câu 23: Với k là số nguyên dương, c là hằng số, giới hạn lim bằng k x x A. 0 . B.  . C.  . D. k x . 2
x  3x  2  , khi x  1
Câu 24: Tìm a sao cho f x   x 1
liên tục tại x  1. o 2ax1 , khi x  1 A. a  2 .
B. a  0 . C. a  1. D. a  1  .
Trang 3/6 - Mã đề thi 132
Câu 25: Số cách chọn ra 5 bạn từ một tổ có 10 bạn là A. 10 C . B. 5 C . C. 10 5 . D. 5 A . 5 10 10
Câu 26: Cho tứ diện ABCD . Điểm M thuộc đoạn AC ( M khác A , M khác C ). Mặt phẳng   đi
qua M song song với AB và AD , cắt tứ diện đã cho theo giao tuyến là A. Hình vuông. B. Hình bình hành. C. Hình chữ nhật. D. Hình tam giác.
Câu 27: Cho cấp số nhân u có số hạng đầu u , công bội q . Tính số hạng thứ n . n  1 A. n 1 u u q   .
B. u u n 1 q . n 1   n 1
C. u u n 1 q . D. n u u q . n 1   n 1
Câu 28: Với k , n là hai số nguyên dương tùy ý thỏa mãn k n , mệnh đề nào dưới đây đúng? k n k n n k ! k ! n k ! k ! ! A. C  . B. A  . C. C  . D. A  . n n! nn k! nn k! n k ! 2x 1
Câu 29: Hàm số f x 
liên tục trên khoảng nào sau đây? 2 x  4x  3  1  A.  1   ;1 . B. 0; 2 . C. 2; 4 . D. ;3   .  2  3x  3  m a
Câu 30: Biết giới hạn lim
 , m là số thực, a, b là số nguyên và a tối giản. Tính 2a b . x2 x  2 b b 1 A. 1. B. 1  . C. 0 . D. . 2 1 1
Câu 31: Cho hàm số f x 3 2
x x x  . Tập nghiệm của bất phương trình f 'x  0 là 3 2 A. . B.   1 . C.  . D.   ;1  .
Câu 32: Cho hàm số y f x xác định và có đạo hàm trên tập số thực. Biết f '  1  5; f   1  6 . Tìm 2
f x  f x  30 giới hạn lim . x 1  x 1 A. 29  . B. 0 . C. 110 . D.  . x Câu 33: Tính lim bằng  x 1  x 1 A. 0 . B.  . C.  . D. 1.
Câu 34: Hình chóp tứ giác có tất cả số mặt là A. 4 . B. 6 . C. 7 . D. 5 .
Câu 35: Cho hình chóp S.ABC có G là trọng tâm của tam giác ABC. Tính d  ,
G SBC khi biết d  ,
A SBC  3 (đơn vị dài). 2 1 A. . B. 3 . C. 1. D. . 3 3 Câu 36: Giới hạn 1 lim bằng n  2020 1 1 A. 0 . B. . C. . D.  . 3 2 3   
Câu 37: Cho cos x  , x   ; 0   . Tính tan x . 4  2  7 7 7 7 A.  . B. . C. . D. . 3 3 4 9
Trang 4/6 - Mã đề thi 132
Câu 38: Tìm khẳng định đúng trong các khẳng định sau:
A. Nếu hai mặt phẳng cùng song song với mặt phẳng thứ ba thì chúng song song với nhau.
B. Nếu ba mặt phẳng phân biệt cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến đó phải đồng quy.
C. Trong không gian, hai đường thẳng cùng vuông góc với đường thẳng thứ ba thì hai đường thẳng đó song song với nhau.
D. Nếu một đường thẳng song song với một mặt phẳng thì nó song song với một đường thẳng nào đó trong mặt phẳng đó.
Câu 39: Có bao nhiêu tiếp tuyến của đồ thị hàm số 3
y x 1 song song với đường thẳng 3x y 1  0 ? A. 3 . B. 2 . C. 0 . D. 1.
Câu 40: Số cách xếp 4 bạn A, B, C, D đứng thành hàng ngang sao cho A và B luôn cạnh nhau là A. 12 . B. 24 . C. 6 . D. 48 . ----- Hết -----
Họ và tên thí sinh:......................................................... Số báo danh:...............................................
Cán bộ coi thi không giải thích gì thêm. Học sinh không được sử dụng tài liệu.
Trang 5/6 - Mã đề thi 132 made Cautron dapan 132 1 B 132 2 C 132 3 A 132 4 C 132 5 B 132 6 A 132 7 D 132 8 B 132 9 D 132 10 C 132 11 D 132 12 D 132 13 A 132 14 D 132 15 B 132 16 C 132 17 C 132 18 A 132 19 D 132 20 C 132 21 B 132 22 B 132 23 A 132 24 C 132 25 B 132 26 D 132 27 A 132 28 B 132 29 A 132 30 C 132 31 B 132 32 C 132 33 B 132 34 D 132 35 C 132 36 A 132 37 A 132 38 D 132 39 D 132 40 A
Trang 6/6 - Mã đề thi 132 ĐÁP ÁN CHI TIẾT
Câu 1. Cho hai điểm ,
A B thuộc đồ thị hàm số y = sin x trên đoạn [0;π ]. Các điểm C, D thuộc trục π
Ox thỏa mãn ABCD là hình chữ nhật và CD = Độ dài cạnh BC bằng 3 . A.1. B. 3 . C. 1 . D. 2 . 2 2 2 Lời giải Chọn B
Giả sử D(a;0) với 0 < a < π .  π  π 
ABCD là hình chữ nhật; A( ;asina); ⇒ Ba+ ;sina+  3 3     π  π
Do ABCD là hình chữ nhậtsina = sin a + ⇒  a =  vì 0 < a < π  3  3 Độ dài cạnh 3 BC = . 2
Câu 2. Gọi S là tập hợp tất cả các giá trị của tham số m sao cho giá trị lớn nhất của hàm số 2
y = x − 2x + m trên đoạn [0; ]
3 bằng 5. Tổng tất cả các phần tử của S là A.8. B. 12 − . C. 2 − . D. 2 . Lời giải Chọn C
Xét hàm số f (x) 2
= x − 2x + m trên đoạn [0; ] 3 .
Có f ′(x) = 2x − 2 ; f ′(x) = 0 ⇔ x =1.
Ta có f (0) = m, f ( )
1 = m −1, f (3) = m + 3.
Khi đó max y = m + 3 hoặc max y =1− m . [0; ]3 [0; ] 3
Ta xét các Trường hợp sau:
TH1: max y = m + 3 = 5 ⇒ m = 2 . [0; ] 3
Thử lại với m = 2 . Khi đó 2 2
y = x − 2x + 2 = x − 2x + 2, x ∀ ∈[0; ] 3 nên max y = 5 . [0; ]3
Do đó m = 2 (thỏa mãn).
TH2: max y =1− m = 5 ⇒ m = 4 − . [0; ]3 Thử lại với m = 4 − . Khi đó 2
y = x − 2x − 4 nên max y = 5 . [0; ]3 Do đó m = 4 − (thỏa mãn).
Vậy có hai giá trị thỏa mãn là m = 2;m = 4 − .
Tổng tất cả các phần tử của S là 2− 4 = 2. −
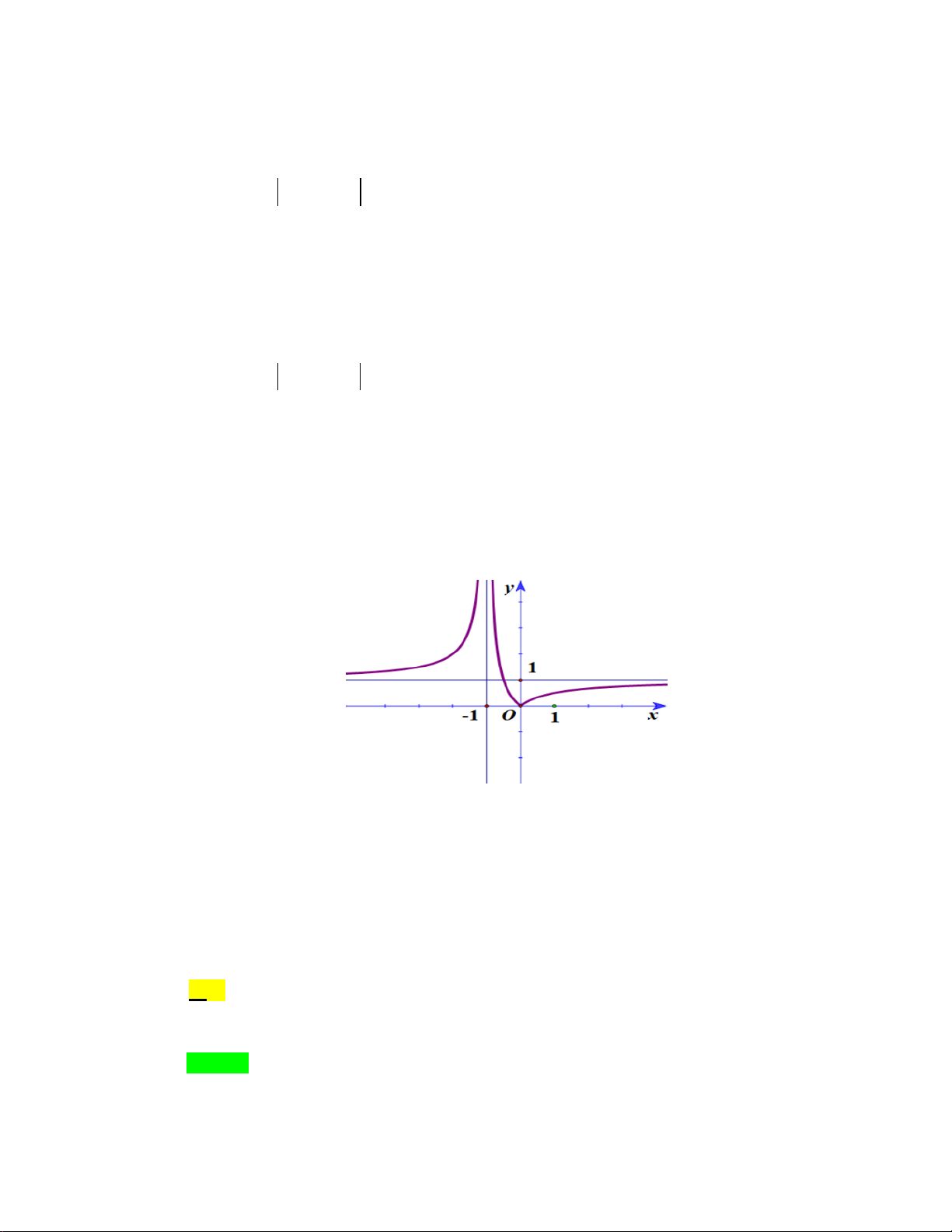
Câu 3. Cho đồ thị hàm số y = f (x) như hình vẽ. Xét các khẳng định sau
i) lim f (x) = +∞ .
ii) lim f (x) = +∞ . x 1+ →− x 1− →−
iii) lim f (x) =1.
iv) lim f (x) = +∞ . x→−∞ x→+∞
Hỏi có bao nhiêu khẳng định đúng? A. 3. B. 1. C. 2. D. 4. Lời giải Chọn A
Qua đồ thị hàm số y = f (x) ta có:
lim f (x) = +∞ ; lim f (x) = +∞ ; lim f (x) =1. x 1+ →− x 1− →− x→−∞ Vậy chon đáp án A.
Câu 4. Cho hình chóp S.ABCD , đáy ABCD là hình vuông cạnh bằng a , tam giác SAB đều. Gọi M
là điểm trên cạnh AD sao cho AM = x, x∈(0;a) . Mặt phẳng (α ) qua M và song song với 2
(SAB) lần lượt cắt các cạnh CB,CS,SD tại N,P, .
Q Khi diện tích tứ giác MNPQ bằng 2a 3 9
thì x bằng bao nhiêu? A. a . B. 2a . C. a . D. a . 2 3 3 4 Lời giải Chọn C
Kẻ đường thẳng qua M và song song với AB , cắt BC tại N .
Kẻ đường thẳng qua N và song song với SB , cắt SC tại P .
Kẻ đường thẳng qua M và song song với SA , cắt SD tại Q .
Suy ra tứ giác MNPQ là thiết diện của hình chóp S.ABCD cắt bởi (α ) . (
 α ) ∩(SCD) = PQ  Có (
SCD) ∩ ( ABCD) = CD (  ABCD  )∩(α ) = MN
⇒ PQ,CD, MN hoặc đôi một song song, hoặc đồng quy.
Mà CD//MN ⇒ PQ// .
CD (PQ < CD) (1)
Gọi H là hình chiếu vuông góc của S lên ( ABCD) .
Ta có: SA = SB ⇒ HA = HB . Suy ra H thuộc đường trung trực đoạn AB .
⇒ HC = HD ⇒ SC = SD ⇒ SB ∆ C = SA
∆ D (c − c − c) ⇒  =  PCN QDM ⇒ P ∆ CN = QDM ∆
(c − g −c) ⇒ PN = QM (2)
Từ (1) và (2) ta có tứ giác MNPQ là hình thang cân. Ta có: PQ SQ AM = =
⇒ PQ = AM = x . CD SD AD
Gọi E = PN ∩QM ⇒ E
∆ NM cân tại E. Mà ( )  = ( )  , , = 60o PN NM SB AB ⇒ E
∆ NM là tam giác đều cạnh a và E
∆ PQ là tam giác đều cạnh x . 2 2 a 3 x 3 ⇒ S = S − = − ∆ S MNPQ EMN EPQ ∆ 4 4 2 2 2 2 Ta có: 2a 3
a 3 x 3 2a 3 a S = ⇔ − = ⇔ x = . MNPQ 9 4 4 9 3
Câu 5. Cho cấp số cộng (u với u = 2 và u
= 2020 . Công sai của cấp số cộng đã cho bằng n ) 1 2020 A. 2017 . B. 2018 . C. 1. D. 2019 . 2018 2019 2020 Lời giải Chọn B
Gọi d là công sai của cấp số cộng (u . n ) Khi đó u = u + 2019d . 2020 1 2018
Hay 2020 = 2 + 2019d ⇔ d = . 2019
Câu 6. Cho hình lập phương ABC .
D EFGH . Góc giữa hai đường thẳng AB , EH là A. 0 90 . B. 0 0 . C. 0 45 . D. 0 60 . Lời giải Chọn A E H G F A D B C
Vì AD song song với EH nên góc giữa hai đường thẳng AB , EH bằng góc giữa hai đường thẳng
AB , AD . Đó là góc  BAD .
Do ABCD là hình vuông nên góc  0 BAD = 90 .
Vậy góc giữa hai đường thẳng AB , EH bằng 0 90 .
Câu 7. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a , mặt bên SAB là tam giác đều nằm trong
mặt phẳng vuông góc với đáy. Tính khoảng cách giữa hai đường thẳng S , A BC . a 5 a 3
A. a 2 . B. a . C. . . 2 D. 2 Lời giải Chọn D S H A D I B C
Gọi I là trung điểm của AB . Do SAB là tam giác đều nằm trong mặt phẳng vuông góc với
đáy nên SI ⊥ ( ABCD).
Ta có AD / /BC ⇒ BC / / (SAD) nên
d (BC;SA) = d (BC;(SAD)) = d ( ;
B (SAD)) = 2d (I;(SAD))
Trong mp(SAI ) kẻ IH ⊥ SA tại H , mà AD ⊥ IH nên IH ⊥ (SAD) ⇒ IH = d (I;(SAD)) a 3 a . . d (BC;SA) a 3
= 2d (I;(SAD)) = 2IH = 2. SI IA 2 2 = 2. = 2 2 SI + IA 2 2 3a a 2 + 4 4 a Vậy d (BC SA) 3 ; = . 2
Câu 8. Sau đợt nghỉ dịch Covid-19, từ ngày 04 tháng 5 năm 2020, học sinh trường THPT Nguyễn Thị
Giang đi học trở lại. Nhà trường yêu cầu tất cả các học sinh đều phải mang khẩu trang. Qua khảo
sát, lớp 11A có 16 học sinh nữ và 24 học sinh nam, trong đó chỉ có một nửa số học sinh nữ và
một nửa số học sinh nam đeo khẩu trang theo quy định. Nếu chọn ngẫu nhiên một học sinh của
lớp 11A để kiểm tra, hãy tính xác suất để chọn được học sinh nữ hoặc hoặc học sinh đeo khẩu trang. 9 A. 10. B. 7 . C. 2 . D. 1 . 10 3 2 Lời giải Chọn B
Số phần tử không gian mẫu : n(Ω) = 40 .
Gọi A là biến cố chọn được học sinh nữ hoặc học sinh đeo khẩu trang.
Ta có n( A) = 16 +12 = 28 n( A) Vậy P( A) 28 = = = 7 = n(Ω) 40 10
Câu 9. Cho hình chóp S.ABC có đáy là tam giác vuông cân tại B , AB = a , SA ⊥ AB , SC ⊥ BC ,
SB = 2a . Gọi M , N lần lượt là trung điểm của S ,
A BC và α là góc giữa MN và ( ABC). Giá trị cosα bằng A. 3 . B. 2 11 . C. 2 6 . D. 6 . 2 11 5 3 Lời giải Chọn D
Vẽ SD ⊥ ( ABC) AB ⊥ SA Khi đó ta có  ⇒ AB ⊥ AD AB ⊥ SDBC ⊥ SC  ⇒ BC ⊥ CD BC ⊥ SD
Suy ra ABCD là hình vuông
Gọi H là trung điểm của AD khi đó MH SD ⇒ MH ⊥ ( ABC) ⇒ α = 
MNH (α là góc giữa MN và ( ABC)). SD 2 2
= SB − BD = ( a) − (a )2 2 2 2 = a 2 . 1 a 2 MH = SD = , HN = a , 2 2 6
MN = MH + HN = 2 2 2 Vậy cosα HN a = = 6 = . MN a 6 3 2
Câu 10. Tất cả các nghiệm của phương trình cos 2x = 0 là A. π π
x = + k2π (k ∈) .
B. x = + kπ (k ∈) . 2 4 C. π π π
x = + k (k ∈) .
D. x = + kπ (k ∈) . 4 2 2 Lời giải Chọn C cos 2x = 0 π π π
⇔ 2x = + kπ (k ∈) ⇔ x = + k (k ∈) . 2 4 2
Câu 11. Có 6 chiếc ghế được kê thành một hàng ngang. Xếp ngẫu nhiên 6 học sinh, gồm 3 học sinh lớp
A , 2 học sinh lớp B , 1 học sinh lớp C vào hàng ghế đó, sao cho mỗi ghế có đúng một em
học sinh. Xác suất để học sinh lớp C chỉ ngồi cạnh học sinh lớp B là A. 3 . B. 1 . C. 2 . D. 1 . 20 6 15 5 Lời giải Chọn D
Ta có n(Ω) = 6!= 720 .
Gọi X là biến cố cần tìm. Khi đó:
Trường hợp 1: Học sinh lớp C ngồi đầu dãy hoặc cuối dãy.
+ Xếp học sinh lớp C ngồi đầu dãy hoặc cuối dãy có 2 cách.
+ Chọn 1 học sinh trong 2 học sinh lớp B và xếp cạnh học sinh lớp C có 2 cách.
+ Xếp 4 học sinh còn lại vào 4 vị trí có 4!= 24 cách.
Khi đó số cách xếp là: 2.2.24 = 96 cách.
Trường hợp 2: Học sinh lớp C không ngồi đầu dãy.
+ Số cách xếp học sinh lớp C ngồi giữa hai học sinh lớp B là 2 cách (ta xem nhóm 3 học
sinh này như một học sinh D )
+ Số cách xếp 3 học sinh lớp A và học sinh D vào 4 vị trí là 4!= 24 cách.
Khi đó số cách xếp là 2.24 = 48 cách.
Từ 2 trường hợp, suy ra số phần tử của biến cố X là n( X ) = 96 + 48 =144 cách.
Vậy xác suất của biến cố cần tìm là P( X ) n( X ) 144 1 = = = . n(Ω) 720 5
Câu 12. Đạo hàm của hàm số y = sin2x là A. 2cosx . B. 2 − cos2x .
C. 2sin2x .
D. 2cos2x . Lời giải Chọn D
Ta có y ' = (2x)'.cos2x = 2cos2x .
Câu 13. Cho cấp số nhân (u u = 2 u =1 n ) với 1 và 2
. Công bội của cấp số nhân đã cho bằng? A. 1 . B. 1 − . C. 2. D. 1. 2 Lời giải Chọn A
Gọi q là công bội của cấp số nhân u 1 Ta có: 2 q = = . u 2 1
Câu 14. Cho tứ diện đều ABCD có cạnh AB = a . Tích vô hướng   A . B CD bằng 2 a 2 −a A. 2 . B. 2 . C. 2 a . D. 0 . Lời giải Chọn D Cách 1: D A C B  
       A .
B CD = (CB −CA).CD = . CB CD − . CA CD 0 0 = . CB . CD cos 60 − . CA . CD cos 60 = 0 . Cách 2:
Gọi M là trung điểm của CD. CD ⊥ AM Do: 
⇒ CD ⊥ (MAB) ⇒ CD ⊥ AB CD ⊥ BM
Vậy:   A . B CD = 0 .
Câu 15. Cho hai đường thẳng a và b chéo nhau. Có bao nhiêu mặt phẳng chứa a và song song với b ? A. 0 . B. 1. C. Vô số. D. 2. Lời giải Chọn B
Theo định lý 3 bài đường thẳng song song với mặt phẳng của sách giáo khoa, chọn B.
Câu 16. Một vật chuyển động thẳng xác định bởi phương trình 3 1 2
S = t − t + 2t −1 ( t là thời gian tính 2
bằng giây, S là đường đi tính bằng mét). Tính vận tốc (m / s) của vật tại thời điểm t = 2(s) 0 ?
A. 14(m / s) .
B. 9(m / s) .
C. 12(m / s) .
D. 6(m / s) .
Lời giải Chọn C Ta có: 2
v(t) = S (′t) = 3t −t + 2 ⇒ v(2) =12.
Câu 17. Cho tam thức bậc hai y = f (x) có đồ thị như hình vẽ bên dưới. Tìm số nghiệm của phương  3π 
trình f (sin x) = 2 − với x ∈ π −  ; . 2    A. 4. B. 2. C. 3. D. 1. Lời giải
Chọn C Giả sử ( ) 2
f x = ax + bx + c . Vì đồ thị hàm số đi qua các điểm ( 1; − 0) , (3;0) và (0; 3 − ) nên ta  .a(− )2 1 + . b (− ) 1 + c = 0 
a − b + c = 0 a = 1 có hệ  2  .3 a .3 b c 0 9   a 3b c 0 b  + + = ⇔ + + = ⇔  = 2 − .  2 .0 a .0 b c 3 c 3  = − c = 3 − + + = −   
Ta được f (x) 2
= x − 2x − 3.  x = + Ta có f ( x) 2 2 sin 1 2 sin = 2
− ⇔ sin x − 2sin x − 3 = 2
− ⇔ sin x − 2sin x −1 = 0 ⇔  sin x = 1− 2
⇔ sin x = 1− 2 ≈ 0.414 −  3π 
Ta có bảng biến thiên của hàm số y = sin x trên π −  ; . 2     3π 
Từ bảng biến thiên suy ra phương trình sin x = 1− 2 có 3 nghiệm thuộc khoảng π −  ; . 2     3π 
Do đó, phương trình f (sin x) = 2
− có 3 nghiệm thuộc khoảng π −  ; . 2    Câu 18. Hàm số 2x +1 y = có đạo hàm là x −1 A. 3 y ' = − . B. 1 y ' = . C. 1 y ' = − . D. y ' = 2 . (x − )2 1 (x − )2 1 (x − )2 1 Lời giải Chọn A (2x ) 1 ′ .(x ) 1 (x ) 1 ′ + − − − .(2x + ) Ta có: 1
2x − 2 − 2x −1 3 y ' = = = − . (x − )2 1 (x − )2 1 (x − )2 1
Câu 19. Tam giác mà ba đỉnh của nó là ba trung điểm của ba cạnh tam giác ABC được gọi là tam giác
trung bình của tam giác ABC. Ta xây dựng dãy tam giác A B C , A B C , A B C ,... 1 1 1 2 2 2 3 3 3 sao cho A B C A B C
1 1 1 là một tam giác đều cạnh bằng 3 và với mỗi số nguyên dương n ≥ 2, tam giác n n n là
tam giác trung bình của tam giác A S − B − C n n n− . 1 1
1 Với mỗi số nguyên dương n đặt n là diện tích
hình tròn ngoại tiếp tam giác A B C
S + S +...+ S + n ... n n n. Tính 1 2 A. 15π π . B. 5π. C. 9 . D. 4π. 4 2 Lời giải Chọn D
Xét tam giác đều ABC có A ,′ B ,′C′ lần lượt là trung điểm của BC, C , A A . B Khi đó A ∆ ′B C ′ ′
là tam giác trung bình của A ∆ BC.
Bán kính đường tròn ngoại tiếp tam giác ABC : 3 R = A . B 3
Bán kính đường tròn ngoại tiếp tam giác 3 A′B C ′ ′ : R′ = A′B′ 3 ′ ′ ′ Suy ra R A B 1 = = . R AB 2
Gọi S là diện tích hình tròn ngoại tiếp tam giác ABC và S′ là diện tích hình tròn ngoại tiếp 2 S′ R′ 1 A ∆ ′B C ′ ,′ khi đó = = 2 S R 4
Do đó dãy số (S là một cấp số nhân có công bội 1
q = và S là diện tích hình tròn ngoại tiếp n ) 4 1 2  
tam giác A B C có cạnh bằng 3 nên 2 3
S = π R = π. .A B  = 3π. 1 1 1 1 1 1 1  3    Vậy 1 1
S + S +...+ S + = S = π = π n ... . 3 . 4 . 1 2 1 1− q 1 1− 4 Câu 20. Cho hàm số  π
f (x) = xcos .x Tính giá trị f  ′ −  .  2  A. 0. B. 1. C. π π − . D. . 2 2 Lời giải Chọn C
Ta có: f (x) (xcos x)′ cos x .x(cos x)′ ′ = = +
= cos x − xsin x Do đó  π   π   π   π  π f ′ − = cos − − − .sin − = −         .  2   2   2   2  2
Câu 21. Có bao nhiêu giá trị nguyên dương của m để phương trình 3sin x − 4cos x − m = 0 có nghiệm A. 11. B. 5. C. 6 . D. 10. Lời giải Chọn B
Ta có 3sin x − 4cos x − m = 0 ⇔ 3sin x − 4cos x = m .
Điều kiện cần và đủ để phương trình trên có nghiệm là + (− )2 2 2 3
4 ≥ m ⇔ m ≤ 5
Vì m nguyên dương nên m ∈{1;2;3;4; } 5
Câu 22. Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O . Biết SA = SC và SB = SD . Khẳng
định nào sau đây sai?
A. AC ⊥ (SDB) .
B. CD ⊥ (SBD).
C. BD ⊥ (SAC).
D. SO ⊥ ( ABCD) . Lời giải Chọn B S A D O B C
Cách 1: Giả sử CD ⊥ (SBD), suy ra CD ⊥ BD (Vô lý). Vậy đáp án B sai.
Cách 2: Vì ABCD là hình thoi tâm O nên AC ⊥ BD ( ) 1 .
Vì SA = SC nên tam giác SAC cân tại S , suy ra SO ⊥ AC (2) .
Vì SB = SD nên tam giác SBD cân tại S , suy ra SO ⊥ BD (3) .
Từ (1) và (2) suy ra AC ⊥ (SDB) . Từ (1) và (3) suy ra BD ⊥ (SAC).
Từ (2) và (3) suy ra SO ⊥ ( ABCD) .
Vậy các đáp án A, C, D đúng và đáp án B sai.
Câu 23. Với k là số nguyên dương, c là hằng số, giới hạn lim c bằng k x→+∞ x A.c . B. 0 . C. −∞ . D. +∞ . Lời giải Chọn B
Ta có lim c = c và lim k
x = +∞ nên lim c = 0 . x→+∞ x→+∞ k x→+∞ x 2
−x + 3x − 2
Câu 24. Tìm a sao cho hàm số  ≠ f (x) khi x 1 =  x −1
liên tục tại x =1. 0  2ax −1 khi x =1 A. 0 . B.1. C. 2 . D. 1 − . Lời giải Chọn B 2 −x + 3x − 2 x −1 −x + 2
Ta có: lim f (x) ( )( ) = lim = lim = lim(−x + 2) =1. x 1 → x 1 → x 1 → x 1 x −1 x −1 → f ( ) 1 = 2a −1.
Hàm số đã cho liên tục tại x =1 ⇔ lim f (x) = f ( )
1 ⇔ 1 = 2a −1 ⇔ a =1. 0 x 1 →
Câu 25. Số cách chọn ra 5 bạn từ tổ có 10 bạn là A. 10 5 C . B. 510 C . C. 10 5 . D. 510 A . Lời giải Chọn B
Số cách chọn ra 5 bạn từ tổ có 10 bạn là 510 C .
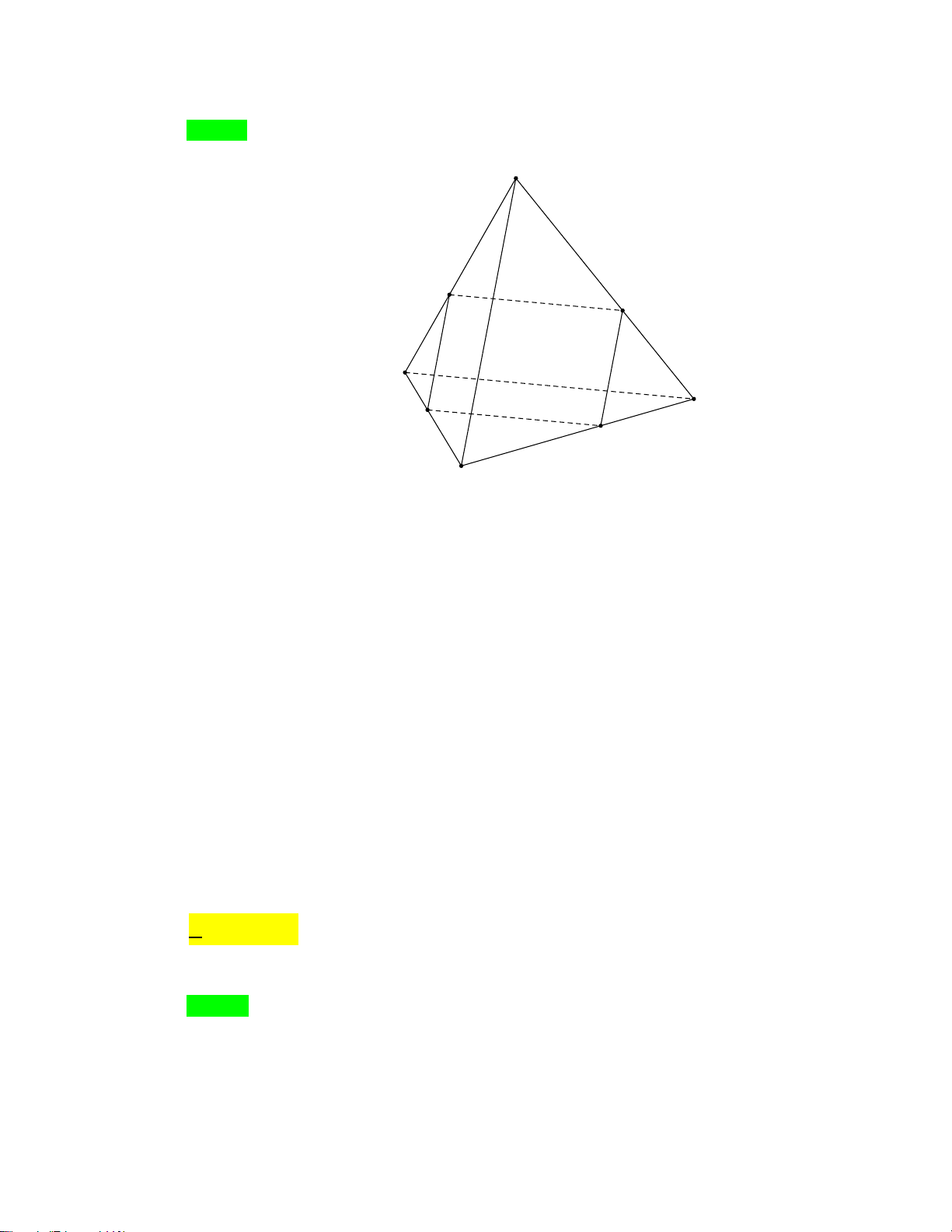
Câu 26. Cho tứ diện ABC .
D Điểm M thuộc đoạn AC ( M khác ,
A M khácC ). Mặt phẳng (α) đi qua
M song song với AB và CD, cắt tứ diện đã cho theo giao tuyến là A. Hình vuông. B. Hình bình hành. C. Hình chữ nhật. D. Tam giác. Lời giải Chọn B D Q P A B M N C Ta có AB || (α)  +) AB (ABC)  ⊂
 ⇒ (ABC) ∩ (α) = MN | AB | (N ∈ BC). M (α) (ABC) ∈ ∩  CD || (α)  +) CD (BCD)  ⊂
 ⇒ (BCD) ∩ (α) = NP | CD (P ∈ BD). N (α) (BCD) ∈ ∩  AB || (α)  +) AB (ABD)  ⊂
 ⇒ (ABD) ∩ (α) = PQ | AB | (Q ∈ AD). P (α) (ABD) ∈ ∩ 
Theo cách dựng thì thiết diện MNPQ là hình bình hành.
Câu 27. Cho cấp số nhân (u có số hạng đầu u , công bội q . Tính số hạng thứ n . n ) 1 A. 1 u u . n q − = .
B. u = u n − q .
C. u = u n + q .
D. u = u q . n . n n 1 1 ( ) n 1 1 ( ) n 1 1 Lời giải Chọn A Câu hỏi lý thuyết.
Công thức tính số hạng tổng quát của một cấp số nhân: 1 u u . n q − = . n 1
Câu 28. Với k, n là hai số nguyên dương tùy ý thỏa mãn k ≤ n , mệnh đề nào dưới đây đúng ? k n − k k (! )! k n! k k! A. C = . A = . C = . k n A = . n B. C. D. ! n! n (n − k)! n (n − k)! n k! Lời giải Chọn B Câu hỏi lý thuyết. k n!
Số chỉnh hợp chập k của n (k,n +
∈ , k ≤ n) được tính bởi công thức A = n ( . n − k )! Câu 29. Hàm số 2x −1 f (x) =
liên tục trên khoảng nào sau đây? 2 x − 4x + 3 A. ( 1; − 1) B. (0;2) C. (2;4) D.  1 ;3  2    Lời giải Chọn A
Hàm số là hàm phân thức hữu tỉ, có tập xác định D =  \ {1; }
3 nên liên tục trên từng khoảng ( ; −∞ ) 1 , (1;3) và (3;+∞) .
Câu 30. Biết giới hạn 3x + 3 lim
− m = a , m là số thực, ,ab là số nguyên và a tối giản. Tính 2a−b . x→2 x − 2 b b A. 1 B. 1 − C. 0 D. 1 2 Lời giải Chọn C Để 3x + 3 lim
− m = a , với ,ab là số nguyên thì điều kiện cần là phương trình x→2 x − 2 b
3x + 3 − m = 0 phải có nghiệm x = 2 , suy ra m = 3 . Khi đó ta được: 3x + 3 − 3 3(x − 2) 3 1 lim = lim = lim = . x→2 − x→2 x 2
(x − 2)( 3x+3 +3) x→2 3x+3 +3 2
Suy ra a = 1, b = 2 ⇒ 2a − b = 0 .
Câu 31. Cho hàm số f (x) 1 3 2 1
= x − x + x + . Tập nghiệm của bất phương trình f '(x) ≤ 0là 3 2 A. .  B. { } 1 . C. . ∅ D.(−∞ ) ;1 . Lời giải Chọn B
Ta có f (x) 2 '
= x − 2x +1 = (x − )2 1 ≥ 0.
Vậy f '(x) ≤ 0 ⇔ x −1 = 0 ⇔ x =1.
Câu 32. Cho hàm số y = f (x) xác định và có đạo hàm trên tập số thực. Biết f ′( ) 1 = 5 ; f ( ) 1 = 6 . Tìm giới 2
f (x) − f (x) − 30 hạn lim . x 1 → x −1 A. 29 − . B. 0 . C. 110 . D. +∞ . Lời giải Chọn C
Vì x −1 xác định khi x ≥ 0 và y = f (x) xác định và có đạo hàm trên tập số thực nên 2
f (x) − f (x) − 30 xác định và có đạo hàm khi x >0. x  −1  x ≠ 1
Áp dụng quy tắc L’Hospital ta có 2
f (x) − f (x) − 30
2 f (x) f ′(x) − f ′(x) lim = lim
= lim2 x 2 f (x) f ′(x) − f ′(x)   x 1 → x 1 x −1 → 1 x 1 → 2 x = 22 f ( ) 1 f ′( ) 1 − f ′( ) 1  
 = 2.(2.5.6 − 5) =110 .
Câu 33. Tính lim x bằng x 1− → x −1 A. 0 . B. −∞ . C. +∞ . D. 1. Lời giải Chọn B Ta có: lim (x − ) 1 = 0, x −1< 0
x < và lim (x) =1 > 0 x 1− → với mọi 1 x 1− →
Do đó: lim x = −∞ . x 1− → x −1
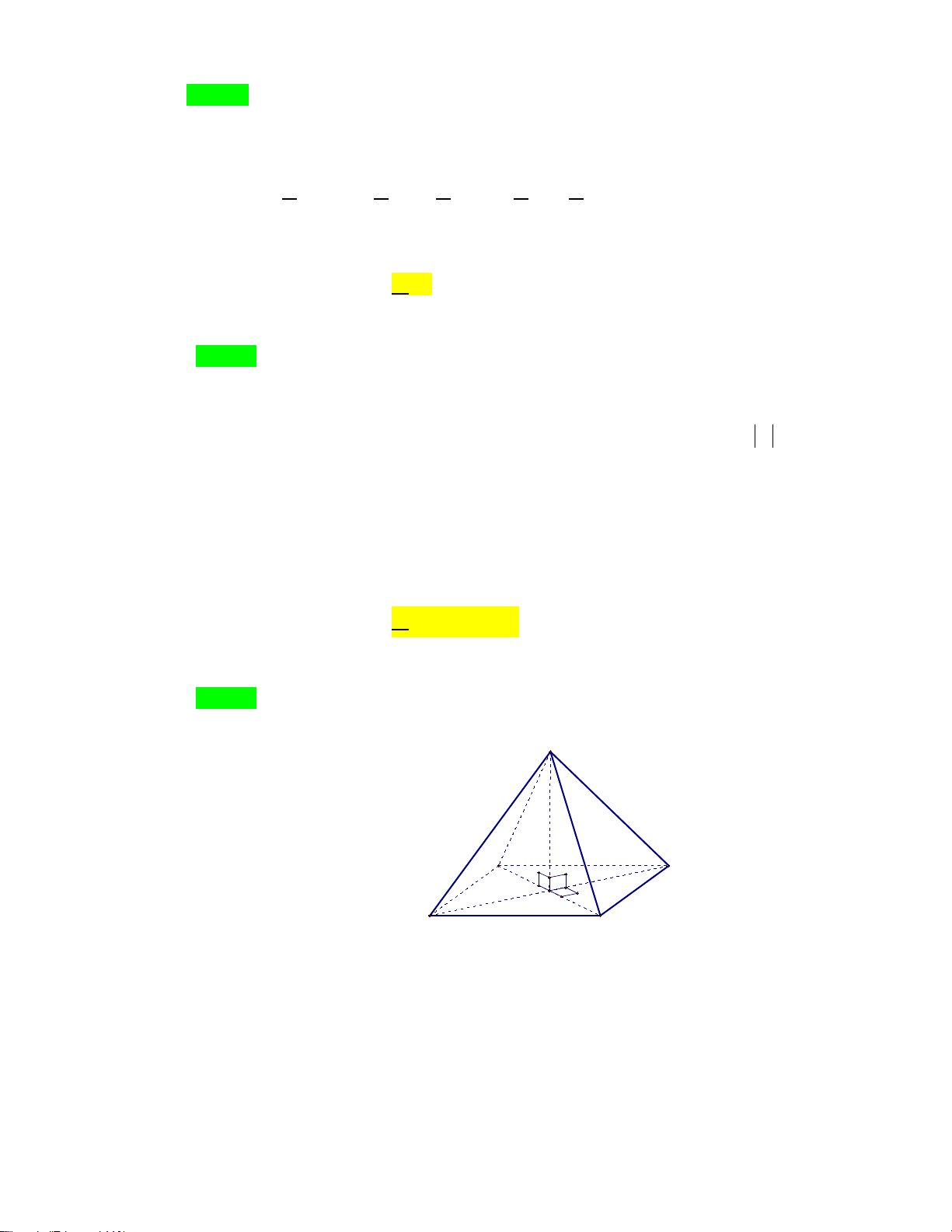
Câu 34. Hình chóp tứ giác có tất cả số mặt là A. 4 . B. 6 . C. 7 . D. 5. Lời giải Chọn D S A D B C
Dễ thấy hình chóp tứ giác có tất cả số mặt là: 5.
Câu 35. Cho hình chóp S.ABC có G là trọng tâm của tam giác ABC . Tính d (G,(SBC)) khi biết d ( ,
A (SBC)) = 3(đơn vị dài). A. 2 . B. 3. C. 1. D. 1 . 3 3 Lời giải Chọn C
Gọi I là trung điểm BC ⇒ AG cắt (SBC) tại I . GI 1
d (G,(SBC)) Ta có 1 1 = ⇒ = ⇒ = = . AI d (
d (G, SBC ) d ( , A SBC ) , A (SBC)) ( ) ( ) 1 3 3 3 Câu 36. Giới hạn 1 lim bằng n + 2020 A. 0 . B. 1 . C. 1 . D. +∞ . 3 2 Lời giải Chọn A 1 Ta có 1 n 0 lim = lim = = 0. n + 2020 2020 1 1+ n Câu 37. Cho 3  π cos x , x  ;0 = ∈ − . Tính tan x . 4 2    A. 7 − . B. 7 . C. 7 . D. 7 . 3 3 4 9 Lời giải Chọn B Ta có: 2 1 1 1 7 1+ tan x = ⇒ tan x = ± −1 = ± −1 = ± 2 2 2 cos x cos x  3  3  4   Vì  π x ;0 ∈ − 7 
nên cos x > 0 ⇒ cos x = . Vậy đáp án B đúng. 2    3
Câu 38. Tìm khẳng định đúng trong các khẳng định sau:
A. Nếu hai mặt phẳng cùng song song với mặt phẳng thứ ba thì chúng song song với nhau.
B. Nếu ba mặt phẳng phân biệt cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến đó phải đồng quy.
C. Trong không gian, hai đường thẳng cùng vuông góc với đường thẳng thứ ba thì hai đường
thẳng đó song song với nhau.
D. Nếu một đường thẳng song song với một mặt phẳng thì nó song song với một đường thẳng
nào đó trong mặt phẳng. Lời giải
+ Nếu hai mặt phẳng cùng song song với mặt phẳng thứ ba thì chúng song song với nhau
Sai vì chúng có thể trung nhau
+ Nếu ba mặt phẳng phân biệt cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến đó phải đồng quy.
Sai vì chúng có thể song song
+ Trong không gian, hai đường thẳng cùng vuông góc với đường thẳng thứ ba thì hai đường
thẳng đó song song với nhau.
Sai vì hai đường thẳng chéo nhau vẫn có thể cùng vuông góc với một đường thẳng thứ 3. Chọn D
Câu 39. Có bao nhiêu tiếp tuyến của đồ thị hàm số 3
y = x −1 song song với đường thẳng 3x − y +1 = 0 A.3. B. 2 . C. 0 . D.1. Lời giải Chọn D Ta có 2
y ' = 3x ; 3x − y +1 = 0 ⇒ y = 3x +1
Vì tiếp tuyến song song với đường thẳng y = 3x +1 Nên 2
3x = 3 ⇒ x∈{-1;1}
Phương trình tiếp tuyến có dạng: y = y '(x x − x + y 0 ) ( 0 ) 0
Với x =1⇒ y ' = 3(x − )
1 + 0 = 3x − 3 , nhận x =1. Với x = 1
− ⇒ y ' = 3(x + )
1 − 2 = 3x +1, nên x = 1 − không thỏa.
Câu 40. Số cách sắp xếp 4 bạn ,
A B, C, D đứng thành hàng ngang sao cho A và B luôn đứng cạnh nhau là A.12. B. 24 . C. 6 . D. 48 . Lời giải Chọn A + ,
A B đứng cạnh nhau coi như một người, đỏi chỗ ba người này có 3! cách Hai người ,
A B đứng cạnh nhau đổi chỗ cho nhau có 2! cách.
Vậy số cách sắp xếp là 3!.2!=12 cách.
-------------------- HẾT --------------------
Document Outline

  • de-kscl-toan-11-thang-5-nam-2020-truong-thpt-nguyen-thi-giang-vinh-phuc
  • Tổ-9-ĐỢT-29-KSCL-LỚP-11-TRƯỜNG-THPT-NGUYỄN-THỊ-GIANG-2019-2020
    • ĐÁP ÁN CHI TIẾT
    • Câu 1. Cho hai điểm thuộc đồ thị hàm số trên đoạn . Các điểm thuộc trục thỏa mãn là hình chữ nhật và . Độ dài cạnh bằng
    • Câu 2. Gọi là tập hợp tất cả các giá trị của tham số sao cho giá trị lớn nhất của hàm số trên đoạn bằng . Tổng tất cả các phần tử của là
    • Câu 39. Có bao nhiêu tiếp tuyến của đồ thị hàm số song song với đường thẳng
    • Câu 40. Số cách sắp xếp bạn đứng thành hàng ngang sao cho và luôn đứng cạnh nhau là