Đề KSCL Toán 11 thi THPT QG 2020 lần 2 trường THPT chuyên Vĩnh Phúc

Ngày 24 tháng 05 năm 2020, trường THPT chuyên Vĩnh Phúc, tỉnh Vĩnh Phúc tổ chức kỳ thi khảo sát chất lượng các môn thi THPT Quốc gia lần thứ hai năm học 2019 – 2020 dành cho học sinh khối lớp 11.

 

15 8 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 11

Môn: Toán 11

Thông tin:

28 trang 7 tháng trước

Tác giả:

Profile Kim Oanh
Trang 1/5 - Mã đề thi 123
SỞ GD & ĐT VĨNH PHÚC
TRƯỜNG THPT CHUYÊN VĨNH PHÚC
(Đề thi có: 05 trang)
ĐỀ THI KHẢO SÁT CHẤT LƯỢNG THPT QG LẦN 2
NĂM HỌC 2019 - 2020
MÔN: TOÁN KHỐI 11
Thời gian làm bài: 90 phút;
(Không kể thời gian giao đề)
Mã đề thi 123
Họ, tên thí sinh:..........................................................................
Số báo danh:...............................................................................
Câu 1: Cho khai triển
( )
2 22
01 2 2
1
n
n
n
x x a ax ax a x++ = + + + +
, với
2
n ≥
và
0
a
,
1
a
,
2
a
, ...,
là
các hệ số. Biết rằng
3
4
14 41
a
a
=
, khi đó tổng
012 2n
Sa aa a= ++++
bằng
A.
11
3S =
. B.
13
3S =
. C.
10
3S =
. D.
12
3S =
.
Câu 2: Cho
,,
abc
là các số thực đôi một khác nhau thuộc đoạn
0; 2


. Giá trị nhỏ nhất của biểu thức
222
111
( )( )( )
P
ab bc ca
=++
−−−
là :
A.
1
3
. B.
4
9
. C.
9
4
D.
.
Câu 3: Tổng tất cả các nghiệm thuộc khoảng
( )
0 ;360

của phương trình
( )
2
sin 45
2
x + °=−
bằng:
A.
180°
. B.
0
540
C.
0
450
D.
0
90
Câu 4: Cho
(
)
2
lim 5 5
x
x ax x
→−∞
+ ++ =
thì giá trị của
a
là một nghiệm của phương trình nào trong
các phương trình sau?
A.
2
11 10 0xx− +=
B.
2
5 60xx− +=
C.
2
8 15 0xx−+=
D.
2
9 10 0xx
+−=
Câu 5: Phương trình
( 1) sin cos 5m xx+ +=
có nghiệm
x ∈
khi và chỉ khi
A.
3
1
m
m
≥
≤−
B.
1
3
m
m
≥
≤−
. C.
13m−≤ ≤
. D.
31m
−≤ ≤
.
Câu 6: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình bình hành tâm
O
,
I
là trung điểm cạnh
SC
.
Khẳng định nào sau đây sai?
A. Đường thẳng
IO
song song với mặt phẳng
( )
SAD
.
B. Mặt phẳng
( )
IBD
cắt hình chóp
.S ABCD
theo thiết diện là một tứ giác.
C. Đường thẳng
IO
song song với mặt phẳng
( )
SAB
.
D. Giao tuyến của hai mặt phẳng
( )
IBD
và
( )
SAC
là
.
Câu 7: Tập xác định của hàm số
2
tan
sin 1
x
y
x
=
+
là
A.
2, .
2
D kk
π
π

= +∈



B.
.D =
C.
{ }
,.D kk
π
= ∈
D.
,.
2
D kk
π
π

= +∈



Câu 8: Số nghiệm phương trình
( )
2
23 320x xx− −+=
là
A. 0. B. 1. C. 2. D. 3.
Trang 2/5 - Mã đề thi 123
Câu 9: Thầy X có
15
cuốn sách gồm
4
cuốn sách toán,
5
cuốn sách lí và
6
cuốn sách hóa. Các
cuốn sách đôi một khác nhau. Thầy X chọn ngẫu nhiên
8
cuốn sách để làm phần thưởng cho một học
sinh. Tính xác suất để số cuốn sách còn lại của thầy X có đủ
3
môn.
A.
5
6
. B.
661
715
. C.
660
713
. D.
6
7
.
Câu 10: Cho cấp số nhân
()
n
u
có số hạng đầu
1
5u =
và công bội
2q = −
. Số hạng thứ sáu của
()
n
u
là:
A.
6
320u = −
.
B.
6
160u =
.
C.
6
320u =
.
D.
6
160u = −
.
Câu 11: Tìm tất cả các giá trị của tham số
m
để phương trình sau có ba nghiệm phân biệt lập thành
một cấp số nhân:
( )
32 2
7 2 6 80x x m mx
.
− + + −=
A.
1m = −
hoặc
7m.=
B.
1m =
hoặc
7m.= −
C.
1m.=
D.
7m.= −
Câu 12: Trong các phát biểu sau, phát biểu nào là sai?
A. Dãy số có tất cả các số hạng bằng nhau là một cấp số nhân.
B. Một cấp số cộng có công sai dương là một dãy số dương.
C. Một cấp số cộng có công sai dương là một dãy số tăng.
D. Dãy số có tất cả các số hạng bằng nhau là một cấp số cộng.
Câu 13: Tập nghiệm của bất phương trình
22
12 12xx x x−− >+ −
là
A.
( )
( )
; 3 4;−∞ − ∪ +∞
B.
( ) ( )
6; 2 3; 4− − ∪−
C.
( ) ( )
; 4 3;−∞ − ∪ +∞
D.
(
)
4;3
−
Câu 14: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình bình hành, mặt bên
SAB
là tam giác vuông
tại
A
,
3SA a=
,
2SB a=
. Điểm
nằm trên đoạn
AD
sao cho
2
AM MD=
. Gọi
( )
P
là mặt
phẳng qua
M
và song song với
( )
SAB
. Tính diện tích thiết diện của hình chóp cắt bởi mặt phẳng
( )
P
.
A.
2
43
3
a
. B.
2
53
6
a
. C.
2
43
9
a
. D.
2
53
18
a
.
Câu 15: Tìm tất cả các giá trị của a dương sao cho giá trị nhỏ nhất của hàm số
(
)
(
)
22
4 4 22y f x x ax a a= = − + −+
trên đoạn
[ ]
0; 2
bằng 3.
A.
5 10
a = +
B.
53a = +
C.
12
a = +
D.
2a =
Câu 16: Bạn An ra vườn hái 6 bông hoa vàng và 5 bông hoa đỏ cho vào giỏ. Có bao nhiêu cách để
bạn An lấy 3 bông hoa từ giỏ đó sao cho chúng có đủ cả hai màu?
A.
135
. B.
462
. C.
810
. D.
.
Câu 17: Trong các khẳng định sau đây, khẳng định nào sai?
A. Gọi
( )
PA
là xác suất của biến cố
A
ta luôn có
( )
01PA<≤
.
B. Phép thử ngẫu nhiên là phép thử mà ta không biết được chính xác kết quả của nó nhưng ta có
thể biết được tập hợp tất cả các kết quả có thể xảy ra của phép thử.
C. Không gian mẫu là tập hợp tất cả các kết quả có thể xảy ra của phép thử.
D. Biến cố là tập con của không gian mẫu.
Câu 18: Từ một tổ gồm 10 học sinh, giáo viên chủ nhiệm chọn ra 4 học sinh để dọn vệ sinh lớp trong
đó có 1 bạn lau bảng, 2 bạn quét lớp và 1 bạn kê bàn ghế. Số cách chọn là
A.
5000.
B.
2500.
C.
2520.
D.
5040.
Câu 19: Biểu thức
( )
( )
22
2 2 22m x mx+ − −+
luôn nhận giá trị dương khi và chỉ khi:
A.
4m ≤−
hoặc
0m ≥
. B.
40m−< <
.
Trang 3/5 - Mã đề thi 123
C.
0m <
hoặc
4
m >
D.
4m <−
hoặc
0m >
.
Câu 20: Tổng
0 1 22
2 2 ... 2
nn
nn n n
CC C C
+ + ++
bằng:
A.
3
n
B.
C.
1
2
n
+
D.
2
n
n
C
Câu 21: Trong không gian cho bốn điểm không đồng phẳng, có thể xác định nhiều nhất bao nhiêu
mặt phẳng phân biệt từ các điểm đó?
A.
6
. B.
4
. C.
2
. D.
3
.
Câu 22: Tính giới hạn:
22 2
11 1
lim 1 1 ... 1
23
n


−− −




.
A.
1
4
. B.
1
2
. C.
1
. D.
3
2
.
Câu 23: Tính tổng vô hạn sau:
2
11 1
1 ... ...
22 2
n
S =++ ++ +
.
A.
4
. B.
1
1
1
2
.
1
2
1
2
n
−
−
. C.
2
. D.
21
n
−
.
Câu 24: Cho hình thang vuông
ABCD
, đường cao
2, , 4
AB a AD a BC a= = =
. Gọi I là trung điểm
CD, J là điểm di động trên cạnh BC. Tính BJ sao cho AJ và BI vuông góc với nhau.
A.
3
4
a
. B.
4
5
a
. C.
a
. D.
5
6
a
.
Câu 25: Cho dãy số
1
1
4
nn
u
u un
+
=
= +
. Tìm số hạng thứ
5
của dãy số.
A.
16
. B.
. C.
12
. D.
.
Câu 26: Số nghiệm của các phương trình
2
4 5 4 17xx x− −= −
là:
A. 3 B. 1 C. 2 D. 4
Câu 27: Từ các chữ số
0,1, 2,7,8,9
tạo được bao nhiêu số tự nhiên lẻ có
5
chữ số đôi một khác
nhau?
A.
312
. B.
600
. C.
360
. D.
288
.
Câu 28: Dãy số nào sau đây không phải là cấp số nhân?
A.
1; 2; 3; 4; 5
. B.
1; 2; 4; 8; 16
. C.
1; 1; 1; 1; 1−−
. D.
1; 2; 4; 8; 16
−−
.
Câu 29: Cho phương trình
cos 2 2
4
xm
π

+ −=


với
m
là tham số. Tìm tập hợp tất cả các giá trị của
m
để phương trình có nghiệm.
A.
.∅
B.
C.
[ 1; 3].
−
D.
[ 3; 1].−−
Câu 30: Cho tam giác ABC có
0
53
60 , 10,
3
A ar 
. Tính diện tích của tam giác ABC.
A.
50
. B.
20 2
. C.
25 3
. D.
.
Câu 31: Tam giác mà ba đỉnh của nó là ba trung điểm ba cạnh của tam giác
ABC
được gọi là tam
giác trung bình của tam giác
ABC
.
Ta xây dựng dãy các tam giác
111 2 2 2 3 3 3
, , ,...ABC A BC ABC
sao cho
111
ABC
là một tam giác đều cạnh
bằng
3
và với mỗi số nguyên dương
2n ≥
, tam giác
nnn
ABC
là tam giác trung bình của tam giác
111nnn
ABC
−−−
. Với mỗi số nguyên dương
n
, kí hiệu
n
S
tương ứng là diện tích hình tròn ngoại tiếp tam
giác
nnn
ABC
. Tính tổng
12
... ...
n
SS S S= + ++ +
?
Trang 4/5 - Mã đề thi 123
A.
15
.
4
S
π
=
B.
4.S
π
=
C.
9
.
2
S
π
=
D.
5.S
π
=
Câu 32: Trong loạt đá luân lưu giữa đội tuyển Việt Nam và Thái Lan, ông Park Hang Seo phải lập
danh sách 5 cầu thủ từ 10 cầu thủ trên sân (trừ thủ môn) và thứ tự đá luân lưu của họ. Hỏi ông Park có
bao nhiêu cách lập danh sách biết ông sẽ để Quế Ngọc Hải là người sút phạt đầu tiên của đội Việt
Nam?
A. 126. B.
15120.
C.
3024.
D.
30240.
Câu 33: Phát biểu nào sau đây là sai ?
A.
lim
n
uc=
(
n
uc
=
là hằng số ). B.
lim 0
n
q =
( )
1q >
.
C.
1
lim 0
n
=
. D.
1
lim 0
k
n
=
( )
1k >
.
Câu 34: Cho hình chóp tứ giác
( )
SABCD
, đáy là hình bình hành,
AC
và
BD
cắt nhau tại
O
. Giao
tuyến của hai mặt phẳng
(
)
SAB
và
( )
SCD
là đường thẳng:
A. qua
S
và song song với
AB
B.
AC
C.
SO
D. qua
S
và song song với
BD
Câu 35: Cho 4 điểm
(
) ( ) ( ) ( )
1; 2 , 0; 3 , 3; 4 , 1; 8A BC D− −−
. Ba điểm nào trong 4 điểm đã cho là
thẳng hàng?
A.
,,ABD
. B.
,,BCD
. C.
,,AC D
. D.
,,ABC
.
Câu 36: Cho
7
0
lim
1. 4 2
x
xa
b
xx
→

=

+ +−

(
a
b
là phân số tối giản). Tính tổng
Lab= +
.
A.
43L
=
. B.
23L =
. C.
13L
=
. D.
53L =
.
Câu 37: Cho hình lập phương
.ABCD A B C D
′′′′
(hình vẽ bên dưới). Góc giữa hai đường thẳng
AC
và
AD
′
bằng
A.
45°
. B.
30°
. C.
60°
. D.
90°
.
Câu 38: Thiết diện của một mặt phẳng với một tứ diện chỉ có thể là:
A. Một tứ giác hoặc một ngũ giác. B. Một tam giác và một hình bình hành.
C. Một tam giác hoặc một tứ giác. D. Một tam giác hoặc một ngũ giác.
Câu 39: Cho hình hộp
.ABCD A B C D
′′′′
. Gọi
là điểm trên cạnh
AC
sao cho
3AC MC=
.
Lấy
N
trên cạnh
CD
′
sao cho
CN xCD
′′
=
. Với giá trị nào của
x
thì
//MN BD
′
.
A.
1
2
x =
. B.
1
3
x =
. C.
1
4
x =
. D.
2
3
x =
.
Câu 40: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Trong không gian hai đường thẳng không có điểm chung thì chéo nhau.
B. Trong không gian hai đường thẳng lần lượt nằm trên hai mặt phẳng phân biệt thì chéo nhau.
C. Trong không gian hai đường thẳng phân biệt không song song thì chéo nhau.
D. Trong không gian hai đường chéo nhau thì không có điểm chung.
Trang 5/5 - Mã đề thi 123
Câu 41: Tập hợp tất cả các giá trị của tham số
m
để phương trình
( )
( )
sin 1 cos 0x xm− −=
có đúng
2 nghiệm phân biệt trên
;
32
ππ

−


là:
A.
1
0;
2



B.
1
;1
2


C.
1
;1
2



D.
1
;1
2



Câu 42: Cho hình hộp
.ABCD A B C D
′′′′
, gọi
là trung điểm
CD
,
( )
P
là mặt phẳng đi qua
và
song song với
BD
′
và
CD
′
. Thiết diện của hình hộp cắt bởi mặt phẳng
( )
P
là hình gì?
A. Ngũ giác. B. Tứ giác. C. Tam giác. D. Lục giác.
Câu 43: Trong các dãy số sau, dãy số nào là dãy số giảm?
A.
2
n
un=
. B.
21
1
n
n
u
n
+
=
−
C.
3
1
n
un= −
. D.
2
n
un=
.
Câu 44: Cho hình chóp
.S ABC
có
2SA BC a= =
. Gọi
,
N
lần lượt là trung điểm của
AB
, và
SC
,
3MN a=
. Tính số đo góc giữa hai đường thẳng
SA
và
BC
.
A.
120°
. B.
150°
. C.
30°
. D.
60°
.
Câu 45: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình thang
( )
//AB CD
. Gọi
,
IJ
lần lượt là trung
điểm của các cạnh
,AD BC
và G là trọng tâm tam giác
SAB
. Biết thiết diện của hình chóp cắt bởi mặt
phẳng
( )
IJG
là hình bình hành. Hỏi khẳng định nào sao đây đúng?
A.
1
3
AB CD=
B.
3
2
AB CD=
C.
3AB CD=
D.
2
3
AB CD=
Câu 46: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình bình hành. Đặt
SA a=

;
SB b=

;
SC c=

;
SD d
=

. Khẳng định nào sau đây đúng?
A.
acdb
+=+


. B.
abcd+=+


. C.
adbc+=+


. D.
0abcd
+++ =


.
Câu 47: Cho hình lập phương
.
ABCD A B C D
′′′′
có cạnh bằng
a
. Gọi
O
là tâm hình vuông
ABCD
và điểm
S
thỏa mãn
OS OA OB OC OD OA OB OC OD
′′′′
=++++ + + +
        
. Tính độ dài đoạn
OS
theo
a
.
A.
6OS a=
. B.
4OS a=
. C.
OS a=
. D.
2OS a=
.
Câu 48: Một công ty nhận được 50 hồ sơ xin việc của 50 người khác nhau muốn xin việc vào công
ty, trong đó có 20 người biết tiếng Anh, 17 người biết tiếng Pháp và 18 người không biết cả tiếng
Anh và tiếng Pháp. Công ty cần tuyển 5 người biết ít nhất một thứ tiếng Anh hoặc Pháp. Tính xác
suất để trong 5 người được chọn có đúng 3 người biết cả tiếng Anh và tiếng Pháp?
A.
351
.
201376
B.
1
.
23
C.
5
.
100688
D.
1755
.
100688
Câu 49: Giá trị lớn nhất của hàm số
1 cos 2yx= +
bằng
A.
2.
B.
1.
C.
2.
D.
0.
Câu 50: Một gia đình cần khoan một cái giếng để lấy nước. Họ thuê một đội khoan giếng nước. Biết
giá của mét khoan đầu tiên là
80.000
đồng, kể từ mét khoan thứ hai giá của mỗi mét khoan tăng thêm
5.000
đồng so với giá của mét khoan trước đó. Biết cần phải khoan sâu xuống
50 m
mới có nước. Hỏi
phải trả bao nhiêu tiền để khoan cái giếng đó?
A.
4.000.000
đồng. B.
10.125.000
đồng. C.
52.500.000
đồng. D.
52.000.000
đồng.
-----------------------------------------------
----------- HẾT ----------
mamon made cautron dapan
TOAN 11 123 1 C
TOAN 11 123 2 C
TOAN 11 123 3 C
TOAN 11 123 4 D
TOAN 11 123 5 B
TOAN 11 123 6 B
TOAN 11 123 7 D
TOAN 11 123 8 C
TOAN 11 123 9 B
TOAN 11 123 10 D
TOAN 11 123 11 B
TOAN 11 123 12 B
TOAN 11 123 13 A
TOAN 11 123 14 D
TOAN 11 123 15 A
TOAN 11 123 16 A
TOAN 11 123 17 A
TOAN 11 123 18 C
TOAN 11 123 19 D
TOAN 11 123 20 A
TOAN 11 123 21 B
TOAN 11 123 22 B
TOAN 11 123 23 C
TOAN 11 123 24 B
TOAN 11 123 25 B
TOAN 11 123 26 C
TOAN 11 123 27 D
TOAN 11 123 28 A
TOAN 11 123 29 D
TOAN 11 123 30 C
TOAN 11 123 31 B
TOAN 11 123 32 C
TOAN 11 123 33 B
TOAN 11 123
34 A
TOAN 11 123 35 A
TOAN 11 123 36 A
TOAN 11 123 37 C
TOAN 11 123 38 C
TOAN 11 123 39 D
TOAN 11 123 40 D
TOAN 11 123 41 D
TOAN 11 123 42 A
TOAN 11 123 43 B
TOAN 11 123 44 D
TOAN 11 123 45 C
TOAN 11 123 46 A
TOAN 11 123 47 B
TOAN 11 123 48 D
TOAN 11 123 49 A
TOAN 11 123 50 B
HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1. Cho khai triển
( )
2 22
01 2 2
1
n
n
n
x x a ax ax a x++ = + + + +
, với
2n ≥
và
0
a
,
1
a
,
2
a
, ...,
2n
a
là các
hệ số. Biết rằng
3
4
14 41
a
a
=
, khi đó tổng
012 2n
Sa aa a= ++++
bằng
A.
11
3
S =
. B.
13
3S =
. C.
10
3S =
. D.
12
3S
=
.
Lời giải
Chọn C
Đặt
( )
2
() 1
n
fx x x= ++
.
Khi đó:
( ) ( )
22 2 2
0 00
()1 1 ().1 () (1)
n nn
nn
k knkk kkkk
n nn
k kk
fx xx xx Cxx Cxx Cxx
−
= = =
= ++ = + + = + = + = + =
∑ ∑∑
0 0 00 00
.
n k nk nk
kk ii kk ii k iki
nknknk
k i ki ki
Cx Cx CxCx CCx
+
= = = = = =
 
= = =
 
 
∑ ∑ ∑∑ ∑∑
Số hạng của
3
x
tương ứng với:
{ }
3
0 ( , ) (3;0),(2;1)
0
ki
k n ki
ik
+=
≤≤⇒ ∈
≤≤
.
Do đó
30 21 3 2
332
2
n n nn
a CC CC C C=+=+
.
Số hạng của
4
x
tương ứng với:
{
}
4
0 ( , ) (4;0),(3;1),(2;2)
0
ki
k n ki
ik
+=
≤≤⇒ ∈
≤≤
.
Do đó
403122 4 32
4 432
3
n n n n nn
a CC CC CC C C C= + + =++
.
Theo bài ra:
3
4
14 41
a
a
=
nên:
3 2 4 32
32 4 32
23
41 82 14 42 14
14 41
n n n nn
nnnnn
C C C CC
CCCCC
+ ++
= ⇔+=++
43 2
72
14 68 0 ( 1) ( 3)( 2) 34 0
12 6
nn n
n
CC C n n n n
−

⇔ + − =⇔− − −+ − =


2
( 1) (7 33 370) 0 10 ( 2, )n n n n n do n n⇔ − − − =⇒= ≥ ∈
Khi đó tổng
10
012 2
(1) 3
n
Sa aa a f=++++ = =
.
Câu 2. Cho
,,abc
là các số thực đôi một khác nhau thuộc đoạn
0; 2


. Giá trị nhỏ nhất của biểu thức
222
111
( )( )( )
P
ab bc ca
=++
−−−
là :
A.
1
3
. B.
4
9
. C.
9
4
. D.
25
4
.
Lời giải
Chọn C
Bài toán này ta sử dụng hai bất đẳng thức:
2
22
()
(1)
2
xy
xy
+
+≥
. Dấu bằng xẩy ra khi
xy
=
.
11 4
, 0 (2)
xy
x y xy
+≥ ∀ >
+
. Dấu bằng xẩy ra khi
xy
=
.
Không mất tính tổng quát ta giả sử
02cba≤<<≤
.
Khi đó:
22 22
( ) ,( )ac a bc b
−≤ −≤
.
2 2 2 222
1 1 1 1 11
( )( )( )( )
P
ab bc ca ab a b
= + + ≥ ++
−−− −
.
Áp dụng (1) ta có:
2
22
11
11
() 2
ab b
ab b

+

−

+≥
−
.
Áp dụng bất đẳng thức (2) ta có:
22
2
11 4
8
22
ab b abb
a

+

− −+

≥=
.
Do đó:
2
2 2 2 222 2 22 2
11
1 1 1 1 11 1 81 99
( )( )( )( ) 2 4
ab b
P
ab bc ca ab a b a a a a

+

−

= + + ≥ ++≥ +≥+=≥
−−− −
.
Vậy GTNN của
P
là
9
4
. Dấu bằng xẩy ra khi
0 2, 1, 0
2
abb
c a bc
a
−=
= ⇔= = =
=
và các hoán vị của
nó.
Câu 3. Tổng tất cả các nghiệm thuộc khoảng
( )
0 ;360°°
của phương trình
( )
2
sin 45
2
x + °=−
bằng
A.
180°
. B.
540°
. C.
450°
. D.
90°
.
Lời giải
Chọn C
Ta có:
( )
2
sin 45
2
x
+ °=−
( ) (
)
sin 45 sin 45x⇔ + °= − °
45 45 360
45 180 45 360
xk
xk
+ °=− °+ °
⇔
+ °= °+ °+ °
( )
90 360
,
180 360
xk
k
xk
=− °+ °
⇔∈
= °+ °
.
• Với
90 360xk=− °+ °
,
k ∈
So điều kiện
( )
0 ;360x ∈° °
{ }
15
0 90 360 360
1
44
k
k
k
k
k
°<− °+ °< °
<<
⇒ ⇔ ⇔∈

∈
∈
270x⇒= °
.
• Với
180 360xk= °+ °
,
k
∈
So điều kiện
( )
0 ;360x ∈° °
0 180 360 360k
k
°< °+ °< °
⇒
∈
{ }
11
0
22
k
k
k
−<<
⇔ ⇔∈
∈
180x⇒= °
.
Vậy tổng tất cả các nghiệm thuộc khoảng
( )
0 ;360°°
của phương trình là
270 180 450
°+ °= °
.
Câu 4. Cho
(
)
2
lim 5 5
x
x ax x
→−∞
+ ++ =
thì giá trị của
a
là một nghiệm của phương trình nào trong các
phương trình sau?
A.
2
11 10 0xx− +=
. B.
2
5 60
xx− +=
. C.
2
8 15 0xx−+=
. D.
2
9 10 0
xx
+−=
.
Lời giải
Chọn D
Ta có:
(
)
2
lim 5 5
x
x ax x
→−∞
+ ++ =
2
5
lim 5
5
x
ax
x ax x
→−∞
+
⇔=
+ +−
2
5
lim 5
5
11
x
a
x
a
xx
→−∞
+
⇔=
− ++ −
5
2
a
⇔=
−
10a⇔=−
.
Ta thấy
10a = −
là nghiệm của phương trình
2
9 10 0xx+−=
. Do đó, chọn đáp án D.
Câu 5. Phương trình
( 1) sin cos 5m xx+ +=
có nghiệm
x
∈
khi và chỉ khi
A.
3
1
m
m
≥
≤−
. B.
1
3
m
m
≥
≤−
. C.
13m
−≤ ≤
. D.
31m−≤ ≤
.
Lời giải
Chọn B
Phương trình
( 1) sin cos 5m xx+ +=
có nghiệm
x ∈
khi và chỉ khi
( )
( )
2
2
11 5m + +≥
2
2 30
mm
⇔ + −≥
1
3
m
m
≥
⇔
≤−
.
Câu 6. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình bình hành tâm
O
,
I
là trung điểm cạnh
SC
.
Khẳng định nào sau đây sai?
A. Đường thẳng
IO
song song với mặt phẳng
( )
SAD
.
B. Mặt phẳng
( )
IBD
cắt hình chóp
.
S ABCD
theo thiết diện là một tứ giác.
C. Đường thẳng
IO
song song với mặt phẳng
( )
SAB
.
D. Giao tuyến của hai mặt phẳng
(
)
IBD
và
(
)
SAC
là
IO
.
Lời giải
Chọn B
.
A Đúng vì
( )
( )
//
//
IO SA
IO SAD
SA SAD
⇒
⊂
.
C Đúng vì
( )
( )
//
//
IO SA
IO SAB
SA SAB
⇒
⊂
.
D Đúng vì
( ) ( )
( ) ( )
( )
( )
I IBD SAC
IBD SAC IO
O IBD SAC
∈∩
⇒∩=
∈∩
.
B sai vì mặt phẳng
( )
IBD
cắt hình chóp
.S ABCD
theo thiết diện là tam giác
IBD
.
Câu 7. Tập xác định của hàm số
2
tan
sin 1
x
y
x
=
+
là
A.
2,
2
D kk
π
π

= +∈



. B.
D
=
.
C.
{ }
,D kk
π
= ∈

. D.
,
2
D kk
π
π

= +∈



.
Lời giải
Chọn D
Điều kiện:
( )
2
in
*
co
s 10
0s
x
x
+
≠
≠
Vì
in1s 1x−≤ ≤
2
1s in 12
x⇒≤ +≤
nên
( )
* cos 0,
2
x x kk
π
π
⇔≠ +⇔ ≠∈
.
Vậy tập xác định của hàm số là
,
2
D kk
π
π

= +∈



.
Câu 8. Số nghiệm phương trình
( )
2
23 320x xx
− −+=
là
A. 0. B. 1. C. 2. D. 3.
Lời giải
Chọn C
Điều kiện:
3
2 30
2
xx−≥⇔ ≥
.
Khi đó
( )
( )
(
)
2
2
3
2
2 30
2 30
23 320 1
1 20
3 20
2
x
x
x
x xx x
xx
xx
x
=
−=
−=
− −+=⇔ ⇔ ⇔ =
− −=
− +=
=
.
So sánh điều kiện ta thấy chỉ có
3
2
x =
và
2x =
thỏa mãn. Vậy phương trình có 2 nghiệm.
Câu 9 . Thầy X có
15
cuốn sách gồm
4
cuốn sách toán,
5
cuốn sách lí và
6
cuốn sách hóa. Các cuốn
sách đôi một khác nhau. Thầy X chọn ngẫu nhiên
8
cuốn sách để làm phần thưởng cho một học
sinh. Tính xác suất để số cuốn sách còn lại của thầy X có đủ
3
môn.
A.
5
.
6
B.
661
.
715
C.
660
.
713
D.
6
.
7
Lời giải
Chọn B
Chọn ra 8 cuốn sách bất kì từ 15 cuốn có :
8
15
( ) 6435nCΩ= =
(cách chọn)
Gọi A là biến cố : “7 cuốn sách còn lại có đủ 3 môn “
Khi đó
A
là biến cố : “ 7 cuốn cách còn lại không có đủ 3 môn “
Số kết quả thuận lợi của biến cố
A
là :
( )
44 53 62
4 11 5 10 6 9
. . . 486nA CC CC CC=++=
(cách)
Vậy :
(
)
486 661
() 1 () 1 1
( ) 6435 715
nA
PA PA
n
=−=− =−=
Ω
Câu 10. Cho cấp số nhân
()
n
u
có số hạng đầu
1
5u =
và công bội
2q = −
. Số hạng thứ sáu của
()
n
u
là:
A. . B. .
C. . D. .
Lời giải
Chọn D
Ta có
()
n
u
là cấp số nhân nên :
1
1
.
n
n
u uq
−
=
Với
6n
=
ta được :
5
6
5.( 2) 160u =−=−
Câu 11. Tìm tất cả các giá trị của tham số m để phương trình sau có ba nghiệm phân biệt lập thành một
cấp số nhân:
( )
32 2
7 2 6 80x x m mx− + + −=
A.
1m = −
hoặc
7m =
. B.
1m =
hoặc
7m = −
.
C.
1m =
. D.
7m = −
.
Lời giải
Chọn C
Điều kiện cần: Do phương trình có 3 nghiệm lập thành cấp số nhân, lại theo định lý Vi-et cho
phương trình bậc ba nên ta có hệ phương trình:
( ) ( ) (
123 123 13
222
12 23 13 12 23 13 12 23 13
23
13 2 123 2 2
7 75
26 26 26
,8 8 2
xxx xxx xx
xx x x xx m m xx xx xx m m xx xx xx m
xx x xxx x x
++= ++= +=


++= +⇒ ++= +⇒ ++= +


= = = =

Thế
2x =
vào phương trình ban đầu ta được
2
8 28 4( 6 ) 8 0mm− + + −=
6
320
u = −
6
160u
=
6
320
u =
6
160u
= −
1
7
m
m
=
⇔
= −
Điều kiện đủ:
-TH1: Với
1m =
thay vào ta được phương trình:
1
32
2
3
1
7 14 8 0 2
4
x
xx x x
x
=
− + −=⇔ =
=
Suy ra với
1m =
thì phương trình có 3 nghiệm
123
,,xx x
lập thành cấp số nhân.
- TH2: Với
7
m = −
thay vào ta được phương trình:
1
32
2
3
6,14
7 82 8 0 0,09
13, 2
x
xx x x
x
−
− + −=⇔ −
Ta thấy
13
0xx <
nên phương trình không thể có 3 nghiệm lập thành cấp số nhân.
Vậy
1m =
thỏa mãn.
Câu 12. Trong các phát biểu sau, phát biểu nào sai?
A. Dãy số có tất cả các số hạng bằng nhau là một cấp số nhân.
B. Một cấp số cộng có công sai dương là một dãy số dương.
C. Một cấp số cộng có công sai dương là một dãy số tăng.
D. Dãy số có tất cả các số hạng bằng nhau là một cấp số cộng.
Lời giải
Chọn B
A. “Dãy số có tất cả các số hạng bằng nhau là một cấp số nhân”. Đây là phương án đúng, CSN
đó có công bội
1q =
.
B. “Một cấp số cộng có công sai dương là một dãy số dương”. Đây là một kết luận sai vì tồn tại
dãy số có công sai d dương nhưng số hạng đầu có thể là số 0 hoặc số âm, ví dụ dãy số
{}
n
u
với
2
n
un=−+
có công sai
1d =
nhưng
1
1u = −
.
C. “Một cấp số cộng có công sai dương là một dãy số tăng”. Đây là một kết luận đúng vì
11
0
nn n n
u ud u u
++
− = >⇒ >
.
D. “Dãy số có tất cả các số hạng bằng nhau là một cấp số cộng”. Đây là một kết luận đúng vì
cấp số cộng đó có công sai
0d =
.
Câu 13. Tập nghiệm của bất phương trình
22
12 12xx x x
−− >+ −
là
A.
( ) ( )
; 3 4;−∞ − ∪ + ∞
. B.
( ) ( )
6; 2 3;4− − ∪−
. C.
( ) ( )
; 4 3;−∞ − ∪ + ∞
. D.
( )
4;3−
.
Lời giải
Chọn A
Ta có
22
12 12xx x x−− >+ −
( )
22
12 12
xx xx⇔ −− >− −−
2
12 0xx⇔ −− >
4
3
x
x
>
⇔
<−
Vậy tập nghiệm của bất phương trình đã cho là
( ) ( )
; 3 4;S = −∞ − ∪ + ∞
.
Câu 14. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình bình hành, mặt bên
SAB
là tam giác vuông tại
A
,
3SA a=
,
2SB a=
. Điểm
M
nằm trên đoạn
AD
sao cho
2AM MD=
. Gọi
( )
P
là mặt
phẳng qua
M
và song song với
(
)
SAB
. Tính diện tích thiết diện của hình chóp cắt bởi mặt
phẳng
( )
P
.
A.
2
43
3
a
. B.
2
53
6
a
. C.
2
43
9
a
. D.
2
53
18
a
.
Lời giải
Chọn D
Ta có
(
) ( )
( ) ( )
( ) ( )
//
//
P SAB
SAB SAD SA Mx SA
P SAD Mx
∩=⇒
∩=
. Gọi
{ }
Mx SD N∩=
.
( ) ( )
( ) ( )
( ) ( )
//
//
P SAB
SAB ABCD AB My AB
P ABCD My
∩=⇒
∩=
. Gọi
{ }
My BC Q∩=
.
Do
( ) ( )
( ) ( )
,
// // //
P MQ SCD CD
CD MQ Nt CD MQ
P SCD Nt
⊃⊃
⇒
∩=
. Gọi
{
}
Nt SC P∩=
.
Do
//
//
MN SA
MQ AB MN MQ
SA AB
⇒⊥
⊥
.
Thiết diện của hình chóp cắt bởi mặt phẳng
( )
P
là hình thang vuông
MNPQ
, vuông tại
,MN
.
Có
22
MQ AB SB SA a== −=
,
13
33
MN a
MN
SA
=⇒=
,
22
33
PN SN a
PN
CD SD
==⇒=
Diện tích thiết diện của hình chóp cắt bởi mặt phẳng
( )
P
là
( )
1
.
2
MNPQ
S MN NP MQ= +
=
2
1 3 2 53
2 3 3 18
a aa
a

+=


.
Câu 15. Tìm tất cả các giá trị của
a
dương sao cho giá trị nhỏ nhất của hàm số
( )
( )
22
4 4 22y f x x ax a a= = − + −+
trên đoạn
[ ]
0; 2
bằng 3.
A.
5 10a = +
. B.
53a = +
. C.
12
a = +
. D.
2
a =
.
Lời giải
Chọn A
ĐTHS là một parabol có hoành độ đỉnh là
2
a
.
+) TH1:
0 20 4
2
a
a< <⇔<<
. GTNN của hàm số trên
[ ]
0; 2
là
2 23
2
a
fa

=− +=


1
()
2
aL⇔=−
.
+) TH2:
24
2
a
a≥⇔≥
. GTNN của hàm số trên
[ ]
0; 2
là
( )
2
2 10 18 3f aa=− +=
5 10 ( / )
5 10 ( )
a tm
aL
= +
⇔
= −
.
Câu 16 . Bạn An ra vườn hái 6 bông hoa vàng và 5 bông hoa đỏ cho vào giỏ. Có bao nhiêu cách để bạn
An lấy 3 bông hoa từ giỏ đó sao cho chúng có đủ hai màu?
A.
135
. B.
462
. C.
810
. D.
90
.
Lời giải
Chọn A
Số cách lấy 3 bông hoa bất kì là
3
11
165C =
.
Số cách lấy 3 bông hoa màu vàng là
3
6
20C
=
.
Số cách lấy 3 bông hoa màu đỏ là
3
5
10C =
.
Số cách lấy 3 bông hoa có đủ hai màu là
165 20 10 135−−=
.
Câu 17. Trong các khẳng định sau đây, khẳng định nào sai?
A. Gọi
( )
PA
là xác suất của biến cố
A
, ta luôn có
( )
01PA<≤
.
B. Phép thử ngẫu nhiên là phép thử mà ta không biết được chính xác kết quả của nó nhưng ta
có thể biết được tập hợp tất cả các kết quả có thể xảy ra của phép thử.
C. Không gian mẫu là tập hợp tất cả các kết quả có thể xảy ra của phép thử.
D. Biến cố là tập con của không gian mẫu.
Lời giải
Chọn A
- Theo tính chất của xác suất ta có với mọi biến cố
A
thì
( )
01PA≤≤
nên phương án A sai.
Câu 18. Từ một tổ gồm 10 học sinh, giáo viên chủ nhiệm chọn ra 4 học sinh để dọn vệ sinh lớp trong đó
có 1 bạn lau bảng, 2 bạn quét lớp và 1 bạn kê bàn ghế. Số cách chọn là
A.
5000
. B.
2500
. C.
2520
. D.
5040
.
Lời giải
Chọn C
Mỗi cách chọn ra 4 học sinh để dọn vệ sinh lớp thỏa mãn yêu cầu bài được thực hiện như sau:
+ Chọn 1 học sinh từ 10 học sinh để lau bảng: có
1
10
C
cách.
+ Chọn 2 học sinh từ 9 học sinh còn lại để quét lớp: có
2
9
C
cách.
+ Chọn 1 học sinh từ 7 học sinh còn lại để kê bàn ghế: có
1
7
C
cách.
Theo quy tắc nhân ta có
1 21
10 9 7
. . 2520C CC=
cách để giáo viên phân công trực nhật thỏa mãn yêu
cầu bài toán.
Câu 19. Biểu thức
( )
( )
22
2 2 22m x mx+ − −+
luôn nhận giá trị dương khi và chỉ khi
A.
4m ≤
hoặc
0m ≥
. B.
40m−< <
.
C.
0
m <
hoặc
4m >
. D.
4m <−
hoặc
0m >
.
Lời giải
Chọn D
Đặt
( )
( )
( )
22
2 2 22fx m x m x=+ − −+
.
Nên
(
)
fx
là tam thức bậc hai có hệ số
0,am
>∀
.
Suy ra để
(
)
0
fx
>
với mọi giá trị
x
khi và chỉ khi
( )
( )
2
22
4
0 2 2 20 4 0
0
m
m m mm
m
<−
′
∆<⇔ − − + <⇔− − <⇔
>
.
Vậy
4
m <−
hoặc
0m >
thì biểu thức
( )
( )
22
2 2 22m x mx+ − −+
luôn nhận giá trị dương.
Câu 20. Tổng
0 1 22
2 2 ... 2
nn
nn n n
CC C C
+ + ++
bằng
A.
3
n
. B.
4
n
. C.
1
2
n+
. D.
2
n
n
C
.
Lời giải
Chọn A
Đặt
( )
0 1 22
1 ...
n
nn
nn n n
S x C xC x C x C=+ = + + ++
(với
*
n ∈
).
Thay
2x
=
vào biểu thức
S
ta được:
( )
0 1 22
2 2 ... 2 1 2 3
n
nn n
nn n n
CC C C+ + ++ =+ =
.
Vậy tổng
0 1 22
2 2 ... 2 3
nn n
nn n n
CC C C+ + ++ =
.
Câu 21. Trong không gian cho bốn điểm không đồng phẳng, có thể xác định nhiều nhất bao nhiêu mặt
phẳng phân biệt từ các điểm đó?
A.
6
. B.
4
. C.
2
. D.
3
.
Lời giải
Chọn B
Do bốn điểm không đồng phẳng nên qua ba điểm bất kỳ trong bốn điểm ta luôn xác định được duy
nhất một mặt phẳng. Vậy số mặt phẳng nhiều nhất bằng
3
4
4C =
.
Câu 22. Tính giới hạn:
22 2
11 1
lim 1 1 ... 1
23 n


−− −




.
A.
1
4
. B.
1
2
. C.
1
. D.
3
2
.
Lời giải
Chọn B
22 2
1 1 1 1111 11
lim 1 1 ... 1 lim 1 1 1 1 ... 1 1
2 3 2233
n nn

    
− − −= −+−+ −+
    

    

1324 1 1
lim ...... .
2233
nn
nn
−+

=


1 11
lim .
22
n
n
+

= =


.
Câu 23. Tính tổng vô hạn sau:
2
11 1
1 ... ...
22 2
n
S
=++ ++ +
A. 4. B.
1
1
1
2
.
1
2
1
2
n
−
−
. C. 2. D.
21
n
−
.
Lời giải
Chọn C
Ta có 1;
1
2
;
2
1
2
;…;
1
2
n
;… lập thành cấp số nhân lùi vô hạn với số hạng đầu tiên
1
1u =
và công bội
1
2
q
=
.
S
là tổng của một cấp số nhân lùi vô hạn với
1
1u =
và
1
2
q =
nên ta có
1
11
2
11
1
1
22
u
S
q
= = = =
−
−
.
Câu 24. Cho hình thang vuông
ABCD
, đường cao
2AB a=
,
AD a=
,
4
BC a=
. Gọi
I
là trung điểm
của
CD
,
J
là điểm di động trên cạnh
BC
. Tính
BJ
sao cho
AJ
và
BI
vuông góc.
A.
3
4
a
. B.
4
5
a
. C.
a
. D.
5
6
a
.
Lời giải
Chọn B
Biểu diễn
BI

theo hai vectơ
BA

và
BC

.
Ta có
BI

1
2
=
( )
BD BC+
 
11
22
BD BC
= +
 
( )
11
22
BA AD BC= ++
  
11 1
22 2
BA AD BC=++
  
1 11 1
.
2 24 2
BA BC BC=++
  
15
28
BA BC= +
 
.
• Đặt
BJ k BC=
 
. Biểu diễn
AJ

theo hai vectơ
BA

và
BC

.
Ta có
AJ BJ BA= −
  
k BC BA= −
 
.
• Do
AJ
và
BI
vuông góc nên
AJ

.
BI

0=
.
Suy ra:
(
)
15
0
28
BA BC k BC BA

+ −=


   
15 5
. . . .0
228 8
kk
BA BC BA BA BC BC BC BA⇔ −+ − =
       
22
15
0
28
k
BA BC⇔− + =
( do
BA BC⊥
nên
.0BA BC =
 
)
22
15
.4 .16 0
28
k
aa⇔− + =
1
5
k⇔=
.
Vậy
1
5
BJ BC=
 
, suy ra
14
.
55
a
BJ BC= =
Câu 25. Cho dãy số
1
1
4
nn
u
u un
+
=
= +
. Tìm số hạng thứ
5
của dãy số.
A.
16
. B.
14
. C.
12
. D.
15
.
Lời giải
Chọn B
Ta có
1
4u =
,
21
15
uu= +=
,
32
27uu= +=
,
43
3 10uu= +=
,
54
4 14uu= +=
.
Câu 26. Số nghiệm của các phương trình
2
4 5 4 17xx x− −= −
là
A.
3
. B.
1
. C.
2
. D.
4
.
Lời giải
Chọn C
2
2
2
2
2
17
4 17 0
4
4 5 4 17
4 5 4 17
8 12 0
4 5 4 17
22 0
x
x
xx x
xx x
xx
xx x
x
−≥
≥

− −= − ⇔ ⇔
− −= −

−+=

− −=− +

−=

17
4
2
6
6
22
22
22
x
x
x
x
x
x
x
≥
=
=
⇔⇔
=
=
=
= −

.
Câu 27. Từ các chữ số
0; 1; 2; 7; 8; 9
tạo được bao nhiêu số tự nhiên lẻ có
5
chữ số đôi một khác
nhau?
A.
312
. B.
600
. C.
360
. D.
288
.
Lời giải
Chọn D
Gọi số cần tìm là
n abcde=
.
( điều kiện:
{ }
, , , , 0;1;2;7;8;9 ; 0
abcde a∈≠
và
, , , , abcde
đôi một khác nhau)
Vì
n
lẻ nên
{ }
1; 7; 9e
∈
⇒
e
có
3
cách chọn.
{ } { }
1; 2; 7; 8; 9 \ae∈
⇒
a
có
4
cách chọn.
Sau khi chon
,ae
còn lại
4
chữ số. Ta lấy
3
chữ số trong
4
chữ số còn lại rồi sắp xếp có thứ tự vào
3 vị trí
, ,
bcd
ta có
3
4
A
cách sắp xếp.
Vậy ta có
3
4
3.4. 288A =
số cần tìm.
Câu 28. Dãy số nào sau đây không phải là cấp số nhân?
A.
1; 2;3;4;5
. B.
1; 2; 4;8;16
. C.
1; 1;1; 1;1−−
. D.
1; 2; 4; 8;16−−
.
Lời giải
Chọn A
Do
23
12
≠
nên dãy số trong phương án A không phải là cấp số nhân.
Các phương án B, C, D đều là cấp số nhân.
Câu 29. Cho phương trình
cos 2 2
4
xm
π

+ −=


, với
m
là tham số. Tìm tập hợp tất cả các giá trị của
m
để phương trình có nghiệm.
A.
∅
. B.
. C.
[ ]
1; 3−
. D.
[ ]
3; 1−−
.
Lời giải
Chọn D
cos 2 2
4
xm
π

+ −=


cos 2 2
4
xm
π

⇔ +=+


.
Vậy phương trình có nghiệm khi và chỉ khi
12 1
m−≤ + ≤
31m⇔− ≤ ≤−
.
Câu 30. Cho tam giác
ABC
có
0
53
60 , 10,
3
A ar
= = =
. Tính diện tích của tam giác
ABC
.
A. 50. B.
20 2
. C.
25 3
. D. 20.
Lời giải
Chọn C
Gọi
O
làm tâm đường tròn nội tiếp tam giác
ABC
.
,,
KHE
lần lượt là hình chiếu vuông góc của
O
lên các cạnh
,,
AB AC BC
. Khi đó ta có
AH AK=
,
CH CE=
,
BE BK=
.
Mặt khác ta có
AH AC CH= −
AC CE= −
( )
AC BC BE=−−
AC BC BE=−+
AC BC BK=−+
AC BC AB AK
=−+−
AC BC AB AH=−+−
b a c AH=−+−
2
bac
AH
−+
⇒=
2
abc
a
++
= −
pa
= −
.
Từ
tan
OH
OAH
AH
=
tan
OH
AH
OAH
⇒=
tan 30
r
=
°
5=
.
Mà
AH p a= −
nên ta có
5
pa−=
5pa⇔=+
15=
.
Vậy diện tích tam giác
ABC
là
S pr=
25 3.=
Câu 31. Tam giác mà ba đỉnh của nó là trung điểm ba cạnh của tam giác
ABC
được gọi là tam giác
trung bình của tam giác
ABC
.
Ta xây dựng dãy các tam giác
111
ABC
,
222
ABC
,
333
ABC
… sao cho tam giác
111
ABC
là tam giác
đều cạnh bằng
3
và với mỗi số nguyên dương
2n ≥
, tam giác
nnn
ABC
là tam giác trung bình
của tam giác
111nnn
ABC
−−−
. Với mỗi số nguyên dương
n
, kí hiệu
n
S
tương ứng là diện tích hình
tròn ngoại tiếp tam giác
nnn
ABC
. Tính tổng
12
... ...
n
SS S S= + ++ +
A.
15
4
S
π
=
. B.
4
S
π
=
. C.
9
2
S
π
=
. D.
5S
π
=
.
Lời giải
Chọn B
Tam giác
111
ABC
có bán kính đường tròn ngoại tiếp là
1
2 3. 3
.3
32
R = =
( )
2
1
1
.3
S
R
ππ
⇒= =
.
Tam giác
222
ABC
có bán kính đường tròn ngoại tiếp là
2
3
2
R =
(
)
2
21
2
11
. .3
44
SS
R
ππ
⇒= = =
.
E
K
H
O
A
C
B
Tam giác
333
ABC
có bán kính đường tròn ngoại tiếp là
3
3
4
R =
( )
2
33 2
11
. .3
16 4
SR S
ππ
⇒= = =
…………………
Tam giác
nnn
ABC
có bán kính đường tròn ngoại tiếp là
1
3
2
n
n
R
−
=
1
1
4
nn
SS
−
⇒=
.
Suy ra
S
là tổng của cấp số nhân lùi vô hạn, có
11
3uS
π
= =
, công bội
1
4
q =
.
Vậy
1
4
1
1
4
S
S
π
= =
−
.
Câu 32. Trong loạt đá luân lưu giữa đội tuyển Việt Nam và Thái Lan, ông Park Hang Seo phải lập danh
sách 5 cầu thủ từ 10 cầu thủ trên sân (trừ thủ môn) và thứ tự đá luân lưu của họ. Hỏi ông Park
có bao nhiêu cách lập danh sách biết ông sẽ để Quế Ngọc Hải là người sút phạt đầu tiên của đội
tuyển Việt Nam?
A.
126
. B.
15120
. C.
3024
. D.
30240
.
Lời giải
Chọn C
Chọn người đá đầu tiên: Có 1 cách.
Chọn 4 người còn lại: Có
4
9
3024
A =
cách.
Vậy số cách lập danh sách là:
3024
cách
Câu 33. Phát biểu nào sau đây là sai?
A.
lim
n
uC=
(
n
uC=
,
C
là hằng số ). B.
( )
lim 0 1
n
qq
= >
.
C.
1
lim 0
n
=
. D.
( )
1
lim 0 1
k
k
n
= >
.
Lời giải
Chọn B
Vì
lim 0
n
q =
nếu
1q <
Câu 34. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình bình hành,
AC
và
BD
cắt nhau tại
O
. Giao
tuyến của hai mặt phẳng
( )
SAB
và
( )
SCD
là đường thẳng
A.qua
S
và song song với
AB
. B.
AC
.
C.
SO
. D. qua
S
và song song với
BD
.
Lời giải
Chọn A
Ta có:
(
) ( )
( )
( )
( )
( )
//
S SAB SCD
AB CD
SAB SCD d
AB SAB
CD SCD
∈∩
⇒∩ =
⊂
⊂
với
d
đi qua
S
và
// //d AB CD
.
Câu 35. Cho 4 điểm
( )
( )
( )
(
)
1; 2 , 0; 3 , 3; 4 , 1; 8A BC D− −−
.
Ba điểm nào trong 4 điểm đã cho là thẳng hàng?
A.
,,ABD
. B.
,,
BCD
. C.
,,AC D
. D.
,,ABC
.
Lời giải
Chọn A
Ta có:
( ) ( )
1; 5 , 2; 10 .AB AD=−=−
 
Nhận thấy:
2
AD AB=
 
⇒
,AB AD
 
cùng phương.
Vậy ba điểm
,,ABD
thẳng hàng.
Câu 36. Cho
7
0
lim
1. 4 2
x
xa
b
xx
→

=

+ +−

(
a
b
là phân số tối giản). Tính tổng
L ab= +
.
A.
43L =
. B.
23L =
. C.
13L
=
. D.
53L =
.
Lời giải
Chọn A
Ta xét
7
0
1. 4 2
lim
x
xx
T
x
→

+ +−
=



( ) (
)
77
0
1. 4 2 2 1 1
lim
x
xx x
T
x
→

+ + − + +−

=


Ta xét
( )
( )
7
7
1
00
1 44
11
lim lim .
4
42
42
xx
xx
x
T
x
xx
→→
+ +−
+
= = =
++
++
Ta xét
( )
7
2
0
2 11
lim .
x
x
T
x
→
+−
=
Đặt
7
7
1 1.t x xt= +⇒ = −
Ta có:
0 1.xt→⇒→
Khi đó,
( )
2
7 65432
11
21
22
lim lim .
1 17
tt
t
T
t tttttt
→→
−
= = =
− ++++++
d
O
C
A
B
D
S
12
1 2 15
.
4 7 28
TTT⇒=+ =+=
Vậy
28, 15.ab= =
Do đó,
28 15 43.L ab=+= + =
Câu 37. Cho hình lập phương
.ABCD A B C D
′′′′
(hình vẽ bên dưới). Góc giữa hai đường thẳng
AC
và
AD
′
bằng
A.
45
°
. B.
30°
. C.
60°
. D.
90°
.
Lời giải
Chọn C
Ta có
// AC A C
′′
nên
( )
( )
, , 60
o
AC AD AC AD DAC
′ ′′ ′ ′′
= = =
( vì tam giác
DA C
′′
đều).
Câu 38. Thiết diện của một mặt phẳng với một tứ diện chỉ có thể là:
A. Một tứ giác hoặc một ngũ giác. B. Một tam giác và một hình bình hành.
C. Một tam giác hoặc một tứ giác. D. Một tam giác hoặc một ngũ giác.
Lời giải
Chọn C
Thiết diện của một mặt phẳng với một tứ diện là tam giác khi mặt phẳng cắt ba mặt tứ diện; và
là một tứ giác khi mặt phẳng cắt bốn mặt của tứ diện. Thiết diện không thể là ngũ giác vì ngũ
giác có năm cạnh mà tứ diện chỉ có bốn mặt.
Câu 39. Cho hình hộp
.ABCD A B C D
′′′′
. Gọi
M
là điểm trên cạnh
AC
sao cho
3AC MC=
. Lấy
N
trên
cạnh
CD
′
sao cho
CN xCD
′′
=
. Với giá trị nào của
x
thì
//
MN BD
′
.
A.
1
2
x =
. B.
1
3
x =
. C.
1
4
x =
. D.
2
3
x =
.
Lời giải
Chọn D
Gọi
I BM CD= ∩
.
Ta có
//AB CD
suy ra
1
2
MC MI
MA MB
= =
. Do đó
1
3
IM
IB
=
.
Mặt khác, ta có
//
MN BD
′
suy ra
1
3
IM IN
IB ID
= =
′
. Do đó
1
2
NI ND
ND NC
= =
′′
.
Nên
2
3
NC C D
′′
=
. Vậy
2
3
x =
.
Câu 40. Trong các mệnh đề sau, mệnh đề nào đúng?
A. Trong không gian hai đường thẳng không có điểm chung thì chéo nhau.
B. Trong không gian hai đường thẳng lần lượt nằm trên hai mặt phẳng phân biệt thì chéo nhau.
C. Trong không gian hai đường thẳng phân biệt không song song thì chéo nhau.
D. Trong không gian hai đường thẳng chéo nhau thì không có điểm chung.
Lời giải
Chọn D
Phương án A sai vì trong không gian hai đường thẳng không có điểm chung có thể song song.
Phương án B sai vì trong không gian hai đường thẳng nằm trên hai mặt phẳng phân biệt có thể song
song hoặc cắt nhau.
Phương án C sai vì trong không gian hai đường thẳng lần lượt nằm trên hai mặt phẳng phân biệt thì có
thể song song hoặc chéo nhau hoặc cắt nhau.
Phương án D đúng vì trong không gian hai đường thẳng chéo nhau thì không có điểm chung.
Câu 41. Tập hợp tất cả các giá trị của tham số
m
để phương trình

sin 1 cos 0
x xm
có đúng hai
nghiệm phân biệt trên
;
32

−


ππ
là
A.
1
0;
2




. B.
1
;1
2

. C.
1
;1
2




. D.
1
;1
2


.
Lời giải
Chọn D

sin 1
sin 1 cos 0 (*)
cos

x
x xm
xm
2( )
2
cos
=+∈
⇔
=
x kk
xm
π
π
.
Với
2( )
2
=+∈x kk
π
π
thì không có
;
32

∈−


x
ππ
.
Như vậy phương trình
*
có đúng hai nghiệm phân biệt trên
;
32

−


ππ
⇔
phương trình
cos xm
có hai nghiệm phân biệt trên
;
32

−


ππ
1
;1
2
m

⇔∈


(hình vẽ minh họa bên dưới).
Do đó
1
;1
2

∈


m
.
Câu 42. Cho hình hộp
.
′′′′
ABCD A B C D
, gọi
M
là trung điểm
CD
,
()P
là mặt phẳng đi qua
M
và song
song với
′
BD
và
′
CD
. Thiết diện của hình hộp cắt bởi mặt phẳng
()P
là hình gì?
A. Ngũ giác. B. Tứ giác. C. Tam giác. D. Lục giác.
Lời giải
Chọn A
Dựng thiết diện của hình hộp cắt bởi mặt phẳng
()P
như sau:
+ Qua M, kẻ đường thẳng d song song
′
CD
, d cắt
′
DD
tại trung điểm N của
′
DD
và d cắt
′
DC
tại P.
+ Qua P, kẻ đường thẳng song song
′
BD
, đường thẳng đó cắt
′′
BC
tại Q.
+ Qua M, kẻ đường thẳng song song
′
BD
, đường thẳng đó cắt
′
BC
tại R, QR cắt BC tại S.
+ Qua N, kẻ đường thẳng song song
′
BD
, đường thẳng đó cắt
′′
BD
tại T, QT cắt
′′
AD
tại U.
Vậy thiết diện của hình hộp cắt bởi mặt phẳng
()P
là ngũ giác MNUQS.
Câu 43. Trong các dãy số sau, dãy số nào là dãy số giảm?
A.
2
n
un=
. B.
23
1
n
n
u
n
+
=
+
. C.
3
1
n
un= −
. D.
2
n
un=
.
Lời giải
Chọn B
Ta có :
1
23 1 1
22
11 2
nn
n
uu
nn n
+
+
= =+ ⇒=+
++ +
.
Xét
( )( )
*
1
11 1
2 2 0,
2 1 12
nn
uu n
n n nn
+

− = + − + =− < ∀∈

+ + ++

*
1
,
nn
u un
+
⇔ < ∀∈
.
Vậy dãy số
( )
n
u
với
23
1
n
n
u
n
+
=
+
là dãy số giảm.
Câu 44. Cho hình chóp
.S ABC
có
2SA BC a= =
. Gọi
M
,
N
lần lượt là trung điểm của
AB
và
SC
,
3
MN a=
. Tính số đo góc giữa hai đường thẳng
SA
và
BC
.
A.
120
°
. B.
150
°
. C.
30
°
. D.
60
°
.
Lời giải
Chọn D
Ta có:
MN MA AS SN= ++
   
.
MN MB BC CN= ++
   
2MN AS BC⇒=+
  
( ) ( )
22
4 MN AS BC⇒=+
  
222
4 2.MN AS BC AS BC⇔ =++
    
( )
222
4 2. . .cos ,MN AS BC AS BC AS BC⇔ =++
 
( )
22 2
41
cos ,
2. . 2
MN AS BC
AS BC
AS BC
−−
⇔= =
 
( )
, 60AS BC
°
⇒=
 
.
Vậy
( )
, 60
AS BC
°
=
.
Câu 45. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình thang
( )
//AB CD
. Gọi
I
,
J
lần lượt là trung
điểm của các cạnh
AD
,
BC
và
G
là trọng tâm của tam giác
SAB
. Biết thiết diện của hình chóp
cắt bởi mặt phẳng
( )
IJG
là hình bình hành. Hỏi khẳng định nào sau đây đúng?
A.
1
3
AB CD=
. B.
3
2
AB CD=
. C.
3AB CD=
. D.
2
3
AB CD=
.
Lời giải
Chọn C
Vì mặt phẳng
( )
IJG
chứa
IJ
song song với
AB
,
CD
nên giao tuyến của mặt phẳng
( )
IJG
và
( )
SAB
là đường thẳng
MN
qua
G
và song song với
AB
. Vậy thiết diện của hình chóp cắt
bởi mặt phẳng
(
)
IJG
là hình thang
IJNM
.
Ta có
( )
1
2
IJ AB CD
= +
và
2
3
MN AB=
.
Điều kiện để hình thang
IJNM
là hình bình hành là
IJ MN=
.
IJ MN=
( )
21
32
AB AB CD⇔= +
11
62
AB CD⇔=
3AB CD⇔=
.
Câu 46. Cho hình chóp
.S ABCD
có đáy
ABCD
là bình hành. Đặt
SA a=

;
SB b=

;
SC c=

;
SD d=

.
Khẳng định nào sau đây đúng?
A.
ac db+= +

. B.
abcd+=+

. C.
ad bc+=+

. D.
0abcd+++ =

.
Lời giải
Chọn A
Giả sử
O
là giao điểm của hai đường chéo của hình bình hành
ABCD
.
Khi đó
O
là trung điểm của
AC
và
BD
.
Nên ta có
2
SA SC SO
+=
  
và
2
SB SD SO+=
  
.
Vậy
SA SC SB SD
+=+
   
hay
acbd
+=+

.
Câu 47. Cho hình lập phương
.
ABCD A B C D
′′′′
có cạnh bằng
a
. Gọi
O
là tâm hình vuông
ABCD
và
điểm
S
thỏa mãn
OS OA OB OC OD OA OB OC OD
′′′′
=++++ + + +
        
. Tính độ dài đoạn
OS
theo
a
.
A.
6OS a
=
. B.
4OS a=
. C.
OS a=
. D.
2OS a=
.
Lời giải
Chọn B
Gọi
O
′
là tâm của hình vuông
ABCD
′′′′
. Ta có:
DDOS OA OB OC O OA OB OC O
′′′′
=+++++ + +
        
OA OC OB OD OA OC OB OD
′′′′
=++++ + + +
       
002 2OO OO
′′
=++ +
 
4OO
′
=

.
Suy ra,
44OS OS OO a
′
= = =
 
.
Câu 48. Một công ty nhận được 50 hồ sơ xin việc của 50 người khác nhau muốn xin việc vào công ty,
trong đó có 20 người biết tiếng Anh, 17 người biết tiếng Pháp và 18 người không biết cả tiếng
Anh và tiếng Pháp. Công ty cần tuyển 5 người biết ít nhất một thứ tiếng Anh hoặc Pháp. Tính
xác suất để trong 5 người được chọn có đúng 3 người biết cả tiếng Anh và tiếng Pháp?
A.
351
201376
. B.
1
23
. C.
5
100688
. D.
1755
100688
.
Lời giải
Chọn D
Số người biết tiếng Anh hoặc tiếng Pháp là:
50 18 32−=
.
Số người biết cả tiếng Anh và tiếng Pháp là:
( )
20 17 32 5+ −=
.
Số phần tử của không gian mẫu là số cách chọn 5 người trong 32 người biết tiếng Anh hoặc
tiếng Pháp. Suy ra:
( )
5
32
nC
Ω=
.
Gọi
A
là biến cố “trong 5 người được chọn có đúng 3 người biết cả tiếng Anh và tiếng Pháp”.
Chọn 3 người biết cả tiếng Anh và tiếng Pháp: có
3
5
C
cách.
Ứng với mỗi cách chọn 3 người nói trên, có
2
27
C
cách chọn 2 người còn lại.
Suy ra,
( )
32
5 27
.nA CC=
.
Vậy xác suất của biến cố
A
là:
(
)
( )
( )
nA
pA
n
=
Ω
1755
100688
=
.
Câu 49. Giá trị lớn nhất của hàm số
1 cos 2
yx= +
bằng
A.
2
. B.
1
. C.
2
. D.
0
.
Lời giải
Chọn A
Ta có:
1 cos 2 1 1 cos 2 2 1 cos 2 2xx x−≤≤⇒+≤⇒+≤
.
Khi đó giá trị lớn nhất của hàm số
1 cos 2yx= +
bằng
2
, đạt được khi:
(
)
cos 2 1 ,
x xk kZ=⇔= ∈
π
.
Kết luận: giá trị lớn nhất của hàm số
1 cos 2yx= +
bằng
2
.
Câu 50. Một gia đình cần khoan một cái giếng để lấy nước. Họ thuê một đội khoan giếng nước. Biết giá
của mét khoan đầu tiên là
80.000
đồng, kể từ mét khoan thứ hai giá của mỗi mét khoan tăng
thêm
5.000
đồng so với giá của mét khoan trước đó. Biết cần phải khoan sâu xuống
50
m
mới
có nước. Hỏi phải trả bao nhiêu tiền để khoan cái giếng đó?
A.
4.000.000
đồng. B.
10.125.000
đồng. C.
52.500.000
đồng. D.
52.000.000
đồng.
Lời giải
Chọn B
Nhận xét: Giá tiền mỗi mét khoan là một cấp số cộng có số hạng đầu
1
80.000
u =
đồng, công
sai
5.000d =
đồng. Do đó số tiền để khoan cái giếng đó là:
(
) ( )
1 2 50 50 1
50
... 2 49 25 2*80.000 49*5000 10.125.000
2
Tu u u S u d= + ++ = = + = + =
đồng.
Kết luận:
10.125.000T =
đồng.
-------------------- HẾT --------------------
| 1/28
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GD & ĐT VĨNH PHÚC
ĐỀ THI KHẢO SÁT CHẤT LƯỢNG THPT QG LẦN 2
TRƯỜNG THPT CHUYÊN VĨNH PHÚC NĂM HỌC 2019 - 2020
(Đề thi có: 05 trang) MÔN: TOÁN KHỐI 11
Thời gian làm bài: 90 phút;
(Không kể thời gian giao đề) Mã đề thi 123
Họ, tên thí sinh:..........................................................................
Số báo danh:............................................................................... n
Câu 1: Cho khai triển ( 2 1+ x + x ) 2 2n
= a + a x + a x ++ a x n ≥ a a a a 0 1 2 2n , với
2 và 0 , 1, 2 , ..., 2nlà a a
các hệ số. Biết rằng 3 4 =
, khi đó tổng S = a + a + a ++ a bằng 14 41 0 1 2 2n A. 11 S = 3 . B. 13 S = 3 . C. 10 S = 3 . D. 12 S = 3 .
Câu 2: Cho a,b,c là các số thực đôi một khác nhau thuộc đoạn 0;2 
 . Giá trị nhỏ nhất của biểu thức 1 1 1 P = + + là : 2 2 2 (a − b) (b − c) (c − a) A. 1 . B. 4 . C. 9 D. 25 . 3 9 4 4
Câu 3: Tổng tất cả các nghiệm thuộc khoảng (0;360) của phương trình (x + °) 2 sin 45 = − 2 bằng: A. 180° . B. 0 540 C. 0 450 D. 0 90 Câu 4: Cho ( 2
lim x + ax + 5 + x = thì giá trị của a là một nghiệm của phương trình nào trong →−∞ ) 5 x các phương trình sau? A. 2
x −11x +10 = 0 B. 2
x − 5x + 6 = 0 C. 2
x − 8x +15 = 0 D. 2
x + 9x −10 = 0
Câu 5: Phương trình (m +1)sin x + cos x = 5 có nghiệm x ∈  khi và chỉ khi A. m ≥ 3 m ≥  B. 1 . C. 1 − ≤ m ≤ 3. D. 3 − ≤ m ≤1. m ≤ 1 − m ≤ 3 −
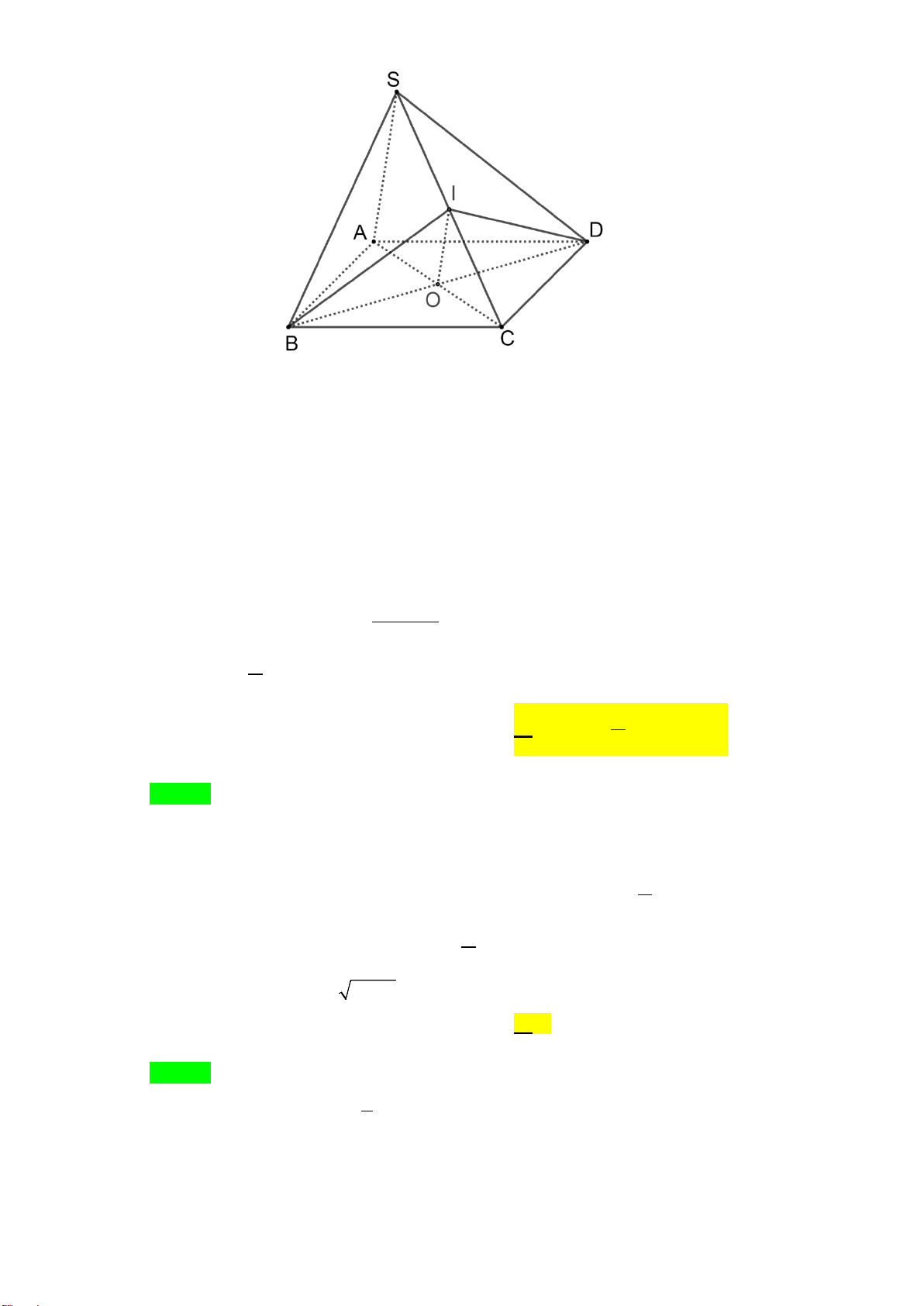
Câu 6: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O, I là trung điểm cạnh SC .
Khẳng định nào sau đây sai?
A. Đường thẳng IO song song với mặt phẳng (SAD).
B. Mặt phẳng (IBD) cắt hình chóp S.ABCD theo thiết diện là một tứ giác.
C. Đường thẳng IO song song với mặt phẳng (SAB) .
D. Giao tuyến của hai mặt phẳng (IBD) và (SAC) là IO . Câu 7: tan x
Tập xác định của hàm số y = là 2 sin x +1 π 
A. D =    + k2π ,k ∈. B. D = .   2  π 
C. D =  {kπ,k ∈ }  .
D. D =    + kπ ,k ∈.  2 
Câu 8: Số nghiệm phương trình x − ( 2 2
3 x − 3x + 2) = 0 là A. 0. B. 1. C. 2. D. 3.
Trang 1/5 - Mã đề thi 123
Câu 9: Thầy X có 15 cuốn sách gồm 4 cuốn sách toán, 5 cuốn sách lí và 6 cuốn sách hóa. Các
cuốn sách đôi một khác nhau. Thầy X chọn ngẫu nhiên 8 cuốn sách để làm phần thưởng cho một học
sinh. Tính xác suất để số cuốn sách còn lại của thầy X có đủ 3 môn. A. 5 . B. 661 . C. 660 . D. 6 . 6 715 713 7
Câu 10: Cho cấp số nhân (u có số hạng đầu u = 5 và công bội q = 2
− . Số hạng thứ sáu của (u n ) n ) 1 là: A. u = 320 − . u =160 . u = 320 . u = 160 − . 6 B. 6 C. 6 D. 6
Câu 11: Tìm tất cả các giá trị của tham số m để phương trình sau có ba nghiệm phân biệt lập thành một cấp số nhân: 3 2 x − x + ( 2 7
2 m + 6m) x −8 = 0. A. m = 1
− hoặc m = 7.
B. m = 1 hoặc m = 7 − .
C. m = 1. D. m = 7 − .
Câu 12: Trong các phát biểu sau, phát biểu nào là sai?
A. Dãy số có tất cả các số hạng bằng nhau là một cấp số nhân.
B. Một cấp số cộng có công sai dương là một dãy số dương.
C. Một cấp số cộng có công sai dương là một dãy số tăng.
D. Dãy số có tất cả các số hạng bằng nhau là một cấp số cộng.
Câu 13: Tập nghiệm của bất phương trình 2 2
x − x −12 > x +12 − x là A. ( ; −∞ 3
− ) ∪(4;+∞) B. ( 6 − ; 2 − ) ∪( 3 − ;4) C. ( ; −∞ 4
− ) ∪(3;+∞) D. ( 4; − 3)
Câu 14: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, mặt bên SAB là tam giác vuông
tại A , SA = a 3 , SB = 2a . Điểm M nằm trên đoạn AD sao cho AM = 2MD . Gọi (P) là mặt
phẳng qua M và song song với (SAB) . Tính diện tích thiết diện của hình chóp cắt bởi mặt phẳng (P). 2 4a 3 2 5a 3 2 4a 3 2 5a 3 A. . B. . C. . D. . 3 6 9 18
Câu 15: Tìm tất cả các giá trị của a dương sao cho giá trị nhỏ nhất của hàm số y = f (x) 2 = x − ax + ( 2 4 4
a − 2a + 2) trên đoạn [0;2] bằng 3. A. a = 5 + 10 B. a = 5 + 3 C. a =1+ 2 D. a = 2
Câu 16: Bạn An ra vườn hái 6 bông hoa vàng và 5 bông hoa đỏ cho vào giỏ. Có bao nhiêu cách để
bạn An lấy 3 bông hoa từ giỏ đó sao cho chúng có đủ cả hai màu? A. 135. B. 462 . C. 810 . D. 90.
Câu 17: Trong các khẳng định sau đây, khẳng định nào sai?
A. Gọi P( A) là xác suất của biến cố A ta luôn có 0 < P( A) ≤1.
B. Phép thử ngẫu nhiên là phép thử mà ta không biết được chính xác kết quả của nó nhưng ta có
thể biết được tập hợp tất cả các kết quả có thể xảy ra của phép thử.
C. Không gian mẫu là tập hợp tất cả các kết quả có thể xảy ra của phép thử.
D. Biến cố là tập con của không gian mẫu.
Câu 18: Từ một tổ gồm 10 học sinh, giáo viên chủ nhiệm chọn ra 4 học sinh để dọn vệ sinh lớp trong
đó có 1 bạn lau bảng, 2 bạn quét lớp và 1 bạn kê bàn ghế. Số cách chọn là A. 5000. B. 2500. C. 2520. D. 5040.
Câu 19: Biểu thức ( 2 m + ) 2
2 x − 2(m − 2) x + 2 luôn nhận giá trị dương khi và chỉ khi: A. m ≤ 4 − hoặc m ≥ 0. B. 4 − < m < 0 .
Trang 2/5 - Mã đề thi 123
C. m < 0 hoặc m > 4 D. m < 4 − hoặc m > 0. Câu 20: Tổng 0 1 2 2
C + 2C + 2 C +...+ 2n n C n n n n bằng: A. 3n B. 4n C. 1 2n+ D. n C2n
Câu 21: Trong không gian cho bốn điểm không đồng phẳng, có thể xác định nhiều nhất bao nhiêu
mặt phẳng phân biệt từ các điểm đó? A. 6 . B. 4 . C. 2 . D. 3 . Câu 22:      Tính giới hạn: 1 1 1
lim  1− 1− ...1−  . 2 2 2  2 3 n       A. 1 . B. 1 . C. 1. D. 3 . 4 2 2 1 1 1
Câu 23: Tính tổng vô hạn sau: S =1+ + +...+ +... 2 2 2 2n . 1 −1 1 n A. 4 . B. 2 . . C. 2 . D. 2n −1. 2 1 −1 2
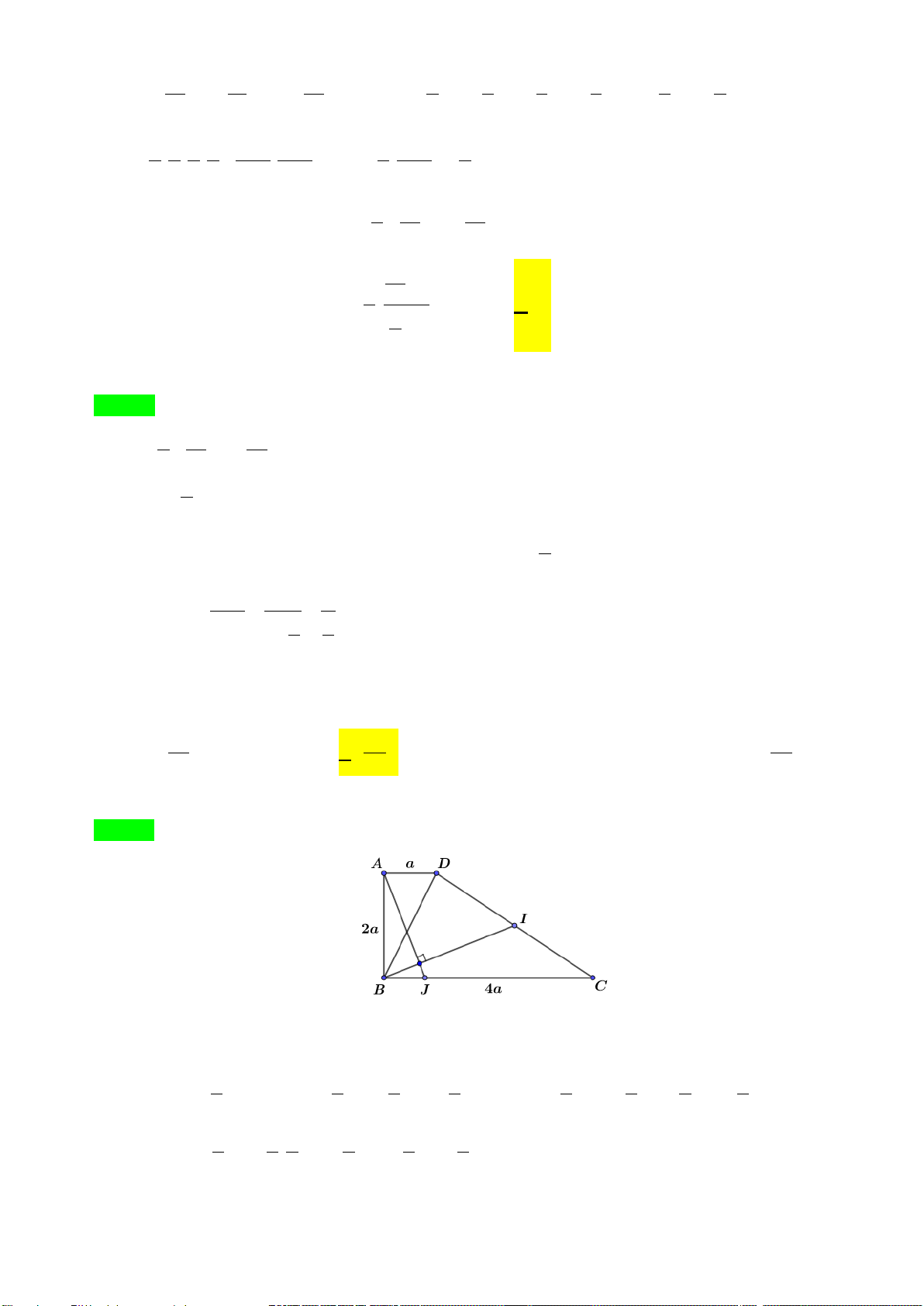
Câu 24: Cho hình thang vuông ABCD , đường cao AB = 2a, AD = a, BC = 4a . Gọi I là trung điểm
CD, J là điểm di động trên cạnh BC. Tính BJ sao cho AJ và BI vuông góc với nhau. A. 3 a . B. 4 a . C. a . D. 5 a . 4 5 6 u  = 4
Câu 25: Cho dãy số 1 u
. Tìm số hạng thứ 5 của dãy số. = +  + u n n 1 n A. 16 . B. 14. C. 12. D. 15.
Câu 26: Số nghiệm của các phương trình 2
x − 4x − 5 = 4x −17 là: A. 3 B. 1 C. 2 D. 4
Câu 27: Từ các chữ số 0,1,2,7,8,9 tạo được bao nhiêu số tự nhiên lẻ có 5 chữ số đôi một khác nhau? A. 312. B. 600 . C. 360. D. 288 .
Câu 28: Dãy số nào sau đây không phải là cấp số nhân? A. 1; 2; 3; 4; 5. B. 1; 2; 4; 8; 16 .
C. 1; −1; 1; −1; 1.
D. 1; − 2; 4; −8; 16 .  π 
Câu 29: Cho phương trình cos 2x + − m =  
2 với m là tham số. Tìm tập hợp tất cả các giá trị của  4 
m để phương trình có nghiệm. A. . ∅ B. .  C. [ 1; − 3]. D. [ 3 − ; 1] − .
Câu 30: Cho tam giác ABC có  0 5 3
A  60 ,a  10,r  3 . Tính diện tích của tam giác ABC. A. 50. B. 20 2 . C. 25 3 . D. 20 .
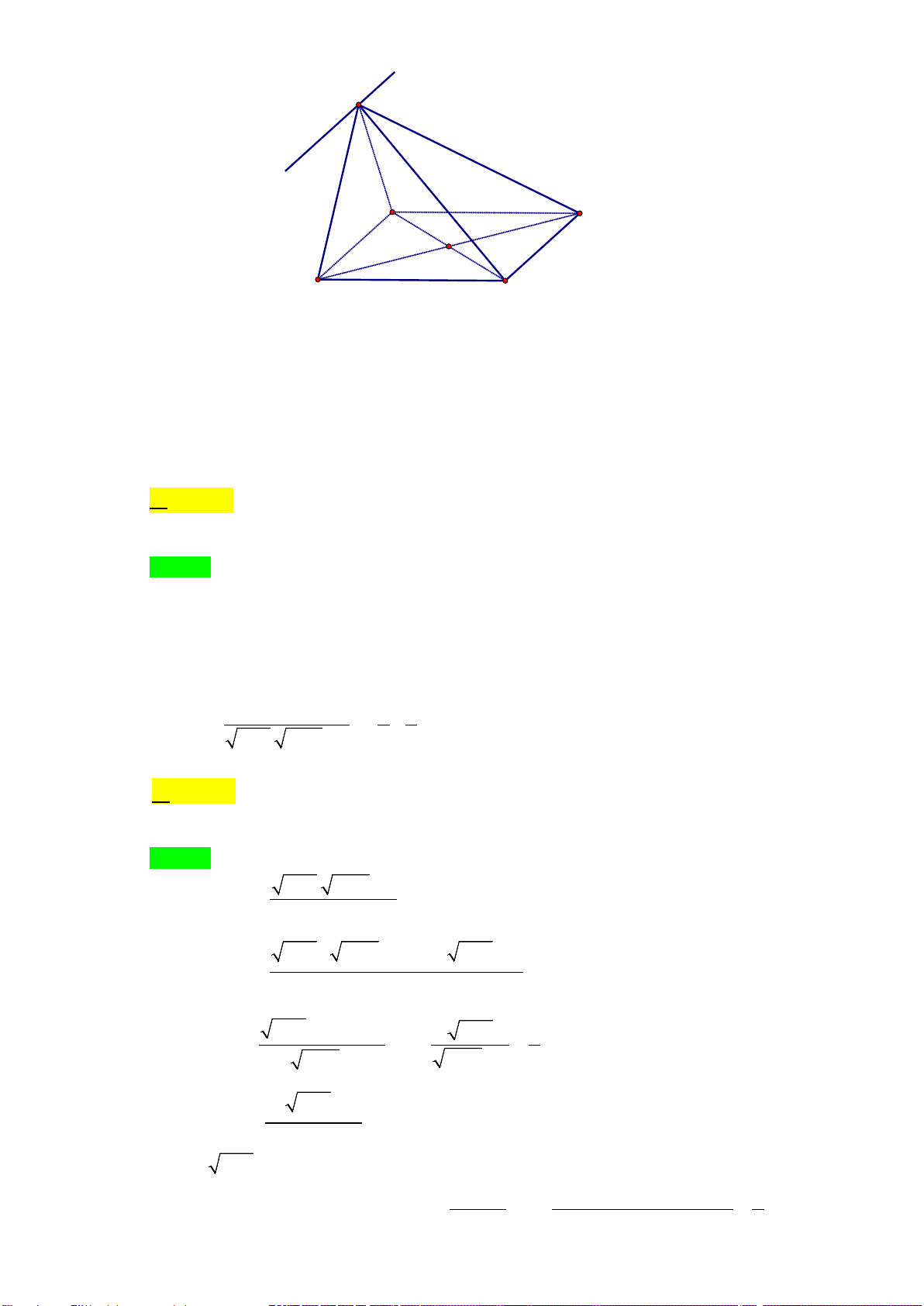
Câu 31: Tam giác mà ba đỉnh của nó là ba trung điểm ba cạnh của tam giác ABC được gọi là tam
giác trung bình của tam giác ABC .
Ta xây dựng dãy các tam giác A B C , A B C , A B C ,... sao cho A B C là một tam giác đều cạnh 1 1 1 2 2 2 3 3 3 1 1 1
bằng 3 và với mỗi số nguyên dương n ≥ 2 , tam giác A B C là tam giác trung bình của tam giác n n n A
. Với mỗi số nguyên dương n , kí hiệu S tương ứng là diện tích hình tròn ngoại tiếp tam − B − C
n 1 n 1 n 1 − n
giác A B C . Tính tổng S = S + S +...+ S + ? n ... n n n 1 2
Trang 3/5 - Mã đề thi 123 A. 15π π S = . B. S = 4π. C. 9 S = . D. S = 5π. 4 2
Câu 32: Trong loạt đá luân lưu giữa đội tuyển Việt Nam và Thái Lan, ông Park Hang Seo phải lập
danh sách 5 cầu thủ từ 10 cầu thủ trên sân (trừ thủ môn) và thứ tự đá luân lưu của họ. Hỏi ông Park có
bao nhiêu cách lập danh sách biết ông sẽ để Quế Ngọc Hải là người sút phạt đầu tiên của đội Việt Nam? A. 126. B. 15120. C. 3024. D. 30240.
Câu 33: Phát biểu nào sau đây là sai ?
A. limu = c u = c n q = n ( n là hằng số ). B. lim 0 ( q > ) 1 . C. 1 lim = 0 . D. 1 lim = 0 (k > ) 1 . n k n
Câu 34: Cho hình chóp tứ giác (SABCD) , đáy là hình bình hành, AC và BD cắt nhau tại O. Giao
tuyến của hai mặt phẳng (SAB) và (SCD) là đường thẳng:
A. qua S và song song với AB B. AC C. SO
D. qua S và song song với BD
Câu 35: Cho 4 điểm A(1; 2
− ), B(0;3),C ( 3 − ;4), D( 1;
− 8) . Ba điểm nào trong 4 điểm đã cho là thẳng hàng? A. , A B, D .
B. B,C, D . C. , A C, D . D. , A B,C . Câu 36: a Cho lim xa =  
( là phân số tối giản). Tính tổng L = a + b . x→0 7
x +1. x + 4 − 2  b b A. L = 43 . B. L = 23 . C. L =13. D. L = 53.
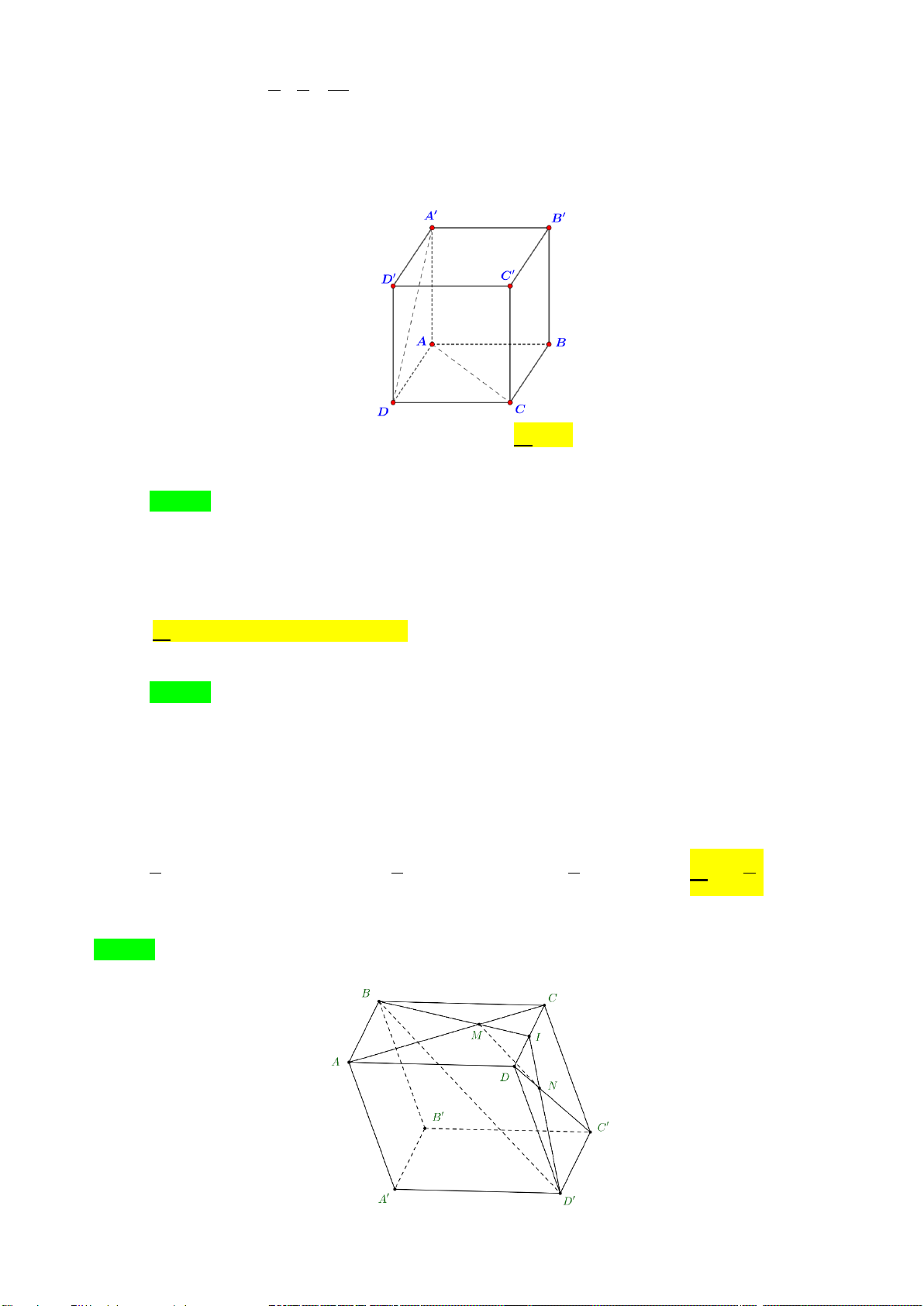
Câu 37: Cho hình lập phương ABC . D A′B C ′ D
′ ′ (hình vẽ bên dưới). Góc giữa hai đường thẳng AC
và A′D bằng A. 45°. B. 30° . C. 60°. D. 90° .
Câu 38: Thiết diện của một mặt phẳng với một tứ diện chỉ có thể là:
A. Một tứ giác hoặc một ngũ giác.
B. Một tam giác và một hình bình hành.
C. Một tam giác hoặc một tứ giác.
D. Một tam giác hoặc một ngũ giác.
Câu 39: Cho hình hộp ABC . D A′B C ′ D
′ ′ . Gọi M là điểm trên cạnh AC sao cho AC = 3MC .
Lấy N trên cạnh C D ′ sao cho C N ′ = xC D
′ . Với giá trị nào của x thì MN // BD′. A. 1 x = . B. 1 x = . C. 1 x = . D. 2 x = . 2 3 4 3
Câu 40: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Trong không gian hai đường thẳng không có điểm chung thì chéo nhau.
B. Trong không gian hai đường thẳng lần lượt nằm trên hai mặt phẳng phân biệt thì chéo nhau.
C. Trong không gian hai đường thẳng phân biệt không song song thì chéo nhau.
D. Trong không gian hai đường chéo nhau thì không có điểm chung.
Trang 4/5 - Mã đề thi 123
Câu 41: Tập hợp tất cả các giá trị của tham số m để phương trình (sin x − )
1 (cos x − m) = 0 có đúng  π π 
2 nghiệm phân biệt trên −  ; là: 3 2     1 1  1   1  A. 0;  B. ;1 C. ;1 D.  ;1 2      2  2     2 
Câu 42: Cho hình hộp ABC . D A′B C ′ D
′ ′ , gọi M là trung điểm CD, (P) là mặt phẳng đi qua M và song song với B D
′ và CD′. Thiết diện của hình hộp cắt bởi mặt phẳng (P) là hình gì? A. Ngũ giác. B. Tứ giác. C. Tam giác. D. Lục giác.
Câu 43: Trong các dãy số sau, dãy số nào là dãy số giảm? 2n +1 A. u = n u = n − = n 2 . B. u = u n n C. 3 n 1. D. 2 . n −1 n
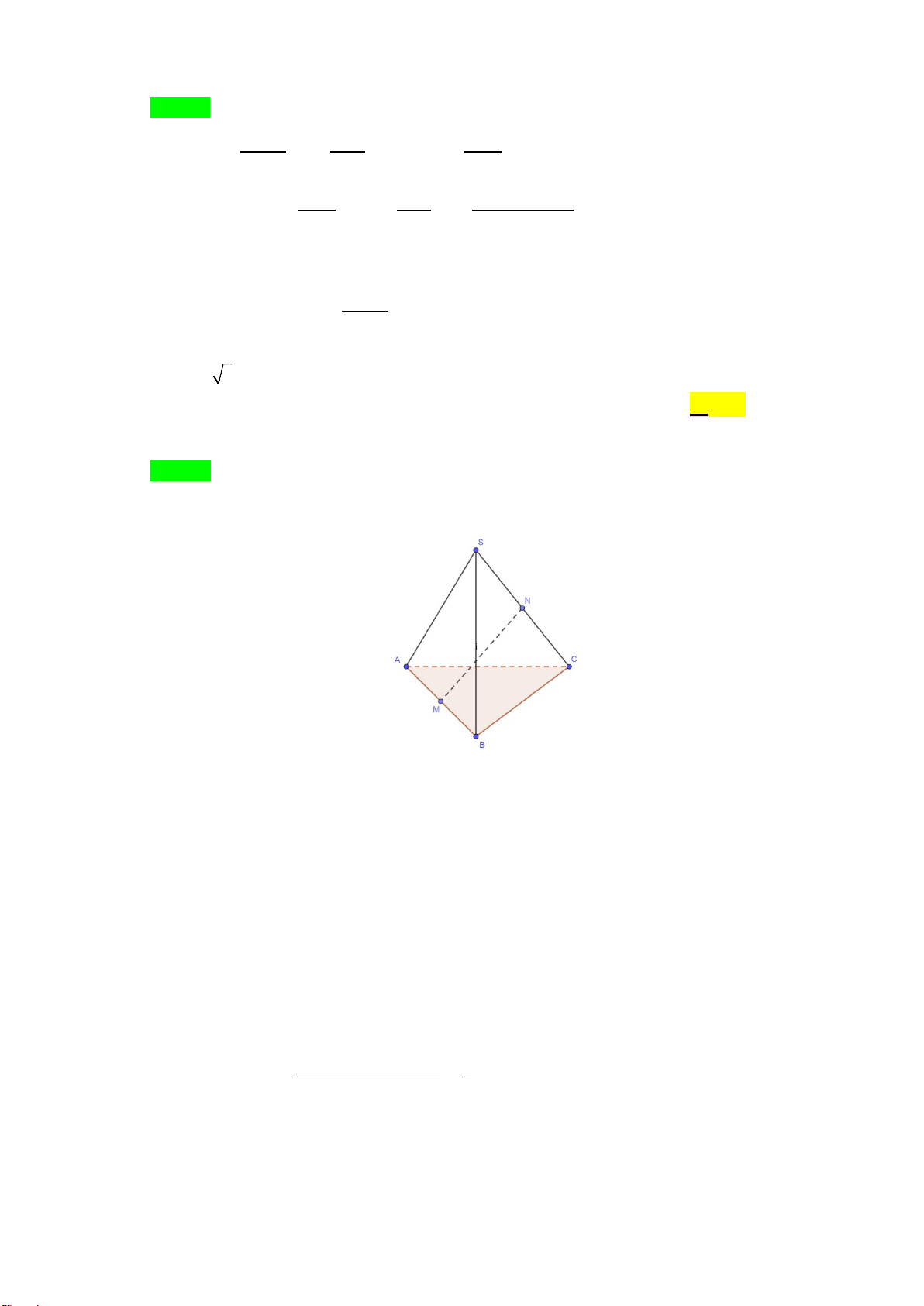
Câu 44: Cho hình chóp S.ABC có SA = BC = 2a . Gọi M , N lần lượt là trung điểm của AB , và
SC , MN = a 3 . Tính số đo góc giữa hai đường thẳng SA và BC . A. 120° . B. 150° . C. 30° . D. 60°.
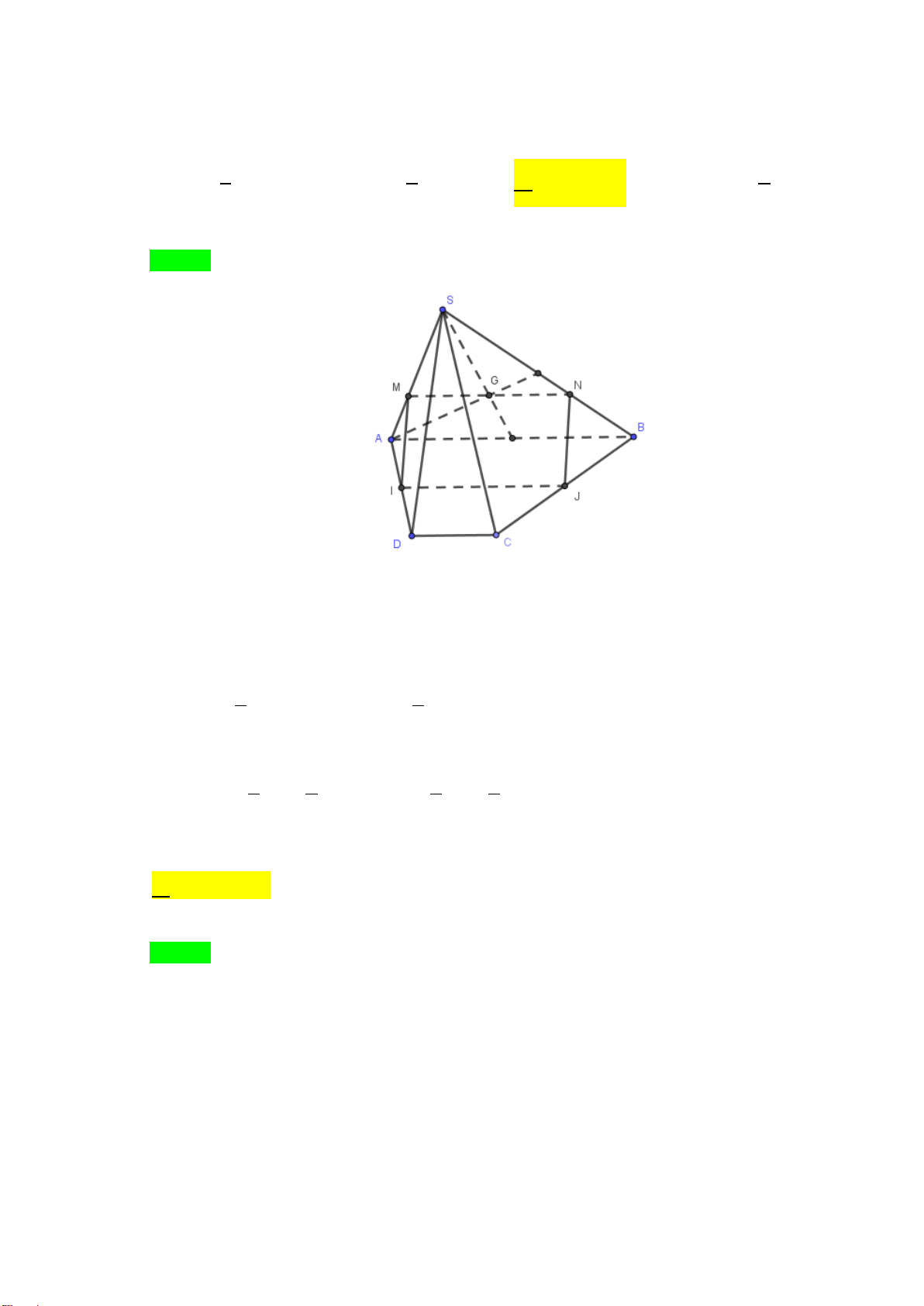
Câu 45: Cho hình chóp S.ABCD có đáy ABCD là hình thang ( AB / /CD) . Gọi I, J lần lượt là trung
điểm của các cạnh AD, BC và G là trọng tâm tam giác SAB . Biết thiết diện của hình chóp cắt bởi mặt
phẳng (IJG) là hình bình hành. Hỏi khẳng định nào sao đây đúng? A. 1 AB = CD B. 3 AB = CD
C. AB = 3CD D. 2 AB = CD 3 2 3   
Câu 46: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Đặt SA = a ; SB = b ;   
SC = c ; SD = d . Khẳng định nào sau đây đúng?                 
A. a + c = d + b .
B. a + b = c + d .
C. a + d = b + c .
D. a + b + c + d = 0 .
Câu 47: Cho hình lập phương ABC . D A′B C ′ D
′ ′ có cạnh bằng a . Gọi O là tâm hình vuông ABCD
        
và điểm S thỏa mãn OS = OA + OB + OC + OD + OA′ + OB′ + OC′ + OD′ . Tính độ dài đoạn OS theo
a . A. OS =6a.
B. OS = 4a .
C. OS = a .
D. OS = 2a .
Câu 48: Một công ty nhận được 50 hồ sơ xin việc của 50 người khác nhau muốn xin việc vào công
ty, trong đó có 20 người biết tiếng Anh, 17 người biết tiếng Pháp và 18 người không biết cả tiếng
Anh và tiếng Pháp. Công ty cần tuyển 5 người biết ít nhất một thứ tiếng Anh hoặc Pháp. Tính xác
suất để trong 5 người được chọn có đúng 3 người biết cả tiếng Anh và tiếng Pháp? 351 1 5 1755 A. . B. . C. . D. . 201376 23 100688 100688
Câu 49: Giá trị lớn nhất của hàm số y = 1+ cos 2x bằng A. 2. B. 1. C. 2. D. 0.
Câu 50: Một gia đình cần khoan một cái giếng để lấy nước. Họ thuê một đội khoan giếng nước. Biết
giá của mét khoan đầu tiên là 80.000 đồng, kể từ mét khoan thứ hai giá của mỗi mét khoan tăng thêm
5.000 đồng so với giá của mét khoan trước đó. Biết cần phải khoan sâu xuống 50 m mới có nước. Hỏi
phải trả bao nhiêu tiền để khoan cái giếng đó? A. 4.000.000 đồng. B. 10.125.000 đồng. C. 52.500.000 đồng. D. 52.000.000 đồng.
----------------------------------------------- ----------- HẾT ----------
Trang 5/5 - Mã đề thi 123 mamon made cautron dapan TOAN 11 123 1 C TOAN 11 123 2 C TOAN 11 123 3 C TOAN 11 123 4 D TOAN 11 123 5 B TOAN 11 123 6 B TOAN 11 123 7 D TOAN 11 123 8 C TOAN 11 123 9 B TOAN 11 123 10 D TOAN 11 123 11 B TOAN 11 123 12 B TOAN 11 123 13 A TOAN 11 123 14 D TOAN 11 123 15 A TOAN 11 123 16 A TOAN 11 123 17 A TOAN 11 123 18 C TOAN 11 123 19 D TOAN 11 123 20 A TOAN 11 123 21 B TOAN 11 123 22 B TOAN 11 123 23 C TOAN 11 123 24 B TOAN 11 123 25 B TOAN 11 123 26 C TOAN 11 123 27 D TOAN 11 123 28 A TOAN 11 123 29 D TOAN 11 123 30 C TOAN 11 123 31 B TOAN 11 123 32 C TOAN 11 123 33 B TOAN 11 123 34 A TOAN 11 123 35 A TOAN 11 123 36 A TOAN 11 123 37 C TOAN 11 123 38 C TOAN 11 123 39 D TOAN 11 123 40 D TOAN 11 123 41 D TOAN 11 123 42 A TOAN 11 123 43 B TOAN 11 123 44 D TOAN 11 123 45 C TOAN 11 123 46 A TOAN 11 123 47 B TOAN 11 123 48 D TOAN 11 123 49 A TOAN 11 123 50 B
HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1. Cho khai triển ( 2
1+ x + x )n 2 2n
= a + a x + a x ++ a x n ≥ a a a a 0 1 2 2n , với
2 và 0 , 1, 2 , ..., 2n là các a a hệ số. Biết rằng 3 4 =
, khi đó tổng S = a + a + a ++ a bằng 14 41 0 1 2 2n A. 11 S = 3 . B. 13 S = 3 . C. 10 S = 3 . D. 12 S = 3 . Lời giải Chọn C Đặt = ( 2 ( ) 1+ + )n f x x x . Khi đó: n n n f (x) = ( 2
1+ x + x )n = ( 2
x + x + )n k 2 k n−k k 2
1 = ∑C (x + x ) .1 = ∑C (x + x )k k k
= ∑C x (x +1)k = n n n k =0 k =0 k =0 n k n k n k k k i i   k k i i   k i k i
= ∑C x ∑C x = ∑ ∑C x C x = ∑ ∑C C x + nk   n k   n k . k=0  i=0  k=0  i=0  k=0  i=0  Số hạng của 3
x tương ứng với:  k + i = 3 
0 ≤ k ≤ n ⇒ (k,i)∈{(3;0),(2;1 } ) .  0 ≤ i ≤  k Do đó 3 0 2 1 3 2
a = C C + C C = C + C . n n n 2 3 3 2 n Số hạng của 4
x tương ứng với:  k + i = 4 
0 ≤ k ≤ n ⇒ (k,i)∈{(4;0),(3;1),(2;2 } ) .  0 ≤ i ≤  k Do đó 4 0 3 1 2 2 4 3 2
a = C C + C C + C C = C + C + C . n n n n 3 4 4 3 2 n n Theo bài ra: a a 3 4 = nên: 14 41 3 2 4 3 2 C + C C + C + C n 2 n n 3 n n 3 2 4 3 2 =
⇔ 41C + C = C + C + C n
82 n 14 n 42 n 14 14 41 n 4 3 2  7 n 2 14C C C n n n n −  ⇔ + − = ⇔ − − − + − = n n 68 n 0 ( 1) ( 3)( 2) 34 0 12 6    2
⇔ (n −1)n(7n − 33n − 370) = 0 ⇒ n =10 (do n ≥ 2,n∈) Khi đó tổng 10
S = a + a + a ++ a = f = . n (1) 3 0 1 2 2
Câu 2. Cho a,b,c là các số thực đôi một khác nhau thuộc đoạn 0; 2 
 . Giá trị nhỏ nhất của biểu thức 1 1 1 P = + + là : 2 2 2 (a − b) (b − c) (c − a) 1 4 9 25 A. . B. . C. . D. . 3 9 4 4 Lời giải Chọn C
Bài toán này ta sử dụng hai bất đẳng thức: 2 2 2 (x y) x y + + ≥
(1) . Dấu bằng xẩy ra khi x = y . 2 1 1 4 + ≥ x
∀ , y > 0 (2) . Dấu bằng xẩy ra khi x = y . x y x + y
Không mất tính tổng quát ta giả sử 0 ≤ c < b < a ≤ 2. Khi đó: 2 2 2 2
(a − c) ≤ a , (b − c) ≤ b . 1 1 1 1 1 1 P = + + ≥ + + . 2 2 2 2 2 2 (a − b) (b − c) (c − a) (a − b) a b 2  1 1  +   Áp dụng (1) ta có: 1
1  a −b b  + ≥ . 2 2 (a − b) b 2 2 2  1 1   4  +    
Áp dụng bất đẳng thức (2) ta có:  a − b b
a − b + b  8 ≥ = . 2 2 2 a Do đó: 2  1 1  +   1 1 1 1 1
1  a −b b  1 8 1 9 9 P = + + ≥ + + ≥ + ≥ + = ≥ . 2 2 2 2 2 2 2 2 2 2 (a − b) (b − c) (c − a) (a − b) a b 2 a a a a 4
a − b = b
Vậy GTNN của P là 9 . Dấu bằng xẩy ra khi  c = 0 ⇔ a = 2,b =1,c = 0 và các hoán vị của 4  a =  2 nó.
Câu 3. Tổng tất cả các nghiệm thuộc khoảng (0 ;°360°) của phương trình (x + °) 2 sin 45 = − bằng 2 A. 180°. B. 540° . C. 450°. D. 90° . Lời giải Chọn C x + 45° = 45 − ° + k360° Ta có: (x + °) 2 sin 45 = −
⇔ sin (x + 45°) = sin ( 45 − °) ⇔ 2 
x + 45° = 180° + 45° + k360° x = 90 − ° + k360° ⇔ ,(k ∈  ).
x = 180° + k360° • Với x = 90
− ° + k360° , k ∈ 1 5 0° < 90
− ° + k360° < 360°  < k <
So điều kiện x ∈(0 ;°360°) ⇒  ⇔ 4 4 ⇔ k ∈{ } 1 k ∈ k ∈ ⇒ x = 270° .
• Với x =180° + k360° , k ∈  1 1
0° <180° + k360° < 360° − < k <
So điều kiện x ∈(0 ;°360°) ⇒  ⇔  2 2 ⇔ k ∈{ } 0 k ∈ k ∈ ⇒ x =180° .
Vậy tổng tất cả các nghiệm thuộc khoảng (0 ;°360°) của phương trình là 270° +180° = 450° . Câu 4. Cho ( 2 lim
x + ax + 5 + x = thì giá trị của a là một nghiệm của phương trình nào trong các →−∞ ) 5 x phương trình sau? A. 2
x −11x +10 = 0 . B. 2
x − 5x + 6 = 0 . C. 2
x −8x +15 = 0 . D. 2
x + 9x −10 = 0 . Lời giải Chọn D 5 a + Ta có: ( 2 lim +
x + ax + 5 + x = ax 5 ⇔ lim = 5 ⇔ lim x = 5 →−∞ ) 5 x x→−∞ 2
x + ax + 5 − x x→−∞ a 5 − 1+ + −1 2 x x a ⇔ = 5 ⇔ a = 10 − . 2 − Ta thấy a = 10
− là nghiệm của phương trình 2x +9x −10 = 0 . Do đó, chọn đáp án D.
Câu 5. Phương trình (m +1)sin x + cos x = 5 có nghiệm x ∈  khi và chỉ khi A. m ≥ 3 m ≥  . B. 1 . C. 1 − ≤ m ≤ 3. D. 3 − ≤ m ≤1. m ≤ 1 − m ≤ 3 − Lời giải Chọn B
Phương trình (m +1)sin x + cos x = 5 có nghiệm x ∈  khi và chỉ khi (m + ) + ≥ ( )2 2 1 1 5 m ≥1 2
⇔ m + 2m − 3 ≥ 0 ⇔  . m ≤ 3 −
Câu 6. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O , I là trung điểm cạnh SC .
Khẳng định nào sau đây sai?
A. Đường thẳng IO song song với mặt phẳng (SAD).
B. Mặt phẳng (IBD) cắt hình chóp S.ABCD theo thiết diện là một tứ giác.
C. Đường thẳng IO song song với mặt phẳng (SAB) .
D. Giao tuyến của hai mặt phẳng (IBD) và (SAC) là IO . Lời giải Chọn B . IO // SA A Đúng vì  ⇒ . SA ⊂ 
(SAD) IO //(SAD) IO // SA C Đúng vì  ⇒ . SA ⊂ 
(SAB) IO //(SAB)
I ∈(IBD)∩(SAC) D Đúng vì 
⇒ (IBD) ∩(SAC) .  ∈  ( )∩( ) = IO O IBD SAC
B sai vì mặt phẳng (IBD) cắt hình chóp S.ABCD theo thiết diện là tam giác IBD .
Câu 7. Tập xác định của hàm số tan x y = là 2 sin x +1 A. π D   k2π ,k  = + ∈ . B. D =  . 2    C. D = π
 {kπ ,k ∈ }  . D. D   kπ ,k  = + ∈ . 2    Lời giải Chọn D 2 s  in x +1 ≠ 0 Điều kiện:  (*) cos x ≠ 0 Vì 1 − ≤ sin x ≤1 2 π
⇒1≤ sin x +1≤ 2 nên ⇔ (*)
cos x ≠ 0 ⇔ x ≠ + kπ ,k ∈ . 2
Vậy tập xác định của hàm số là π D   kπ ,k  = + ∈ . 2   
Câu 8. Số nghiệm phương trình x − ( 2 2
3 x − 3x + 2) = 0 là A. 0. B. 1. C. 2. D. 3. Lời giải Chọn C Điều kiện: 3
2x − 3 ≥ 0 ⇔ x ≥ . 2  3 x =  2  2x −3 = 0 2x − 3 = 0  Khi đó 2x − 3 ( 2
x − 3x + 2) = 0 ⇔  ⇔  ⇔ x =1 . 2
x −3x + 2 = 0 ( x − ) 1 (x − 2) = 0 x = 2  
So sánh điều kiện ta thấy chỉ có 3
x = và x = 2 thỏa mãn. Vậy phương trình có 2 nghiệm. 2
Câu 9 . Thầy X có 15 cuốn sách gồm 4 cuốn sách toán, 5 cuốn sách lí và 6 cuốn sách hóa. Các cuốn
sách đôi một khác nhau. Thầy X chọn ngẫu nhiên 8 cuốn sách để làm phần thưởng cho một học
sinh. Tính xác suất để số cuốn sách còn lại của thầy X có đủ 3 môn. A. 5 . B. 661. C. 660 . D. 6 . 6 715 713 7 Lời giải Chọn B
Chọn ra 8 cuốn sách bất kì từ 15 cuốn có : 8
n(Ω) = C = 6435(cách chọn) 15
Gọi A là biến cố : “7 cuốn sách còn lại có đủ 3 môn “
Khi đó A là biến cố : “ 7 cuốn cách còn lại không có đủ 3 môn “
Số kết quả thuận lợi của biến cố A là : n( A) 4 4 5 3 6 2
= C .C + C .C + C .C = 486 (cách) 4 11 5 10 6 9 n( A) Vậy : 486 661 P( ) A =1− P( ) A =1− = 1− = n(Ω) 6435 715
Câu 10. Cho cấp số nhân (u có số hạng đầu u = 5 và công bội q = 2
− . Số hạng thứ sáu của (u n ) n ) 1 là: A. u = 320 − u =160 6 . B. 6 . C. u = 320 u = 160 − 6 . D. 6 . Lời giải Chọn D
Ta có (u là cấp số nhân nên : 1 n ) u u . n q − = n 1
Với n = 6 ta được : 5 u = 5.( 2) − = 160 − 6
Câu 11. Tìm tất cả các giá trị của tham số m để phương trình sau có ba nghiệm phân biệt lập thành một cấp số nhân: 3 2 x − x + ( 2 7
2 m + 6m) x −8 = 0 A. m = 1 − hoặc m = 7 .
B. m =1 hoặc m = 7 − . C. m =1. D. m = 7 − . Lời giải Chọn C
Điều kiện cần: Do phương trình có 3 nghiệm lập thành cấp số nhân, lại theo định lý Vi-et cho
phương trình bậc ba nên ta có hệ phương trình: 
x + x + x = 7 
x + x + x = 7  x + x = 5 1 2 3 1 2 3 1 3   
x x + x x + x x = 2( 2
m + 6m) ⇒ x x + x x + x x = 2( 2
m + 6m) ⇒ x x + x x + x x = 2( 2 m + 6 1 2 2 3 1 3 1 2 2 3 1 3 1 2 2 3 1 3  2  3  x x x , x x x 8 x 8  = = = x =   2 1 3 2 1 2 3 2 2
Thế x = 2 vào phương trình ban đầu ta được 2
8 − 28 + 4(m + 6m) − 8 = 0 m = 1 ⇔  m = 7 − Điều kiện đủ:  x =1 1
-TH1: Với m =1 thay vào ta được phương trình: 3 2
x 7x 14x 8 0  − + − = ⇔ x = 2 2  x =  4 3
Suy ra với m =1 thì phương trình có 3 nghiệm x , x , x lập thành cấp số nhân. 1 2 3  x  6, − 14 1 - TH2: Với m = 7
− thay vào ta được phương trình: 3 2
x 7x 82x 8 0  − + − = ⇔ x  0 − ,09 2   x 13,2 3
Ta thấy x x < 0 nên phương trình không thể có 3 nghiệm lập thành cấp số nhân. 1 3
Vậy m =1 thỏa mãn.
Câu 12. Trong các phát biểu sau, phát biểu nào sai?
A. Dãy số có tất cả các số hạng bằng nhau là một cấp số nhân.
B. Một cấp số cộng có công sai dương là một dãy số dương.
C. Một cấp số cộng có công sai dương là một dãy số tăng.
D. Dãy số có tất cả các số hạng bằng nhau là một cấp số cộng. Lời giải Chọn B
A. “Dãy số có tất cả các số hạng bằng nhau là một cấp số nhân”. Đây là phương án đúng, CSN
đó có công bội q =1.
B. “Một cấp số cộng có công sai dương là một dãy số dương”. Đây là một kết luận sai vì tồn tại
dãy số có công sai d dương nhưng số hạng đầu có thể là số 0 hoặc số âm, ví dụ dãy số {u với n}
u = − + n có công sai d =1 nhưng u = 1 − . n 2 1
C. “Một cấp số cộng có công sai dương là một dãy số tăng”. Đây là một kết luận đúng vì u − = > ⇒ > . + u d u + u n n 0 1 n 1 n
D. “Dãy số có tất cả các số hạng bằng nhau là một cấp số cộng”. Đây là một kết luận đúng vì
cấp số cộng đó có công sai d = 0 .
Câu 13. Tập nghiệm của bất phương trình 2 2
x − x −12 > x +12 − x là
A. (−∞;−3) ∪(4;+ ∞) . B. ( 6 − ;− 2) ∪( 3;
− 4). C. (−∞;− 4) ∪(3;+ ∞) . D. ( 4; − 3). Lời giải Chọn A Ta có 2 2
x − x −12 > x +12 − x 2 ⇔ x − x − > −( 2 12 x − x −12) 2
⇔ x − x −12 > 0 x > 4 ⇔  x < 3 −
Vậy tập nghiệm của bất phương trình đã cho là S = (−∞;−3) ∪(4;+ ∞) .
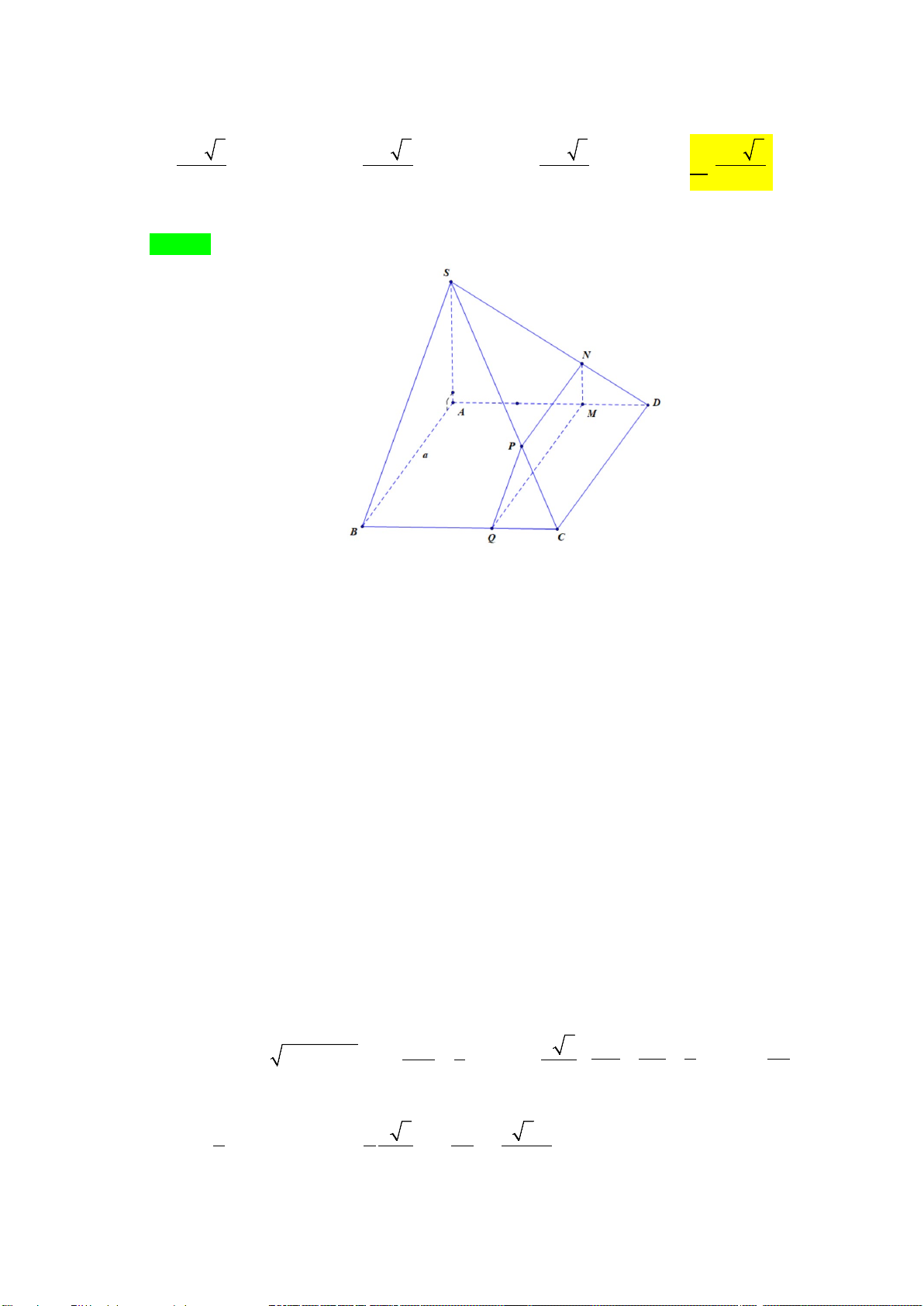
Câu 14. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, mặt bên SAB là tam giác vuông tại
A , SA = a 3 , SB = 2a . Điểm M nằm trên đoạn AD sao cho AM = 2MD . Gọi (P) là mặt
phẳng qua M và song song với (SAB) . Tính diện tích thiết diện của hình chóp cắt bởi mặt phẳng (P) . 2 4a 3 2 5a 3 2 4a 3 2 5a 3 A. . B. . C. . D. . 3 6 9 18 Lời giải Chọn D (  P) // (SAB)  Ta có (
SAB) ∩ (SAD) = SA ⇒ Mx // SA . Gọi Mx ∩ SD = {N} . (  P
 ) ∩ (SAD) = Mx (  P) // (SAB) ( 
SAB) ∩ ( ABCD) = AB ⇒ My // AB . Gọi My ∩ BC = { } Q . (  P
 ) ∩ ( ABCD) = My (
P)⊃ MQ,(SCD) ⊃ CD Do CD  // MQ
⇒ Nt // CD // MQ . Gọi Nt ∩ SC = { } P . (  P
 ) ∩ (SCD) = NtMN // SA
Do MQ // AB ⇒ MN ⊥ MQ . SA ⊥  AB
Thiết diện của hình chóp cắt bởi mặt phẳng (P) là hình thang vuông MNPQ , vuông tại M , N . Có 2 2 MQ PN SN a
= AB = SB − SA = a , MN 1 a 3 = ⇒ MN = , 2 2 = = ⇒ PN = SA 3 3 CD SD 3 3
Diện tích thiết diện của hình chóp cắt bởi mặt phẳng (P) là 2 1 S
= MN NP + MQ = 1 a 3  2a  5 3aa + = . MNPQ .( ) 2 2 3 3    18
Câu 15. Tìm tất cả các giá trị của a dương sao cho giá trị nhỏ nhất của hàm số y = f (x) 2 = x − ax + ( 2 4 4
a − 2a + 2) trên đoạn [0;2] bằng 3. A. a = 5+ 10 . B. a = 5 + 3 . C. a =1+ 2 . D. a = 2 . Lời giải Chọn A
ĐTHS là một parabol có hoành độ đỉnh là a . 2 +) TH1: 0 a
< < 2 ⇔ 0 < a < 4. GTNN của hàm số trên [0;2] là  a f  = 2 − a + 2 =   3 2  2  1
⇔ a = − (L) . 2
+) TH2: a ≥ 2 ⇔ a ≥ 4. GTNN của hàm số trên [0;2] là f ( ) 2
2 = a −10a +18 = 3 2
a = 5+ 10 (t / m) ⇔  .
a = 5− 10 (L)
Câu 16 . Bạn An ra vườn hái 6 bông hoa vàng và 5 bông hoa đỏ cho vào giỏ. Có bao nhiêu cách để bạn
An lấy 3 bông hoa từ giỏ đó sao cho chúng có đủ hai màu? A. 135. B. 462 . C. 810. D. 90. Lời giải Chọn A
Số cách lấy 3 bông hoa bất kì là 3 C =165 . 11
Số cách lấy 3 bông hoa màu vàng là 3 C = 20 . 6
Số cách lấy 3 bông hoa màu đỏ là 3 C =10 . 5
Số cách lấy 3 bông hoa có đủ hai màu là 165 − 20 −10 =135.
Câu 17. Trong các khẳng định sau đây, khẳng định nào sai?
A. Gọi P( A) là xác suất của biến cố A, ta luôn có 0 < P( A) ≤1.
B. Phép thử ngẫu nhiên là phép thử mà ta không biết được chính xác kết quả của nó nhưng ta
có thể biết được tập hợp tất cả các kết quả có thể xảy ra của phép thử.
C. Không gian mẫu là tập hợp tất cả các kết quả có thể xảy ra của phép thử.
D. Biến cố là tập con của không gian mẫu. Lời giải Chọn A
- Theo tính chất của xác suất ta có với mọi biến cố A thì 0≤ P( A)≤1 nên phương án A sai.
Câu 18. Từ một tổ gồm 10 học sinh, giáo viên chủ nhiệm chọn ra 4 học sinh để dọn vệ sinh lớp trong đó
có 1 bạn lau bảng, 2 bạn quét lớp và 1 bạn kê bàn ghế. Số cách chọn là A. 5000. B. 2500 . C. 2520 . D. 5040. Lời giải Chọn C
Mỗi cách chọn ra 4 học sinh để dọn vệ sinh lớp thỏa mãn yêu cầu bài được thực hiện như sau:
+ Chọn 1 học sinh từ 10 học sinh để lau bảng: có 1 C cách. 10
+ Chọn 2 học sinh từ 9 học sinh còn lại để quét lớp: có 2 C cách. 9
+ Chọn 1 học sinh từ 7 học sinh còn lại để kê bàn ghế: có 1 C cách. 7
Theo quy tắc nhân ta có 1 2 1
C .C .C = 2520 cách để giáo viên phân công trực nhật thỏa mãn yêu 10 9 7 cầu bài toán.
Câu 19. Biểu thức ( 2 m + ) 2
2 x − 2(m − 2) x + 2 luôn nhận giá trị dương khi và chỉ khi
A. m ≤ 4 hoặc m ≥ 0 . B. 4 − < m < 0 .
C. m < 0 hoặc m > 4 .
D. m < −4 hoặc m > 0. Lời giải Chọn D
Đặt f (x) = ( 2 m + ) 2
2 x − 2(m − 2) x + 2.
Nên f (x) là tam thức bậc hai có hệ số a > 0, m ∀ .
Suy ra để f (x) > 0 với mọi giá trị x khi và chỉ khi m < −
∆′ < 0 ⇔ (m − 2)2 − 2( 4 2 m + 2) 2
< 0 ⇔ −m − 4m < 0 ⇔  . m > 0
Vậy m < − 4 hoặc m > 0 thì biểu thức ( 2 m + ) 2
2 x − 2(m − 2) x + 2 luôn nhận giá trị dương. Câu 20. Tổng 0 1 2 2
C + 2C + 2 C +...+ 2n n C n n n n bằng A. 3n . B. 4n . C. 1 2n+ . D. n C . 2n Lời giải Chọn A
Đặt S = ( + x)n 0 1 2 2 1
= C + xC + x C +... n n + x C (với * n∈ n n n n  ).
Thay x = 2 vào biểu thức S ta được: 0 1 2 2
C + 2C + 2 C +...+ 2n n
C = (1+ 2)n = 3n . n n n n Vậy tổng 0 1 2 2
C + 2C + 2 C +...+ 2n n C = 3n . n n n n
Câu 21. Trong không gian cho bốn điểm không đồng phẳng, có thể xác định nhiều nhất bao nhiêu mặt
phẳng phân biệt từ các điểm đó? A. 6 . B. 4 . C. 2 . D. 3. Lời giải Chọn B
Do bốn điểm không đồng phẳng nên qua ba điểm bất kỳ trong bốn điểm ta luôn xác định được duy
nhất một mặt phẳng. Vậy số mặt phẳng nhiều nhất bằng 3 C = 4 . 4
Câu 22. Tính giới hạn:  1  1   1
lim  1− 1− ...1  −  . 2 2 2  2 3 n       1 1 A. . B. . C. 1. D. 3 . 4 2 2 Lời giải Chọn B  1  1   1   1  1  1  1   1  1
lim  1− 1− ...1− =
 lim 1− 1+ 1− 1+ ...1− 1  +  2 2 2  2 3 n   2 2 3 3 n n              
 1 3 2 4 n −1 n +1 lim . . . . . .   + = 1 n 1 1  = lim . = . 2 2 3 3 n n      2 n  2
Câu 23. Tính tổng vô hạn sau: 1 1 1 S =1+ + + ...+ + ... 2 2 2 2n 1 −1 A. 4. B. 1 2 . n . C. 2. D. 2n −1 . 2 1 −1 2 Lời giải Chọn C
Ta có 1; 1 ; 1 ;…; 1 ;… lập thành cấp số nhân lùi vô hạn với số hạng đầu tiên u =1 và công bội 2 2 2 2n 1 1 q = . 2
S là tổng của một cấp số nhân lùi vô hạn với u =1 và 1 1 q = nên ta có 2 u 1 1 1 S = = = = 2 . 1− q 1 1 1− 2 2
Câu 24. Cho hình thang vuông ABCD , đường cao AB = 2a , AD = a , BC = 4a . Gọi I là trung điểm
của CD , J là điểm di động trên cạnh BC . Tính BJ sao cho AJ và BI vuông góc. A. 3a . B. 4a . C. a . D. 5a . 4 5 6 Lời giải Chọn B   
Biểu diễn BI theo hai vectơ BA và BC .            Ta có BI 1 = (BD + BC) 1 1 = BD + BC 1 = (BA+ AD) 1 + BC 1 1 1
= BA + AD + BC 2 2 2 2 2 2 2 2      1 1 1 1
= BA + . BC + BC 1 5 = BA + BC . 2 2 4 2 2 8     
• Đặt BJ = k BC . Biểu diễn AJ theo hai vectơ BA và BC .
    
Ta có AJ = BJ − BA = kBC − BA.  
• Do AJ và BI vuông góc nên AJ . BI = 0 .     Suy ra:  1 5 BA BC  + (kBC −BA) =   0  2 8          k 1 5k 5 ⇔ B . A BC − B . A BA +
BC.BC − BC.BA = 0 2 2 8 8   1 2 5k 2 ⇔ − BA +
BC = 0 ( do BA ⊥ BC nên B . A BC = 0 ) 2 8 1 2 5k 2 ⇔ − .4a + .16a = 0 1 ⇔ k = . 2 8 5   Vậy 1
BJ = BC , suy ra 1 4a BJ = BC = . 5 5 5 u  = 4
Câu 25. Cho dãy số 1 u
. Tìm số hạng thứ 5 của dãy số. = +  + u n n 1 n A. 16. B. 14. C. 12. D. 15. Lời giải Chọn B
Ta có u = 4 , u = u +1 = 5 ,u = u + 2 = 7 , u = u + 3 =10 , u = u + 4 =14 . 1 2 1 3 2 4 3 5 4
Câu 26. Số nghiệm của các phương trình 2
x − 4x − 5 = 4x −17 là A. 3. B. 1. C. 2 . D. 4 . Lời giải Chọn C  17  4x −17 ≥ 0 x ≥    4 2 2
x − 4x − 5 = 4x −17 ⇔  x − 4x − 5 = 4x −17 ⇔  2
x − 8x + 12 = 0   2   x 4x 5 4x 17  − − = − +  2  x − 22 = 0  17 x ≥  4   x = 2   x = 6 ⇔   x = 6 ⇔  .    x = 22   x = 22     x = − 22
Câu 27. Từ các chữ số 0; 1; 2; 7; 8; 9 tạo được bao nhiêu số tự nhiên lẻ có 5 chữ số đôi một khác nhau? A. 312. B. 600 . C. 360. D. 288 . Lời giải Chọn D
Gọi số cần tìm là n = abcde .
( điều kiện: a, b, c, d, e∈{0;1;2;7;8; }
9 ;a ≠ 0 và a, b, c, d, e đôi một khác nhau)
Vì n lẻ nên e∈{1;7; }
9 ⇒ e có 3 cách chọn. a ∈{1;2;7;8; } 9 \{ }
e ⇒ a có 4 cách chọn.
Sau khi chon a,e còn lại 4 chữ số. Ta lấy 3 chữ số trong 4 chữ số còn lại rồi sắp xếp có thứ tự vào 3 vị trí ,
b c, d ta có 3 A cách sắp xếp. 4 Vậy ta có 3
3.4.A = 288 số cần tìm. 4
Câu 28. Dãy số nào sau đây không phải là cấp số nhân? A. 1;2;3;4;5. B. 1;2;4;8;16 . C. 1;−1;1;−1;1. D. 1;− 2;4;−8;16 . Lời giải Chọn A Do 2 3
≠ nên dãy số trong phương án A không phải là cấp số nhân. 1 2
Các phương án B, C, D đều là cấp số nhân.
Câu 29. Cho phương trình  π cos 2x  + − m =  
2 , với m là tham số. Tìm tập hợp tất cả các giá trị của m  4 
để phương trình có nghiệm. A. ∅ . B. . C. [ 1; − ]3. D. [ 3 − ;− ] 1 . Lời giải Chọn D  π  π cos 2x  + − m =    2 ⇔ cos 2x + = 2 +   m .  4   4 
Vậy phương trình có nghiệm khi và chỉ khi 1
− ≤ 2 + m ≤1 ⇔ 3 − ≤ m ≤ 1 − .
Câu 30. Cho tam giác ABC có  0 5 3
A = 60 ,a =10,r =
. Tính diện tích của tam giác ABC . 3 A. 50.
B. 20 2 . C. 25 3 . D. 20. Lời giải Chọn C B E K O A H C
Gọi O làm tâm đường tròn nội tiếp tam giác ABC . K, H, E lần lượt là hình chiếu vuông góc của O
lên các cạnh AB, AC, BC . Khi đó ta có AH = AK , CH = CE , BE = BK .
Mặt khác ta có AH = AC − CH = AC − CE = AC − (BC − BE) = AC − BC + BE
= AC − BC + BK = AC − BC + AB − AK
= AC − BC + AB − AH = b − a + c − AH
b a c a + b + c AH − + ⇒ = =
− a = p − a . 2 2 Từ  tan OH OAH OH = ⇒ AH = r = = 5 . AH  tan OAH tan 30°
Mà AH = p − a nên ta có p − a = 5 ⇔ p = 5 + a =15 .
Vậy diện tích tam giác ABC là S = pr = 25 3.
Câu 31. Tam giác mà ba đỉnh của nó là trung điểm ba cạnh của tam giác ABC được gọi là tam giác
trung bình của tam giác ABC .
Ta xây dựng dãy các tam giác A B C , A B C , A B C … sao cho tam giác A B C là tam giác 1 1 1 2 2 2 3 3 3 1 1 1
đều cạnh bằng 3 và với mỗi số nguyên dương n ≥ 2 , tam giác A B C là tam giác trung bình n n n của tam giác A
. Với mỗi số nguyên dương n , kí hiệu S tương ứng là diện tích hình − B − C
n 1 n 1 n 1 − n
tròn ngoại tiếp tam giác A B C . Tính tổng S = S + S +...+ S + n ... n n n 1 2 A. 15π π S = . B. S = 4π . C. 9 S = . D. S = 5π . 4 2 Lời giải Chọn B
Tam giác A B C có bán kính đường tròn ngoại tiếp là 2 3. 3 ⇒ S = π. R = 3π 1 ( 1)2 1 1 1 R = . = 3 1 3 2 .
Tam giác A B C có bán kính đường tròn ngoại tiếp là 3 2 2 2 R = 2 2 ⇒ S = π ( 1 1 . R = .3π = S . 2 )2 2 1 4 4
Tam giác A B C có bán kính đường tròn ngoại tiếp là 3 3 3 3 R = 3 4 ⇒ S = π (R )2 1 1 . = .3π = S 3 3 2 16 4 …………………
Tam giác A B C có bán kính đường tròn ngoại tiếp là 3 1 = ⇒ = . n n n R S S n n 1 2 − n n 1 4 −
Suy ra S là tổng của cấp số nhân lùi vô hạn, có u = S = 3π , công bội 1 1 1 q = . 4 Vậy S1 S = = 4π 1 . 1− 4
Câu 32. Trong loạt đá luân lưu giữa đội tuyển Việt Nam và Thái Lan, ông Park Hang Seo phải lập danh
sách 5 cầu thủ từ 10 cầu thủ trên sân (trừ thủ môn) và thứ tự đá luân lưu của họ. Hỏi ông Park
có bao nhiêu cách lập danh sách biết ông sẽ để Quế Ngọc Hải là người sút phạt đầu tiên của đội tuyển Việt Nam? A.126. B.15120. C.3024. D. 30240. Lời giải Chọn C
Chọn người đá đầu tiên: Có 1 cách.
Chọn 4 người còn lại: Có 4 A = 3024 cách. 9
Vậy số cách lập danh sách là: 3024 cách
Câu 33. Phát biểu nào sau đây là sai?
A. limu = C (u = C , C là hằng số ). B. lim n q = 0 ( q > ) 1 . n n C. 1 lim = 0 . D. 1 lim = 0 k > . k ( )1 n n Lời giải Chọn B Vì lim n
q = 0 nếu q <1
Câu 34. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, AC và BD cắt nhau tại O . Giao
tuyến của hai mặt phẳng (SAB) và (SCD) là đường thẳng
A.qua S và song song với AB . B. AC . C. SO .
D. qua S và song song với BD . Lời giải Chọn A d S A D O B C
S ∈(SAB) ∩ (SCD)  AB // CD Ta có: 
với d đi qua S và d // AB // CD . ⊂  ( )
⇒ (SAB) ∩ (SCD) = d AB SAB CD ⊂  (SCD)
Câu 35. Cho 4 điểm A(1; 2
− ), B(0;3),C ( 3 − ;4), D( 1; − 8) .
Ba điểm nào trong 4 điểm đã cho là thẳng hàng? A. , A B, D .
B. B,C, D . C. , A C, D . D. , A B,C . Lời giải Chọn A   Ta có: AB = ( 1; − 5), AD = ( 2 − ; 10).    
Nhận thấy: AD = 2AB ⇒ AB, AD cùng phương. Vậy ba điểm ,
A B, D thẳng hàng. Câu 36. a Cho lim xa =  
( là phân số tối giản). Tính tổng L = a + b . x→0 7
x +1. x + 4 − 2  b b A. L = 43 . B. L = 23 . C. L =13. D. L = 53. Lời giải Chọn A 7  + + −  Ta xét x 1. x 4 2 T = lim  x→0  x   
 7 x +1.( x+ 4 −2)+ 2(7 x+1− )1 T lim  = x→0  x   
7 x +1(x + 4 − 4) 7 Ta xét x +1 1 T = lim = lim = . 1 x→0 x( x + 4 + 2) x→0 x + 4 + 2 4 2(7 x +1− )1 Ta xét T = lim . 2 x→0 x Đặt 7 7
t = x +1 ⇒ x = t −1. 2(t − ) 1
Ta có: x → 0 ⇒ t →1. Khi đó, 2 2 T = lim = lim = . 2 7 6 5 4 3 2 t 1 → t 1 t −1
→ t + t + t + t + t + t +1 7 1 2 15
⇒ T = T +T = + = . 1 2 4 7 28
Vậy a = 28, b =15. Do đó, L = a + b = 28 +15 = 43.
Câu 37. Cho hình lập phương ABC . D A′B C ′ D
′ ′ (hình vẽ bên dưới). Góc giữa hai đường thẳng AC và A′D bằng A. 45°. B. 30° . C. 60°. D. 90° . Lời giải Chọn C
Ta có AC // A′C′ nên ( ′ )  = ( ′ ′ ′ )  =  , , ′ ′ = 60o AC A D A C A D DA C
( vì tam giác DA′C′đều).
Câu 38. Thiết diện của một mặt phẳng với một tứ diện chỉ có thể là:
A. Một tứ giác hoặc một ngũ giác.
B. Một tam giác và một hình bình hành.
C. Một tam giác hoặc một tứ giác.
D. Một tam giác hoặc một ngũ giác.
Lời giải Chọn C
Thiết diện của một mặt phẳng với một tứ diện là tam giác khi mặt phẳng cắt ba mặt tứ diện; và
là một tứ giác khi mặt phẳng cắt bốn mặt của tứ diện. Thiết diện không thể là ngũ giác vì ngũ
giác có năm cạnh mà tứ diện chỉ có bốn mặt.
Câu 39. Cho hình hộp ABC . D A′B C ′ D
′ ′ . Gọi M là điểm trên cạnh AC sao cho AC = 3MC . Lấy N trên cạnh C D ′ sao cho C N ′ = xC D
′ . Với giá trị nào của x thì MN // BD′. A. 1 x = . B. 1 x = . C. 1 x = . D. 2 x = . 2 3 4 3 Lời giải Chọn D
Gọi I = BM ∩CD .
Ta có AB //CD suy ra MC MI 1 = = . Do đó IM 1 = . MA MB 2 IB 3
Mặt khác, ta có MN // BD′ suy ra IM IN 1 = = . Do đó NI ND 1 = = . IB ID′ 3 ND′ NC′ 2 Nên 2 NC′ = C D ′ . Vậy 2 x = . 3 3
Câu 40. Trong các mệnh đề sau, mệnh đề nào đúng?
A. Trong không gian hai đường thẳng không có điểm chung thì chéo nhau.
B. Trong không gian hai đường thẳng lần lượt nằm trên hai mặt phẳng phân biệt thì chéo nhau.
C. Trong không gian hai đường thẳng phân biệt không song song thì chéo nhau.
D. Trong không gian hai đường thẳng chéo nhau thì không có điểm chung. Lời giải Chọn D
Phương án A sai vì trong không gian hai đường thẳng không có điểm chung có thể song song.
Phương án B sai vì trong không gian hai đường thẳng nằm trên hai mặt phẳng phân biệt có thể song song hoặc cắt nhau.
Phương án C sai vì trong không gian hai đường thẳng lần lượt nằm trên hai mặt phẳng phân biệt thì có
thể song song hoặc chéo nhau hoặc cắt nhau.
Phương án D đúng vì trong không gian hai đường thẳng chéo nhau thì không có điểm chung.
Câu 41. Tập hợp tất cả các giá trị của tham số m để phương trình sin x 
1 cos xm 0 có đúng hai π π
nghiệm phân biệt trên  ;  −  là 3 2     1 1  1  1  A. 0;  . B. ;1  . C.  ;1 . D.  ;1.  2     2    2    2  Lời giải Chọn D sin x π 1
x = +k π k ∈  2 ( ) sin x 
1 cos xm 0 (*)    ⇔  2 . cos x   m  cos x = m π π Với π x  
= + k2π (k ∈) thì không có x∈ −  ; . 2 3 2    π π
Như vậy phương trình  
* có đúng hai nghiệm phân biệt trên ;  −  ⇔ phương trình 3 2    π π cos x 1
m có hai nghiệm phân biệt trên  ;  −   ⇔ m
∈ ;1 (hình vẽ minh họa bên dưới). 3 2      2   1 Do đó m ;1 ∈ . 2   
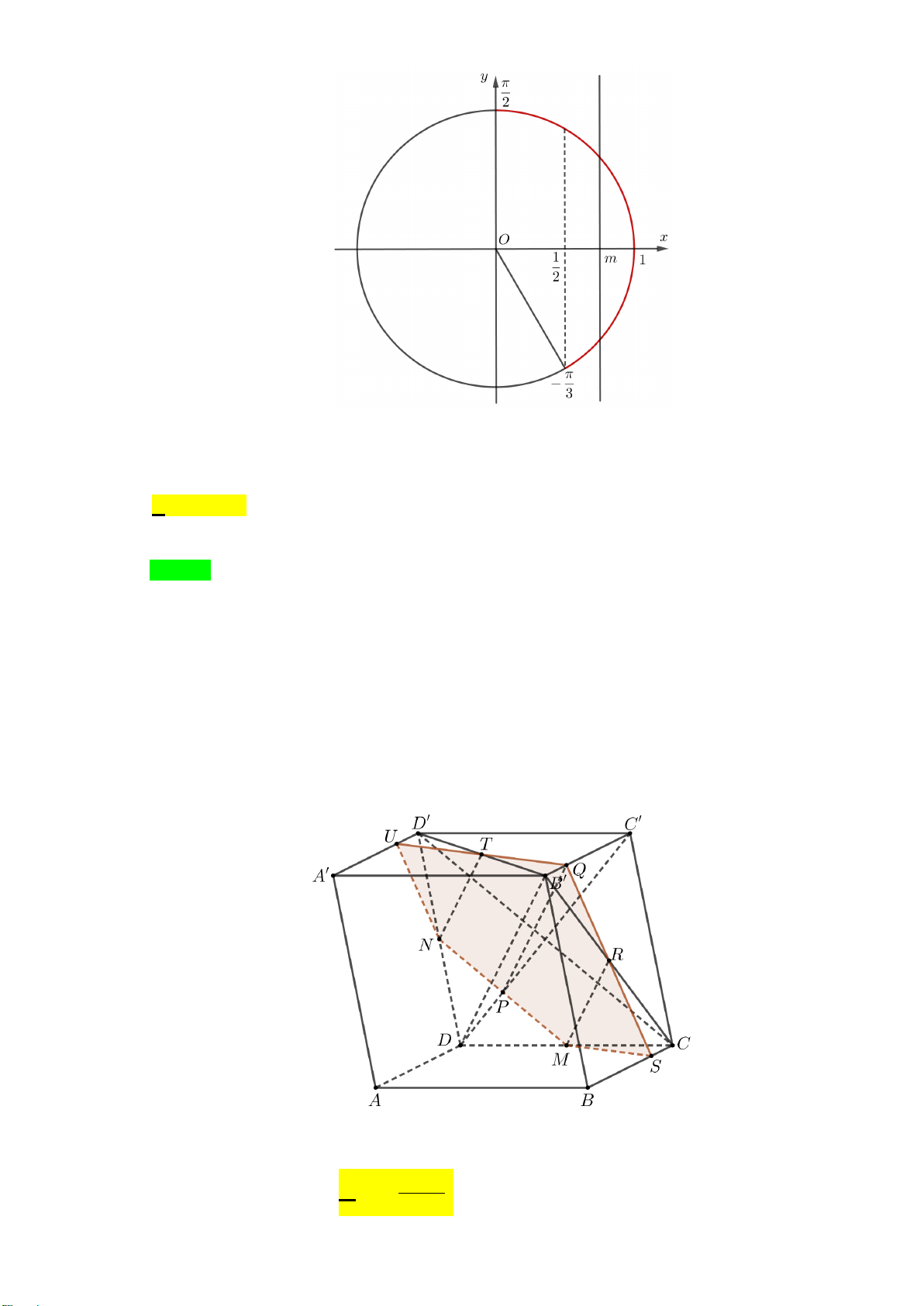
Câu 42. Cho hình hộp ABC . D ′
A B′C′D′ , gọi M là trung điểm CD , (P) là mặt phẳng đi qua M và song
song với B′D và CD′ . Thiết diện của hình hộp cắt bởi mặt phẳng (P) là hình gì? A. Ngũ giác. B. Tứ giác. C. Tam giác. D. Lục giác. Lời giải Chọn A
Dựng thiết diện của hình hộp cắt bởi mặt phẳng (P) như sau:
+ Qua M, kẻ đường thẳng d song song CD′ , d cắt DD′tại trung điểm N của DD′ và d cắt DC′tại P.
+ Qua P, kẻ đường thẳng song song B′D , đường thẳng đó cắt B′C′tại Q.
+ Qua M, kẻ đường thẳng song song B′D , đường thẳng đó cắt B′C tại R, QR cắt BC tại S.
+ Qua N, kẻ đường thẳng song song B′D , đường thẳng đó cắt B′D′ tại T, QT cắt ′ A D′ tại U.
Vậy thiết diện của hình hộp cắt bởi mặt phẳng (P) là ngũ giác MNUQS.
Câu 43. Trong các dãy số sau, dãy số nào là dãy số giảm?
A. u = n . B. 2n + 3 = . C. 3 = − . D. 2 = . n 2 u u n u n n 1 n n +1 n Lời giải Chọn B Ta có : 2n + 3 1 1 u = = + ⇒ u = + . n 2 n+ 2 1 n +1 n +1 n + 2 Xét  1   1  1 * u − = + − + = − < ∀ ∈ + u     n n n 2 2 0, 1   n + 2   n +1 (n + ) 1 (n + 2) * ⇔ u < ∀ ∈ + u n n n , 1  .
Vậy dãy số (u với 2n + 3 = là dãy số giảm. n ) un n +1
Câu 44. Cho hình chóp S.ABC có SA = BC = 2a . Gọi M , N lần lượt là trung điểm của AB và SC ,
MN = a 3 . Tính số đo góc giữa hai đường thẳng SA và BC . A. 120°. B. 150°. C. 30° . D. 60° . Lời giải Chọn D
   
Ta có: MN = MA + AS + SN .
   
MN = MB + BC + CN
  
⇒ 2MN = AS + BC    ⇒ ( )2 =( + )2 4 MN AS BC
2 2 2  
⇔ 4MN = AS + BC + 2AS.BC   2 2 2
⇔ 4MN = AS + BC + 2.AS.BC.cos( AS,BC)   ⇔ (AS BC) 2 2 2
4MN − AS − BC 1 cos , = = 2.AS.BC 2 (  AS, BC) 60° ⇒ = .
Vậy ( AS, BC) 60° = .
Câu 45. Cho hình chóp S.ABCD có đáy ABCD là hình thang ( AB // CD) . Gọi I , J lần lượt là trung
điểm của các cạnh AD , BC và G là trọng tâm của tam giác SAB . Biết thiết diện của hình chóp
cắt bởi mặt phẳng (IJG) là hình bình hành. Hỏi khẳng định nào sau đây đúng? A. 1 AB = CD . B. 3 AB = CD .
C. AB = 3CD . D. 2 AB = CD . 3 2 3 Lời giải Chọn C
Vì mặt phẳng (IJG) chứa IJ song song với AB , CD nên giao tuyến của mặt phẳng (IJG)
và (SAB) là đường thẳng MN qua G và song song với AB . Vậy thiết diện của hình chóp cắt
bởi mặt phẳng (IJG) là hình thang IJNM . Ta có 1
IJ = ( AB + CD) và 2 MN = AB . 2 3
Điều kiện để hình thang IJNM là hình bình hành là IJ = MN . IJ = MN 2 1
⇔ AB = ( AB + CD) 1 1
⇔ AB = CD ⇔ AB = 3CD . 3 2 6 2
       
Câu 46. Cho hình chóp S.ABCD có đáy ABCD là bình hành. Đặt SA = a ; SB = b; SC = c ; SD = d .
Khẳng định nào sau đây đúng?                 
A. a + c = d + b .
B. a + b = c + d .
C. a + d = b + c .
D. a + b + c + d = 0 . Lời giải Chọn A
Giả sử O là giao điểm của hai đường chéo của hình bình hành ABCD .
Khi đó O là trung điểm của AC và BD .      
Nên ta có SA + SC = 2SO và SB + SD = 2SO .
       
Vậy SA + SC = SB + SD hay a + c = b + d .
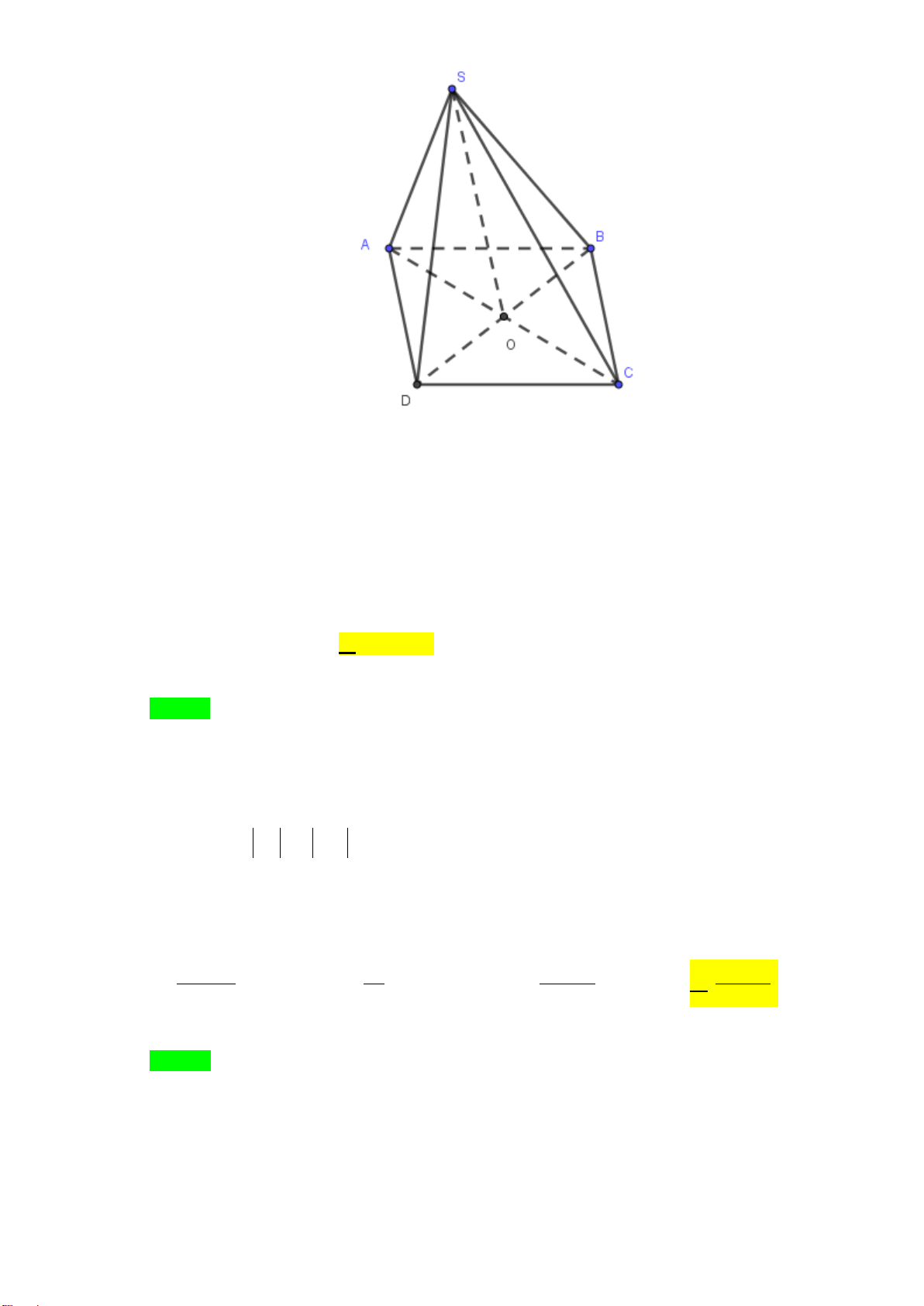
Câu 47. Cho hình lập phương ABC . D A′B C ′ D
′ ′ có cạnh bằng a . Gọi O là tâm hình vuông ABCD và
        
điểm S thỏa mãn OS = OA + OB + OC + OD + OA′ + OB′ + OC′ + OD′. Tính độ dài đoạn OS theo a .
A. OS = 6a .
B. OS = 4a .
C. OS = a .
D. OS = 2a . Lời giải Chọn B
Gọi O′ là tâm của hình vuông A′B C ′ D ′ ′ . Ta có:
        
OS = OA + OB + OC + D
O + OA′ + OB′ + OC′ + D O ′
            
= OA + OC + OB + OD + OA′ + OC′ + OB′ + OD′ = 0 + 0 + 2OO′ + 2OO′ = 4OO′.  
Suy ra, OS = OS = 4 OO′ = 4a .
Câu 48. Một công ty nhận được 50 hồ sơ xin việc của 50 người khác nhau muốn xin việc vào công ty,
trong đó có 20 người biết tiếng Anh, 17 người biết tiếng Pháp và 18 người không biết cả tiếng
Anh và tiếng Pháp. Công ty cần tuyển 5 người biết ít nhất một thứ tiếng Anh hoặc Pháp. Tính
xác suất để trong 5 người được chọn có đúng 3 người biết cả tiếng Anh và tiếng Pháp? A. 351 . B. 1 . C. 5 . D. 1755 . 201376 23 100688 100688 Lời giải Chọn D
Số người biết tiếng Anh hoặc tiếng Pháp là: 50 −18 = 32 .
Số người biết cả tiếng Anh và tiếng Pháp là: (20 +17) −32 = 5.
Số phần tử của không gian mẫu là số cách chọn 5 người trong 32 người biết tiếng Anh hoặc
tiếng Pháp. Suy ra: n(Ω) 5 = C . 32
Gọi A là biến cố “trong 5 người được chọn có đúng 3 người biết cả tiếng Anh và tiếng Pháp”.
Chọn 3 người biết cả tiếng Anh và tiếng Pháp: có 3 C cách. 5
Ứng với mỗi cách chọn 3 người nói trên, có 2
C cách chọn 2 người còn lại. 27 Suy ra, n( A) 3 2 = C .C . 5 27
Vậy xác suất của biến cố n A
A là: p( A) ( ) = 1755 = . n(Ω) 100688
Câu 49. Giá trị lớn nhất của hàm số y = 1+ cos 2x bằng A. 2 . B. 1. C. 2 . D. 0 . Lời giải Chọn A Ta có: 1
− ≤ cos 2x ≤1⇒1+ cos 2x ≤ 2 ⇒ 1+ cos 2x ≤ 2 .
Khi đó giá trị lớn nhất của hàm số y = 1+ cos 2x bằng 2 , đạt được khi:
cos 2x =1 ⇔ x = kπ ,(k ∈ Z ) .
Kết luận: giá trị lớn nhất của hàm số y = 1+ cos 2x bằng 2 .
Câu 50. Một gia đình cần khoan một cái giếng để lấy nước. Họ thuê một đội khoan giếng nước. Biết giá
của mét khoan đầu tiên là 80.000 đồng, kể từ mét khoan thứ hai giá của mỗi mét khoan tăng
thêm 5.000 đồng so với giá của mét khoan trước đó. Biết cần phải khoan sâu xuống 50m mới
có nước. Hỏi phải trả bao nhiêu tiền để khoan cái giếng đó? A. 4.000.000 đồng.
B. 10.125.000 đồng. C. 52.500.000 đồng. D. 52.000.000 đồng. Lời giải Chọn B
Nhận xét: Giá tiền mỗi mét khoan là một cấp số cộng có số hạng đầu u = 80.000 đồng, công 1
sai d = 5.000 đồng. Do đó số tiền để khoan cái giếng đó là: 50
T = u + u +...+ u = S =
2u + 49d = 25 2*80.000 + 49*5000 =10.125.000 đồng. 1 2 50 50 ( 1 ) ( ) 2
Kết luận: T =10.125.000 đồng.
-------------------- HẾT --------------------
Document Outline

  • de-kscl-toan-11-thi-thpt-qg-2020-lan-2-truong-thpt-chuyen-vinh-phuc
    • KSCL THPT QG LAN 2_1_TOAN 11_123
    • KSCL THPT QG LAN 2_1_TOAN 11_dapancacmade
      • Data
  • Tổ-23-đợt-29-ĐỀ-KSCL-LẦN-2-CHUYÊN-VĨNH-PHÚC-