Đề lập đội tuyển thi HSG QG môn Toán THPT năm 2025 – 2026 sở GD&ĐT Tuyên Quang

SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI LẬP ĐỘI TUYỂN DỰ THI CHỌN HỌC SINH GIỎI TUYÊN QUANG
QUỐC GIA THPT NĂM HỌC 2025 – 2026 Môn thi: Toán ĐỀ CHÍN H THỨC
Thời gian: 180 phút (không kể thời gian giao đề)
Ngày thi thứ nhất: 11/9/2025
(Đề này có 01 trang)  22 x  2, x   1 2
Bài 1 (5,0 điểm). Cho dãy số  x xác định bởi: 23  . n   * 23x  22x  x , n     n2 n 1  n a) Tính lim x . n x x x b) Đặt 1 2 n * y    ... 
, n   . Chứng minh rằng dãy số  y bị chặn. n  n 2 2 2 2n
Bài 2 (5,0 điểm). Tìm tất cả các hàm số f : 0;   0; thỏa mãn 2
x  f (x)  f ( y)  (x  y) f  yf (x); với mọi x, y  0;.
Bài 3 (5,0 điểm). Với k là một số nguyên dương ta kí hiệu  (k) là tổng tất cả các ước
nguyên dương của k. Chứng minh rằng:   2025 p  1   1945 p  1 a) 
, với mọi số nguyên tố p; 2025 1945 p 1 p 1
b)  (mn)  n (m)   (n)  n, với mọi * , m n   .
Bài 4 (5,0 điểm). Trên mặt phẳng, cho 4 điểm phân biệt ,
A B, C, D trong đó không có 3
điểm nào thẳng hàng. Chứng minh rằng tồn tại một đường tròn () đi qua 3 trong 4 điểm này
và điểm còn lại thuộc miền trong của () hoặc nằm trên (). -----Hết-----
Ghi chú: - Thí sinh không được sử dụng tài liệu và máy tính cầm tay trong khi làm bài.
- Giám thị coi thi không giải thích gì thêm.
Họ và tên thí sinh:.................................................................Số báo danh:................
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI LẬP ĐỘI TUYỂN DỰ THI CHỌN HỌC SINH GIỎI TUYÊN QUANG
QUỐC GIA THPT NĂM HỌC 2025 – 2026 Môn thi: Toán
Thời gian: 180 phút (không kể thời gian giao đề) ĐỀ CHÍNH THỨC
Ngày thi thứ hai: 12/9/2025
(Đề này có 01 trang)
Bài 5 (7,0 điểm). Cho đa thức P(x) có hệ số hữu tỉ, bậc bằng 2026 và có 2026 nghiệm thực
x  x  ...  x
lập thành một cấp số cộng với công sai d  0. Chứng minh rằng: 1 2 2026 1 2 2 a) 2 2 x  x   x  d  i 
d  với mọi i  1, 2,..., 2026; i i  2 2025  2 2027 2 , 2027 1 2   b) 2
d là số hữu tỉ.
Bài 6 (7,0 điểm). Cho tam giác ABC nhọn, không cân và AB  AC. Các đường cao
BE, CF của tam giác ABC cắt nhau tại H. Gọi M , K lần lượt là trung điểm của BC và
EF; N là giao điểm của AM và EF; P là hình chiếu vuông góc của N trên cạnh BC.
a) Chứng minh rằng ba điểm ,
A K , P thẳng hàng.
b) Đường tròn đường kính AP cắt lại các cạnh AB, AC lần lượt tại Q và .
R Gọi X , Y lần
lượt là trung điểm của CQ và B .
R Chứng minh rằng hai đường thẳng XY và HN vuông góc với nhau.
Bài 7 (6,0 điểm). Cho A là một tập con có 23 phần tử của tập S  1; 2;...; 533  5 . Đặt
A  x  n x  
A , n  S. Chứng minh rằng: n
a) Với mọi i, j  S, tập A  A khác tập rỗng khi và chỉ khi i  j  B   x  y x, y   A ; i j
b) Tồn tại 22 phần tử t , t ,..., t phân biệt của S sao cho các tập A , A ,..., A đôi một 1 2 22 t t t 1 2 22 giao nhau bằng rỗng. -----Hết-----
Ghi chú: - Thí sinh không được sử dụng tài liệu và máy tính cầm tay trong khi làm bài.
- Giám thị coi thi không giải thích gì thêm.
Họ và tên thí sinh:.................................................................Số báo danh:................ HƯỚNG DẪN CHẤM
ĐỀ THI LẬP ĐỘI TUYỂN DỰ THI CHỌN HỌC SINH GIỎI QUỐC GIA THPT, NĂM HỌC 2025-2026 ĐỀ CHÍNH THỨC ----- NGÀY THI THỨ NHẤT 11.9.2025 -----  22 x  2, x   1 2
Bài 1 (5,0 điểm). Cho dãy số  x xác định bởi: 23  . n   * 23x  22x  x , n     n2 n 1  n a) Tính lim x . n x x x b) Đặt 1 2 n * y    ... 
, n   . Chứng minh rằng dãy số  y bị chặn. n  n 2 2 2 2n Nội dung Điểm   1
a) Phương trình đặc trưng của dãy  x  : 2 23 22 1     1. Suy ra số hạng n    23 1,0 n  1  
tổng quát của dãy  x có dạng *
x  A  B  , n    ; , A B  .  n  n    23  22 n  1  
Từ x  2, x  suy ra    Do đó * x  1 23. , n    . 1,0 1 2 A 1, B 23. n   23  23  n   1   
Vậy lim x  lim 1 23   1. n   0,5  23      n  1   1 b) Ta có * x  1 23  1  2, n    . n   1,0 n 1  23  23  Suy ra x x x x x x 2 2 2 1 2 n 1 2 y    ...     ... n     ...  n 2 n 2 n 2 2 2 2 2 2 2 2 2 2n 1,5 1 1  1  *  1  ...   2 1   2, n    . n 1   2 2   2n 
Vậy dãy  y bị chặn. n 
Bài 2 (5,0 điểm). Tìm tất cả các hàm số f : 0;   0; thỏa mãn 2
x  f (x)  f ( y)  (x  y) f  yf (x); với mọi x, y  0;. Nội dung Điểm
Giả sử f là một hàm số cần tìm. Cho x  y  1, ta được f (1)  f  f (1) (1). 1,0
Giả sử x , x  0;  thỏa mãn f  x  f x  a  0. Khi đó ta có 1   2  1 2   2
x a  f ( y)  (x  y) f (ay)  1,0 1   1  ; y   0 (2). 2 x
a  f ( y)  (x  y) f (ay)  2   2  2 2 x x Từ (2) suy ra 1 2    x  x
x x  y x  x
 0  x  x . Vậy f là 1 2   1 2  1 2   1 2 x  y x  y 1,0 1 2 đơn ánh.
Vì f là đơn ánh nên từ (1) suy ra f (1)  1. Cho x  1, y  0;, ta được 1 1,0
1  f ( y)  (1 y) f ( y)  f ( y)  . y 1 1
Thử lại f ( y) 
thỏa mãn bài toán. Vậy f ( y)  , y
  0 là hàm số duy nhất cần y y 1,0 tìm.
Bài 3 (5,0 điểm). Với k là một số nguyên dương ta kí hiệu  (k) là tổng tất cả các ước nguyên
dương của k. Chứng minh rằng:   2025 p  1   1945 p  1 a) 
, với mọi số nguyên tố p; 2025 1945 p 1 p 1
b)  (mn)  n (m)   (n)  n, với mọi * , m n   . Nội dung Điểm a) Ta thấy t p  *
t    có tất cả các ước nguyên dương là 2 1, , ,..., t p p p . Suy ra t 1   1,0   p t p  t 1 2
 1 p  p  ...  p  . p 1 t 1 p  1    t p  1 t 1 1 p 1 p   p p Do đó    . Vậy t p 1 t p 1  p   1  t p   1 p 1 1,0   2025 p  1   1945 p p  1   . 2025 1945 p 1 p 1 p 1
b) Kí hiệu S là tập tất cả các ước nguyên dương của k. Khi đó  (k)  x k  và bất x S  k   0,5
đẳng thức cần chứng minh tương đương với x  n   x    x  n  (*). x S  x S  x S  mn  m  n   Ta có n x    nx  x 
 (1), với nS  ns s  S . m m 0,5 x S  x S  x n  S  m  m m s  S  s n
Mặt khác s  S  nS    
 s  n Do đó S  nS  n (2). n  m    n  m  n . 0,5 s  nS  s n m   S  S Hơn nữa n mn   S  nS  S (3). n  m  mn 0,5 nS  S  m mn Từ (3) suy ra x  x  x  x  x      (4). 0,5 x S  x S   nS x S  x n  S x S   nS mn n  m  n m n  m   
Thay (1) và (2) vào (4) suy ra x  n   x    x  n  hay x S  x S  x S  0,5 mn  m  n
 (mn)  n (m)   (n)  . n
Bài 4 (5,0 điểm). Trên mặt phẳng, cho 4 điểm phân biệt ,
A B, C, D trong đó không có 3 điểm
nào thẳng hàng. Chứng minh rằng tồn tại một đường tròn () đi qua 3 trong 4 điểm này và điểm
còn lại thuộc miền trong của () hoặc nằm trên (). Nội dung Điểm
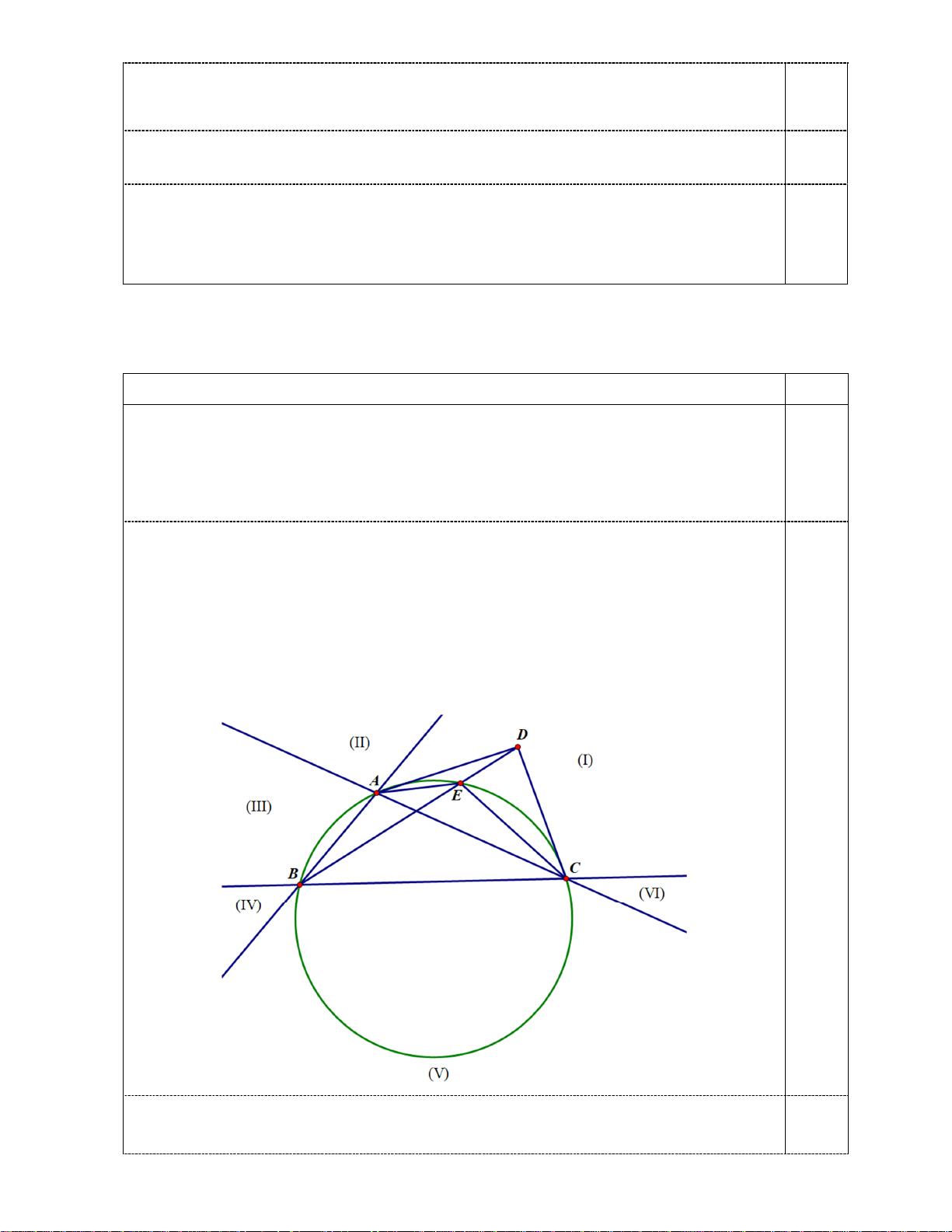
Trong các đường tròn đi qua 3 điểm lấy từ 4 điểm đã cho, gọi ( ) là đường tròn có
bán kính lớn nhất. Không mất tính tổng quát, giả sử ( ) đi qua 3 điểm , A , B C. 1,0
Trường hợp 1: D thuộc ( ) hoặc miền trong của ( ). Chọn ()  ( ) thỏa mãn bài toán.
Trường hợp 2: D không thuộc ( ) và không thuộc miền trong của ( ). Khi đó D
có thể thuộc vào một trong các miền (I), (II), (III), (IV), (V), (VI) như hình vẽ, trong đó: 
Miền (I) giới hạn bởi tia đối của tia AB, tia đối của tia CB và cung AC (không tính
bờ). Tương tự cho các miền (III), miền (V);
Miền (II) giới hạn bởi tia đối của tia AB và tia đối của tia AC (không tính bờ). Tương
tự cho miền (IV), miền (VI). 1,0
 Nếu D thuộc miền (II) thì chọn () là đường tròn ngoại tiếp tam giác DBC thoả 1,0
mãn bài toán. Tương tự với D thuộc các miền (IV) và (VI).
 Nếu D thuộc miền (I) thì gọi E là giao điểm thứ hai của BD và ( ). Khi đó hai  góc AEB và 
BEC có ít nhất một góc nhọn, giả sử  0 AEB  90 . Ta thấy   0  
ADB  AEB  90  sin ADB  sin AE . B Do đó AB AB 2,0 R    R , ( )    ABD sin AEB sin ADB
mâu thuẫn với cách chọn ( ). Vậy D không thuộc miền (I).
Tương tự thì D không thuộc miền (III) và (V) trong trường hợp 2. ----- NGÀY THI THỨ 2 12.9.2025 -----
Bài 5 (7,0 điểm). Cho đa thức P(x) có hệ số hữu tỉ, bậc bằng 2026 và có 2026 nghiệm thực
x  x  ...  x
lập thành một cấp số cộng với công sai d  0. Chứng minh rằng: 1 2 2026 1 2 2 a) 2 2 x  x   x  d  i 
d  với mọi i  1, 2,..., 2026; i i  2 2025  2 2027 2 , 2027 1 2   b) 2
d là số hữu tỉ. Nội dung Điểm 1 2 2 a) Ta có 2 2 x  x   x  x  x  x  (1). 1,0 i 2027i  i 2027i   i 2027i  2   x  x
 x  (i 1)d  x  (2026  i)d  2x  2025d Mặt khác i 2027i 1 1 1  (2). 1,5 x  x
 x  (i 1)d  x  (2026  i)d  (2i  2027)d  i 2027i 1 1 1 2 2 Từ (1), (2) suy ra 2 2 x  x   x  d  i  d  i   (3). 0,5 i i  2 2025  2 2027 2 , 1, 2026 2027 1 2   b) Giả sử 2026 2025
P(x)  a x  a x
 ...  a x  a ; a  ,  i
  0,1,..., 2026; a  0. 2026 2025 1 0 i 2026 2026 a a 1,0 Theo Định lí Viet, ta có 2025   x  và 2024  x x  (4). i a j k i 1 a 2026 
1 jk 2026 2026 2 2 2026 2026 (4)      a  a Do đó 2 2025 2024 x  x  2 x x   2    (5). 1,0 i  i   j k    i 1   i 1  
1 jk 2026 a a    2026  2026 2026 2026 2026 1 1 2 2 Từ (3) suy ra 2 x  x  x   x  d  i  d     (6). 1,0 i  2 2 i i  2 2025  2 2027 2 2027 1   i 1  2 i 1  4 i 1  2026 2 x   a  a i a Vì 2025 2024  2  i 1  2025  
 và 2x  2025d      nên từ (5) và (6) a a 1 1,0  1013 1013a 2026  2026 2026 suy ra 2 d  . 
Bài 6 (7,0 điểm). Cho tam giác ABC nhọn, không cân và AB  AC. Các đường cao BE, CF
của tam giác ABC cắt nhau tại H. Gọi M , K lần lượt là trung điểm của BC và EF; N là giao
điểm của AM và EF; P là hình chiếu vuông góc của N trên cạnh BC.
a) Chứng minh rằng ba điểm ,
A K , P thẳng hàng.
b) Đường tròn đường kính AP cắt lại các cạnh AB, AC lần lượt tại Q và .
R Gọi X , Y lần
lượt là trung điểm của CQ và B .
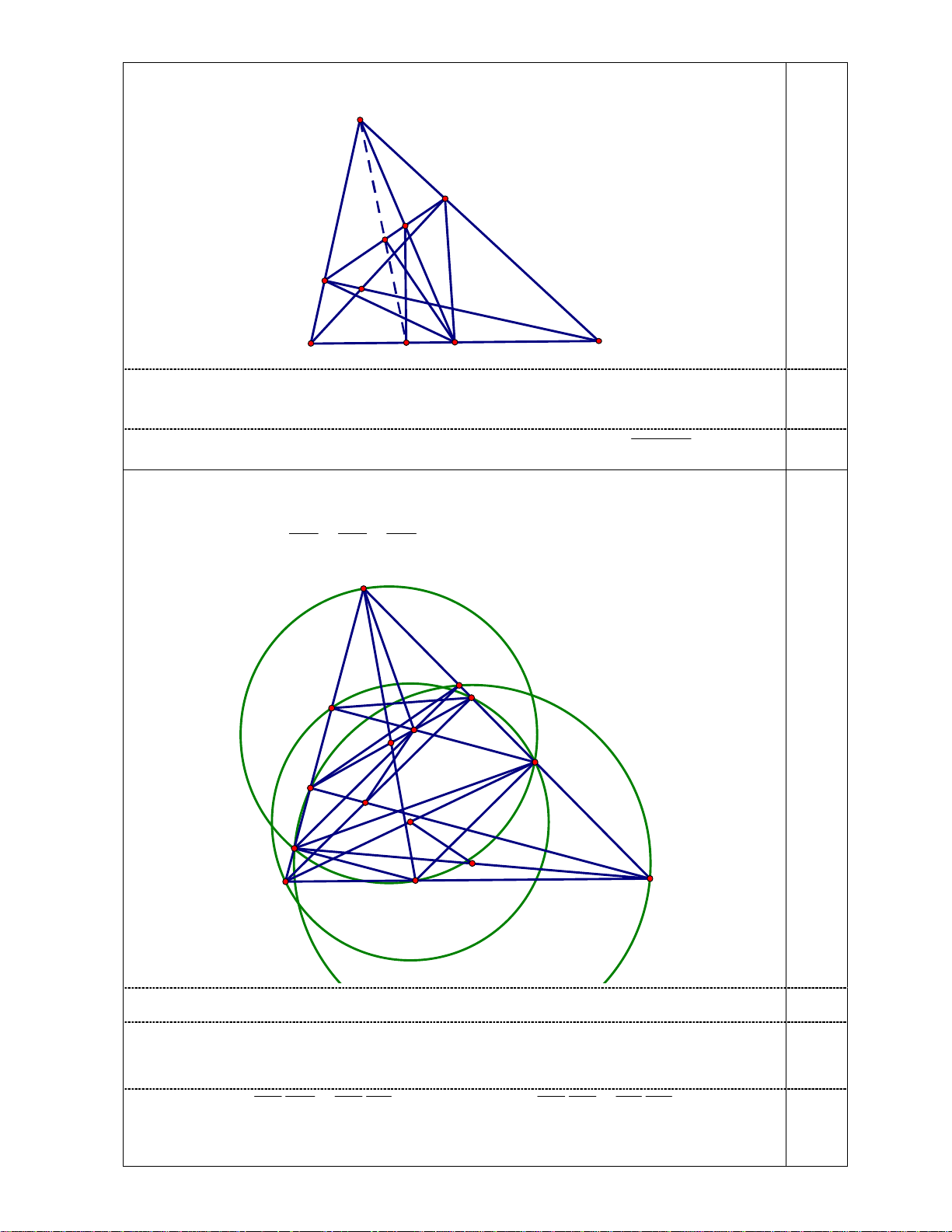
R Chứng minh rằng hai đường thẳng XY và HN vuông góc với nhau. Nội dung Điểm 1 a) Ta có MF 
BC  ME  M
 EF cân tại M nên  0 MKN  90 . 1,0 2 Mặt khác  0
MPN  90 . Suy ra 4 điểm N , K , P, M thuộc đường tròn đường kính MN. A E N K F H B P M C
Ta thấy AM , AK lần lượt là đường trung tuyến của tam giác ABC và tam giác AEF. 1,0 Mà A  EF  A
 BC nên AKE  AMB.   0    Suy ra 0
AKE  NMP  180  EKP  AKE  EKP  180 . Do đó , A K , . P 1,0
b) Ta có PQ  AB nên PQ // CF. Kết hợp với A  BP  A
 EN  g.g  suy ra QB PB NE  
 QN // BE  QN  A . R QF PC NF A U E V 1,5 K N R F H Y Q X B C P
Tương tự ta cũng có RN  AQ nên N là trực tâm tam giác AQR. 0,5
Gọi QU , RV là các đường cao của tam giác AQR. Ta thấy B, V , E, R thuộc đường 1,0
tròn Y  đường kính BR; C, U , F, Q thuộc đường tròn  X  đường kính C . Q Suy ra   N .
Q NU  NV .NR  ; 
 HC.HF  HB.HE  . N / X  N /Y  H / X  H /Y  1,0
Vậy NH là trục đẳng phương của hai đường tròn  X , Y ; do đó XY  HN.
Bài 7 (6,0 điểm). Cho A là một tập con có 23 phần tử của tập S  1; 2;...; 533  5 . Đặt
A  x  n x   A , n
  S. Chứng minh rằng: n
a) Với mọi i, j  S, tập A  A khác tập rỗng khi và chỉ khi i  j  B   x  y x, y   A ; i j
b) Tồn tại 22 phần tử t , t ,..., t phân biệt của S sao cho các tập A , A ,..., A đôi một giao 1 2 22 t t t 1 2 22 nhau bằng rỗng. Nội dung Điểm
a) Ta thấy A  A    x
 , y  A : x  i  y  j  x  y  i  j  i  j  . B i j 1,0
Đảo lại, nếu i  j  B thì tồn tại x, y  A sao cho i  j  x  y . Khi đó
x  j  y  i
i  j  x  y   A  A  .   i j 1,0
x  i  y  j 
Vậy A  A    i  j  . B i j
b) Theo a) thì A  A    i  j  . B i j 0,5 Ta thấy 2
B  C  1  254. 23 0,5
Chọn t  1. Đặt C  S \   t   B . Khi đó C  5335  254  0 và C  S. 1  1  1 1 1
Chọn t  min t t  C . Vì 0  B nên t  t  t  t  t  t  B bởi nếu ngược lại 2  1 2 1 2 1 2 1 0,5
thì tồn tại   B sao cho t  t    t  t   , trái với cách chọn t . 2 1 2 1 2
Đặt C  C \   t   B . Khi đó C  C  254  5335  2 254  0 và C  C . 2 1  2  2 1 2 1 0,5
Chọn t  min t t  C
thì t  t  t  t  t  t  t  . B 3  2  3 2 1 3 2 3 2
Nếu t  t  B thì tồn tại   B sao cho t  t    t  t   C  t  C , vô 1,0 3 1 3 1 3 1 1 3 2
lí. Vậy t  t  . B 3 1
Lặp lại lí luận trên đến khi có tập C . Khi đó C
 5335  21 254  1 và 21 21 0,5
C  C  ...  C . 21 20 1
Chọn t  C thì t
 t  ...  t và nếu tồn tại i 1; 2;...; 2 
1 sao cho t  t  B 22 21 22 21 1 22 i
thì tồn tại   B sao cho t  t  t  t    t
 t    C  t  C , vô lí. 22 i 22 i 22 i i 22 21 0,5
Vậy t , t ,..., t thỏa mãn t  t  B  A  A  ,  i   j. 1 2 22 i j t t i j -----Hết-----
Ghi chú: Nếu thí sinh làm bài theo cách khác, với kiến thức trong chương trình THPT (hoặc
THPT chuyên), thì vẫn cho điểm các phần đúng tương ứng.
MA TRẬN ĐỀ THI CHỌN ĐỘI TUYỂN DỰ THI CHỌN HỌC SINH GIỎI QUỐC GIA THPT, NĂM HỌC 2025 - 2026 Môn thi: TOÁN -----
Mức độ nhận thức Nội dung Cộng Nhận biết Thông hiểu Vận dụng Vận dụng cao
- Số hạng tổng quát của dãy số.
- Tính chất giải tích của dãy số: Giới hạn dãy số, dãy số bị chặn. Số ý: 2 Giải tích Số ý: 1 Số ý: 1 Số điểm: 5,0 Số điểm: 2,5 Số điểm: 2,5
- Đồng dư và quan hệ chia hết trên tập số nguyên.
- Cấp của một số nguyên theo modun. Số học
- Các hàm số học: Phi hàm Euler  (n) , Hàm tổng các ước  (n). Số ý: 2 Số điểm: 5,0 Số ý: 1 Số ý: 1 Số điểm: 2,0 Số điểm: 3,0
- Phương trình hàm đại số: Phương pháp sử dụng ánh xạ, phương pháp thế. Đại số
- Đa thức: Hệ số, nghiệm, bậc và giá trị của đa thức. Số ý: 3 Số điểm: 12,0 Số ý: 1 Số ý: 1 Số ý: 1 Số điểm: 3,0 Số điểm: 4,0 Số điểm: 5,0
- Hệ thức lượng trong tam giác.
- Hệ thức lượng trong đường tròn: Phương tích, trục đẳng phương. Hình học Số ý: 2
- Một số định lí cơ bản của hình học. phẳng Số điểm: 7,0 Số ý: 1 Số ý: 1 Số điểm: 3,0 Số điểm: 4,0
- Nguyên lí khởi đầu cực trị; Bất biến và đơn biến.
- Phép đếm cơ bản và nâng cao. Số ý: 3 Tổ hợp
- Lực lượng tập hợp; các phép toán của tập hợp. Số điểm: 11,0 Số ý: 1 Số ý: 1 Số ý: 1 Số điểm: 2,0 Số điểm: 5,0 Số điểm: 4,0 Số ý: 5 Số ý: 4 Số ý: 3 Số ý: 12 Tổng Số điểm: 12,5 Số điểm: 14,5 Số điểm: 13,0 Số điểm: 40,0 Ghi chú:
- Ngày 1 gồm 4 bài toán thuộc các phân môn: Giải tích, Đại số, Tổ hợp, Số học.
- Ngày 1 gồm 3 bài toán thuộc các phân môn: Đại số, Hình học, Tổ hợp. -----Hết-----
Document Outline