Đề mẫu thi KTHP Giải Tích 1 (60 phút) - GT1 60. Môn Giải tích 1 (GT01) | Trường Đại học Giao thông Vận tải.

lOMoAR cPSD| 58833082
ĐỀ MẪU THI KTHP GIẢI T˝CH 1 (60 phœt) Chương
Hàm số và giới hạn 1 𝑒𝑥 Câu 1: Giới hạn lim −1 bằng 𝑥→ 0 𝑥 A. 1 B. C. -1 D. 4
Câu 2: Giới hạn lim ln(1+𝑥) bằng 𝑥→ 0 𝑥 A. 0 B. C. 1 D. -1
Câu 3: Giới hạn lim (2𝑥2 + 𝑥 − 1) bằng 𝑥→ −∞ A. −∞ B. -2 C. +∞ D. -3
Câu 4: Khi 𝑥 → 0, VCB 1 − cos 𝑥 tương ương với A. 𝑥 1 B. 𝑥2 2 C. 𝑥 D. – 𝑥 Câu 5: Giới hạn lim 𝑥 bằng 1+ 10𝑥−2 𝑥→ 5 A. B. C. +∞ D. −∞ lOMoAR cPSD| 58833082
Câu 6: Tìm giới hạn lim 𝑥−arcsin𝑥 𝑥→ 0 𝑥−tan𝑥 A. 1 B. C. − D. 2 Câu 7: Tìm giới hạn 𝑥→ 0 2 𝑥 A. 1 B. C. D. −
Câu 8: Tìm giới hạn lim 1− cos 𝑥 𝑥→ 0 𝑥 sin 2𝑥 A. 0 B. C. 1 D. - 1 𝑒2𝑥+𝑒−2𝑥 −2 2
Câu 9: Tìm 𝑘 ể hàm 𝑓(𝑥) = { nếu 𝑥 ≠ 0, 2𝑥 liên tục: 2𝑘 + 1 nếu 𝑥 = 0. A. − B. C. 1 D. 2
Câu 10: Tìm 𝑘 ể hàm 𝑓(𝑥) = { nếu 𝑥 ≠ 0, sin2 𝑥
liên tục: 2𝑘 + 1 nếu 𝑥 = 0. A. -3/4 B. -3/2 C. 1 D. -2 Chương
Đạo hàm và vi phân 2
Câu 11: Nếu 𝑦 = cos 3𝑥 thì 𝑦′ = A. 3cos 3𝑥 B. −3 sin 3𝑥 C. −cos 3𝑥 D. − cos 3𝑥 lOMoAR cPSD| 58833082
Câu 12: Công thức ạo hàm nào sau ây úng? ′ 1 ( √ 𝑥 ) = A. √ 𝑥 ′ B. (1) = 12 𝑥 𝑥 ′ 1 C. (cot = cos 2 𝑥 𝑥) ′ 1 D. (tan = cos 2 𝑥) 𝑥
Câu 13: Nếu 𝑦 = arctan 2𝑥 thì 𝑦′ =
A. 2arccot 2𝑥 B. 2 tan 2𝑥 C. D. −
Câu 14: Nếu 𝑓(𝑥) = (𝑥2 − 2)3(𝑥2 − 4) thì 𝑓′(2) =? A. 2 B. 0 C. -2 D. 1
Câu 15: Nếu 𝑓(𝑥) = sin(𝜋sin 𝑥) thì 𝑓′ (𝜋) =? 6 𝜋 A. 2 𝜋 B. − 2 C. 0 𝜋 D. 2
Câu 16: Nếu 𝑓(𝑥) = arctan3 𝑥 + cot 2𝑥 thì 𝑓′(𝑥) =? 2 A. 𝑥 − 2 2𝑥 sin 3(1+ 𝑥 2 ) arctan 2 B. 3 arctan 2 𝑥 2 1+𝑥 2 + sin 2 2 𝑥 C. 3 arctan2 𝑥 − 22 2𝑥 s 2 in 3 arctan 2 2 − 𝑥 sin 2 D. 1+𝑥 2𝑥 lOMoAR cPSD| 58833082 Câu 17: Nếu 𝑓 thì 𝑓′(𝑥) =? 𝑥 A. 1 + 𝑥 2 +1 1 B. 𝑥 √ 𝑥 2 +1 2 𝑥 2 +1 C. √ 𝑥 2 +1 2 𝑥 2𝑥 +1 D. 2+1) 𝑥(𝑥 Câu 18: Nếu 𝑦 = 𝑒 𝑥 − 𝑥
𝑥 +−𝑒𝑒− 𝑥 thì 𝑑𝑦 =? 𝑒 A. 𝑑𝑦 𝑥+𝑒−𝑥 𝑑𝑥 𝑒 B. 𝑑𝑦 𝑥+𝑒−𝑥 𝑑𝑥 𝑒 C. 𝑑𝑦𝑑𝑥 D. 𝑑𝑦 𝑑𝑥 𝑥
Câu 19: Nếu 𝑓(𝑥) = {1+
𝑒1/𝑥 nếu 𝑥 ≠ 0, 0 nếu 𝑥 = 0.
thì 𝑓−′(0) =?; 𝑓+′(0) =? A. 1 và 0 B. 1 và 2 C. -1 và 2 D. 0 và 1
𝑥2 + sin(𝑥 − 2) 𝑘ℎ𝑖 𝑥 ≤ 2 Câu 20: Cho 𝑓(𝑥) = {
𝑥2 . T nh 𝑓+′(2) v 𝑓−′(2)
+ 6𝑥 − 6 𝑘ℎ𝑖 𝑥 > 2
A. Kh ng tồn tại 𝑓+′(2); 𝑓−′(2)=5
B. 𝑓+′(2) = 5; 𝑓−′(2) = 4
C. 𝑓+′(2) = 𝑓−′(2) = 5
D. 𝑓+′(2) = 4; 𝑓−′(2) = 5 Chương Tích phân 3
Câu 21: Tích phân ∫ sin (3𝑥)𝑑𝑥 = A. cos (3𝑥) + 𝐶 B. cos (3𝑥) + 𝐶 C. − cos (3𝑥) + 𝐶 D. sin (3𝑥) + 𝐶 lOMoAR cPSD| 58833082
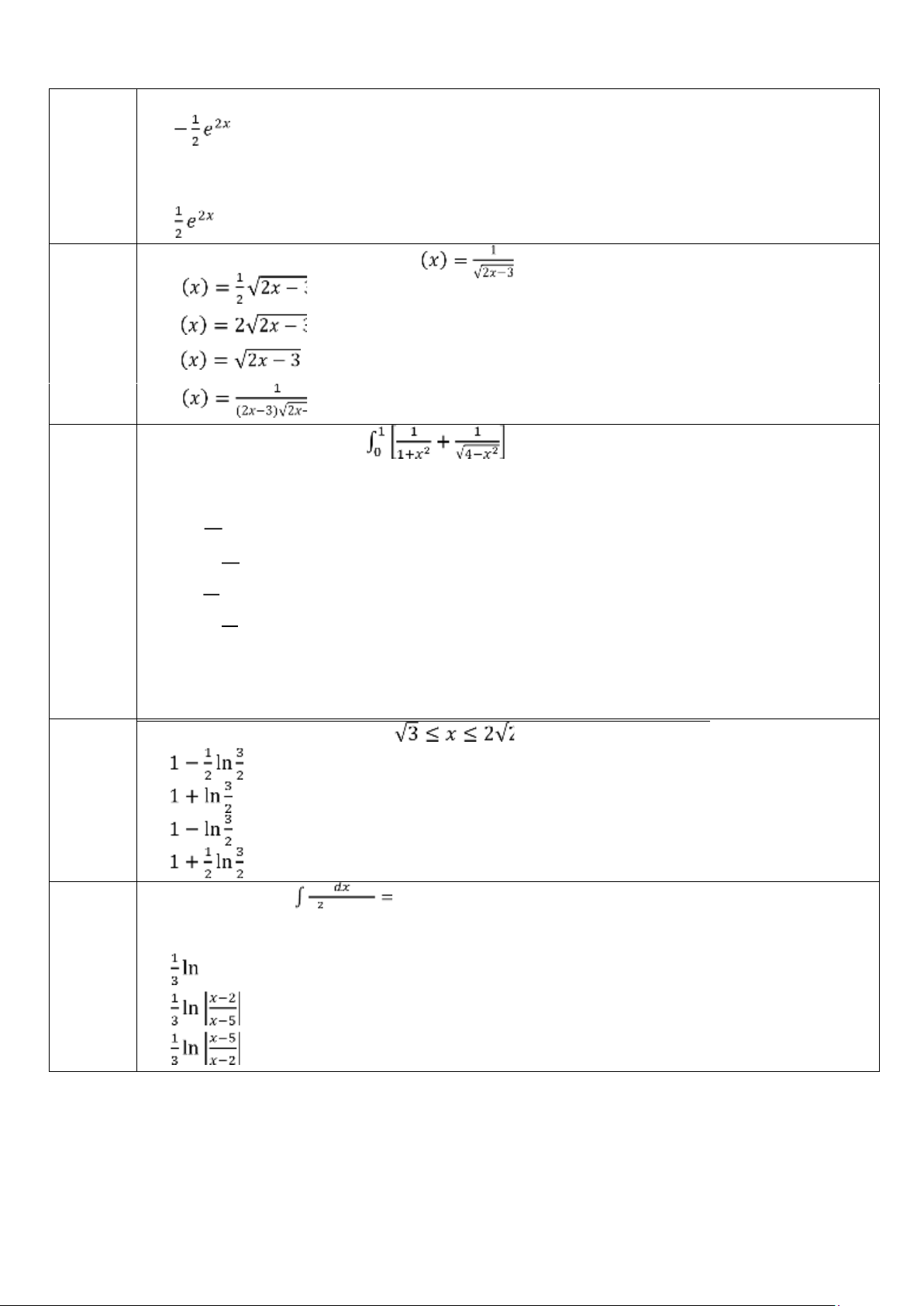
Câu 22: Tích phân ∫ 𝑒2𝑥𝑑𝑥 = A. + 𝐶 B. 2𝑒2𝑥 + 𝐶 C. −2𝑒2𝑥 + 𝐶 D. + 𝐶 Câu 23: Tìm hàm c ác 𝐹(𝑥) biết 𝐹′ A. 𝐹 + 𝐶 B. 𝐹 + 𝐶 C. 𝐹 + 𝐶 + 𝐶 D. 𝐹
Câu 24: Tính tích phân 𝐼 𝑑𝑥 = 7𝜋 A. 𝐼 = 12 5𝜋 B. 𝐼 = − 12 𝜋 C. 𝐼 = 12 𝜋 C. 𝐼 = − 12
Câu 25: Độ dài cung 𝑦 = ln 𝑥, là A. B. C. D. Câu 26: Tích phân 𝑥 −7𝑥+10
A. ln|(𝑥 − 2)(𝑥 − 5)| + 𝐶 B.
|(𝑥 − 2)(𝑥 − 5)| + 𝐶 C. + 𝐶 D. + 𝐶 lOMoAR cPSD| 58833082
Câu 27: Diện tích hình phẳng giữa hai ường cong 𝑦 = 𝑥2 và 𝑦 = là A. B. 2 C. 1 D. Câu 28: Tính A. 0 B. C. D. +∞ 𝑥 Câu 29:
Tính tích phân 𝑥+𝑒2𝑥 √2+2𝑒 A. 2ln(𝑒𝑥 ) + 𝐶 B. + 𝐶
C. 2 arcsin(𝑒𝑥 + 1) + 𝐶
D. 2 arctan(𝑒𝑥 + 1) + 𝐶 +∞ 𝛼+cos𝑥 Câu 30: Tích phân ∫1
(1+2𝑥)3/2 𝑑𝑥 hội tụ khi và chỉ khi A. 𝛼 < −1 B. 𝛼 = 0 C. 𝛼 tùy ý
D. Không có giá trị 𝛼 nào Chương Chuỗi 4 Câu 31: Chuỗi 𝑞𝑛 hội tụ nếu A. 𝑞 ≥ 1 B. 𝑞 < 1 C.|𝑞| < 1 D. 𝑞 > 1 𝑛 Câu 32: Chuỗi hội tụ nếu 𝑒 𝑒 𝑒 A. B. C. D. lOMoAR cPSD| 58833082
Câu 33: Cho chuỗi dương ∑+𝑛=0∞ 𝑎𝑛 . Mệnh ề nào sau ây úng? A.
Nếu 𝑎𝑛 → 0 khi 𝑛 → ∞ thì chuỗi trên hội tụ. A. Nếu thì chuỗi hội tụ.
C. Nếu chuỗi phân kỳ thì 𝑎𝑛 → 0 khi 𝑛 → ∞.
D. Nếu 𝑎𝑛 → 0 khi 𝑛 → ∞ thì chuỗi trên phân kỳ. Câu 34: Chuỗi
A. hội tụ và có tổng là 2
B. hội tụ và có tổng là 1 C. Phân kỳ
D. hội tụ và có tổng là Câu 35: Chuỗi 𝑛=1 𝑛 𝑛
hội tụ nếu và chỉ nếu A. 𝑝 > 3; 𝑞 > 0 B. 𝑝 > 3; 𝑞 < 0 C.
𝑝 < 3; 𝑞 > 0 D. 𝑝 < 3; 𝑞 < 0 1 ; ( 2 ∞ + ) ∑ 𝑛=1 3 √ 𝑛 𝑛
Câu 36: Chuỗi nào trong ba chuỗi sau phân kỳ? ; 𝜋 2𝑛 𝑛 (3) ∑+𝑛=1∞ (𝑛+1 ) A. Chuỗi (2) và (3) B. Chuỗi (2) C. Chuỗi (1) và (3) D. Chuỗi (3) Câu 37: Chuỗi
𝑛=1 𝑛2+𝐴2 (𝐴 là tham số) hội tụ tuyệt ối khi và chỉ khi A. 𝐴 ≥ 1 B. 𝐴 tùy ý C. 𝐴 > 2 D. 𝐴 > 1 4 𝑛
Câu 38: Cho chuỗi ∑+𝑛=1 ∞ 8 𝑛 + 𝛼𝑛 −
5 (𝛼 là tham số). Mệnh ề nào úng?
A. Chuỗi trên luôn hội tụ.
B. Chuỗi hội tụ khi và chỉ khi 𝛼 < 0
D. Chuỗi hội tụ khi và chỉ khi 𝛼 > 0
D. Chuỗi hội tụ khi và chỉ khi 𝛼 ≥ 0 lOMoAR cPSD| 58833082
Câu 39: Tìm miền hội tụ của
𝑛𝑛! (𝑥 − 2)𝑛 A. [−1,1] B. (1,3) C. {2} D. [1,3]
Câu 40: Tìm 𝑝 ể chuỗi ∑+𝑛=1∞ (
𝑛+1)(𝑛𝑛2+3𝑝+1) hội tụ A.
Chuỗi trên luôn luôn phân kỳ B. 𝑝 > 2 C. 𝑝 ≥ 2 D. 𝑝 > 1