SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI
ĐỀ OLYMPIC MÔN TOÁN 10
CỤM TRƯỜNG THPT THANH XUÂN-
NĂM HỌC 2018 – 2019
CẦU GIẤY-THƯỜNG TÍN Môn: Toán
Thời gian: 120 phút (Không kể thời gian phát đề) Câu 1. Cho hàm số 2
y  x  2x  2   1 .
a) Lập bảng biến thiên và vẽ đồ thị  P của hàm số   1 .
b) Tìm m để phương trình 2
x  2x  2  m  0 có hai nghiệm x và x thỏa mãn: 1 2 x  1   3  x . 1 2 Câu 2.
a) Giải bất phương trình sau:  2 x  x 2 4
2x  5x  3  0 2 2
2x  xy  y 5x  y  2  0
b) Giải hệ phương trình sau:  . 2 2
x  y  x  y  4  0 2
x  4x  m
c) Tìm m để bất phương trình: 2    3 2 x  2x  nghiệm đúng x   ? 3 Câu 3.
Cho tam giác ABC ; đặt a  BC,b  AC, c  AB . Gọi M là điểm tùy ý. a)
Tìm giá trị nhỏ nhất của biểu thức 2 2 2
P  MA  MB  MC theo a, b, c . b)
Giả sử a  6 cm, b  2 cm, c  1 3 cm . Tính số đo góc nhỏ nhất của tam giác ABC
và diện tích tam giác ABC . Câu 4.
Trong mặt phẳng tọa độ Oxy cho hình chữ nhật ABCD . Gọi H là hình chiếu của A lên BD ;
I là trung điểm của BH . Biết đỉnh A2; 
1 , phương trình đường chéo BD là: x  5 y 19  0 ,   điể 42 41 m I ;  .  13 13 
a) Viết phương trình tham số đường thẳng AH . Tìm tọa độ điểm H ?
b) Viết phương trình tổng quát cạnh AD . Câu 5.
Cho ba số dương a, b, c thỏa mãn: 2 2 2
a  b  c  1. Chứng minh rằng a b c 3 3    . 2 2 2 2 2 2 b  c c  a a  b 2 HẾT 1
HƯỚNG DẪN GIẢI CHI TIẾT Câu 1. Cho hàm số 2
y  x  2x  2   1 .
a) Lập bảng biến thiên và vẽ đồ thị  P của hàm số   1 .
b)Tìm m để phương trình 2
x  2x  2  m  0 có hai nghiệm x và x thỏa mãn: 1 2 x  1   3  x . 1 2 Lời giải
a) Tập xác định: D  .
Tọa độ đỉnh I 1  ;1 .
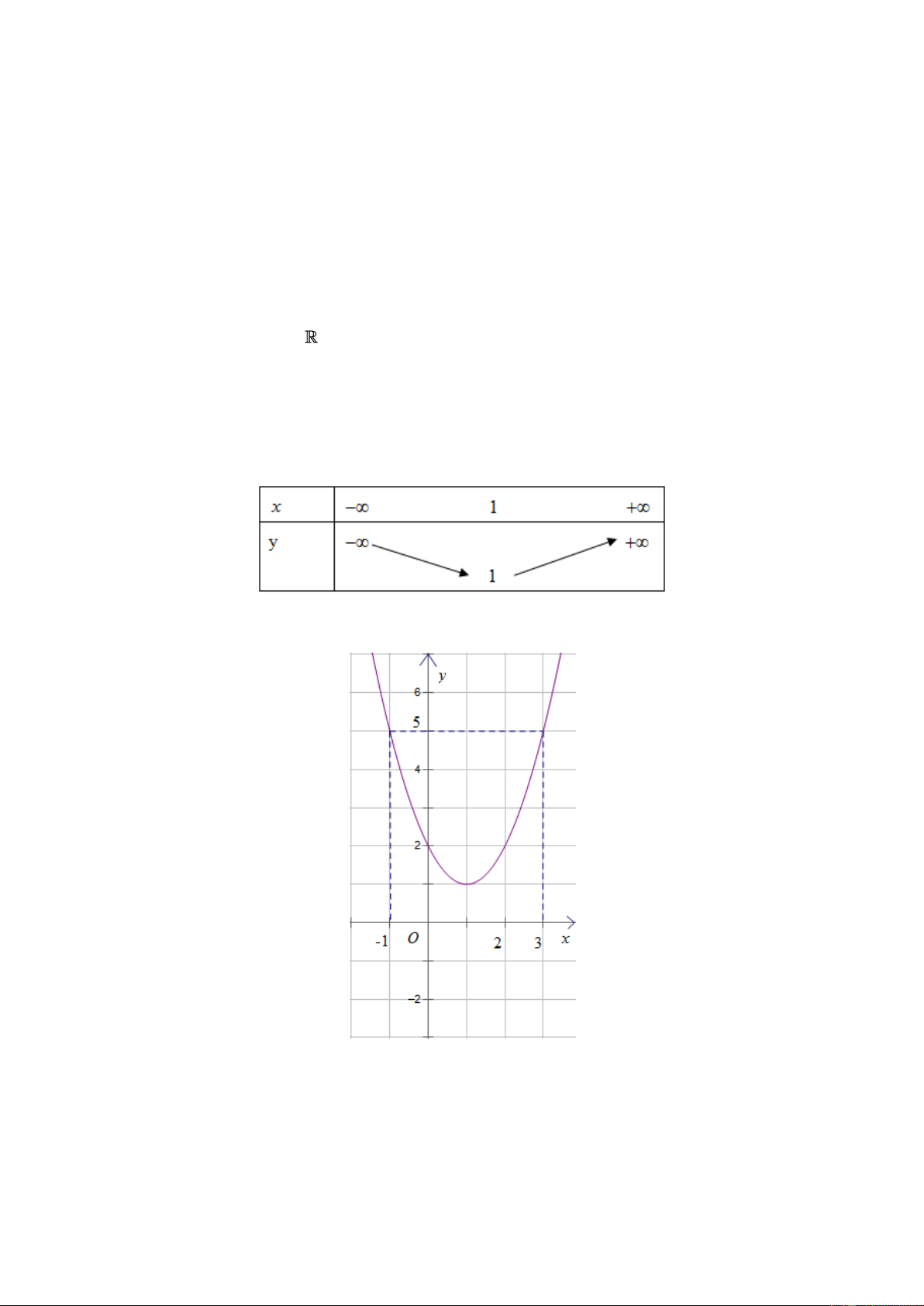
Hệ số a 1  0 nên hàm số đồng biến trên khoảng 1;   và nghịch biến trên khoảng   ;1  . Bảng biến thiên:
+ Đồ thị: P có trục đối xứng là đường thẳng x 1. P đi qua các điểm A0;2 ; B2;2 . b) 2 2
x  2x  2  m  0  x  2x  2  m .   1
Số nghiệm của phương trình  
1 chính là số giao điểm của  P với đường thẳng d : y  m ,
trong đó d  là đường thẳng luôn song song hoặc trùng với Ox .
Dựa vào đồ thị  P ta thấy phương trình  
1 có nghiệm thỏa mãn x  1   3  x  1 2 m   5  m  5  . 2 Câu 2.
a) Giải bất phương trình sau:  2 x  x 2 4
2x  5x  3  0 2 2
2x  xy  y 5x  y  2  0
b) Giải hệ phương trình sau:  . 2 2
x  y  x  y  4  0 2
x  4x  m
c) Tìm m để bất phương trình: 2    3 nghiệm đúng x   ? 2 x  2x  3 Lời giải x  3  a) Điề  u kiện 2
2x  5x  3  0  1  . x   2 1 + Ta thấy x  3
 , x  là nghiệm của bất phương trình đã cho. 2 x  3  + Khi 1        thì 2 2x 5x 3 0 , suy ra 2 2x 5x 3 0 nên: x   2  x   2 x  x 2 4
2x  5x  3  0 2  x  4x  4 0   . x  0   Suy ra trườ 1
ng hợp này bất phương trình có tập nghiệm S   ;  4   ;  . 2      2  1 
Vậy bất phương trình có tập nghiệm là S   ;  4   ;     3 . 2  2 2
2x  xy  y 5x  y  2  0 b)  2 2
x  y  x  y  4  0 Ta có: 2 2 2 2
2x  xy  y  5x  y  2  0  y  2xy  y  xy  2x  x  2 y  4x  2  0
 y y  2x  
1  x  y  2x  
1  2 y  2x   1  0      y x
y  x  2 y  2x   1  2 0   .
 y  2x 1 Như thế:
y  2  x   2 2 2  2
2x  xy  y  5x  y  2  0 x  
2 x  x 2 x 4  0    2 2
x  y  x  y  4  0
y  2x 1   x   2x  2 2
1  x  2x   1  4  0 x 1
y  2  x   y  1 2
2x  4x  2  0    4     .  x y  2x 1      5  2  5
 x  x  4  0  13   y    5  4 13  Vậy hệ có nghiệm  ; x y là: 1  ;1 ;  ;    .  5 5  3 c) Ta có 2
x  2x  3   x  2 1  2  0 , x   nên: 2
x  4x  m 2 2  2
 x  4x  6  x  4x  m 2 3
 x 8x  m  6  0 (1) 2    3     . 2 x  2x  3 2 2
x  4x  m  3x  6x  9 2
2x  2x  9  m  0 (2)
Yêu cầu bài toán trở thành tìm m để mỗi bất phương trình (1), (2) nghiệm đúng với mọi x thuộc . Ta thấy:
(1) đúng với mọi x thuộc 2
    4  3 m  6  2 0  m   . 1   3
(2) đúng với mọi x thuộc 2
    1  2 9  m  17 0  m  . 2   2  2 17  Vậy m   ;   .  3 2  Câu 3.
Cho tam giác ABC ; đặt a  BC,b  AC, c  AB . Gọi M là điểm tùy ý. c)
Tìm giá trị nhỏ nhất của biểu thức 2 2 2
P  MA  MB  MC theo a, b, c . d)
Giả sử a  6 cm, b  2 cm, c  1 3 cm . Tính số đo góc nhỏ nhất của tam giác ABC
và diện tích tam giác ABC . Lời giải
a) Gọi G là trọng tâm tam giác ABC  GA  GB  GC  0 . 2 2 2 Ta có 2 2 2
P  MA  MB  MC  MA  MB  MC . 2 MA   MGGA2 2 2  MG  2M . G GA  GA  2 2
Với MB   MG  GB 2 2  MG  2M . G GB  GB  2
MC  MGGC2 2 2  MG  2M . G GC  GC  2 2 2 2
 MA  MB  MC  MG   2 2 2 3
GA  GB  GC  Khi đó 2 P  MG   2 2 2 3
GA  GB  GC  và 2
P min  MG min  MG min  M  G . 2 2 2  4 4  b  c a  1 2 2 G
 A  m     
b  c  a a  2 2 2 2 2  9 9   2 4  9  2 2 2  4 4  a  c b  1 Mặt khác 2 2 G
 B  m     
a  c  b . b  2 2 2 2 2  9 9   2 4  9  2 2 2 4 4  a  b c  1 2 2 G
 C  m     
a  b  c c  2 2 2 2 2   9 9   2 4  9 1 Suy ra P   2 2 2
a  b  c . min  9 b)
* Ta có a  6 cm, b  2 cm, c  1 3 cm .
Vì b  mina, , b 
c suy ra góc B trong tam giác ABC có số đo nhỏ nhất.
Áp dụng định lí Cosin trong tam giác ABC , ta được: 4 2 2 2
b  a  c  2ac cos B   
a  c  b  2 2 2 2 6 1 3 4 6  2 3 2  cos B      B   . ac 2. 6.1 3 45 2 2 6  6 2 2 Vậy B  45. 1 1 2
* Diện tích tam giác ABC : S  ac sin B  . 6.2.  3 . 2 2 2 Vậy S  3 (đvdt). Câu 4.
Trong mặt phẳng tọa độ Oxy cho hình chữ nhật ABCD . Gọi H là hình chiếu của A lên BD ;
I là trung điểm của BH . Biết đỉnh A2; 
1 , phương trình đường chéo BD là: x  5 y 19  0 ,   điể 42 41 m I ;  .  13 13  c)
Viết phương trình tham số đường thẳng AH . Tìm tọa độ điểm H ?
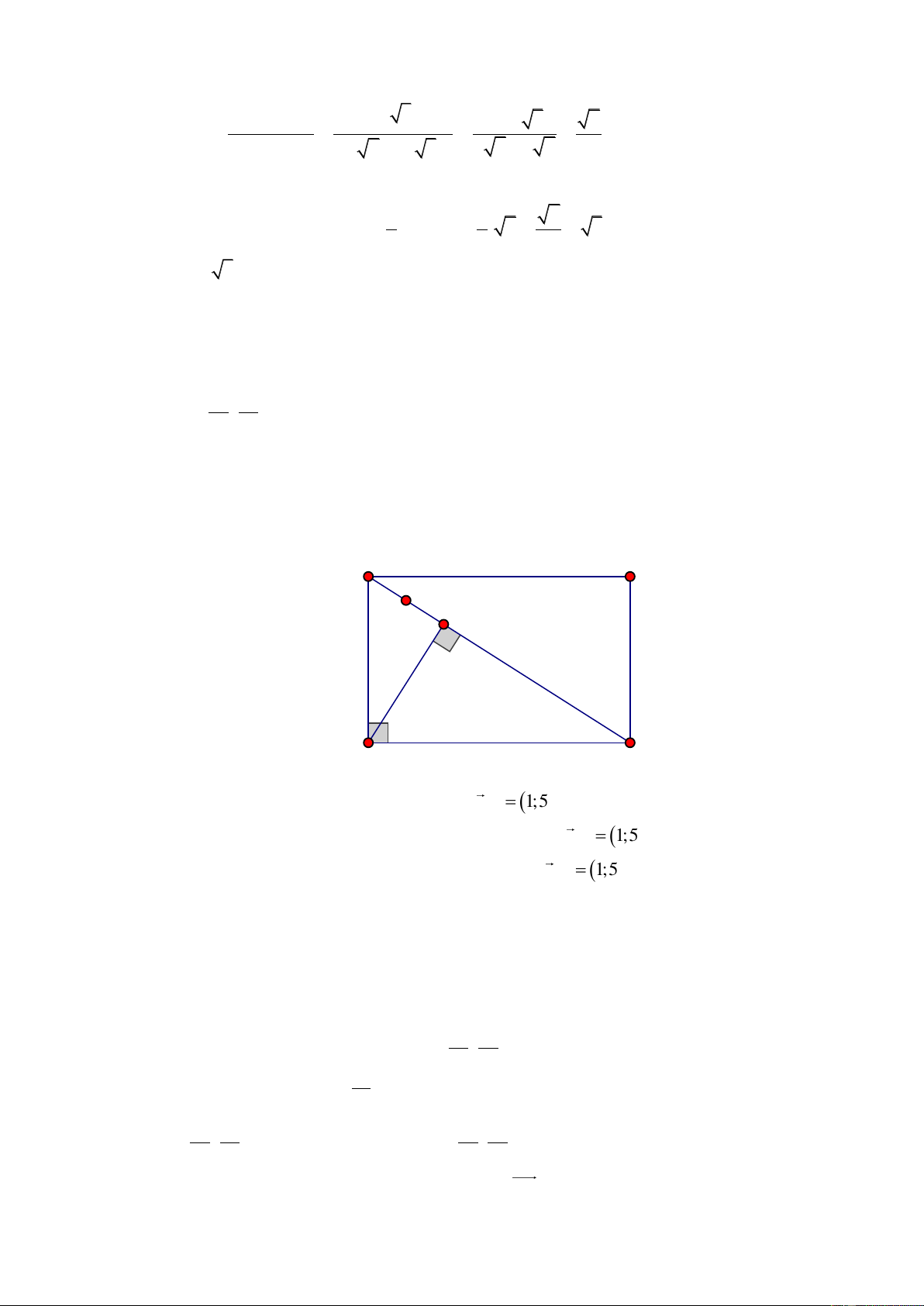
d) Viết phương trình tổng quát cạnh AD . Lời giải a) B C H I A D
BD : x  5 y 19  0 có véc tơ pháp tuyến là n  1;5 . BD 
AH  BD nên AH nhận véc tơ pháp tuyến của BD : n
 1;5 làm vec tơ chỉ phương của BD 
mình. Vậy AH qua A2; 
1 có véc tơ chỉ phương là u
 1;5 nên phương trình tham số của AH  x  2  t
đường thẳng AH là:  .
 y  1 5t b)
H  AH  BD nên tọa độ H thỏa mãn hệ phương trình:  x  2  t x  2  t    32 43  y 1 5t
 y 1 5t  H ;   .    13 13 
x  5y 19  0 6  t    13  42 41  32 43  Vì I ; 
 là trung điểm BH với H ; 
 nên tọa độ B4;3 .  13 13   13 13 
Có AD  AB nên đường thẳng AD nhận véc tơ AB 2; 2 làm véc tơ pháp tuyến. 5
Đường thẳng AD đi qua điểm A2; 
1 và có véc tơ pháp tuyến AB 2; 2 nên có phương trình
tổng quát là: 2 x  2  2 y  
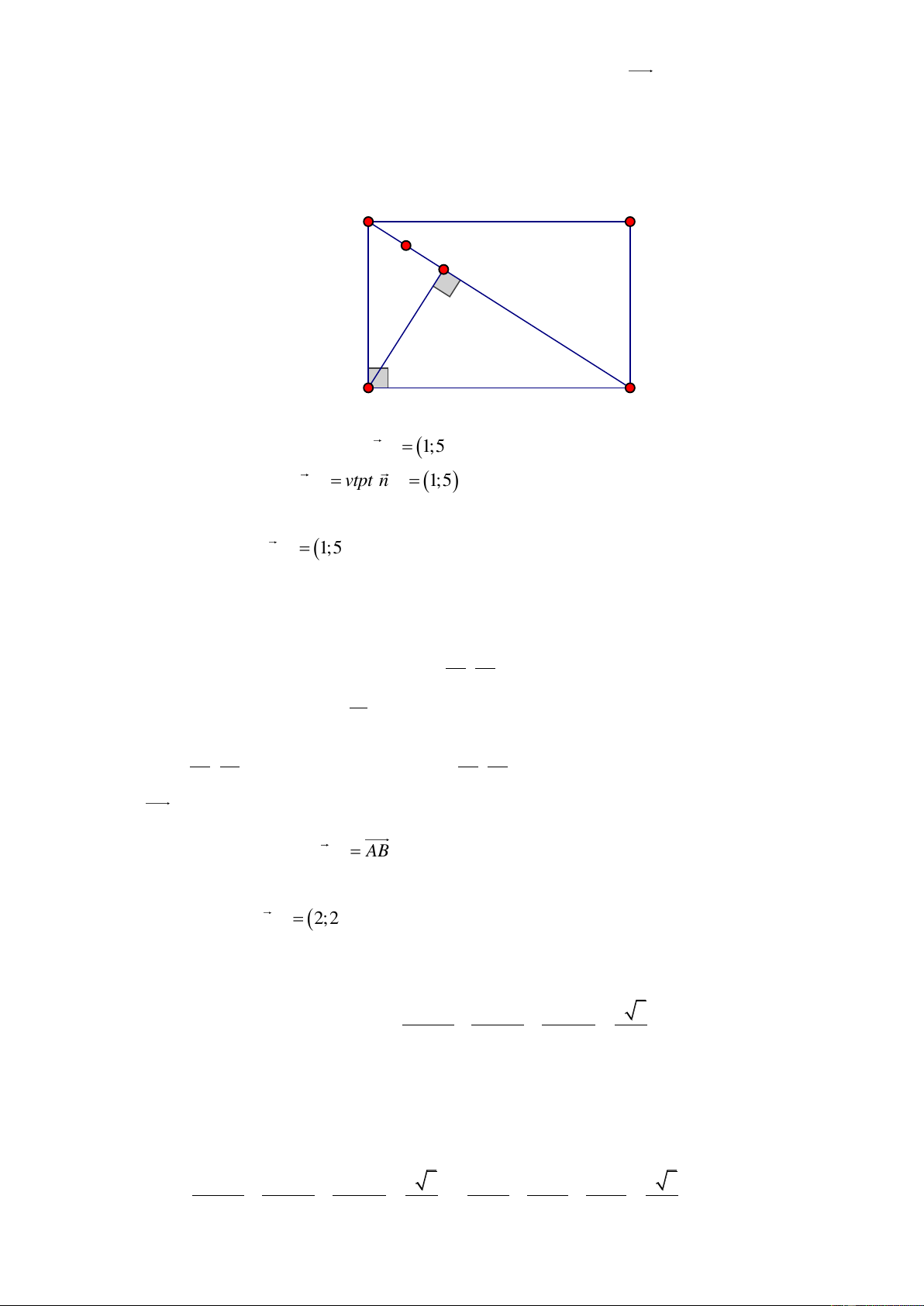
1  0  x  y  3  0 . Lời giải a) B C H I A D
BD : x  5 y 19  0 có vtpt là n  1;5 . BD 
AH  BD nên vtcp u
 vtpt n  1;5 . AH BD  qua A  2;1 x  2  t Vậy AH :    . vtcp u   1;5 y   t AH  1 5 b)
H  AH  BD nên tọa độ H thỏa mãn hệ phương trình:  x  2  t x  2  t    32 43  y 1 5t
 y 1 5t  H ;   .    13 13 
x  5y 19  0 6  t    13  42 41  32 43 
x  2x  x Vì I ; 
 là trung điểm BH với H ; 
 nên tọa độ B : B I H   B4;3 .  13 13   13 13 
y  2 y  y  B I H AB  2; 2 .
Có AD  AB nên vtpt n  AB  2;2 . AD  qua A  2;1 Vậy AD : 
 2x 2 2  y 1        . vtpt n     0 x y 3 0 2;2 AD Câu 5.
Cho ba số dương a, b, c thỏa mãn: 2 2 2
a  b  c  1. Chứng minh rằng a b c 3 3    . 2 2 2 2 2 2 b  c c  a a  b 2 Lời giải:
Do a, b, c  0 thỏa mãn 2 2 2
a  b  c  1 nên a, , b c 0  ;1 . a b c 3 3 a b c 3 3 Ta có        . 2 2 2 2 2 2 2 2 2 b  c c  a a  b 2 1 a 1 b 1 c 2 6 Ta sẽ chứng minh 1 3 3 2  a , a   0;1 (1). 2   1 a 2 Thật vậy 1 3 3 2  a   a 4 2 1 a    a 2 1 a  2 1 a (*). 2  1 a 2 3 3 27
Áp dụng bất đẳng thức AM-GM cho ba số dương 2 a  2  a   2 2 , 1 , 1 a  ta có:
a   a   a 4
2a .1 a .1 a  2 1 1 3 2 2 2 8 2 2 2   2  a . 2 1 a . 2 1 a   27 27 27  . a  2 2 1 a   . 3 3 1
Dấu “=” xảy ra khi và chỉ khi 2 2
2a  1 a  a  . 3 Vậy (*) luôn đúng. Tương tự b 3 3 1 ta có: 2  b , b
  0;1 (2). Dấu “=” xảy ra  b  . 2   1 b 2 3 c 3 3 1 2  c c , c
  0;1 (3). Dấu “=” xảy ra  c  . 2   1 c 2 3
Lấy (1), (2), (3) cộng theo vế ta có: a b c 3 3    . 2 2 2 2 2 2 b  c c  a a  b 2 1
Dấu “=” xảy ra  a  b  c  . 3 7