















Preview text:
1 TOANTHAYCU.COM
ĐỀ ÔN TẬP KẾT THÚC CHƯƠNG HSLG VÀ PTLG 0834332133 NĂM HỌC 2024-2025
MÔN THI: TOÁN 11- DÙNG CHUNG 3 LOẠI SÁCH
(Thời gian làm bài 90 phút, không kể thời gian giao đề) ĐỀ THỬ SỨC 01
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu
thí sinh chỉ chọn một phương án.
Câu 1: Hàm số y = sin x tuần hoàn với chu kỳ bao nhiêu? A. π . B. 2π . C. 3π . D. 4π .
Câu 2: Giá trị nào dưới đây của x là một nghiệm của phương trình tan x = 3 ? A. π π π π x = . B. x = . C. x = . D. x = . 6 4 3 2
Câu 3: Mệnh đề nào dưới đây đúng? A. cos cos
2cos x y .cos x y x y + − + = . 2 2 B. cos cos
2sin x y .sin x y x y + − + = . 2 2 C. cos cos
2cos x y .cos x y x y + − + = − . 2 2 D. cos cos
2sin x y .sin x y x y + − + = − . 2 2
Câu 4: Trong các đẳng thức sau đây, đẳng thức nào đúng?
A. sin (180° −α ) = −sinα .
B. cos(180° −α ) = cosα
C. tan (180° −α ) = tanα .
D. cot (180° −α ) = −cotα
Câu 5: Nghiệm của phương trình cot x = − 3 là A. π π
x = + kπ ,k ∈ .
B. x = − + kπ ,k ∈. 2 3 C. π π
x = + kπ ,k ∈ .
D. x = − + kπ ,k ∈. 4 6
Câu 6: Khẳng định nào sau đây đúng?
A. sin 2x = sin .xcosx . B. 2
cos2x = 2cos x −1. C. 2
cos2x = 2sin x −1. D. sin 2x = 2sin x .
Câu 7: Góc có số đo 80° đổi sang đơn vị radian bằng A. 5π . B. π . C. 2π . D. 4π . 9 9 9 9
Câu 8: Cho hàm số y = cosx . Khẳng định nào dưới đây sai?
A. Tập xác định của hàm số là D = .
B. Hàm số tuần hoàn với chu kỳ π . C. Hàm số chẵn.
D. Tập giá trị của hàm số là [ 1; − ] 1 .
Trần Đình Cư - 0834332133 2
Câu 9: Cho góc lượng giác α , biết π < α < π . Khẳng định nào sai? 2 A. sinα > 0. B. cotα < 0 . C. tanα < 0. D. cosα>0.
Câu 10: Công thức nghiệm của phương trình sin x = sinα là x = α + k2π x = α + k2π A. ,k ∈ . B. ,k ∈ .
x = π −α + k2π
x = π +α + k2π C. x = α
± + k2π ,k ∈ . D. x = α
± + kπ ,k ∈ .
Câu 11: Rút gọn biểu thức A = 2sin 2 .xcos3x −sin5x A. 2sin 5x . B. cosx . C. −cos5x . D. si − n x .
Câu 12: Phương trình 2
x = 4x tương đương với phương trình nào dưới đây? A. 2 x + 4x = 0 . B. 2
x + x − 2 = 4x + x − 2 . C. 2
x + x + 3 = 4x + x + 3 . D. 2 1 1 x + = 4x + . x x
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở
mỗi câu, thí sinh chọn đúng hoặc sai .
Câu 1: Từ một vị trí ban đầu trong không gian, vệ tinh X chuyển động theo quỹ đạo là một đường tròn
quanh trái đất và luôn cách tâm trái đất một khoảng bằng 9200km . Sau 2 giờ thì vệ tinh X hoàn
thành hết một vòng di chuyển. Các mệnh đề sau đúng hay sai?
a) Quãng đường vệ tinh X chuyển động được sau 1 giờ xấp xỉ 28902,65(km).
b) Quãng đường vệ tinh X chuyển động được sau 1,5 giờ xấp xỉ 43353,98(km) .
c) Sau khoảng 5,3 giờ thì X di chuyển được quãng đường 240000km .
d) Giả sử vệ tinh di chuyển theo chiều dương của đường tròn, sau 4,5 giờ thì quỹ đạo chuyển
động của vệ tinh thu được một góc 9π rad . 2 Câu 2: Cho 1 π
sinα = và < α < π. Mệnh đề sau đúng hay sai: 3 2
a) sin 2α = 2sinα cosα . b) 2 2 cosα = . 3 c) 4 2 tan 2α = − . 7 d) π 9 4 2 tan α − − = . 4 7
Câu 3: Cho hàm số y = f (x) = cos2x + cos x . Xét tính đúng - sai của các phát biểu sau:
a) Tập xác định của hàm số trên là .
Trần Đình Cư - 0834332133 3
b) Hàm số trên là hàm số chẵn.
c) Đặt t = cos x thì hàm số trở thành y = f (t) 2 = 2t + t −1.
d) Giá trị nhỏ nhất của hàm số y = f (x) là 0 .
Câu 4: Cho phương trình sin x = 0. 1− cos x
a) Tập xác định của hàm số sin x y =
là D = \{k2π,k ∈ } . 1− cos x b) Hàm số sin x y =
có chu kì tuần hoàn là T = π. 1− cos x
c) Phương trình sin x = 0 có tập nghiệm là S = {kπ,k ∈ } .
d) Số điểm biểu diễn nghiệm của phương trình sin x = 0 trên đường tròn lượng giác là 1− cos x 2.
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1: Trong chặng đua nước rút, bánh xe của một vận động viên đua xe đạp quay được 30 vòng
trong8 giây. Chọn chiều dương của chuyển động bánh xe cùng chiều quay của kim đồng hồ.
Biết rằng bán kính của bánh xe là 35 cm . Độ dài quãng đường mà vận động viên đua xe đạp
đã đi được trong 4 phút là bao nhiêu mét? .
Câu 2: Một sợi cáp R được gắn vào một cột thẳng đứng ở vị trí cách mặt đất 33 .
m Một sợi cáp S
khác cũng được gắn vào cột đó ở vị trí cách mặt đất 25 .
m Biết rằng hai sợi cáp trên cùng được
gắn với mặt đất tại một vị trí cách chân cột 35m . Gọi α là góc giữa hai sợi cáp trên. Biết tan a
α = với a, b∈ a
, tối giản. Tính 10a + 4 . b b b
Trần Đình Cư - 0834332133 4
Câu 3: Huyết áp của một người được cho thông qua hàm số p(t) =120 + 30.sin(160πt) , trong đó
p(t) là huyết áp tính bằng mmHg tại thời điểm t ≥ 0 tính bằng phút. Huyết áp tối đa và huyết
áp tối thiểu gọi là huyết áp tâm thu và huyết áp tâm trương. Hiệu số của Huyết áp tâm trương
và huyết áp tâm thu của người này là bao nhiêu?
Câu 4: Giả sử một vật dao động điều hoà xung quanh vị trí cân bằng theo phương trình 2cos5 π x t = − 6
Ở đây, thời gian t tính bằng giây và quãng đường x tính bằng centimét. Hãy cho biết trong
khoảng thời gian từ 0 đến 6 giây, vật đi qua vị trí cân bằng bao nhiêu lần?
Câu 5: Huyết áp là áp lực máu cần thiết tác động lên thành động mạch nhằm đưa máu đi nuôi dưỡng
các mô trong cơ thể. Nhờ lực co bóp của tim và sức cản của động mạch mà huyết áp được tạo
ra. Giả sử huyết áp của một người thay đổi theo thời gian được cho bởi công thức:
p(t) =120 +15cos150πt
trong đó p(t) là huyết áp tính theo đơn vị mmHg và thời gian t tính theo đơn vị phút. Huyết
áp cao nhất và huyết áp thấp nhất lần lượt được gọi là huyết áp tâm thu và huyết áp tâm trương.
Tìm chỉ số huyết áp của người đó, biết rằng chỉ số huyết áp được viết là huyết áp tâm thu/huyết áp tâm trương.
Câu 6: Tính tổng tất cả các nghiệm của phương trình sin 2x = cos x trong đoạn [0;2π ], . HẾT
Trần Đình Cư - 0834332133
ĐÁP ÁN ĐỀ SỐ 01
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn.
(Mỗi câu trả lời đúng thí sinh được 0,25 điểm)
BẢNG ĐÁP ÁN TRẮC NGHIỆM Câu 1 2 3 4 5 6 7 8 9 10 11 12 Chọn B C A D D B D B D A D C
PHẦN II. Câu trắc nghiệm đúng sai.
Điểm tối đa của 01 câu hỏi là 1 điểm
-Thí sinh chỉ lựa chọn chính xác 01 ý trong 1 câu hỏi được 0,1 điểm.
-Thí sinh chỉ lựa chọn chính xác 02 ý trong 1 câu hỏi được 0,25 điểm.
-Thí sinh chỉ lựa chọn chính xác 03 ý trong 1 câu hỏi được 0,5 điểm.
-Thí sinh lựa chọn chính xác cả 04 ý trong 1 câu hỏi được 1,0 điểm. Câu 1 Câu 2 Câu 3 Câu 4 a) Đ a) Đ a) Đ a) Đ b) Đ b) S b) Đ b) S c) S c) Đ c) Đ c) Đ d) Đ d) S d) S d) S
PHẦN III. Câu trắc nghiệm trả lời ngắn.
(Mỗi câu trả lời đúng thí sinh được 0,5 điểm) Câu 1 2 3 4 5 6 Chọn 1979 1100 60 9 1,29 9,24
LỜI GIẢI CHI TIẾT
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu thí
sinh chỉ chọn một phương án.
Câu 1: Hàm số y = sin x tuần hoàn với chu kỳ bao nhiêu? A. π . B. 2π . C. 3π . D. 4π . Lời giải Chọn B
Câu 2: Giá trị nào dưới đây của x là một nghiệm của phương trình tan x = 3 ? A. π π π π x = . B. x = . C. x = . D. x = . 6 4 3 2 Lời giải Chọn C
Câu 3: Mệnh đề nào dưới đây đúng? A. cos cos
2cos x y .cos x y x y + − + = . 2 2 B. cos cos
2sin x y .sin x y x y + − + = . 2 2 C. cos cos
2cos x y .cos x y x y + − + = − . 2 2 D. cos cos
2sin x y .sin x y x y + − + = − . 2 2 Lời giải Chọn A
Câu 4: Trong các đẳng thức sau đây, đẳng thức nào đúng?
A. sin (180° −α ) = −sinα .
B. cos(180° −α ) = cosα
C. tan (180° −α ) = tanα .
D. cot (180° −α ) = −cotα Lời giải Chọn D
Mối liên hệ hai cung bù nhau.
Câu 5: Nghiệm của phương trình cot x = − 3 là A. π π
x = + kπ ,k ∈ .
B. x = − + kπ ,k ∈. 2 3 C. π π
x = + kπ ,k ∈ .
D. x = − + kπ ,k ∈. 4 6 Lời giải Chọn D π π
cot x = − 3 ⇔ cot x = cot − ⇔
x = − + kπ ,k ∈ . 6 6
Câu 6: Khẳng định nào sau đây đúng?
A. sin 2x = sin .xcosx . B. 2
cos2x = 2cos x −1. C. 2
cos2x = 2sin x −1. D. sin 2x = 2sin x . Lời giải Chọn B
Câu 7: Góc có số đo 80° đổi sang đơn vị radian bằng A. 5π . B. π . C. 2π . D. 4π . 9 9 9 9 Lời giải Chọn D Ta có: 80.π 4π 80° = = rad . 180 9
Câu 8: Cho hàm số y = cosx . Khẳng định nào dưới đây sai?
A. Tập xác định của hàm số là D = .
B. Hàm số tuần hoàn với chu kỳ π . C. Hàm số chẵn.
D. Tập giá trị của hàm số là [ 1; − ] 1 . Lời giải Chọn B
Câu 9: Cho góc lượng giác α , biết π < α < π . Khẳng định nào sai? 2 A. sinα > 0. B. cotα < 0 . C. tanα < 0. D. cosα>0. Lời giải Chọn D
Vì π < α < π nên điểm biểu diễn của α thuộc cung phần tư thứ 2, do đó 2
sinα > 0;cosα <0;tanα <0;cotα <0 .
Câu 10: Công thức nghiệm của phương trình sin x = sinα là x = α + k2π x = α + k2π A. ,k ∈ . B. ,k ∈ .
x = π −α + k2π
x = π +α + k2π C. x = α
± + k2π ,k ∈ . D. x = α
± + kπ ,k ∈ . Lời giải Chọn A
Câu 11: Rút gọn biểu thức A = 2sin 2 .xcos3x −sin5x A. 2sin 5x . B. cosx . C. −cos5x . D. si − n x . Lời giải Chọn D Ta có: 1 A = 2sin 2 .
x cos3x − sin 5x = 2. sin
(2x −3x) +sin(2x +3x) −sin5x 2
= sin (−x) + sin 5x − sin 5x = sin (−x) = −sin x .
Câu 12: Phương trình 2
x = 4x tương đương với phương trình nào dưới đây? A. 2 x + 4x = 0 . B. 2
x + x − 2 = 4x + x − 2 . C. 2
x + x + 3 = 4x + x + 3 . D. 2 1 1 x + = 4x + . x x Lời giải Chọn C x = 0 Ta có: 2 x = 4x ⇔ , vậy S = {0; } 4 . x = 4 x = 0 +) Giải phương trình A: 2
x + 4x = 0 ⇔
. Do đó hai phương trình không tương đương. x = 4 − x ≥ 2 x ≥ 2 +) Giải phương trình B: 2 x x 2 4x x 2 + − = + − ⇔
⇔ x = 0 ⇔ x = 0. Do đó hai 2 x = 4x x = 4
phương trình không tương đương. x ≥ 3 − x ≥ 3 − x = 0 +) Giải phương trình C: 2
x + x + 3 = 4x + x + 3 ⇔ ⇔ x = 0 ⇔ . Do đó hai 2 x = 4x x = 4 x = 4
phương trình tương đương. x ≠ 0 1 1 x ≠ 0 +) Giải phương trình D: 2 x 4x + = + ⇔
⇔ x = 0 ⇔ x = 4. Do đó hai phương 2 x x x = 4x x = 4
trình không tương đương.
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở
mỗi câu, thí sinh chọn đúng hoặc sai .
Câu 1: Từ một vị trí ban đầu trong không gian, vệ tinh X chuyển động theo quỹ đạo là một đường tròn
quanh trái đất và luôn cách tâm trái đất một khoảng bằng 9200km . Sau 2 giờ thì vệ tinh X hoàn
thành hết một vòng di chuyển. Các mệnh đề sau đúng hay sai?
a) Quãng đường vệ tinh X chuyển động được sau 1 giờ xấp xỉ 28902,65(km).
b) Quãng đường vệ tinh X chuyển động được sau 1,5 giờ xấp xỉ 43353,98(km) .
c) Sau khoảng 5,3 giờ thì X di chuyển được quãng đường 240000km .
d) Giả sử vệ tinh di chuyển theo chiều dương của đường tròn, sau 4,5 giờ thì quỹ đạo chuyển
động của vệ tinh thu được một góc 9π rad . 2 Lời giải
a) Một vòng di chuyển của X chính là chu vi đường tròn: C = 2π R = 2π.9200 =18400π (km) .
Sau 1 giờ, vệ tinh di chuyển nửa đường tròn với quãng đường: 1 C = 9200π ≈ 28902,65(km) . 2
Suy ra mệnh đề Đúng.
b) Sau 1,5 giờ, vệ tinh di chuyển được 3 đường tròn với quãng đường: 4 3 3
C = .18400π = 43353,98(km) . suy ra mệnh đề Đúng. 4 4
c) Số giờ để vệ tinh X di chuyển được quãng đường 240000km là: 240000 ≈ 8,3. 9200π
Suy ra mệnh đề Sai.
d) Sau 4,5 giờ thì số vòng mà vệ tinh X di chuyển được là: 9 . 4
Vậy số đo góc lượng giác thu được là: 9 9π .2π =
( rad ). Suy ra mệnh đề Đúng. 4 2 Câu 2: Cho 1 π
sinα = và < α < π. Mệnh đề sau đúng hay sai: 3 2
a) sin 2α = 2sinα cosα . b) 2 2 cosα = . 3 c) 4 2 tan 2α = − . 7 d) π 9 4 2 tan α − − = . 4 7 Lời giải
a) Ta có sin 2α = 2sinα cosα . Suy ra mệnh đề đúng.
b) Với π < α < π thì ta có 2 1 2 2
cosα = − 1− sin α = − 1− = −
. Suy ra mệnh đề sai. 2 9 3
c) Với π < α < π thì ta có 2 1 2 2
cosα = − 1− sin α = − 1− = − . 2 9 3 1 α Suy ra sin 3 2 tanα = = = − . cosα 2 2 4 − 3 2 2.− 2 tanα 4 Do đó 4 2 tan 2α = = = −
. Suy ra mệnh đề đúng 2 2 1− tan α 7 2 1− − 4 tan − tan π α d) π α Ta có 4 tan −1 tan α − = = 4 π tanα +1 1+ tanα.tan 4
Với π < α < π thì ta có 2 1 2 2
cosα = − 1− sin α = − 1− = − . 2 9 3 1 α Suy ra sin 3 2 tanα = = = − . cosα 2 2 4 − 3 2 − −1 Vậy π tanα −1 4 9 + 4 2 tan α − = = = − 4 tanα +1 2 7 − +1 4
Suy ra mệnh đề sai.
Câu 3: Cho hàm số y = f (x) = cos2x + cos x . Xét tính đúng - sai của các phát biểu sau:
a) Tập xác định của hàm số trên là .
b) Hàm số trên là hàm số chẵn.
c) Đặt t = cos x thì hàm số trở thành y = f (t) 2 = 2t + t −1.
d) Giá trị nhỏ nhất của hàm số y = f (x) là 0 . Lời giải
a) Tập xác định của hàm số trên là . Mệnh đề đúng. x
∀ ∈ ⇒ −x∈ b) Vì
⇒ f (x) là hàm số chẵn suy ra mệnh đề đúng. f (−x) = cos( 2
− x) + cos(−x) = f (x) c) Ta có 2
y = cos 2x + cos x = 2cos + cos x −1.
Đặt:t = cos x , t ∈[ 1; − ]
1 , khi đó f (t) 2
= 2t + t −1. Suy ra mệnh đề đúng. 2 d) Đặt:
t = cos x , t ∈[ 1; − ]
1 , khi đó f (t) 2 1 9 9
= 2t + t −1 = 2 t + − ≥ − ; t ∀ ∈[ 1; − ]1. 4 8 8 Suy ra m = f (t) 9 min
= − . Do đó mệnh đề sai. [ 1 − ] ;1 8
Câu 4: Cho phương trình sin x = 0. 1− cos x
a) Tập xác định của hàm số sin x y =
là D = \{k2π,k ∈ } . 1− cos x b) Hàm số sin x y =
có chu kì tuần hoàn là T = π. 1− cos x
c) Phương trình sin x = 0 có tập nghiệm là S = {kπ,k ∈ } .
d) Số điểm biểu diễn nghiệm của phương trình sin x = 0 trên đường tròn lượng giác là 2. 1− cos x Lời giải
a) Điều kiện xác định của hàm số sin x y =
là cos x ≠ 0 ⇔ x ≠ k2π ,k ∈ Z nên mệnh đề đúng. 1− cos x
b) Chu kì tuần hoàn của hàm số y = sin x và hàm số y = cos x đều bằng 2π nên chu kì tuần hoàn của hàm số sin x y =
cũng bằng 2π. Mệnh đề sai. 1− cos x
c) sin x = 0 ⇔ x = kπ ,k ∈ .
Mệnh đề đúng. sin x cos x ≠ 0 x ∈ D d) = 0 ⇔ ⇔
. Dựa vào đồ thị hàm số y = sin x , y = cos x và đường thẳng 1− cos x si n x 0 = x ∈ S
y =1 ta được nghiệm của phương trình trên [0;2π ] là x = π . Vậy có 1 điểm biểu diễn nghiệm
trên đường tròn lượng giác. Mệnh đề sai
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1: Trong chặng đua nước rút, bánh xe của một vận động viên đua xe đạp quay được 30 vòng trong
8 giây. Chọn chiều dương của chuyển động bánh xe cùng chiều quay của kim đồng hồ. Biết rằng
bán kính của bánh xe là 35 cm . Độ dài quãng đường mà vận động viên đua xe đạp đã đi được
trong 4 phút là bao nhiêu mét? . Lời giải Trả lời: 1979
Gọi V van của bánh xe.
Sau 1 giây, van V của bánh xe quay được 30 = 3,75 . 8
Sau 4 phút, van V của bánh xe quay được 3,75⋅240 = 900 .
Suy ra sau 4 phút, van V của bánh xe quay được một góc có số đo là α = 900.2π =1800π.
Mỗi góc ở tâm với số đo 1 rad chắn một cung có độ dài bằng bán kính bánh xe R = 0,35 m .
Do đó, độ dài quãng đường mà vận động viên đua xe đạp đã đi được trong 4 phút là l = .
Rα =1800π ⋅0,35 ≈1979(m).
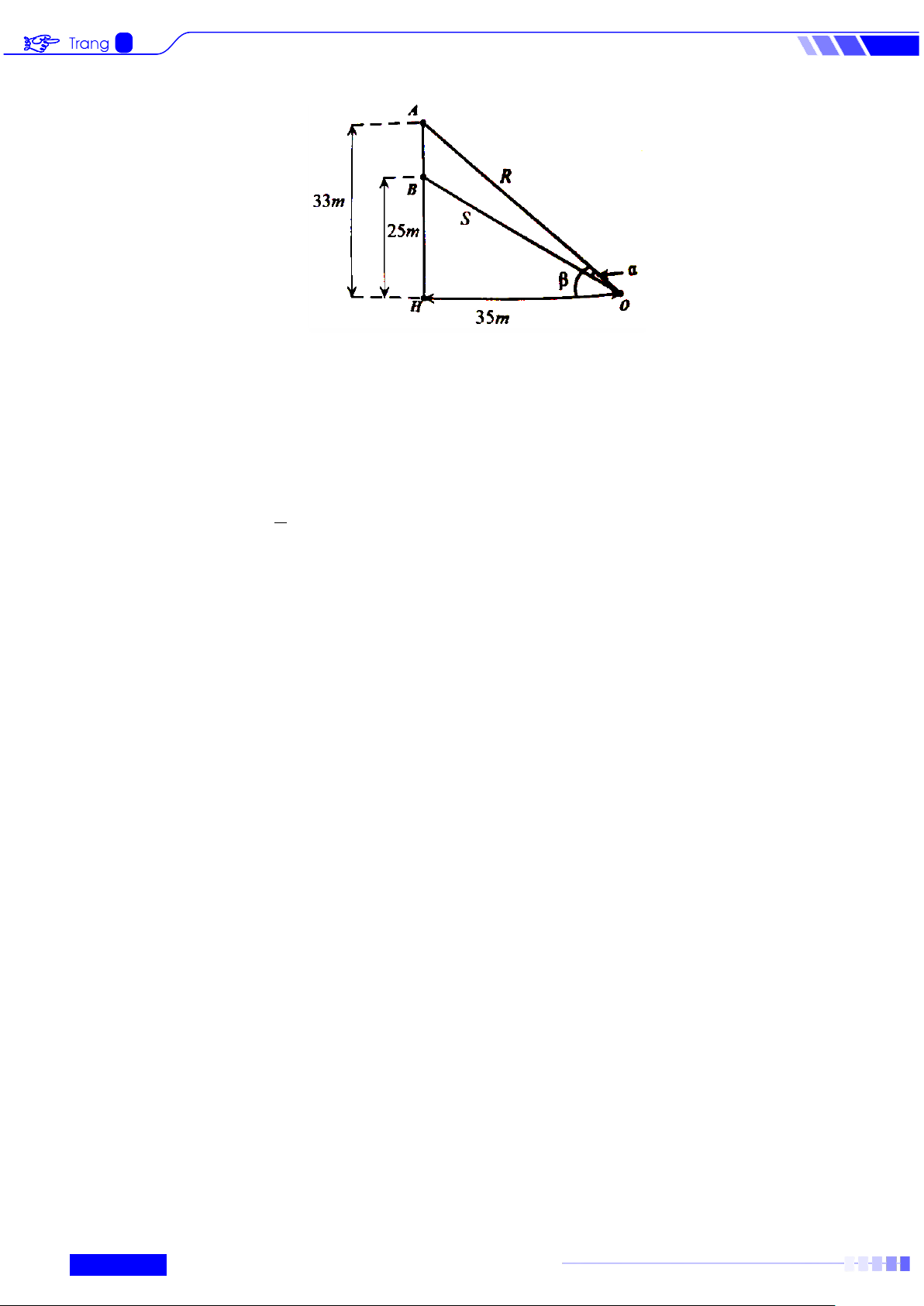
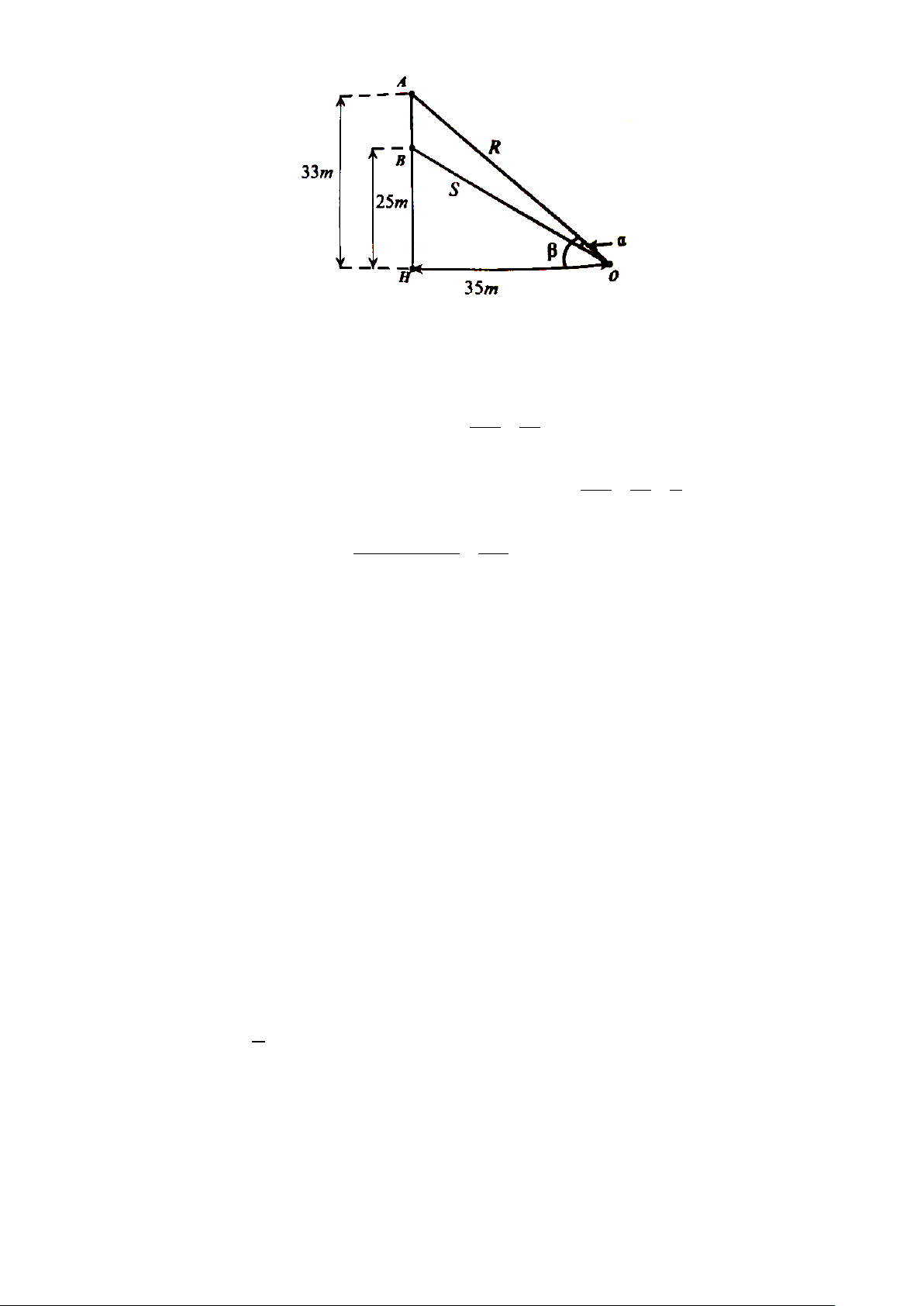
Câu 2: Một sợi cáp R được gắn vào một cột thẳng đứng ở vị trí cách mặt đất 33 .
m Một sợi cáp S khác
cũng được gắn vào cột đó ở vị trí cách mặt đất 25 .
m Biết rằng hai sợi cáp trên cùng được gắn
với mặt đất tại một vị trí cách chân cột 35m . Gọi α là góc giữa hai sợi cáp trên. Biết tan a α = b với a, b∈ a
, tối giản. Tính 10a + 4 . b b Lời giải
Trả lời: 1100
Xét tam giác AOH vuông tại H có AH 33 tan β = = . HO 35 Đặt
BOH = γ . Xét tam giác BOH vuông tại H có BH 25 5 tanγ = = = . HO 35 7 β − γ Suy ra α = (β −γ ) tan tan 28 tan tan = = . 1+ tan β.tanγ 205 Do đó, a = 28, 205. b =
Vậy 10a + 4b =10.28 + 4.205 =1100.
Câu 3: Huyết áp của một người được cho thông qua hàm số p(t) =120 + 30.sin(160πt) , trong đó p(t)
là huyết áp tính bằng mmHg tại thời điểm t ≥ 0 tính bằng phút. Huyết áp tối đa và huyết áp tối
thiểu gọi là huyết áp tâm thu và huyết áp tâm trương. Hiệu số của Huyết áp tâm trương và huyết
áp tâm thu của người này là bao nhiêu? Lời giải Trả lời: 60 Ta có: Ta có: 1
− ≤ sin(160πt) ≤1 ⇔ 90 ≤120 + 30sin(160πt) ≤150 . Suy ra HA tâm thu: 90 HA tâm trương 150 Hiệu số bằng 60.
Câu 4: Giả sử một vật dao động điều hoà xung quanh vị trí cân bằng theo phương trình 2cos5 π x t = − 6
Ở đây, thời gian t tính bằng giây và quãng đường x tính bằng centimét. Hãy cho biết trong
khoảng thời gian từ 0 đến 6 giây, vật đi qua vị trí cân bằng bao nhiêu lần? Lời giải Trả lời: 9
Vị trí cân bằng của vật dao động điều hòa là vị trí vật đứng yên, khi đó x = 0 , ta có π π 2cos 5t 0 cos 5t − = ⇔ − = 0 6 6 π π 2π π
⇔ 5t − = + k,k ∈ ⇔ t =
+ k ,k ∈ 6 2 15 5
Trong khoảng thời gian từ 0 đến 6 giây, tức là 0 ≤ t ≤ 6 hay 2π π 2 90 − 2π 0 ≤
+ k ≤ 6 ⇔ − ≤ k ≤ 15 5 3 3π
Vì k ∈ nên k ∈{0;1;2;3;4;5;6;7;8}.
Vậy trong khoảng thời gian từ 0 đến 6 giây, vật đi qua vị trí cân bằng 9 lần.
Câu 5: Huyết áp là áp lực máu cần thiết tác động lên thành động mạch nhằm đưa máu đi nuôi dưỡng các
mô trong cơ thể. Nhờ lực co bóp của tim và sức cản của động mạch mà huyết áp được tạo ra. Giả
sử huyết áp của một người thay đổi theo thời gian được cho bởi công thức:
p(t) =120 +15cos150πt
trong đó p(t) là huyết áp tính theo đơn vị mmHg và thời gian t tính theo đơn vị phút. Huyết
áp cao nhất và huyết áp thấp nhất lần lượt được gọi là huyết áp tâm thu và huyết áp tâm trương.
Tìm chỉ số huyết áp của người đó, biết rằng chỉ số huyết áp được viết là huyết áp tâm thu/huyết áp tâm trương. Lời giải
Trả lời: 1,29 Ta có: 1
− ≤ cos150πt ≤1, t ∀ ∈ ⇒ 15
− ≤ 15cos150πt ≤15, t ∀ ∈
Hay: 105 ≤ p(t) ≤135, t ∀ ∈
Vậy chỉ số huyết áp của người đó là: 135 ≈1,29 105
Câu 6: Tính tổng tất cả các nghiệm của phương trình sin 2x = cos x trong đoạn [0;2π ], . Lời giải
Trả lời: 9,42 π k2π x π = + Ta có: 6 3
sin 2x = cos x ⇔ sin 2x = sin − x ⇔ (k ∈). 2 π x = + k2π 2 Vì π π π π x [ π ] 5 3 0;2 x ; ; ; ∈ ⇒ ∈ 6 6 2 2
Vậy tổng các nghiệm của phương trình là: π 5π 3π π S = + + + = 3π ≈ 9,42 6 6 2 2 1 TOANTHAYCU.COM
ĐỀ ÔN TẬP KẾT THÚC CHƯƠNG HSLG VÀ PTLG 0834332133 NĂM HỌC 2024-2025
MÔN THI: TOÁN 11- DÙNG CHUNG 3 LOẠI SÁCH
(Thời gian làm bài 90 phút, không kể thời gian giao đề) ĐỀ THỬ SỨC 02
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu
thí sinh chỉ chọn một phương án.
Câu 1: Hàm số y = sinx tuần hoàn theo chu kỳ: A. . B. π . C. 2π . D. k2π .
Câu 2: Số nào là nghiệm của phương trình 3 cos x = ? 2 π π π π A. 5 . B. 11 . C. 13 . D. 13 . 6 6 6 6
Câu 3: Công thức nào sau đây sai?
A. cos(a −b) = sin asin b + cos acos . b
B. cos(a + b) = sin asin b − cos acos . b
C. sin (a −b) = sin acosb − cos asin . b
D. sin (a + b) = sin acosb + cosasin . b Câu 4: Góc o
36 có số đo bằng rađian là π π π π A. . B. . C. . D. . 18 5 36 6
Câu 5: Phương trình: sin x = 0 có tập nhghiệm là A. x = π .
B. x = k2π . C. x = 0 .
D. x = kπ . π
Câu 6: Cho góc lượng giác (OM ,ON ) có số đo bằng . Hỏi trong các số sau, số nào là số đo của 7
một góc lượng giác có cùng tia đầu, tia cuối với góc lượng giác (OM ,ON ) ? π − π π π A. 6 . B. 11 . C. 9 . D. 29 . 7 7 7 7
Câu 7: Trong các công thức sau, công thức nào sai A. 2 2
cos 2x = cos x − sin x .
B. cos 2x = 2cos x . C. 2
cos 2x = 2cos x −1.
D. sin 2x = 2sin xcos x .
Câu 8: Nghiệm của phương trình cot x = − 3 là: π π π π A. x = .
B. x = − + kπ .
C. x = + kπ .
D. x = − + kπ . 6 6 6 3 π Câu 9: Cho cos – 12 α =
và < α < π . Giá trị của tanα là 13 2 2 5 5 5 A. . B. − . C. . D. − . 3 12 12 12
Câu 10: Trong các công thức sau, công thức nào sai?
Trần Đình Cư - 0834332133 2 1 1
A. cos a cosb = cos
(a – b)+ cos(a +b).
sin asin b = cos a – b – cos a + b . 2 B. ( ) ( ) 2 1 1
C. sin a cosb = sin
(a – b)+sin(a +b).
D. sin a cosb = sin
(a −b)−cos(a +b). 2 2
Câu 11: Cho các mệnh đề sau
. Hàm số y = tan x luôn luôn tăng.
. Hàm số y = tan x luôn luôn tăng trên từng khoảng xác định.
. Hàm số y = tan x tăng trong các khoảng (π + k2 ;2
π π + k2π),k ∈ . .
. Hàm số y = tan x tăng trong các khoảng (k ;
2π π + k2π),k ∈ .
Có bao nhiêu mệnh đề đúng? A. 0 . B. 3. C. 1. D. 2 .
Câu 12: Phương trình lượng giác: cos2 x +1,5 = 0 tương đương với phương trình
A. 2cos x +1,5 = 0 . B. 2
2cos x −1,5 = 0 . C. 2
0,5 − 2sin x = 0 . D. 2 sin x + 0,5 = 0 .
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở
mỗi câu, thí sinh chọn đúng hoặc sai .
Câu 1: Huyết áp của mỗi người thay đổi trong ngày. Giả sử huyết áp tâm trương của một người nào
đó ở trạng thái nghỉ ngơi tại thời điểm t được cho bởi công thức: π ( ) = 80 + 7sin t B t . 12 a) Ta có: π 0 = 15 . 12 b) Ta có: 5π 1 sin = − . 6 2
c) Huyết áp tâm trương của người này vào thời điểm 8 giờ sáng là 80,255 mmHg.
d) Huyết áp tâm trương của người này vào thời điểm 2 giờ 30 phút chiều là 80,463 mmHg. π Câu 2: Cho biết 4
sinα = và < α < π . Các mệnh đề sau đây đúng hay sai? 5 2 a) cosα < 0 .
b) sin 2α > 0 . c) 7 cos 2α = − . 25 d) 2 π α 4 cos − = . 4 2 5
Câu 3: Cho hàm số f (x) 1 1 = + . 2 2 cos x sin x a) f ( ) 1 1 3 = + . 2 2 cos 3 sin 3
Trần Đình Cư - 0834332133 3 b) π
Tập xác định của hàm số là D \ kπ ,k = + ∈ . 2
c) Hàm số đã cho là hàm số lẻ.
d) Giá trị nhỏ nhất của hàm số là 4.
Câu 4: Cho phương trình: cos2x −3sin x − 2 = 0 . a) Ta có 2
cos2x =1− 2.sin x .
b) Đặt t = sin x, 1
− ≤ t ≤1 thì phương trình trở thành 2
2t + 3t −1= 0 . π
c) x = − + k2π ,(k ∈) là một họ nghiệm của phương trình. 2
d) Phương trình có 3 nghiệm thuộc khoảng (0;2π ) .
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
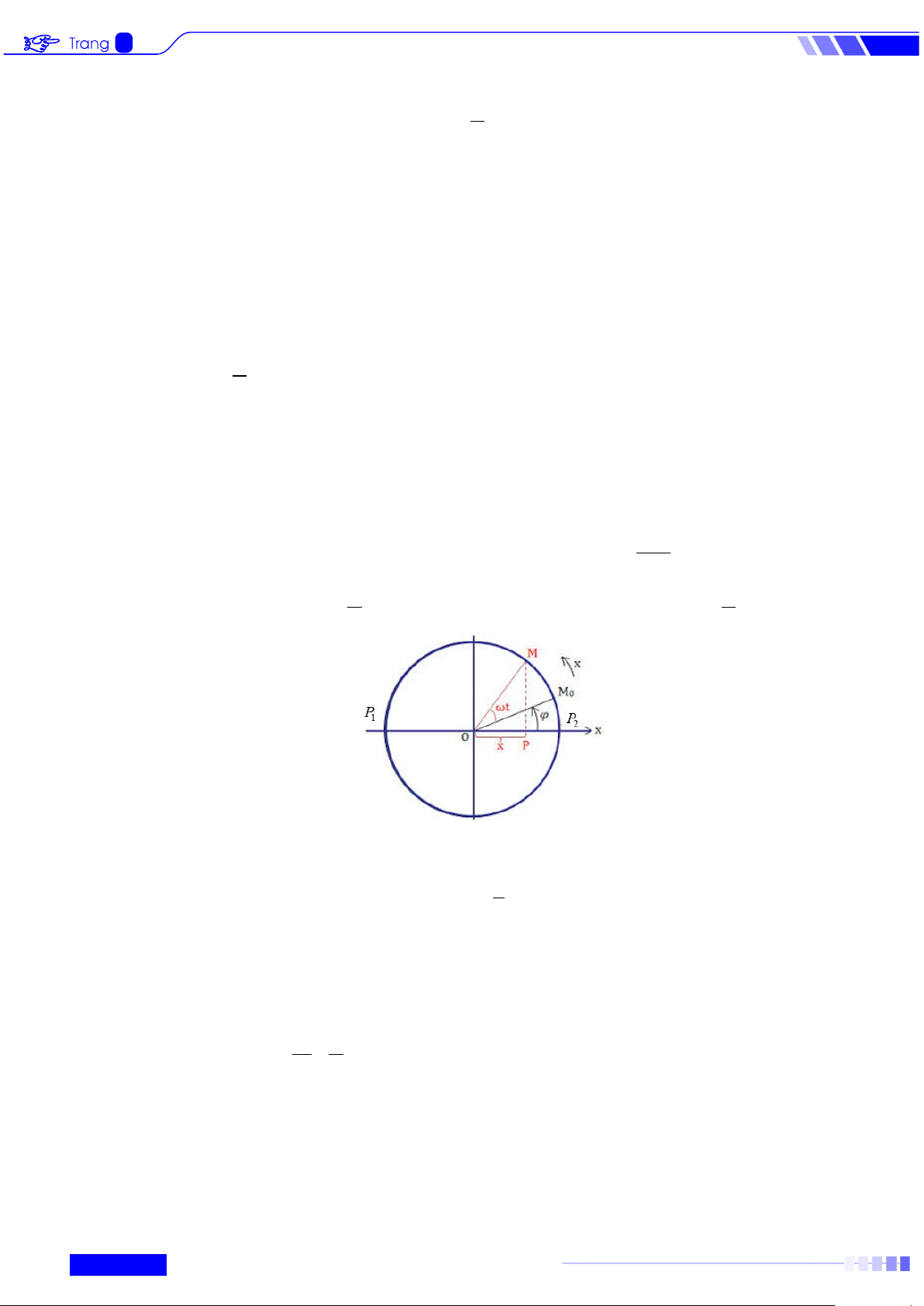
Câu 1: Một điểm P dao động điều hòa từ vị trí 1P đến 2 P , sao cho 1P 2
P =10cm . Ta coi P là hình
chiếu của điểm M chuyển động tròn đều trên đường tròn 1 P 2 ; P O
lên đoạn PP . Tốc độ 2 1 2
góc của điểm M là π ϖ π
= . Tại thời điểm t = 0 thì góc ϕ = ( 2 OP ,OM0 ) = 4 3
Tính khoảng cách OP tại thời điểm t = 2 giây, kết quả làm tròn đến hàng phần trăm.
Câu 2: Cho hai góc α;β thỏa mãn (α + β ) 1 sin = và tanα = 2
− tan β . Tính sin (α − β ) , kết quả 3
làm tròn đến hàng phần mười.
Câu 3: Hàng ngày, mực nước của một con kênh lên xuống theo thủy triều. Độ sâu h(m) của mực
nước trong kênh tính theo thời gian t trong một ngày (0 ≤ t ≤ 24) cho bởi công thức ( ) π π cos t h t a b = + + ( 0; a > b >
0). Biết rằng mực nước của con kênh vào lúc 4 sáng là 12 3
9,5(m) và mực nước thấp nhất của con kênh là 8(m). Hỏi mực nước của con kênh vào lúc
4 giờ chiều là nhiêu mét?
Trần Đình Cư - 0834332133 4 π
Câu 4: Một vật dao động điều hòa với phương trình x = 4cos(6πt + ) , ( x tính bằng cm, t tính bằng 3
giây). Xác định thời điểm vật qua vị trí x = 2cm theo chiều dương lần thứ 2 kể từ thời điểm ban đầu.
Câu 5: Khi đu quay hoạt động, vận tốc v của cabin M theo phương tiếp xúc với vòng quay có độ
lớn không đổi là 0,2(m / s). Giả sử α = (Ox,OM ), v là vận tốc của cabin M theo phương x
ngang phụ thuộc góc α . Khi đu quay hoạt động, giá trị lớn nhất của vx là bao nhiêu?
Câu 6: Khoảng cách từ tâm của một guồng nước đến mặt nước và bán kính của guồng đều bằng 2m
. Xét gàu G của guồng. Ban đầu gàu G nằm vị trí A . Gọi h(α ) là hàm biểu diễn chiều cao
của gàu G so với mặt nước theo góc α = ( ,
OA OG) . Guồng nước quay hết mỗi vòng là 24
giây. Lần đầu tiên gàu G cách mặt nước 3m là sau khi quay bao nhiêu giây? HẾT
Trần Đình Cư - 0834332133
ĐÁP ÁN ĐỀ SỐ 02
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn.
(Mỗi câu trả lời đúng thí sinh được 0,25 điểm)
BẢNG ĐÁP ÁN TRẮC NGHIỆM Câu 1 2 3 4 5 6 7 8 9 10 11 12 Chọn C B B B D D D B D D C D
PHẦN II. Câu trắc nghiệm đúng sai.
Điểm tối đa của 01 câu hỏi là 1 điểm
-Thí sinh chỉ lựa chọn chính xác 01 ý trong 1 câu hỏi được 0,1 điểm.
-Thí sinh chỉ lựa chọn chính xác 02 ý trong 1 câu hỏi được 0,25 điểm.
-Thí sinh chỉ lựa chọn chính xác 03 ý trong 1 câu hỏi được 0,5 điểm.
-Thí sinh lựa chọn chính xác cả 04 ý trong 1 câu hỏi được 1,0 điểm. Câu 1 Câu 2 Câu 3 Câu 4 a) Đ a) Đ a) Đ a) Đ b) S b) S b) S b) S c) S c) Đ c) S c) Đ d) Đ d) S d) Đ d) Đ
PHẦN III. Câu trắc nghiệm trả lời ngắn.
(Mỗi câu trả lời đúng thí sinh được 0,5 điểm) Câu 1 2 3 4 5 6 Chọn 4,33 -0,3 12,5 0,56 0,2 2
LỜI GIẢI CHI TIẾT
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu thí
sinh chỉ chọn một phương án.
Câu 1: Hàm số y = sinx tuần hoàn theo chu kỳ: A. . B. π . C. 2π . D. k2π . Lời giải Chọn C
Ta có: Hàm số y = sinx tuần hoàn theo chu kỳ 2π
Câu 2: Số nào là nghiệm của phương trình 3 cos x = ? 2 π π π π A. 5 . B. 11 . C. 13 . D. 13 . 6 6 6 6 Lời giải Chọn B π x = + k2π Ta có 3 π 6 cos x = ⇔ cos x = cos ⇔ (k ∈ ) . 2 6 π
x = − + k2π 6 π π
Nhận thấy với nghiệm x = − + k2π , với 11 k =1⇒ x = . 6 6
Câu 3: Công thức nào sau đây sai?
A. cos(a −b) = sin asinb + cos acos . b
B. cos(a + b) = sin asinb − cos acos . b
C. sin (a −b) = sin acosb − cos asin . b
D. sin (a + b) = sin acosb + cos asin . b Lời giải Chọn B
Ta có: cos(a −b) = sin asin b − cos a cos . b Câu 4: Góc o
36 có số đo bằng rađian là π π π π A. . B. . C. . D. . 18 5 36 6 Lời giải Chọn B π π π Ta có: o o 1 = rad ⇒ 36 = 36. rad = rad 180 180 5
Câu 5: Phương trình: sin x = 0 có tập nhghiệm là A. x = π .
B. x = k2π . C. x = 0 .
D. x = kπ . Lời giải Chọn D
Ta có sin x = 0 ⇔ x = kπ . π
Câu 6: Cho góc lượng giác (OM ,ON ) có số đo bằng . Hỏi trong các số sau, số nào là số đo của một 7
góc lượng giác có cùng tia đầu, tia cuối với góc lượng giác (OM ,ON ) ? π − π π π A. 6 . B. 11 . C. 9 . D. 29 . 7 7 7 7 Lời giải Chọn D π
Ta có: (OM ,ON ) = + k2π,(k ∈ Z) 7 π Với 29
k = 2 ⇒ (OM ,ON) = 7
Câu 7: Trong các công thức sau, công thức nào sai A. 2 2
cos 2x = cos x − sin x .
B. cos 2x = 2cos x . C. 2
cos 2x = 2cos x −1.
D. sin 2x = 2sin xcos x . Lời giải Chọn B Ta có: 2 2 2 2
cos 2x = cos x − sin x = 2cos x −1 =1− 2sin x
Câu 8: Nghiệm của phương trình cot x = − 3 là: π π π π A. x = .
B. x = − + kπ .
C. x = + kπ .
D. x = − + kπ . 6 6 6 3 Lời giải Chọn B π
Ta có: cot x = − 3 ⇔ x = − + kπ (k ∈). 6 π Câu 9: Cho cos – 12 α =
và < α < π . Giá trị của tanα là 13 2 A. 2 . B. 5 − . C. 5 . D. 5 − . 3 12 12 12 Lời giải Chọn D π 2 Ta có:
< α < π nên sinα > 0. Từ đó ta có 2 2 12 25 sin α =1− cos α =1− − = 2 13 169 5 ⇒ sinα = 13 sinα 5 ⇒ tanα = = − . cosα 12
Câu 10: Trong các công thức sau, công thức nào sai? A. 1
cos a cosb = cos 1
(a – b)+ cos(a +b).
sin asin b = cos a – b – cos a + b . 2 B. ( ) ( ) 2 C. 1
sin a cosb = sin 1
(a – b)+sin(a +b).
D. sin a cosb = sin
(a −b)−cos(a +b). 2 2 Lời giải Chọn D 1
Ta có: sin a cosb = sin
(a – b)+sin(a +b) 2
Câu 11: Cho các mệnh đề sau
. Hàm số y = tan x luôn luôn tăng.
. Hàm số y = tan x luôn luôn tăng trên từng khoảng xác định.
. Hàm số y = tan x tăng trong các khoảng (π + k2 ;2
π π + k2π),k ∈ . .
. Hàm số y = tan x tăng trong các khoảng (k ;
2π π + k2π),k ∈ .
Có bao nhiêu mệnh đề đúng? A. 0 . B. 3. C. 1. D. 2 . Lời giải




