Đề ôn tập Môn Lý thuyết xác xuất và thống kê ứng dụng | Trường Đại học Tài chính - Marketing

Đề 01
Câu 1. (2 điểm) Một kho hàng có 15 hộp sản phẩm được đóng gói giống nhau bao gồm 2
loại: loại I và loại II. Trong đó có 10 hộp loại I, mỗi hộp chứa 8 chính phẩm và 2 phế phẩm; 5
hộp loại II, mỗi hộp chứa 7 chính phẩm và 3 phế phẩm.
a) Lấy ngẫu nhiên hai hộp sản phẩm từ kho hàng, tính xác suất lấy được hai hộp cùng loại.
b) Lấy ngẫu nhiên một hộp rồi từ hộp đó lấy ngẫu nhiên 2 sản phẩm. Tính xác suất cả 2
sản phẩm lấy ra đều là chính phẩm.
Câu 2. (2 điểm) Khoảng thời gian từ khi sản phẩm được sử dụng cho đến khi bị hư hỏng do
lỗi của nhà sản xuất của một loại sản phẩm là biến ngẫu nhiên tuân theo quy luật phân phối
chuẩn với trung bình là 15 tháng và độ lệch chuẩn là 3 tháng.
a) Nếu quy định thời gian bảo hành là 12 tháng thì tỷ lệ sản phẩm bảo hành là bao nhiêu?
b) Muốn tỷ lệ sản phẩm bảo hành tối đa là 10% thì phải quy định thời gian bảo hành là bao lâu?
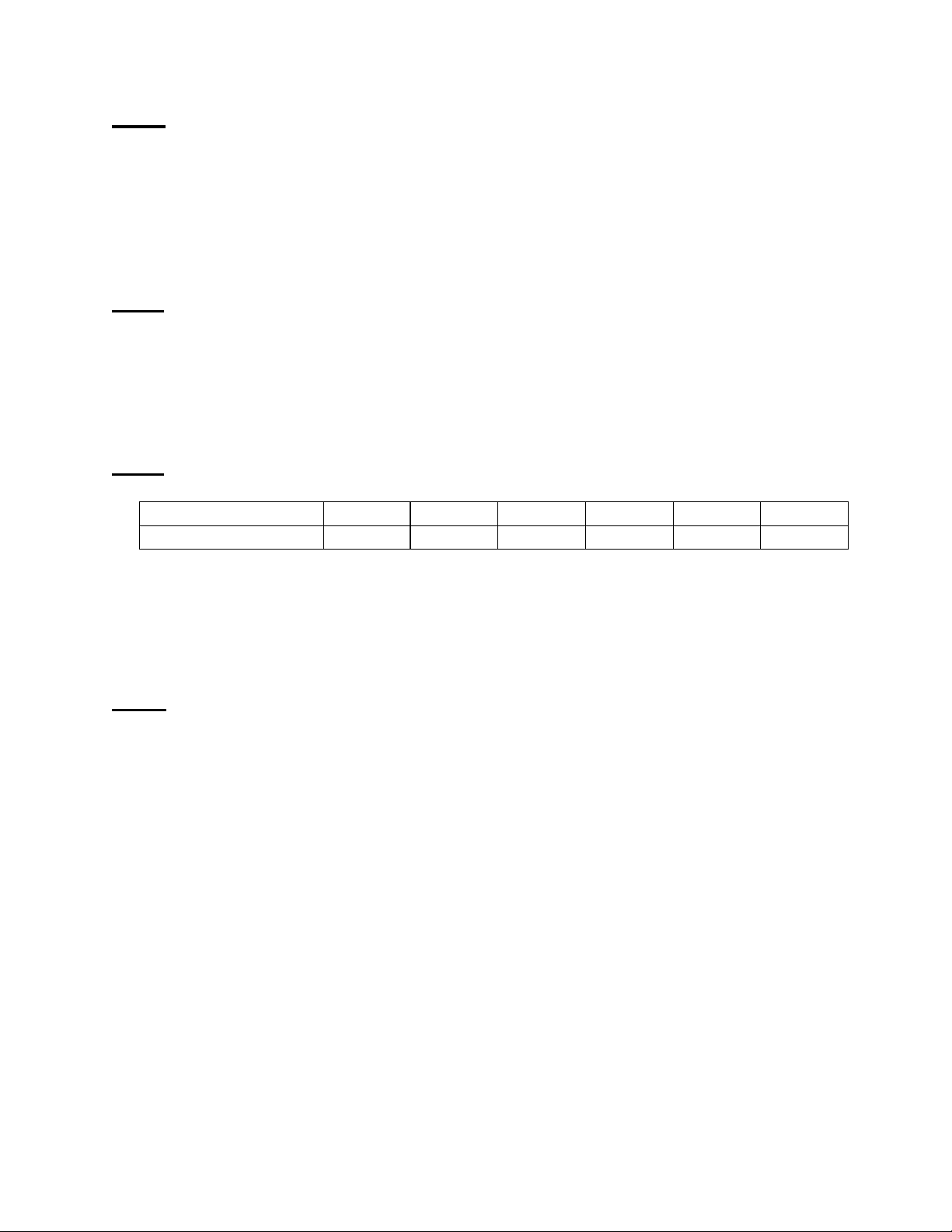
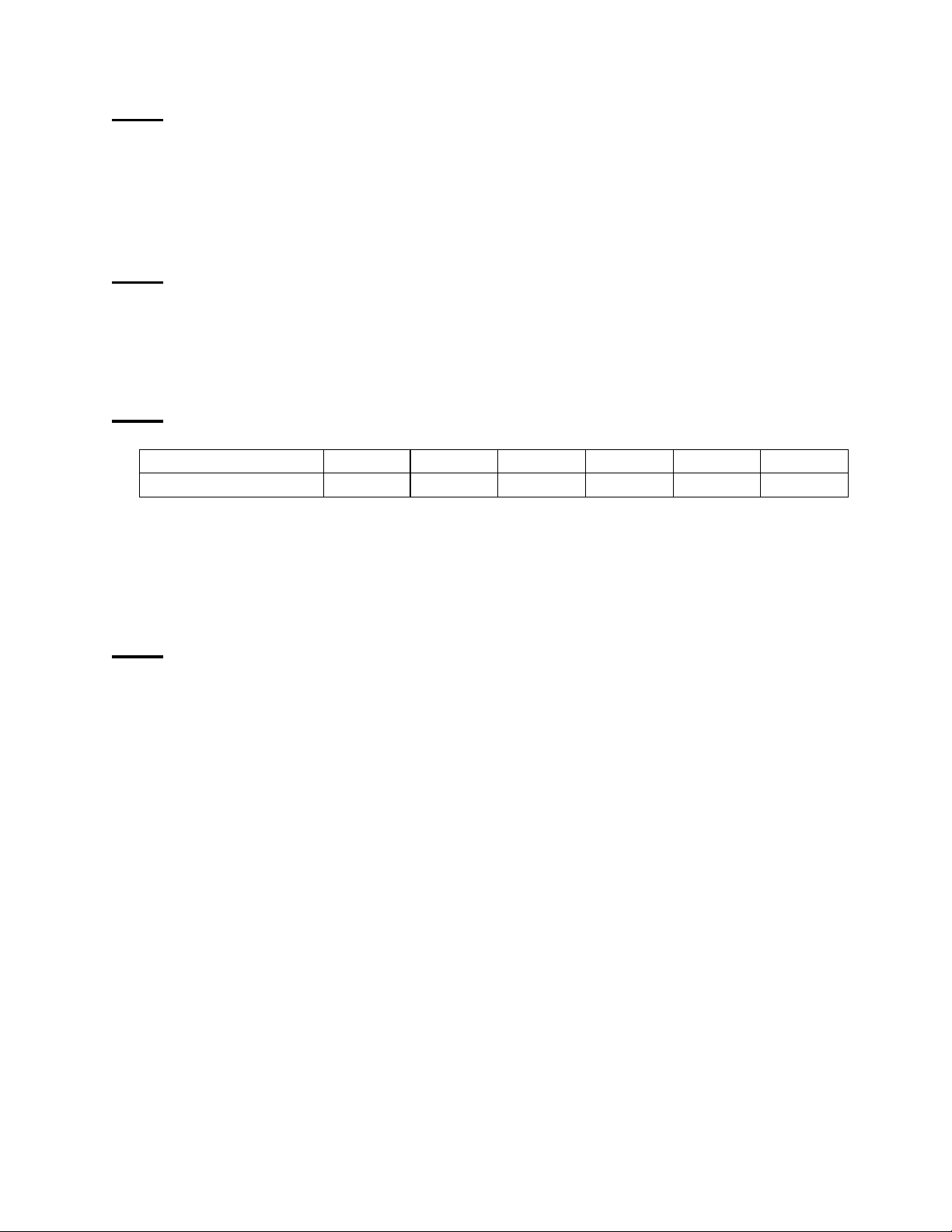
Câu 3. (3 điểm) Tại một nông trường để điều tra kết quả sử dụng loại phân bón mới trên một
loại trái cây, người ta lấy một mẫu ngẫu nhiên cân thử và thu được số liệu như sau: Trọng lượng (gam) 45 – 55 55 – 60 60 – 65 65 – 70 70 – 75 75 – 80 Số trái cây 10 35 75 130 35 15
a) Với độ tin cậy 95% , hãy ước lượng trọng lượng trung bình của loại trái cây trên của nông trường.
b) Trước kia, trọng lượng trung bình của mỗi loại trái cây trên là 64gam. Với mức ý
nghĩa 5%, hãy đánh giá xem loại phân bón mới có mang lại hiệu quả thực sự là làm
tăng trọng lượng trung bình của trái cây lên hay không?
Câu 4. (3 điểm) Để ước lượng tỷ lệ sinh viên bị cận thị tại một trường Đại học, người ta
chọn ngẫu nhiên 200 sinh viên thì thấy có 118 sinh viên bị cận thị.
a) Với độ tin cậy 90%, hãy ước lượng tỷ lệ sinh viên bị cận thị của trường Đại học này?
b) Trước đây 5 năm, tỷ lệ sinh viên bị cận thị tại trường Đại học này là 45%. Với mức ý
nghĩa 5%, hãy cho biết tỷ lệ sinh viên bị cận thị hiện nay tại trường Đại học này có
tăng lên so với 5 năm trước không? Đề 02
Câu 1. (2 điểm) Có 2 kiện hàng được đóng gói giống nhau. Kiện thứ nhất 12 sản phẩm tốt và
3 sản phẩm kém chất lượng, kiện thứ hai có 10 sản phẩm tốt và 5 sản phẩm kém chất lượng.
Lấy ngẫu nhiên một kiện rồi từ kiện đó lấy ngẫu nhiên 2 sản phẩm.
a) Tính xác suất 2 sản phẩm lấy ra là 2 sản phẩm tốt.
b) Biết 2 sản phẩm lấy ra là 2 sản phẩm tốt, tính xác suất 2 sản phẩm đó được lấy ra từ kiện thứ nhất.
Câu 2. (2 điểm) Một loại chi tiết máy do một phân xưởng sản xuất được coi là đạt tiêu chuẩn
kỹ thuật nếu đường kính của nó sai lệch so với đường kính thiết kế không quá 0,012mm. Biết
rằng đường kính của các chi tiết máy do phân xưởng sản xuất là biến ngẫu nhiên tuân theo
phân phối chuẩn, với độ lệch chuẩn là 0,005mm.
a) Tính tỷ lệ chi tiết máy đạt tiêu chuẩn kỹ thuật do phân xưởng này sản xuất.
b) Chọn ngẫu nhiên 20 chi tiết máy do phân xưởng này sản xuất. Tính xác suất để chọn
được ít nhất 18 chi tiết máy đạt tiêu chuẩn kỹ thuật.
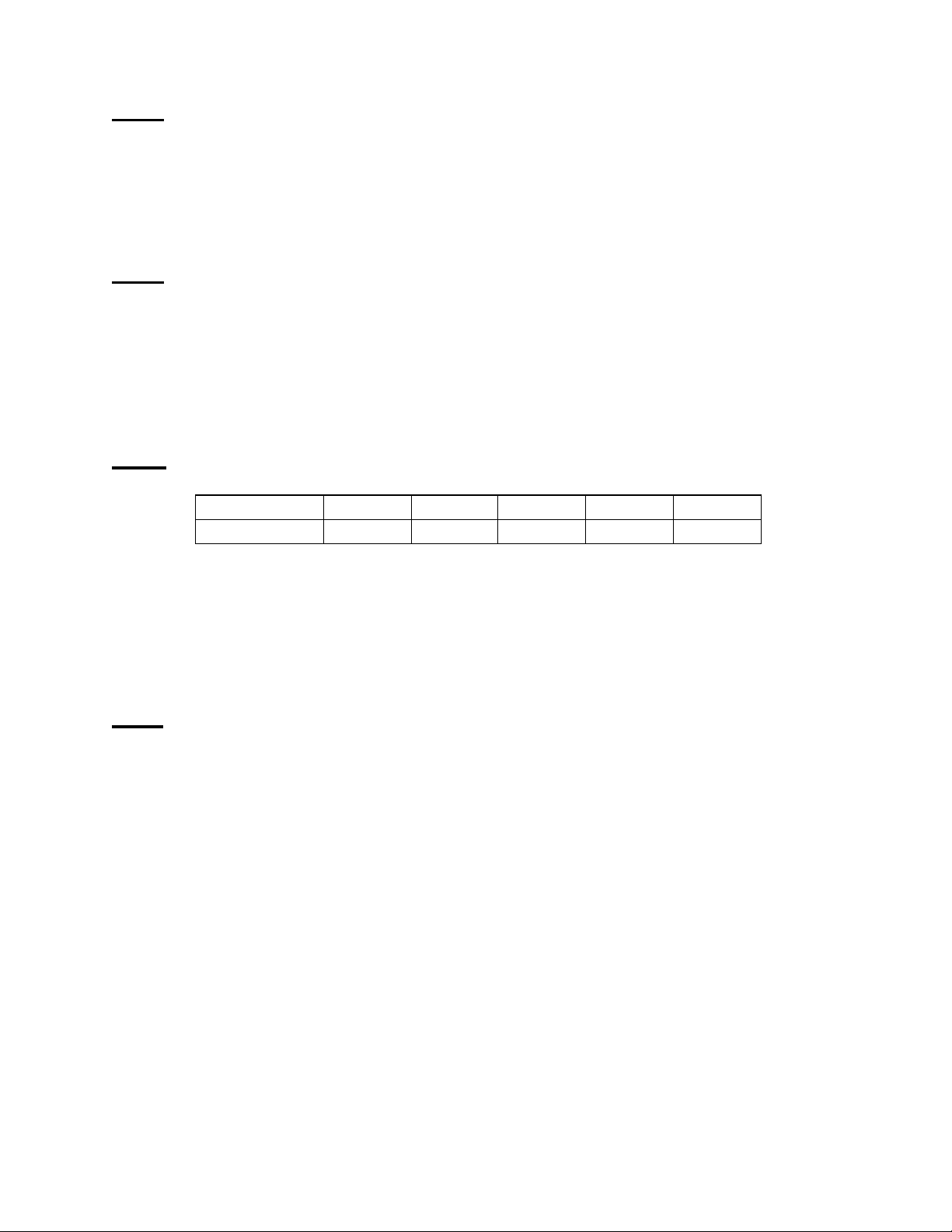
Câu 3. (3 điểm) Điều tra mức lương (đơn vị : triệu đồng/tháng) của một số công nhân tại
một xí nghiệp, ta có bảng số liệu như sau: Mức lương 1,8 – 2
2 – 2,2 2,2 – 2,4 2,4 – 2,6 2,6 – 2,8 Số công nhân 10 15 25 20 8
Biết rằng mức lương của công nhân tại xí nghiệp này là biến ngẫu nhiên phân phối chuẩn.
a) Hãy ước lượng mức lương trung bình của các công nhân thuộc xí nghiệp này, với độ tin cậy 95%.
b) Giám đốc của xí nghiệp cho rằng lương trung bình của công nhân thuộc xí nghiệp này
là 2,5 triệu đồng/tháng. Với mức ý nghĩa 5%, hãy cho biết lời của vị giám đốc này có
phù hợp thực tế không?
Câu 4. (3 điểm) Khảo sát 150 chung cư, khách sạn trên địa bàn thành phố người ta ghi nhận
được chỉ có 60 chung cư hoặc khách sạn đảm bảo an toàn về phòng cháy chữa cháy.
a) Hãy ước lượng tỷ lệ chung cư, khách sạn đảm bảo về an toàn phòng cháy chữa cháy
trên địa bàn với độ tin cậy 95%.
b) Có thông tin cho rằng có không quá 35% chung cư hoặc khách sạn đảm bảo an toàn
phòng cháy chữa cháy. Hãy cho nhận định về thông tin trên với mức ý nghĩa 5%. Đề 03
Câu 1. (2 điểm) Một cỗ máy có 3 bộ phận 1, 2, 3. Xác suất hỏng của các bộ phận trong thời
gian làm việc theo thứ tự là 0,2; 0,4 và 0,3.
a) Tính xác suất có hai bộ phận hỏng.
b) Cuối ngày làm việc được biết rằng có 2 bộ phận bị hỏng. Tính xác suất để hai bộ phận
hỏng đó là bộ phận 1 và 2.
Câu 2. (2 điểm) Có ba kiện hàng: kiện thứ nhất có 7 sản phẩm loại A và 3 sản phẩm loại B,
kiện thứ hai có 8 sản phẩm loại A và 2 sản phẩm loại B, kiện thứ ba có 6 sản phẩm loại A và
4 sản phẩm loại B. Chọn ngẫu nhiên mỗi kiện hàng 3 sản phẩm.
a) Tính xác suất để chọn được 9 sản phẩm loại A.
b) Tính xác suất để chọn được ít nhất 2 sản phẩm loại A.
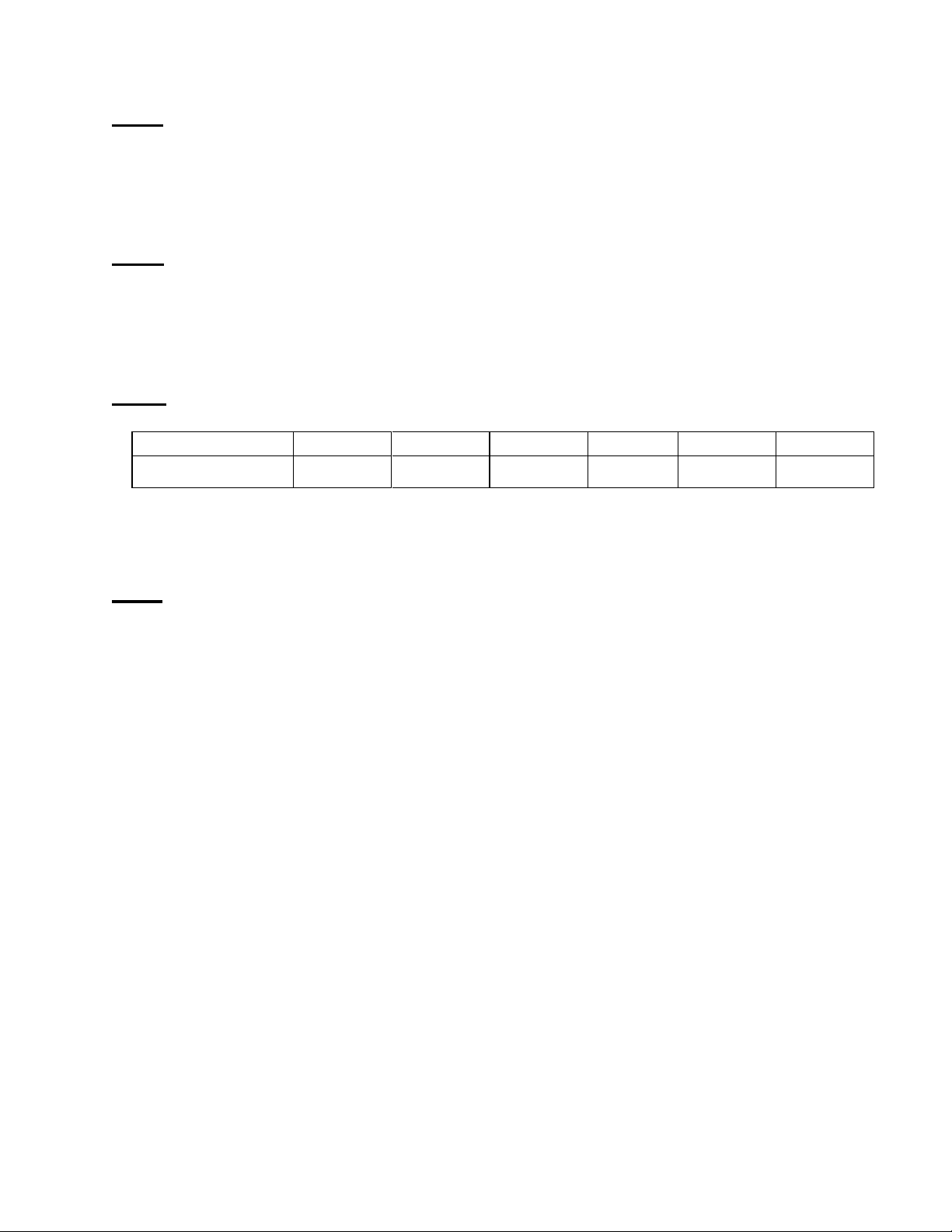
Câu 3. (3 điểm) Quan sát chiều cao của một nhóm người Việt Nam,người ta được số liệu sau: Chiều cao (cm) 140-145 145-150 150-155 155-160 160-165 165-170 Số người 2 3 7 9 10 4
a) Hãy ước lượng chiều cao trung bình của người Việt Nam ở độ tin cậy 95%;
b) Nếu muốn sai số trong ước lượng chiều cao trung bình này không quá 1 cm ở độ tin
cậy 95% thì cần quan sát thêm bao nhiêu người nữa?
Câu 4. (3 điểm) Khảo sát ngẫu nhiên 200 người, người ta thấy có 38 người hút thuốc lá.
a) Hãy ước lượng tỷ lệ người hút thuốc lá với độ tin cậy là 95%.
b) Người ta cho rằng có không quá 20% số người hút thuốc lá, nhận định trên đúng
không với mức ý nghĩa 5%. Đề 04
Câu 1. (2 điểm) Tỉ lệ sinh viên tốt nghiệp trường Đại học M được xếp loại Giỏi; Khá; Trung
bình lần lượt là 25%; 35%; 40%. Xác suất có việc làm sau khi tốt nghiệp trường M đối với
sinh viên Giỏi là 95%; đối với sinh viên Khá là 80%; đối với sinh viên Trung bình là 60%.
a) Chọn ngẫu nhiên một sinh viên đã tốt nghiệp trường Đại học M, tính xác suất sinh
viên đó sẽ có việc làm.
b) Chọn ngẫu nhiên một sinh viên đã tốt nghiệp trường M có việc làm. Tính xác suất đó
là sinh viên tốt nghiệp loại Giỏi.
Câu 2. (2 điểm) Một lô hàng gồm có 6 sản phẩm loại I và 4 sản phẩm loại II. Lấy ngẫu
nhiên đồng thời 3 sản phẩm từ lô hàng trên. Gọi X là số sản phẩm loại II được lấy ra.
a) Lập bảng phân phối xác suất của X.
b) Tính số sản phẩm loại II trung bình được lấy ra và cho biết xác suất có ít nhất 1 sản
phẩm loại II được lấy ra là bao nhiêu ?
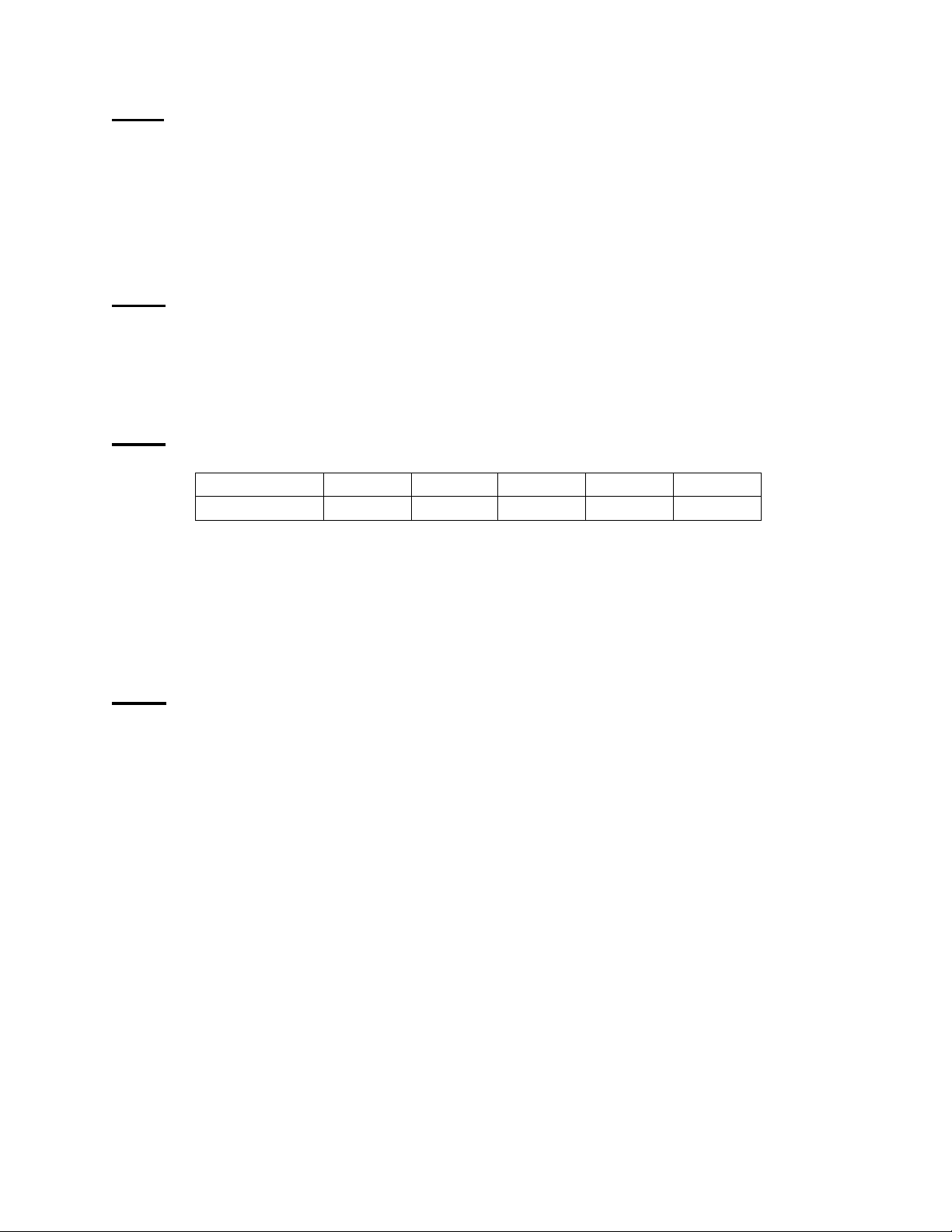
Câu 3. (3 điểm) Điều tra mức lương (đơn vị : triệu đồng/tháng) của một số công nhân tại
một xí nghiệp, ta có bảng số liệu như sau: Mức lương 1,8 – 2 2 – 2,2
2,2 – 2,4 2,4 – 2,6 2,6 – 2,8 Số công nhân 10 15 25 20 8
Biết rằng mức lương của công nhân tại xí nghiệp này là biến ngẫu nhiên phân phối chuẩn.
a) Hãy ước lượng mức lương trung bình của các công nhân thuộc xí nghiệp này, với độ tin cậy 95%.
b) Giám đốc của xí nghiệp cho rằng lương trung bình của công nhân thuộc xí nghiệp này
là 2,5 triệu đồng/tháng. Với mức ý nghĩa 5%, hãy cho biết lời của vị giám đốc này có
phù hợp thực tế không?
Câu 4. (3 điểm) Để ước lượng tỷ lệ sinh viên bị cận thị tại một trường Đại học, người ta
chọn ngẫu nhiên 200 sinh viên thì thấy có 118 sinh viên bị cận thị.
a) Với độ tin cậy 90%, hãy ước lượng tỷ lệ sinh viên bị cận thị của trường Đại học này?
b) Trước đây 5 năm, tỷ lệ sinh viên bị cận thị tại trường Đại học này là 45%. Với mức ý
nghĩa 5%, hãy cho biết tỷ lệ sinh viên bị cận thị hiện nay tại trường Đại học này có
tăng lên so với 5 năm trước không? Đề 05
Câu 1. (2 điểm) Có 2 kiện hàng được đóng gói giống nhau. Kiện thứ nhất 12 sản phẩm tốt và
3 sản phẩm kém chất lượng, kiện thứ hai có 10 sản phẩm tốt và 5 sản phẩm kém chất lượng.
Lấy ngẫu nhiên một kiện rồi từ kiện đó lấy ngẫu nhiên 2 sản phẩm.
a) Tính xác suất 2 sản phẩm lấy ra là 2 sản phẩm tốt.
b) Biết 2 sản phẩm lấy ra là 2 sản phẩm tốt, tính xác suất 2 sản phẩm đó được lấy ra từ kiện thứ nhất.
Câu 2. (2 điểm) Xác suất bán được một hợp đồng bảo hiểm là 12,5%. Một đại lý kinh doanh
bảo hiểm gặp 12 khách hàng trong một tuần:
a) Tính xác suất để người này bán được 2 hợp đồng bảo hiểm trong một tuần.
b) Cần phải gặp ít nhất bao nhiêu khách hàng để đại lý này bán được hợp đồng bảo hiểm
trong một tuần với xác suất 75%.
Câu 3. (3 điểm) Tại một nông trường để điều tra kết quả sử dụng loại phân bón mới trên một
loại trái cây, người ta lấy một mẫu ngẫu nhiên cân thử và thu được số liệu như sau: Trọng lượng (gam) 45 – 55 55 – 60 60 – 65 65 – 70 70 – 75 75 – 80 Số trái cây 10 35 75 130 35 15
a) Với độ tin cậy 95% , hãy ước lượng trọng lượng trung bình của loại trái cây trên của nông trường.
b) Trước kia, trọng lượng trung bình của mỗi loại trái cây trên là 64gam. Với mức ý
nghĩa 5%, hãy đánh giá xem loại phân bón mới có mang lại hiệu quả thực sự là làm
tăng trọng lượng trung bình của trái cây lên hay không?
Câu 4. (3 điểm) Khảo sát 150 chung cư, khách sạn trên địa bàn thành phố người ta ghi nhận
được chỉ có 60 chung cư hoặc khách sạn đảm bảo an toàn về phòng cháy chữa cháy.
a) Hãy ước lượng tỷ lệ chung cư, khách sạn đảm bảo về an toàn phòng cháy chữa cháy
trên địa bàn với độ tin cậy 95%.
b) Có thông tin cho rằng có không quá 35% chung cư hoặc khách sạn đảm bảo an toàn
phòng cháy chữa cháy. Hãy cho nhận định về thông tin trên với mức ý nghĩa 5%. Đề 06
Câu 1. (2 điểm) Tỷ lệ người dân nghiện rượu ở một nước lạc hậu là 30%. Biết rằng tỷ lệ
người bị viêm gan trong số người nghiện rượu là 60%, còn tỷ lệ người bị viêm gan trong số
người không nghiện rượu là 40%.
a) Lấy ngẫu nhiên một người, tính xác suất để người đó bị viêm gan.
b) Nếu người đó không bị viêm gan, tính xác suất để người đó nghiện rượu
Câu 2. (2 điểm) Trong một hộp gồm 6 lọ thuốc trong đó có 4 lọ đạt tiêu chuẩn. Lấy ngẫu
nhiên lần lượt không hoàn lại từng lọ để kiểm tra, nếu gặp lọ đạt tiêu chuẩn thì dừng lại. Gọi X là số lần kiểm tra.
a) Lập bảng phân phối xác suất của X.
b) Tính xác suất để phải kiểm tra ít nhất 2 lần.
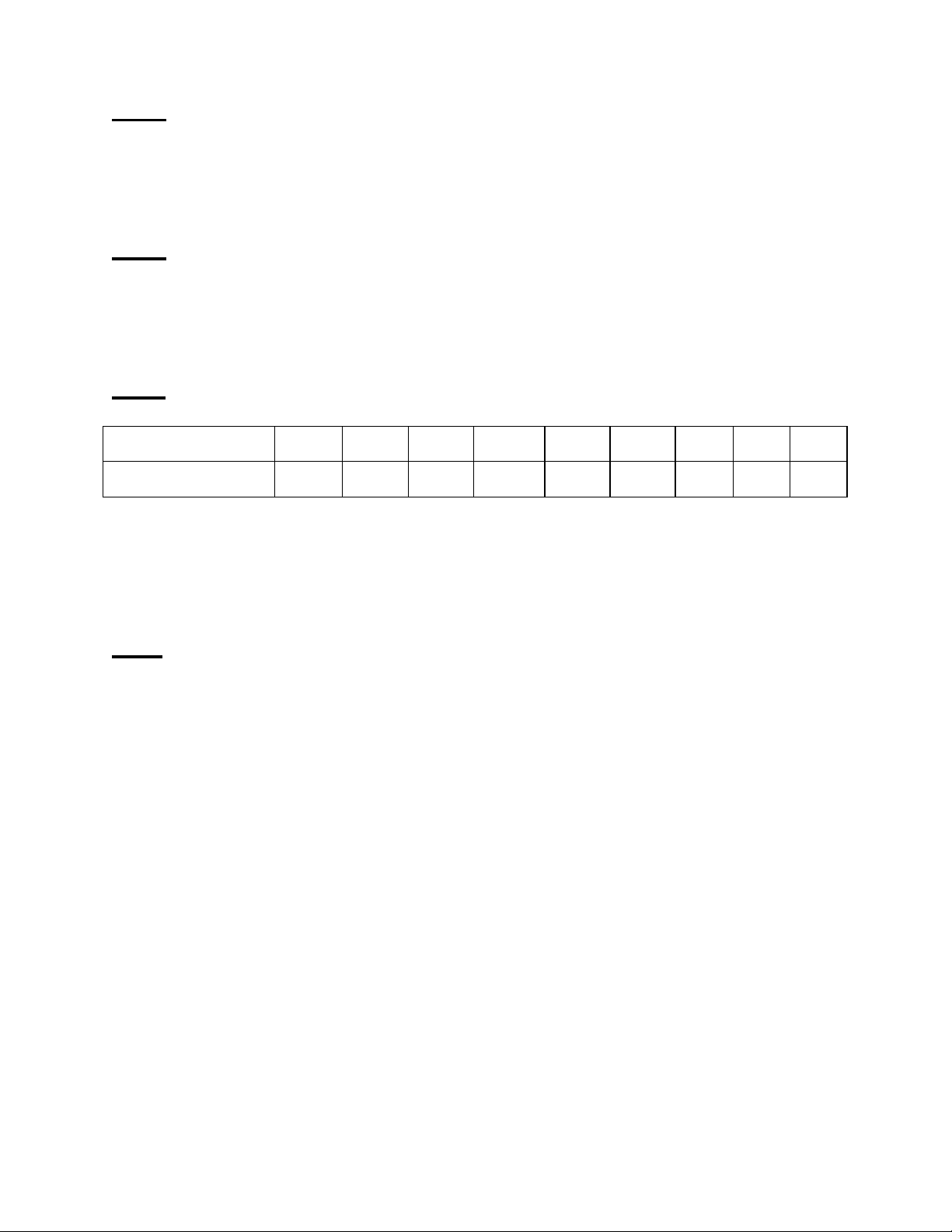
Câu 3. (3 điểm) Số liệu thống kê về doanh số bán hàng (triệu đồng/ngày) của một siêu thị
trong một số ngày cho ở bảng sau: Doanh số 24 30 36 42 48 54 60 65 70 Số ngày 5 12 25 35 24 15 12 10 6
a) Ước lượng doanh số bán trung bình trong một ngày của siêu thị, với độ tin cậy 95%?
b) Trước đây doanh số bán trung bình của siêu thị là 35 triệu đồng/ ngày. Số liệu ở bảng
trên được thu thập sau khi siêu thị áp dụng một phương pháp bán hàng mới. Hãy cho biết
phương thức bán hàng mới có làm tăng doanh số bán hàng của siêu thị lên hay không? Kết
luận với mức ý nghĩa 5%.
Câu 4. (3 điểm) Khảo sát ngẫu nhiên 200 người, người ta thấy có 38 người hút thuốc lá.
a) Hãy ước lượng tỷ lệ người hút thuốc lá với độ tin cậy là 95%.
b) Người ta cho rằng có không quá 20% số người hút thuốc lá, nhận định trên đúng
không với mức ý nghĩa 5%.