-
Thông tin
-
Quiz
Đề ôn thi giữa HK1 Toán 12 năm 2024 – 2025 trường Quốc tế Á Châu – TP HCM
Xin giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề ôn thi giữa học kì 1 môn Toán 12 năm học 2024 – 2025 trường Quốc tế Á Châu, thành phố Hồ Chí Minh. Mời các bạn cùng tham khảo chi tiết bài viết dưới đây nhé.
Chủ đề: Đề giữa HK1 Toán 12 100 tài liệu
Môn: Toán 12 3.9 K tài liệu
Thông tin:
Tác giả:
Preview text:
Trường Quốc tế Á Châu
Nhóm toán – khối 12 ÔN THI GIỮA HKI Tổ Toán MÔN TOÁN – KHỐI 12 Quốc tế Á Châu Năm học : 2024 -2025
Họ và tên học sinh: ......................... Lớp: ............ ĐỀ 1
PHẦN I. TRẮC NGHIỆM 4 ĐÁP ÁN
CÂU HỎI TRẮC NGHIỆM Câu 1:
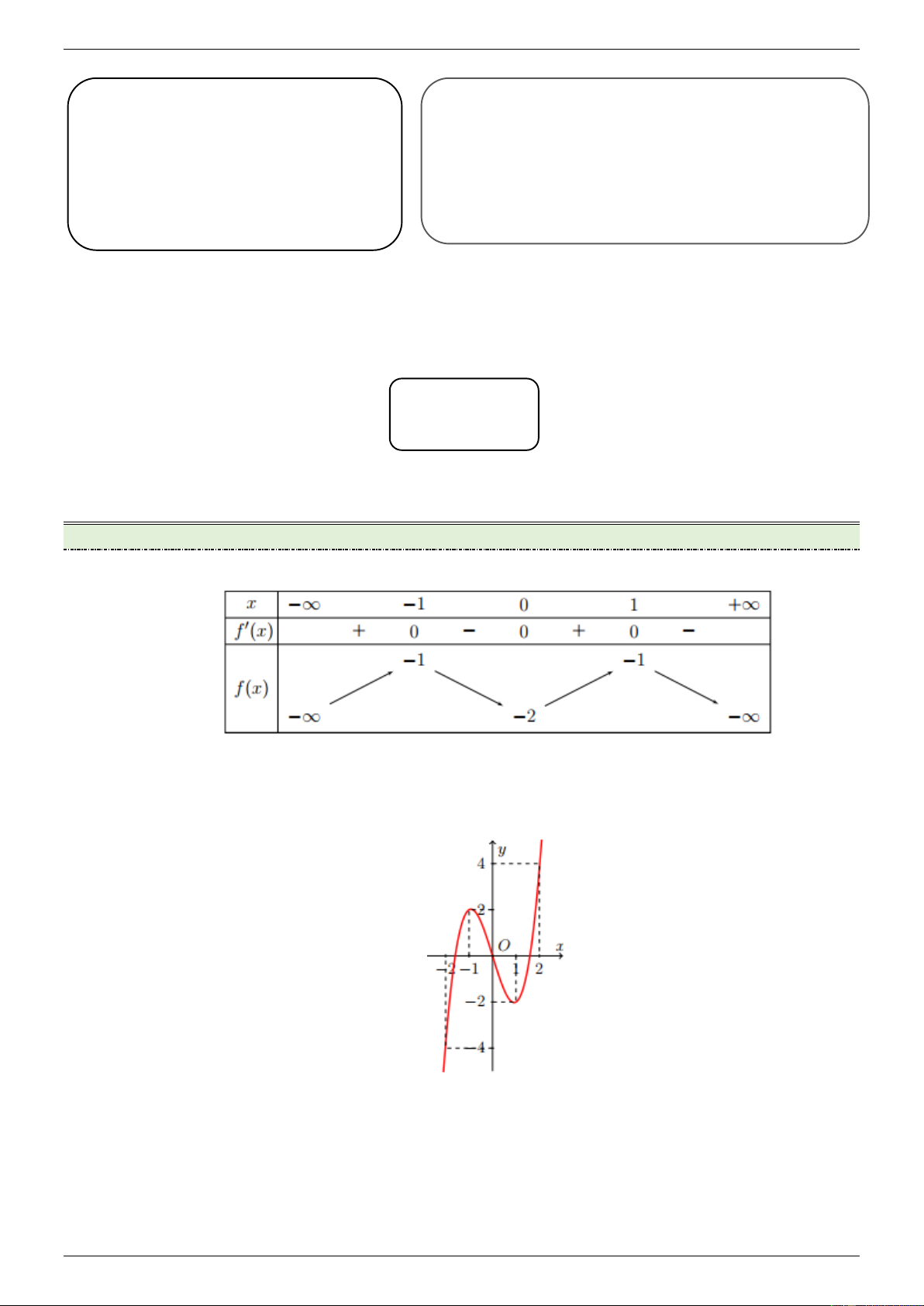
Cho hàm số y f x có bảng biến thiên như sau. Hỏi hàm số đồng biến trên khoảng nào A. 0; 1
B. 1;0 C. ;1
D. 1; Câu 2:
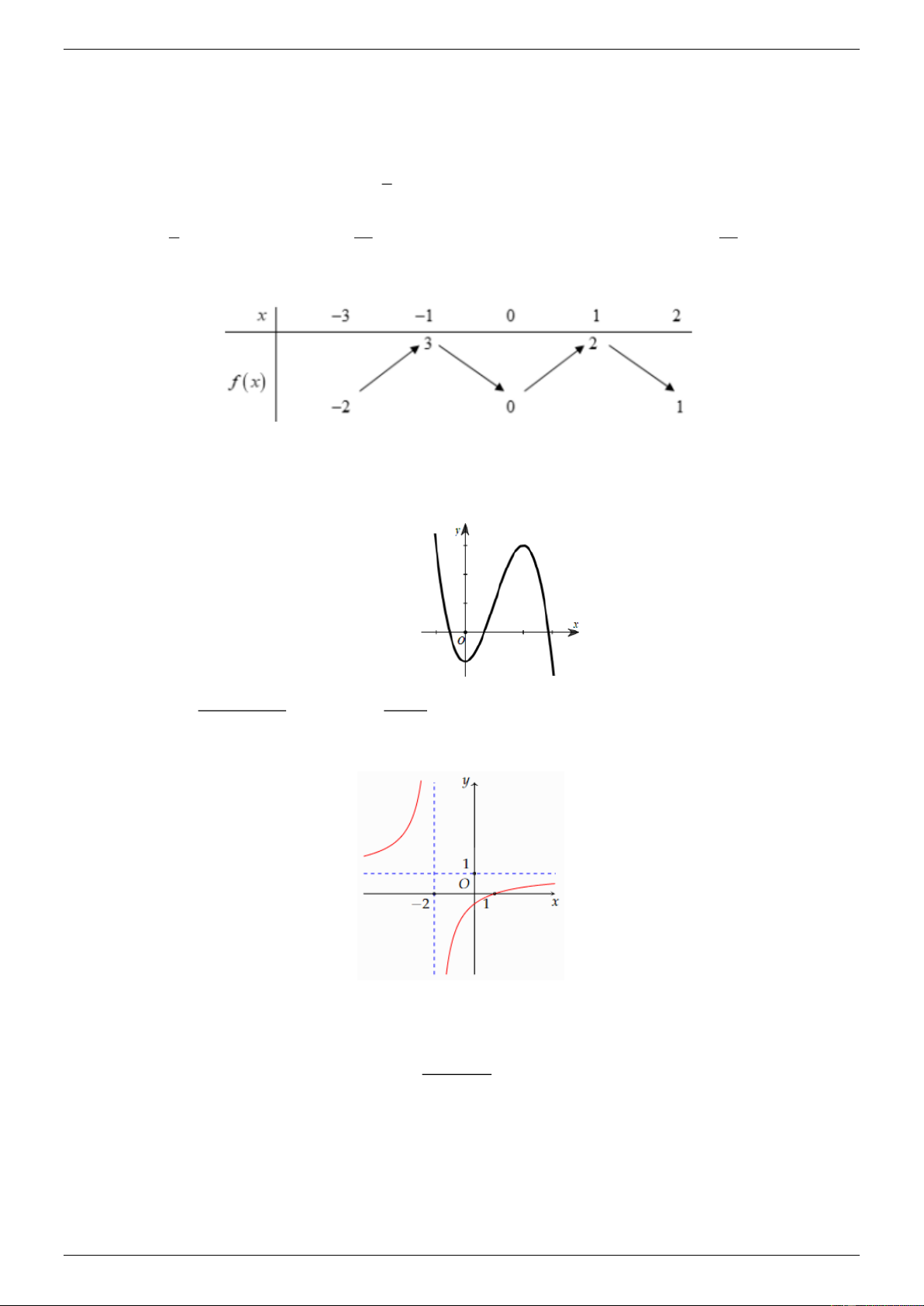
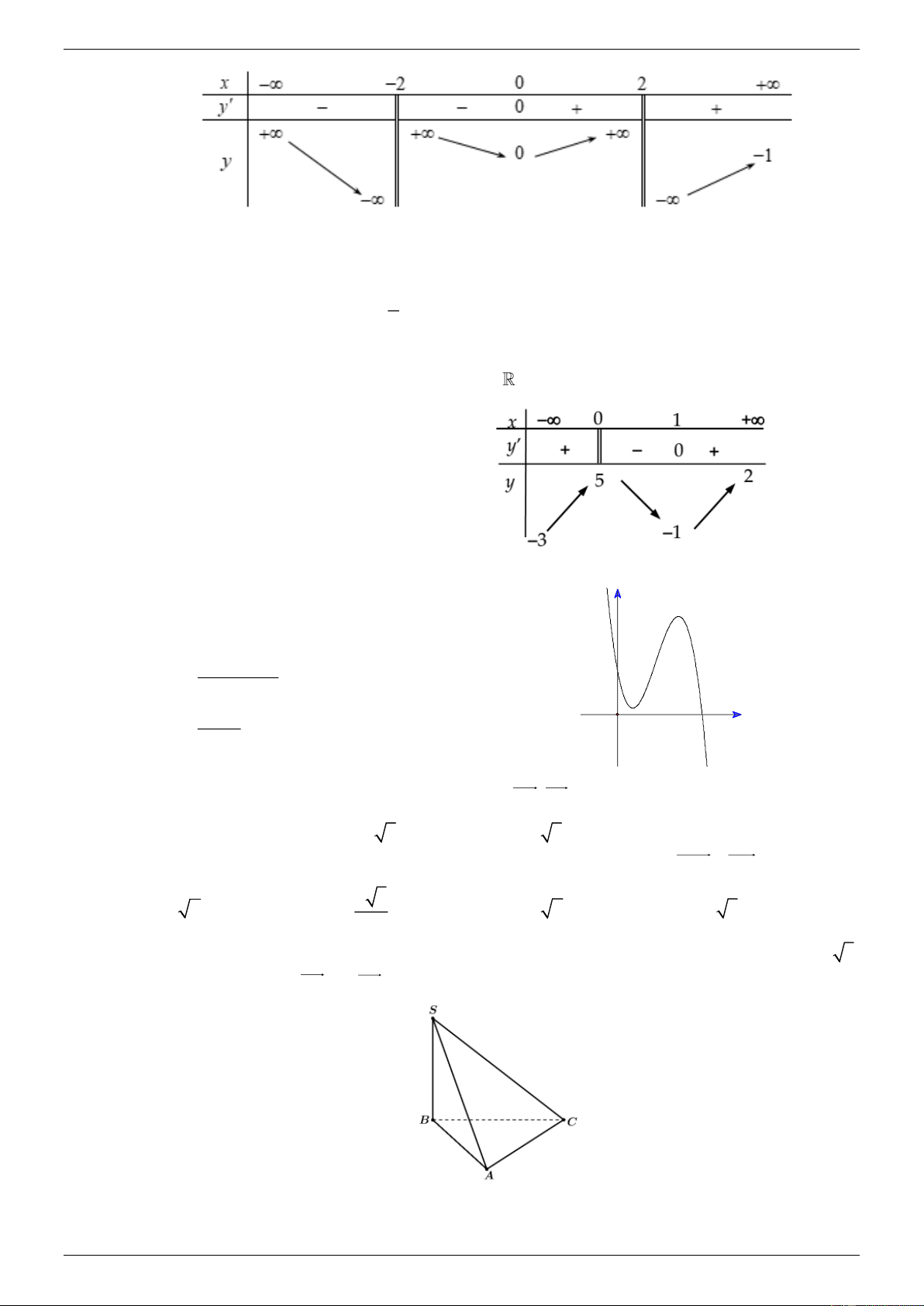
Cho hàm số y f x xác định liện tục trên đoạn 2; 2 và có đồ thị là đường cong trong hình vẽ bên dưới
Hàm số f x đạt cực đại tại điểm nào dưới đây? A. x 2 .
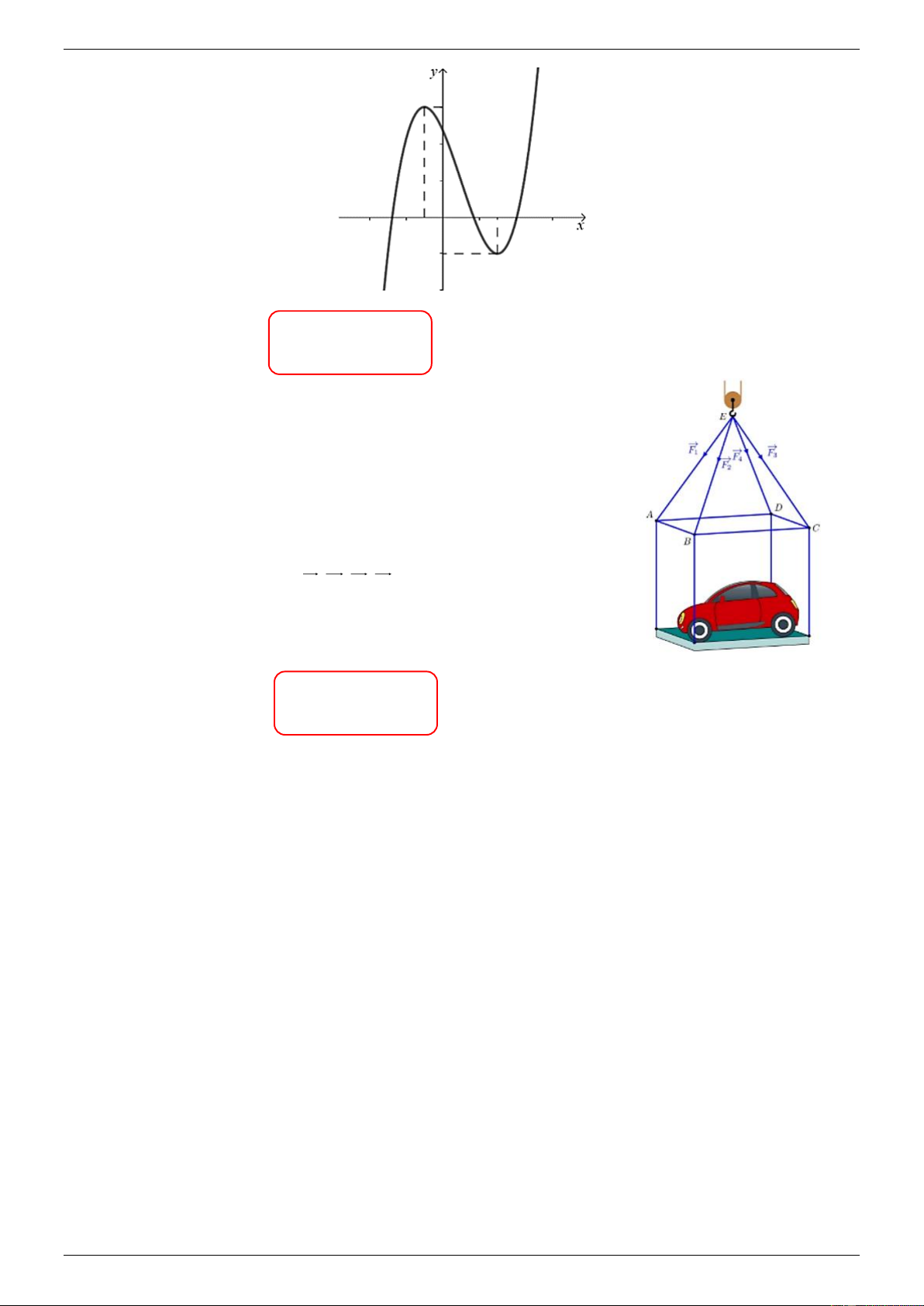
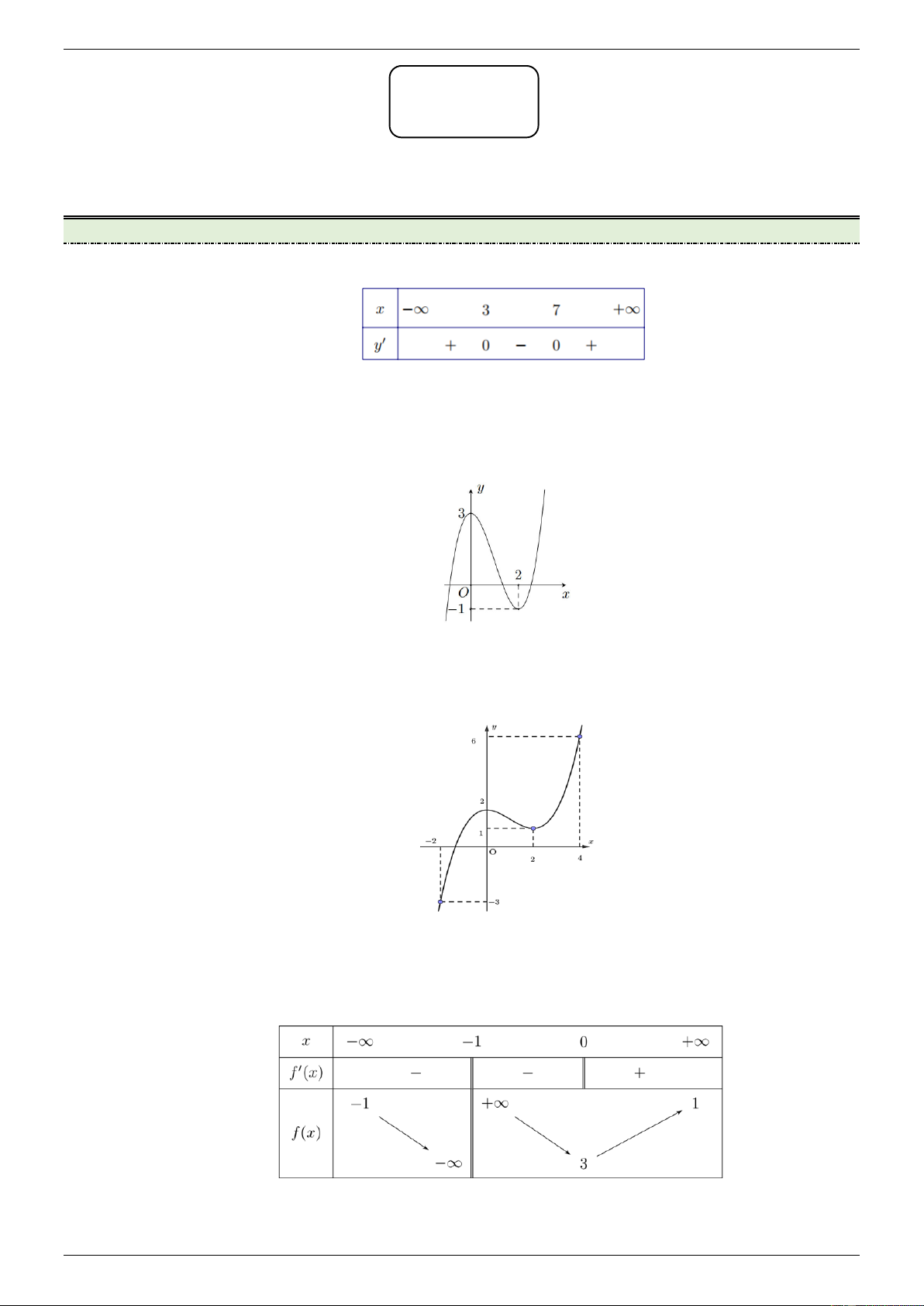
B. x 1 . C. x 1 . D. x 2 Câu 3: Đồ thị hàm số 3 2
y x 3x 9x 5 có điểm cực tiểu là A 3; 32 . B. 1;0 . C. x 1 . D. x 3
Ôn tập thi giữa HKI – 2024-2025 Trang 1
Trường Quốc tế Á Châu
Nhóm toán – khối 12 2 3 2024 Câu 4:
Cho hàm số y f ' x x
1 2 x .3x 1 .2x 3
. Hàm số y f x có bao nhiêu cực trị? A 1. B. 2 . C. 3 . D. 4 . 1 Câu 5:
Giá trị lớn nhất của hàm số 3 2 y
x 2x 3x 4 trên đoạn 1;5 là 3 8 10 A. . B. . C. 10 4 . D. . 3 3 3 Câu 6:
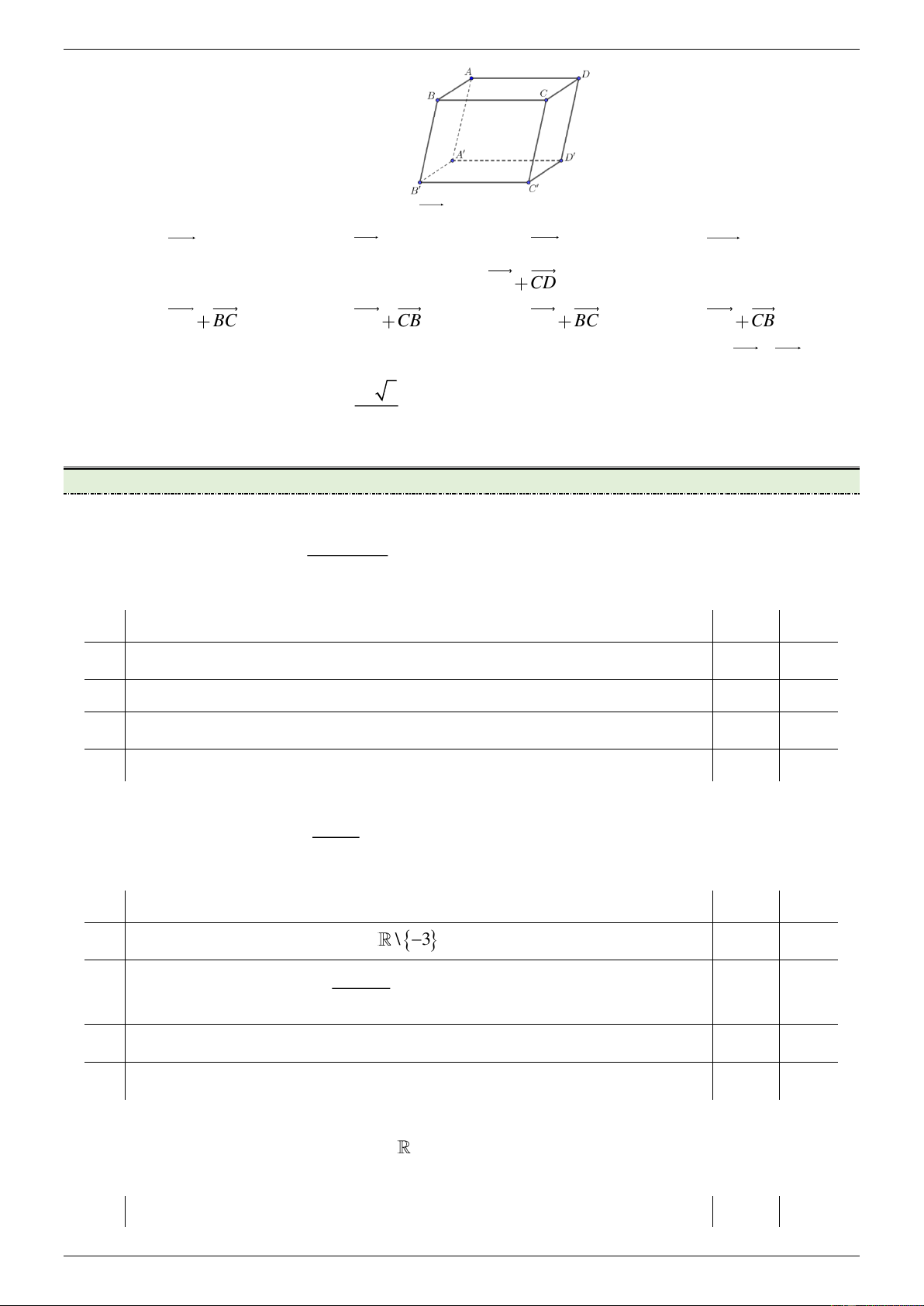
Cho hàm số y f x liên tục trên 3; 2 và có bảng biến thiên như sau:
Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên 1; 2 . Tính M m . A. 3 B. 2 C. 1 D. 4 Câu 7:
Đồ thị hàm số nào dưới đây có dạng như đường cong sau? 2 x 2x 1 2x 1 A. y . B. y . C. 3 2
y x 3x 1. D. 3 2
y x 3x 1 . x 3 x 2 Câu 8:
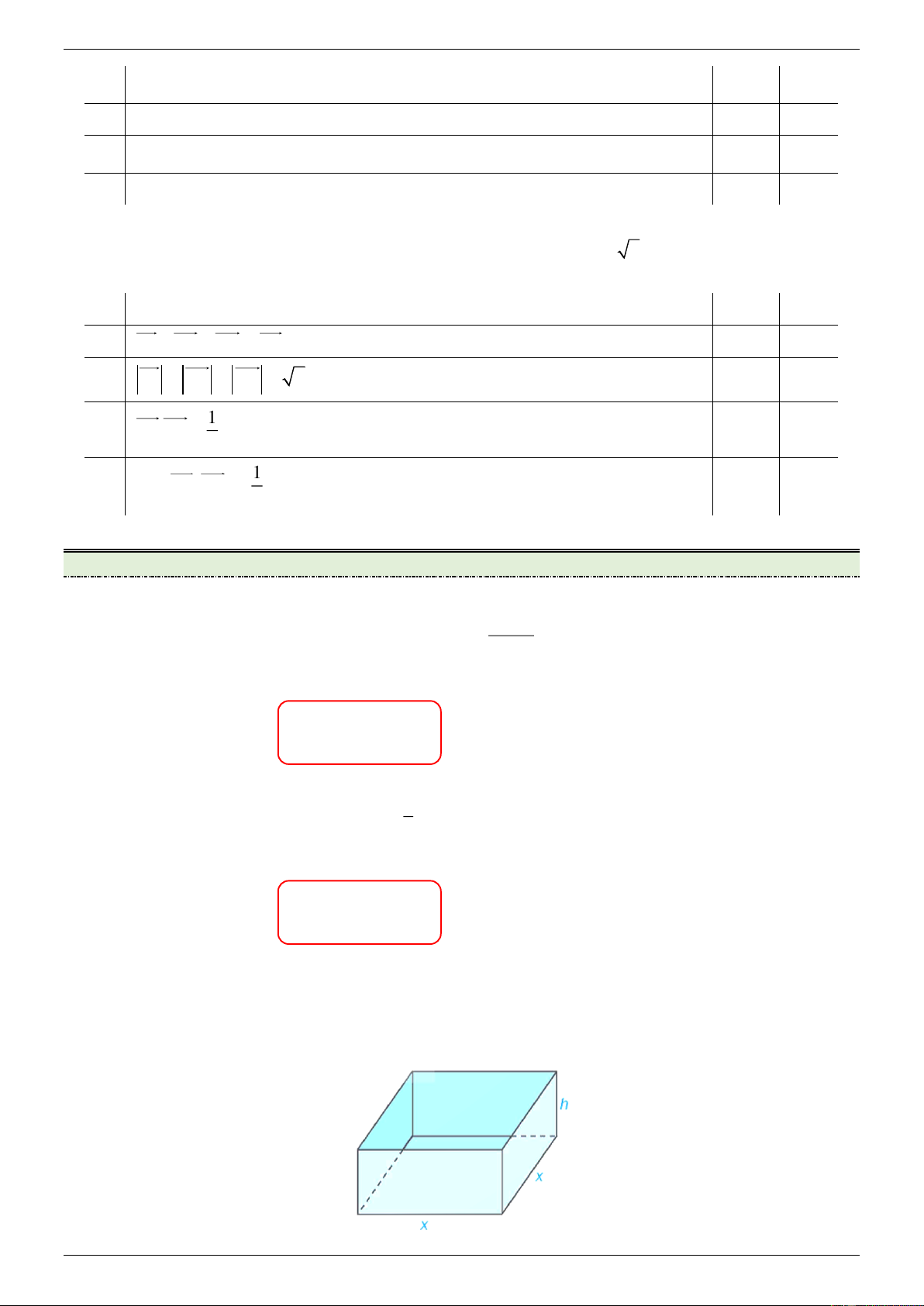
Cho hàm số f (x) có đồ thị như hình vẽ bên dưới.
Đường tiệm cận ngang của đồ thị hàm số là A. x 1. B. y 2 . C. x 2 . D. y 1 . 2 x x 3 Câu 9:
Tiệm cận xiên của đồ thị hàm số y có phương trình là x 1
A. y 2x 1.
B. y x 2 .
C. y 2 x .
D. y x 1.
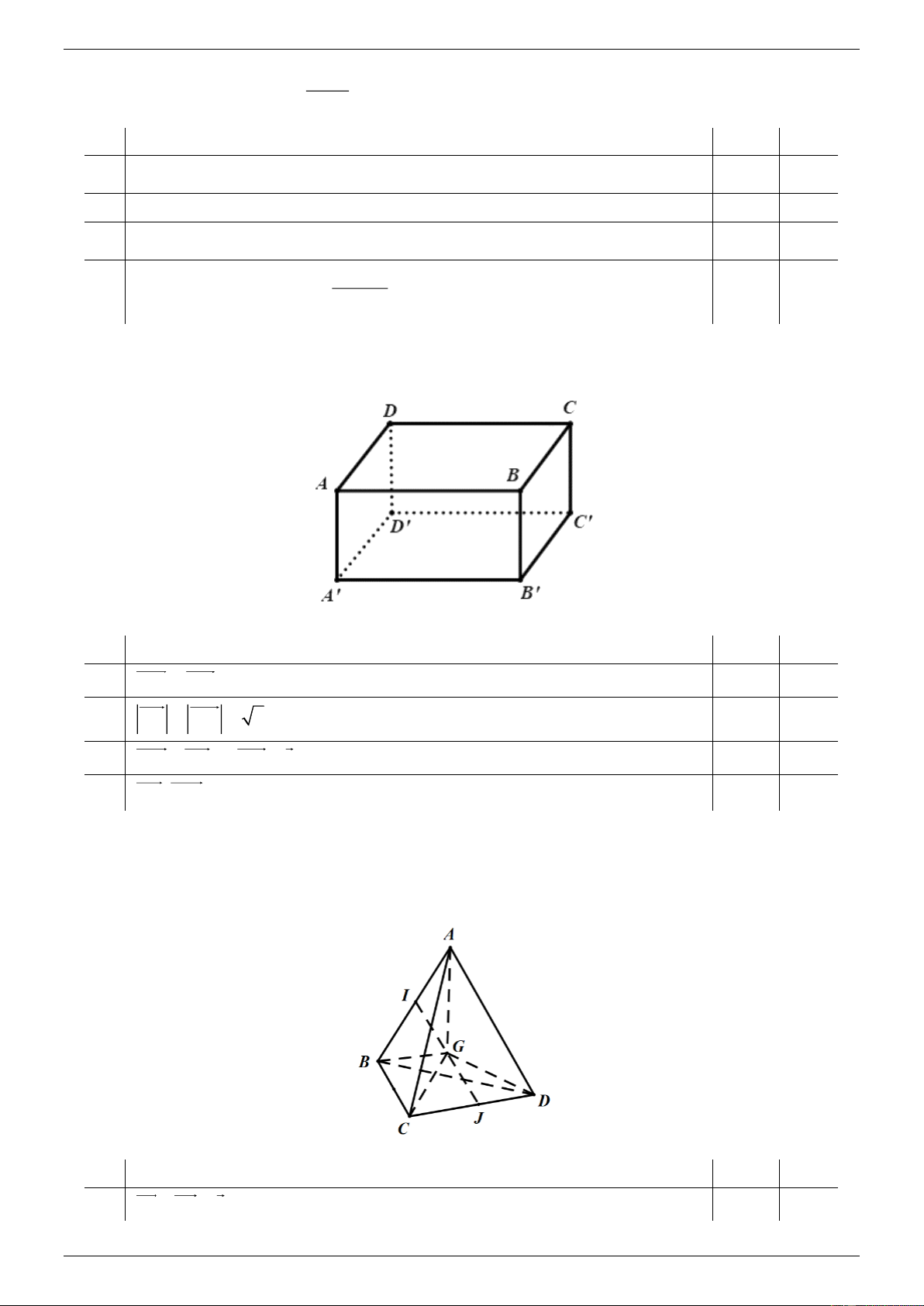
Câu 10: Cho hình hộp chữ nhật ABC .
D A ' B 'C ' D ' . Trang 2
Ôn tập thi giữa HKI – 2024 – 2025
Trường Quốc tế Á Châu
Nhóm toán – khối 12
Vectơ nào sau đây cùng phương với BC ? A. DC . B. DA . C. BB ' .
D. C 'C .
Câu 11: Trong không gian, cho tứ diện ABCD . Ta có AB CD bằng A. AD BC . B. DA CB . C. DA BC . D. AD CB .
Câu 12: Cho tam giác ABC có AB AC 7a và BAC 120 . Độ dài của vectơ tổng AB AC bằng? 5a 3 A. 10a . B. . C. 5a . D. 7a . 2
PHẦN II. TRẮC NGHIỆM ĐÚNG SAI
CÂU HỎI TRẮC NGHIỆM ĐÚNG /SAI x x
Câu 1: Cho hàm số y f x 2 2 4 . x 2 Mệnh đề Đúng Sai
(a) Hàm số y f x đồng biến trên khoảng ;
4 và 0;.
(b) Giá trị cực tiểu của hàm số y 6 .
(c) Hàm số y f x có giá trị lớn nhất bằng 2 và giá trị nhỏ nhất bằng 6 .
(d) Đồ thị hàm số có đường tiệm cận xiên là y x . x
Câu 2: Cho hàm số y f x 1
có đồ thị C . x 3 Mệnh đề Đúng Sai
(a) Tập xác định của hàm số là D \ 3 . 2
(b) Đạo hàm của hàm số y ' . 3 x2
(c) Hàm số đồng biến trên ; 4 .
(d) Đường thẳng y 1 là tiệm cận ngang của đồ thị hàm số C . 2
Câu 3: Cho hàm số y f x liên tục trên
có đạo hàm f x 3
x x 1 x 2 . Mệnh đề Đúng Sai
Ôn tập thi giữa HKI – 2024-2025 Trang 3
Trường Quốc tế Á Châu
Nhóm toán – khối 12
(a) Hàm số nghịch biến trên 0; .
(b) Hàm số đạt cực đại tại tại x 0 .
(c) Giá trị lớn nhất của hàm số trên 2024 ;
1 là f 2 .
(d) Hàm số không có giá trị lớn nhất và nhỏ nhất trên tập xác định.
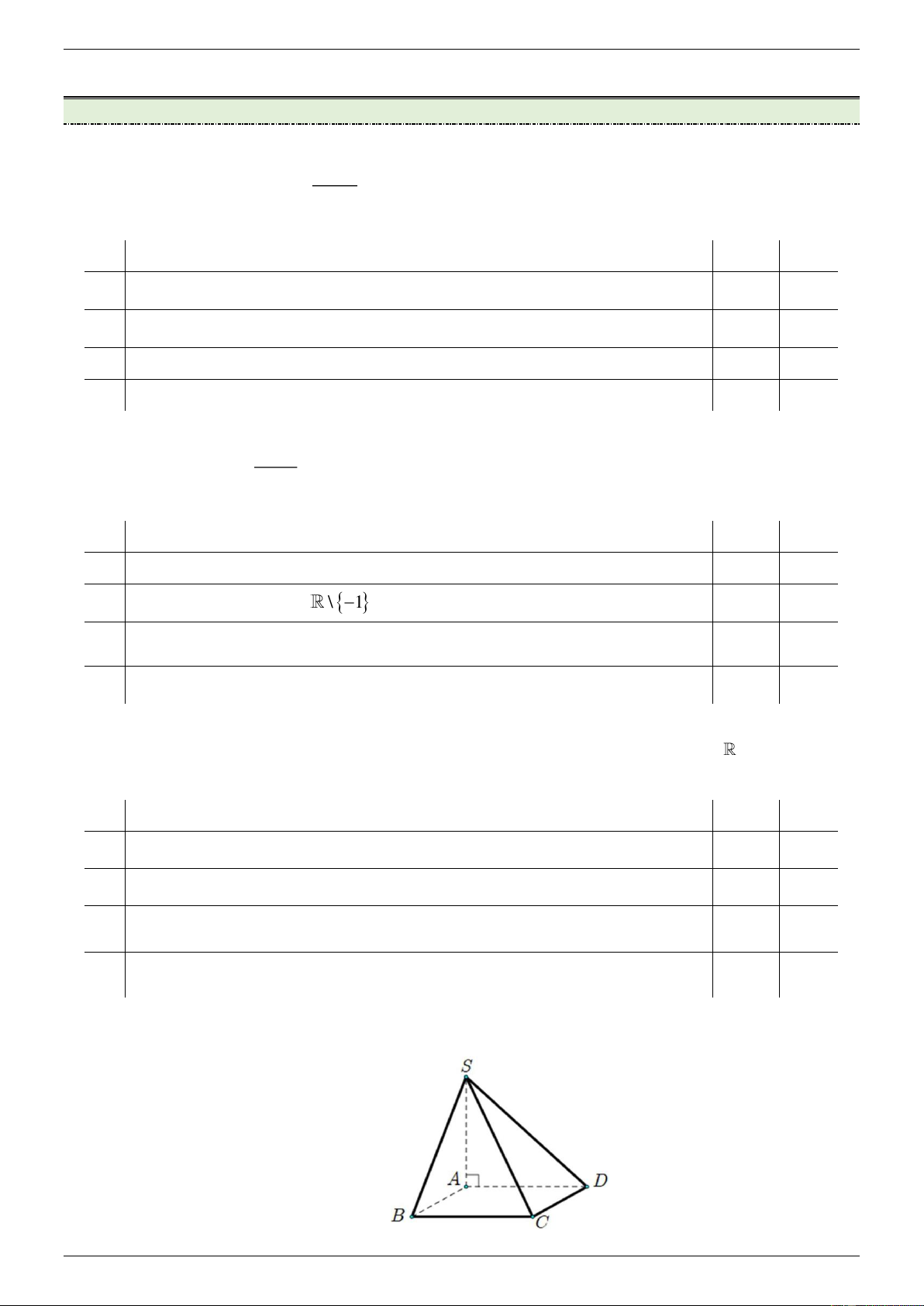
Câu 4: Cho hình chóp S.ABC có SA SB SC AB AC 1 và BC 2 . Mệnh đề Đúng Sai
(a) SA AB BC SC .
(b) SA AB BC 2 . 1
(c) SC.AB . 2 (d) SC AB 1 cos , . 2
PHẦN III. TRẢ LỜI NGẮN TRẢ LỜI NGẮN x 4
Câu 1: Cho hàm số y f x có đạo hàm là f ' x 2 , x
0. Số điểm cực trị của hàm số đã cho 2 3x là? Điền đáp số: 1
Câu 2: Tính giá trị lớn nhất của hàm số 3 2 y
x 2x 3x 1 trên đoạn 2;5 . 3 Điền đáp số:
Câu 3: Một nhà sản xuất muốn thiết kế một chiếc hộp có dạng hình hộp chữ nhật không có nắp, có đáy là
hình vuông cạnh x cm , chiều cao h cm và diện tích của tất cả các mặt bằng 2 108 cm như hình
dưới đây. Tìm chiều cao h cm sao cho thể tích của hộp là lớn nhất. Trang 4
Ôn tập thi giữa HKI – 2024 – 2025
Trường Quốc tế Á Châu
Nhóm toán – khối 12 Điền đáp số: 2 4x 2x 2
Câu 4: Số đường tiệm cận ngang của đồ thị hàm số y bằng? 3x 1 Điền đáp số: Câu 5: Cho hàm số 3 2
y ax bx cx d có đồ thị như hình sau. Hỏi
các hệ số a, b, c, d có bao nhiêu số dương?
Điền đáp số:
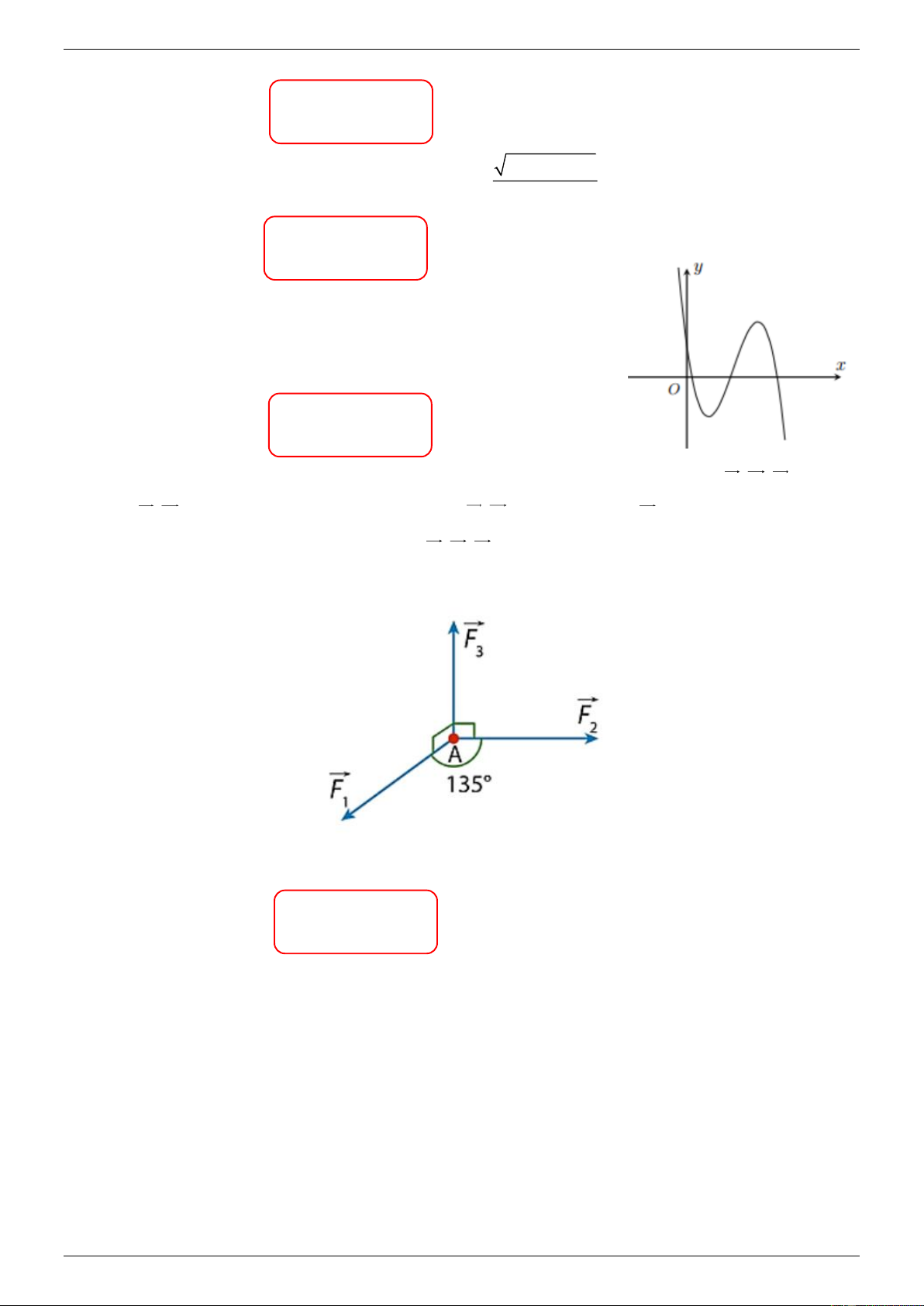
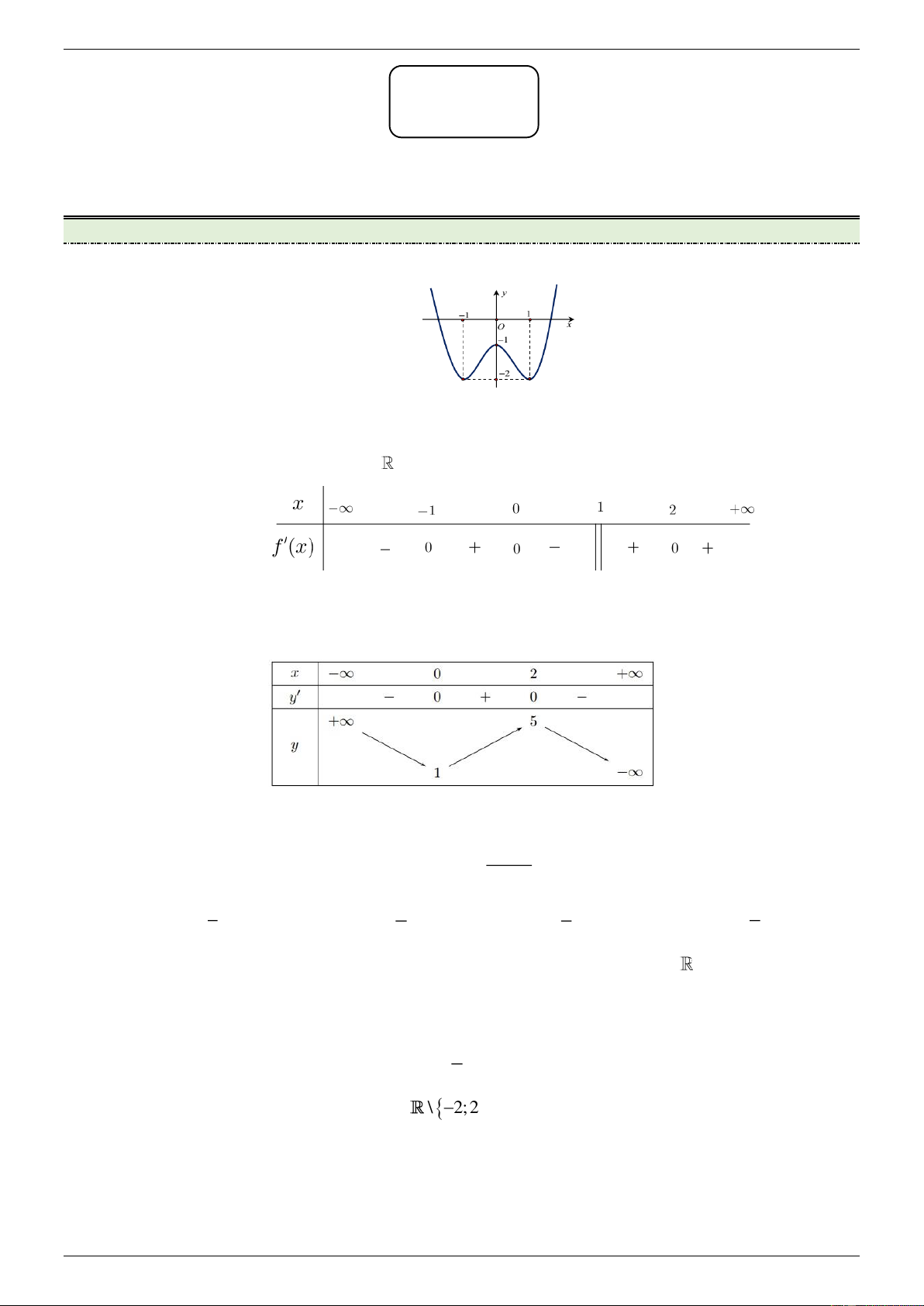
Câu 6: Một chất điểm A nằm trên mặt phẳng nằm ngang , chịu tác động bởi ba lực F , F , F . Các lực 1 2 3
F , F có giá nằm trong mặt phẳng và F , F 135 , còn lực F có giá vuông góc với 1 2 0 1 2 3
và hướng lên trên. Độ lớn hợp lực của F , F , F bằng bao nhiêu (làm tròn kết quả đến hàng phần 1 2 3
mười) biết rằng độ lớn của ba lực đó lần lượt là 20N,15N,10N . Điền đáp số:
-------------------------------Hết-------------------------------
Ôn tập thi giữa HKI – 2024-2025 Trang 5
Trường Quốc tế Á Châu
Nhóm toán – khối 12 ĐỀ 2
PHẦN I. TRẮC NGHIỆM 4 ĐÁP ÁN
CÂU HỎI TRẮC NGHIỆM Câu 1:
Cho hàm số y f x có bảng xét dấu đạo hàm y như sau:
Hàm số đã cho nghịch biến trên khoảng nào trong các khoảng dưới đây? A. ;3 . B. ; 7 . C. 3;7 . D. 3; . Câu 2:
Cho hàm số y f x có bảng biến thiên như sau:
Hàm số đã cho đạt cực đại tại A. x 2 . B. x 2 . C. x 1 . D. x 1 . Câu 3:
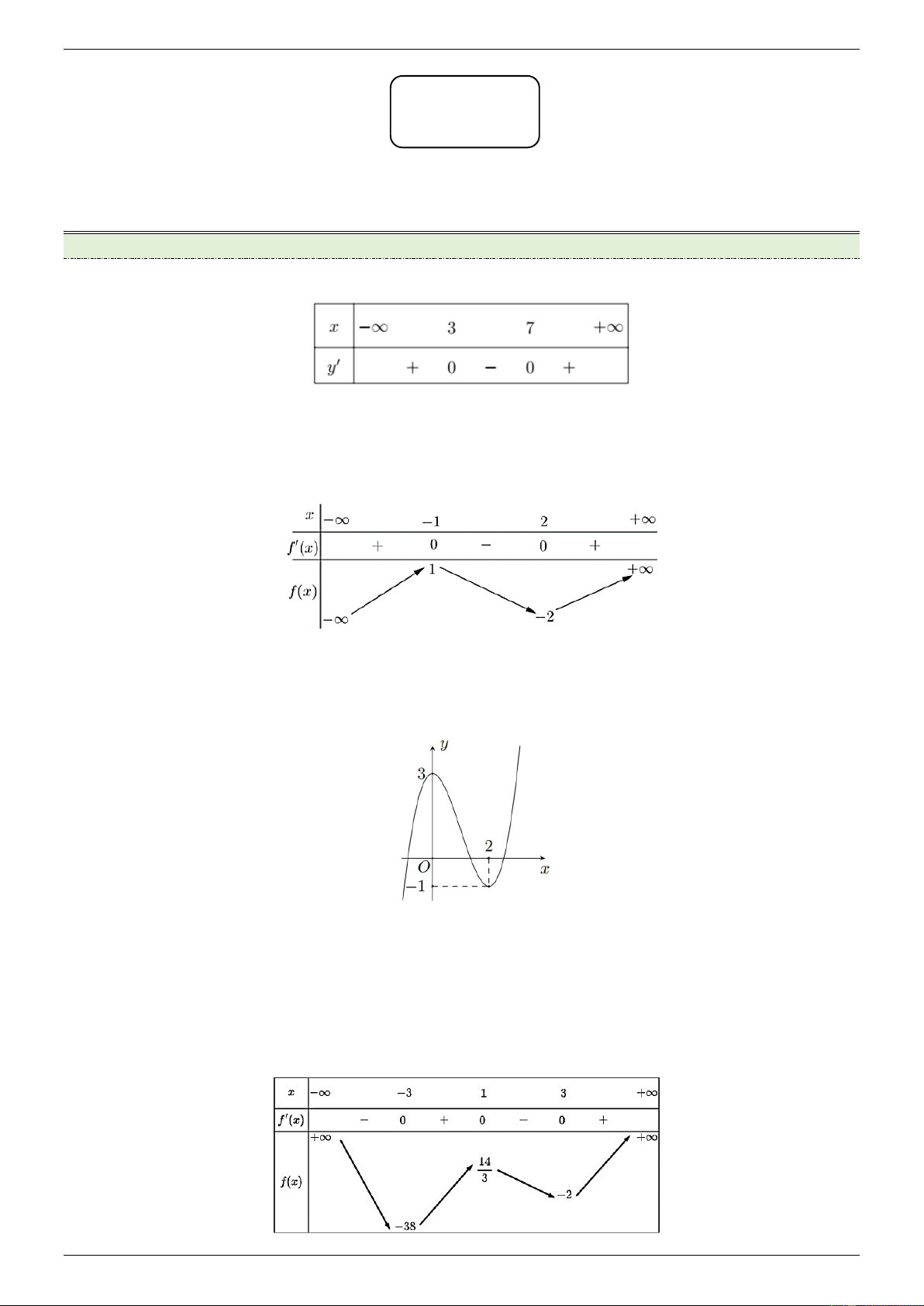
Cho hàm số y f x có đồ thị như hình dưới đây.
Giá trị cực tiểu của hàm số đã cho bằng A. 3 . B. 0 . C. 2 . D. 1 . Câu 4:
Cho hàm số y f x x x x2025 2 ' 1 1 2
. Hàm số y f x có bao nhiêu cực trị? A 1. B. 2 . C. 3 . D. 4 . Câu 5:
Cho hàm số y f x có bảng biến thiên như hình vẽ bên dưới Trang 6
Ôn tập thi giữa HKI – 2024 – 2025
Trường Quốc tế Á Châu
Nhóm toán – khối 12
Giá trị nhỏ nhất của hàm số trên đoạn 3; 3 bằng bao nhiêu? A. 38 . B. 3 . C. 2 . D. 3 . Câu 6:
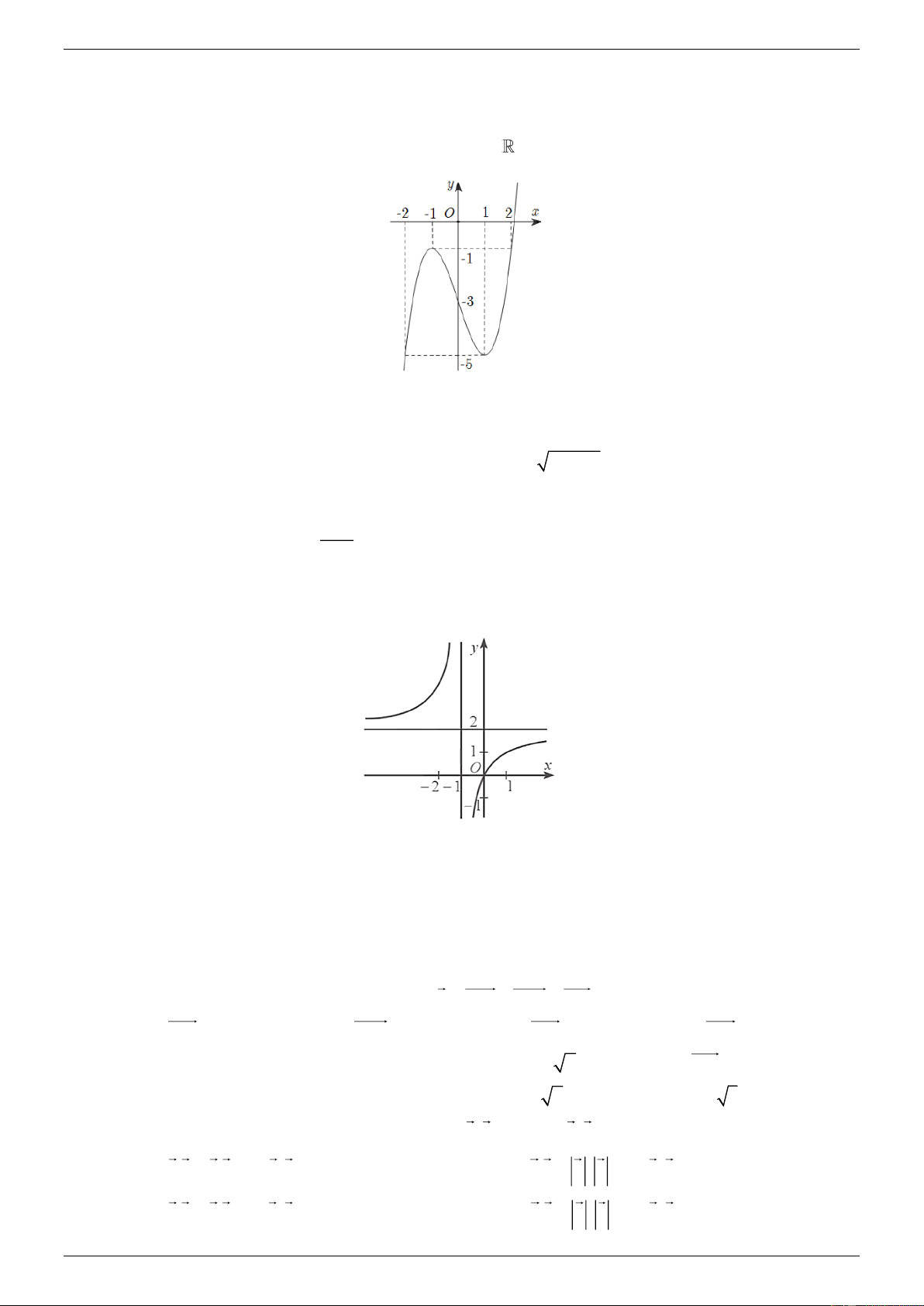
Cho hàm số y f x xác định và liên tục trên
có đồ thị hàm số như hình vẽ dưới đây.
Giá trị nhỏ nhất m và giá trị lớn nhất M của hàm số đã cho trên đoạn 2; 2 lần lượt là
A. m 5, M 1.
B. m 2, M 2 .
C. m 1, M 0 .
D. m 5, M 0 . Câu 7:
Trên đoạn 1;5, giá trị lớn nhất của hàm số f x 11 2x bằng A. 3 . B. 1. C. 5 . D. 0 . 1 Câu 8:
Cho hàm số y x 2
. Tiệm cận xiên của đồ thị hàm số là đường thẳng x 1
A. y x 1.
B. y x 1.
C. y x 2 .
D. y x 1 . Câu 9:
Cho hàm số y f x có đồ thị như hình vẽ dưới đây.
Phát biểu nào dưới đây là đúng về đường tiệm của đồ thị hàm số
A. Tiệm cận đứng là đường thẳng x 2 , tiệm cận ngang là đường thẳng y 1.
B. Tiệm cận đứng là đường thẳng x 1 , tiệm cận ngang là đường thẳng y 2 .
C. Tiệm cận đứng là đường thẳng x 2 , tiệm cận ngang là đường thẳng y 1.
D. Tiệm cận đứng là đường thẳng x 1 , tiệm cận ngang là đường thẳng y 2 .
Câu 10: Cho hình hộp ABC . D AB C D
. Vectơ v B A B C B B
bằng vectơ nào dưới đây?
A. DB . B. B D . C. BD . D. B D .
Câu 11: Cho hình lập phương ABC . D AB C D
có cạnh bằng a 2 . Độ dài vectơ AB bằng A. 2a . B. a . C. a 2 . D. a 3 .
Câu 12: Trong không gian, cho hai vectơ phân biệt a, b . Khi đó, a .b bằng A. . a b . a .
b cos a,b . B. .
a b a . b .cos a,b . C. . a b . a .
b sin a,b . D. .
a b a . b .sin a,b .
Ôn tập thi giữa HKI – 2024-2025 Trang 7
Trường Quốc tế Á Châu
Nhóm toán – khối 12
PHẦN II. TRẮC NGHIỆM ĐÚNG SAI
CÂU HỎI TRẮC NGHIỆM ĐÚNG /SAI x x
Câu 1 : Cho hàm số y f x 2 2 3 x 2 Mệnh đề Đúng Sai
(a) Hàm số y f x đồng biến trên khoảng ;
2 và 2; .
(b) Hàm số đã cho có 2 cực trị
(c) Không tồn tại giá trị lớn nhất và giá trị nhỏ nhất của hàm số y f x
(d) Đồ thị hàm số có đường tiệm cận xiên là y x . x
Câu 2: Cho hàm số y f x 2 1
có đồ thị C x 1 Mệnh đề Đúng Sai
(a) Tập xác định của hàm số là D \ 1 1
(b) Đạo hàm của hàm số y ' x 2 1
(c) Hàm số đồng biến trên ; 1
(d) Đường thẳng y 2 là tiệm cận ngang của đồ thị hàm số C .
Câu 3: Cho hàm số y f x liên tục trên
có đạo hàm f x x x 2 ' 1 . Mệnh đề Đúng Sai
(a) Hàm số đồng biến biến trên 1;0
(b) Hàm số đạt cực đại tại tại x 0 và đạt cực tiểu tại x 1
(c) Giá trị nhỏ nhất của hàm số trên 0;9 là 900
(d) Đồ thị hàm số đã cho không có đường tiệm cận đứng.
Câu 4: Cho hình hộp chữ nhật ABC . D AB C D
có AB AD 1 và AA 2 . Mệnh đề Đúng Sai
(a) AD BC
(b) BD CD 2
(c) AC CA 2C C 0
(d) AD AB 2 Trang 8
Ôn tập thi giữa HKI – 2024 – 2025
Trường Quốc tế Á Châu
Nhóm toán – khối 12
PHẦN III. TRẢ LỜI NGẮN TRẢ LỜI NGẮN 2 x 2x 3
Câu 1: Cho hàm số y f x có đạo hàm là f x x
. Số điểm cực tiểu của hàm số x 2 , 0 2 đã cho là? Điền đáp số: 4
Câu 2: Giá trị lớn nhất của hàm số 3 y 2x x trên đoạn 1 ; 1 bằng 3 Điền đáp số:
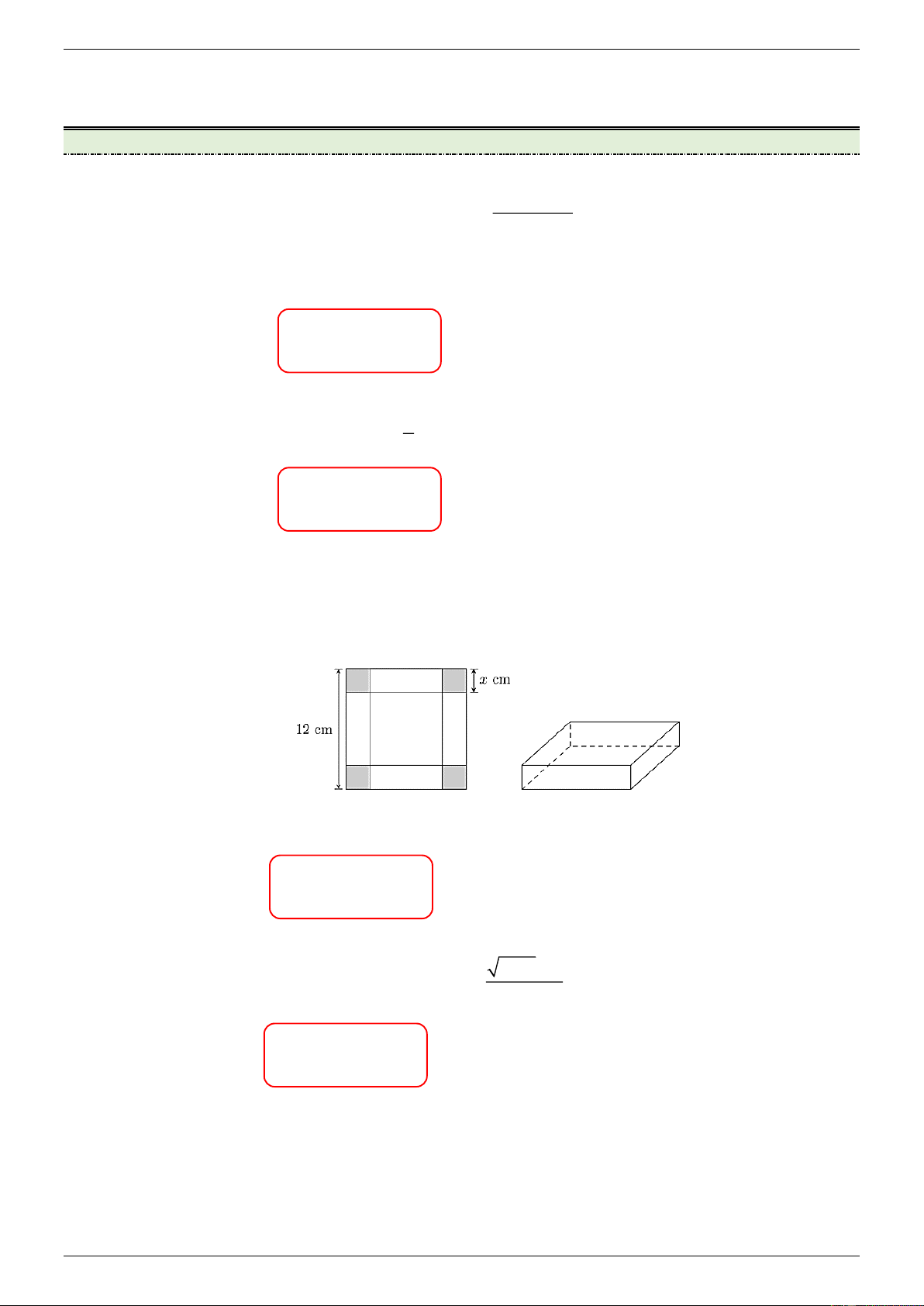
Câu 3: Cho một tấm nhôm hình vuông cạnh 12 (cm), người ta cắt ở bốn góc bốn hình vuông bằng nhau,
mỗi hình vuông có cạnh bằng x (cm), rồi gập tấm nhôm lại để được một cái hộp có dạng hình hộp
chữ nhật không có nắp (tham khảo hình vẽ).
Giá trị của x bằng bao nhiêu centimét để thể tích của khối hộp đó là lớn nhất? Điền đáp số: x 4 4
Câu 4: Số đường tiệm cận đứng của đồ thị hàm số y là 2 x 400 Điền đáp số: Câu 5: Cho hàm số 3 2
y ax bx cx d có đồ thị như hình bên. Hỏi các hệ số a, b, c, d có bao nhiêu số dương?
Ôn tập thi giữa HKI – 2024-2025 Trang 9
Trường Quốc tế Á Châu
Nhóm toán – khối 12
Điền đáp số:
Câu 6: Một chiếc ô tô được đặt trên mặt đáy dưới của một khung sắt có
dạng hình hộp chữ nhật với đáy trên là hình chữ nhật ABCD , mặt phẳng
ABCD song song với mặt phẳng nằm ngang. Khung sắt đó được buộc
vào móc E của chiếc cần cẩu sao cho các đoạn dây cáp E ,
A EB, EC, ED
có độ dài bằng nhau và cùng tạo với mặt phẳng ABCD một góc bằng
60 . Chiếc cần cẩu kéo khung sắt lên theo phương thẳng đứng. Trọng
lượng của chiếc xe ô bằng bao nhiêu Newton (làm tròn kết quả đến hàng
đơn vị)? Biết rằng các lực căng F , F , F , F đều có cường độ là 4500 N 1 2 3 4
và trọng lượng của khung sắt là 2 700 N. Điền đáp số:
-------------------------------Hết------------------------------- Trang 10
Ôn tập thi giữa HKI – 2024 – 2025
Trường Quốc tế Á Châu
Nhóm toán – khối 12 ĐỀ 3
PHẦN I. TRẮC NGHIỆM 4 ĐÁP ÁN
CÂU HỎI TRẮC NGHIỆM Câu 1:
Cho hàm số y f x có đồ thị như hình vẽ bên dưới
Hàm số đã cho nghịch biến trên khoảng nào? A. 1;0 . B. 1;1 . C. ;0 . D. 0; 1 . Câu 2:
Cho hàm số f x liên tục trên
và có bảng xét dấu của f x như sau:
Số điểm cực trị của hàm số đã cho là A. 1. B. 4 . C. 2 . D. 3 . Câu 3:
Hàm số y f x có bảng biến thiên như sau
Giá trị cực đại của hàm số đã cho bằng A. 1. B. 0 . C. 2 . D. 5 . 3 2x Câu 4:
Đường tiệm cận ngang của đồ thị hàm số y là 5x 1 1 2 3 1 A. x . B. y . C. y . D. y . 5 5 5 5 3 Câu 5:
Cho hàm số y f x có đạo hàm là f x 2
x x
1 2 3x , x . Khẳng định nào sau đây là đúng?
A. Hàm số đạt cực đại tại x 0 .
B. Hàm số đạt cực đại tại x 1 . 2
C. Hàm số nghịch biến trên khoảng 1;
. D. Hàm số đồng biến trên khoảng 1;0 . 3 Câu 6:
Hàm số y f x có đạo hàm trên \ 2 ;
2 , có bảng biến thiên như sau:
Ôn tập thi giữa HKI – 2024-2025 Trang 11
Trường Quốc tế Á Châu
Nhóm toán – khối 12
Khẳng định nào sau đây là đúng?
A. Đồ thị hàm số có đúng 2 tiệm cận đứng.
B. Đồ thị hàm số có 3 tiệm cận đứng.
C. Đồ thị hàm số có 2 đường tiệm cận ngang.
D. Đồ thị hàm số không có tiệm cận ngang. 4 Câu 7:
Trên đoạn [1;5] , hàm số y x
đạt giá trị nhỏ nhất tại điểm? x A. x 2 . B. x 5 . C. x 1 . D. x 4 . Câu 8:
Cho hàm số y f x xác định và liên tục trên
và có bảng biến thiên như hình vẽ sau
Mệnh đề nào dưới đây đúng?
A. Hàm số có giá trị nhỏ nhất bằng 3 .
B. Hàm số có giá trị nhỏ nhất bằng 1 .
C. Hàm số có giá trị lớn nhất bằng 2 .
D. Hàm số có giá trị lớn nhất bằng 5 . Câu 9:
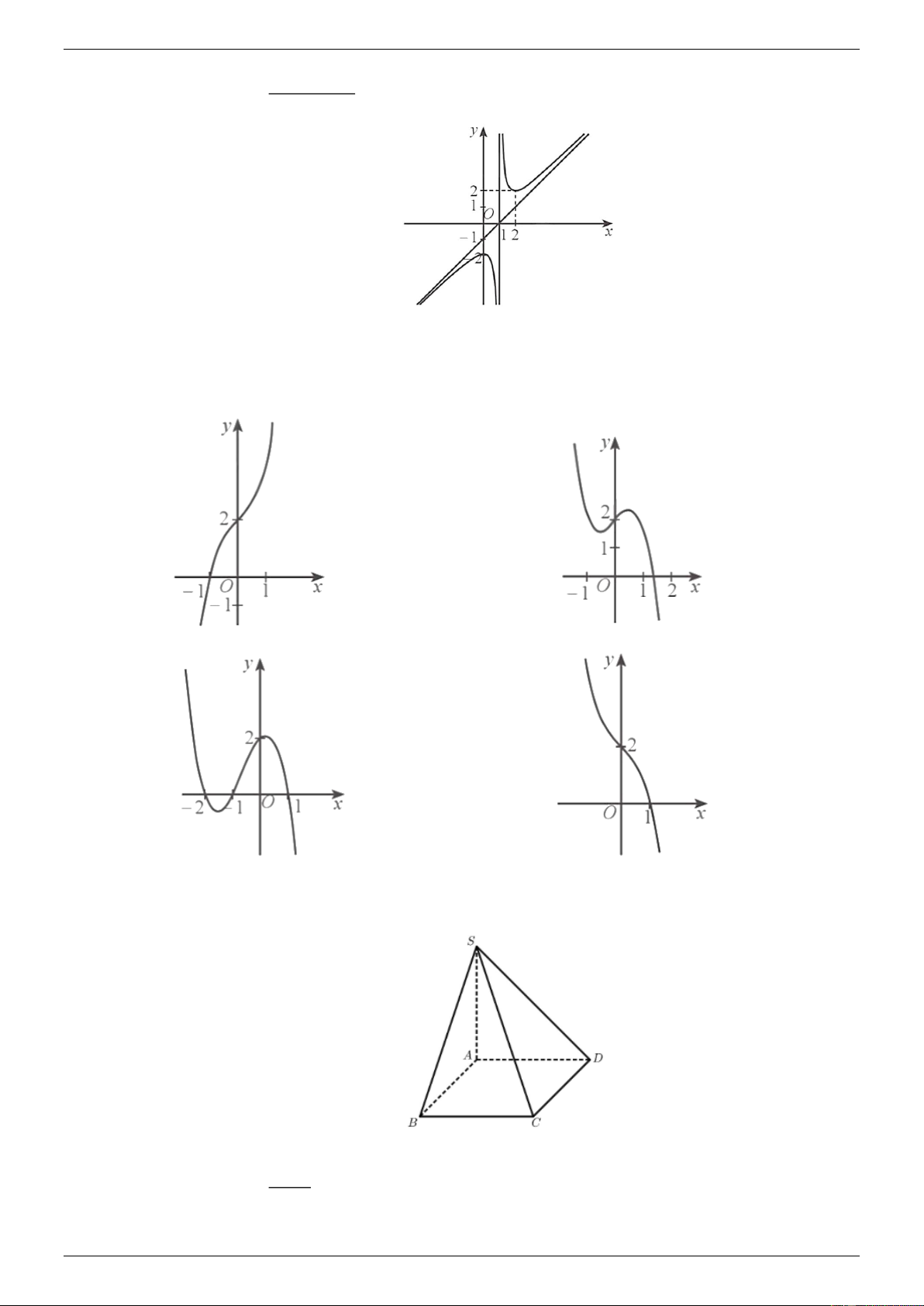
Đường cong trong hình bên là đồ thị của hàm số nào dưới đây? y A. 3 2
y x 3x 1. B. 3
y 2x x 1. 2 x 2x 2 C. y . x 1 x x 1 D. y . O 2x 1
Câu 10: Cho tứ diện đều ABCD có cạnh bằng 2 . Khi đó AB .CA bằng A. 2 . B. 2 3 . C. 2 3 . D. 2 .
Câu 11: Cho hình lập phương ABC . D
A BCD cạnh bằng 2 . Độ dài của vectơ A C A A bằng 2 3 A. 2 2 . B. . C. 2 6 . D. 2 3 . 2
Câu 12: Cho hình chóp S.ABC có đáy là tam giác đều cạnh a , SB vuông góc với mặt đáy và SB a 3
. Góc giữa hai vectơ AB và AS là A. o 30 . B. o 60 . C. o 45 . D. o 90 . Trang 12
Ôn tập thi giữa HKI – 2024 – 2025
Trường Quốc tế Á Châu
Nhóm toán – khối 12
PHẦN II. TRẮC NGHIỆM ĐÚNG SAI
CÂU HỎI TRẮC NGHIỆM ĐÚNG /SAI Câu 1 : Cho hàm số 2 4 x y f x . x Mệnh đề Đúng Sai
(a) Hàm số y f x nghịch biến trên khoảng 2; 2 .
(b) Hàm số y f x đạt cực đại tại x 2 .
(c) Cực tiểu của hàm số là 2 .
(d) Đồ thị hàm số có đường tiệm cận xiên là y x . 2x 1
Câu 2: Cho hàm số y
có đồ thị C . x 1 Mệnh đề Đúng Sai
(a) Điều kiện xác định của hàm số là x 1
(b) Hàm số đồng biến trên \ 1 . y x (c) max 1 khi 2 . 0;2
(d) Đồ thị C có giao điểm của hai đường tiệm cận là I 1; 2 .
Câu 3: Cho hàm số y f x có đạo hàm f x 2 x 2 4
x 2x với mọi x thuộc . Mệnh đề Đúng Sai
(a) Hàm số y f x đạt cực tiểu tại x 2 .
(b) Hàm số đồng biến trên 0; .
max f x f 2 (c) . ; 2
min f x f 0 (d) . 2 ; 2
Câu 4: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB a , AD 2a , cạnh bên
SA vuông góc với đáy, SA a . Gọi M là trung điểm của CD (tham khảo hình vẽ)
Ôn tập thi giữa HKI – 2024-2025 Trang 13
Trường Quốc tế Á Châu
Nhóm toán – khối 12 Mệnh đề Đúng Sai
(a) SB MB SC SD . (b) SA SM 2 21 cos , . 21 (c)
AM SA a 21 . 1 2
(d) SM . AB a . 2
PHẦN III. TRẢ LỜI NGẮN TRẢ LỜI NGẮN
Câu 1: Kí hiệu A x ; y là điểm cực đại của đồ thị hàm số 3 2
y x 3x 1. Giá trị của x y bằng? o o o o Điền đáp số:
Câu 2: Một vật chuyển động theo quy luật 3 2
S 2t 24t 9t 3 với t là khoảng thời gian tính từ lúc
vật bắt đầu chuyển động và S là quãng đường vật đi được trong khoảng thời gian đó. Hỏi trong
khoảng thời gian 10 giây kể từ lúc bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được bằng bao nhiêu? Điền đáp số:
Câu 3: Một khách sạn có 50 phòng. Hiện tại mỗi phòng cho thuê với giá 400 nghìn đồng một ngày thì toàn
bộ phòng được thuê hết. Biết rằng cứ mỗi lần tăng giá thêm 20 nghìn đồng thì có thêm 2 phòng
trống. Hỏi Giám đốc của khách sạn phải chọn giá phòng mới là bao nhiêu để thu nhập của khách
sạn trong ngày là lớn nhất (đơn vị nghìn đồng)? Điền đáp số: 2 x 2x 2
Câu 4: Biết rằng đồ thị của hàm số y
có đường tiệm cận đứng là x a và đường tiệm cận xiên x 1 a m
là y mx n . Tính giá trị của P . n Điền đáp số:
Câu 5: Cho hàm số f x 3 2
ax bx cx d a,b,c,d có đồ thị là đường cong như hình bên dưới Trang 14
Ôn tập thi giữa HKI – 2024 – 2025
Trường Quốc tế Á Châu
Nhóm toán – khối 12
Giá trị của f 5 bằng?
Điền đáp số:
Câu 6: Một em nhỏ cân nặng 20 kg trượt trên cầu trượt dài 3 m . Biết rằng cầu trượt có góc nghiêng so
với phương nằm ngang là o
30 . Biết rằng công AJ sinh bởi lực F có độ dịch chuyển d được
tính bởi công thức A F .d . Tính công sinh bởi trọng lực P khi em nhỏ trượt hết chiều dài cầu
trượt biết gia tốc rơi tự do là 2 g 9,8 m/s . Điền đáp số:
-------------------------------Hết-------------------------------
Ôn tập thi giữa HKI – 2024-2025 Trang 15
Trường Quốc tế Á Châu
Nhóm toán – khối 12 ĐỀ 4
PHẦN I. TRẮC NGHIỆM 4 ĐÁP ÁN
CÂU HỎI TRẮC NGHIỆM Câu 1:
Cho hàm số y f x có bảng xét dấu đạo hàm y như sau:
Hàm số đã cho nghịch biến trên khoảng nào trong các khoảng dưới đây? A. ;3 . B. ; 7 . C. 3;7 . D. 3; . Câu 2:
Cho hàm số y f x có đồ thị như hình dưới đây.
Giá trị cực đại của hàm số đã cho bằng A. 3 . B. 0 . C. 2 . D. 1 . Câu 3:
Cho hàm số y f x có đồ thị hàm số như hình vẽ dưới đây.
Giá trị nhỏ nhất của hàm số trên đoạn 0; 4 bằng bao nhiêu? A. 3 . B. 2 . C. 1. D. 6 . Câu 4:
Cho hàm số y f x có bảng biến thiên như hình vẽ sau:
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là A. 3 . B. 2 . C. 1. D. 0 . Trang 16
Ôn tập thi giữa HKI – 2024 – 2025
Trường Quốc tế Á Châu
Nhóm toán – khối 12 2
ax bx c Câu 5: Cho hàm số y
(với a, m 0 ) có đồ thị là đường cong như hình dưới đây. mx n
Tiệm cận xiên của đồ thị hàm số là đường thẳng
A. y x 1.
B. y x 1.
C. y x 1 .
D. y x 1. Câu 6: Đồ thị hàm số 3
y x x 2 là đường cong nào trong các đường cong sau? A. . B. . C. . D. . Câu 7:
Cho hình chóp tứ giác S.ABCD . Trong các vectơ có điểm đầu và điểm cuối phân biệt thuộc tập
hợp các đỉnh của hình chóp tứ giác, có bao nhiêu vectơ có giá nằm trong mặt phẳng SCD ? A. 3 . B. 2 . C. 6 . D. 0 . 3x 1 Câu 8: Cho hàm số y
. Phát biểu nào sau đây là đúng? 1 x
Ôn tập thi giữa HKI – 2024-2025 Trang 17
Trường Quốc tế Á Châu
Nhóm toán – khối 12
A. Hàm số đã cho đồng biến trên \ 1 .
B. Hàm số đã cho nghịch biến trên \ 1 .
C. Hàm số đã cho đồng biến trên các khoảng ;1 và 1;.
D. Hàm số đã cho nghịch biến trên các khoảng ;1 và 1;. Câu 9:
Trên đoạn 1;5, giá trị lớn nhất của hàm số f x 11 2x bằng A. 3 . B. 1. C. 5 . D. 0 .
Câu 10: Cho hình chóp S.ABCD có đáy là hình bình hành tâm O . Tính tổng SA SB SC SD . A. 2SO . B. 4SO . C. 3SO . D. 0 .
Câu 11: Cho hình lập phương ABC . D AB C D
. Khẳng định nào sau đây là sai? A. A ; B A D
90 . B. A ; B A C
45. C. AC;B D
90. D. A ; A CB 45 .
Câu 12: Cho hình lăng trụ ABC.A ' B 'C ' , M là trung điểm của BB ' . Đặt CA a , CB b , AA c .
Khẳng định nào sau đây đúng? 1 1
A. AM b c a .
B. AM a c b . 2 2 1 1
C. AM a c b .
D. AM b a c . 2 2
PHẦN II. TRẮC NGHIỆM ĐÚNG SAI
CÂU HỎI TRẮC NGHIỆM ĐÚNG /SAI
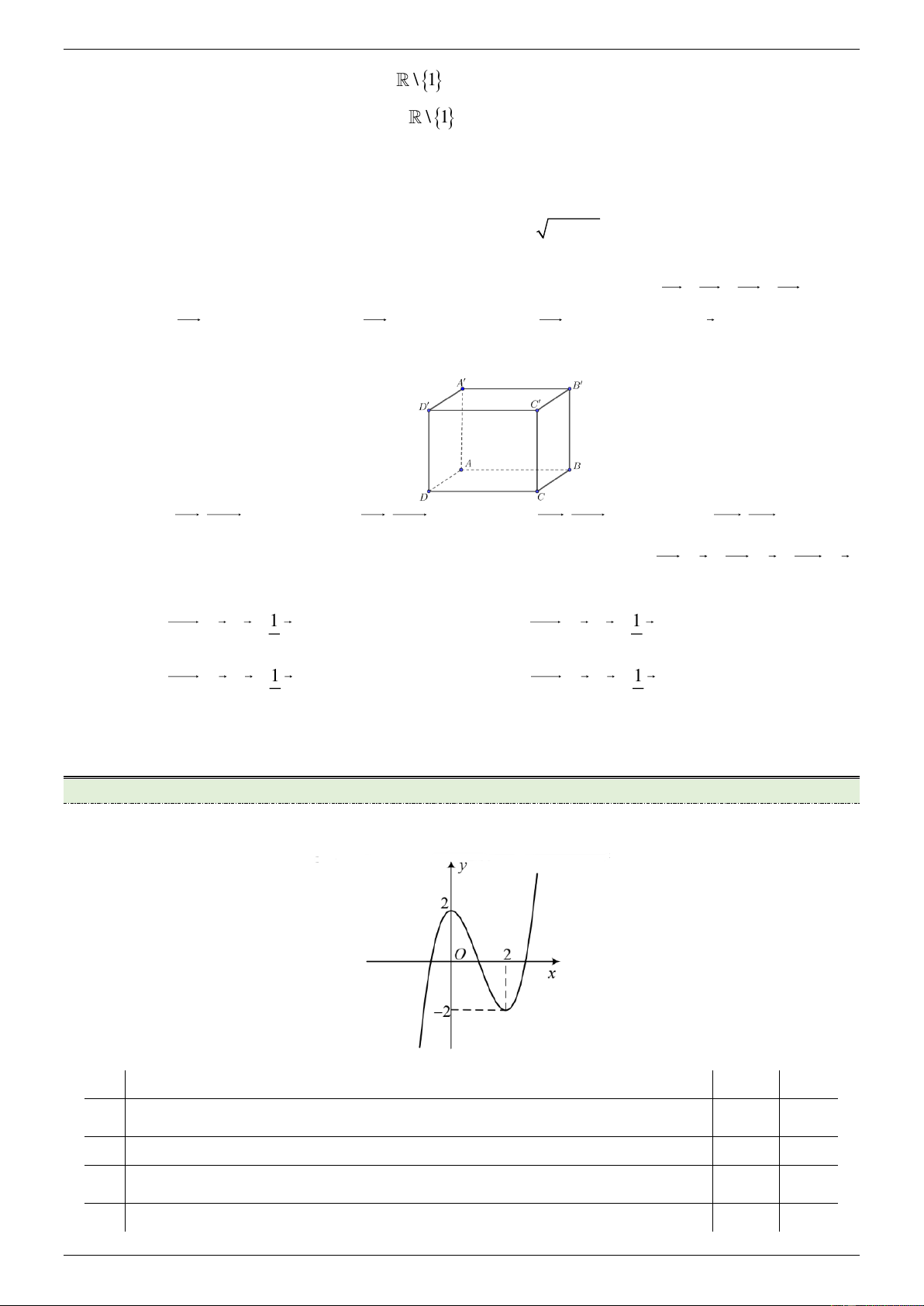
Câu 1. Cho hàm số y f x có đồ thị như hình dưới đây. Mệnh đề Đúng Sai
(a) Hàm số đã cho đồng biến trên khoảng 2; .
(b) Hàm số đã cho đạt cực đại tại x 0 ; đạt cực tiểu tại x 2 .
(c) Trên đoạn 0; 2 , giá trị lớn nhất của hàm số đã cho bằng 0 .
(d) Đồ thị hàm số không có đường tiệm cận. Trang 18
Ôn tập thi giữa HKI – 2024 – 2025
Trường Quốc tế Á Châu
Nhóm toán – khối 12 x
Câu 2. Cho hàm số y f x 2 1
có đồ thị là C . x 1 Mệnh đề Đúng Sai
(a) Hàm số đã cho nghịch biến trên từng khoảng ;
1 và 1; .
(b) Hàm số đã cho không có cực trị.
(c) C có tiệm cận đứng là x 1 , tiệm cận ngang là y 2 . 4
(d) Đạo hàm của hàm số y ' . x 2 1
Câu 3. Cho hình hộp chữ nhật ABCD.A B C D
có AB AD 1 và AA 2 . Mệnh đề Đúng Sai (a)
AD BC . (b) BD CD 2 (c)
AC CA 2C C 0. (d)
AD . AB 2 .
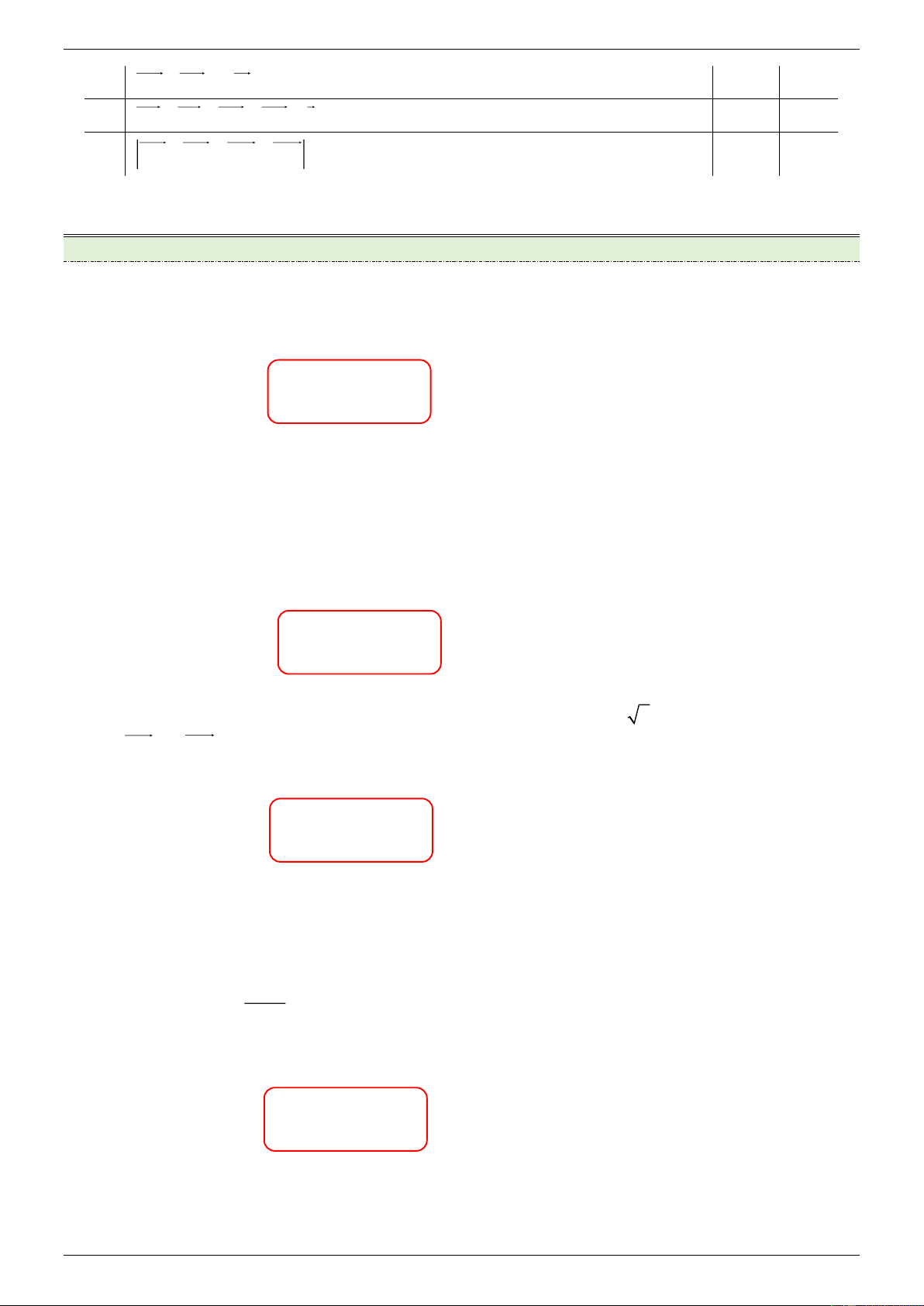
Câu 4. Cho tứ diện ABCD . Gọi I , J lần lượt là trung điểm của AB và CD , G là trung điểm của IJ (tham khảo hình vẽ). Mệnh đề Đúng Sai
(a) GI JG 0 .
Ôn tập thi giữa HKI – 2024-2025 Trang 19
Trường Quốc tế Á Châu
Nhóm toán – khối 12 (b)
AC BD 2IJ .
(c) GA GB GC GD 0 . (d)
MA MB MC MD nhỏ nhất khi M G .
PHẦN III. TRẢ LỜI NGẮN TRẢ LỜI NGẮN Câu 1: Cho hàm số 4 2
y x 2x 1. Hàm số có giá trị cực đại bằng bao nhiêu? Điền đáp số:
Câu 2: Một học sinh được giao thiết kế một cái hộp thỏa mãn: Tổng chiều dài và chiều rộng bằng 12 cm ;
tổng chiều rộng và chiều cao bằng 24 cm . Giáo viên ấy yêu cầu học sinh thiết kế sao cho thể tích
cái hộp là lớn nhất, giá trị thể tích lớn nhất bằng bao nhiêu ( kết quả làm tròn đến hàng chục). Điền đáp số:
Câu 3: Cho hình lăng trụ tam giác đều ABC.AB C
có AB a và AA a 2 . Số đo góc giữa hai vectơ
AB và BC bằng bao nhiêu độ? Điền đáp số:
Câu 4: Một doanh nghiệp sản xuất một loại sản phẩm. Giả sử tổng chi phí (đơn vị: triệu đồng) để sản xuất
và bán hết x sản phẩm đó được cho bởi f x 2
0,0001x 0, 2x 10 000 x 1 . f x
Tỉ số M x x
1 được gọi là chi phí trung bình cho một sản phẩm khi bán ra. Hãy cho x
biết doanh nghiệp cần sản xuất bao nhiêu sản phẩm để chi phí trung bình là nhỏ nhất. Điền đáp số:
Câu 5: Từ một tấm bìa mỏng hình vuông cạnh 6 dm, bạn Nhi cắt bỏ bốn tam giác cân bằng nhau có cạnh
đáy là cạnh của hình vuông ban đầu và đỉnh là đỉnh của một hình vuông nhỏ phía trong rồi gập lên, Trang 20
Ôn tập thi giữa HKI – 2024 – 2025