

Preview text:
ÔN GIỮA KỲ 1 - LỚP 12
GV. Ñaëng Coâng Vinh Böûu THPT Nguyễn Hữu Cầu
Thứ ......... ngày ..... tháng ..... năm ..... Lớp: 12A... ĐỀ 1
KIỂM TRA GIỮA KỲ 1 (2024-2025) Thời gian 75 phút
Họ và tên: .......................................................
- GT: Chương I (đến hết bài đường tiệm cận).
- HH: Chương II (Vectơ và các phép toán trong không gian).
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn(3 điểm) Câu 1:
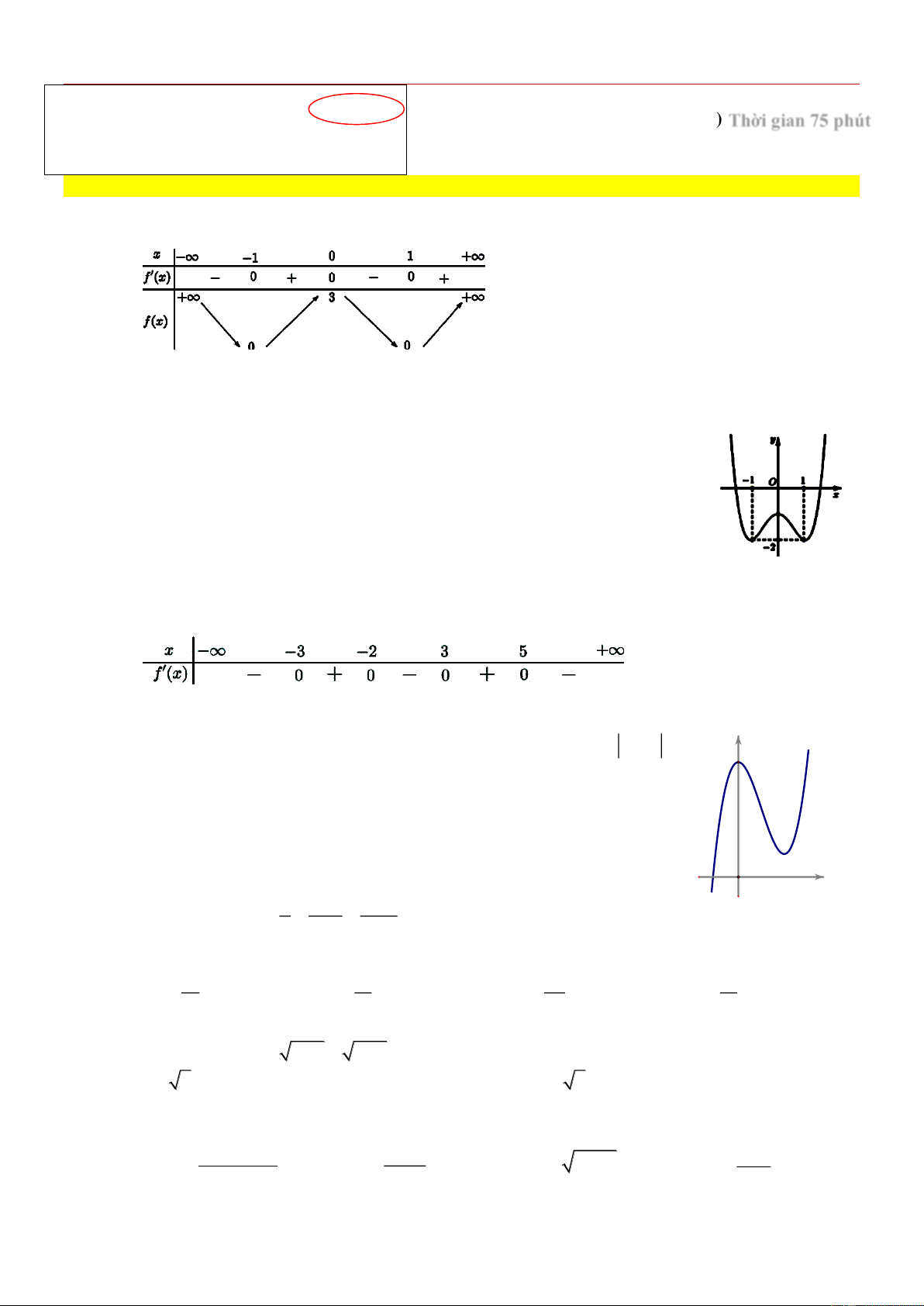
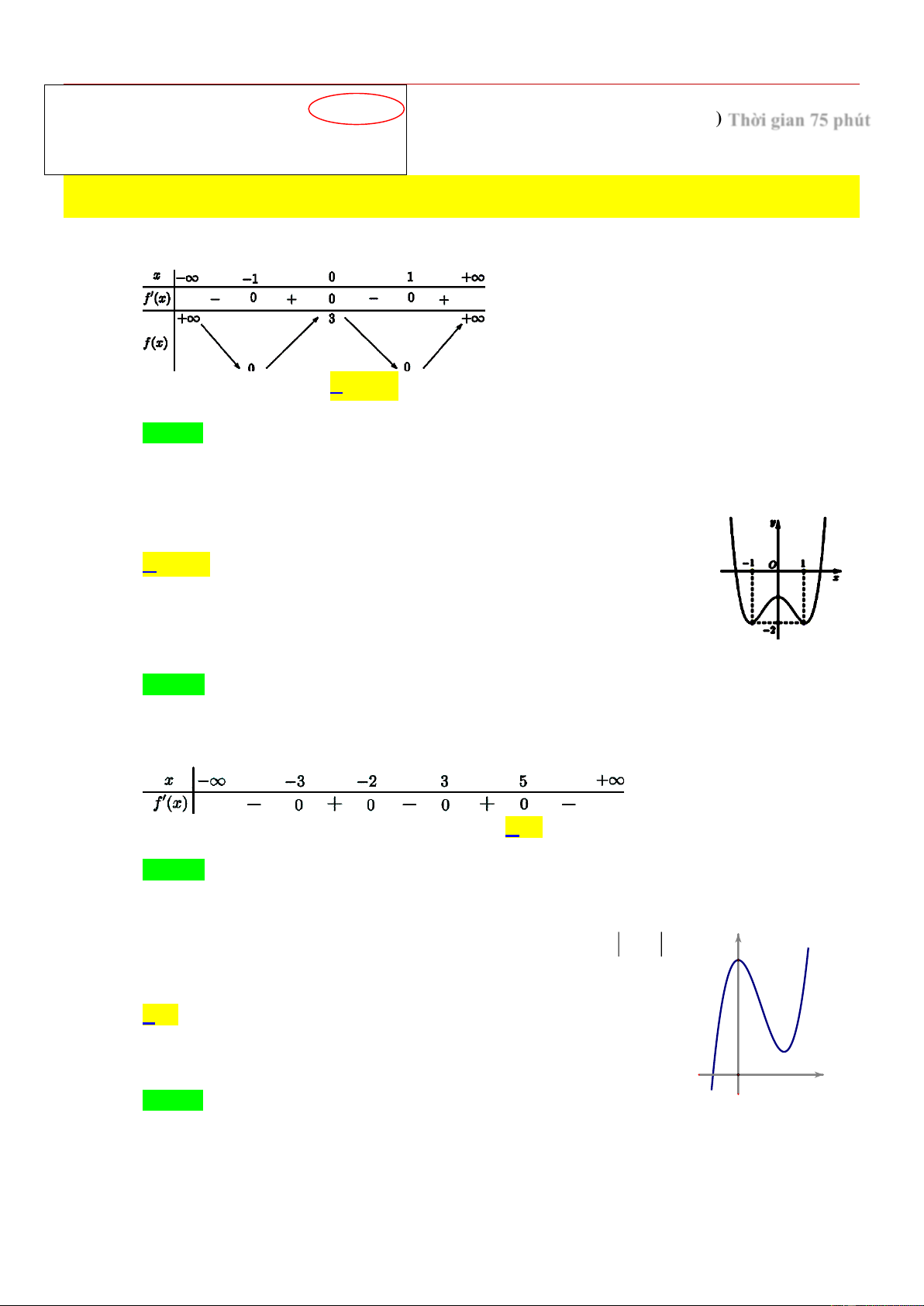
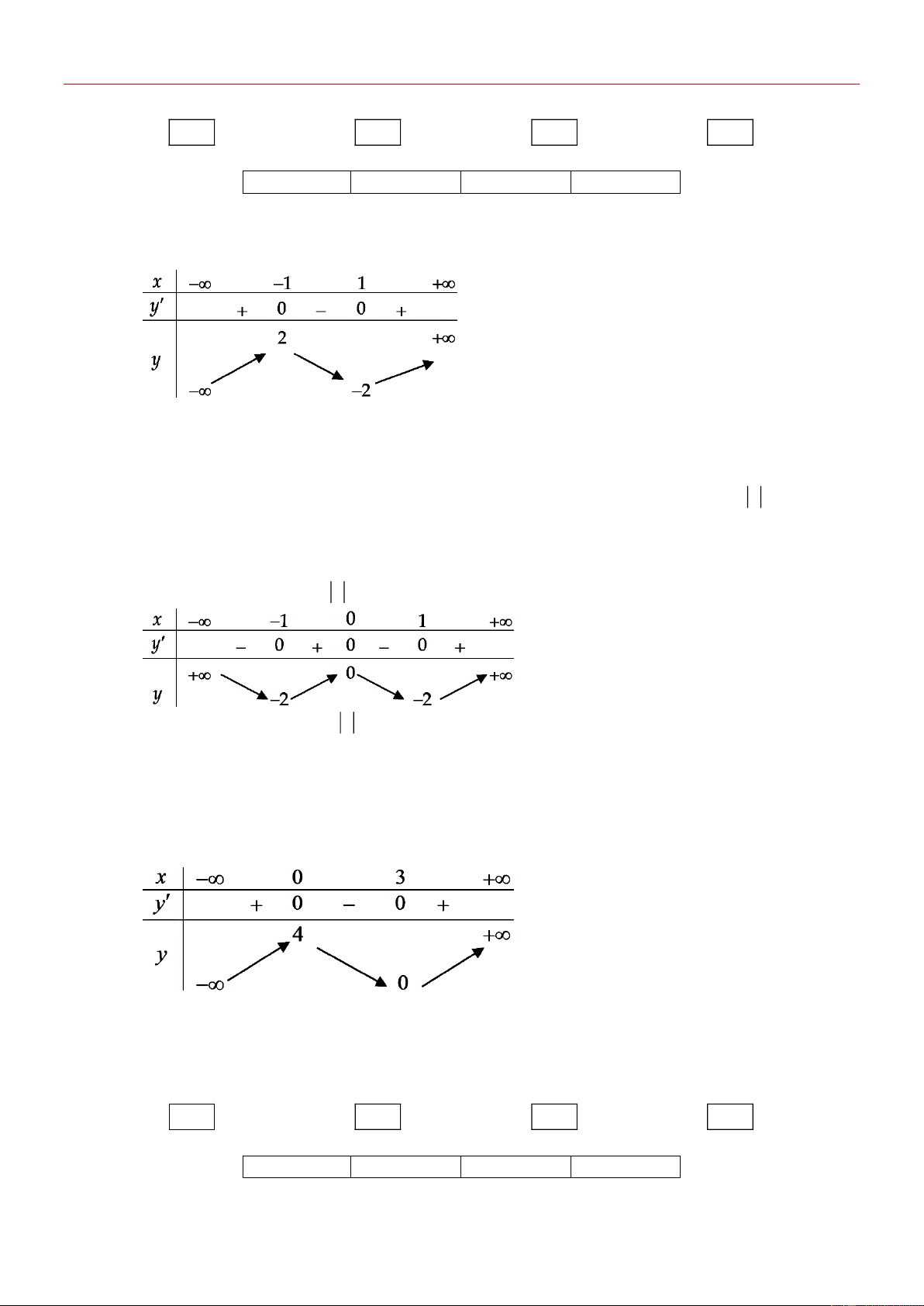
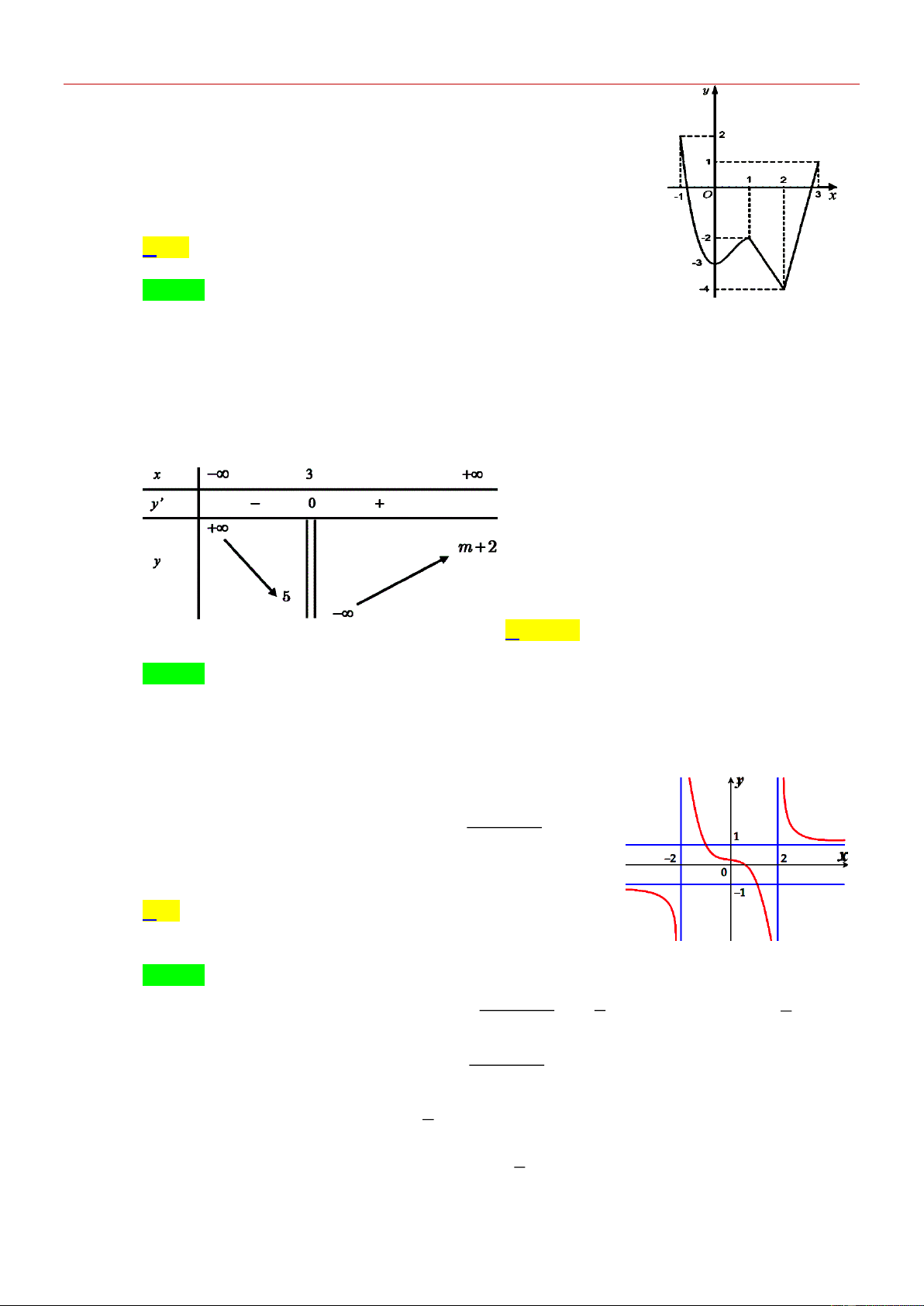
[NB] Cho hàm số y f x có bảng biến thiên như hình vẽ. Hàm số đã cho nghịch biến trên
khoảng nào dưới đây? A. 1; . B. 0 ;1 . C. 1 ;0 . D. 0; . Câu 2:
[NB] Cho hàm số y f (x) có đồ thị là đường cong trong hình vẽ. Hàm số
đã cho nghịch biến trong khoảng nào dưới đây? A. (0;1) . B. ( ; 0). C. (0; ) . D. ( 1 ;1) . Câu 3:
[NB] Cho hàm số f (x) có bảng xét dấu đạo hàm như hình vẽ. Số điểm cực trị của hàm số đã cho là A. 2. B. 3. C. 4. D. 5. Câu 4:
[NB] Cho hàm số y f (x) có đồ thị như hình vẽ. Hàm số y f x y f(x) có mấy cực trị? A. 2. B. 3. C. 4. D. 5. O x 1 1 1 Câu 5: [TH] Hàm số y
đạt giá trị lớn nhất trên đoạn x x 1 x 2 5 ; 3 bằng 13 11 47 11 A. . B. . C. . D. . 12 6 60 6 Câu 6:
[TH] Hàm số y 1 x 1 x có giá trị lớn nhất, giá trị nhỏ nhất lần lượt là A. 2 và1. B. 1và 0 . C. 2 và 2 . D. 2 và1. Câu 7:
[TH] Đồ thị của hàm số nào dưới đây có tiệm cận đứng? 2 x 3x 2 2 x x A. y . B. y . C. 2 y x 1 . D. y . x 1 2 x 1 x 1 ÔN GIỮA KỲ 1 - LỚP 12
GV. Ñaëng Coâng Vinh Böûu x 1 Câu 8:
[VD] Tìm số đường tiệm cận của đồ thị hàm số y .
4 3x 1 3x 5 A. 1. B. 2. C. 3. D. 4. Câu 9:
[TH] Cho hình lăng trụ AB . C A B C
. Đặt a AA , b AB , A' C'
c AC . Gọi G là trọng tâm của tam giác A B C . Vectơ G' AG bằng 1 a
A. AG a 3b c . 3 B' 1
B. AG a b c . c 3 A C 1
C. AG a b 3c . b 3 1 B
D. AG 3a b c . 3
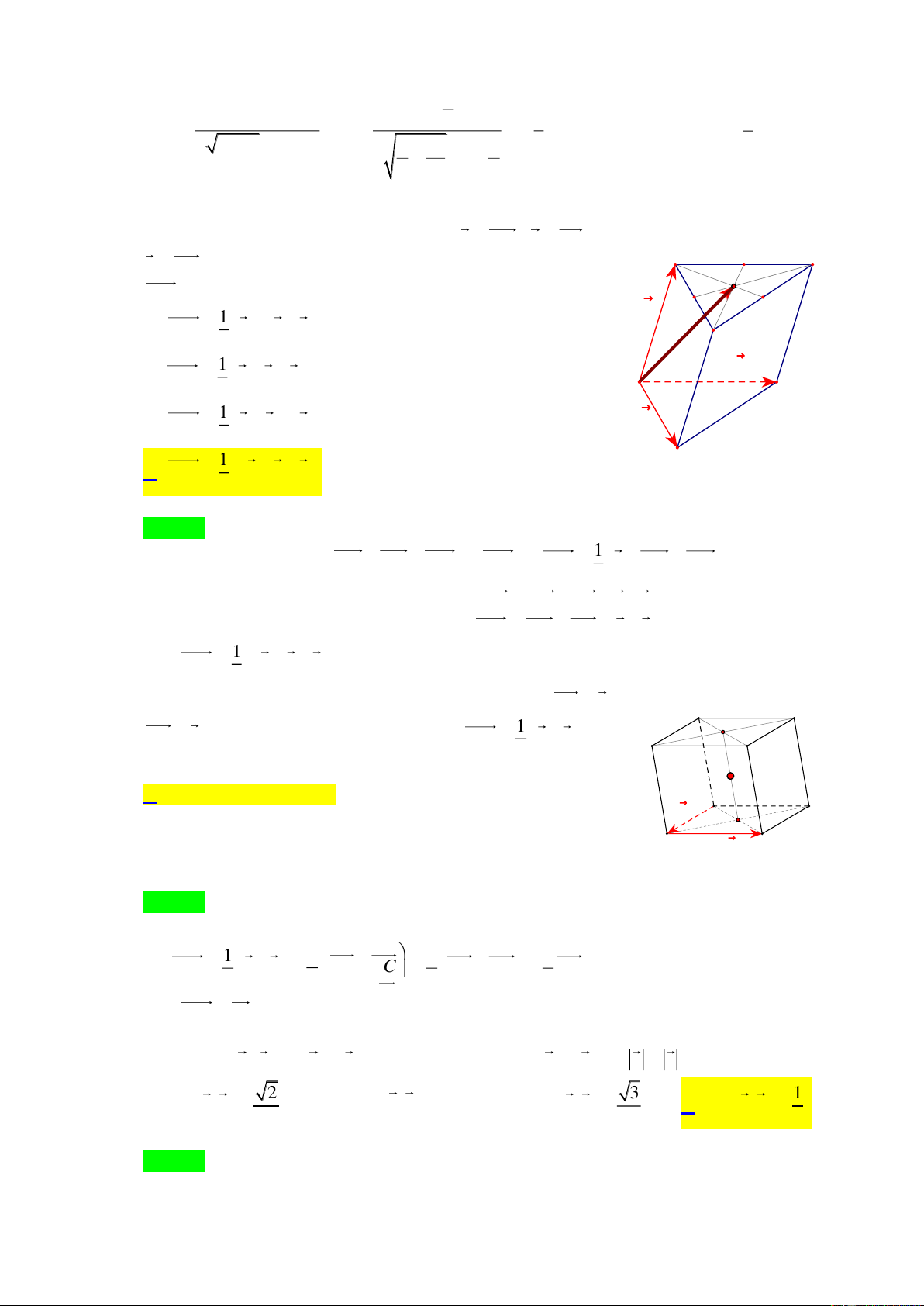
Câu 10: [VD] Cho hình hộp ABC .
D A' B 'C ' D ' có tâm O . Đặt AB a , A' D' 1 I'
BC b . Điểm M xác định bởi đẳng thức OM ab. B' C' 2
Khẳng định nào sau đây đúng? O
A. M là trung điểm BB ' . A D
B. M là tâm hình bình hành BCC ' B ' . a I
C. M là trung điểm CC ' . B C b
D. M là tâm hình bình hành ABB ' A' .
Câu 11: [VDC] Cho a , b có a 2b vuông góc với vectơ 5a 4b và a b . Khi đó: A. a b 2 cos , . B. cos , a b 1 . C. a b 3 cos , . D. a b 1 cos , . 2 2 2
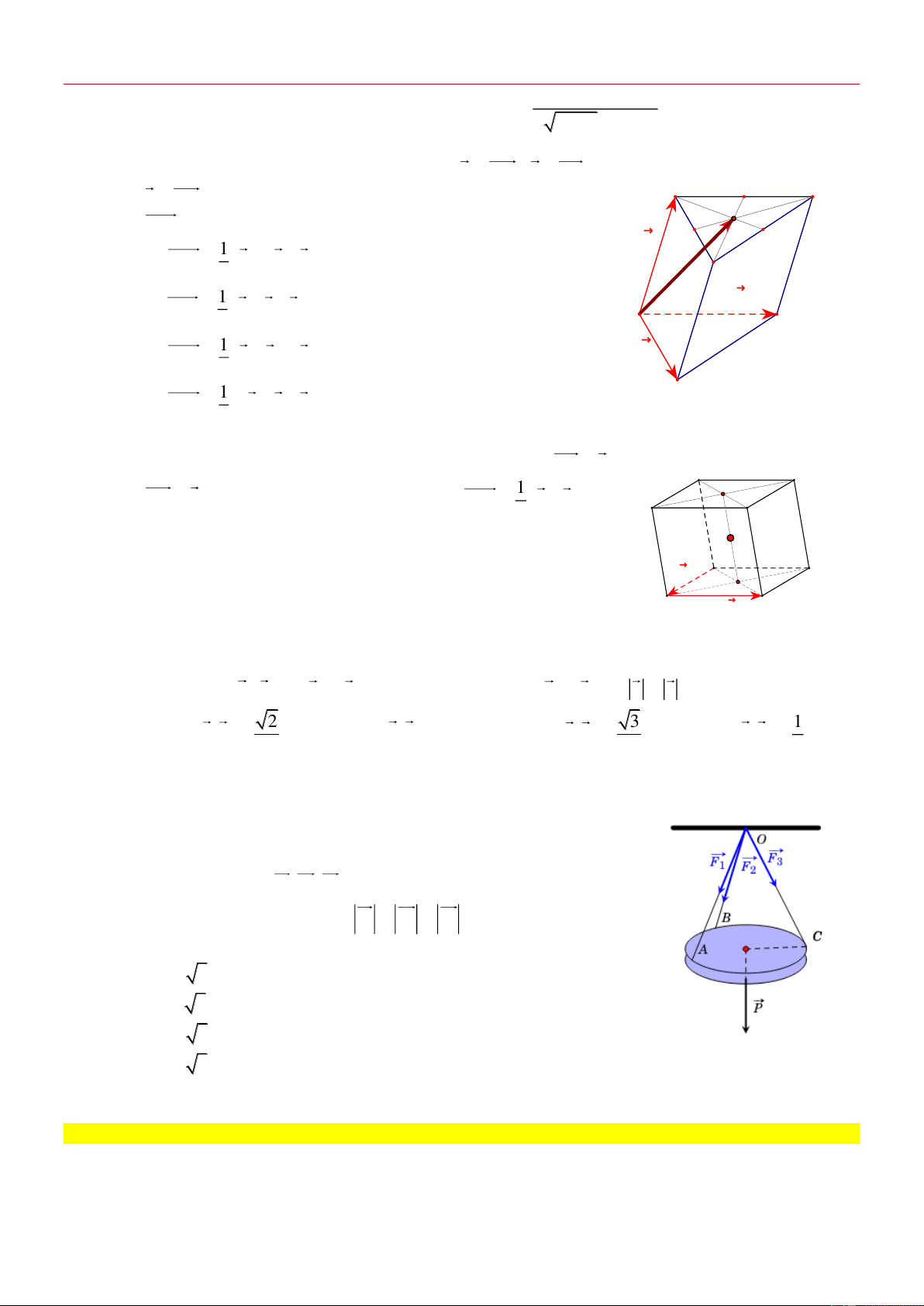
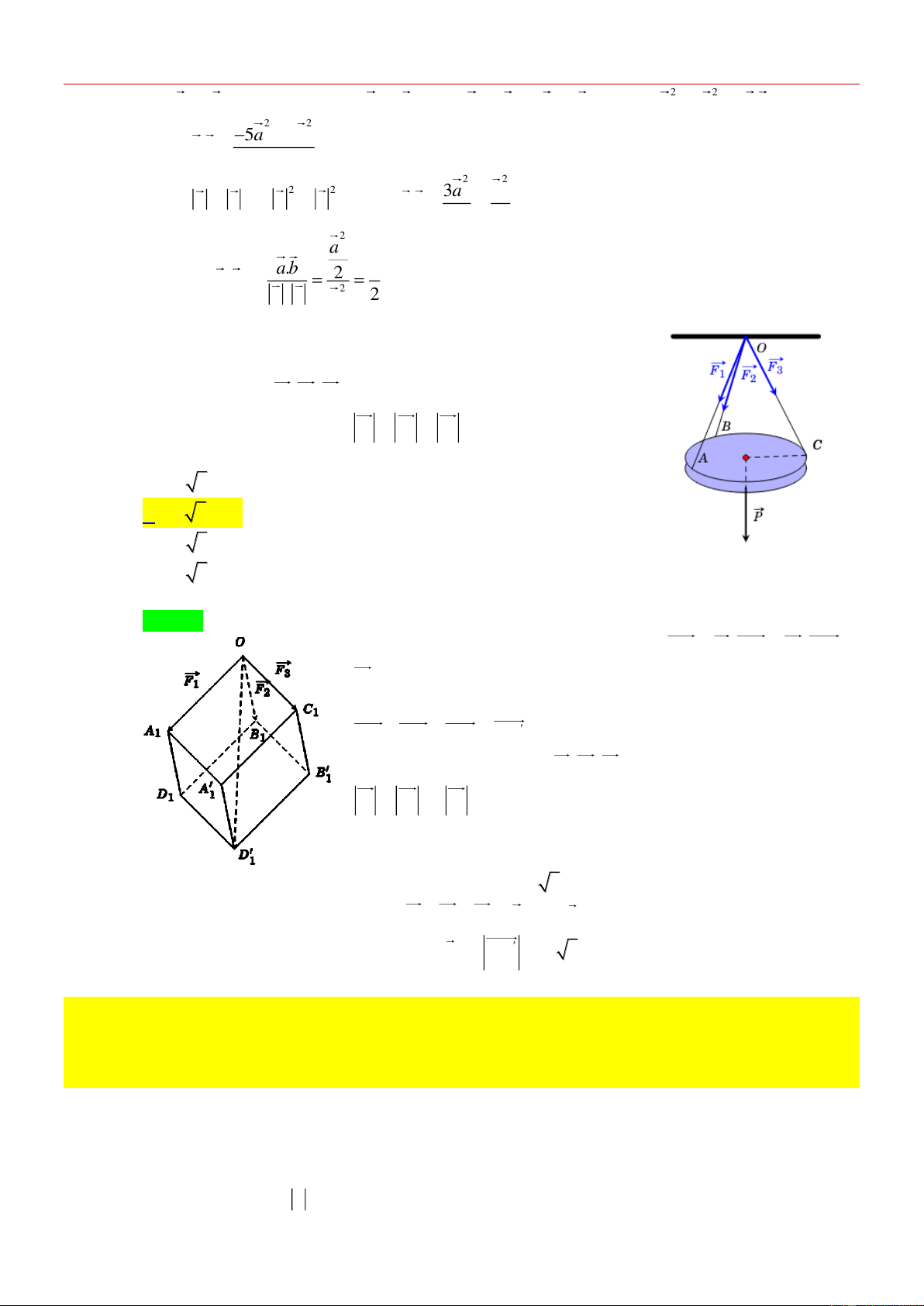
Câu 12: [VDC] Một chiếc đèn tròn được treo song song với mặt phẳng
nằm ngang bởi ba sợi dây không dãn xuất phát từ điểm O trên
trần nhà và lần lượt buộc vào ba điểm , A ,
B C trên đèn tròn sao
cho các lực căng F , F , F lần lượt trên mối dây O , A O , B OC đôi 1 2 3
một vuông góc với nhau và F F F 15 (N). Trọng lượng 1 2 3
của chiếc đèn tròn đó. A. 14 3( N) . B. 15 3( N) . C. 17 3( N) . D. 16 3( N) .
PHẦN II. Câu trắc nghiệm đúng sai (4,5 điểm) Câu 1:
Cho hàm số f x 3 x 3 .
x Các khẳng định sau đâu đúng hay sai?
a) [NB] Hàm số f x đồng biến trên ; 1 và 1; .
b) [NB] Nếu u, v thỏa mãn 0 u v 1 thì f u f v. ÔN GIỮA KỲ 1 - LỚP 12
GV. Ñaëng Coâng Vinh Böûu
c) [TH] Hàm số f x đồng biến trên 1 ;0.
d) [VD] Hàm số y f 2x 1 đồng biến trên ;
0 và 1;. A. . B. . C. . D. . Câu 2:
Cho hàm số bậc ba có bảng biến thiên như hình vẽ. Khẳng định sau đây đúng hay sai?
a) [NB] Hàm số f x có hai điểm cực trị.
b) [NB] Cực đại hàm số bằng 0.
c) [NB] Điểm A0; 4 là điểm cực đại của đồ thị hàm số.
d) [TH] Đường thẳng qua hai điểm cực trị của đồ thị hàm số là 4x 3y 12 0. A. . B. . C. . D. . Câu 3:
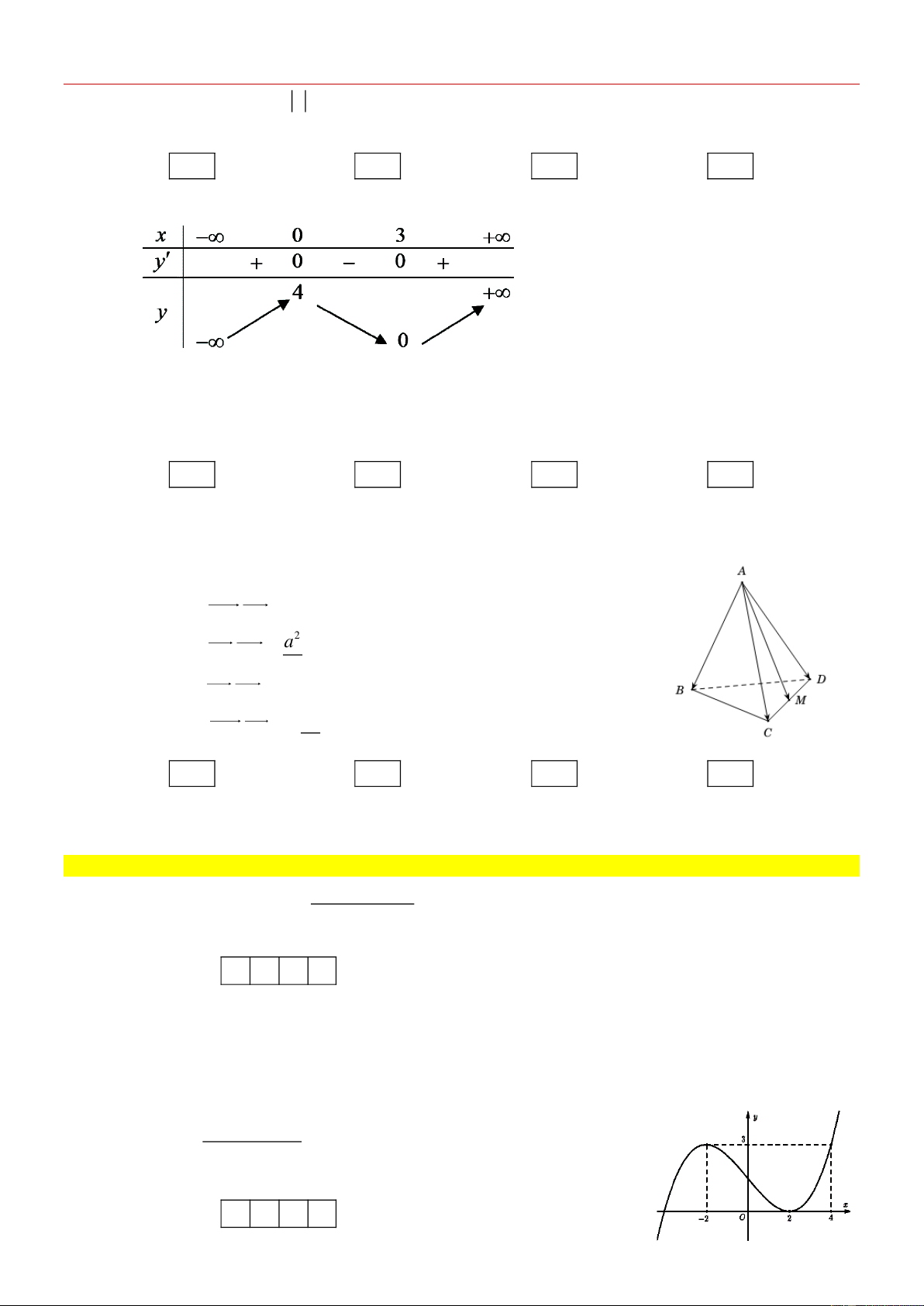
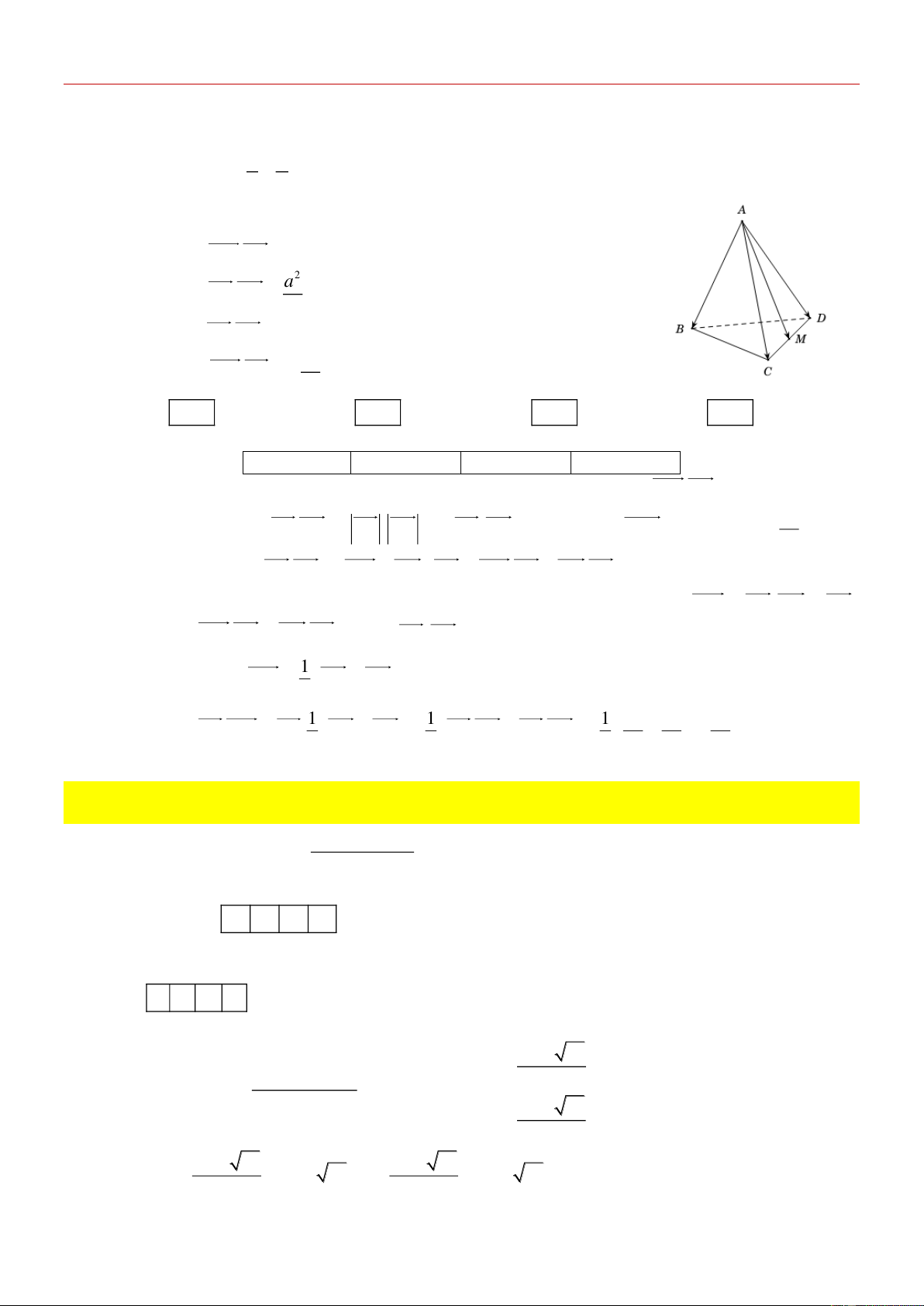
Cho tứ diện đều ABCD có cạnh bằng a và M là trung điểm của .
CD Các mệnh đề sau đúng hay sai?
a) [NB] AM.CD 0. 2 a
b) [NB] A . B AC . 2
c) [TH] A . B CD 0 2 a
d) [VD] AM .AB . 2 A. . B. . C. . D. .
PHẦN III. Câu trắc nghiệm trả lời ngắn (2,5 điểm) 2 3x 13x 19 Câu 1:
[TH] Cho hàm số y
. Đường thẳng d đi qua hai điểm cực trị của đồ thị hàm số x 3
có dạng d : y ax b . Tính giá trị biểu thức M 98a 99b . Kết quả: A. . B. . C. . D. . Câu 2:
[TH] Cho hàm số bậc ba có đồ thị như hình vẽ. Hỏi đồ thị hàm số g x 1
có tổng số bao nhiêu đường tiệm cận đứng f 2 4 x 3
và tiệm cận ngang? Kết quả: ÔN GIỮA KỲ 1 - LỚP 12
GV. Ñaëng Coâng Vinh Böûu A. . B. . C. . D. . 2 2x 3x 2 Câu 3:
[TH] Cho hàm số y
. Biết đồ thị hàm số có điểm cực tiểu là B ; a b và có 2x 3
đường tiệm cận xiên là y mx n . Khi đó T a 2b 3m 4n bằng bao nhiêu? (làm tròn đến
2 chữ số thập phân) Kết quả: A. . B. . C. . D. . Câu 4:
[VDC] Giả sử doanh số (tính bằng số sản phẩm) của một sản phẩm mới (trong vòng một số
năm nhất định) tuân theo quy luật logistic được mô hình hoá bằng hàm số 5000 f (t) , t 0 , 1 5 t e
trong đó thời gian t được tính bằng năm, kể từ khi phát hành sản phẩm mới. Khi đó, đạo hàm f (
t) sẽ biểu thị tốc độ bán hàng. Hỏi sau khi phát hành bao nhiêu năm thì tốc độ bán hàng là
lớn nhất? (làm tròn đến 2 chữ số thặp phân) Kết quả: A. . B. . C. . D. . Câu 5:
[VD] Cho tứ diện đều ABCD cạnh .
a Gọi M là trung điểm của BC. Tính cos A , B DM .
(làm tròn đến hai chữ số thập phân) Kết quả: A. . B. . C. . D. . ÔN GIỮA KỲ 1 - LỚP 12
GV. Ñaëng Coâng Vinh Böûu THPT Nguyễn Hữu Cầu
Thứ ......... ngày ..... tháng ..... năm ..... Lớp: 12A... ĐỀ 1
KIỂM TRA GIỮA KỲ 1 (2024-2025) Thời gian 75 phút
Họ và tên: .......................................................
- GT: Chương I (đến hết bài đường tiệm cận).
- HH: Chương II (Vectơ và các phép toán trong không gian).
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn (Thí sinh trả lời tư câu l đến câu 12. Mỗi câu
hỏi thi sinh chi chọn một phuơng án). (3 điểm) [8 câu Giải tích + 4 câu Hình học] Câu 1:
[NB] Cho hàm số y f x có bảng biến thiên như hình vẽ. Hàm số đã cho nghịch biến trên
khoảng nào dưới đây? A. 1; . B. 0 ;1 . C. 1 ;0 . D. 0; . Lời giải Chọn B
Dựa vào bảng biến thiên, hàm số đã cho nghịch biến trên các khoảng ; 1 và 0 ;1 . Vậy chọn đáp án 0 ;1 . Câu 2:
[NB] Cho hàm số y f (x) có đồ thị là đường cong trong hình vẽ. Hàm số
đã cho nghịch biến trong khoảng nào dưới đây? A. (0;1) . B. ( ; 0). C. (0; ) . D. ( 1 ;1) . Lời giải Chọn A
đồ thị hàm số đi xuống trên khoảng (0;1) nên hàm số nghịch biến trên khoảng (0;1) . Câu 3:
[NB] Cho hàm số f (x) có bảng xét dấu đạo hàm như hình vẽ. Số điểm cực trị của hàm số đã cho là A. 2. B. 3. C. 4. D. 5. Lời giải Chọn C
Dựa vào bảng xét dấu đạo hàm ta thấy đạo hàm đổi dấu qua các điểm 3
; 2;3;5. Vậy hàm số có 4 điểm cực trị. Câu 4:
[NB] Cho hàm số y f (x) có đồ thị như hình vẽ. Hàm số y f x y f(x) có mấy cực trị? A. 2. B. 3. C. 4. D. 5. Lời giải O x Chọn B ÔN GIỮA KỲ 1 - LỚP 12
GV. Ñaëng Coâng Vinh Böûu
Từ đồ thị của y f (x) y suy ra đồ f(x)
thị của y f x
Giữ nguyên phần đồ thị f x 0
(tức là giữ nguyên phần đồ thị phía trên trục Ox )
Lấy đối xứng phần đồ thị f x 0 qua trục Ox
(tức là lấy đối xứng phần đồ thị phía dưới trục Ox ) O x
Hợp 2 phần đồ thị vừa tìm chính là đồ thị của y f x 1 1 1 Câu 5: [TH] Hàm số y
đạt giá trị lớn nhất trên đoạn 5 ; 3 bằng x x 1 x 2 13 11 47 11 A. . B. . C. . D. . 12 6 60 6 Lời giải Chọn C 1 1 1 D \ 0; 1 ; 2 ; y 0, x D 2 x x 2 1 x 22 47
Vậy hàm số nghịch biến trên đoạn 5 ;
3 , nên max f x f 5 . 5; 3 60 Câu 6:
[TH] Hàm số y 1 x 1 x có giá trị lớn nhất, giá trị nhỏ nhất lần lượt là A. 2 và1. B. 1và 0 . C. 2 và 2 . D. 2 và1. Lời giải Chọn C 1 1 D 1 ; 1 ; y 2 1 x 2 1 x
y 0 1 x 1 x x 0 1 ; 1 y 1 2; y 1 2 Tính
. Vậy max y 2; min y 2 . y 0 2 1 ; 1 1 ; 1 Câu 7:
[TH] Đồ thị của hàm số nào dưới đây có tiệm cận đứng? 2 x 3x 2 2 x x A. y . B. y . C. 2 y x 1 . D. y . x 1 2 x 1 x 1 Lời giải Chọn D x x D: lim , lim
nên đường thẳng x 1
là tiệm cận đứng của đồ thị x 1 x x 1 1 x 1 x 1 Câu 8:
[VD] Tìm số đường tiệm cận của đồ thị hàm số y .
4 3x 1 3x 5 A. 1. B. 2. C. 3. D. 4. Lời giải Chọn B 1
Tập xác định: D ; \ 1 3 x x 1 4 3x 1 3x 5 1
4 3x 1 3x 5 + Ta có: lim lim , do x
4 3x 1 3x 5 x 9 x lim 2 1 1 x 1 1 9 x 1
đó đường thẳng x 1 là đường tiệm cận đứng của đồ thị ÔN GIỮA KỲ 1 - LỚP 12
GV. Ñaëng Coâng Vinh Böûu 1 1 x 1 1 1 + lim lim x
do đó đường thẳng y là đường
x 4 3x 1 3x 5 x 3 1 5 3 3 4 3 2 x x x
tiệm cận ngang của đồ thị
Vậy đồ thị hàm số có 2 đường tiệm cận. Câu 9:
[TH] Cho hình lăng trụ AB . C A B C
. Đặt a AA , b AB , A' C'
c AC . Gọi G là trọng tâm của tam giác A B C . Vectơ G' AG bằng 1 a
A. AG a 3b c . 3 B' 1
B. AG a b c . c 3 A C 1 C. AG
ab3c. b 3 1 D. B AG
3abc. 3 Lời giải Chọn D 1
Theo tính chất trọng tâm AA AB AC 3AG AG
a AB AC 3
Theo tính chất hình bình hành ABB A
ta có AB AA AB a b
Theo tính chất hình bình hành ACC A
ta có AC AA AC a c 1 Vậy AG
3abc. 3
Câu 10: [VD] Cho hình hộp ABC .
D A' B 'C ' D ' có tâm O . Đặt AB a , A' D' 1 I'
BC b . Điểm M xác định bởi đẳng thức OM ab. B' C' 2
Khẳng định nào sau đây đúng? O
A. M là trung điểm BB ' . A D
B. M là tâm hình bình hành BCC ' B ' . a I
C. M là trung điểm CC ' . B C b
D. M là tâm hình bình hành ABB ' A' . Lời giải Chọn A
I , I ' là tâm các mặt đáy ABC ,
D A' B 'C ' D ' tâm O là trung điểm II ' . 1 1 Từ OM a 1
b AB BC AB 1 AD
DB (quy tắc 3 điểm với phép trừ) 2 2 2 2 AD
Nên OM IB , do đó OIBM là hình bình hành.
Vậy M là trung điểm BB ' .
Câu 11: [VDC] Cho a , b có a 2b vuông góc với vectơ 5a 4b và a b . Khi đó: A. a b 2 cos , . B. cos , a b 1 . C. a b 3 cos , . D. a b 1 cos , . 2 2 2 Lời giải Chọn D ÔN GIỮA KỲ 1 - LỚP 12
GV. Ñaëng Coâng Vinh Böûu
Vì a 2b vuông góc với 5a 4b nên a 2b.5a 4b 2 2
0 5a 8b 6 . a b 0 2 2 5 a 8b . a b . 6 2 2 3a a Ta có a 2 2
b a b ; Do đó . a b . 6 2 2 a . a b 1 Vậy a b 2 cos , . 2 a . b 2 a
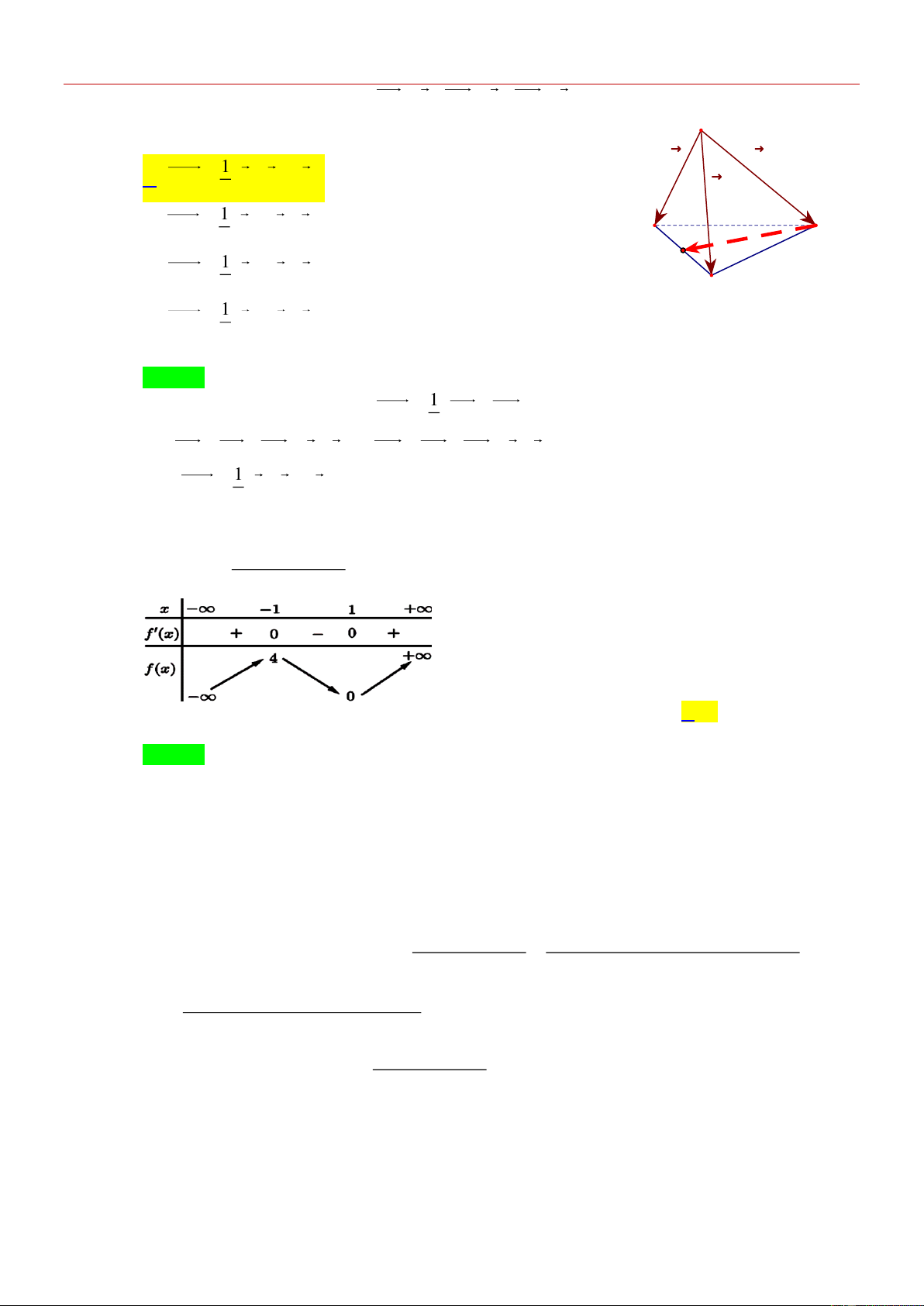
Câu 12: [VDC] Một chiếc đèn tròn được treo song song với mặt phẳng
nằm ngang bởi ba sợi dây không dãn xuất phát từ điểm O trên
trần nhà và lần lượt buộc vào ba điểm , A ,
B C trên đèn tròn sao
cho các lực căng F , F , F lần lượt trên mối dây O , A O , B OC đôi 1 2 3
một vuông góc với nhau và F F F 15 (N). Trọng lượng 1 2 3
của chiếc đèn tròn đó. A. 14 3( N) . B. 15 3( N) . C. 17 3( N) . D. 16 3( N) . Lời giải Chọn B
Gọi A , B ,C lần lượt là các điểm sao cho OA F ,OB F ,OC 1 1 1 1 1 1 2 1
F . Lấy các điểm D , A , B , D sao cho OA D B C A D B là hình 3 1 1 1 1 1 1 1 1 1 1 1
hộp (như hình bên). Khi đó, áp dụng quy tắc hình hộp ta có OA OB OC OD . 1 1 1 1
Măt khác, do các lực căng F , F , F đôi một vuông góc và 1 2 3
F F F 15( N) nên hình hộp OA D B C A D B có ba 1 2 3 1 1 1 1 1 1 1
cạnh OA ,OB , OC đôi một vuông góc và bằng nhau. Vì thể hình 1 1 1
hộp đó là hình lập phương có độ dài cạnh bằng 15. Suy ra độ dài
đường chéo OD của hình lập phương đó bằng 15 3 . 1
Do chiếc đèn ở vị trí cân bằng nên F F F P , với P là trong lực tác dụng lên chiếc đèn. 1 2 3
Suy ra trọng lượng của chiếc đèn là | P | OD 15 3( N) 1
PHẦN II. Câu trắc nghiệm đúng sai. Thi sinh trả lời tù̀ câu 1 đến câu 4. Trong mỗi ý a) , b) , c) , d) ở
mỗi câu, thí sinh chọn đúng hoặc sai. (4,5 điểm) [2 câu Giải tích + 1 câu Hình học]
Trả lời đúng 1/4 ý thì được 0,25 điểm; Trả lời đúng 2/4 ý được 0,5 điểm; Trả lời đúng 3/4 ý được 1,0
điểm; Trả lời đúng 4/4 ý được 1,5 điểm Câu 1:
Cho hàm số f x 3 x 3 .
x Các khẳng định sau đâu đúng hay sai?
a) [NB] Hàm số f x đồng biến trên ; 1 và 1; .
b) [NB] Nếu u, v thỏa mãn 0 u v 1 thì f u f v.
c) [TH] Hàm số f x đồng biến trên 1 ;0. ÔN GIỮA KỲ 1 - LỚP 12
GV. Ñaëng Coâng Vinh Böûu
d) [VD] Hàm số y f 2x 1 đồng biến trên ;
0 và 1;. A. . B. . C. . D. . Lời giải a) Đ b) S c) d) x 1
* a) Ta có: f x 2
3x 3; f x 0 . x 1 BBT:
Dựa vào BBT, hàm số f x đồng biến trên ;
1 và 1; . (a: đúng)
b) Do hàm số f x nghịch biến trên 1
;1 và u, v thỏa mãn 0 u v 1 nên f u f v. (b: sai)
c) Sử dụng phép biến đổi đồ thị. Từ đồ thị hàm số y f x suy ra đồ thị y f x bằng cách:
+) Giữ nguyên phần đồ thị y f x ứng với x 0, bỏ phần đồ thị y f x ứng với x 0.
+) Lấy đối xứng phần đồ thị được giữ của đồ thị y f x qua trục tung.
Lúc đó, BBT của y f x như sau:
Dựa vào BBT, hàm số f x đồng biến trên 1
;0. (c: đúng). d) Cách 1: x x Ta có: y
f x 2 1 1 1 2 2 1 0 . 2x 1 1 x 0
Vậy hàm số y f 2x 1 đồng biến trên ;
0 và 1;. Câu 2:
Cho hàm số bậc ba có bảng biến thiên như hình vẽ. Khẳng định sau đây đúng hay sai?
a) [NB] Hàm số f x có hai điểm cực trị.
b) [NB] Cực đại hàm số bằng 0.
c) [NB] Điểm A0; 4 là điểm cực đại của đồ thị hàm số.
d) [TH] Đường thẳng qua hai điểm cực trị của đồ thị hàm số là 4x 3y 12 0. A. . B. . C. . D. . Lời giải a) Đ b) S c) Đ d) Đ
* a) Hàm số f x có hai điểm cực trị là x 0; x 3 (a: đúng)
b) Cực đại hàm số bằng 4. (b: sai) ÔN GIỮA KỲ 1 - LỚP 12
GV. Ñaëng Coâng Vinh Böûu
c) Đồ thị có điểm cực đại là A0;4 . (c: đúng)
d) Đồ thị hàm số đã cho có 2 điểm cực trị là A0;4 và B3;0. x y
AB : 1 4x 3y 12 0. 3 4 Câu 3:
Cho tứ diện đều ABCD có cạnh bằng a và M là trung điểm của .
CD Các mệnh đề sau đúng hay sai?
a) [NB] AM.CD 0. 2 a
b) [NB] A . B AC . 2
c) [TH] A . B CD 0 2 a
d) [VD] AM .AB . 2 A. . B. . C. . D. . Lời giải a) Đ b) Đ c) Đ d) S
* a) Đúng: Tam giác ACD đều suy ra AM vuông góc với CD nên AM.CD 0 . a b) Đúng: AB AC AB AC AB AC 2 Ta có . . cos , A . B A . C cos BAC . a . a cos 60 . 2
c) Đúng: Ta có A .
B CD AM MB.CD AM.CD M . B CD .
Mặt khác AM , BM là trung tuyến của các tam giác đều AC ,
D BCD nên AM C , D MB CD
Suy ra AM.CD M . B CD 0
A ,BCD 90 . 1
d) Sai: Ta có AM AC AD 2 a a a
Suy ra AB AM AB
AC AD AB AC AB AD 2 2 2 1 1 1 . . . . 2 2 2 2 2 2
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6. (2,5 điểm) [5 câu Giải
tích + 1 câu Hình học] 2 3x 13x 19 Câu 1:
[TH] Cho hàm số y
. Đường thẳng d đi qua hai điểm cực trị của đồ thị hàm số x 3
có dạng d : y ax b . Tính giá trị biểu thức M 98a 99b . Kết quả: A. . B. . C. . D. . Lời giải 1 8 7 5
*Cách 1 (tìm tọa độ 2 điểm cực trị - viết PT đường thẳng) 9 21 x 2 Đạ 3x 18x 20 3 o hàm y ; Giải y 0
; Tọa độ 2 điểm cực trị là x 32 9 21 x 3 9 21 9 21 A ; 5 2 21, B ; 5 2 21 3 3 ÔN GIỮA KỲ 1 - LỚP 12
GV. Ñaëng Coâng Vinh Böûu 9 21 5 2 21 .a b a 6 Đườ 3
ng thẳng d : y ax b thỏa . 9 21 b 13 5 2 21 .a b 3
Vậy d : y 6x 13 ; Giá trị M 98a 99b 986 99 1 3 1875. f x
*Cách 2 (áp dụng công thức PT đường thẳng qua hai điểm cực trị hàm phân thức là g x f x đường y ) g x 2 PT đườ 3x 13x 19
ng thẳng qua 2 điểm cực trị của đồ thị hàm số y là đường x 3 2
3x 13x 19 y
y 6x 13. x 3
Giá trị M 98a 99b 986 99 1 3 1875. Câu 2:
[TH] Cho hàm số bậc ba có đồ thị như hình vẽ. Hỏi đồ thị hàm số g x 1
có tổng số bao nhiêu đường tiệm cận đứng f 2 4 x 3
và tiệm cận ngang? Kết quả: A. . B. . C. . D. . Lời giải 4 2 4 x 2 x 6 Xét f 2
4 x 3 0 f 2
4 x 3 2 4 x 4 x 0
Vậy đồ thị hàm số g x có ba đường tiệm cận đứng. Xét f 2 lim
4 x lim g x 0 y 0 là đường tiệm cận ngang của đồ thị. x x
KL: Vậy đồ thị hàm số g x có 4 đường tiệm cận. 2 2x 3x 2 Câu 3:
[TH] Cho hàm số y
. Biết đồ thị hàm số có điểm cực tiểu là B ; a b và có 2x 3
đường tiệm cận xiên là y mx n . Khi đó T a 2b 3m 4n bằng bao nhiêu? (làm tròn đến
2 chữ số thập phân) Kết quả: A. . B. . C. . D. . Lời giải 3 , 5 0 5 x 2 4x 12x 5 2 Đạo hàm y , y 0 . 2x 32 1 x 2 1 1 1 1
Vậy đồ thị hàm số có điểm cực tiểu là B ; a ;b 2 2 nên 2 2 ÔN GIỮA KỲ 1 - LỚP 12
GV. Ñaëng Coâng Vinh Böûu 2 3 2 1 2 2 3 y 2x x . Vậy TCX y
x nên m 1; n 0 2 0 2 2 3 2x 3 2 x 2
KL: Giá trị T a 2b 3m 1 7 4n 1 3 0 3,5 2 2 Câu 4:
[VDC] Giả sử doanh số (tính bằng số sản phẩm) của một sản phẩm mới (trong vòng một số
năm nhất định) tuân theo quy luật logistic được mô hình hoá bằng hàm số 5000 f (t) , t 0 , 1 5 t e
trong đó thời gian t được tính bằng năm, kể từ khi phát hành sản phẩm mới. Khi đó, đạo hàm f (
t) sẽ biểu thị tốc độ bán hàng. Hỏi sau khi phát hành bao nhiêu năm thì tốc độ bán hàng là
lớn nhất? (làm tròn đến 2 chữ số thặp phân) Kết quả: A. . B. . C. . D. . Lời giải 1 , 6 1 5 00015 t e 25000 t e Ta có: f ( t)
. Tốc độ bán hàng là lớn nhất khi f ( t) lớn nhất. 1 5 t e 2 15 t e 2 t Đặ 25000e t h(t) . 1 5 t e 2 2 5000 t e 1 5 t
e 2 2 5 t
e 15 t
e 25000 t e h ( t) 1 5 t e 4 2 5000 t e 1 5 t
e 1 5 t e 10 t e 2 5000 t e 1 5 t e 1 5 t e 4 15 t e 3 2 5000 t e 1 5 t e t t 1 h ( t) 0
15e 0 e t ln 5(tm) 1 5 t e 0 3 5
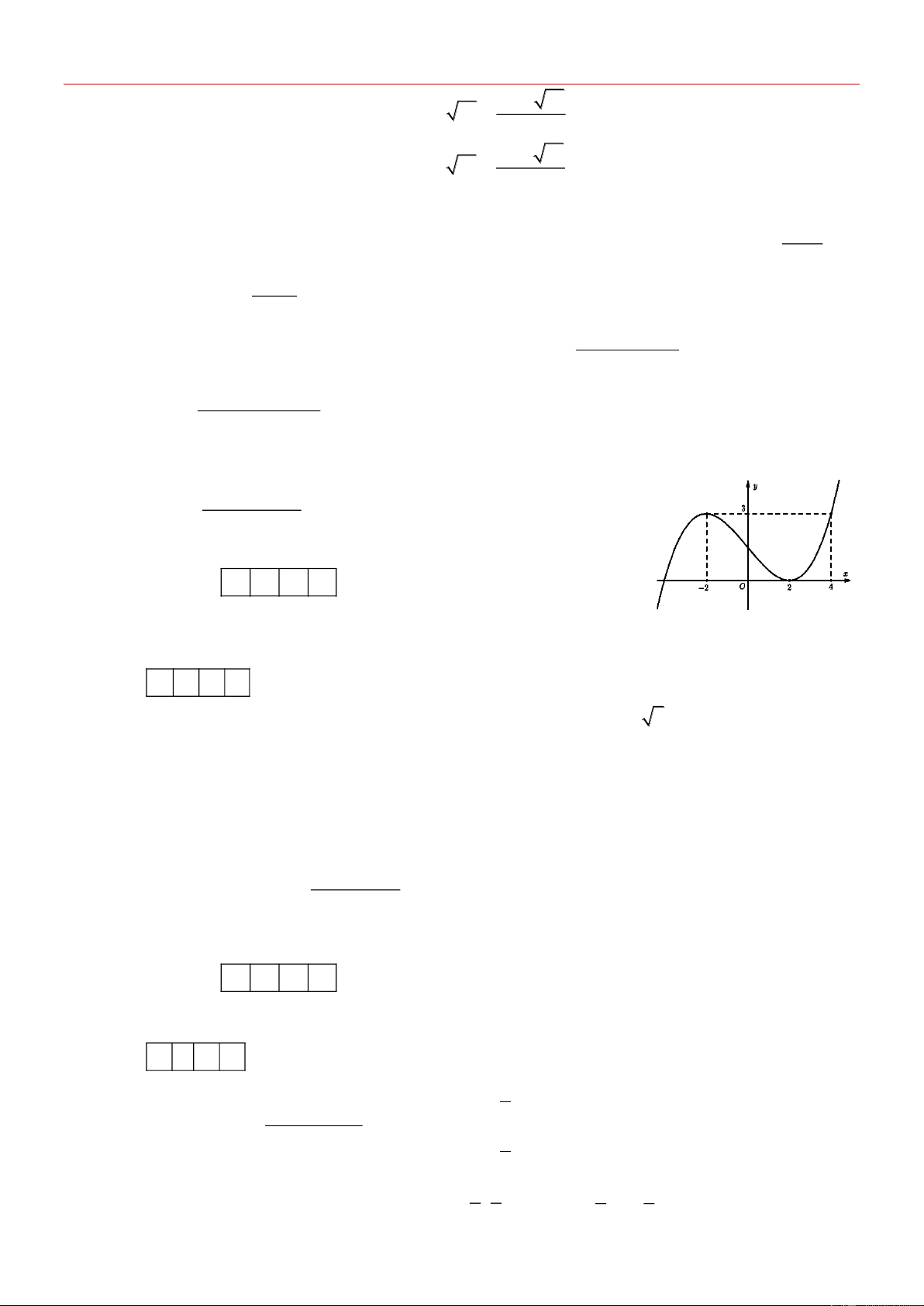
Ta có bảng biến thiên với t [0; ) :
Vậy sau khi phát hành khoảng ln 5 1, 6 năm thì thì tốc độ bán hàng là lớn nhất. Câu 5:
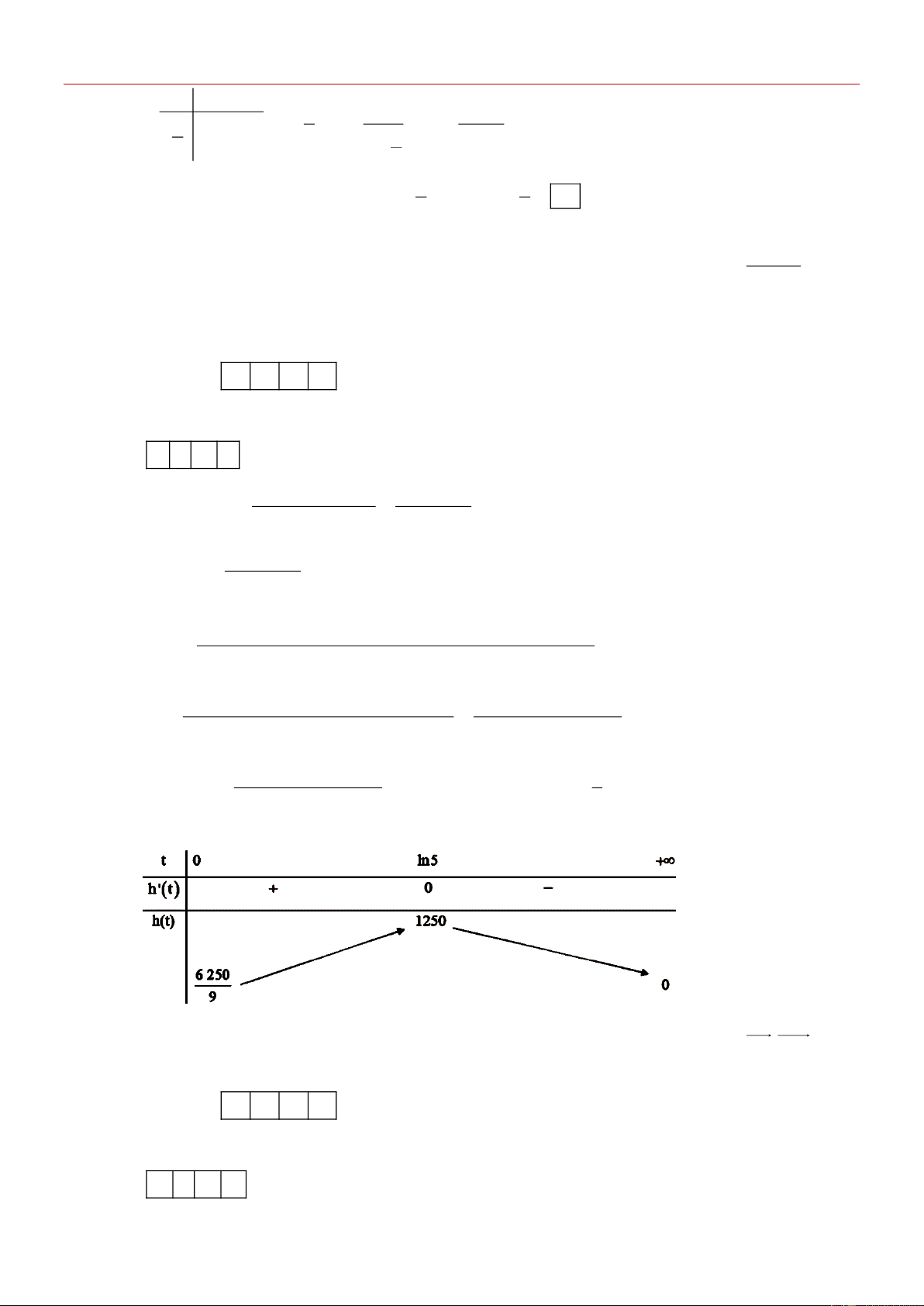
[VD] Cho tứ diện đều ABCD cạnh .
a Gọi M là trung điểm của BC. Tính cos A , B DM .
(làm tròn đến hai chữ số thập phân) Kết quả: A. . B. . C. . D. . Lời giải 0 , 2 9 ÔN GIỮA KỲ 1 - LỚP 12
GV. Ñaëng Coâng Vinh Böûu a 3 a 3
Xét tứ diện ABCD cạnh a ta có: DM ; AM . 2 2 Ta có
AB DM A .BDM AM.DM 2 AM.DM cos , . . 2 AB . DM a 3 3 a . a 2 Tính A . B DM : ta có A .
B DM AB AM AD A . B AM A . B AD AM
AB AM AB AD AB AD 2 a 3 3 1 a AB . .cos , . .cos , . a . . a . a . 2 2 2 4 Vậy AB DM 3 cos , 0,29 . 6 ÔN GIỮA KỲ 1 - LỚP 12
GV. Ñaëng Coâng Vinh Böûu THPT Nguyễn Hữu Cầu
KIỂM TRA GIỮA KỲ 1 (2024-2025) Thời gian 75 phút Lớp: 12A... ĐỀ 2
- GT: Chương I (đến hết bài đường tiệm cận).
Họ và tên: .......................................................
- HH: Chương II (Vectơ và các phép toán trong không gian).
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn(3 điểm) [8 câu Giải tích + 4 câu Hình học] Câu 1:
[NB] Cho hàm số y f (x) có bảng biến thiên như hình vẽ. Hàm số đã cho nghịch biến trên
khoảng nào dưới đây? A. 1 ;0 . B. ; 0. C. 1; . D. 0 ;1 . Câu 2:
[NB] Cho hàm số y f (x) có đồ thị là đường cong trong hình vẽ.
Hàm số đã cho đồng biến trên khoảng nào dưới đây? A. ( ; 2) . B. (0; 2) . C. ( 2 ;2) . D. (2; ) . Câu 3:
[NB] Cho hàm số y f x có bảng biến thiên như hình vẽ. Giá trị
cực đại của hàm số đã cho bằng A. –1. B. 3. C. 1. D. –5. Câu 4:
[NB] Cho hàm số y f x liên tục trên
và có bảng xét dấu đạo hàm như hình vẽ. Số điểm
cực trị của hàm số là A. 1. B. 2. C. 3. D. 4. Câu 5:
[NB] Cho hàm số y f (x) liên tục trên đoạn 1 ; 3 và có đồ thị như
hình vẽ. Gọi M , m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn 1 ;
3 . Giá trị của M m là A. 2. B. –6. C. –5. D. –2. Câu 6:
[NB] Hàm số y f x liên tục trên các khoảng xác định và có bảng
biến thiên như hình vẽ. Định tham số m để đồ thị hàm số có tiệm cận đứng x x và tiệm cận o
ngang y y sao cho x y 30 . o o o A. m 1. B. m 10 . C. m 8 . D. m 8 . ÔN GIỮA KỲ 1 - LỚP 12
GV. Ñaëng Coâng Vinh Böûu Câu 7:
[TH] Cho hàm số y f x có đồ thị như hình vẽ. Tìm số đườ 2
ng tiệm cận của đồ thị hàm số g x .
3 f x 2 A. 1. B. 2. C. 3. D. 4. Câu 8:
[TH] Cho tứ diện ABCD . Đặt AB a , AC b , AD c . Gọi
M là trung điểm của đoạn BC . Đẳng thức nào dưới đây A đúng? 1 a c A. DM
ab2c. 2 b 1 B. DM
a2bc. B D 2 1 M C. DM
a2bc. 2 C 1 D. DM
a2bc. 2 Câu 9:
[VD] Cho hàm số y f x có bảng biến thiên như hình vẽ. Hỏi đồ thị hàm số
y g x 4 x 1
có bao nhiêu tiệm cận đứng? 2
f x 4 f x A. 0. B. 2. C. 3. D. 4.
Câu 10: [VD] Cho tứ diện ABCD và điểm G thỏa mãn
GA GB GC GD 0 ( G là trọng tâm của tứ diện). Gọi G o
là giao điểm của GA và mặt phẳng BCD . Khẳng định nào
dưới đây đúng? A. GA 2 G G . o
B. GA 4G G . o
C. GA 3G G . o
D. GA 2G G . o
Câu 11: [VDC] Cho hai vectơ a và b có a 5, b 12, a b 13 . Khi đó cosin của góc giữa hai véc-
tơ a b và a b bằng 12 5 119 119 A. . B. . C. . D. . 13 12 169 169 ÔN GIỮA KỲ 1 - LỚP 12
GV. Ñaëng Coâng Vinh Böûu
Câu 12: [VDC] Cho u a 3b vuông góc với v 7a 5b và đồng thời có x a 4b vuông góc với
y 7a 2b . Khi đó góc giữa hai vectơ a và b bằng A. , a b 75 . B. , a b 60 . C. , a b 120 . D. , a b 45 .
PHẦN II. Câu trắc nghiệm đúng sai (4,5 điểm). [2 câu Giải tích + 1 câu Hình học] Câu 1:
Cho hàm số f x 3 2
x 3x . Các khẳng định sau đúng hay sai?
a) [NB] Hàm số f x nghịch biến trên 0; 2.
b) [TH] Hàm số f x 1 nghịch biến trên 1 ; 1 .
c) [TH] Hàm số f x nghịch biến trên 2;3.
d) [VD] Hàm số y f 4 2x đồng biến trên 1; 2. A. . B. . C. . D. . Câu 2:
Cho hàm số bậc ba có đồ thị như hình vẽ. Các khẳng định sau đúng hay sai?
a) [NB] Hàm số f x có hai điểm cực trị.
b) [NB] Hàm số f x đạt cực tiểu tại điểm x 1.
c) [NB] Cực đại của hàm số f x bằng 3.
d) [TH] Độ dài đoạn AB 2. A. . B. . C. . D. . Câu 3:
Một chiếc ô tô được đặt trên mặt đáy dưới của một khung sắt có
dạng hình hộp chữ nhật với đáy trên là hình chữ nhật ABC , D mặt phẳng (ABC )
D song song với mặt phẳng nằm ngang. Khung sắt đó
được buộc vào móc E của chiếc cần cẩu sao cho các đoạn dây cáp E , A E ,
B EC, ED có độ dài bằng nhau và cùng tạo với mặt phẳng ( ABC )
D một góc bằng 60 . Chiếc cần cẩu kéo khung sắt lên theo
phương thẳng đứng. Biết rằng các lực căng F , F , F , F đều có 1 2 3 4
cường độ là 4700 N và trọng lượng của khung sắ là 3000 N . Các
khẳng định sau đúng hay sai?
a) [NB] F F F F . 1 2 3 4
b) [NB] F F F F . 1 3 2 4
c) [TH] F F 8141 N (làm tròn đến hàng đơn vị). 1 3
d) [TH] Trọng lượng của chiếc xe ô tô là 16282 N (làm tròn đến hàng đơn vị). ÔN GIỮA KỲ 1 - LỚP 12
GV. Ñaëng Coâng Vinh Böûu
PHẦN III. Câu trắc nghiệm trả lời ngắn (2,5 điểm). [5 câu Giải tích + 1 câu Hình học] Câu 1:
[TH] Biết đồ thị hàm số 3 2
y ax bx cx d có hai điểm cực trị A1; 7, B2; 8 . Tính
giá trị y 10 Kết quả: A. . B. . C. . D. . 2 x 2x 2 Câu 2:
[TH] Biết rằng tất cả các khoảng nghịch biến của hàm số y là hai khoảng x 1
a; b,b; c với a b c . Tính giá trị của P 100a10bc . Kết quả: A. . B. . C. . D. . 4 Câu 3:
[TH] Tính giá trị nhỏ nhất của hàm số y 3x
trên khoảng 0; . (làm tròn đến hai chữ 2 x số thập phân) Kết quả: A. . B. . C. . D. . Câu 4:
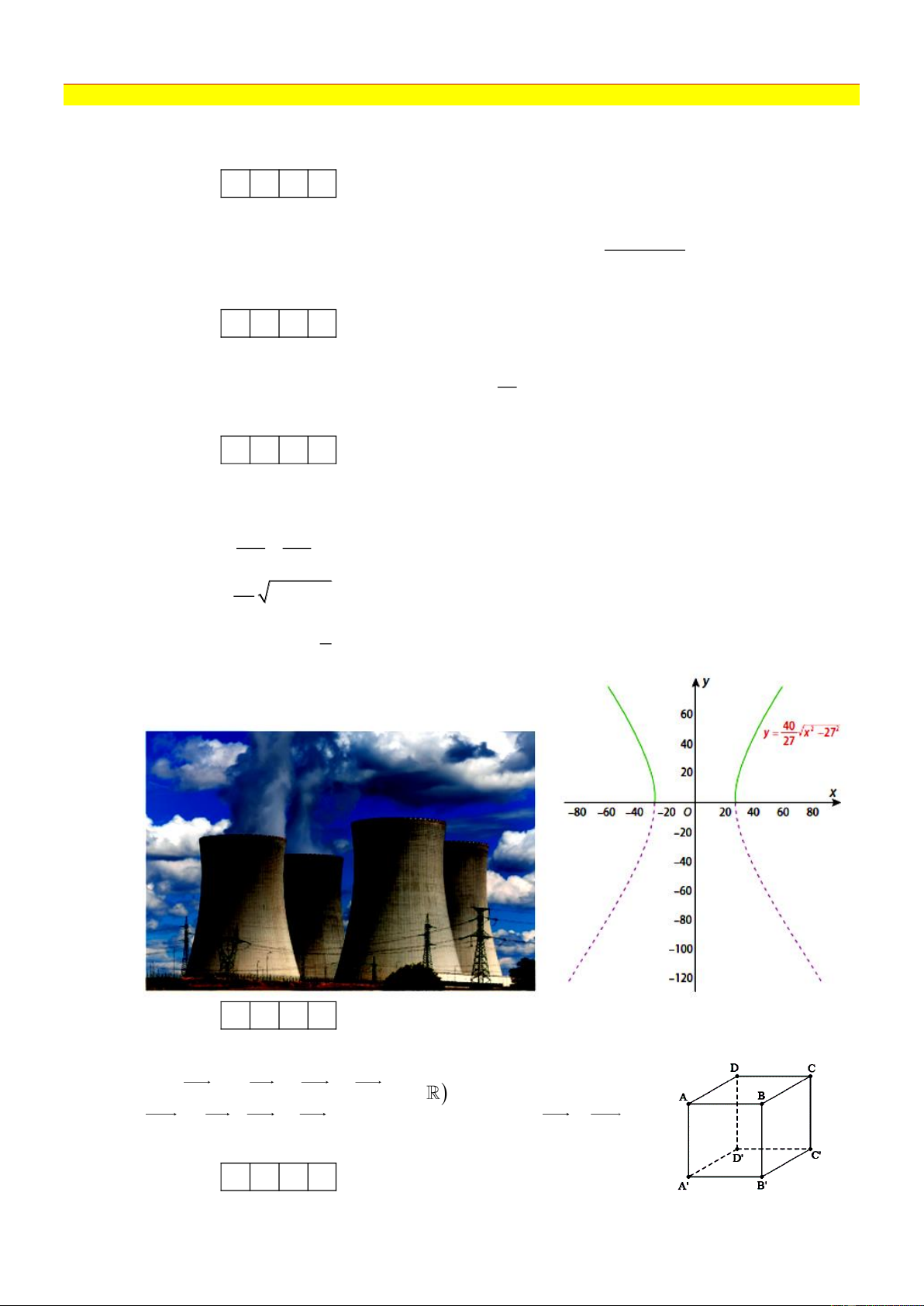
[VD] Một ống khói của nhà máy điện hạt nhân có mặt cắt là một hypebol H có phương trình 2 2 x y chính tắc là
1 (Hình vẽ). Xét hai nhánh bên trên Ox của H là đồ thị C của 2 2 27 40 40 hàm số 2 2 y
x 27 (phần nét liền đậm). Biết rằng phương trình hai đường tiệm cận xên 27 a
của C có dạng y
x (với a, b nguyên dương). Tính giá trị 2 2
Q a b . b Kết quả: A. . B. . C. . D. . Câu 5:
[VDC] Trong không gian, cho hình lập phương ABC . D A B C D biết rằng AN 4
AB k AA 2AD k và
AM 2AB AA 3AD . Tìm giá trị k thích hợp để AN AM (số
k được làm tròn đến hàng đơn vị). Kết quả: A. . B. . C. . D. . ÔN GIỮA KỲ 1 - LỚP 12
GV. Ñaëng Coâng Vinh Böûu THPT Nguyễn Hữu Cầu
KIỂM TRA GIỮA KỲ 1 (2024-2025) Thời gian 75 phút Lớp: 12A... ĐỀ 2
- GT: Chương I (đến hết bài đường tiệm cận).
Họ và tên: .......................................................
- HH: Chương II (Vectơ và các phép toán trong không gian).
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn(3 điểm) [8 câu Giải tích + 4 câu Hình học] Câu 1:
[NB] Cho hàm số y f (x) có bảng biến thiên như hình vẽ. Hàm số đã cho nghịch biến trên
khoảng nào dưới đây? A. 1 ;0 . B. ; 0. C. 1; . D. 0 ;1 . Lời giải Chọn D
Dựa vào bảng biến thiên ta có hàm số đã cho nghịch biến trên các khoảng 0 ;1 và ; 1 . Câu 2:
[NB] Cho hàm số y f (x) có đồ thị là đường cong trong hình vẽ.
Hàm số đã cho đồng biến trên khoảng nào dưới đây? A. ( ; 2) . B. (0; 2) . C. ( 2 ;2) . D. (2; ) . Lời giải Chọn B
Dựa vào đồ thị hàm số ta có hàm số đồng biến trên khoảng (0; 2) . Câu 3:
[NB] Cho hàm số y f x có bảng biến thiên như hình vẽ. Giá trị cực đại của hàm số đã cho bằng A. –1. B. 3. C. 1. D. –5. Lời giải Chọn B
Nhìn vào bảng biến thiên ta thấy giá trị cực đại của hàm số đã cho bằng 3 (tại x 1 ) Câu 4:
[NB] Cho hàm số y f x liên tục trên
và có bảng xét dấu đạo hàm như hình vẽ. Số điểm
cực trị của hàm số là A. 1. B. 2. C. 3. D. 4. Lời giải Chọn C
Đạo hàm đổi dấu 3 lần khi x “đi qua” các điểm x 3
; x 0; x 3 . Vậy hàm số có 3 điểm cực trị. ÔN GIỮA KỲ 1 - LỚP 12
GV. Ñaëng Coâng Vinh Böûu Câu 5:
[NB] Cho hàm số y f (x) liên tục trên đoạn 1 ; 3 và có đồ thị
như hình vẽ. Gọi M , m lần lượt là giá trị lớn nhất và nhỏ nhất của
hàm số đã cho trên đoạn 1 ;
3 . Giá trị của M m là A. 2. B. –6. C. –5. D. –2. Lời giải Chọn D
m min f x f 2 4 1 ;3 Từ đồ thị ta có: . M f
x f M m 2 max 1 2 1 ;3 Câu 6:
[NB] Hàm số y f x liên tục trên các khoảng xác định và có bảng biến thiên như hình vẽ.
Định tham số m để đồ thị hàm số có tiệm cận đứng x x và tiệm cận ngang y y sao cho o o x y 30 . o o A. m 1. B. m 10 . C. m 8 . D. m 8 . Lời giải Chọn C
Từ BBT ta có: TCĐ x 3 , nên x 3 o
TCN y m 2 , nên y m 2 o
Từ GT x y 30 3m 2 30 m 8 . o o Câu 7:
[TH] Cho hàm số y f x có đồ thị như hình vẽ. Tìm số đườ 2
ng tiệm cận của đồ thị hàm số g x 3f x . 2 A. 1. B. 2. C. 3. D. 4. Lời giải Chọn C 2 2 2
Khi x thì f x 1
, nên g x y 3 f x . Vậy có TCN là 2 5 5 2
Khi x thì f x 1 , nên g x y f x 2 3 . Vậy có TCN là 2 2
Xét mẫu f x f x 2 3 2 0 3
Từ đồ thị của f x ta thấy phương trình f x 2
có duy nhất một nghiệm. Vậy có một TCĐ 3
KL: đồ thị hàm số g x có 3 đường tiệm cận. ÔN GIỮA KỲ 1 - LỚP 12
GV. Ñaëng Coâng Vinh Böûu Câu 8:
[TH] Cho tứ diện ABCD . Đặt AB a , AC b , AD c . Gọi
M là trung điểm của đoạn BC . Đẳng thức nào dưới đây A đúng? 1 a c A. DM
ab2c. 2 b 1 B. DM
a2bc. B D 2 1 M C. DM
a2bc. 2 C 1 D. DM
a2bc. 2 Lời giải Chọn A 1
M là trung điểm của BC nên DM DB DC 2
Mà DB AB AD a c và DC AC AD b c 1 Nên DM
ab2c 2 Câu 9:
[VD] Cho hàm số y f x có bảng biến thiên như hình vẽ. Hỏi đồ thị hàm số
y g x 4 x 1
có bao nhiêu tiệm cận đứng? 2
f x 4 f x A. 0. B. 2. C. 3. D. 4. Lời giải Chọn D
x a, a ; 1
f x 0 x 1 (ng kép) Xét mẫu 2
f x 4 f x 0 f x 4 x 1 (ng kép) x , b b 1; 2 2 Nên có thể viết 2
f x 4 f x h x x a x
1 x b x
1 ; h x 0 1 x 1 x 1 2 4 x x 1
Do đó hàm số trở thành y g x 2
f x 4 f x
h x x a x 2
1 x b x 2 1 2 x 1
h x x a x
1 x b x 1 4 x 1
Vậy đồ thị hàm số y g x có 4 tiệm cận đứng. 2
f x 4 f x




