










Preview text:
SỞ GD & ĐT TP.HỒ CHÍ MINH
ĐỀ THAM KHẢO TUYỂN SINH 10
PHÒNG GD & ĐT QUẬN 1 NĂM HỌC 2022-2023 ĐỀ THAM KHẢO MÔN : TOÁN 9 --------------------
Đề thi gồm 8 câu hỏi tự luận MÃ ĐỀ : Quận 5 – 1
Thời gian: 120 phút (không kể thời gian phát đề) x
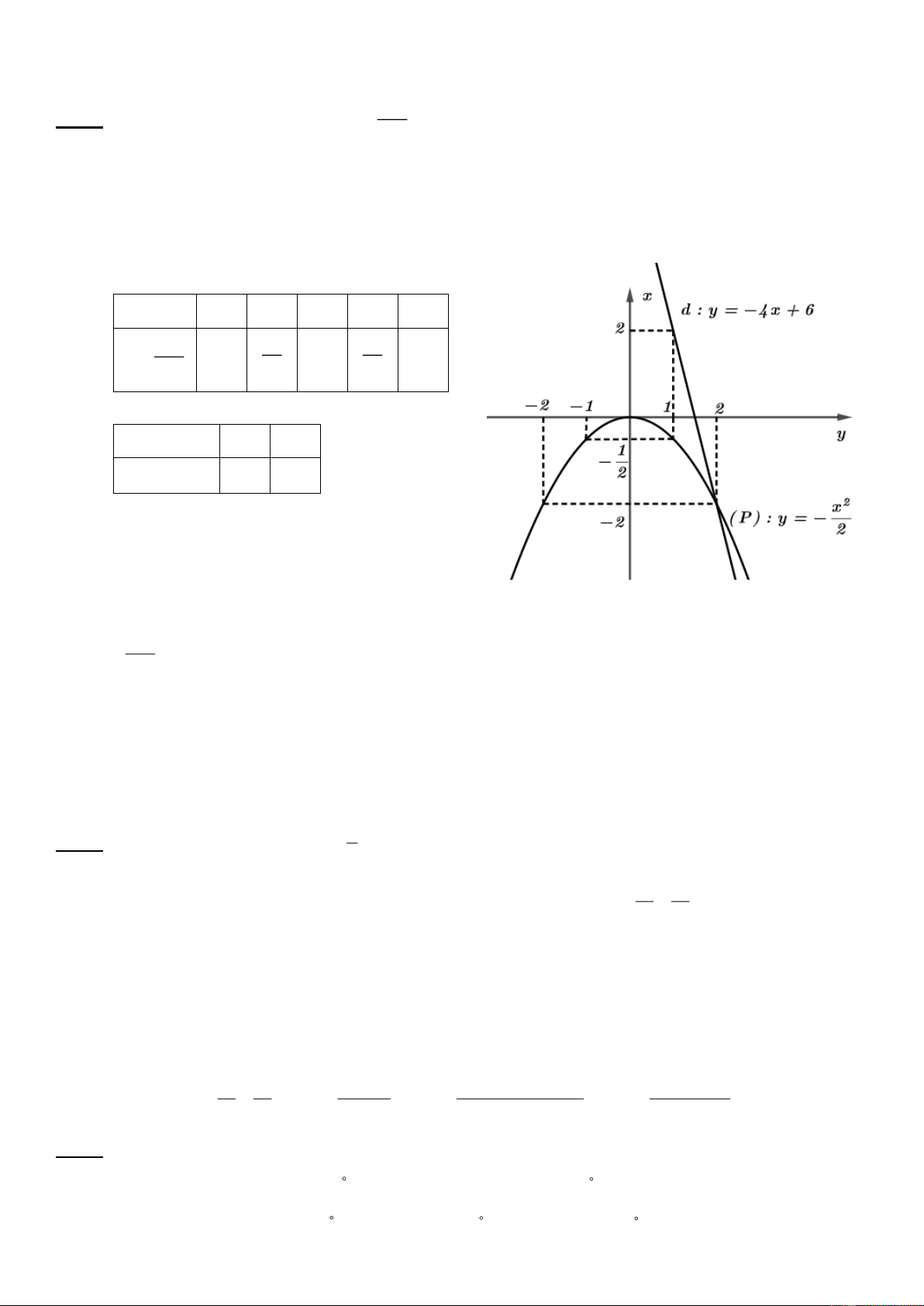
Bài 1: (1.5 điểm) Cho parabol P 2 : y
và đường thẳng d : y 4 x 6 2
a) Vẽ đồ thị P và d trên cùng hệ trục tọa độ;
b) Tìm tọa độ giao điểm của P và d bằng phép toán. 1
Bài 2: (1.0 điểm) Cho phương trình 2
x x 1 0 1 2 x x
Không giải phương trình hãy tính giá trị của biểu thức sau: 1 2 A
x x với x , x là hai 1 2 x x 1 2 2 1
nghiệm của phương trình (1).
Bài 3: (0.75 điểm) Để tính múi giờ của một địa điểm ta làm như sau:
- Ở Đông bán cầu (kí hiệu là Ð): múi giờ = kinh độ Đông: 15
- Ở Tây bán cầu (kí hiệu là T): múi giờ (= 360 Kinh độ Tây): 15
(Kết quả làm tròn đến hàng đơn vị)
Để tính giờ của một địa điểm, ta tính theo công thức: T GMT H với T là giờ tại nơi đó, GMT
là giờ gốc, H được quy đổi như sau: Múi giờ 0 1 2 3 4 5 6 7 8 9 10 11 H 0 1 2 3 4 5 6 7 8 9 10 11 Múi giờ 13 14 15 16 17 18 19 20 21 22 23 H 12 11 10 9 8 7 6 5 4 3 2 1 a) Lúc 19 0
h 0 ở Hà Nội 105 Ð ngày 15/6/2021 thì lúc đó ở Los Angeles 120 T là mấy giờ?
b) Một chiếc máy bay cất cánh ở sân bay tại New York 75 T với vận tốc 750 km / h trên quãng
đường chim bay dài 14250 km để hạ cánh xuống sân bay Tân Sơn Nhất của Việt Nam 105 Ð
đúng 2 giờ sáng ngày 01/10/2021. Hỏi máy bay cất cánh tại New York ngày nào? Lúc mấy giờ?
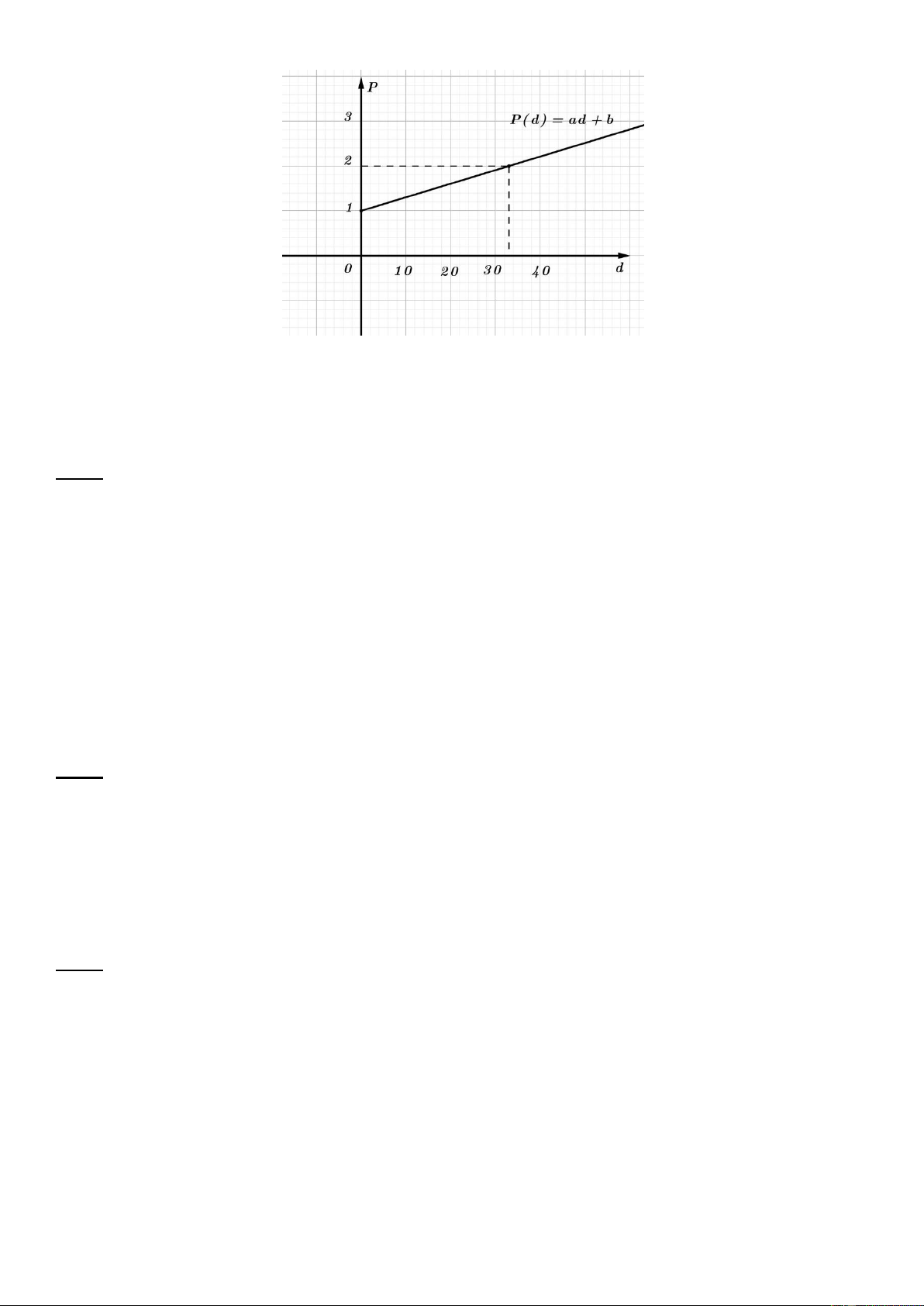
Bài 4: (0.75 điểm) Áp suất của nước P (đơn vị: atm ) lên một người thợ lặn ở độ sâu d (tính theo feet) là
một hàm số bậc nhất P(d ) ad b có đồ thị như hình bên Trang - 1 -
a) Tính các hệ số a và b biết các điểm A0;
1 và B 33; 2 thuộc đồ thị hàm số.
b) Tính áp suất của nước lên người thợ lặn ở độ sâu 100 feet (kết quả làm tròn đến hàng đơn vị). Biết
feet là đơn vị đo độ dài, 1 feet 0,3048 . m
Bài 5: (1.0 điểm) Hãng viễn thông Văn có ba phương án trả tiền cước điện thoại cho mỗi cuộc gọi:
- Phương án I: Trả tổng cộng 99 cent cho 20 phút đầu, sau đó từ phút 21 trở đi thì mỗi phút trả 5 cent.
- Phương án II: Kể từ lúc đầu tiên, mỗi phút trả 10 cen . t
- Phương án III: Trả 25 cent tiền thuê bao, sau đó kể từ phút đầu tiên mỗi phút trả 8 cent .
Anh Toán là nhân viên Sale bất động sản. Trung bình thì mỗi tháng anh Toán thực hiện 200 cuộc
gọi với 10% cuộc gọi 1 phút, 10% cuộc gọi 5 phút, 30% cuộc gọi 10 phút, 30% cuộc gọi 20 phút,
20% cuộc gọi 30 phút. Hỏi anh Toán nên chọn phương án nào của hãng viễn thông Văn để có lợi nhất?
Bài 6: (1.0 điểm) Thầy Bảo, nhân viên y tế, được trường phân công mua một số hộp khẩu trang để phục vụ
cho công tác phòng chống dịch Covid của nhà trường. Thầy dự định mua một số hộp khẩu trang tại
nhà thuốc Pharmacity. Khi tham khảo giá trên thì tổng số tiền thầy sẽ trả là 600 nghìn đồng. Tuy
nhiên, khi đến mua trực tiếp, Pharmacity có chương trình khuyến mãi mỗi hộp khẩu trang được
giảm 2 nghìn đồng nên thầy quyết định mua thêm 2 hộp. Khi đó tổng số tiền phải trả là 672 nghìn
đồng. Hỏi thầy Bảo đã mua tất cả bao nhiêu hộp khẩu trang?
Bài 7: (1.0 điểm) Một bồn nước hình trục có bán kính đáy là 3 m, chiều cao là 4 m. Người ta đổ nước vào
trong bồn sao cho chiều cao của nước bằng đúng một nửa chiều cao của bồn và tiếp tục đặt vào
trong bồn một phao nước có dạng hình cầu bằng kim loại không thấm nước có bán kính là 50 cm và
chìm hoàn toàn trong nước.
a) Hỏi khi đó mực nước trong bồn cao bao nhiêu mét (làm tròn đến chữ số thập phân thức ba)?
b) Sau đó, người ta lại bơm thêm nước vào bồn bằng một vòi có công suất chảy là 3 0, 0024 cm cho
mỗi giây. Hỏi sau bao nhiêu phút thì bồn đầy nước (làm tròn đến hàng đơn vị)? Trang - 2 -
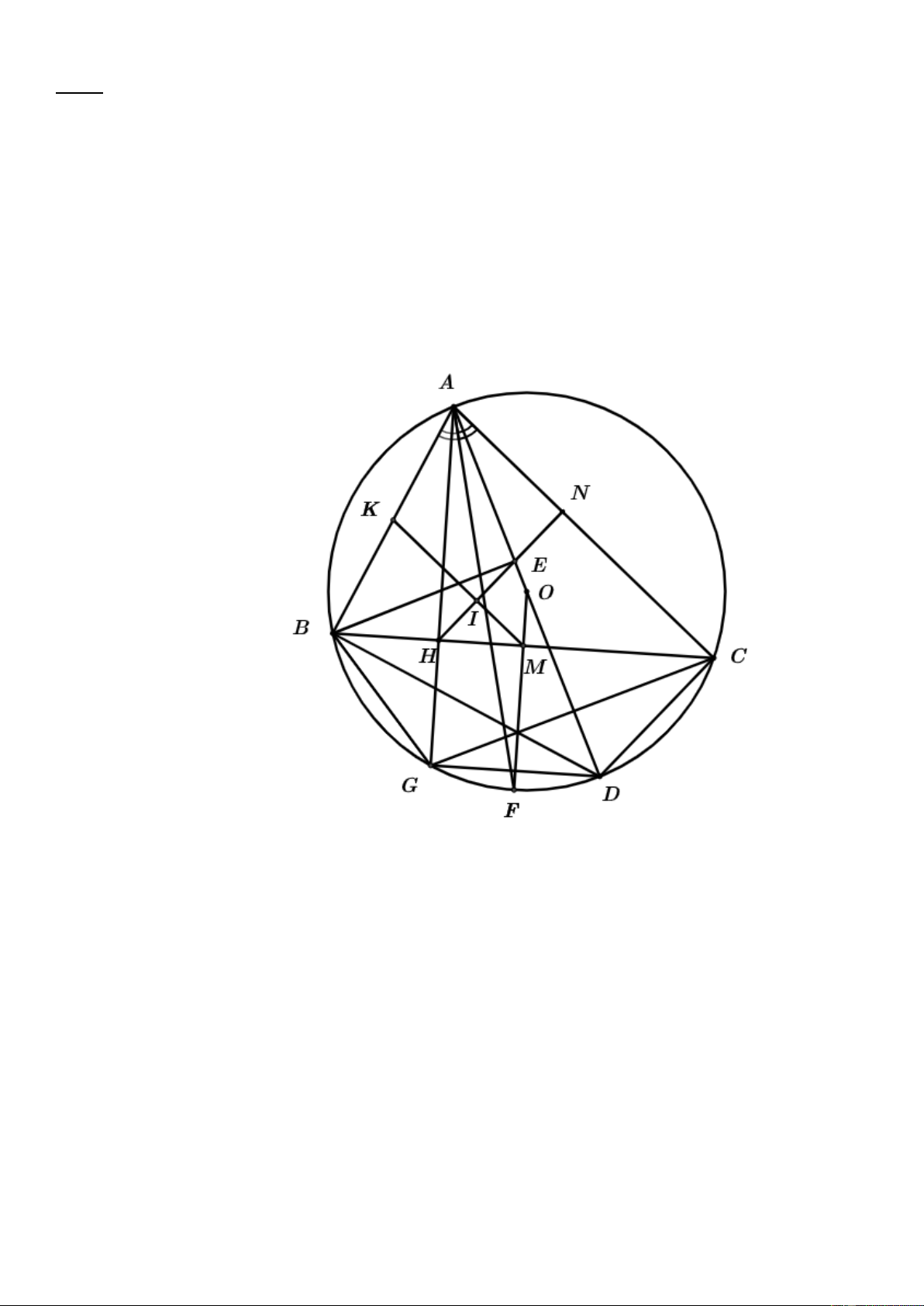
Bài 8: (3.0 điểm) Cho tam giác ABC nhọn AB AC nội tiếp đường tròn O . Kẻ AD là đường kính
của O , AH vuông góc với BC tại H , BE vuông góc với AD tại E. Gọi G là giao điểm của
AH với O .
a) Chứng minh tứ giác ABHE nội tiếp và GD song song . BC
b) Gọi N là giao điểm giữa HE và .
AC Chứng minh tam giác AHN vuông tại N.
c) Tia phân giác của góc BAC cắt đường tròn O tại F. Gọi M là giao điểm của OF và BC, K là
trung điểm của AB, I là giao điểm của KM và HE . Chứng minh rằng A . B EI A . E EM.
-------------------------------------------- Trang - 3 - HƯỚNG DẪN GIẢI x
Bài 1: (1.5 điểm) Cho parabol P 2 : y
và đường thẳng d : y 4 x 6 2
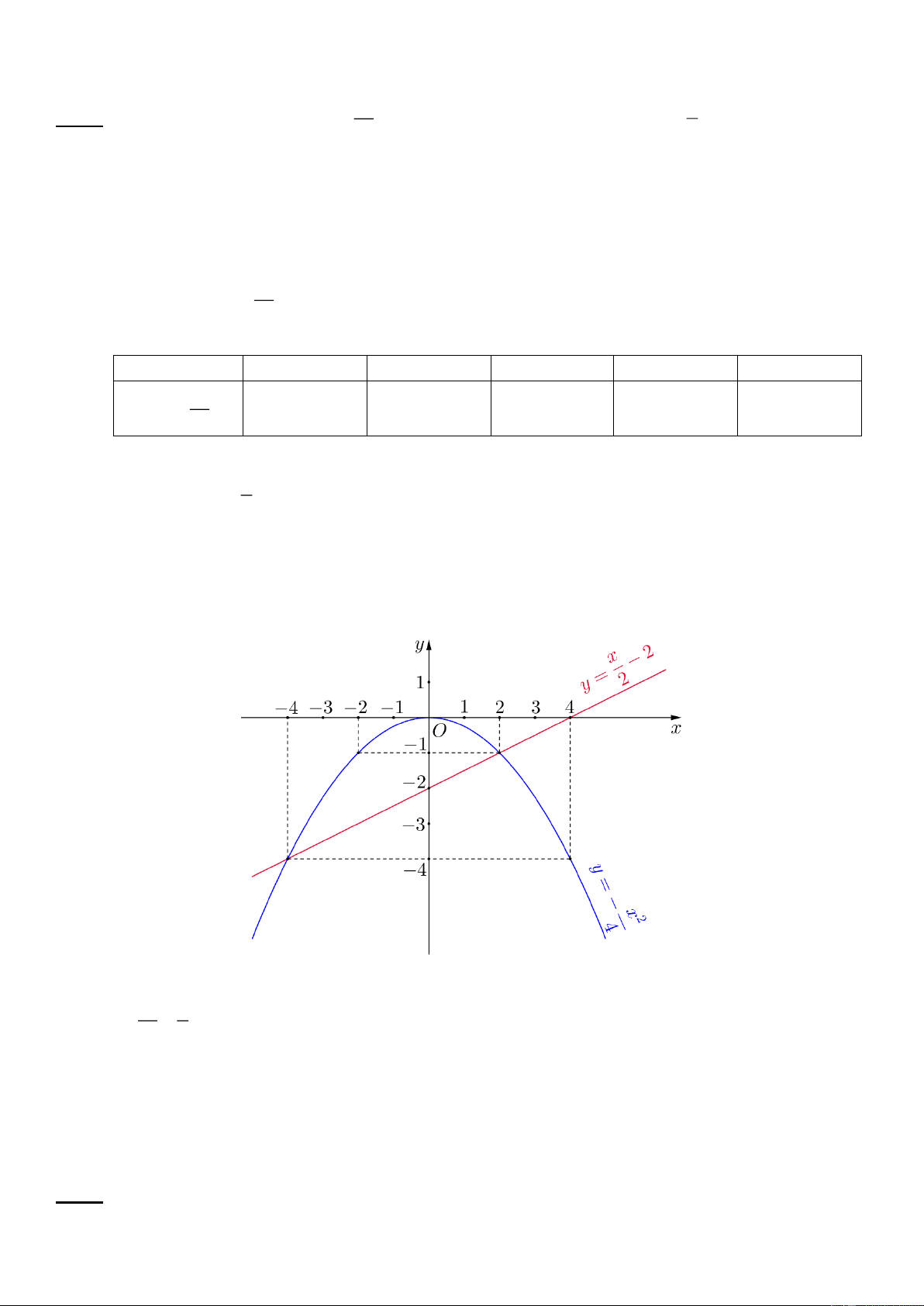
a) Vẽ đồ thị P và d trên cùng hệ trục tọa độ;
b) Tìm tọa độ giao điểm của P và d bằng phép toán. Lời giải a) x 2 1 0 1 2 2 x 1 1 y 2 0 2 2 2 2 x 1 2 y 4 x 6 2 2
b) Phương trình hoành độ giao điểm của parabol (P) và đường thẳng d : 2 x 4 x 6 2 2
x 8x 12 0
x 2 y 2
x 6 y 18
Vậy (P) và d cắt nhau tại hai điểm M 2; 2 và N 6; 1 8 1
Bài 2: (1.0 điểm) Cho phương trình 2
x x 1 0 1 2 x x
Không giải phương trình hãy tính giá trị của biểu thức sau: 1 2 A
x x với x , x là hai 1 2 x x 1 2 2 1
nghiệm của phương trình (1). Lời giải x x 2
Áp dụng định lí Vi-ét ta có: 1 2 x x 2 1 2 2 2 x x x x
x x 2x x 2 2 2 1 2 1 2 1 2 2 2 1 2 Khi đó: A x x x x x x 2 2 1 2 1 2 1 2 x x x x x x 2 2 1 1 2 1 2
Bài 3: (0.75 điểm) Để tính múi giờ của một địa điểm ta làm như sau:
- Ở Đông bán cầu (kí hiệu là Ð): múi giờ = kinh độ Đông: 15
- Ở Tây bán cầu (kí hiệu là T): múi giờ = ( 360 Kinh độ Tây): 15 Trang - 4 -
(Kết quả làm tròn đến hàng đơn vị)
Để tính giờ của một địa điểm, ta tính theo công thức: T GMT H với T là giờ tại nơi đó, GMT
là giờ gốc, H được quy đổi như sau: Múi giờ 0 1 2 3 4 5 6 7 8 9 10 11 H 0 1 2 3 4 5 6 7 8 9 10 11 Múi giờ 13 14 15 16 17 18 19 20 21 22 23 H 12 11 10 9 8 7 6 5 4 3 2 1 a) Lúc 19 0
h 0 ở Hà Nội 105 Ð ngày 15/6/2021 thì lúc đó ở Los Angeles 120 T là mấy giờ?
b) Một chiếc máy bay cất cánh ở sân bay tại New York 75 T với vận tốc 750 km / h trên quãng
đường chim bay dài 14250 km để hạ cánh xuống sân bay Tân Sơn Nhất của Việt Nam 105 Ð
đúng 2 giờ sáng ngày 01/10/2021. Hỏi máy bay cất cánh tại New York ngày nào? Lúc mấy giờ? Lời giải
a) Hà Nội thuộc múi giờ: 105:15 7
Los Angeles thuộc múi giờ: (360 120) :15 16
Chênh lệch giờ từ Hà Nội đến Los Angeles là; 16 7 9
Giờ của Los Angeles là 19 9 28 24 4 giờ ngày 16/6/2021
b) Thời gian để máy bay đi hết quãng đường là 14250 : 750 19 giờ
Vậy để hạ cánh lúc 2 giờ ngày 01/10/2021 thì cất cánh lúc 7 giờ ngày 30/09/2021.
Bài 4: (0.75 điểm) Áp suất của nước P (đơn vị: atm ) lên một người thợ lặn ở độ sâu d (tính theo feet) là
một hàm số bậc nhất P(d ) ad b có đồ thị như hình bên
a) Tính các hệ số a và b biết các điểm A0;
1 và B 33; 2 thuộc đồ thị hàm số. Trang - 5 -
b) Tính áp suất của nước lên người thợ lặn ở độ sâu 100 feet (kết quả làm tròn đến hàng đơn vị). Biết
feet là đơn vị đo độ dài, 1 feet 0,3048 . m Lời giải a) Vì A0;
1 và B 33; 2 thuộc đồ thị hàm số nên: 1 . a 0 b 1 a 33 . a 33 b 2 b 1 1
Phương trình hàm số P(d) d 1 33
b) Với 100 feet 100.0, 3048 30, 48 m
Với d 30, 48 m thì áp suất của nước lên người thợ lặn là P 1 30, 48
.30, 48 1 2 (atm) 33
Bài 5: (1.0 điểm) Hãng viễn thông Văn có ba phương án trả tiền cước điện thoại cho mỗi cuộc gọi:
- Phương án I: Trả tổng cộng 99 cent cho 20 phút đầu, sau đó từ phút 21 trở đi thì mỗi phút trả 5 cent.
- Phương án II: Kể từ lúc đầu tiên, mỗi phút trả 10 cen . t
- Phương án III: Trả 25 cent tiền thuê bao, sau đó kể từ phút đầu tiên mỗi phút trả 8 cent .
Anh Toán là nhân viên Sale bất động sản. Trung bình thì mỗi tháng anh Toán thực hiện 200 cuộc
gọi với 10% cuộc gọi 1 phút, 10% cuộc gọi 5 phút, 30% cuộc gọi 10 phút, 30% cuộc gọi 20 phút,
20% cuộc gọi 30 phút. Hỏi anh Toán nên chọn phương án nào của hãng viễn thông Văn để có lợi nhất? Lời giải
Giả sử người đó có 100 cuộc gọi trong một tháng
Theo phương án I, người đó phải trả:
99.100 30 20.20.5 10900 (cent)
Theo phương án II, người đó phải trả:
1.105.1010.30 20.3030.20.10 15600 (cent)
Theo phương án III, người đó phải trả:
25.100 1.10 5.10 10.30 20.30 30.20.8 14980 (cent)
Như vậy, phương án I cho tiền cước lợi nhất.
Bài 6: (1.0 điểm) Thầy Bảo, nhân viên y tế, được trường phân công mua một số hộp khẩu trang để phục vụ
cho công tác phòng chống dịch Covid của nhà trường. Thầy dự định mua một số hộp khẩu trang tại
nhà thuốc Pharmacity. Khi tham khảo giá trên thì tổng số tiền thầy sẽ trả là 600 nghìn đồng. Tuy
nhiên, khi đến mua trực tiếp, Pharmacity có chương trình khuyến mãi mỗi hộp khẩu trang được Trang - 6 -
giảm 2 nghìn đồng nên thầy quyết định mua thêm 2 hộp. Khi đó tổng số tiền phải trả là 672 nghìn
đồng. Hỏi thầy Bảo đã mua tất cả bao nhiêu hộp khẩu trang? Lời giải
Gọi giá tiền mỗi hộp khẩu trang dự định mua là x (nghìn đồng), điều kiện x 2.
Giá tiền mỗi hộp khẩu trang thực tế là x 2 (nghìn đồng) Ta có: 600 672 2 x x 2
600(x 2) 2(x 2)x 672x 0 x(x 2) 2
2x 76x 1200 0 x 50 x 12
Vậy giá tiền mỗi hộp khẩu trang thực tế là: 50 2 48 nghìn đồng
Số hộp khẩu trang đã mua là: 672 : 48 14 hộp
Bài 7: (1.0 điểm) Một bồn nước hình trục có bán kính đáy là 3 m, chiều cao là 4 m. Người ta đổ nước vào
trong bồn sao cho chiều cao của nước bằng đúng một nửa chiều cao của bồn và tiếp tục đặt vào
trong bồn một phao nước có dạng hình cầu bằng kim loại không thấm nước có bán kính là 50 cm và
chìm hoàn toàn trong nước.
a) Hỏi khi đó mực nước trong bồn cao bao nhiêu mét (làm tròn đến chữ số thập phân thức ba)?
b) Sau đó, người ta lại bơm thêm nước vào bồn bằng một vòi có công suất chảy là 3 0, 0024 cm cho
mỗi giây. Hỏi sau bao nhiêu phút thì bồn đầy nước (làm tròn đến hàng đơn vị)? Lời giải
a) Thể tích nước có sẵn trong bồn: 2 3
V .3 .2 18 (m ) 3 4 1
Thể tích quả cầu kim loại 3 V ' (m ) 3 2 6 109
Lượng nước có trong bồn khi đó 3 V V ' (m ) 6 109 Chiều cao mực nước là
:9 2,0185 (m) 6
Mực nước dâng lên được 0, 0185 (m)
b) Thời gian đầy bồn nước là 2 .3 (4 2,0185) T 23343,997 6 3 h 0 ' 0, 0024 Trang - 7 -
Bài 8: (3.0 điểm) Cho tam giác ABC nhọn AB AC nội tiếp đường tròn O . Kẻ AD là đường kính
của O , AH vuông góc với BC tại H , BE vuông góc với AD tại E. Gọi G là giao điểm của
AH với O .
a) Chứng minh tứ giác ABHE nội tiếp và GD song song . BC
b) Gọi N là giao điểm giữa HE và .
AC Chứng minh tam giác AHN vuông tại N.
c) Tia phân giác của góc BAC cắt đường tròn O tại F. Gọi M là giao điểm của OF và BC, K là
trung điểm của AB, I là giao điểm của KM và HE . Chứng minh rằng A . B EI A . E EM. Lời giải a)
Xét tứ giác ABHE có: 0
AH BC (gt) AHB 90 0
BE AD (gt) AEB 90 0
AHB AEB 90 (hai đỉnh kề của một tứ giác cùng nhìn một cạnh với một góc bằng nhau)
Suy ra tứ giác ABHE nội tiếp Ta có: 0
AGD 90 (góc nội tiếp chắn nửa đường tròn (O) AG GD (1)
Mà AG BC (gt) (2)
Từ (1) và (2) suy ra GD / /BC .
b) Vì BC / /GD (chứng minh trên)
CBD BDG (so le trong) Trang - 8 -
CD BG sdCD sd BG Ta có: 1
BAG sd BG (góc nội tiếp) 2 1
CAD sdCD (góc nội tiếp) 2
Suy ra: BAG CAD Xét AEN và ABH có:
BAG CAD
ABH AEN ( ABHE là tứ giác nội tiếp) A EN C
AD g g 0
AHB ANE 90 (2 góc tương ứng)
HN AN A
HN vuông tại N .
c) Vì AF là tia phân giác của BAC BAF CAF BF FC FO BC
M là trung điểm BC
KM là đường trung bình của tam giác ABC KM / /AC (3)
Mà HN AC (4)
Từ (3) và (4) suy ra HN KM hay 0 EIM 90 .
Tứ giác ABHE là tứ giác nội tiếp OEM MEH HBO OBA (5) Mặt khác: 0 0 0
BEO OMB 90 90 180 BEOM là tứ giác nội tiếp
OEM OBM (2 góc nội tiếp cùng chắn cung OM ) (6)
Từ (5) và (6) suy ra: IEM ABO (7) Mặt khác: ABO
cân tại O OBA OAB (8)
Từ (7) và (8) suy ra IEM OAB Xét ABE và M EI có + 0
AEB EIM 90 (chứng minh trên)
+ IEM OAB (chứng minh trên) A BE E
MI (g g) AB AE .
AB EI AE.EM (điều phải chứng minh). EM EI
-------------------------------------------
SỞ GD & ĐT TP.HỒ CHÍ MINH ĐỀ THAM KHẢO TUYỂN SINH 10
PHÒNG GD & ĐT QUẬN 5 NĂM HỌC 2022-20232
ĐỀ THAM KHẢO MÔN : TOÁN 9
-------------------- Đề thi gồm 8 câu hỏi tự luận
MÃ ĐỀ : Quận 5 – 2 Thời gian: 120 phút (không kể thời gian phát đề) Trang - 9 - 2 x x
Bài 1: (1.5 điểm). Cho hàm số y
có đồ thị là parabol P và hàm số y
2 có đồ thị là đường 4 2 thẳng D .
a) Vẽ đồ thị P và D trên cùng hệ trục tọa độ;
b) Tìm tọa độ giao điểm của P và D bằng phép toán.
Bài 2: (1.0 điểm) Cho phương trình 2
x m 2 5
1 x 6m 2m 0 ( m là tham số).
a) Chứng minh rằng phương trình trên luôn có hai nghiệm x ; x với mọi m ; 1 2
b) Tìm m để phương trình có hai nghiệm x ; x thỏa mãn 2 2 x x 1 . 1 2 1 2
Bài 3: (0.75 điểm) Quy tắc sau đây cho ta biết CAN, CHI của năm X nào đó. Để xác định CAN, ta cần
tìm số dư r trong phép chia X cho 10 và tra vào bảng 1. Để xác định CHI, ta tìm số dư s trong
phép chia X cho 12 và tra vào bảng 2.
Ví dụ: Năm 1982 có CAN là Nhâm, có CHI là Tuất. Bảng 1 r 0 1 2 3 4 5 6 7 8 9 CAN Canh Tân Nhâm Quý Giáp Ất Bính Đinh Mậu Kỷ Bảng 2 s 0 1 2 3 4 5 6 7 8 9 10 11 CHI Thân Dậu Tuất Hợi Tí Sửu Dần Mão Thìn Tỵ Ngọ Mùi
a) Em hãy sử dụng quy tắc trên để xác định CAN, CHI của năm 2021;
b) Bạn Loan nhớ rằng mẹ bạn ấy sinh năm Giáp Thìn nhưng không rõ là năm bao nhiêu.
Bài 4: (0.75 điểm) Một xí nghiệp may cứ mỗi tháng thì trả tiền lương cho công nhân viên, tiền vật liệu,
tiền điện, tiền thuế,… tổng cộng là 410000000 (VNĐ). Mỗi chiếc áo được bán với giá là 350000
(VNĐ). Gọi số tiền lời (hoặc lỗ) mà xí nghiệp thu được sau mỗi tháng là L (VNĐ) và mỗi tháng xí
nghiệp bán được A chiếc áo.
a) Lập hàm số của L theo A ;
b) Nếu trong một tháng, công ty bán được 1000 chiếc áo thì công ty lời hay lỗ bao nhiêu?
c) Mỗi tháng phải bán ít nhất bao nhiêu chiếc áo để xí nghiệp không bị lỗ?
d) Hỏi cần phải bán trung bình bao nhiêu chiếc áo mỗi tháng để sau 1 năm xí nghiệm thu được tiền lời là 1380000000 (VNĐ)?
Bài 5: (1.0 điểm) Lớp 9A có 40 học sinh, trong đó nam nhiều hơn nữ. Trong giờ ra chơi, cô giáo đưa cả
lớp 260000 đồng để mỗi bạn nam mua một ly Coca giá 5000 đồng/ly, mỗi bạn nữ mua một bánh
phô mai giá 8000 đồng/cái và được căn tin thối lại 3000 đồng. Hỏi lớp 9A có bao nhiêu học sinh
nam và bao nhiêu học sinh nữ?
Bài 6: (1.0 điểm) Tính chiều cao của một ngọn núi (làm tròn đến mét), cho biết tại hai địa điểm cách nhau
550 m, người ta nhìn thấy đỉnh núi với góc nâng lần lượt là 33 và 37 . Trang - 10 -
Bài 7: (1.0 điểm) Vào dịp khai trương, nhà sách khuyến mãi mỗi cây viết bi Thiên Long được giảm 20%
so với giá niêm yết, còn mỗi quyển tập ABC chỉ được giảm 10% so với giá niêm yết. Bạn An vào
nhà sách mua 20 quyển tập ABC và 10 cây viết bi Thiên Long. Khi tính tiền, bạn An đưa 175000
đồng và được thối lại 3000 đồng. Tính giá niêm yết của mỗi quyển tập và mỗi cây viết bi mà bạn
An đã mua. Biết rằng khi An nhìn vào hóa đơn, tổng số tiền phải trả khi chưa giảm giá là 195000 đồng.
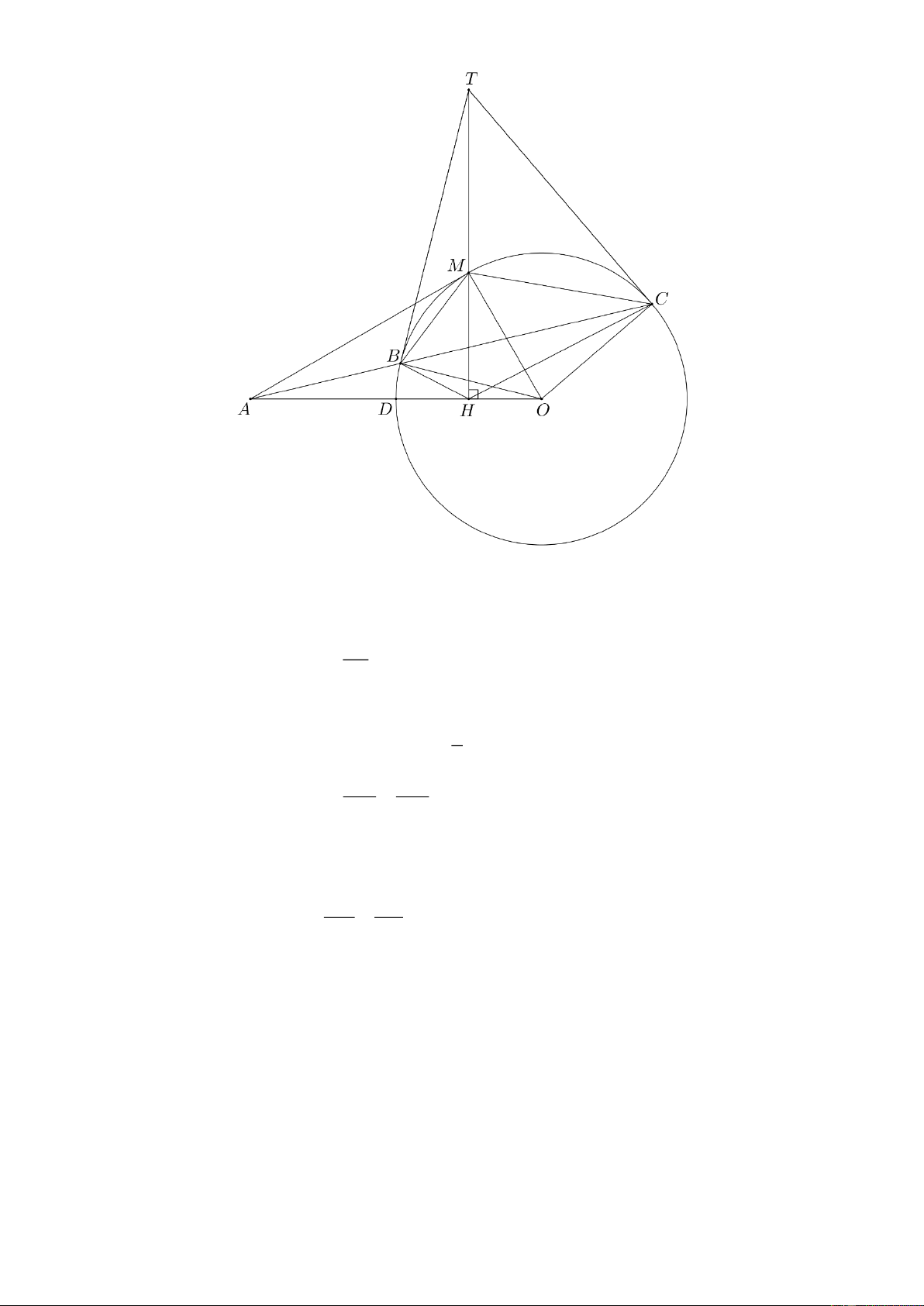
Bài 8: (3.0 điểm) Cho đường tròn ;
O R và điểm A ở ngoài đường tròn O với OA 2R . Đoạn thẳng
OA cắt đường tròn O tại D . Gọi H là trung điểm của OD , đường thẳng vuông góc với OA tại
H cắt đường tròn O tại M .
a) Chứng minh: AM là tiếp tuyến của đường tròn O ;
b) Qua A vẽ cát tuyến ABC đến đường tròn O ( B , C thuộc O , B nằm giữa A và C ). Chứng minh: 2
AH AO AB AC AM và đường thẳng MH chứa tia phân giác của BHC ;
c) Tiếp tuyến tại B và C của đường tròn O cắt nhau tại T . Chứng minh: Ba điểm M , H , T thẳng hàng.
-------------------------------------------- Trang - 11 - HƯỚNG DẪN GIẢI 2 x x
Bài 1: (1.5 điểm). Cho hàm số y
có đồ thị là parabol P và hàm số y
2 có đồ thị là đường 4 2 thẳng D .
a) Vẽ đồ thị P và D trên cùng hệ trục tọa độ;
b) Tìm tọa độ giao điểm của P và D bằng phép toán. Lời giải 2 x
a) Hàm số: y 4
Bảng giá trị tương ứng của x và y : x 4 2 0 2 4 2 x y 4 1 0 1 4 4
Đồ thị hàm số là một Parabol đi qua các điểm 4 ; 4 ; 2 ; 1 ; 0;0 ; 2; 1 ; 4; 4 x
Hàm số: y 2 2
x 0 y 2
y 0 x 4
Đồ thị hàm số là đường thẳng đi qua 0; 2 và 4;0 Vẽ:
b) Hoành độ giao điểm của P và D là nghiệm của phương trình: 2 x x 2 2
x 2x 8 2
x 2x 8 0 4 2 2 1 1. 8
9 0 Phương trình có hai nghiệm phân biệt: x 2 ; x 4 1 2
+ Với x 2 y 1 1 1
+ Với x 4 y 4 2 2
Vậy D cắt P tại hai điểm phân biệt là 2; 1 và 4 ; 4 .
Bài 2: (1.0 điểm) Cho phương trình 2
x m 2 5
1 x 6m 2m 0 ( m là tham số).
a) Chứng minh rằng phương trình trên luôn có hai nghiệm x ; x với mọi m ; 1 2 Trang - 12 -
b) Tìm m để phương trình có hai nghiệm x ; x thỏa mãn 2 2 x x 1 . 1 2 1 2 Lời giải
a) Phương trình đã cho là phương trình bậc hai của x có: 2 2
m 2 m m 2 2 2 5 1 4.1. 6 2
25m 10m 1 24m 8m m 2m 1 m 1 0 với m
Vậy phương trình đã cho luôn có hai nghiệm x ; x với mọi giá trị của m . 1 2
x x 5m 1
b) Theo định lý Vi-et, ta có: 1 2 2
x x 6m 2m 1 2 2 Do đó: 2 2
x x 1 x x
2x x 1 m 2 5 1
2 6m 2m 1 1 2 2 1 2 1 2 m 0 2 2
25m 10m 112m 4m 1 0 2
13m 6m 0 m13m 6 0 13 m 6 13 Vậy với m 0;
thì phương trình có hai nghiệm x ; x thỏa mãn 2 2 x x 1 . 6 1 2 1 2
Bài 3: (0.75 điểm) Quy tắc sau đây cho ta biết CAN, CHI của năm X nào đó. Để xác định CAN, ta cần
tìm số dư r trong phép chia X cho 10 và tra vào bảng 1. Để xác định CHI, ta tìm số dư s trong
phép chia X cho 12 và tra vào bảng 2.
Ví dụ: Năm 1982 có CAN là Nhâm, có CHI là Tuất. Bảng 1 r 0 1 2 3 4 5 6 7 8 9 CAN Canh Tân Nhâm Quý Giáp Ất Bính Đinh Mậu Kỷ Bảng 2 s 0 1 2 3 4 5 6 7 8 9 10 11 CHI Thân Dậu Tuất Hợi Tí Sửu Dần Mão Thìn Tỵ Ngọ Mùi
a) Em hãy sử dụng quy tắc trên để xác định CAN, CHI của năm 2021;
b) Bạn Loan nhớ rằng mẹ bạn ấy sinh năm Giáp Thìn nhưng không rõ là năm bao nhiêu. Lời giải
a) Vì 2021 chia cho 10 dư 1 và 2021 chia cho 12 dư 5 nên năm 2021 có CAN là Tân, có CHI là Sửu.
b) Gọi năm sinh của mẹ bạn Loan là x ( x Z ; 1930 x 2000 )
Vì Mẹ bạn Loan sinh năm Giáp Thìn nên x chia cho 10 dư 4 và chia cho 12 dư 8
x 16 chia hết cho cả 10 và 12 hay x 16 là một bội chung của 10 và 12
Mà BCNN 10;12 60 x 16 B60 0;60;120;180;;1920;1980;2040;
x44;104;164;;1904;1964;2024; . Thực tế ta thấy x 1964 là một giá trị hợp lí.
Vậy mẹ bạn Loan sinh năm 1964 .
Bài 4: (0.75 điểm) Một xí nghiệp may cứ mỗi tháng thì trả tiền lương cho công nhân viên, tiền vật liệu,
tiền điện, tiền thuế,… tổng cộng là 410000000 (VNĐ). Mỗi chiếc áo được bán với giá là 350000
(VNĐ). Gọi số tiền lời (hoặc lỗ) mà xí nghiệp thu được sau mỗi tháng là L (VNĐ) và mỗi tháng xí
nghiệp bán được A chiếc áo.
a) Lập hàm số của L theo A ;
b) Nếu trong một tháng, công ty bán được 1000 chiếc áo thì công ty lời hay lỗ bao nhiêu?
c) Mỗi tháng phải bán ít nhất bao nhiêu chiếc áo để xí nghiệp không bị lỗ?
d) Hỏi cần phải bán trung bình bao nhiêu chiếc áo mỗi tháng để sau 1 năm xí nghiệm thu được tiền lời là 1380000000 (VNĐ)? Trang - 13 - Lời giải
a) Số tiền bán áo thu được mỗi tháng là 350000A (VNĐ)
Số tiền lời (hoặc lỗ) mà xí nghiệp thu được sau mỗi tháng là L 350000A 410000000 (VNĐ)
Vậy hàm số của L theo A là L 350000A 410000000 .
b) Với A 1000 thì L 350000.1000 410000000 6 0000000(VNĐ)
Vậy nếu trong một tháng, công ty bán được 1000 chiếc áo thì công ty lỗ 60000000 (VNĐ).
c) Để xí nghiệp không bị lỗ thì L 0 350000A 410000000 0 35A 8200 41000 A 7 8200 Ta có:
1171, 43 ; mà số áo bán ra là một số nguyên dương A 1172 7
Vậy mỗi tháng cần phải bán ít nhất 1172 chiếc áo để xí nghiệp không bị lỗ.
d) Số tiền lời (hoặc lỗ) mà xí nghiệp thu được sau 1 năm (12 tháng) là M 12L (VNĐ)
Do đó, sau 1 năm xí nghiệm thu được tiền lời là 1380000000 (VNĐ) 12L 1380000000
L 115000000 350000A410000000 115000000 35A 52500 A 1500
Vậy cần phải bán trung bình mỗi tháng 1500 chiếc áo để sau 1 năm xí nghiệp thu được số tiền lời là 1380000000 (VNĐ).
Bài 5: (1.0 điểm) Lớp 9A có 40 học sinh, trong đó nam nhiều hơn nữ. Trong giờ ra chơi, cô giáo đưa cả
lớp 260000 đồng để mỗi bạn nam mua một ly Coca giá 5000 đồng/ly, mỗi bạn nữ mua một bánh
phô mai giá 8000 đồng/cái và được căn tin thối lại 3000 đồng. Hỏi lớp 9A có bao nhiêu học sinh
nam và bao nhiêu học sinh nữ? Lời giải
a) Gọi x là số học sinh nam, y là số học sinh nữ của lớp 9A ( x ; y nguyên dương, x ; y 40 )
Vì lớp 9A có 40 học sinh nên ta có phương trình x y 40 1
Số tiền mua Coca là 5000x (đồng), số tiền mua phô mai là 8000 y (đồng).
Vì cô giáo đưa cả lớp 260000 đồng và được căn tin thối lại 3000 đồng nên ta có phương trình:
5000x 8000 y 260000 3000 5x 8 y 260 3 5x 8 y 257 2 Từ
1 và 2 ta có hệ phương trình:
x y 40 8
x 8y 320 3 x 63 x 21 (thỏa mãn) 5
x 8y 257 5
x 8y 257
y 40 x y 19
Vậy lớp 9A có 21 học sinh nam và 19 học sinh nữ.
Bài 6: (1.0 điểm) Tính chiều cao của một ngọn núi (làm tròn đến mét), cho biết tại hai địa điểm cách nhau
550 m, người ta nhìn thấy đỉnh núi với góc nâng lần lượt là 33 và 37 . Lời giải
Gọi chiều cao của ngọn núi (cạnh CD ) là x (mét) ( x 0 ) A
CD vuông tại C ta có: AC DC cot DAC AC xcot33 B
CD vuông tại C ta có: BC DC cot DBC BC xcot37 Trang - 14 -
Mà AB AC BC 550m nên ta có: xcot 33 xcot 37 550 550 x 2584 (m) cot 33 cot 37
Vậy chiều cao của ngọn núi là 2584 mét.
Bài 7: (1.0 điểm) Vào dịp khai trương, nhà sách khuyến mãi mỗi cây viết bi Thiên Long được giảm 20%
so với giá niêm yết, còn mỗi quyển tập ABC chỉ được giảm 10% so với giá niêm yết. Bạn An vào
nhà sách mua 20 quyển tập ABC và 10 cây viết bi Thiên Long. Khi tính tiền, bạn An đưa 175000
đồng và được thối lại 3000 đồng. Tính giá niêm yết của mỗi quyển tập và mỗi cây viết bi mà bạn
An đã mua. Biết rằng khi An nhìn vào hóa đơn, tổng số tiền phải trả khi chưa giảm giá là 195000 đồng. Lời giải
Gọi giá niêm yết của mỗi cây viết bi Thiên Long là x (nghìn đồng), giá niêm yết của mỗi quyển tập
ABC là y (nghìn đồng) ( 0 x ; y 195 )
Vì tổng số tiền phải trả khi chưa giảm giá là 195000 đồng nên ta có phương trình: 10x 20 y 195
2x 4y 39 1
Vì khi tính tiền (đã giảm giá) bạn An đưa 175000 đồng và được thối lại 3000 đồng nên ta có phương trình: 80 90 10x
20y 175 3 8x 18y 172 4x 9y 86 2 100 100
2x 4y 39
4x 8y 78 y 8 Từ
1 và 2 ta có hệ phương trình: (thỏa mãn)
4x 9y 86
4x 9y 86 x 3,5
Vậy giá niêm yết của mỗi cây viết là 3500 đồng, giá niêm yết của mỗi quyển tập là 8000 đồng.
Bài 8: (3.0 điểm) Cho đường tròn ;
O R và điểm A ở ngoài đường tròn O với OA 2R . Đoạn thẳng
OA cắt đường tròn O tại D . Gọi H là trung điểm của OD , đường thẳng vuông góc với OA tại
H cắt đường tròn O tại M .
a) Chứng minh: AM là tiếp tuyến của đường tròn O ;
b) Qua A vẽ cát tuyến ABC đến đường tròn O ( B , C thuộc O , B nằm giữa A và C ). Chứng minh: 2
AH AO AB AC AM và đường thẳng MH chứa tia phân giác của BHC ;
c) Tiếp tuyến tại B và C của đường tròn O cắt nhau tại T . Chứng minh: Ba điểm M , H , T thẳng hàng. Lời giải Trang - 15 -
a) Do H là trung điểm của OD và MH OD M
OD có MH vừa là trung tuyến, vừa là đường cao M
OD cân tại M MO MD, mà MO OD R M
OD là tam giác đều.
Do OA 2R và OA cắt đường tròn O tại D D là trung điểm của OA MD là trung tuyến OA của A
MO, mà MD OD A
MO vuông tại M AM OM 2
Ta có: M thuộc đường tròn O , AM OM AM là tiếp tuyến tại M của đường tròn O . 1 b) Xét A MB và A
CM có: AMB ACM sđ MB ; MAC chung 2 AM AB AM B ” ACM (g.g) 2 AM A . B AC 1 AC AM A
MO vuông tại M có đường cao MH 2
AM AH. AO 2 Từ 1 và 2 2
AH AO AB AC AM
Do AH AO AB AH AC AC
, mà OAC chung AH B ” ACO (c.g.c) AB AO
AHB ACO Tứ giác OHBC là tứ giác nội tiếp OHC OBC O
BC cân tại O OBC OCB hay OBC ACO AHB OHC
Mà AHB BHM OHC CHM 90 BHM CHM
Vậy đường thẳng MH chứa tia phân giác của BHC .
c) Tiếp tuyến tại B , C của đường tròn O cắt nhau tại T TB OB và TC OC
OBT OCT 90 OBT OCT 90 90 180 Tứ giác OBTC là tứ giác nội tiếp
Mà tứ giác OHBC nội tiếp 5 điểm O , H , B , T , C cùng thuộc một đường tròn
Tứ giác OHTC là tứ giác nội tiếp OHT OCT 180 OHT 90 TH OA
Như vậy ta có: TH OA, MH OA. Suy ra ba điểm M , H , T thẳng hàng.
------------------------------------------- Trang - 16 -
SỞ GD & ĐT TP.HỒ CHÍ MINH ĐỀ THAM KHẢO TUYỂN SINH 10
PHÒNG GD & ĐT QUẬN 5 NĂM HỌC 2022-20232
ĐỀ THAM KHẢO MÔN : TOÁN 9
-------------------- Đề thi gồm 8 câu hỏi tự luận
MÃ ĐỀ : Quận 5 – 3 Thời gian: 120 phút (không kể thời gian phát đề) 2 x
Bài 1: (1.5 điểm). Cho hàm số y
có đồ thị là parabol P và hàm số y x 4 có đồ thị là đường 2 thẳng D .
a) Vẽ đồ thị P và D trên cùng hệ trục tọa độ;
b) Tìm tọa độ giao điểm của P và D bằng phép toán.
Bài 2: (1.0 điểm) Cho phương trình 2
5x 3x 15 0 .Không giải phương trình. Hãy tính giá trị biểu thức
A x x 2 2x 2x với x ; x là hai nghiệm nếu có của phương trình đã cho. 1 2 1 2 1 2
Bài 3: (0.75 điểm) Một nhà máy sản xuất xi măng có sản lượng hang năm được xác định theo hàm số
T 12, 5n 360 . Với T là sản lượng (đơn vị tấn) và n là số năm tính từ năm 2010.
a) Hãy tính sản lượng xi măng của nhà máy vào năm 2020.
b) Theo hàm số trên thì nhà máy đạt sản lượng 510 tấn vào năm nào?
Bài 4: (0.75 điểm) Trong tháng Giêng hai tổ công nhân đã may được 800 chiếc áo. Tháng Hai, tổ 1 may
vượt mức 15% , tổ hai may vượt mức 20% so với tháng Giêng do đó cả hai tổ đã may được 945 cái
áo. Hỏi trong tháng Giêng mỗi tổ đã may được bao nhiêu chiếc áo?
Bài 5: (1.0 điểm) Trong tháng 4 năm 2021, một công nhân được nhận tiền lương là 7 800 000 đồng gồm
tiền lương trong 24 ngày làm việc bình thường và 4 ngày làm việc đặc biệt (gồm chủ nhật và ngày
lễ). Biết tiền lương của một ngày làm việc đặc biệt nhiều hơn tiền lương của một ngày bình thường
là 200 000 đồng. Tính tiền lương của một ngày làm việc bình thường.
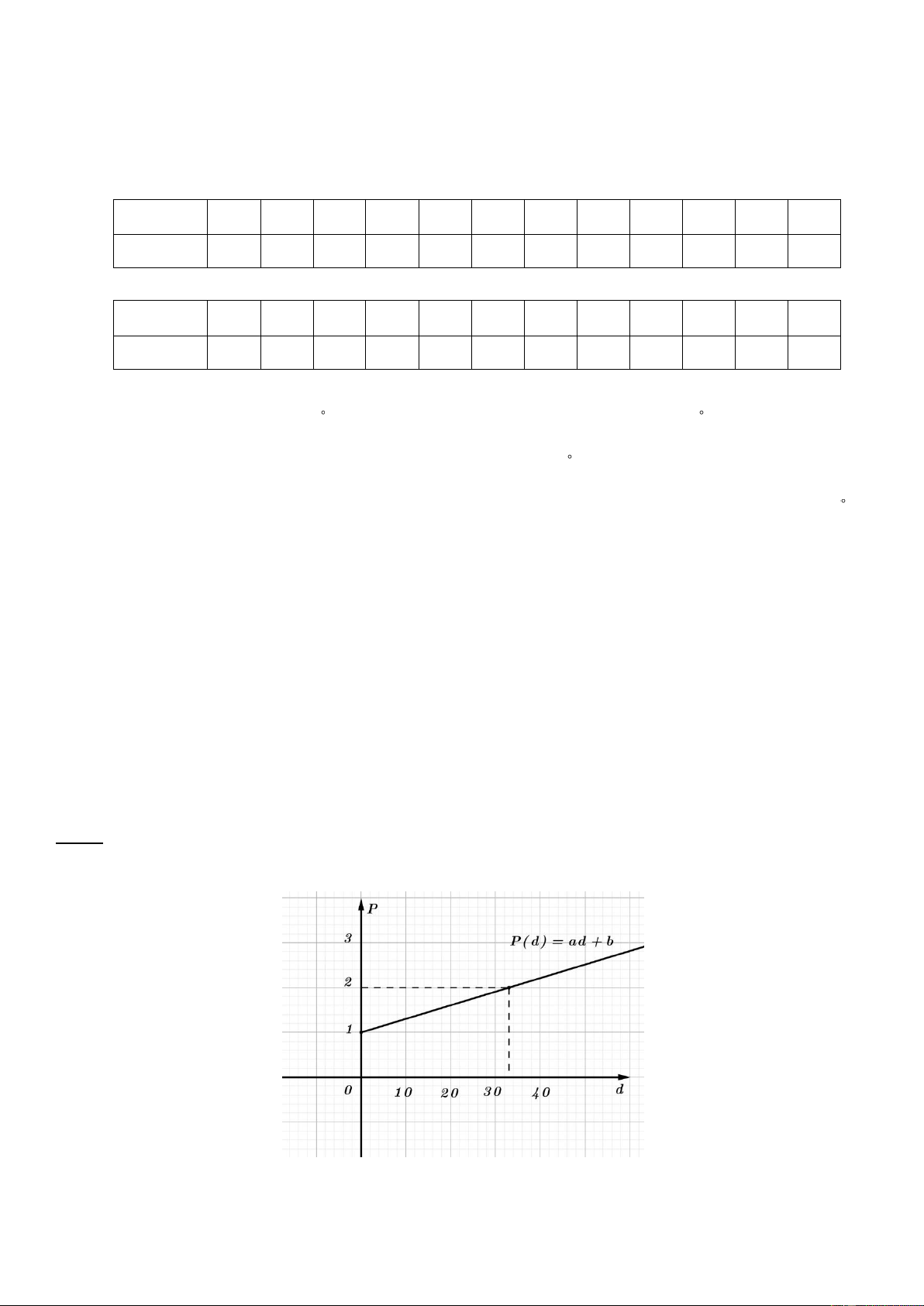
Bài 6: (1.0 điểm) Quãng đường giữa hai thành phố A và B dài 120 km. Lúc 6 giờ sáng, một ô tô xuất phát
từ A đi về B. Người ta thấy mối liên hệ giữa khoảng cách của ô tô so với A và thời điểm đi của ô tô Trang - 17 - là một hàm số bậc nhất
y ax b có đồ thị như hình sau:
a) Xác định các hệ số a, b?
b) Lúc 8 giờ sáng ôtô cách B bao xa?
Bài 7: (1.0 điểm) Một cái ly thủy tinh hình nón, bán kính đáy bằng 2 cm và chiều cao bằng 6 cm
a) Tính thể tích cái ly (biết bề dày của cái ly không đáng kể)( làm tròn đến chữ số thập phân thứ nhất)
b) Người ta rót rượu vào ly, biết chiều cao của rượu trong ly bằng 3 cm. Tính thể tích rượu chứa trong
ly ( làm tròn đến chữ số thập phân thứ nhất).
Bài 8: (3.0 điểm) Cho tam giác ABC nhọn (AB < AC). Đường tròn tâm O đường kính BC cắt AB, AC lần
lượt tại E và F. Gọi H là giao điểm của BF và CE. Gọi D là giao điểm của AH và BC. Gọi M là
trung điểm của HC. Gọi I là giao điểm của DF và CE.
a) Chứng minh: AH BC và FHC BAC
b) Chứng minh FDE 2FCE và I . E IM I . D IF
c) Qua I vẽ đường thẳng song song với MF cắt HF , AC lần lượt tại K và S. Lấy T đối xứng K qua I.
Chứng minh tứ giác SHTC nội tiếp.
-------------------------------------------- Trang - 18 - HƯỚNG DẪN GIẢI 2 x
Bài 1: (1.5 điểm). ). Cho hàm số y
có đồ thị là parabol P và hàm số y x 4 có đồ thị là đường 2 thẳng D .
a) Vẽ đồ thị P và D trên cùng hệ trục tọa độ;
b) Tìm tọa độ giao điểm của P và D bằng phép toán. Lời giải a) Học sinh tự vẽ
b) Hoành độ giao điểm của P và D là nghiệm của phương trình: 2 x x 4 2 x 2 x 8 2
x 2x 8 0 2 2 1 1. 8
9 0 Phương trình có hai nghiệm phân biệt: x 2 ; x 4 1 2
+ Với x 2 y 1 1 1
+ Với x 4 y 4 2 2
Vậy D cắt P tại hai điểm phân biệt là 2; 1 và 4 ; 4 .
Bài 2: (1.0 điểm) Cho phương trình 2
5x 3x 15 0 .Không giải phương trình. Hãy tính giá trị biểu thức
A x x 2 2x 2x với x ; x là hai nghiệm nếu có của phương trình đã cho. 1 2 1 2 1 2 Lời giải
Vì x ; x là hai nghiệm của phương trình. 1 2 Áp dụng định lý vi-et: b 3
S x x 1 2 a 5 c P x x 3 1 2 a
A x x 2 2x 2x 1 2 1 2 2
A x x
4x x 2 x x 1 2 1 2 1 2 2 3 3 321 A 4.3 2. 5 5 25
Bài 3: (0.75 điểm) Một nhà máy sản xuất xi măng có sản lượng hang năm được xác định theo hàm số
T 12, 5n 360 . Với T là sản lượng (đơn vị tấn) và n là số năm tính từ năm 2010.
a) Hãy tính sản lượng xi măng của nhà máy vào năm 2020.
b) Theo hàm số trên thì nhà máy đạt sản lượng 510 tấn vào năm nào? Lời giải
a) Sản lượng xi măng vào năm 2020 là: T 12,52020 2010 360 485 (tấn)
b) Theo đề bài ta có: 510 12, 5n 360 n 12 (năm)
Vậy nhà máy đạt sản lượng 510 tấn vào năm 2022 Trang - 19 -
Bài 4: (0.75 điểm) Trong tháng Giêng hai tổ công nhân đã may được 800 chiếc áo. Tháng Hai, tổ 1 may
vượt mức 15% , tổ hai may vượt mức 20% so với tháng Giêng do đó cả hai tổ đã may được 945 cái
áo. Hỏi trong tháng Giêng mỗi tổ đã may được bao nhiêu chiếc áo? Lời giải
Gọi x (chiếc áo) là số chiếc áo của tổ 1 may trong tháng Giêng.
y (chiếc áo) là số chiếc áo của tổ 2 may trong tháng Giêng. ( x, y * ) x y 800 x 300
Theo đề bài ta có hệ phương trình: 11
5%x 120%y 945 y 500
Vậy tổ 1 may được 300 chiếc áo, tổ 2 may được 500 chiếc áo.
Bài 5: (1.0 điểm) Trong tháng 4 năm 2021, một công nhân được nhận tiền lương là 7 800 000 đồng gồm
tiền lương trong 24 ngày làm việc bình thường và 4 ngày làm việc đặc biệt (gồm chủ nhật và ngày
lễ). Biết tiền lương của một ngày làm việc đặc biệt nhiều hơn tiền lương của một ngày bình thường
là 200 000 đồng. Tính tiền lương của một ngày làm việc bình thường. Lời giải
Gọi x (đồng) là tiền lương ngày làm việc đặc biệt
y (đồng) là tiền lương ngày làm việc bình thường ( x, y 0 )
x y 200000 x 450000
Theo đề bài ta có hệ phương trình:
4x 24 y 7800000 y 250000
Vậy tiền lương của một ngày làm việc bình thường là 250000 đồng
Bài 6: (1.0 điểm) Quãng đường giữa hai thành phố A và B dài 120 km. Lúc 6 giờ sáng, một ô tô xuất phát
từ A đi về B. Người ta thấy mối liên hệ giữa khoảng cách của ô tô so với A và thời điểm đi của ô tô
là một hàm số bậc nhất y ax b có đồ thị như hình sau:
a) Xác định các hệ số a, b?
b) Lúc 8 giờ sáng ôtô cách B bao xa? Lời giải
6a b 0 a 40
a) Theo đề bài ta có hệ phương trình sau : 9
a b 120 b 24 0
Vậy a 40, b 2
40. Hàm số : y 40x 240 Trang - 20 -
b) Thay x 8vào y 40x 240
y 40.8 240 80
Vậy lúc 8h sáng ô tô cách B : 120 80 40(km)
Bài 7: (1.0 điểm) Một cái ly thủy tinh hình nón, bán kính đáy bằng 2 cm và chiều cao bằng 6 cm
a) Tính thể tích cái ly (biết bề dày của cái ly không đáng kể)( làm tròn đến chữ số thập phân thứ nhất)
b) Người ta rót rượu vào ly, biết chiều cao của rượu trong ly bằng 3 cm. Tính thể tích rượu chứa trong
ly ( làm tròn đến chữ số thập phân thứ nhất). Lời giải 2 .2 .6 a) Thể tích cái ly : 3 25,1(cm ) 3 b)
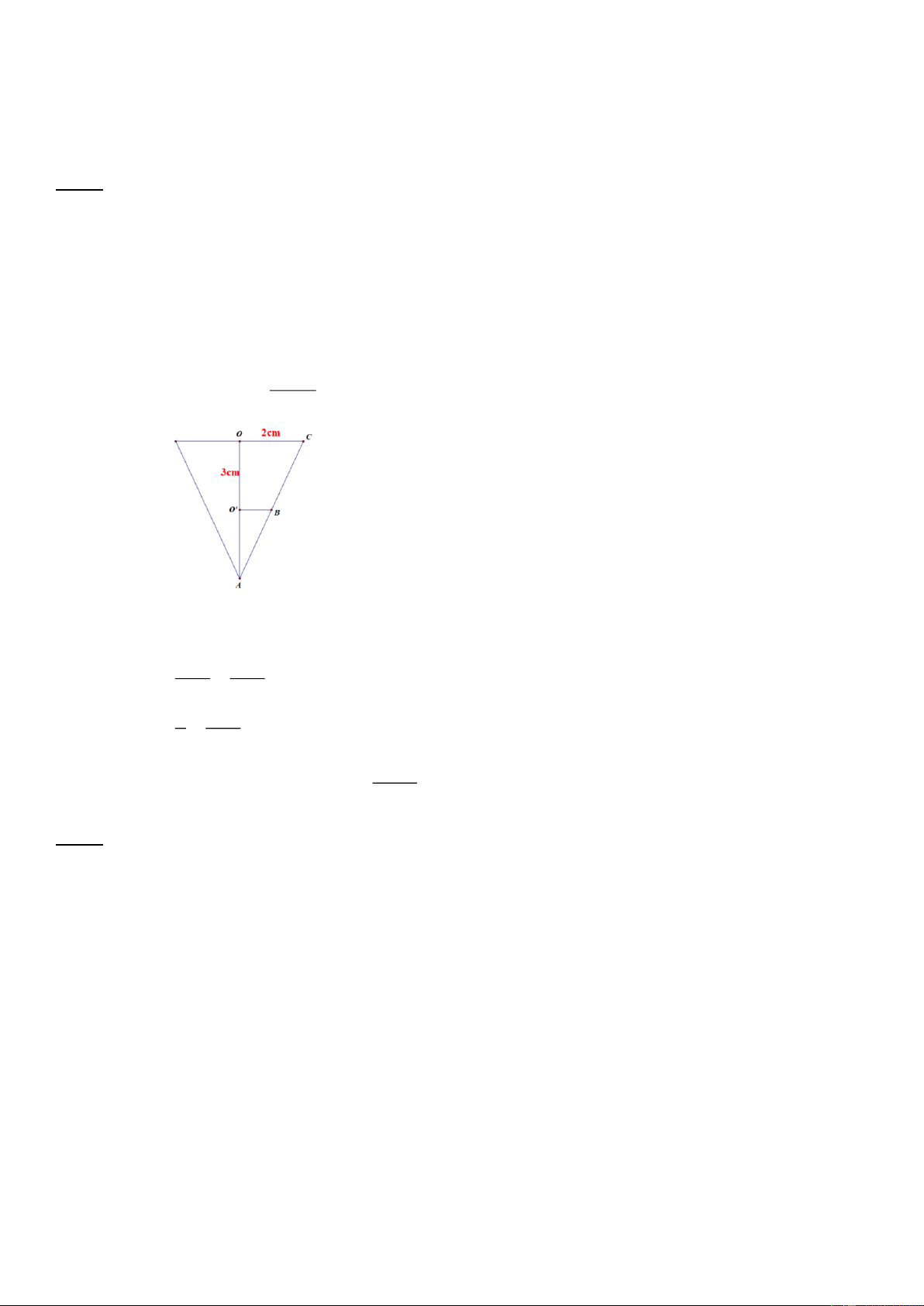
Theo đề bài ta có hình vẽ sau : Xét O
AC có : O’B // OC O ' A O ' B OA OC 3 O ' B
O ' B 1(cm) 6 2 2 .1 .3
Thể tích rượu chứa trong ly : 3,1 3 cm 3
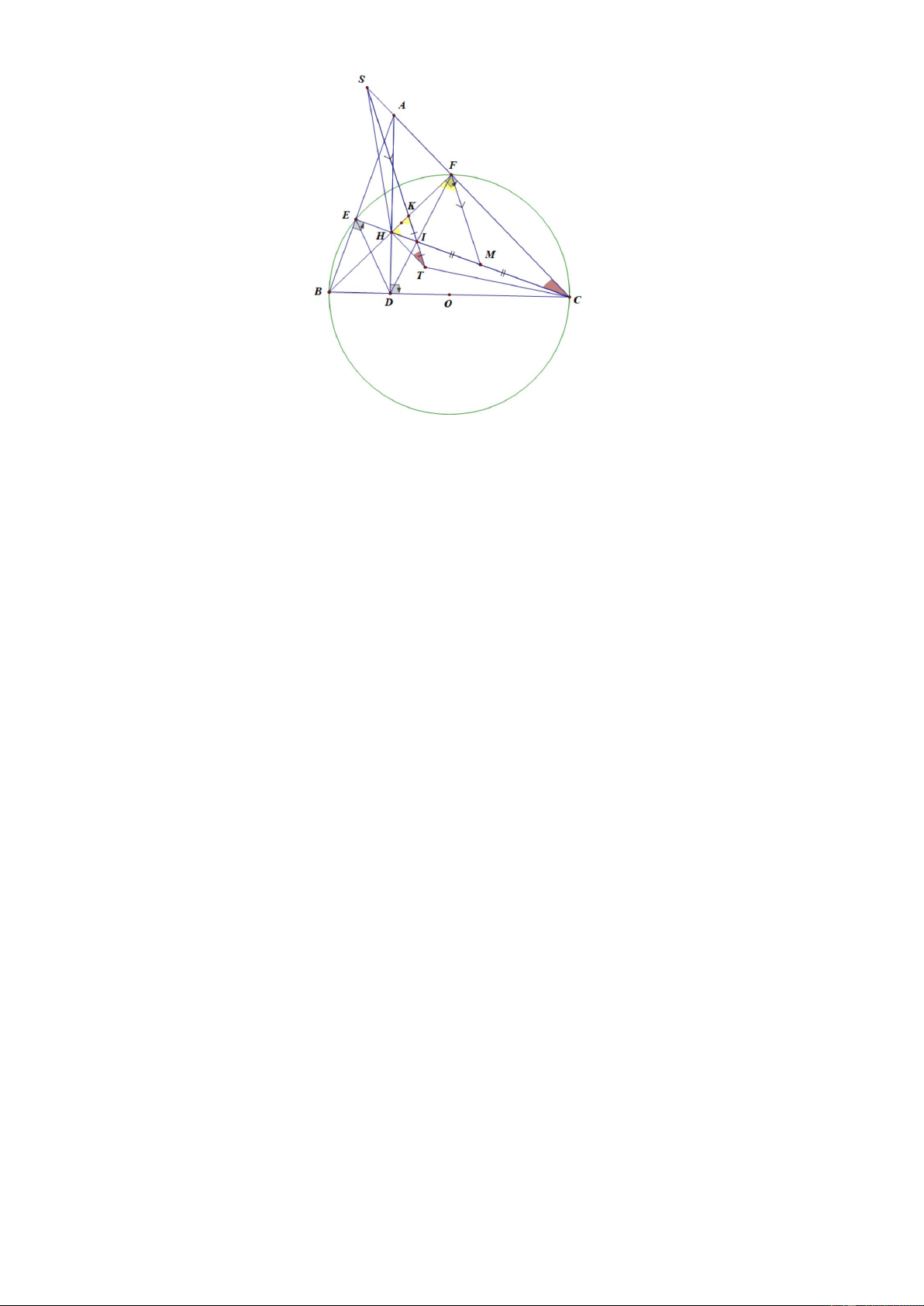
Bài 8: (3.0 điểm) Cho tam giác ABC nhọn (AB < AC). Đường tròn tâm O đường kính BC cắt AB, AC lần
lượt tại E và F. Gọi H là giao điểm của BF và CE. Gọi D là giao điểm của AH và BC. Gọi M là
trung điểm của HC. Gọi I là giao điểm của DF và CE.
a) Chứng minh: AH BC và FHC BAC
b) Chứng minh FDE 2FCE và I . E IM I . D IF
c) Qua I vẽ đường thẳng song song với MF cắt HF , AC lần lượt tại K và S. Lấy T đối xứng K qua I.
Chứng minh tứ giác SHTC nội tiếp. Lời giải Trang - 21 - a) Chứng minh BEC vuông tại E và BFC vuông tại F
Suy ra H là trực tâm ABC
=> AH BC
Tứ giác AEHF nội tiếp => FHC BAC
b) Ta có: EDH ECF (tứ giác AEDC nội tiếp)
HDF HCF ( tứ giác HDCF nội tiếp)
EDH HDF
HD là phân giác của EDF
EDF 2ECF
Ta có: EMF 2ECF ( góc ngoài F MC ) E DI ∽ F
MI(g g)
IE.IM I . D IF
c) Ta có: FHM HFM ( H FM cân tại M)
HFM HKI (2 góc đồng vị, FM // KI)
KHI HKI H
KI cân tại I => HI = KI => H IT cân tại I H KT vuông tại H
HTS HCS (cùng phụ FHC )
Tứ giác HTCS nội tiếp
------------------------------------------- Trang - 22 -




