





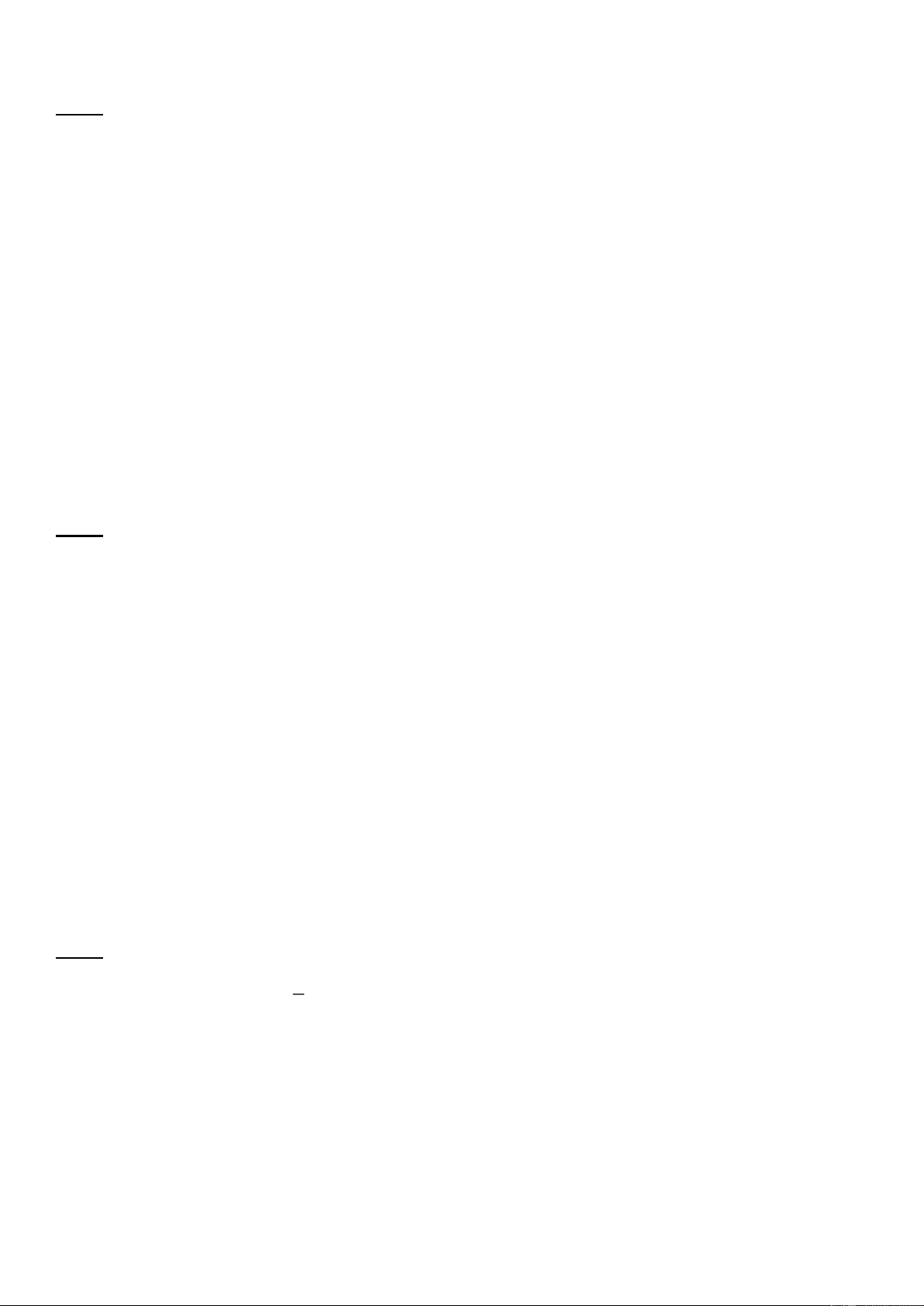








Preview text:
SỞ GD & ĐT TP.HỒ CHÍ MINH ĐỀ THAM KHẢO TUYỂN SINH 10
PHÒNG GD & ĐT QUẬN 3 NĂM HỌC 2022-20232
ĐỀ THAM KHẢO MÔN : TOÁN 9
-------------------- Đề thi gồm 8 câu hỏi tự luận
MÃ ĐỀ : Quận 3 – 1 Thời gian: 120 phút (không kể thời gian phát đề)
Bài 1: (1.5 điểm). Cho P : 2
y x và đường thẳng D : y 3x 4
a) Vẽ P và D trên cùng một hệ trục.
b) Tìm tọa độ giao điểm của P và D bằng phép tính.
Bài 2: (1.0 điểm) Cho phương trình bậc hai: 2
x 2mx 1 0 1
a) Chứng minh rằng phương trình
1 luôn có hai nghiệm phân biệt x và x . 1 2
b) Tìm các giá trị m để 2 2
x x x x 7 . 1 2 1 2
Bài 3: (1.0 điểm) Một cửa hàng đồng loạt giảm giá các sản phẩm. Trong đó có chương trình nếu mua một
gói kẹo thứ hai trở đi sẽ được giảm 10% so với giá ban đầu là 50000 đồng.
a) Nếu gọi số gói kẹo đã mua là x, số tiền phải trả là y. Hãy biểu diễn diễn y theo x.
b) Bạn Thư muốn mua 10 gói kẹo thì hết bao nhiêu tiền.
Bài 4: (1.0 điểm) Trong kỳ thi HKII môn toán lớp 9. Một phòng thi của trường có 24 thí sinh dự thi. Các
thí sinh đều phải làm bài trên giấy thi của trường phát. Cuối buổi thi, sau khi thu bài, giám thị coi thi
đếm được tổng số tờ giấy thi là 53 tờ. Hỏi trong phòng thi đó có bao nhiêu thí sinh làm bài 2 tờ giấy
thi, bao nhiêu thí sinh làm bài 3 tờ giấy thi? Biết rằng có 3 thí sinh chỉ làm 1 tờ giấy thi.
Bài 5: (1.0 điểm) Trong một phòng họp có 360 người họp, được sắp xếp ngồi đều trên các dãy ghế. Nếu
bớt đi 3 dãy ghế thì mỗi dãy ghế phải xếp thêm 4 ghế mới đủ chỗ. Hỏi lúc đầu có bao nhiêu dãy ghế
và mỗi dãy xếp mấy ghế?
Bài 6: (1.0 điểm) Để ước lượng khối lượng của cây gỗ
trồng trong rừng người ta cần xác định chiều cao h
của cây (đo bằng mét) và chu vi C của vòng tròn
thân cây ngang tầm ngực (đo bằng mét). Theo cách
đo đạc trong lâm nghiệp, độ cao ngang tầm ngực là
1,4 mét tính từ mặt đất. Từ đó người ta có thể quấn
thước dây vòng quanh thân cây ở độ cao này và ghi
lại số đo chu vi C.
a) Áp dụng công thức thể tích hình trụ V = S.h trong
đó S là diện tích vòng tròn thân cây có chu vi C nói
trên và h là chiều cao của cây sẽ tính được thể tích Trang - 1 -
của cây. Nếu một cây có chu vi C của vòng tròn thân cây ngang tầm ngực là 1,28m và chiều cao là
20,4m thì cây có thể tích bao nhiêu (làm tròn đến chữ số thập phân thứ nhất)?
b) Cho biết loại cây nói trên có khối lượng riêng là D = 1,05 tấn/m3 khối lượng m = V . D. Hãy ước
lượng khối lượng của cây đó tính theo đơn vị là kg (làm tròn đến hàng trăm).
Bài 7: (1.0 điểm) Một cửa hàng Pizza có chương trình khuyến mãi: giảm 30% cho bánh Pizza hải sản có
giá bán ban đầu là 210000 đồng/cái. Nếu khách hàng có thẻ VIP thì sẽ được giảm thêm 5% trên giá
đã giảm. Hỏi một nhóm nhân viên văn phòng đặt mua 60 cái bánh Pizza hải sản ở cửa hàng trong đó
có 25 cái dùng thẻ VIP thì phải trả tất cả bao nhiêu tiền (làm tròn nghìn đồng)?
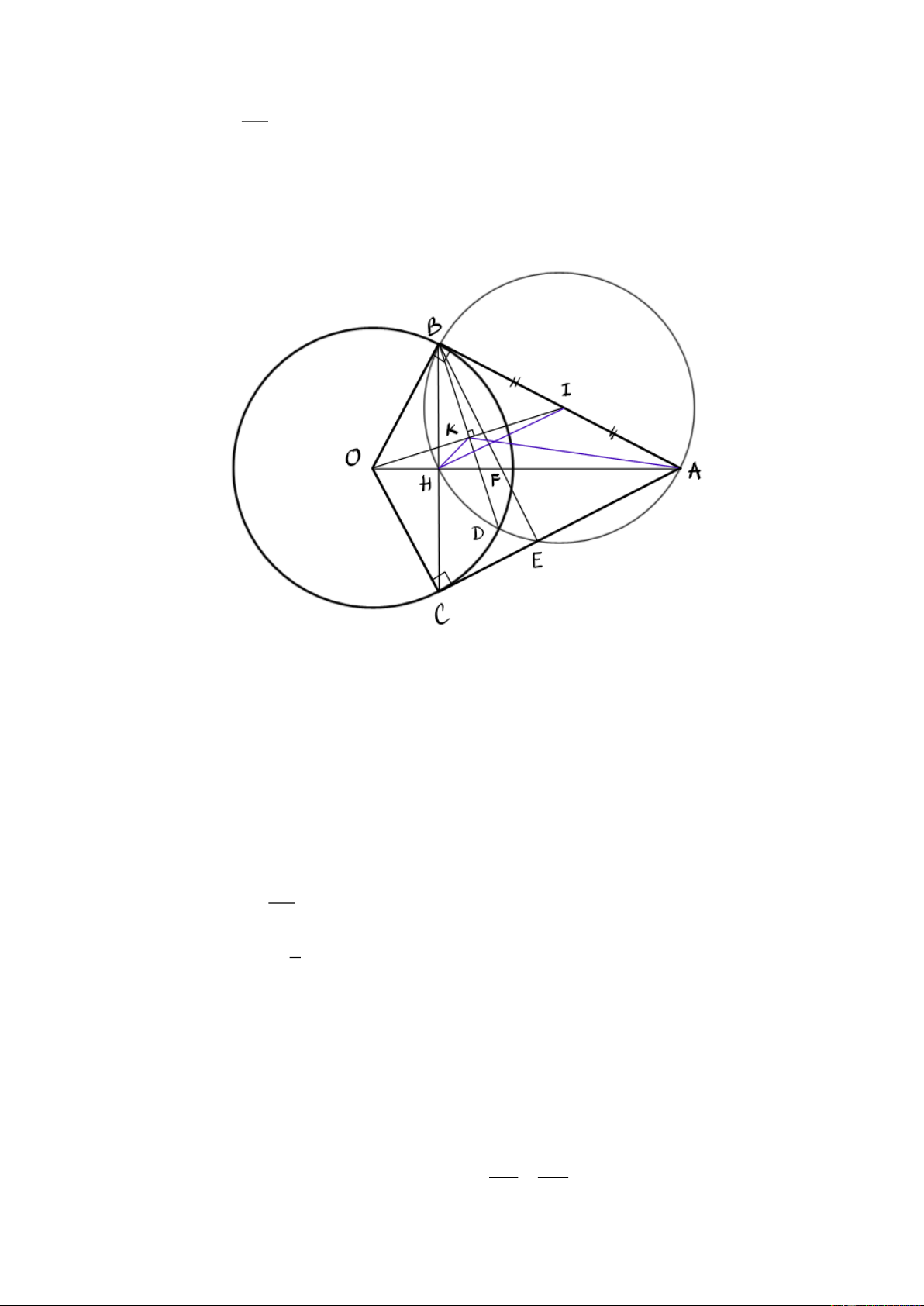
Bài 8: (2.5 điểm) Từ điểm A ở ngoài đường tròn ;
O R vẽ hai tiếp tuyến AB, AC với đường tròn O
B,C là tiếp điểm . Gọi H là giao điểm của AO và BC. Gọi I là trung điểm của AB. Từ B kẻ
đường thẳng vuông góc với OI tại K, đường thẳng này cắt đường tròn O tại D (D khác B).
a) Chứng minh tứ giác ABOC nội tiếp và OK.OI OH.OA. AB b) Đường tròn I ;
cắt AC tại E. Gọi F là giao điểm của BE và OA. Chứng minh F đối xứng với 2 O qua H.
c) Chứng minh đường tròn ngoại tiếp AFB đi qua điểm K
-------------------------------------------- Trang - 2 - HƯỚNG DẪN GIẢI
Bài 1: (1.5 điểm). Cho P : 2
y x và đường thẳng D : y 3x 4
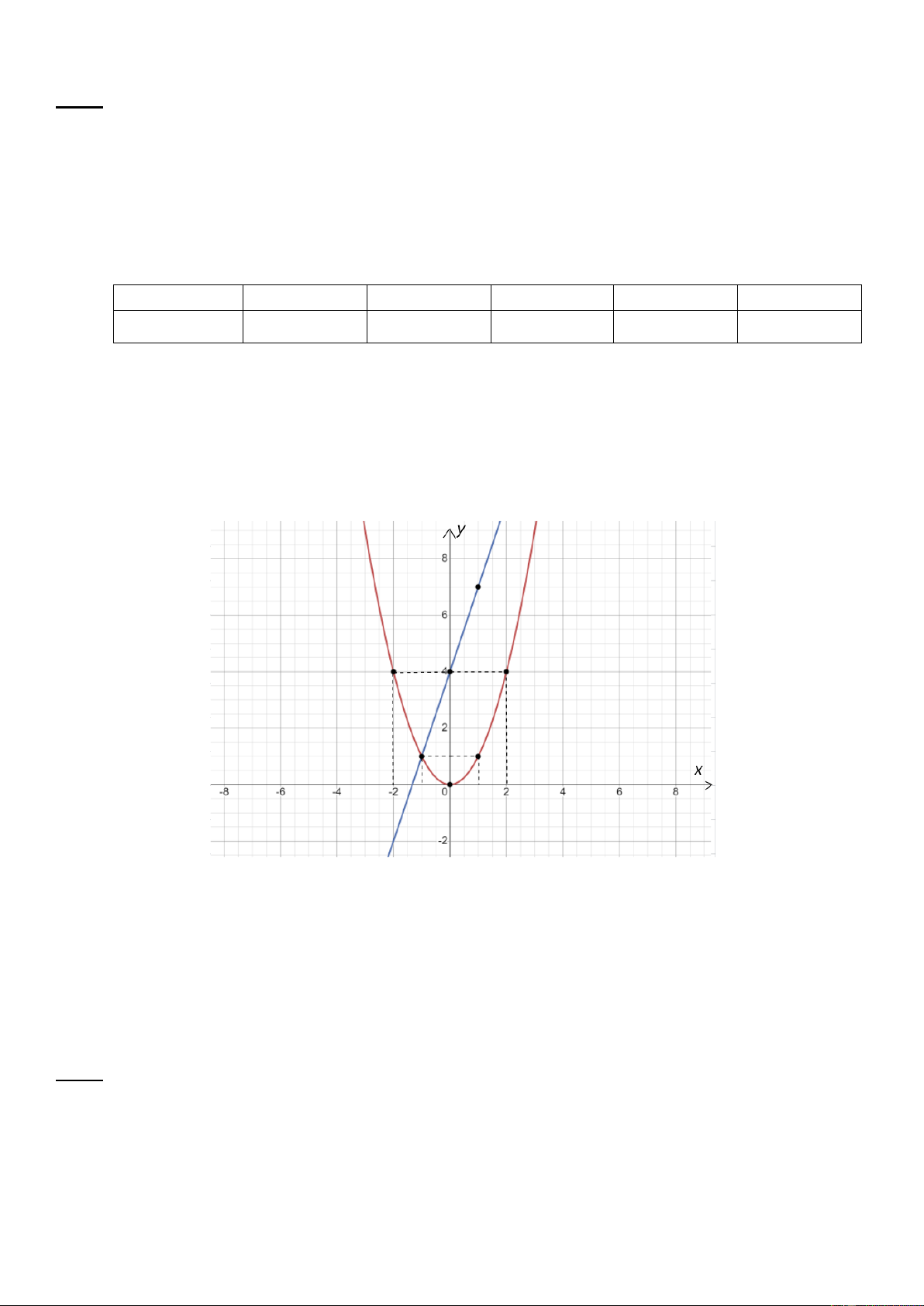
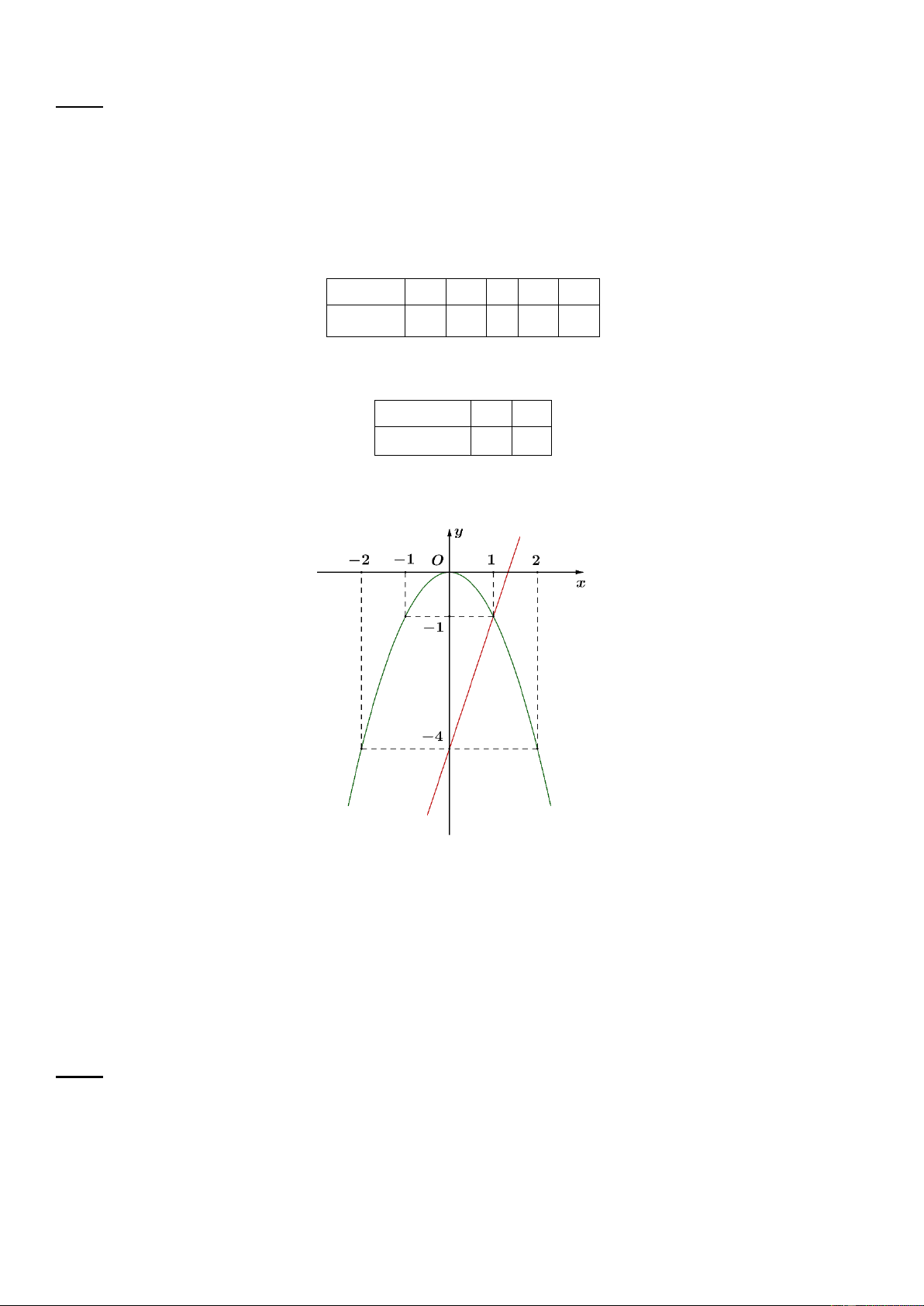
a) Vẽ P và D trên cùng một hệ trục.
b) Tìm tọa độ giao điểm của P và D bằng phép tính. Lời giải a) Hàm số: 2 y x
Bảng giá trị tương ứng của x và y : x –2 -1 0 1 2 2 y x 4 1 0 1 4
Đồ thị hàm số là một Parabol đi qua các điểm (−𝟐; 𝟒); (−𝟏; 𝟏); 0;0 ; (𝟏; 𝟏); (𝟐; 𝟒)
Hàm số: y 3x 4
x 0 y 4 x 1 y 1
Đồ thị hàm số là đường thẳng đi qua 0;4 và 1 ; 1 Vẽ:
b) Hoành độ giao điểm của P và D là nghiệm của phương trình: 2 x 3x 4 2
x 3x 4 0 a 1,b 3 ,c 4
a b c 1 (3) (4) 0 Phương trình có hai nghiệm phân biệt: x 1 ; x 4 1 2 + Với x 1 y 1 1 1
+ Với x 4 y 16 2 2
Vậy D cắt P tại hai điểm phân biệt là 1 ; 1 và 4;16 .
Bài 2: (1.0 điểm) Cho phương trình bậc hai: 2
x 2mx 1 0 1
a) Chứng minh rằng phương trình
1 luôn có hai nghiệm phân biệt x và x . 1 2
b) Tìm các giá trị m để 2 2
x x x x 7 . 1 2 1 2 Lời giải a) Trang - 3 - Cách 1:
Phương trình đã cho là phương trình bậc hai của x có: 2 2 ( ) m 1.( 1
) m 11 m
0 m
Vậy phương trình đã cho luôn có hai nghiệm x ; x với mọi giá trị của m . 1 2
Cách 2 : vì a, c trái dấu nên phương trình luôn có 2 nghiệm phân biệt
x x 2m
b) Theo định lý Vi-et, ta có: 1 2 x x 1 1 2 Do đó: 2 2
x x x x 7 x x
3x x 7 m2 2 3.( 1 ) 7 1 2 2 1 2 1 2 1 2 2 4m 3 7 2 4m 4 2
m 1 m 1
Vậy với m
1 thì phương trình có hai nghiệm x ; x thỏa mãn 2 2
x x x x 7 . 1 2 1 2 1 2
Bài 3: (1.0 điểm) Một cửa hàng đồng loạt giảm giá các sản phẩm. Trong đó có chương trình nếu mua một
gói kẹo thứ hai trở đi sẽ được giảm 10% so với giá ban đầu là 50000 đồng.
a) Nếu gọi số gói kẹo đã mua là x, số tiền phải trả là y. Hãy biểu diễn diễn y theo x.
b) Bạn Thư muốn mua 10 gói kẹo thì hết bao nhiêu tiền. Lời giải
a) Giá một gói kẹo thì gói thứ hai trở đi: (100% 10%).50000 45000 đồng
Số gói kẹo đã mua là x, số tiền phải trả là y. Theo đề bài ta có:
y 50000 45000 x
1 y 45000x 5000
b) Bạn Thư mua 10 gói kẹo x 10 y 45000.10 5000 455000
Vậy số tiền bạn Thư phải trả khi mua 10 gói kẹo là 455000 đồng
Bài 4: (1.0 điểm) Trong kỳ thi HKII môn toán lớp 9. Một phòng thi của trường có 24 thí sinh dự thi. Các
thí sinh đều phải làm bài trên giấy thi của trường phát. Cuối buổi thi, sau khi thu bài, giám thị coi thi
đếm được tổng số tờ giấy thi là 53 tờ. Hỏi trong phòng thi đó có bao nhiêu thí sinh làm bài 2 tờ giấy
thi, bao nhiêu thí sinh làm bài 3 tờ giấy thi? Biết rằng có 3 thí sinh chỉ làm 1 tờ giấy thi. Lời giải
Gọi x là số thí sinh làm bài 2 tờ giấy thi, y là số thí sinh làm bài 3 tờ giấy thi
,x y ,0 ,x y 2 1
Vì có 3 thí sinh làm bài 1 tờ giấy thi nên ta có x y 24 3 21
Tổng số tờ giấy thi của các thí sinh làm 2 tờ và 3 tờ giấy thi là 2x 3y 53 3 50 Ta có hệ phương trình:
x y 21
2x 2y 42 y 8 x 13 (thỏa mãn)
2x 3y 50
2x 3y 50 x 21 y y 8
Vậy có 13 thí sinh làm bài 2 tờ giấy thi, có 8 thí sinh làm bài 3 tờ giấy thi.
Bài 5: (1.0 điểm) Trong một phòng họp có 360 người họp, được sắp xếp ngồi đều trên các dãy ghế. Nếu
bớt đi 3 dãy ghế thì mỗi dãy ghế phải xếp thêm 4 ghế mới đủ chỗ. Hỏi lúc đầu có bao nhiêu dãy ghế
và mỗi dãy xếp mấy ghế? Lời giải
Gọi x là dãy ghế ban đầu (x nguyên dương, 3 < x < 360) 360
Số ghế mỗi dãy ban đầu là x
Số dãy ghế lúc sau là: x – 3. Trang - 4 - 360
Số ghế mỗi dãy lúc sau là: x 3
Vì mỗi dãy ghế phải xếp thêm 4 ghế so mới đủ chỗ nên ta có phương trình: 360 360
360(x 3) 4x(x 3) 360x 4 x x 3 x(x 3) x(x 3) 2
360x 1080 4x 12x 360x 2
4x 12x 1080 0 x 1
5 (loại) ; x 18 (nhận) 1 2 360
Vậy lúc đầu có 18 dãy ghế và mỗi dãy có 20 (ghế) 18
Bài 6: (1.0 điểm) Để ước lượng khối lượng của cây gỗ trồng trong rừng người ta cần xác định chiều cao h
của cây (đo bằng mét) và chu vi C của vòng tròn thân cây ngang tầm ngực (đo bằng mét). Theo
cách đo đạc trong lâm nghiệp, độ cao ngang tầm ngực là 1,4 mét tính từ mặt đất. Từ đó người ta có
thể quấn thước dây vòng quanh thân cây ở độ cao này và ghi lại số đo chu vi C.
a) Áp dụng công thức thể tích hình trụ V = S.h trong đó S là diện tích vòng tròn thân cây có chu vi C
nói trên và h là chiều cao của cây sẽ tính được thể tích của cây. Nếu một cây có chu vi C của vòng
tròn thân cây ngang tầm ngực là 1,28m và chiều cao là 20,4m thì cây có thể tích bao nhiêu (làm tròn
đến chữ số thập phân thứ nhất)?
b) Cho biết loại cây nói trên có khối lượng riêng là D = 1,05 tấn/m3 khối lượng m = V . D. Hãy ước
lượng khối lượng của cây đó tính theo đơn vị là kg (làm tròn đến hàng trăm). Lời giải
a) Gọi R (m) là bán kính vòng tròn thân cây ngang tầm ngực (R > 0) C 1, 28
Chu vi vòng tròn thân cây ngang tầm ngực là: C 2 R R 0, 2(m) 2 2
Diện tích vòng tròn thân cây ngang tầm ngực: 2 2 2
S R .0, 2 0,126(m ) Thể tích cây là: 3
V S.h 0,126.20, 4 2, 6 (m )
b) Khối lượng của cây: m V .D 2, 6.1, 05 2, 73 (tấn) 2700 (kg)
Bài 7: (1.0 điểm) Một cửa hàng Pizza có chương trình khuyến mãi: giảm 30% cho bánh Pizza hải sản có
giá bán ban đầu là 210000 đồng/cái. Nếu khách hàng có thẻ VIP thì sẽ được giảm thêm 5% trên giá
đã giảm. Hỏi một nhóm nhân viên văn phòng đặt mua 60 cái bánh Pizza hải sản ở cửa hàng trong đó
có 25 cái dùng thẻ VIP thì phải trả tất cả bao nhiêu tiền (làm tròn nghìn đồng)? Lời giải
Giá một cái bánh Pizza hải sản trong chương trình khuyến mãi:
(100% – 30%).210000 = 147000 (đồng)
Giá một cái bánh Pizza hải hải trong chương trình khuyến mãi và có dùng thẻ VIP :
(100% – 5%).147000 = 139650 (đồng)
Nhóm nhân viên văn phòng đặt mua 60 cái bánh Pizza hải sản trong đó có 25 cái dùng thẻ VIP thì
số tiền phải trả là : 147000.(60-25) + 139650.25 = 8636250 (đồng)
Bài 8: (2.5 điểm) Từ điểm A ở ngoài đường tròn ;
O R vẽ hai tiếp tuyến AB, AC với đường tròn O
B,C là tiếp điểm . Gọi H là giao điểm của AO và BC. Gọi I là trung điểm của AB. Từ B kẻ
đường thẳng vuông góc với OI tại K, đường thẳng này cắt đường tròn O tại D (D khác B). Trang - 5 -
a) Chứng minh tứ giác ABOC nội tiếp và OK.OI OH.OA. AB b) Đường tròn I ;
cắt AC tại E. Gọi F là giao điểm của BE và OA. Chứng minh F đối xứng với 2 O qua H.
c) Chứng minh đường tròn ngoại tiếp AFB đi qua điểm K. Lời giải
a) Ta có OB AB,OC AC (AB, AC là tiếp tuyến của (O) ) Suy ra
90o 90o 180o ABO ACO
Do đó tứ giá ABOC nội tiếp.
Lại có: AO là phân giác góc BAC và AB = AC (AB, AC là tiếp tuyến của đường tròn (O))
Suy ra AO là phân giác cũng là đường cao của tam giác cân ABC
AO BC tại H.
∆OBA vuông tại B có đường cao BH 2
OB OH.OA
∆OBI vuông tại B có đường cao BK 2
OB OK.OI
Vậy: OH.OA OK.OI AB
b) Xét đường tròn I ; : 2 1
Ta có: HAE HBE sđ E
H (góc nội tiếp chắn cung HE) 2
Mà HAE OBH (cùng nhìn cạnh OC của tứ giác nội tiếp OBAC)
HBE OBH
BH là phân giác OBF Mà BH OF
Do đó ∆OBF cân tại B có BH là phân giác cũng là đường cao và đường trung tuyến
Suy ra H là trung điểm OF hay F đối xứng O qua H. OA OI
c) Ta có OH.OA OK.OI (chứng minh ở câu a) OK OH
Đồng thời ∆OKA và ∆OAI có AOI chung nên O
KH” O AI (c.g.c) Trang - 6 -
OKH OAI Tứ giác AHKI nội tiếp
IKA IHA (1) 1
Lại có IH IA
AB (∆ABH vuông tại H, HI là trung tuyến) nên ∆IHA cân tại I 2 IHA IAH
mà IAH OBH (cùng phụ BOH ) và OBH HBF (chứng minh trên)
nên IHA HBF (2)
Từ (1) và (2) IKA HBF Mặt khác: 90o BFA HBF BHF HBF (góc ngoài ∆BHF) 90o BKA IKA BKI IKA
Do đó BFA BKA và cùng nhìn cạnh AB
Vậy tứ giác BKFA nội tiếp hay đường tròn ngoại tiếp ∆BFA đi qua K.
-------------------------------------------
SỞ GD & ĐT TP.HỒ CHÍ MINH
ĐỀ THAM KHẢO TUYỂN SINH 10
PHÒNG GD & ĐT QUẬN 3 NĂM HỌC 2022-2023 ĐỀ THAM KHẢO MÔN: TOÁN 9
-------------------------
Đề thi gồm 8 câu hỏi tự luận
MÃ ĐỀ: Quận 3 – 2
Thời gian: 120 phút (không kể thời gian phát đề)
Bài 1: (1.5 điểm) Cho (𝑷) 𝒚 = 𝟐𝒙𝟐 và (D): 𝒚 = 𝟑𝒙 − 𝟏
a) Vẽ (P) và (D) trên cùng một hệ trục tọa độ
b) Tìm tọa độ giao điểm của (P) và (D) bằng phép tính.
Bài 2: (1.0 điểm) Cho phương trình 𝒙𝟐 − 𝟏𝟎𝒙 − 𝟖 = 𝟎 có hai nghiệm x , x . Không giải phương trình hãy 1 2
tính giá trị của biểu thức A = (𝒙 𝟐 𝟐
𝟏 − 𝒙𝟐)(𝒙𝟏 − 𝒙𝟐).
Bài 3: (1.0 điểm) Các nhà khoa học về thống kê đã thiết lập được hàm số sau: A(t) = 𝟎, 𝟎𝟖𝒕 + 𝟏𝟗, 𝟕. Trong
đó A(t) là độ tuổi trung bình các phụ nữ kết hôn lần đầu của thế giới; t là số năm kết hôn, với gốc
thời gian là 1950. Hãy tính độ tuổi trung bình các phụ nữ kết hôn lần đầu lần lượt vào các năm 1950,
2000, 2018, 2020 (làm tròn đến chữ số thập phân thứ hai).
Bài 4: (1.0 điểm) Một trường học có tổng số giáo viên là 80 người, hiện tại tuổi trung bình của giáo viên là
35 tuổi. Trong đó, tuổi tuổi trung bình của giáo viên nữ là 32 tuổi và tuổi trung bình của giáo viên
nam là 38 tuổi. Hỏi 3 trường đó có bao nhiêu giáo viên nam, bao nhiêu giáo viên nữ?
Bài 5: (1.0 điểm) Bé An sống trong gia đình ba thế hệ gồm ông bà nội, ba mẹ, bé An và em trai. Chủ nhật
vừa rồi cả gia đình đi xem phim. Biết giá vé cho trẻ em (vé của bé An và em trai) được giảm giá
50%; vé người cao tuổi được giảm giá 25% (vé của ông bà nội). Vé của ba mẹ không được giảm giá. Trang - 7 -
Ông nội bé An, người phải trả giá vé là 60 nghìn đồng, đang trả tiền cho mọi người. Hỏi ông nội
phải trả bao nhiêu tiền?
Bài 6: (1.0 điểm) Theo năm Dương lịch, chu kỳ Trái Đất quay quanh Mặt Trời là 365 ngày và ngày (tức là
365,25 ngày). Khi đó, 1 ngày này sẽ được tích lũy trong vòng 4 năm nên theo năm Dương lịch thì 4
cứ 4 năm lại có 1 năm là năm nhuận vào các năm chia hết cho 4 (tháng 2 của năm này sẽ có 29 ngày
thay vì có 28 ngày như các năm không nhuận Dương lịch). Tuy nhiên, vẫn có một số ngoại lệ đối
với nguyên tắc trên vì có khi một năm Dương lịch lại ngắn hơn 365,25 ngày nên với những năm có
hai chữ số 0 ở cuối thì năm đó phải chia hết cho 400 mới là năm nhuận Dương lịch.
a) Từ năm 1900 đến năm 2000 có bao nhiêu năm nhuận Dương lịch? Vì sao?
b) Một nhà hộ sinh trong tháng 2 năm 2021 có 29 em bé chào đời là con của 29 gia đình khác nhau. Có
thể chắc chắn rằng có ít nhất 2 em bé chào đời cùng ngày hay không? Vì sao?
Bài 7: (1.0 điểm) Thớt là một dụng cụ sử dụng trong bếp của mỗi gia đình để
thái, chặt, ... Một cái thớt hình trụ có đường kính đáy 22cm, cao 4cm.
a) Tính tổng diện tích hai mặt thớt (làm tròn đến cm2).
b) Cho biết loại gỗ làm thớt có khối lượng 500 kg/m3. Hỏi thớt nặng bao nhiêu gam?
Công thức tính thể tích hình trụ là V = S · h (S là diện tích đáy và h là chiều cao hình trụ).
Bài 8: (3.0 điểm) Cho 𝜟𝑨𝑩𝑪 có 3 góc nhọn nội tiếp đường tròn (O; R). Gọi M, P, Q lần lượt là điểm chính
giữa các cung BC , CA , AB Gọi T là giao điểm của BP và CQ. Đường thẳng vuông góc với BP tại
B và đường thẳng vuông góc với CQ tại C cắt nhau ở I. Vẽ đường kính MN của (O). Gọi K là hình
chiếu của I trên AB.
a) Chứng minh: 𝜟𝑨𝑲𝑰 ~ 𝜟𝑵𝑪𝑴 và tứ giác BICT nội tiếp.
b) PQ cắt AC tại H, MQ cắt BC tại V. Chứng minh 3 điểm H, T, V thẳng hàng.
c) Gọi OI = d, IK = r. Chứng minh: 𝒅𝟐 = 𝑹𝟐 + 𝟐𝑹𝒓.
----------------------HẾT---------------------- Trang - 8 - HƯỚNG DẪN GIẢI
Bài 1: (1.5 điểm) Cho (𝑷) 𝒚 = 𝟐𝒙𝟐 và (D): 𝒚 = 𝟑𝒙 − 𝟏
a) Vẽ (P) và (D) trên cùng một hệ trục tọa độ
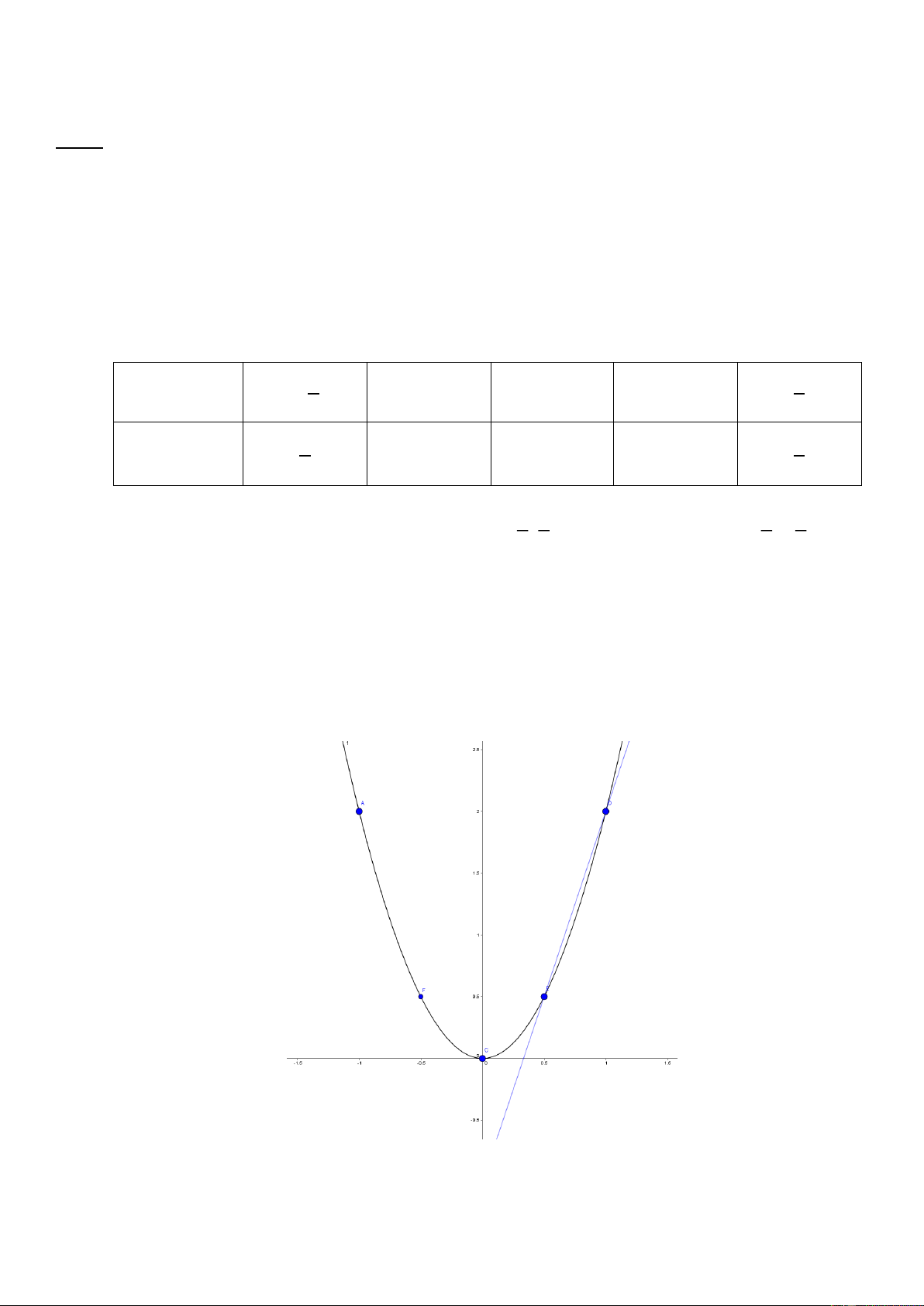
b) Tìm tọa độ giao điểm của (P) và (D) bằng phép tính. Lời giải a)
Hàm số (P): 𝒚 = 𝟐𝒙𝟐
Bảng giá trị tương ứng của x và y : 𝟏 𝟏 x − − 𝟏 𝟎 𝟏 𝟐 𝟐 𝟏 𝟏
(P): 𝒚 = 𝟐𝒙𝟐 𝟐 0 𝟐 𝟐 𝟐 1 1 1 1
Đồ thị hàm số là một Parabol đi qua các điểm ; ; 1
;2 ; 0;0 ; 1;2 ; ; 2 2 2 2
Hàm số (D): 𝒚 = 𝟑𝒙 − 𝟏
𝒙 = 𝟎 ⇒ 𝒚 = −𝟏
𝒙 = 𝟏 ⇒ 𝒚 = 𝟐
Đồ thị hàm số là đường thẳng đi qua 0; 1 và 2 ;1 .
Vẽ đồ thị hàm số (P) và (D) trên cùng một hệ trục tọa độ. b)
Hoành độ giao điểm của P và (D) là nghiệm của phương trình:
𝟐𝒙𝟐 = 𝟑𝒙 − 𝟏 ⇔ 𝟐𝒙𝟐 − 𝟑𝒙 + 𝟏 = 𝟎= 0 Trang - 9 - 1
∆ = (–3)2 – 4.2.1 = 1 > 0 Phương trình có hai nghiệm phân biệt: x = 1; x = . 1 2 2 + Với x = 1 𝒚 1 𝟏 = 2. 1 1 + Với x = 𝒚 . 2 𝟐 = 2 2 1 1
Vậy (D) cắt P tại hai điểm phân biệt là (𝟏; 𝟐) và ; . 2 2
Bài 2: (1.0 điểm) Cho phương trình 𝒙𝟐 − 𝟏𝟎𝒙 − 𝟖 = 𝟎 có hai nghiệm x , x . Không giải phương trình hãy 1 2
tính giá trị của biểu thức A = (𝒙 𝟐 𝟐
𝟏 − 𝒙𝟐)(𝒙𝟏 − 𝒙𝟐). Lời giải
A = x x 2 2 x x = 3 3
x x x x x x 1 2 1 2 1 2 1 2 1 2 2
= x x . x x
3x x x x x x 1 2 1 2 1 2 1 2 1 2 x x 10 1 2 1
Theo định lý Vi-et, ta có: { x .x 8 4 1 2 Do đó: A = 2 10. 1 0 3. 8 8 .10 = 1320.
Bài 3: (1.0 điểm) Các nhà khoa học về thống kê đã thiết lập được hàm số sau: A(t) = 𝟎, 𝟎𝟖𝒕 + 𝟏𝟗, 𝟕. Trong
đó A(t) là độ tuổi trung bình các phụ nữ kết hôn lần đầu của thế giới; t là số năm kết hôn, với gốc
thời gian là 1950. Hãy tính độ tuổi trung bình các phụ nữ kết hôn lần đầu lần lượt vào các năm 1950,
2000, 2018, 2020 (làm tròn đến chữ số thập phân thứ hai). Lời giải
Số năm kết hôn của các phụ nữ kết hôn lần đầu ở các năm 1950, 2000, 2018, 2020 so với gốc
thời gian 1950 lần lượt là: 0, 50, 68, 70 (năm).
Theo công thức tính độ tuổi trung bình các phụ nữ kết hôn lần đầu của thế giới, độ tuổi trung
bình của các phụ nữ kết hôn lần đầu vào năm 1950, 2000, 2018, 2020 lần lượt là (làm tròn đến chữ số thập phân thứ hai):
A(0) = 0,08.0 + 19,7 = 19,70 (tuổi).
A(50) = 0,08.50 + 19,7 = 23,70 (tuổi).
A(68) = 0,08.68 + 19,7 = 25,14 (tuổi).
A(70) = 0,08.70 + 19,7 = 25,30 (tuổi). Trang - 10 -
Bài 4: (1.0 điểm) Một trường học có tổng số giáo viên là 80 người, hiện tại tuổi trung bình của giáo viên là
35 tuổi. Trong đó, tuổi tuổi trung bình của giáo viên nữ là 32 tuổi và tuổi trung bình của giáo viên
nam là 38 tuổi. Hỏi 3 trường đó có bao nhiêu giáo viên nam, bao nhiêu giáo viên nữ? Lời giải
Tổng số tuổi của 80 giáo viên là: 80 . 35 = 2800 (tuổi).
Gọi x là số giáo viên nữ, suy ra tổng số tuổi của các giáo viên nữ là: 32x (tuổi).
Gọi y là số giáo viên nam, suy ra tổng số tuổi của các giáo viên nam là: 38y (tuổi).
Theo tổng số tuổi của 80 giáo viên gồm nam và nữ, ta có phương trình:
y 40 32x 38 y 2800 (1)
Theo tổng số giáo viên của trường học, ta có phương trình: x y 80 (2)
Từ (1), (2), ta tìm được: x 40; y 40 (giáo viên).
Bài 5: (1.0 điểm) Bé An sống trong gia đình ba thế hệ gồm ông bà nội, ba mẹ, bé An và em trai. Chủ nhật
vừa rồi cả gia đình đi xem phim. Biết giá vé cho trẻ em (vé của bé An và em trai) được giảm giá
50%; vé người cao tuổi được giảm giá 25% (vé của ông bà nội). Vé của ba mẹ không được giảm giá.
Ông nội bé An, người phải trả giá vé là 60 nghìn đồng, đang trả tiền cho mọi người. Hỏi ông nội
phải trả bao nhiêu tiền? Lời giải
Gọi x (nghìn đồng) là giá vé.
Ông nội được giảm giá vé 25% nên số tiền ông phải trả là: 0.75x.
Vì ông trả giá vé là 60 nghìn đồng, nên ta tính được giá vé là: 60 : 0.75 = 80 (nghìn đồng).
Gia đình bé An gồm có ông bà nội được giảm 25%, bé An và em được giảm 50%, ba mẹ không
được giảm, ta có phép tính tổng tiền vé là: 10.25
.210.5.210.2.80
= 360 (nghìn đồng).
Bài 6: (1.0 điểm) Theo năm Dương lịch, chu kỳ Trái Đất quay quanh Mặt Trời là 365 ngày và ngày (tức là
365,25 ngày). Khi đó, 1 ngày này sẽ được tích lũy trong vòng 4 năm nên theo năm Dương lịch thì 4
cứ 4 năm lại có 1 năm là năm nhuận vào các năm chia hết cho 4 (tháng 2 của năm này sẽ có 29 ngày
thay vì có 28 ngày như các năm không nhuận Dương lịch). Tuy nhiên, vẫn có một số ngoại lệ đối
với nguyên tắc trên vì có khi một năm Dương lịch lại ngắn hơn 365,25 ngày nên với những năm có
hai chữ số 0 ở cuối thì năm đó phải chia hết cho 400 mới là năm nhuận Dương lịch.
a) Từ năm 1900 đến năm 2000 có bao nhiêu năm nhuận Dương lịch? Vì sao? Trang - 11 -
b) Một nhà hộ sinh trong tháng 2 năm 2021 có 29 em bé chào đời là con của 29 gia đình khác nhau. Có
thể chắc chắn rằng có ít nhất 2 em bé chào đời cùng ngày hay không? Vì sao? Trang - 12 - Lời giải a)
Số năm có 2 chữ số 0 ở cuối là: 2000 1900 1 2 (năm) 100
Vậy 2 năm đó là 1900 và 2000. Theo điều kiện của đề bài, ta có 2000 ⋮ 400, suy ra có 1 năm
nhuận Dương lịch tận cùng là 2 chữ số 0. (1)
Số năm nhuận Dương lịch chia hết cho 4, không tính năm 1900, không tính năm 2000 là: 2000 1900 1 2 24 (năm) (2) 4
Từ (1), (2), suy ra số năm nhuận Dương lịch là 24 + 1 = 25 (năm). b)
Vì năm 2021 không chia hết cho 4 nên được tính là năm không nhuận Dương lịch, suy ra tháng 2 năm 2021 có 28 ngày.
Giả sử mỗi ngày có 1 em bé sinh ra trong nhà hộ sinh, cả tháng 2 năm 2021 sẽ có tổng cộng 28
em bé sinh ra tương ứng với số ngày.
Mà số liệu ghi nhận 29 em bé, nên sẽ có ít nhất 2 em bé chào đời cùng ngày.
Bài 7: (1.0 điểm) Thớt là một dụng cụ sử dụng trong bếp của mỗi gia đình để
thái, chặt, ... Một cái thớt hình trụ có đường kính đáy 22cm, cao 4cm.
a) Tính tổng diện tích hai mặt thớt (làm tròn đến cm2).
b) Cho biết loại gỗ làm thớt có khối lượng 500 kg/m3. Hỏi thớt nặng bao nhiêu gam? Lời giải a)
Diện tích một mặt thớt hình tròn là: 2
.R = 3.14 x 22 ≈ 69 (cm2)
Diện tích hai mặt thớt là: 69 . 2 ≈ 138 (cm2) b)
Thể tích của thớt hình trụ là:
V = Smặt đáy . h ≈ 69 . 4 ≈ 276 (cm3) ≈ 0.000276 (m3)
Khối lượng của thớt là:
m = Dgỗ x Vthớt ≈ 500 x 0.000276 ≈ 0.138 (kg) ≈ 138 (g) Trang - 13 -
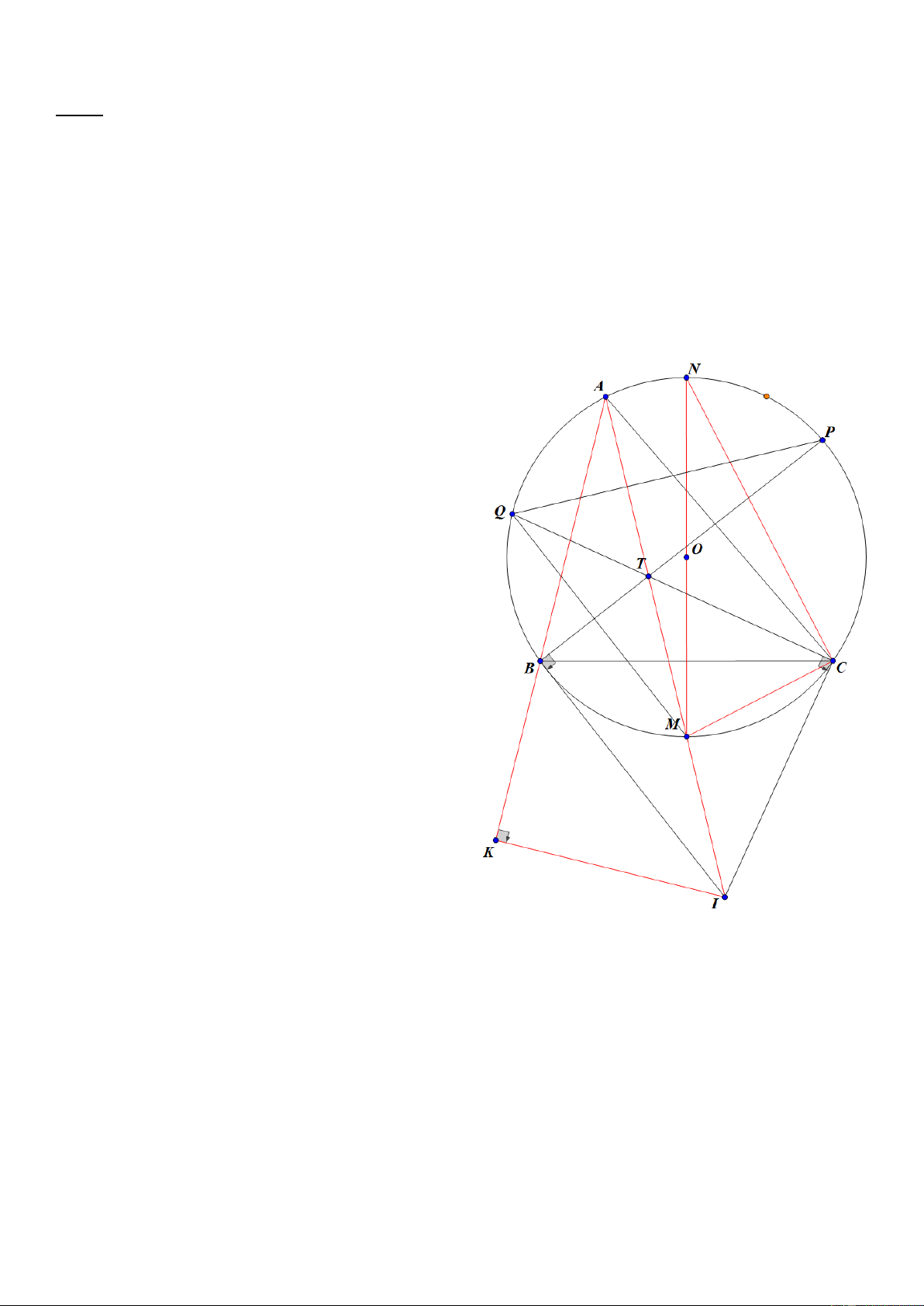
Bài 8: (3.0 điểm) Cho 𝜟𝑨𝑩𝑪 có 3 góc nhọn nội tiếp đường tròn (O; R). Gọi M, P, Q lần lượt là điểm chính
giữa các cung BC , CA , AB Gọi T là giao điểm của BP và CQ. Đường thẳng vuông góc với BP tại
B và đường thẳng vuông góc với CQ tại C cắt nhau ở I. Vẽ đường kính MN của (O). Gọi K là hình
chiếu của I trên AB.
a) Chứng minh: 𝜟𝑨𝑲𝑰 ~ 𝜟𝑵𝑪𝑴 và tứ giác BICT nội tiếp.
b) PQ cắt AC tại H, MQ cắt BC tại V. Chứng minh 3 điểm H, T, V thẳng hàng.
c) Gọi OI = d, IK = r. Chứng minh: 𝒅𝟐 = 𝑹𝟐 + 𝟐𝑹𝒓. Lời giải
a) Xét tứ giác BICT, có: 90o TBI (gt) 90o TCI (gt)
BICT nội tiếp.
Q nằm chính giữa AB
sđ AQ = sđ QB
ACQ QCB
CQ là phân giác góc C của 𝜟𝑨𝑩𝑪 (1)
P nằm chính giữa NC
sđ AP = sđ PC
ABP PBC
BP là phân giác góc B của 𝜟𝑨𝑩𝑪 (2)
M nằm chính giữa BC
sđ BM = sđ MC
BAM MAC
AM là phân giác góc A của 𝜟𝑨𝑩𝑪 (3)
Mà CQ BP = T (4)
Từ (1), (2), (3), (4), suy ra T tâm đường tròn nội tiếp 𝜟𝑨𝑩𝑪 và AM, CQ, BP đồng quy tại T.
Đồng nghĩa với A, T, M thẳng hàng. (5) Vì 90o TCI , ta có: 90o TCI MCI MCT (6) Xét MTC , có Trang - 14 - 1 MTC
(sđ QA + sđ MC ) 2
Mà QA QB và MC MB và QB BM QM 1 1
MTC = (sđ QB + sđ BM ) = sđ QM = MCQ = MCT (7) 2 2
𝜟𝑪𝑴𝑻 cân tại M 180o TMC
2MCT (góc ngoài của 𝜟 cân) (8) Từ (6), (7) suy ra: 90o MCI MTC (9)
Xét 𝜟𝑻𝑪𝑰 vuông tại C, có: 90o ITC TIC (10)
Từ (9), (10) suy ra TIC MCI
𝜟𝑪𝑴𝑰 cân tại M 180o IMC
2MCI (góc ngoài của 𝜟 cân) (11)
Từ (6), (8), (11) 180o TMC IMC
T, M, I thẳng hàng. (12)
Từ (5), (12), suy ra A, T, M, I thẳng hàng.
Xét 𝜟𝑨𝑲𝑰 và 𝜟𝑵𝑪𝑴, có: 90o AKI NCM
KAI CNM (2 góc chắn 2 cung bằng nhau, BN MC )
𝜟𝑨𝑲𝑰 𝜟𝑵𝑪𝑴 (g.g) b) CÁCH 1: 1 QTB =
(sđ QB + sđ CP ) 2
Mà QB QA và CP PA và QA PA QP 1
QTB = QBT = sđ QP 2
𝜟𝑩𝑸𝑻 cân tại Q
QB = QT (13)
Chứng minh tương tự với BTM , ta có: 1 BTM MBP sđ MP 2
𝜟𝑩𝑴𝑻 cân tại M Trang - 15 -
BM = MT (14)
Từ (13), (14) suy ra QM là đường trung trực của BT.
BV = VT (V = QM BC, V QM)
𝜟𝑩𝑽𝑻 cân tại V
VBT VTB mà BP là phân giác CBA
VTB TBA mà 2 góc này ở vị trí so le trong.
VT // AB. (15)
Chứng minh tương tự với 1
QTA MTC QAM sđ QM 2
Suy ra 𝜟𝑨𝑸𝑻 cân tại Q.
QA = QT (16)
Chứng minh tương tự với 1
ATP BTM MAP sđ MP 2
Suy ra 𝜟𝑨𝑷𝑻 cân tại P.
PA = PT (17)
Từ (16), (17) suy ra QP là đường trung trực AT, mà HAC
HA = HT và HTA TAB
Mà AM là phân giác BAC
HTA TAB
HT // AB. (18)
Từ (15), (18), theo tiên đề Ơ-clit:
H, V, T thẳng hàng. b) CÁCH 2:
Xét tứ giác TCPH có: 1 1 CTP CHP
. (sđ QB + sđ PC ) =
. (sđ QA + sđ PC ) (do QA QB ) 2 2
TCPH là tứ giác nội tiếp. 180o HTC HPC (13)
Xét tứ giác VTCM có: 1 1 MVC MTC
. (sđ QB + sđ MC ) =
. (sđ QA + sđ MC ) (do QA QB ) 2 2
VTCM là tứ giác nội tiếp. 180o VTC VMC (14) Trang - 16 -
Xét tứ giác MQPC nội tiếp (O) , có: 180o QMC QPC (15)
V QM và H QP Từ (13), (14), (15) suy ra 180o VTC HTC
H, T, V thẳng hàng. c) Ta có:
𝜟𝑻𝑴𝑪 cân tại M (cmt)
𝜟𝑪𝑴𝑰 cân tại M (cmt)
MT = MC = MI
𝜟𝑨𝑲𝑰 𝜟𝑵𝑪𝑴 (cmt) IK IA
IK.MN I . A MC I .
A MC 2Rr MC MN I .
A IM 2Rr (do MC = MI)
Gọi K, S lần lượt là giao điểm của IO và (O)
Xét 𝜟𝑰𝑴𝑲 và 𝜟𝑰𝑺𝑨, có: AIS chung
IKM IAS (do tứ giác MKSA nội tiếp (O) ) IM IK IS IA 2 2 I .
A IM IK.IS (IO OK ).(IO OS) d R Mà I .
A IM 2Rr 2 2
d R 2Rr
SỞ GD & ĐT TP.HỒ CHÍ MINH
ĐỀ THAM KHẢO TUYỂN SINH 10
PHÒNG GD & ĐT QUẬN 3 NĂM HỌC 2022-2023
ĐỀ THAM KHẢO MÔN : TOÁN 9
-------------------- Đề thi gồm 8 câu hỏi tự luận
MÃ ĐỀ : Quận 3 – 3 Thời gian: 120 phút (không kể thời gian phát đề) Bài 1: Cho 2
(P) : y x và đường thẳng (d ) : y 3x 4 .
a) Vẽ (P) và (d ) trên cùng mặt phẳng tọa độ.
b) Tìm tọa độ giao điểm của (P) và (d ) bằng phép tính. Trang - 17 -
Bài 2: Cho phương trình 2 2x 5x 3
có hai nghiệm x , x . Không giải phương trình hãy tính giá trị của 1 2
biểu thức A x 3x x 3x . 1 2 2 1
Bài 3: Tổng điều tra dân số và nhà ở năm 2019 được tiến hành vào thời điểm 0 giờ ngày 1/4/2019 theo
Quyết định số 772/QD-TTg ngày 26/6/2018 của Thủ tướng Chính phủ. Đây là cuộc Tổng điều tra
dân số và nhà ở lần thứ năm ở Việt Nam kể từ khi đất nước thống nhất vào năm 1975. Theo kết quả
của cuộc tổng điều tra nói trên, tổng dân số của Việt Nam là 96.208.984 người, trong đó nam ít hơn
nữ là 446.862 người và dân tộc Kinh chiếm 85,3% dân số cả nước.
a) Dân tộc Kinh có bao nhiêu người (làm tròn đến hàng đơn vị)?
b) Tính số nam và số nữ của Việt Nam.
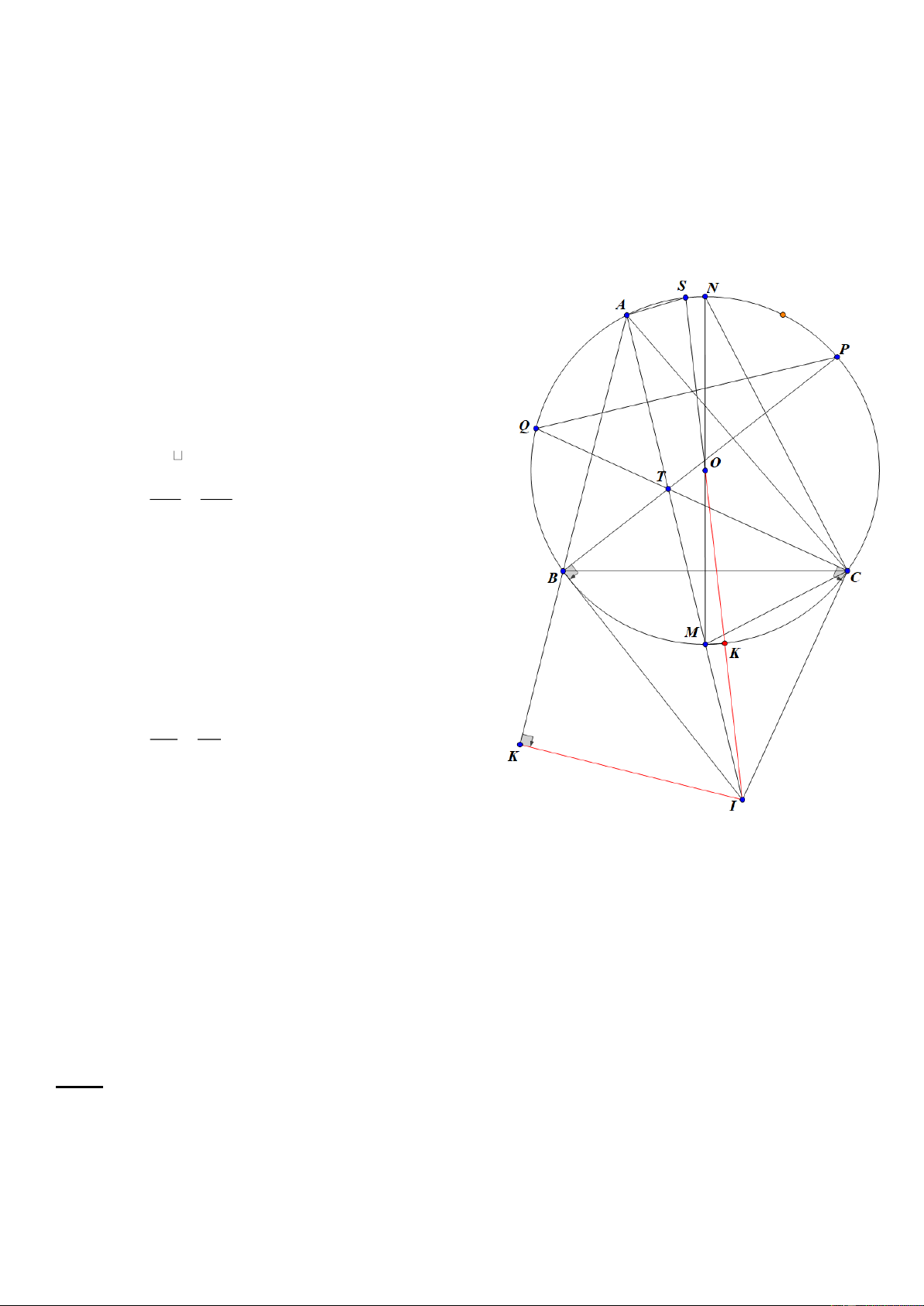
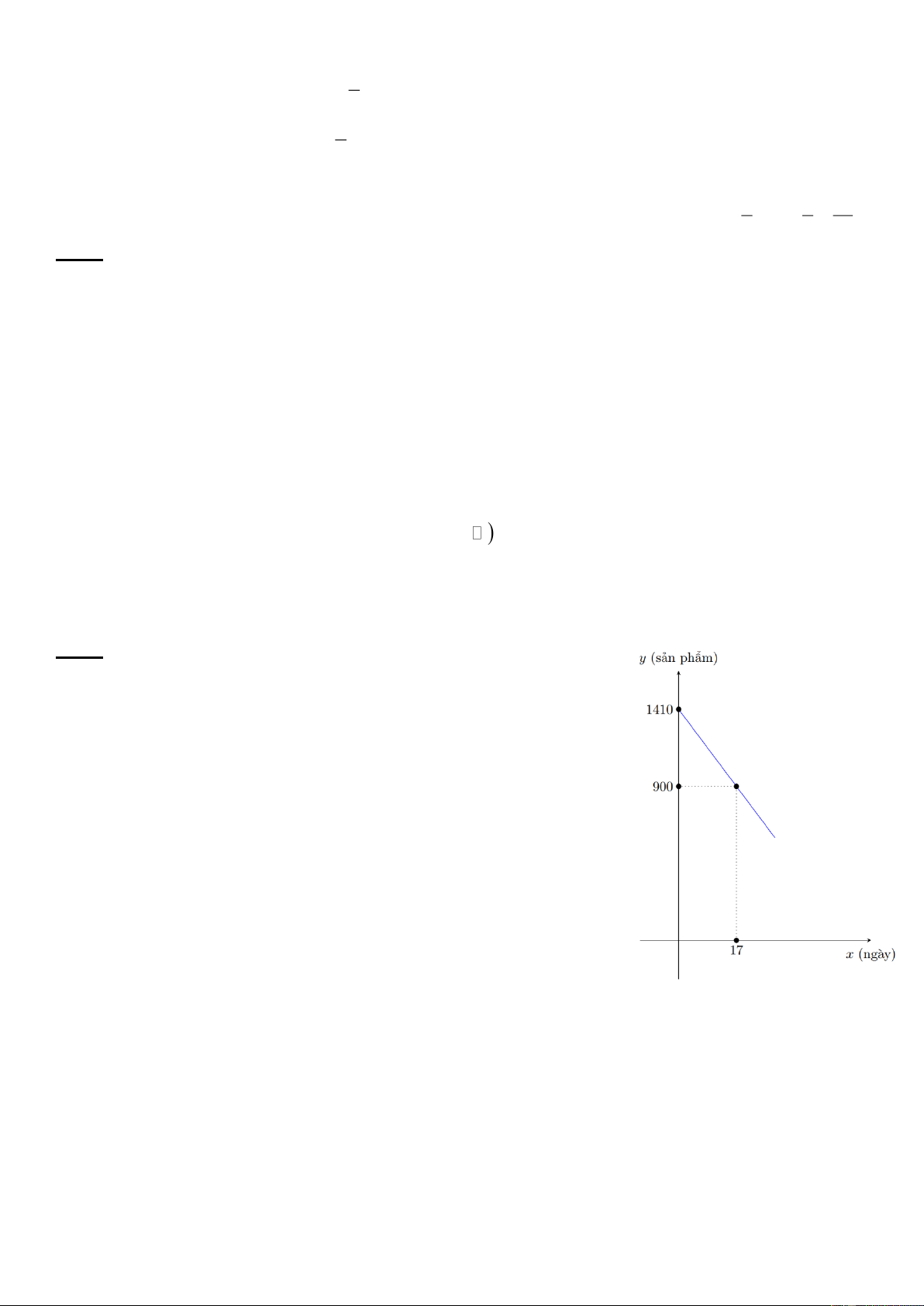
Bài 4: Một xí nghiệp cần bán thanh lý b sản phẩm. Số sản phẩm y
còn lại sau x ngày bán được xác định bởi hàm số: y ax b có đồ thị như bên
a) Hãy dựa vào đồ thị hãy xác định a, b và hàm số y .
b) Xí nghiệp cần bao nhiêu ngày để bán hết số sản phẩm cần thanh lý?
Bài 5: Các bạn học sinh của lớp 9A dự định đóng góp một số tiền để mua tặng cho mỗi em ở Mái ấm tình
thương ba món quà (giá tiền các món quà đều như nhau). Khi các bạn đóng đủ số tiền như dự trù thì
Mái ấm đã nhận chăm sóc thêm 9 em và giá tiền mỗi món quà lại tăng thêm 5% nên số tiền có được
vừa đủ để tặng mỗi em hai món quà. Hỏi có bao nhiêu em ở Mái ấm lúc tặng quà?
Bài 6: Coi cả Trái Đất và Mặt Trăng đều có dạng hình cầu và biết bán
kính của Trái Đất là khoảng 6371 km, bán kính của mặt trăng là khoảng 1737 km.
a) Hãy tính diện tích bề mặt của Trái Đất và diện tích bề mặt của Mặt Trăng.
b) Biết 70,8% diện tích bề mặt Trái Đất là nước. Hãy tính phần
diện tích này? (Làm tròn kết quả đến hàng triệu)
Bài 7: Giá của một mặt hàng là 800.000 đồng. Nếu bán mặt hàng này với giá bằng một nửa giá niêm yết
thì lợi nhuận là 20% . Hỏi phải bán với giá bao nhiêu thì được lợi nhuận 60% ?
Bài 8: Cho tam giác ABC nhọn ( AB AC) nội tiếp đường tròn tâm O có ba đường cao AD, BE, CF cắt nhau tại H .
a) Chứng minh AEHF và ABDE là các tứ giác nội tiếp. Trang - 18 -
b) Đường thẳng EF cắt đường tròn (O) tại các điểm M , N ( M thuộc cung nhỏ AB ). Kẻ đường kính
AK của đường tròn O . Chứng minh tia EB là tia phân giác của góc DEF và K MN cân.
c) Đường trung trực của CE cắt MK tại Q . Chứng minh MA là tiếp tuyến của (MEC) và OQ vuông góc với MC . Trang - 19 - HƯỚNG DẪN GIẢI Bài 1: Cho 2
(P) : y x và đường thẳng (d ) : y 3x 4 .
a) Vẽ (P) và (d ) trên cùng mặt phẳng tọa độ.
b) Tìm tọa độ giao điểm của (P) và (d ) bằng phép tính. Lời giải a) Hàm số: 2 y x
Bảng giá trị tương ứng của x và y : x 2 1 0 1 2 2 y x 4 1 0 1 4
Đồ thị hàm số là một Parabol đi qua các điểm 2 ; 4 ; 1 ; 1 ; 0;0 ; 1; 1 ; 2; 4 .
Hàm số: y 3x 4 x 0 1 y 3x 4 4 1
Đồ thị hàm số là đường thẳng đi qua 0; 4 và 1; 1 . Vẽ:
b) Hoành độ giao điểm của P và D là nghiệm của phương trình: x 1 2 2
x 3x 4 x 3x 4 0 x 4
+ Với x 1 y 1 1 1
+ Với x 4 y 16 2 2
Vậy D cắt P tại hai điểm phân biệt là 1; 1 và 4 ; 1 6.
Bài 2: Cho phương trình 2 2x 5x 3
có hai nghiệm x , x . Không giải phương trình hãy tính giá trị của 1 2
biểu thức A x 3x x 3x . 1 2 2 1 Lời giải Ta có: 2 2 2x 5x 3
2x 5x 3 0. 2 5
4.2.3 1 0 Phương trình có hai nghiệm phân biệt. Trang - 20 - 5 x x 1 2 Theo đị 2 nh lí Vi-et: . 3 x .x 1 2 2 Khi đó:
A x 3x x 3x 10x x 3 x x 10P 3S 2P 2 5 3 99 2 2 2 2
3S 4P 3. 4. . 1 2 2 1 1 2 1 2 2 2 4
Bài 3: Tổng điều tra dân số và nhà ở năm 2019 được tiến hành vào thời điểm 0 giờ ngày 1/4/2019 theo
Quyết định số 772/QD-TTg ngày 26/6/2018 của Thủ tướng Chính phủ. Đây là cuộc Tổng điều tra
dân số và nhà ở lần thứ năm ở Việt Nam kể từ khi đất nước thống nhất vào năm 1975. Theo kết quả
của cuộc tổng điều tra nói trên, tổng dân số của Việt Nam là 96.208.984 người, trong đó nam ít hơn
nữ là 446.862 người và dân tộc Kinh chiếm 85,3% dân số cả nước.
a) Dân tộc Kinh có bao nhiêu người (làm tròn đến hàng đơn vị)?
b) Tính số nam và số nữ của Việt Nam. Lời giải
a) Số người dân tộc Kinh là: 96208984.85.3% 82066263 người.
b) Gọi số nam và số nữ lần lượt là x và y , x y .
x y 96208984 x 47881061
Ta có hệ phương trình: .
x y 446862 y 48327923
Vậy số nam là 47881061 và số nữ là 48327923.
Bài 4: Một xí nghiệp cần bán thanh lý b sản phẩm. Số sản phẩm y còn
lại sau x ngày bán được xác định bởi hàm số: y ax b có đồ thị như bên
a) Hãy dựa vào đồ thị hãy xác định a, b và hàm số y .
b) Xí nghiệp cần bao nhiêu ngày để bán hết số sản phẩm cần thanh lý? Lời giải
a) Nhìn vào hình ta có đồ thị hàm số y ax b đi qua hai điểm 0;1410 và 17;900 .
Thay 0;1400 vào y ax b 1410 0.a b
Thay (17; 900) vào y = ax +b 900 = 17a +b 14
10 0.a b
0.a b 1410 a 30 Ta có hệ pt: 90
0 17a b 17 a b . 900 b 1410 Vậy y 3 0x 1410 . Trang - 21 -
b) Số ngày xí nghiệp bán hết số sản phẩm cần thanh lý: 0 3
0x 1410 x 47
Vậy số ngày xí nghiệp bán hết số sản phẩm cần thanh lý là 47 ngày.
Bài 5: Các bạn học sinh của lớp 9A dự định đóng góp một số tiền để mua tặng cho mỗi em ở Mái ấm tình
thương ba món quà (giá tiền các món quà đều như nhau). Khi các bạn đóng đủ số tiền như dự trù thì
Mái ấm đã nhận chăm sóc thêm 9 em và giá tiền mỗi món quà lại tăng thêm 5% nên số tiền có được
vừa đủ để tặng mỗi em hai món quà. Hỏi có bao nhiêu em ở Mái ấm lúc tặng quà? Lời giải
Gọi x là số em ở mái ấm lúc chưa có thêm 9 em x .
Gọi a là giá tiền một món quà lúc chưa tăng giá. Ta có phương trình: .
x 3.a x 9.2. .
a 1 5% x 21
Vậy có 21 em ở Mái ấm lúc tặng quà.
Bài 6: Coi cả Trái Đất và Mặt Trăng đều có dạng hình cầu và biết bán
kính của Trái Đất là khoảng 6371 km, bán kính của mặt trăng là khoảng 1737 km.
a) Hãy tính diện tích bề mặt của Trái Đất và diện tích bề mặt của Mặt Trăng.
b) Biết 70,8% diện tích bề mặt Trái Đất là nước. Hãy tính phần
diện tích này? (Làm tròn kết quả đến hàng triệu) Lời giải
a) Diện tích bề mặt của Trái Đất: 2 2
S R 2 4 4 .6371 510000000 km
Diện tích bề mặt của Mặt Trăng: 2 2
S R 2 4 4 .1737 38000000 km
b) Diện tích nước bao phủ bề mặt Trái Đất là: 2 510000000.70,8% 361000000 km
Bài 7: Giá của một mặt hàng là 800.000 đồng. Nếu bán mặt hàng này với giá bằng một nửa giá niêm yết
thì lợi nhuận là 20% . Hỏi phải bán với giá bao nhiêu thì được lợi nhuận 60% ? Lời giải
Giá gốc của mặt hàng đó: 800000 : 2.1– 20% 320000 (đồng).
Giá bán lần sau: 320000.1 60% 512000 (đồng).
Bài 8: Cho tam giác ABC nhọn ( AB AC) nội tiếp đường tròn tâm O có ba đường cao AD, BE, CF cắt nhau tại H .
a) Chứng minh AEHF và ABDE là các tứ giác nội tiếp. Trang - 22 -
b) Đường thẳng EF cắt đường tròn (O) tại các điểm M , N ( M thuộc cung nhỏ AB ). Kẻ đường kính
AK của đường tròn O . Chứng minh tia EB là tia phân giác của góc DEF và K MN cân.
c) Đường trung trực của CE cắt MK tại Q . Chứng minh MA là tiếp tuyến của (MEC) và OQ vuông góc với MC . Lời giải A N E F M O H B D C Q K
a) Xét tứ giác AEHF có o
AFH AEH 90 ( BE và CF là các đường cao) o
AFH AEH 180
Tứ giác AEHF nội tiếp đường tròn đường kính AH .
Xét tứ giác ABDE có o
ADB AEB 90 ( AD và BE là các đường cao)
Tứ giác ABDE nội tiếp đường tròn đường kính AB .
b) Tứ giác AFHE nội tiếp FAH FEH 1 .
Tứ giác ABDE nội tiếp FAH BED 2. Từ
1 và 2 FEH BED hay EB là tia phân giác của góc DEF .
Xét tứ giác BFEC có o
BEC BEC 90
Tứ giác BFEC nội tiếp đường tròn đường kính BC .
AFE ACB 1 1
sđ AN sđ BM đ s AM đ s MB 2 2 AN AM
AK MN tại trung điểm của MN
AK là đường trung trực của MN
KM KN hay K
MN cân tại K 1
c) Ta có: AN AM AME ACM sđ E M 2
ME là dây của đường tròn MEC MA là tiếp tuyến của MEC . o
AMK 90 AM MA tại M Trang - 23 -
Tâm đường tròn (MEC) thuộc MK
mà Q là giao điểm MK và đường trung trực của EC
Q là tâm đường tròn (MEC) QM = QC
mà OM = OC (= bk(O)) OQ là đường trung trực MC Vậy OQ MC. Trang - 24 -




