Đề thi chọn học sinh giỏi cấp tỉnh Toán 12 năm 2018 – 2019 sở GD và ĐT Quảng Ngãi

SỞ GIÁO DỤC VÀ ĐÀO TẠO KỲ THI CHỌN HỌC SINH GIỎI CẤP TỈNH QUẢNG NGÃI
LỚP 12 NĂM HỌC 2018-2019 Ngày thi: 18/10/2018 Đ Ề C H Í N H T H Ứ C Môn thi: TOÁN
Thời gian làm bài: 180 phút
Câu 1 (5,0 điểm). 2
2 3 sin x  3 cos x  2sin x
a) Giải phương trình  cos x .
(1 2 cos x) tan x  2  2x y  7 
 3x  2  x 3xy   5
b) Giải hệ phương trình  . 2 2 2
 x (4  y ) 1  1 4x  xy 
Câu 2 (3,0 điểm). 2x 1 Cho hàm số y 
có đồ thị (C). Chứng minh rằng với mọi m đường thẳng x  1
y  2x  m luôn cắt đồ thị (C) tại hai điểm phân biệt A và B . Gọi k , k lần lượt là hệ 1 2
số góc của các tiếp tuyến với (C) tại A và B. Tìm m để biểu thức P  k 2019  k 2019 1 2
đạt giá trị nhỏ nhất.
Câu 3 (3,0 điểm).
a) Cho n là số nguyên dương thỏa mãn n 1  n C  C
 7 n  3 . Tìm hệ số của số hạng n4 n3   n  3  chứa 4
x trong khai triển nhị thức Niu-tơn 2 2x   , x  0. 3   x 
b) Có hai chiếc hộp chứa bi, mỗi viên bi chỉ mang màu xanh hoặc màu đỏ. Lấy ngẫu
nhiên từ mỗi hộp đúng 1 viên bi. Biết tổng số bi trong hai hộp là 20 và xác suất để lấy 55
được 2 viên bi màu xanh là
. Tính xác suất để lấy được 2 viên bi màu đỏ. 84
Câu 4 (4,0 điểm).
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A , tam giác SAB đều và
nằm trong mặt phẳng vuông góc với đáy. Biết AB  7a, BC  7 3a , E là điểm trên
cạnh SC và EC  2ES .
a) Tính thể tích khối chóp E.ABC .
b) Tính khoảng cách giữa hai đường thẳng AC và BE .
Câu 5 (3,0 điểm).
Trong mặt phẳng với hệ tọa độ Oxy , cho hình vuông ABCD và điểm E thuộc cạnh
BC . Đường thẳng qua A và vuông góc với AE cắt CD tại F . Gọi M là trung điểm
EF , đường thẳng AM cắt CD tại K . Tìm tọa độ điểm D biết A 6  ; 6, M  4  ; 2, K  3
 ; 0 và E có tung độ dương.
Câu 6 (2,0 điểm).
Cho các số thực không âm , a ,
b c thỏa c  ,
a c  b . Tìm giá trị nhỏ nhất của biểu thức 2 2 2
 2a  c   2b  c  64 8(a 1)  2
P  (a  b)          . 2 2 2 2 2
 b  c   a  c 
ab  bc  ca
a(a  b)  
--------------------------------Hết--------------------------------
Ghi chú: Cán bộ coi thi không giải thích gì thêm.
SỞ GD-ĐT QUẢNG NGÃI
ĐÁP ÁN - THANG ĐIỂM ĐỀ CHÍNH THỨC
THI CHỌN HỌC SINH GIỎI CẤP TỈNH Môn: TOÁN-Lớp 12
(Đáp án – Thang điểm gồm 5 trang) CÂU NỘI DUNG ĐIỂM Câu 1 2
2 3 sin x  3 cos x  2sin x
a) (2,0đ). Giải phương trình  cos x . (5,0đ)
(1 2 cos x) tan x  1 cos x   2 0,5 
+)Điều kiện cos x  0 . tan x  0  
 3 sin x  cos x  0 (1)
Với điều kiện trên Pt   0,5 2 sin x  3  0 (2)   +) (1)  x  
 k , k   0,5 6   x   k 2  +) 3 (2)   , k   . 2 x   k 2  3
Kết hợp điều kiện, suy ra nghiệm của phương trình là   x    k  6 0,5   , k   . 2  x   k 2  3
b) (3,0đ). Giải hệ phương trình 2
(2x y  7)( 3x  2  x  3xy )  5 (1)   . 2 2 2
 x (4  y ) 1  1 4x  xy (2)   2 x  +) ĐK:  3 .
x  3xy  0  0,5 1 1 +) Từ 2 (2) 
4  y  y  4   (2 ') 2 x x 0,5   2   t 2 Xét hàm số 2 f (t) 
4  t  t, t  ;   
  ta có f '(t)  1  0, t   .   3   2 3 4  t  2 1 0,5 Suy ra 
f (t) đồng biến trên ;  
 . Do đó (2 ')  y  .  3  x 1 Thay y 
vào (1) ta được (2x  7)( 3x  2  x  3)  5 (3) x 0,5 7 5 x 
không là nghiệm nên (3)  g(x)  3x  2  x  3  . 2 2x  7 3 1 10 2 7
Ta có: (3)  g '(x)     0, x   , x  2 2 3x  2 2 x  3 (2x  7) 3 2 0,5  2 7  7
Suy ra g(x) đồng biến trên   ;   và ;     3 2   2 
Mà g(1)  g(6)  0 nên (3) có 2 nghiệm là 1 và 6. 1 0,5
Vậy nghiệm (x;y) của hệ là (1;1), (6; ) . 6 Câu 2 2x 1
Cho hàm số y 
có đồ thị (C). Chứng minh rằng với mọi m đường (3,0đ) x  1
thẳng y  2x  m luôn cắt đồ thị (C) tại hai điểm phân biệt A và B . Gọi
k , k lần lượt là hệ số góc của các tiếp tuyến với (C) tại A và B. Tìm m để 1 2 2019 2019
biểu thức P  k  k
đạt giá trị nhỏ nhất. 1   2  2x 1
+) Phương trình hoành độ giao điểm:
 2x  m ( x  1 ) x 1 0,5 2
 2x  4  m x 1 m  0 (1) Ta có 2
  m  8  0 , m  và x  1
 không là nghiệm của pt(1). 0,5
Vậy đường thẳng y  2x  m và (C) luôn cắt nhau tại hai điểm phân biệt với mọi m.
+) A x ;2x  m , B x ; 2
 x  m . Trong đó x , x là nghiệm phương trình (1). 1 1   2 2  1 2 0,5 1 1 k  , k  1  x  2 2 1  x  2 1 1 2 1 1 1 +) k .k  .   4 1 2  x  2 1  x  2 1
 x  x  x .x  2 1 0,5 1 2 1 2 1 2
P  k 2019  k 2019  2 k .k 2019 2019 2020  2 4  2 . 0,5 1 2 1 2 1 1
 x  x (loai) 0,5 Vậy 2020 P  2 khi k  k   1 2   m  0 . min 1 2   x  2 1  x  2 1 x  x  2 1 2  1 2
Câu 3 a)Cho n là số nguyên dương thỏa mãn n 1  n C  C
 7 n  3 . Tìm hệ số của số 2,0đ n4 n3   (3,0đ) n  3  hạng chứa 4
x trong khai triển nhị thức Niu-tơn 2 2x   , x  0. 3   x 
(n  3)(n  2) n 1  n C  C  7 n  3   7 n  3 n4 n3   2 0,5  n  12 . 12 12  3 Với  k n  12 , 2 k 12 2x   C 2 k 3  k  x   3    24 5 12 0,5  x  k 0 Số hạng chứa 4
x ứng với 24  5k  4  k  4 . 0,5
Vậy hệ số của số hạng chứa 4 x là: 4 8 4 C .2 .3 . 0,5 12
b)Có 2 hộp đựng bi, mỗi viên bi chỉ mang màu xanh hoặc màu đỏ. Lấy
ngẫu nhiên từ mỗi hộp đúng 1 viên bi. Biết tổng số bi trong 2 hộp là 20 0,5 55
và xác suất để lấy được 2 viên bi xanh là
. Tính xác suất để lấy 84 được 2 viên bi đỏ
+) Giả sử hộp thứ nhất có x viên bi , trong đó có a bi xanh, hộp thứ hai có y viên bi
trong đó có b bi xanh (điều kiện: x, y, a,b nguyên dương, x  y, x  a, y  b ). 0,25
x  y  20 (1) 
Từ giả thiết ta có : ab 55  (2)  xy 84  1
+)Từ (2)  55xy  84ab  xy84 , mặt khác : 2 xy 
(x  y)  100  xy  84 (3) 4 0,25 x  14 Từ (1) và (3) suy ra  . y  6  0,25
+)Từ (2) và (3) suy ra ab  55 , mà a  x  14,b  y  6  a  11,b  5 . 0,25
x  a y  b 1
Vậy xác suất để lấy được 2 bi đỏ là P  .  . x y 28
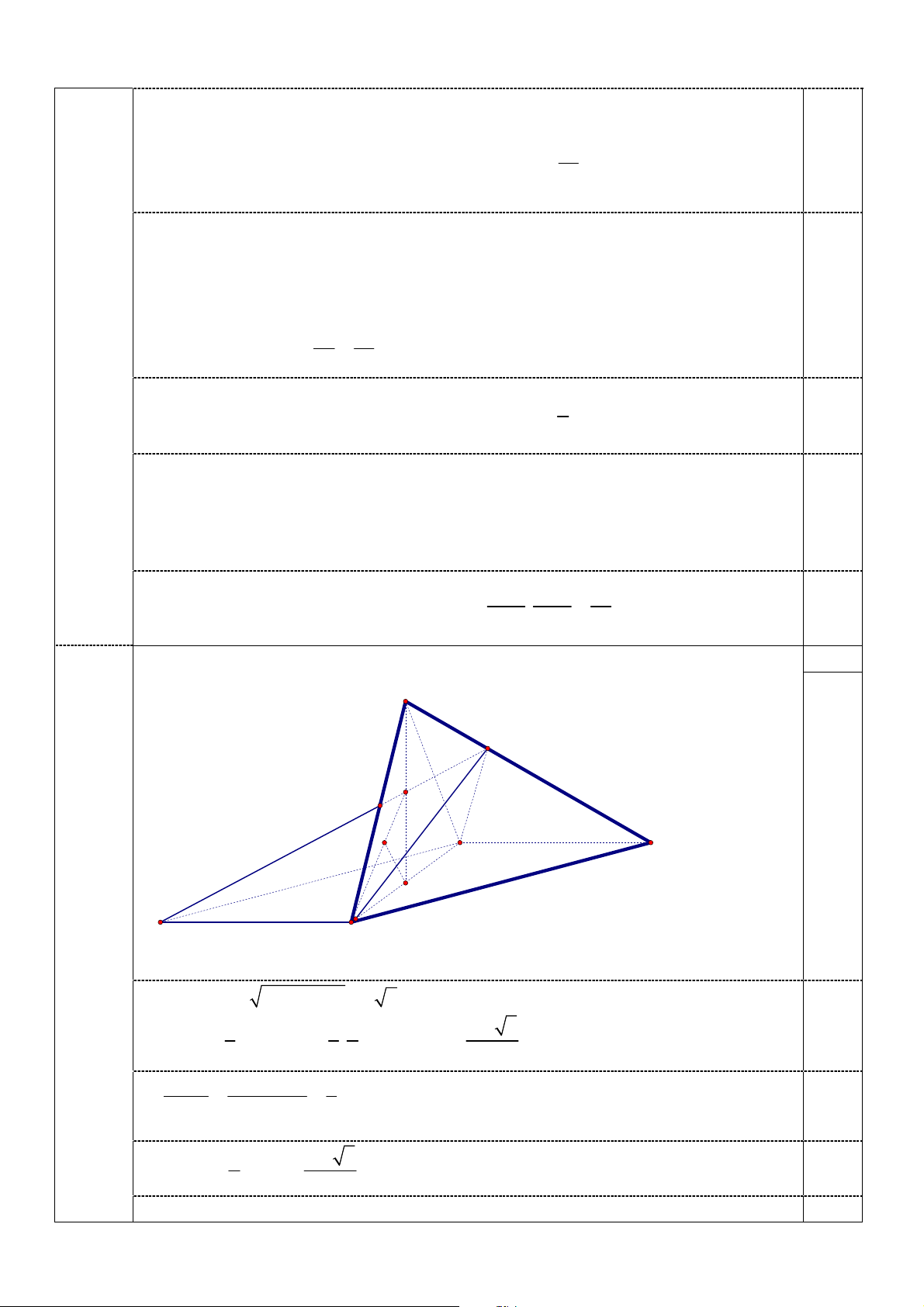
Câu 4 a) (2,0đ). Tính thể tích khối chóp E.ABC . (4,0đ) S E I 0,5 A C K H D B
Gọi H là trung điểm AB, vì A
 BC đều và (SAB)  ( ABC) suy ra SH  ( ABC) Ta có : 2 2 AC 
BC  AB  7 2a . 0,5 1 1 1 343 6 +) 3 V  .S .SH  . .A . B AC.SH  a . S . ABC 3 A  BC 3 2 12 V S . A S . B SE 1 +) S.ABE   . V S . A SB.SC 3 0,5 S . ABC 2 343 6 3  V  V  a E.ABC S . 3 ABC 18 0,5
b) (2,0đ) +) Tính khoảng cách giữa AC và BE.
Lấy điểm D sao cho ACBD là hình bình hành
Vì BD / / AC nên d(AC, BE)  d( AC,(BDE))  d( ,
A (BDE))  2 d(H , (BDE)) . 0,5
+) Gọi I  SH  DE , (BDE)  (SAB) theo giao tuyến BI.
Kẻ HK  BI , (K  BI )  HK  (BDE)  d(H , (BDE))  HK . 0,5 1 7 3
 HI  SH  a . 2 4 0,5
Trong tam giác BHI vuông tại H có HK  BI , suy ra 1 1 1 21 0,5    HK  a . 2 2 2 HK HB HI 2
Vậy d( AC, BE)  21a .
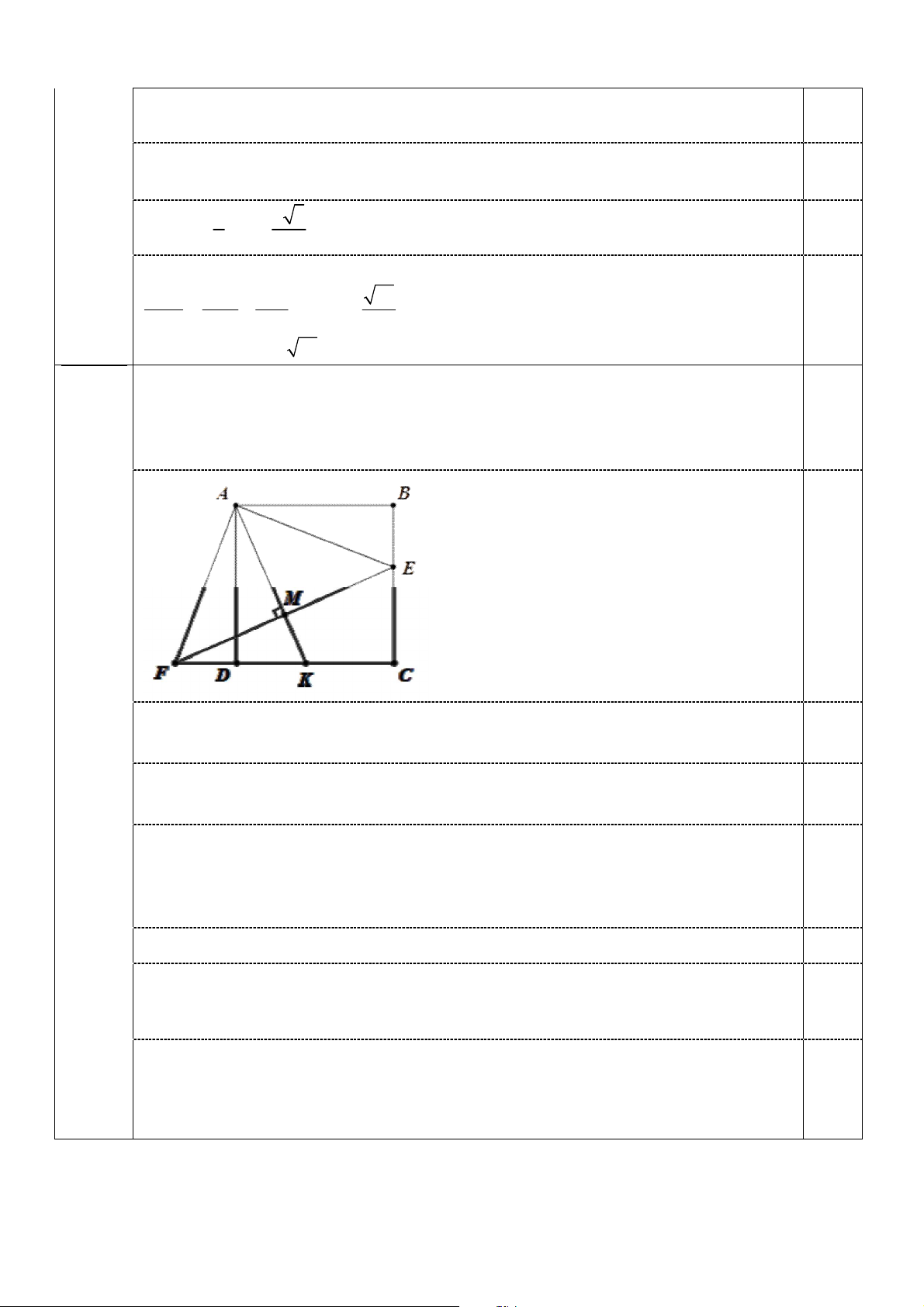
Câu 5 Trong mặt phẳng với hệ tọa độ Oxy , cho hình vuông ABCD và điểm E
(3,0đ) thuộc cạnh BC . Đường thẳng qua A và vuông góc với AE cắt CD tại F .
Gọi M là trung điểm EF , đường thẳng AM cắt CD tại K . Tìm tọa độ điểm
D biết A 6
 ; 6, M 4; 2, K  3
 ; 0 và E có tung độ dương.
Ta có ΔABE = ΔADF vì AB = AD và  
BAE  DAF (cùng phụ với  DAE ).
Suy ra ΔAEF vuông cân và  AM  EF và ME  MA  MF . 0,5
Đường thẳng EF đi qua M và vuông góc với MA nên có phương trình 0,5
x  2 y  8  0 .
+) Phương trình đường tròn ngoại tiếp tam giác AFE:  x  2   y  2 4 2  20  
 x  2   y  2 4 2  20
+) Tọa độ điểm E, F thỏa hệ  0,5
x  2 y  8  0 
Giải hệ ta được tọa độ E 0; 4 , F  8
 ;0 , ( y  0 ). 0,5 E
Với E 0; 4 , F  8  ;0
Đường thẳng CD qua F  8  ;0 và K  3
 ; 0 nên có phương trình y  0 . 0,5
Đường thẳng AD qua A 6
 ;6 và vuông góc với FK nên có phương trình 0,5 x  6  0 .
D  CD  AD  D  6  , 0 .
Câu 6 Cho các số thực không âm , a ,
b c thỏa c  ,
a c  b . Tìm giá trị nhỏ nhất
(2,0đ) của biểu thức 2 2 2
 2a  c   2b  c  64 8(a 1)  2
P  (a  b)          . 2 2 2 2 2
 b  c   a  c 
ab  bc  ca
a(a  b)   1 1 1 1 1 1 +)Ta có  ;  ,  2 2 2 2 2 2 (a  c ) c  c c
ab  bc  ca c c 4 (b ) 4 (a  ) (b )
(a  ).(b  ) 2 2 a a 0,5  c 2 c 2  4(a  ) 4(b  )  64  1 +) Suy ra: 2 2 2
P  (a  b)    8(a  )  c  4 c 4 c c a  (b  ) (a  )
(a  )(b  )  0,25  2 2 2 2  c c
+) Đặt a   x, b  y, (x  0, y  0). Ta có 2 2 2 2  x y 64  1 1 0,25 2
P  (x  y) 4  4  16   4 4  y x xy 2 2 2   (a  c ) c 4 (a  ) 2 3 x y  x y x y        Hay P  4   2    3  16 16       . y x y x y x          x y +)Đặt t   , (t  2) . Xét hàm số 3
f (t)  4(t  2)(t  3t 16) , y x 5 0,5 Ta có: 3 2
f '(t)  4(4t  6t  6t 10) , f '(t)  0  t  . 2 63
Lập bảng biến thiên, suy ra f (t)   . 4 a  1 0,5 a  1  1 1   1
Suy ra P   và P    b  2 hoặc b   4 4  2 c  0   c  0  1 Vậy P   . min 4 Chú ý:
1. Mọi lời giải đúng, khác với hướng dẫn chấm, đều cho điểm tối đa theo từng
câu và từng phần tương ứng.
2. Tổ chấm thảo luận để thống nhất các tình huống làm bài có thể xảy ra của học sinh.
Document Outline

• MTBlankEqn