Đề thi chọn học sinh giỏi cấp tỉnh Toán THPT năm 2018 – 2019 sở GD&ĐT Lào Cai

SỞ GIÁO DỤC VÀ ĐÀO TẠO LÀO CAI
ĐỀ THI CHỌN HỌC SINH GIỎI CẤP TỈNH ĐỀ CHÍNH THỨC
NĂM HỌC 2018 – 2019
Môn: Toán - THPT
Thời gian: 180 phút (Không kể thời gian phát đề) Câu 1. (5,0 điểm). 
 173x 5 x 3y 14 4 y  0
a) Giải hệ phương trình  ,  , x y   . 2
2 2x  y  5  3 3x  2y 11  x  6x 13 
b) Cho a, b, c là các số thực dương. Tìm giá trị nhỏ nhất của biểu thức 2 2 2 a  bc b  ca c  ab 4 P   
 4 a  b  c b  c c  a a  . b Câu 2. (4,0 điểm). 2018   x x 1
a) Cho hàm số y  f  x có đạo hàm f  x   x  3 2 e  e    2
x  2x. Tìm tất cả các  3 
giá trị thực của m để hàm số f  2
x  8x  m có đúng 3 điểm cực trị sao cho 2 2 2
x  x  x  50 , trong đó x , x , x là hoành độ của ba cực trị đó. 1 2 3 1 2 3  1 u  , u  3  1 2  2 b) Cho dãy số u xác định như sau:  . n  u .u 1 n 1  n u   , n   1 n2  u  u  n 1  n
Chứng minh rằng u
có giới hạn hữu hạn và tìm giới hạn đó. n  Câu 3. (3,0 điểm).
a) Trong mặt phẳng với hệ tọa độ Oxy cho hình thang vuông ABCD vuông tại A và D , có
CD  2AD  2AB . Gọi M 2; 4 là điểm thuộc cạnh AB sao cho AB  3AM . Điểm N thuộc
cạnh BC sao cho tam giác DMN cân tại M . Phương trình đường thẳng MN là 2x  y  8  0 .
Tìm tọa độ các đỉnh của hình thang ABCD biết D thuộc đường thẳng d : x  y  0 và điểm A
thuộc đường thẳng d  : 3x  y  8  0
b) Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng a . Biết hình chiếu vuông góc của
S trên mặt phẳng  ABCD là điểm M thỏa mãn AD  3MD . Trên cạnh CD lấy các điểm
I , N sao cho ABM  MBI và MN vuông góc với BI . Biết góc giữa SC và  ABCD bằng
60 . Tính thể tích khối chóp S.AMCB và khoảng cách từ N đến mặt phẳng SBC  . Câu 4.
(3,0 điểm).Tìm tất cả các nghiệm nguyên dương của phương trình x 2 15   2z y . 1 2 2 2 2018 2 2019 2 Câu 5.
(3,0 điểm).Tính tổng 1 2 2018 2019 S C C ... C C . 2019 2019 2019 2019 2019 2018 2 1 Hết 1
HƯỚNG DẪN GIẢI CHI TIẾT 
 173x 5 x 3y 14 4 y  0 Câu 1.
a) Giải hệ phương trình  ,  , x y   . 2
2 2x  y  5  3 3x  2y 11  x  6x 13 
b) Cho a, b, c là các số thực dương. Tìm giá trị nhỏ nhất của biểu thức 2 2 2 a  bc b  ca c  ab 4 P   
 4 a  b  c b  c c  a a  b . Lời giải 5   x  0  4  y  0 a) Điều kiện:  .
2x  y  5  0  3
 x  2y 11 0
Đặt 5  x  a  0 ; 4  y  b  0 ,
phương trình 17  3x 5  x  3y 14 4  y  0 trở thành:   2 2 3 3   2
 a  a      2 17 3 5 .
3 4  b  14  0 
 3a  2.a  3b  2.b  3a  2a  3b  2b (*).
Xét hàm số y  f t  3
 3t  2t trên 0; .
Ta có f t  2
 3t  2  0 , t
 0; nên hàm số y  f t đồng biến trên 0; .
Vì thế với a  0 , b  0 thì 3 3
3a  2a  3b  2b  f a  f b  a  b . Suy ra 5  x 
4  y  5  x  4  y  y  x 1 .
Thay y  x 1 vào phương trình thứ hai trong hệ ta được phương trình: 2
2 3x  4  3 5x  9  x  6x 13 .   Điề 4 u kiện: x   ;5   .  3 
Khi đó, phương trình   x      x    2 2 3 4 2 3 5 9
6  x  6x  5
43x  4  4 95x  9  36    x   1  x  5 2 3x  4  2 3 5x  9  6 6 x   1 15 x   1    x   1  x  5 3x  4 1 5x  9  2 x 1  0   6 15    x  5  3x  4 1 5x  9  2 x  1    6 15    . x  5 *  *  3x  4 1 5x  9  2
Phương trình (**) tương đương vớ 6 15 i   x  5 . 3x  4 1 5x  9  2   Đặ 4 t g  x 6 15  
 x , x   ;5   . 3x  4 1 5x  9  2  3  2 3 5 6  . 1  5. 2 3x  4 2 5x  9
Ta có g x     3x  4   1 2 1  5x9 22 9  7  5   4      , x    ;5   . 3x  4   1 0 2 1 . 3x  4
2  5x  9  22 . 5x  9  3   4 
Suy ra g  x nghịch biến trên  ;5   .  3   4 
Vì thế phương trình g  x  5 có nhiều nhất một nghiệm trên  ;5   .  3 
Ta lại có x  0 là nghiệm nên đây là nghiệm duy nhất. Với x  1  thì y  2 .
Với x  0 thì y  1.
So sánh điều kiện, hệ đã cho có hai nghiệm  ; x y là  1  ; 2   ; 0;  1  . b) 2 2 a  bc
a  bc  ab  ac      2 a b a c a  bc
a ba  c Ta có  a      a b  c b  c b  c b  c b  c . 2 b  ca
b  cb  a 2 c  ab
c  ac b Tương tự ta có:   ; b   c c  a c  a a  b a  b .
a ba  c b  cb  a c  ac b  P   
 a  b  c 4
 4 a  b  c b  c c  a a  b
Áp dụng bất đẳng thức AM-GM
a ba  c b  cb  a 
 2a  b b  c c  a
b  cb  a c  ac b 
 2b  c c  a a  b
c  ac b a ba  c 
 2c  a a  b b  c
 a  ba  c b  cb  a c  ac  b   2  
  4a  b  c b  c c  a a  b   4
 P  a  b  c  4 a  b  c . Đặt 4 4 4
t  a  b  c  0  a  b  c  4 a  b  c  t  4t . 2 2 Ta có 4 4 2
t  t  t  t    2
t  t      2 4 2 1 2 2 1 3 t   1  2t   1  3  3   P  3  .
a  b  c 1 1
Vậy giá trị nhỏ nhất của P là -3 khi 
 a  b  c 
a  b  c 3 . 3 2018   x x 1 Câu 2.
a) Cho hàm số y  f  x có đạo hàm f  x   x  3 2 e  e    2
x  2x. Tìm tất cả các  3 
giá trị thực của m đề hàm số f  2
x  8x  m có đúng 3 điểm cực trị sao cho 2 2 2
x  x  x  50 , trong đó x , x , x là hoành độ của ba cực trị đó. 1 2 3 1 2 3  1 u  , u  3  1 2  2 b) Cho dãy số u xác định như sau:  . n  u .u 1 n 1  n u   , n   1 n2  u  u  n 1  n
Chứng minh rằng u
có giới hạn hữu hạn và tìm giới hạn đó. n  Lời giải a) Cách 1 x  3   
f ' x   x  32018 x x 1 2 e  e    2 x  2x,
f ' x  0  x  0 3    x  2 
Trong đó x  3 là nghiệm bội chẵn.
Xét hàm y  f  2
x  8x  m có y   x   f  2 ' 2 8
' x  8x  m . x  4 x  4   2 2
x  8x  m  3
x  8x  3  m     1 y '  0     2 2
x  8x  m  2
x  8x  2  m 2   2 2
x 8x  m  0
x 8x  m  3
Ta xét hàm g  x 2  x 8x x  4  g ' x – 0 +   g  x -16
Nếu 3 m  1
 6  m 19:
Phương trình (1), (2), (3) đều vô nghiệm. Hàm số đã cho chỉ có 1 cực trị.
Nếu 2  m  1
 6  3m 18  m 19 :
Phương trình (1) có 2 nghiệm bội chẵn, phương trình (2) vô nghiệm hoặc có nghiệm kép và
phương trình (3) vô nghiệm. Hàm đã cho có 1 cực trị.
Do đó không thỏa điều kiện có 3 cực trị. Nếu m   1
 6  2 m 16  m 18:
Phương trình (1) có 2 nghiệm bội chẵn, phương trình (2) có 2 nghiệm bội lẻ và phương trình
(3) vô nghiệm hoặc có nghiệm kép. Do đó thỏa điều kiện có 3 cực trị.
Khi đó giả sử x  4 , ta có x , x là hai nghiệm của phương trình 2 thỏa mãn điều kiện: 1 2 3
x  x  34   x  x 2 2 2  2x x  34. 2 3 2 3 1 2
Áp dụng định lý Viét ta có: 64  2m  2  34  m  17 Thỏa điều kiện. 4 Nếu m   1
 6  m 16 : Phương trình (1) có 2 nghiệm bội chẵn, phương trình (2) có 2
nghiệm đơn, phương trình (3) có 5 nghiệm đơn. Do đó không thỏa điều kiện có 3 cực trị.
Vậy với m 17 thì điều kiện bài toán thỏa. Cách 2
Xét hàm y  f  2
x  8x  m có
y '  2x  8 f ' 2
x  8x  m      .
 x  x  x  m  2018 2 2
x  xm
x  xm 1 2 8 8 3 e  e  
  x  8x  m2 2 2 8 8 2  2 2
x  8x  m  3     2  
Dấu y phụ thuộc vào dấu của  x    2
x  x  m   2 2 8 8
2 x  8x  m   Ta có: x  4 x  4     
2x  8  x  8x  m2 2  2 2
x  8x  m 2 2
 0  x  8x  m  0  x  8x  m      2 2  
x  8x  m  2
x  8x  2  m  
Ta xét hàm g  x 2  x 8x x  4  g x – 0 +   g  x -16
Hàm số có 3 cực trị khi và chỉ khi: m   1
 6  2 m 16  m 18.
Khi đó giả sử x  4 , ta có x , x là hai nghiệm của phương trình 2 thỏa mãn điều kiện: 1 2 3
x  x  34   x  x 2 2 2  2x x  34. 2 3 2 3 1 2
Áp dụng định lý Viét ta có: 64  2m  2  34  m  17 .Thỏa điều kiện. u .u 1    u 1 u 1 n 1 n 1   
b) Theo giả thuyết ta có u   u 1 n n  n2 n2 u  u u  u n 1  n n 1  n u .u 1    u 1 u 1 n 1 n 1    u   u 1 n n  n2 n2 u  u u  u n 1  n n 1  n  1 u    0 u .u 1 1 n 1   2 n  u   0, n  1 n2 u  u  n 1 u  3  0  n  Vì 2 . u 1    u 1 u 1 n 2 n 1   n   u 1 u 1 u 1 n2
 n 1  n  Suy ra n . u 1 n v   v
 v .v  v  v . v n n2 n 1  n n2 n 1  n Đặ u 1 t n .  Đặ x ln v t n n suy ra x  x  x . n2 n 1  n 
Ta có phương trình đặc trưng: 1 5 2
t  t 1  0  t  . 2 5 n n 1 5  1 5  x         n     2 2     Vậy .  1 1   5 1 5  1 v           ln 3 1 u  x  ln 3     0  ,38  0 1 3 1 2 2  2         1 x   ln 2          0,78 2 3 5 3 5 u 3  v     2   2 ln 2  2  Với  2 2 . 1 5 1 5 1, 1 n n   2 2 1 5  1 5  Vì
nên lim x  lim          . n  2   2          u 1
Suy ra lim v  0  lim n  0  limu 1 n u  . 1 n n Vậy rằng u
có giới hạn hữu hạn và giới hạn đó bằng 1. n  Câu 3.
a) Trong mặt phẳng với hệ tọa độ Oxy cho hình thang vuông ABCD vuông tại A và D , có
CD  2AD  2AB . Gọi M 2; 4 là điểm thuộc cạnh AB sao cho AB  3AM . Điểm N thuộc
cạnh BC sao cho tam giác DMN cân tại M . Phương trình đường thẳng MN là 2x  y  8  0 .
Tìm tọa độ các đỉnh của hình thang ABCD biết D thuộc đường thẳng d : x  y  0 và điểm A
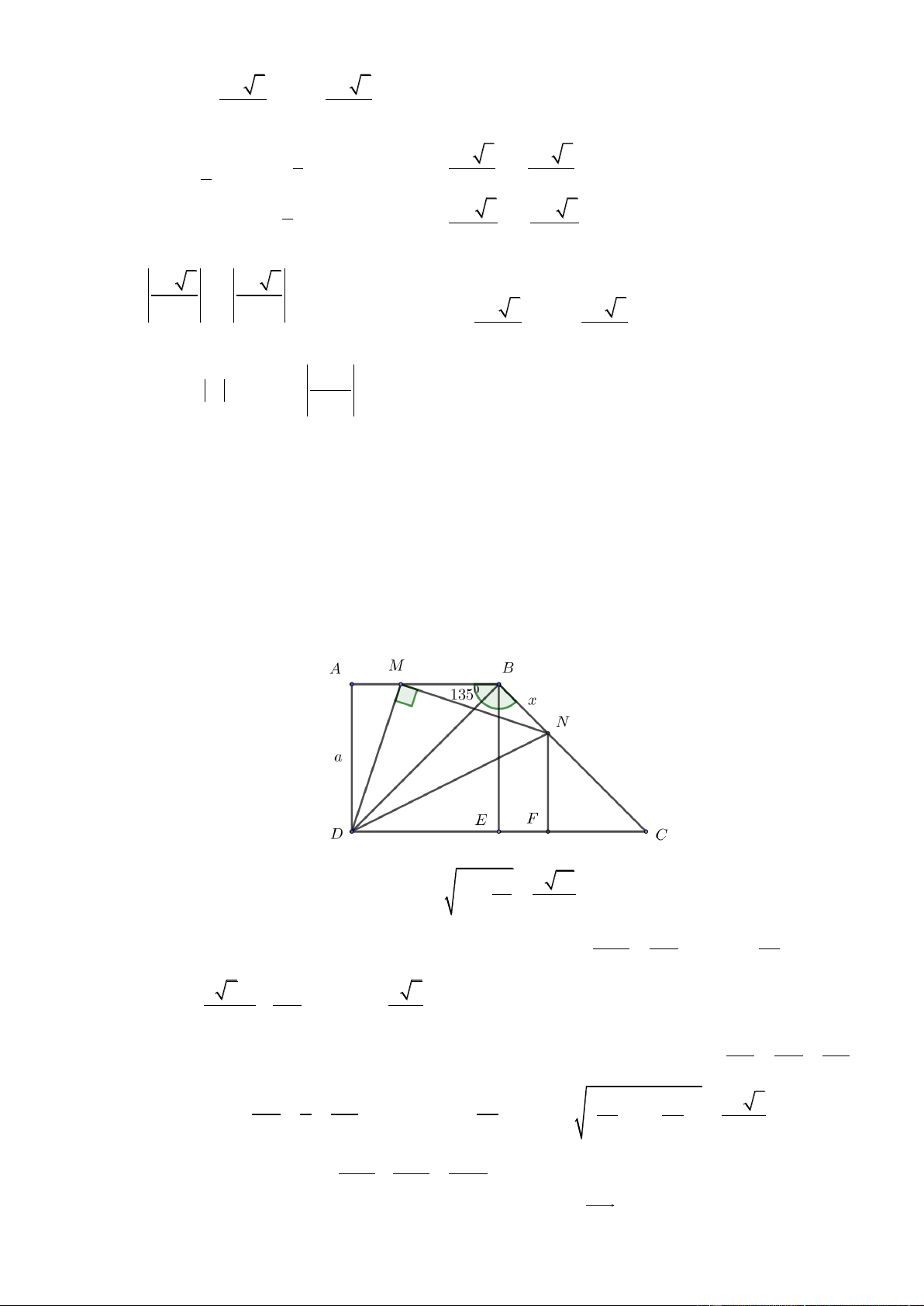
thuộc đường thẳng d  : 3x  y  8  0 Lời giải 2 +) Đặ a a 10
t BN  x , AB  a 2
 MA  MN  a   . 9 3 2 2 10a 4a 2a Xét B  MN có 2 2 2
MN  MB  BN  2.M . B N . B cos MBN 2    x  2. . x .cos135 9 9 3 2 2 2ax 2a a 2  x    2 0  x  . 3 3 3 NF CN CF
Gọi E là chân đường vuông góc hạ từ B , kẻ NF vuông góc với DC . Ta có   BE CB CE NF 2 CF 2 2    2a   4a   2a  2a 5 NF  CF   DN        . a 3 a 3  3   3  3 2 2 2 10a 10a 20a Nhận thấy 2 2 2 MD  MN   
 DN . Suy ra D
 MN vuông tại M . 9 9 9
+) Vì D thuộc đường thẳng d : x  y  0 nên D d; d   MD  d  2; d  4 . 6
Phương trình đường thẳng MN 2x  y  8  0 có vectơ chỉ phương u   1  ;2 .  M .
D u  0  d  2   D 2  ;2 .
+) Điểm A thuộc đường thẳng d : 3x  y  8  0 nên A ; a 3  a  8 ,    a
DA  a  2; 3
 a  6 , MA  a  2;3a  4  D . A MA  0 2
 a  3a  2  1 0  a  2
*) Trường hợp 1: a 1  A1;5
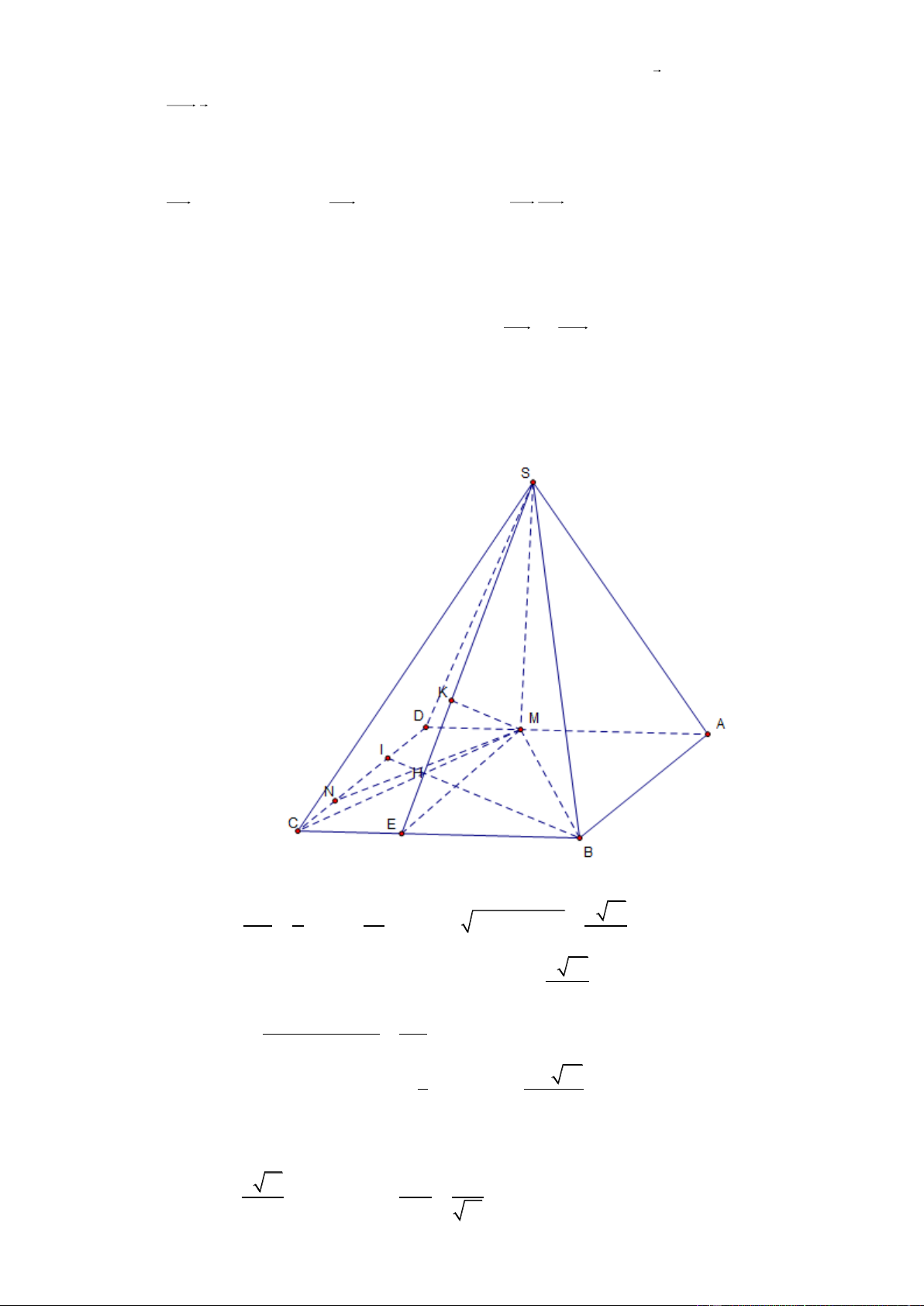
b) Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng a . Biết hình chiếu vuông góc của S
trên mặt phẳng  ABCD là điểm M thỏa mãn AD  3MD . Trên cạnh CD lấy các điểm I , N
sao cho ABM  MBI và MN vuông góc với BI . Biết góc giữa SC và  ABCD bằng 60 .
Tính thể tích khối chóp S.AMCB và khoảng cách từ N đến mặt phẳng SBC  . Lời giải
*) Tính thể tích khối chóp S.AMCB AD a 2a a 10 Ta có 2 2 DM   , AM 
 CM  DM  CD  . 3 3 3 3
SM   ABCD a 30
 SCM  60  SM  CM tan 60  . 3  AM  BC 2 AB Khi đó 5a S   . AMCB 2 6 3 1 5a 30
Thể tích khối chóp S.AMCB là V  SM.S  . 3 AMCB 54
*) Tính khoảng cách từ N đến mặt phẳng SBC  . a 13 AB 3 Ta có BM   cos ABM    cos IBM . 3 BM 13 7 2 Đặ a 2 t 2 2 2
DI  x  IM  x 
IB  a  x 2 ,  a . 9
Áp dụng định lí cosin ta có 2 2 2
IM  MB  IB  2.M . B I . B cos IBM 2 a       2 2 13a x a x  a   2 .
a a  x2 2 2 2  a 9 9 7a 13a  x   IB  . 12 12 a
Gọi H  MN  BI . Ta có ABM  M
 BH  BH  AB  a, IH  IB  BH  . 12 BI CI HI.BI 13a a CN 1 C  BI HNI     NI  
, CN  CD  DI  IN    NI HI CI 60 5 CD 5 1 1
Suy ra d  N,SBC   .d D,SBC   .d M ,SBC  . 5 5
Kẻ ME vuông góc với BC , kẻ MK vuông góc với SE . Suy ra MK  .d M ,SBC . 1 1 1 13 a 130 1 a 130 Ta có     MK 
 d N,SBC  .d M,SBC  . 2 2 2 2 MK MS ME 10a 13 5 65 Câu 4.
Tìm tất cả các nghiệm nguyên dương của phương trình x 2 15   2z y . Lời giải
Theo yêu cầu bài toán thì z 4
2  15 1  2  z  4 .
Khi đó vế phải của phương trình đã cho chia hết cho 16.
Do đó y phải là số lẻ. Từ đó ta được: 2 y 1  mod8 x 2 x 
15  y    1 1mod8 . x 1  5x    1 mod8
Vì vậy ta cũng suy ra được x là số lẻ.
Ta lại lặp luận tiếp để kết luận z phải là số chẵn bằng phản chứng như sau: n Nếu 
z là số lẻ thì z 2n 1 2  2  23  1  2mod3 và 2 y
không thể chia 3 dư 2 nên ta có mâu thuẫn. Vì khi đó 2
2z  y không thể chia hết cho 3 .
Vậy tới đây ta tiếp tục tìm nghiệm của phương trình đã cho với giả thiết là x, y đều lẻ, còn z là số chẵn. Ta có x 2 15 
 2z 15x  2t  2t y y
 y. Với t  2 là số nguyên thoả mãn z  2t . Ta nhận xét rằng
2t  2t    2.2t y y
. Do đó 2t  y và 2t  y không thể cùng chia hết cho 3 hoặc 5 . t 1
2   5x 3x  
2t  y  3x x x       1 5 3  y 
2t  y  5x  x t t 2
Vì vậy 15  2  y2  y     . t t 1  2  y  1 2   115x     t x x   y    2 2 15 15 1  y   2 8 x 1  y 1 y 1     t 2 z  4  Nếu x  1     . y  7 x 1    t   3 y  7   z  6   t 5x 3x
Nếu x  2n  3, n  0 thì từ 2   76   6  2t t  0mod16 . Ta có 2 x 
 2n    2n 2n 3 27 3 27 4 1
13mod16 ;5x 125.4   1 13mod16 Khi đó 3x 5x 
 26mod16 , ta kết luận   1 vô nghiệm. x  Tương tự t 1 15
như thế, nếu x  2n  3, n  0 thì từ 2 
1688  10  2t t  0mod32 . 2 Ta có
x    2n3 15 16 1
162n 3 1mod32
Khi đó 115x  162n  3mod32 , ta kết luận 2 vô nghiệm. 2 2 2 2 1 2 2018 2019 Câu 5. Tính tổng S   1 C    2 C  ...  2018 C    2019 C . 2019 2019 2019 2019  2019 2018 2 1 Lời giải
Xét số hạng tổng quát: k 2 k k 2019! k 2019! T . C . .C . k C k 2019 2019 2019 2020 k 2020 k 2019 k !k ! 2020 k ! k 1 ! k 1 2019 C . k C , k 1;2;...;2019 2019 2019 Suy ra 0 2018 1 2017 2017 1 2018 0 S C .C C .C ... C .C C .C 2019 2019 2019 2019 2019 2019 2019 2019 Xét khai triển: 2019 2019 0 1 2019 2019 0 1 2019 2019 1 x . 1 x C C x ... C x C C x ... C x 2019 2019 2019 2019 2019 2019 2019 2019 Hệ số của 2018 x trong khai triển 1 x . 1 x là: 0 2018 1 2017 2017 1 2018 0 C .C C .C ... C .C C .C 1 2019 2019 2019 2019 2019 2019 2019 2019 4038 Xét khai triển: 0 1 2018 2018 4038 4038 1 x C C x ... C x ... C x 4038 4038 4038 4038 4038 Hệ số của 2018 x trong khai triển 1 x là: 2018 C 2 4038 1 2 2 2 2018 2 2019 2 Từ 1 và 2 ta có 1 2 2018 2019 2018 S C C ... C C C 2019 2019 2019 2019 4038 2019 2018 2 1 9