Đề thi chọn học sinh giỏi tỉnh Toán 12 năm 2019 sở GD&ĐT Bình Phước

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI BÌNH PHƯỚC
CẤP TỈNH LỚP 12 NĂM 2019 Môn: Toán. ĐỀ CHÍNH THỨC
Thời gian làm bài: 180 phút (không kể thời gian phát đề).
(Đề thi gồm có 01 trang) Ngày thi: 22/09/2019. x +
Câu 1. (4 điểm) Cho hàm số y = f ( x) 1 =
có đồ thị (C ) . x −1
a) Khảo sát sự biến thiên và vẽ đồ thị (C ) của hàm số y = f ( x). b) Tìm hai điểm ,
A B thuộc về hai nhánh của đồ thị (C ) sao cho AB ngắn nhất.
Câu 2. (6 điểm)
a) Giải phương trình: (sin 2x + cos 2x) cos x + 2 cos 2x − sin x = 0 . 2 2 2 2
2xy − y − y +1+ 2xy 4x +1 = 0
b) Giải hệ phương trình:  3 3
 x − 2 2x y = 2 x + 6 + 2 
c) Có 27 tấm thẻ được đánh các số tự nhiên từ 1 đến 27 (mỗi thẻ đánh đúng một số). Rút ngẫu nhiên
ba thẻ. Tính xác suất để rút được ba thẻ mà tổng các số trên ba thẻ chia hết cho 3. Câu 3. (4 điểm)
a) Trong mặt phẳng với hệ trục tọa độ Oxy . Cho tam giác ABC nội tiếp đường tròn tâm I ( 2; − − ) 1 , 𝐴𝐴𝐴𝐴𝐴𝐴 � = 90𝑜𝑜, H ( 1 − ; 3
− ) là hình chiếu vuông góc của A lên BC và K ( 1
− ;2) là một điểm thuộc
đường thẳng AC . Tìm tọa độ các đỉnh ,
A B, C . Biết rằng điểm A có hoành độ dương.
b) Cho tam giác ABC ( AB < AC ). Đường phân giác trong góc A cắt đường tròn ngoại tiếp tam giác
ABC tại điểm D . Gọi E là giao điểm của đường trung trực của đoạn thẳng AC và đường phân
giác ngoài của góc A . Gọi H là giao điểm của DE và AC . Đường thẳng qua H và vuông góc
với DE cắt AE tại F. Đường thẳng qua F vuông góc với AE cắt AB tại K. Chứng minh rằng
KH song song BC.
Câu 4. (3 điểm) Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật biết AB = a, BC = 2a, tam giác
SAB đều và nằm trong mặt phẳng vuông góc với mặt phẳng ( ABCD).
a) Tính thể tích khối chóp S.AC . D
b) Tính khoảng cách giữa hai đường thẳng SC và B . D
Câu 5. (2 điểm) Cho a,b,c là các số thực không âm thỏa (a + b)(b + c)(a + c) > 0 và a ≥ max{b, } c . Chứng minh rằng: a 11  b c 
a + 7 (b + c) 15 +  +  + 2 >   b + c 2 a + c a + b a 2  
Câu 6. (1 điểm) Cho dãy số (u xác định bởi n ) 2019u  2019  u = 1;u = 2020; n u = + 1+ u , n ∀ ≥ 2 1 2 n 1 +   n 1− n  n −1   1 1 1 1  Tính lim  + + + ...+  . n→+∞ u u u u  1 2 3 n 
………HẾT………
- Thí sinh không được sử dụng tài liệu và máy tính cầm tay
- Giám thị coi thi không giải thích gì thêm.
LỜI GIẢI CHI TIẾT x + Bài 1.
Cho hàm số y = f ( x) 1 = có đồ thị (C) . x −1
a) Khảo sát sự biến thiên và vẽ đồ thị (C ) của hàm số y = f ( x) .
b) Tìm hai điểm A , B thuộc về hai nhánh của đồ thị (C ) sao cho AB ngắn nhất. Lời giải x +
a) y = f ( x) 1 = x−1
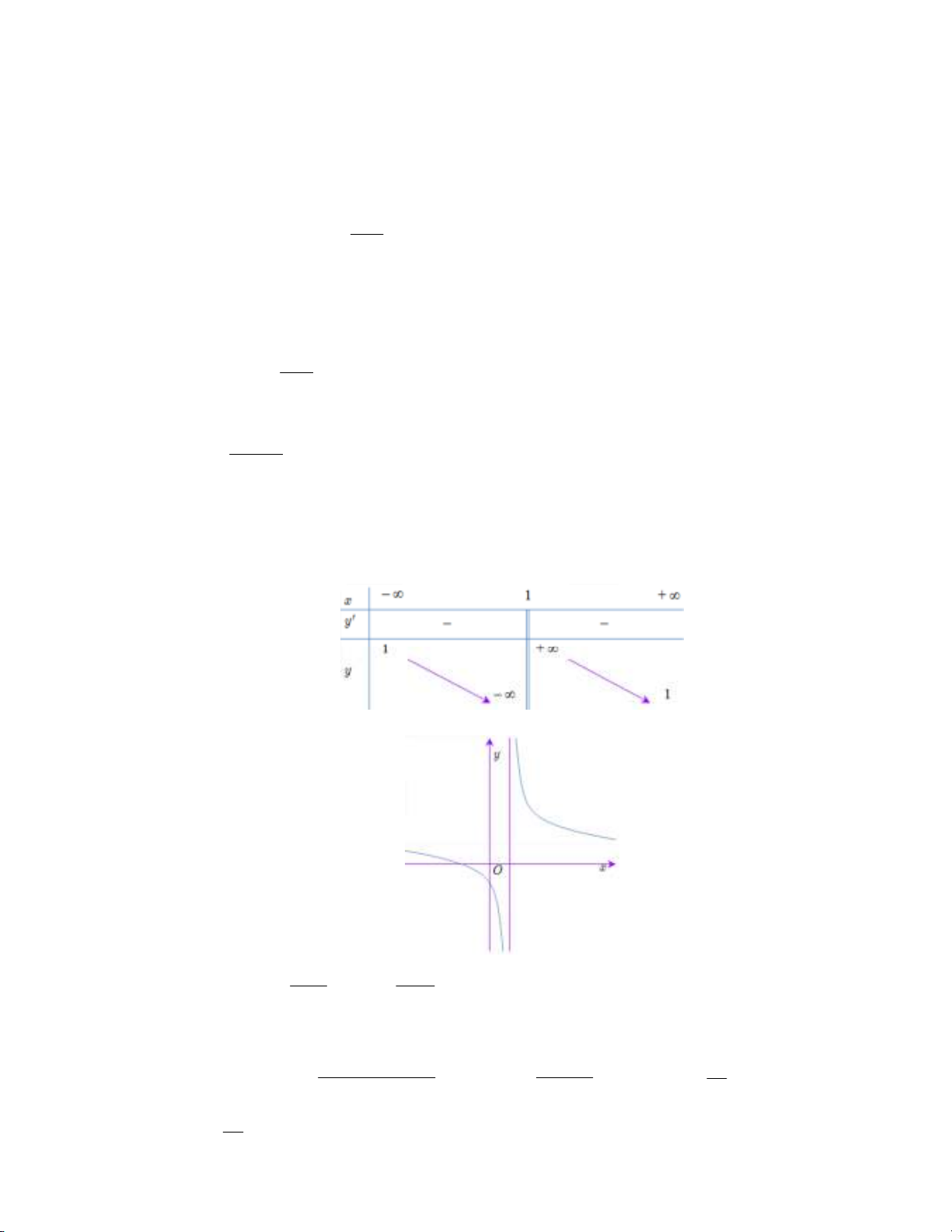
+) Tập xác định: D = ℝ \ { } 1 . −2 +) y′ = < 0 , x
∀ ≠ 1. Hàm số nghịch biến trên các khoảng (− ; ∞ ) 1 và (1;+∞) . (x − )2 1
+) y′ không xác định tại x =1.
+) lim y = 1 nên y = 1 là tiệm cận ngang của đồ thị hàm số. x→±∞
+) lim y = −∞ ; lim y = +∞ nên x =1 là tiệm cận đứng của đồ thị hàm số. − + x 1 → x 1 → +) Đồ thị  x +1   x +1  b) Giả sử 1 A x ; ; 2 B  x ;
, với x < 1 < x . 1   x −1 2 1 2  x −1 1   2 
Đặt x = 1− a ; x = 1+ b với a,b > 0 . 1 2 2 2 x − x a + b 2   2 2 2  2 
AB = ( x − x + 4 = (a + b) ( ) + 4
= (a + b) 1+    2 1 )2 ( 2 1) ( 2   x − )2 1 ( x − )2 1 (ab)  ab  1 2   4 ≥ 4a . b = 16. ab
NHÓM HSG-DIỄN ĐÀN GIÁO VIÊN TOÁN 2 a = b  a = 2
Dấu " = " xảy ra khi và chỉ khi  2 ⇔ 
. Vậy A(1− 2;1− 2), B(1+ 2;1+ 2 ) . 1 =   =  b 2  ab Bài 2.
a) Giải phương trình (sin 2x + cos 2x) cos x + 2 cos 2x − sin x = 0 2 2 2 2
2xy − y − y +1 + 2xy 4x +1 = 0 ( ) 1
b) Giải hệ phương trình  3 3
x − 2 2x y = 2 x + 6 + 2  (2)
c) Có 27 tấm thẻ được đánh các số tự nhiên từ 1 đến 27 (mỗi thẻ đánh đúng một số). Rút ngẫu
nhiên ba thẻ. Tính xác suất để rút được ba thẻ mà tổng các số trên ba thẻ chia hết cho 3 . Lời giải a) ( x + x ) 2 sin 2 cos 2
cos x + 2 cos 2x − sin x = 0 ⇔ 2 sin x cos x + cos 2x (cos x + 2) − sin x = 0 ⇔ x ( 2 sin 2cos x − )
1 + cos 2x (cos x − 2) = 0 ⇔ cos 2x(sin x + cos x − 2) = 0  π kπ x = + cos 2x 0  = 4 2 ⇔ ⇔   .
sin x + cos x − 2 = 0    π  sin x + = 2(PTVN)     4  π kπ 
Vậy nghiệm của phương trình là S =  + | k ∈ ℤ .  4 2 
b)ĐK: x ≥ 0; y ≥ 0 .
Nhận thấy x = 0; y = 0 không phải là nghiệm của hệ phương trình do đó ta chỉ xét x > 0, y > 0 . Ta có: 2 2 2 2 2
2xy − y − y +1 + 2xy
4x +1 = 0 ⇔ 2xy ( 2 1+ 4x +1) 2 = y + y +1 ⇔ 2x ( 1 1 2 1+ 4x +1) = + 1+ 2 y y 2 t
Xét hàm số f (t) = t ( 2
1+ 1+ t ) ,t > 0, f ′(t) 2 = 1+ 1+ t + > 0 . 2 1+ t Hàm số f (t ) đồng biến trên (0;+∞) dó đó ta có   2x ( 1 1 1 1 1 2 1+ 4x +1) = + 1+
⇔ f 2x = f ⇔ 2x = ⇔ y = 2 ( )   y y  y  y 2x
Thay vào phương trình (2) ta có:
NHÓM HSG-DIỄN ĐÀN GIÁO VIÊN TOÁN 3    2 3 3 3 3 
x − 2 = 2 x + 6 + 2 ⇔ x − 8 = 2 x + 6 − 4 ⇔ ( x − 2) 2 x + 2x + 4 − =   (   x + 6 ) 0 2 3 3 + 2 x + 6 + 4  x = 2  2 ⇔ 2
x + 2x + 4 − =   ( x+6) 0 2 3 3 + 2 x + 6 + 4 1
+ Vói x = 2 ⇒ y = thoả mãn yêu cầu. 4 2 + Với 2 x + 2x + 4 − = ( x + 6 ) 0 2 3 3 + 2 x + 6 + 4 x + 6 +1 + 7 2 2 2 ( )2 3 ⇔ ( x + ) 1 + 3 − = 0 ⇔ x +1 + = 0 * 2 ( ) 2 ( ) (3 x+6) 3 + 2 x + 6 + 4 (3 x+6 + )1 +3
Phương trình (*) vô nghiệm. x = 2 
Vậy hệ có nghiệm duy nhất  1 . y =  4
c) Gọi Ω không gian mẫu của phép thử: “Rút 3 thẻ trong 27 thẻ”. Khi đó, n (Ω) 3 = C = 2925 . 27
Gọi biến cố A : “Rút 3 thẻ trong 27 thẻ mà tổng các số trên ba thẻ chia hết cho 3”. Xét 3 tập hợp:
Tập B : “Các thẻ có số chia hết cho 3” ⇒ B = {3;6;9;12;15;18;21; 24;2 } 7 .
Tập C : “Các thẻ có số chia cho 3 dư 1” ⇒ C = {1; 4;7;10;13;16;19;22;2 } 5 .
Tập D : “Các thẻ có số chia cho 3 dư 2” ⇒ D = {2;5;8;11;14;17 ; 20; 23; 2 } 6 .
(Nhận xét: Ba tập hợp B, C, D là đôi một rời nhau với n ( B) = n (C ) = n (D) = 9 ; 27 tấm thẻ đều
được liệt kê 1 trong 3 tập trên, không có tấm thẻ nào được liệt kê 2 lần).
Theo tính chất đồng dư và phép chia hết cho 3, biến cố A xảy ra khi và chỉ khi một trong các khả năng sau xảy ra:
KN1. 3 thẻ rút được đều nằm trong tập B , khi đó n ( A) 3 = C = 84 . 1 9
KN2. 3 thẻ rút được đều nằm trong tập C , khi đó n ( A) 3 = C = 84 . 2 9
KN3. 3 thẻ rút được đều nằm trong tập D , khi đó n ( A) 3 = C = 84 . 3 9
KN4. 3 thẻ rút được có 1 thẻ trong tập B , 1 thẻ trong tập C , 1 thẻ trong tập D , khi đó n ( A) 1 1 1 = C C C = 729 . 4 9 9 9
Do đó, n ( A) = n A + n A + n A + n A = 981. 1 ( ) 2 ( ) 3 ( ) 4 ( )
NHÓM HSG-DIỄN ĐÀN GIÁO VIÊN TOÁN 4 n A 981 109
Vậy xác suất của biến cố A là: P ( A) ( ) = = = . n (ω ) 2925 325 Bài 3.
a) Trong mặt phẳng với hệ toạ độ Oxy .Cho tam giác ABC nội tiếp đường tròn tâm I ( 2 − ;− ) 1 .
Góc AIB bằng 90o , H ( 1 − ; 3
− ) là hình chiếu vuông góc của A lên BC và K ( 1 − ;2) thuộc
đường thẳng AC . Tìm toạ độ A, B, C biết rằng A có hoành độ dương.
b) Cho tam giác ABC ( AB < AC ) . Đường phân giác trong góc A cắt đường tròn ngoại tiếp tam
giác ABC tại D . Gọi E là giao điểm của đường trung trực của đoạn thẳng AC và đường phân
giác ngoài của góc A , H = DE ∩ AC . Đường thẳng qua H và vuông góc với DE cắt AE tại F.
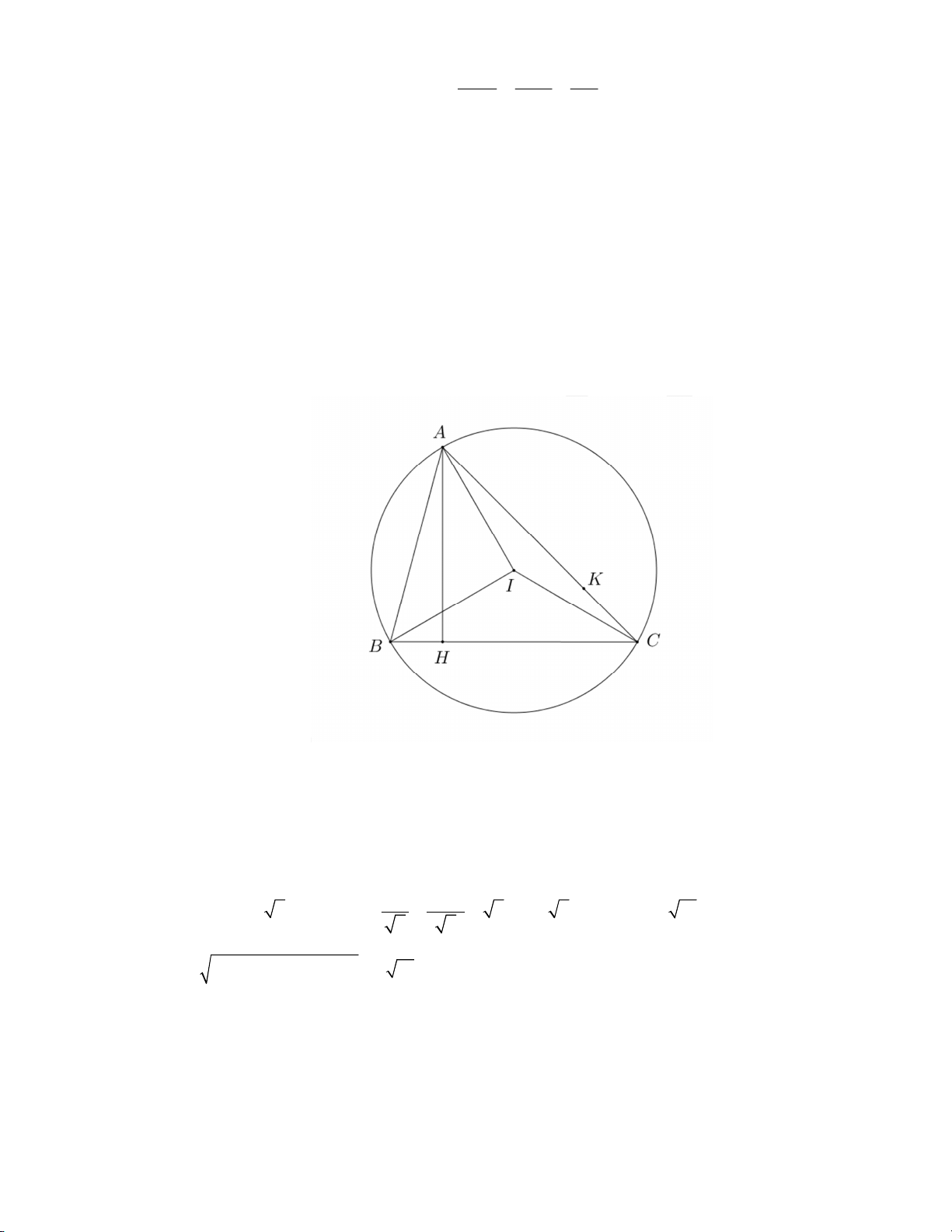
Đường thẳng qua F vuông góc với AE cắt AB tại K. Chứng minh rằng KH //BC . Lời giải a) Ta có 0 AIB = 90 nên 0
ACH = 45 suy ra tam giác AHC vuông cân tại H
Mặt khác IA = IC nên HI ⊥ AC
Phương trình đường thẳng AC qua K (−1;2) và vuông góc với HI có phương trình
−x + 2y − 5 = 0 .
Gọi A(2a − 5;a )∈ AC AC 2HK
Ta có AC = 2 AH ⇒ AH = =
= 2HK = 2d (H; AC) = 2 10 2 2
a = −1 ⇒ A −5; 1 − l 2 2 ( ) ( ( ))
⇔ (4 − 2a) + (−3 − a) = 2 10 ⇔ a = 3⇒ A  (1;3) Vậy A(1;3) .
Phương trình đường thẳng BC qua H (−1;−3) và vuông góc với AH có phương trình
x + 3y + 10 = 0 .
Gọi B (3b − 10;b)∈ BC , ta có IB = (3b − 8;b + ) 1 ; IA = (3;4)
NHÓM HSG-DIỄN ĐÀN GIÁO VIÊN TOÁN 5  
Vì tam giác AIB vuông tại I nên IB IA = ⇔ ( b − ) + (b + ) 20 20 . 0 3 3 8 4 1 = 0 ⇔ b = ⇒ B 10;   3  3 
Vì C = AC ∩ BC nên tọa độ điểm C là nghiệm của hệ phương trình
x + 3y +10 = 0 x = 7 −  ⇔  ⇒ C (−7;− ) 1
−x + 2 y − 5 = 0  y = 1 − b)
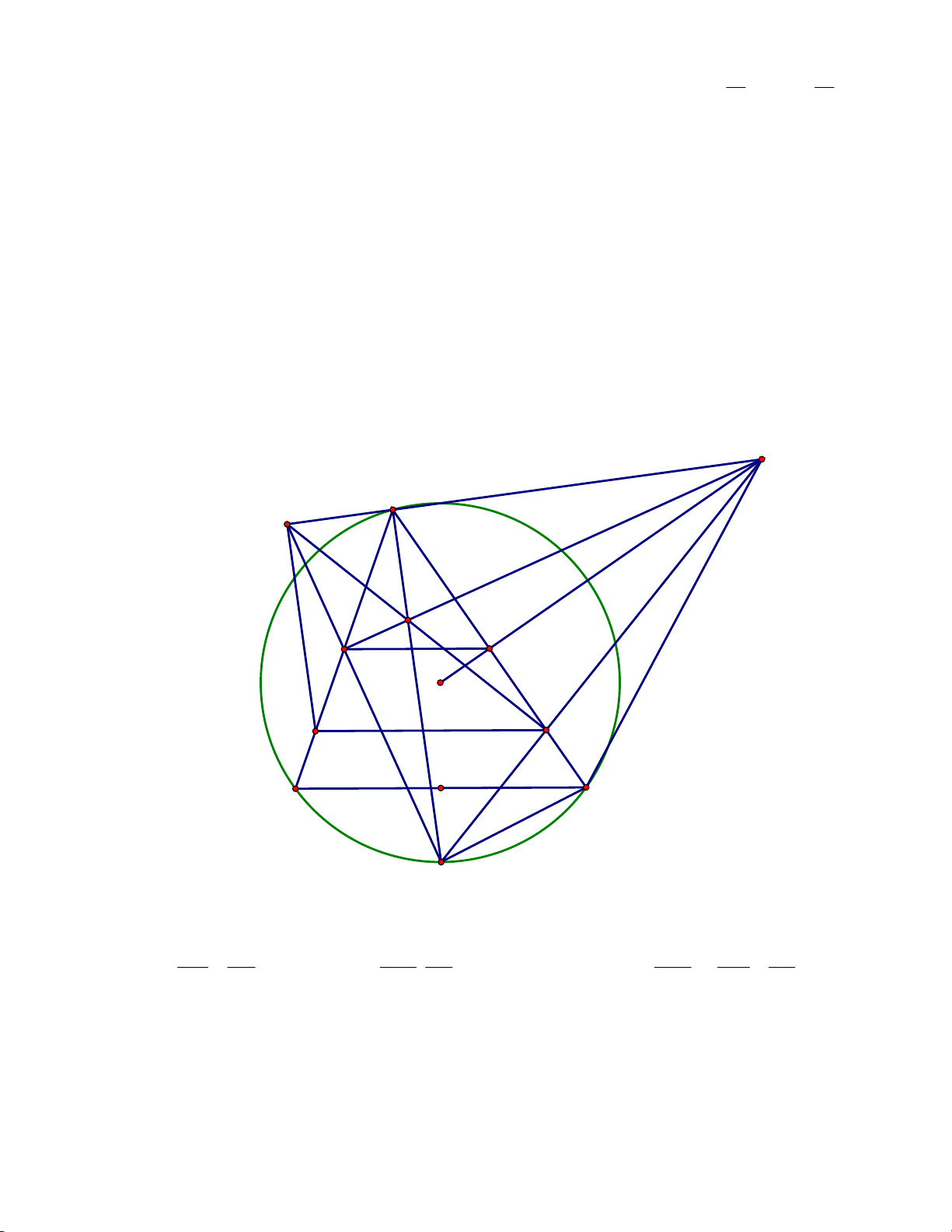
Ta có H = DE ∩ AC E A F I N M O K H B P C D
Gọi M, N, P lần lượt là trung điểm của AB, AC và BC. Khi đó, ta có: MN PC BAC EN BAC NM NE = = cos PCD = cos ;
= cos NEC = cos NEA = cos ⇒ = DC DC 2 EC 2 CD CE Lại có:
MNE = 90° + ANM = 90° + AC ;
B DCE = ACB + BCD + NCE = ACB + NEC + NCE = ACB + 90° Suy ra
MNE = DCE ⇒ M ∆ NE ∼ D ∆ CE (c g c)
. . ⇒ MEN = DEC ⇒ MEN + OEH = DEC + OEH
NHÓM HSG-DIỄN ĐÀN GIÁO VIÊN TOÁN 6 BAC ⇔ MEH = OEC =
= MAD ⇒ DMAE là tứ giác nội tiếp suy ra DM ⊥ ME . (2) 2
Giả sử ME ∩ AD = I , ta đi chứng minh F , I , H ; F , M , D . BAC Có: IEH =
= IAH ⇒ IAEH là tứ giác nội tiếp suy ra IH ⊥ DE ⇒ I, F, H (do FH cũng 2
vuông góc với DE) (1)
Từ (1) kết hợp với DI ⊥ FE ⇒ I là trực tâm tam giác FDE suy ra FD ⊥ IE (3)
Từ (2) và (3) suy ra F, M , D . FA AM
Dễ thấy ∆FAM ∼ ∆HAE ( g g ) 1 . ⇒ = ⇔ A .
B AH = AE.AF và HA AE 2
∆FAK ∼ ∆NAE ( g g ) FA AK 1 . ⇒ = ⇔
AC.AK = AE.AF NA AE 2 AH AC Suy ra A .
B AH = AK.AC ⇔ = ⇒ KH // BC. AK AB
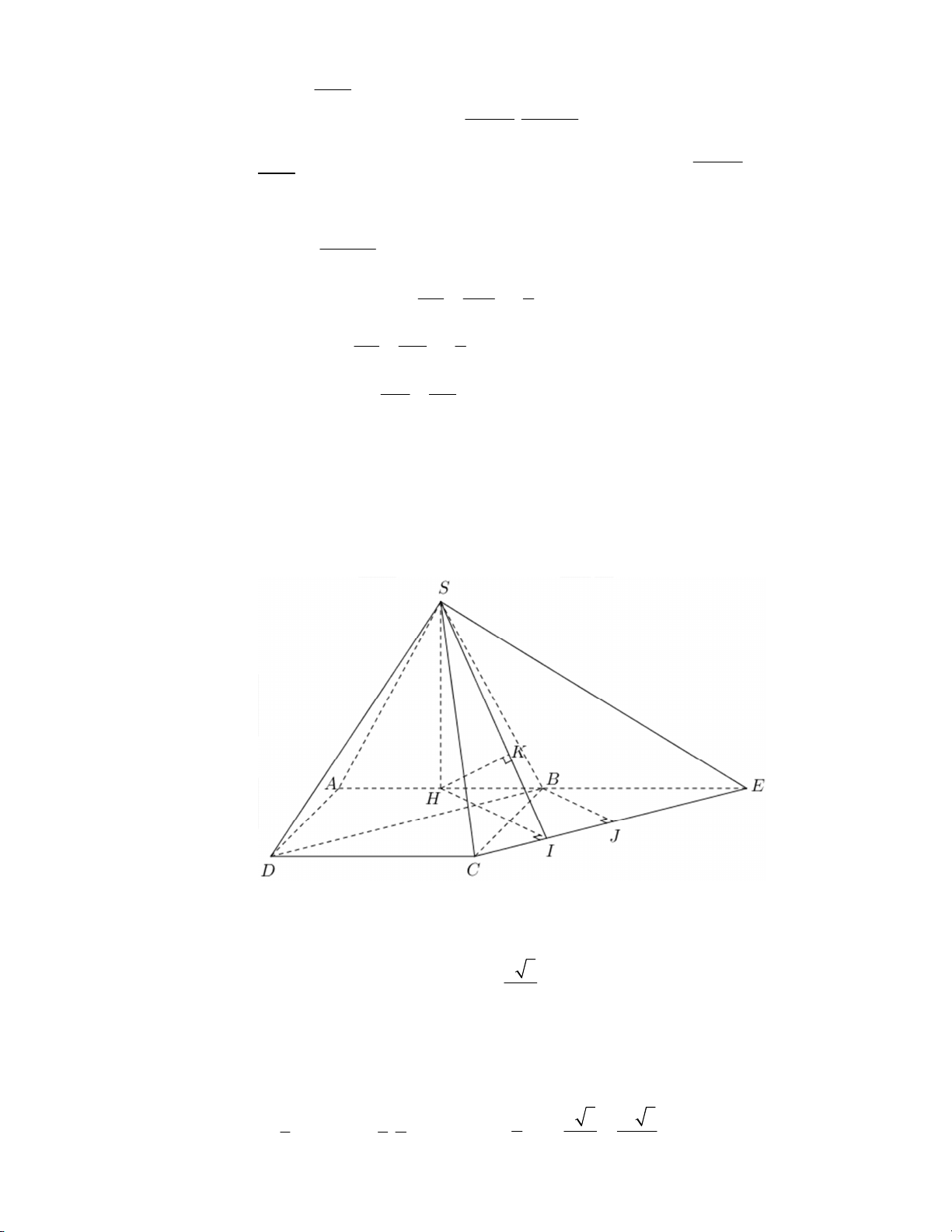
Bài 4. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật biết AB = a , BC = 2a , tam giác SAB
đều và nằm trong mặt phẳng vuông góc với mặt phẳng ( ABCD) .
a) Tính thể tích khối chóp S.ACD .
b) Tính khoảng cách giữa hai đường thẳng SC và BD . Lời giải
a) Tính thể tích khối chóp S.ACD .
Vì ABCD là hình chữ nhật nên AB = CD = a , BC = AD = 2a .
Gọi H là trung điểm của AB . a 3
Vì tam giác SAB đều nên SH ⊥ AB và SH = . 2 (
 SAB) ⊥ ( ABCD)  Khi đó (
 SAB) ∩ ( ABCD) = AB ⇒ SH ⊥ ( ABCD) . SH ⊂ 
(SAB), SH ⊥ AB 1 1 a 3 3 a 3 Ta có V = 1 1 S .SH = . .A . D CD.SH = .2 . a . a = . S . ACD 3 ∆ACD 3 2 6 2 6
NHÓM HSG-DIỄN ĐÀN GIÁO VIÊN TOÁN 7
b) Tính khoảng cách giữa hai đường thẳng SC và BD .
Từ C kẻ đường thẳng song song với BD cắt AB tại điểm E . BD//CE Ta có 
⇒ BECD là hình bình hành ⇒ BE = CD = a . BE //CD  2 Suy ra BE = HE . 3 2
Khi đó d ( BD, SC) = d (BD, (SCE)) = d (B, (SCE )) = d (H , (SCE )) (*). 3
Kẻ HI ⊥ CE ( I ∈CE) , mà CE ⊥ SH ⇒ CE ⊥ (SHI ) ⇒ (SCE ) ⊥ (SHI ) . (
 SCE ) ⊥ (SHI )  Do đó (
 SCE ) ∩ (SHI ) = SI ⇒ HK ⊥ (SCE) HK ⊥ SI  (K ∈SI )
Suy ra HK = d (H, (SCE)) .
Kẻ BJ ⊥ CE ( J ∈CE) ⇒ 3
BJ //HI ⇒ HI = BJ . 2 BE.BC 2a 5
Xét tam giác BCE vuông tại B có BJ = = . 2 2 + 5 BE BC 3a 5 ⇒ HI = . 5 SH .HI 3a 17
Xét tam giác SHI vuông tại H có HK = = . 2 2 + 17 SH HI a a
Từ (*) ⇒ d ( BD SC ) 2 3 17 2 17 , = . = . 3 17 17
Bài 5. Cho a, b, c là các số thực không âm thoả (a + b)(b + c)(a + c) > 0 và a ≥ max{ , b } c . Chứng minh rằng: a 11 b c 
a + 7 (b + c) 15 +  +  + 2 > b c 2  a c a b  + + + a 2   Lời giải b c a 11  b c 
a + 7 (b + c) Đặt x = , y = và P = +  +  + 2 . a a b + c 2 a + c a + b a   Từ a ≥ max{ , b }
c suy ra x ≤ 1, y ≤ 1. 1 11  x y  Khi đó P = +  +
 + 2 1+ 7( x + y) x + y 2 y + 1 x + 1  
Do 0 ≤ x, y ≤ 1 nên x ( − y) 1 1 1
≥ 0 ⇔ x ≥ xy ⇔ x + y ≥ y + xy ⇒ ≤ x + y y ( x + ) 1 2 1 y y y y y ⇒ ≥ ⇒ ≥ ⇒ ≥ . x + 1 x + y x + 1 x + y x + 1 x + y
NHÓM HSG-DIỄN ĐÀN GIÁO VIÊN TOÁN 8 x x Tương tự, ta cũng có ≥ . y + 1 x + y Khi đó 1 11  x y  P ≥ +  +  + + (x + y) 1 11 2 1 7 = +
x + y + 2 1 + 7 ( x + y) x + y 2 x + y x + y x + y 2  
Đặt t = x + y , (0 < t ≤ 2) ta được 1 11 2 P ≥ +
t + 2 1 + 7t = f (t ) t 2 f ′(t) 1 11 14t 1 = − + + = 0 ⇔ t = (thoả) 2 2 t 2 1+ 7t 3  1  15 Suy ra P ≥ f = .    3  2 x = 0 b = 0    1  1
Dấu “=” xảy ra khi và chỉ khi t =
⇔ b + c = a ⇔ a = b = c = 0 (vô lý) 3 9    y = 1 c = a   15 Vậy P > . 2 2019u  2019 
Bài 6. Cho dãy số (u xác định bởi u = 1;u = 2020; n u = + 1+ u , n ≥ 2. n ) 1 2 n 1 +   n 1− n  n −1   1 1 1 1  Tính lim  + + + ...+ . n→+∞ u u u u  1 2 3 n  Lời giải 2019u  2019   u u  Ta có n n n 1 u = + 1+ u = 2019 − + + u n 1 +   n 1 −   n 1 − n  n −1   n n −1  n  u u   u u  u n n 1 − n−2 n−3 = 2019 + + 2019 + + u = ... = 2019 i ∑ +u     . n−3 1  n n −1
 n − 2 n − 3  = i i 1 n 1 +  u  u Suy ra i n 1 u = 2019 ∑ + u = 2019 + + u . n+2   1 n 1 +   + i 1 = i n 1 2019u  n + 2019  u n + 2019 Vậy n n 1 u = + u = u + ⇒ = , n ∀ ∈ . ℕ n 1 + n n   n  n  u n n (2019 + )
1 (2019 + 2)...(2019 + n − ) 1 Do đó u = . n (n − ) 1 ! 1 1 1 1 1 n (k − ) 1 ! Vậy + + + ...+ = 1+ + ∑ u u u u 2020 = + + + k − n k 2019 1 2019 2 ... 2019 2 1 2 3 3 ( )( ) ( ) 1  2!  1 n  (k − )1! k!  =1+ 1− +   ∑ −  2018 2020 2018 = + + +k − + + +k − k 3 (2019 )1(2019 ) 2 ...(2019 ) 2 (2019 )1(2019 ) 2 ...(2019 )1 1 n! 1+ − . 2018
2018.2020.2021...(2019 + n − ) 1
NHÓM HSG-DIỄN ĐÀN GIÁO VIÊN TOÁN 9 n! Do lim = x→∞ ( + n − ) 0 2018.2020.2021... 2019 1  1 1 1 1  2019 Nên lim  + + + ...+  = . n→+∞ u u u u 2018  1 2 3 n 
---------- HẾT ----------
NHÓM HSG-DIỄN ĐÀN GIÁO VIÊN TOÁN 10
Document Outline

• de-thi-chon-hoc-sinh-gioi-tinh-toan-12-nam-2019-so-gddt-binh-phuoc
• 1570370351_WT.HSG-BÌNH-PHƯỚC-2019-2020