Đề thi chọn học sinh giỏi tỉnh Toán 12 năm 2021 – 2022 sở GD&ĐT Nghệ An

Thứ Tư ngày 22 tháng 12 năm 2021, sở Giáo dục và Đào tạo tỉnh Nghệ An tổ chức kỳ thi chọn học sinh giỏi môn Toán lớp 12 cấp tỉnh năm học 2021 – 2022.

29 15 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 12

Môn: Toán 12

Thông tin:

11 trang 8 tháng trước

Tác giả:

Profile Nguyễn Vân
LỜI GIẢI THAM KHẢO ĐỀ THI HSG TỈNH NGHỆ AN NĂM 2021-2022
Câu 1: (7,0 điểm)
a, Tìm tất cả các giá trị thực của tham số
m
để hàm số
63
( ) 5 2y f x x x mx= = − + +
đồng
biến trên khoảng
(0; )+
Giải:
Ta có:
52
' 6 15y x x m= − +
.
Để hàm số đồng
y
đồng biến trên khoảng
thì
'0y
với
(0; )x +
Hay
52
( ) 6 15m h x x x = − +
với
(0; )x +
( )
0;
max ( )m h x
+

Xét hàm số
52
( ) 6 15h x x x= − +
trên
có
42
'( ) 30 30h x x x= − +
0( )
'( ) 0 1( )
1( )
x ktm
h x x ktm
x tm
=
= = −
=
Ta có
( )
0;
(0) 0; (1) 9;lim ( ) max ( ) 9
x
h h h x h x
→+ +
= = = − =
Vậy với
9m
thì hàm số
63
( ) 5 2y f x x x mx= = − + +
đồng biến trên khoảng
(0; )+
b, Giải hệ phương trình
(
)
4 2 2
22
16 15 2 (3 4 17)
( 2 15) 5 1 3 14
y y x y x
y x x y x
− + = − −
+ − + − + + =
Giải:
ĐKXĐ:
1
5
x
−
4 2 2
4 2 2
22
2
2
16 15 2 (3 4 17)
2 (3 8) 8 14 35 0
( 2 1)( 4 15) 0
21
4 15
y y x y x
y y x x x
y x y x
yx
yx
− + = − −
− + + + + =
− − − − =
=+
=+
+) Với
2
4 15yx=+
thay vào phương trình còn lại, ta được:
( )
( )
17
6 5 1 5 18 14 6 .
5 1 5 18
7 5 1 5 18 51 0(*)
x x x x
xx
x x x
−
+ − + =
+ + +
+ + + + =
Vì
1
5
x
−
nên ta có
1 1 1
(*) 7 5. 1 5. 18 51. 0
5 5 5
VT

− − −
+ + + +



Suy ra phương trình (*) vô nghiệm
+) Với
2
21yx=+
thay vào phương trình còn lại, ta được:
( ) ( )
( )
2
22
2
(4 14) 5 1 3 4 14 (2 7) 5 1 3 4 7
(2 7)(2 3)
7 7 5 1 3 4 (2 7)(2 3) 0
5 1 3 4
245 49 (5 7) 147 196 (3 14) 4 28 0
175 25 63 9
4 28 0
245 49 (5 7) 147 196 (3 14)
(
x x x x x x
xx
x x x x
xx
x x x x x
x x x x
xx
x x x x
xx
− + − + = − + − + =
−−
= + + + − − − =
+ + +
+ − + − + − + − + =
−−
+ − + =
+ + + + + +
− −
25 9
7) 4 0(**)
245 49 (5 7) 147 196 (3 14)x x x x

+ + =

+ + + + + +

Vì
1
5
x
−
nên
25 9
40
245 49 (5 7) 147 196 (3 14)x x x x
+ +
+ + + + + +
Nên (**)
0
7
x
x
=
=
Với
01xy= =
Với
7 15xy= =
Vậy tập nghiệm của hệ phương trình
( ) ( )
( ; ) (0;1);(0; 1); 7; 15 ; 7; 15xy − −
Câu 2:(4,0 điểm)
a, Cho hàm số bậc ba
()y f x=
có đồ thị như hình bên. Tìm số
điểm cực trị của hàm số
( )
2
( ) 8g x f x x

= + −

Giải:
Điều kiện:
08x
Ta có:
( ) ( )
11
'( ) ' 8 . 8
8
g x f x x f x x
xx

= − + − + −

−

( )
( )
( )
( )
4
11
8 0;2 2 (1)
0
8
8 2 2;4 (2)
'( ) 0 ' 8 0
8 2 2(3)
80
8 4(4)
8 2 2(5)
x
x x a
xx
x x b
g x f x x
xx
f x x
xx
x x t
=

+ − =
−=

−

+ − =
= + − =
+ − =
+ − =
+ − =
+ − =
Xét hàm số
( ) 8h x x x= + −
trên
0;8
có
11
'( ) ; '( ) 0 4
2 2 8
h x h x x
xx
= − = =
−
Bảng biến thiên
Dựa vào bảng biến thiên ta có
+)Phương trình (1); (5) vô nghiệm
+) (2)
(0;4)
(4;8)
xc
xd
=
=
+) (3)
0
8
x
x
=
=
+) (4)
4( )x kep=
Bảng biến thiên của hàm số
()gx
với
08x
Vậy hàm số
()gx
có 3 điểm cực trị
b, Trong quá trình truy vết lịch sử tiếp xúc của bệnh nhân Covid-19 ở một trường học,
trung tâm y tế xác định được 3 giáo viên và một số học sinh có sự liên quan đến bệnh
nhân đó. Người ta chọn ngẫu nhiên 10 người trong số các giáo viên và học sinh liên quan
để làm xét nghiệm gộp. Biết rằng xác suất để trong 10 người được chọn có 3 giáo viên
bằng
6
lần xác suất trong 10 người được chọn đều là học sinh. Tính xác suất để trong 10
người được chọn làm xét nghiệm có nhiều nhất 2 giáo viên.
Giải:
Gọi số học sinh liên quan đến bệnh nhân Covid -19 là
( )
10nn
Ta có:
( )
10
3n
nC
+
=
Xác suất để chọn 10 người trong đó có 3 giáo viên bằng
3 7 7
3
10 10
33
.
nn
nn
C C C
CC
++
=
Xác suất để chọn 10 người đều là học sinh là
10
10
3
n
n
C
C
+
Theo bài ra ta có:
7 10
7 10
10 10
33
!!
6. 6. 6.
7!( 7)! 10!( 10)!
16
( 7)( 8)( 9) 120 6.5.4
( 7)( 8)( 9) 8.9.10
13
nn
nn
nn
CC
nn
CC
C C n n
n n n
n n n
n
++
= = =
−−
= − − − = =
− − −
=
Vậy xác suất để trong 10 người có nhiều nhất 2 giáo viên là
7
13
10
16
11
1
14
C
P
C
= − =
Câu 3:(1,5 điểm) Cho
,,abc
là các số thực không âm thay đổi thỏa mãn điều kiện
2
1 1 2 1 2 5a b c+ + + + + =
. Tìm giá trị lớn nhất của biểu thức
3 3 3
2P a b c= + +
Giải:
Trước tiên, ta xét bài toán phụ sau:
Cho hai số thực
,xy
không âm. Chứng minh
1 2 1 2 1 1 2( )x y x y+ + + + + +
• Chứng minh: Vì
,xy
không âm nên ta có:
0xy
( ) ( )
22
(1 2 )(1 2 ) 1 2( ) (1 2 ) (1 2 ) 2 (1 2 )(1 2 ) 1 2( ) 2 1 2( ) 1
1 2 1 2 1 1 2( )
1 2 1 2 1 1 2( )
x y x y x y x y x y x y
x y x y
x y x y
+ + + + + + + + + + + + + + + +
+ + + + + +
+ + + + + +
Dấu bằng xảy ra
0
0
x
y
=
=
Quay trở lại bài toán, ta có:
( )
22
22
2
2
5 1 1 2 1 2 1 1 1 2( )
4 1 1 2( ) 1 1 2( )
8
2 2 8
2
a b c a b c
a b c a b c
a
a b c b c
= + + + + + + + + + +
+ + + + + + + +
−
+ + +
Vì
2
8
0 0 0 2 2
2
a
b c a
−
+
Ta có:
3 3 3 3
( ) 3 ( ) ( )b c b c bc b c b c+ = + − + +
vì
0bc
3
2
3 3 3
8
2 ( ) 2
2
a
P a b c a

−
+ + +


Xét hàm số
3
2
3
8
( ) 2
2
a
f a a

−
=+


trên
0;2 2


có:
( )
( )
2
2
2 3 2 2 2
22
33
( ) 6 3 4 ( 2)( 2 12 32) ( 2) 12 2(16 )
2 4 4
0
( ) 0 2
12 2(16 ) 0
a
f a a a a a a a a a a a a a
a
f a a
a a a


= − − = − − − + + = − − + −



=
= =
− + − =
Vì
22
0;2 2 (12 ) 2(16 ) 0
0
( ) 0
2
a a a a
a
fa
a

− + −

=
=
=
Hàm số
()fa
liên tục trên
0;2 2


, đồng thời
( )
(0) 64; (2) 24; 2 2 32 2f f f= = =
Suy ra
[0;2 2]
max
a
( ) (0) 64f a f==
Vậy giá trị lớn nhất của P bằng 64. Dấu bằng xảy ra khi
0; 4a b c= = =
hoặc
0; 4a c b= = =
Câu 4: (6,0 điểm) Cho hình hộp
1 1 1 1
.ABCD A B C D
có đáy
ABCD
là hình thoi cạnh bằng
, 60a ABC =
và
1
()B A ABCD⊥
. Biết góc giữa hai mặt phẳng
( )
1
B CD
và
( )
1 1 1 1
A BC D
bằng
với
1
cot
2
=
. Gọi
M
là trung điểm của
,CD E
là trung điểm của
1
BM
a) Tính thể tích khối hộp
1 1 1 1
.ABCD A B C D
b) Gọi
F
là điểm thuộc đường thẳng
1
DD
sao cho
EF AC⊥
. Tính độ dài đoạn
EF
và
cosin góc giữa hai mặt phẳng
()AEM
và
( )
AEF
Giải:
a) Dễ thấy
ACD
đều suy ra
AM CD⊥
và
3
2
a
AM =
. Khi đó ta có:
( )
1
11
CD B A
CD B AM AMB
CD AM
⊥
⊥ =
⊥
Xét tam giác vuông
1
AMB
có :
1
1
1
cot 2 3
2
AM
AB AM a
AB
= = = =
Ta cũng có
2
3
2 . .sin60
2
ABCD ABC
a
S S BA BC= = =
1 1 1 1
3
.1
3
.
2
ABCD A B C D ABCD
a
V AB S = =
b)
- Từ
1 1 1 1
3 60 ; 120AB a B A A A AB= = =
Kẻ
11
( ); / / ( )D H ABCD FK D H FK ABCD FK AC⊥ ⊥ ⊥
Ta có:
()
FK AC
AC EFK AC EK
EF AC
⊥
⊥ ⊥
⊥
Gọi
Q
là trung điểm của
AM
1
/ / ( )EQ B A EQ ABCD EQ AC ⊥ ⊥
Ta có:
()
EK AC
AC EQK AC QK
EQ AC
⊥
⊥ ⊥
⊥
Dễ thấy
/ / / /AH BD AH AC QK AH ⊥
Suy ra
K
là trung điểm của
MH
22
1 1 1 1 1
1
11
()
2 2 4
1 1 1 1 1
4 4 4 4 4 2
a
DK MK MD MH MD MD DH MD
DK DF a
DF DD AA B A B A
DH DD
= − = − = + − =
= = = = = + =
Ta cũng có:
22
22
11
3
2 . .cos120
2
15
2
a
FM FD DM FD DM
a
B M B A AM
= + − =
= + =
Kẻ
( )
1 1 1 1 1
//FR A B C D FR C D⊥
1
11
11
1 1 1
1
1 1 1
22
1 1 1 1 1 1 1
22
11
3 3 3 3 3
4 4 4 4
1
4 4 4
21
2. . .cos120
4
3
DF
FR a
FR C D B A
C D DD
C R C D
DF a
CR
C D DD
a
B R B C C R C R B C
B F B R RF a
= = = = =
= = = =
= + − =
= + =
Áp dụng công thức đường trung tuyến trong tam giác
1
B FM
ta có:
( )
2 2 2
11
2
15
24
B F FM B M
a
EF
+−
==
- Gọi
là góc giữa hai mặt phẳng
()AEM
và
Ta có:
( )
;( )
sin
( ; )
d F AEM
d F AE
=
+) Ta có:
( ) ( ) ( )
11
;( ) ;( ) ;( )d F AEM d F AB M d K AB M==
( )
( )
( ) ( )
1
1
11
;( )
3
1
;( ) 2
3
;( ) ;( )
2
d K AB M
KM KD
d D AB M DM DM
d K AB M d D AB M
= = + =
=
Kẻ
( ) ( )
11
;( )DT AM DT B AM d D B AM DT⊥ ⊥ =
Ta có:
( )
. . .sin60 2
ADM
DT AM AD DM S= =
( )
( )
1
1
. .sin 60
;( )
22
3
;( )
4
AD DM a a
DT d D B AM
AM
a
d K B AM
= = =
=
+)
2
2 2 2 2
1
6
2 . .cos120
42
HD
a
AF AK KF AD DK AD DK

= + = + − + =


Xét tam giác
AEF
cân tại
E
. Kẻ
11
3
4
a
EE AF EE⊥ =
Kẻ
11
( ; )FF AE d F AE FF⊥ =
Ta có:
( )
1
1 1 1
.
33
. . 2 ( ; )
10 10
EAF
EE AF
aa
FF EA EE AF S FF d F AE
EA
= = = = =
Suy ra
( )
;( )
10 6
sin cos
( ; ) 4 4
d F AEM
d F AE

= = =
Câu 5: (1,5 điểm) Cho tứ diện
ABCD
và điểm
M
nằm trong tứ diện. Qua
M
dựng các
mặt phẳng
/ / BCD , / / ACD , / / ABD
và
/ / ABC .
Biết cắt
AB
tại
E,
cắt
BC
tại
F,
cắt
CD
tại
P,
cắt
AD
tại
Q.
Chứng minh
.
EA FB PC QD
EB FC P A
3
DQ
4
Giải:
Gọi
11
A AM BCD , B AM ACD
,
11
C AM ABD , D AM ABC
+) Trong mặt phẳng
1
ABA
kẻ đường thẳng qua M
song song với
1
AB
cắt AB tại
1
EA MA
E.
EB MA
+) Tương tự ta cũng có:
1
FB MB
,
FC MB
1
PC MC
,
PD MC
1
QD MD
.
QA MD
Khi đó:
EA FB PC QD
EB FC PD QA
1 1 1 1
MA MB MC MD
MA MB MC MD
Đặt
ABCD
V V,
MBCD a
V V ,
MACD b
V V ,
MABD c
V V ,
MABC d
V V .
Khi đó
1
BCD
BD
a
1
C
d M; BCD .S d M; BCD
V
MA
V AA
d A; BCD .S d A; BCD
a
1 1 1
1 1 1 a a
VV
AA MA AA
MA V
11
MA MA MA V V
3
b c d
b c d
aa
V
3V
V
VV
V V V
(1)
Tương tự ta có:
b
3
a
33
dcd
1
a a b
1
c
bd1 c
3 V 3 V 3 V
; ; .
V V V V V V
M
V
B MC MD
MB MC MDVV
(2)
Từ (1), (2) suy ra
1 1 1 1
.
MA MB MC MD
. . .
MA MB MC MD
81
Khi đó
4
1 1 1 1 1 1 1 1
M
3
A MB MC MD MA MB MC MD
. . .
MA MB MC MD
4
M
4
A MB MC MD
Đẳng thức xảy ra khi và chỉ khi
1 1 1 1
MA MB MC MD
3
MA MB MC MD
hay M là trọng tâm tứ diện.
| 1/11
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

LỜI GIẢI THAM KHẢO ĐỀ THI HSG TỈNH NGHỆ AN NĂM 2021-2022
Câu 1: (7,0 điểm)
a, Tìm tất cả các giá trị thực của tham số m để hàm số 6 3
y = f (x) = x − 5x + mx + 2 đồng
biến trên khoảng (0;+) Giải: Ta có: 5 2
y ' = 6x −15x + m .
Để hàm số đồng y đồng biến trên khoảng (0;+) thì y '  0 với x  (0;+) Hay 5 2
m h(x) = 6
− x +15x với x
 (0;+)  m  max h(x) (0;+) Xét hàm số 5 2 h(x) = 6
− x +15x trên (0;+) có 4 2
h '(x) = −30x + 30x x = 0(ktm) 
h '(x) = 0  x = 1 − (ktm)  x =1(tm) 
Ta có h(0) = 0;h(1) = 9;lim h(x) = −  max h(x) = 9 x→+ (0;+)
Vậy với m  9 thì hàm số 6 3
y = f (x) = x − 5x + mx + 2 đồng biến trên khoảng (0; +) 4 2 2
y −16y +15 = 2x(3y − 4x −17) 
b, Giải hệ phương trình  2 ( y + 2x −15)  ( 2 5x +1 − y + x + 3 ) =14 Giải: − ĐKXĐ: 1 x  5 4 2 2
y −16 y +15 = 2x(3y − 4x −17) 4 2 2
y − 2y (3x + 8) + 8x +14x + 35 = 0 2 2
 (y − 2x −1)(y − 4x −15) = 0 2  y = 2x +1   2  y = 4x +15 +) Với 2
y = 4x +15 thay vào phương trình còn lại, ta được: − x ( x + − x + ) 17 6 5 1 5 18 = 14  6 . x 5x +1 + 5x +18
 7( 5x +1+ 5x +18)+51x = 0(*) −  − −  − Vì 1 x  nên ta có 1 1 1 VT (*)  7  5. +1 + 5. +18  +51.  0   5 5 5 5  
Suy ra phương trình (*) vô nghiệm +) Với 2
y = 2x +1 thay vào phương trình còn lại, ta được:
(4x −14) ( 5x +1 − 3x + 4 ) =14  (2x − 7)( 5x +1 − 3x + 4 ) = 7
(2x − 7)(2x − 3) 
= 7  7( 5x +1 + 3x + 4)−(2x −7)(2x −3) = 0 5x +1 + 3x + 4 2
  245x + 49 − (5x + 7) −  147x +196 − (3x +14) − 4x + 28 = 0     2 2 175x − 25x 63x − 9x 2  + − 4x + 28x = 0
245x + 49 + (5x + 7)
147x +196 + (3x +14)    −x(x − 25 9 7)  + + 4 = 0(**)
 245x + 49 + (5x + 7)
147x +196 + (3x +14)  − Vì 1 x  nên 25 9 + + 4  0 5
245x + 49 + (5x + 7)
147x +196 + (3x +14)  = Nên (**) x 0   x = 7
Với x = 0  y = 1 
Với x = 7  y =  15
Vậy tập nghiệm của hệ phương trình ( ; x y) (0;1);(0; 1 − );(7; 15);(7;− 15)
Câu 2:(4,0 điểm)
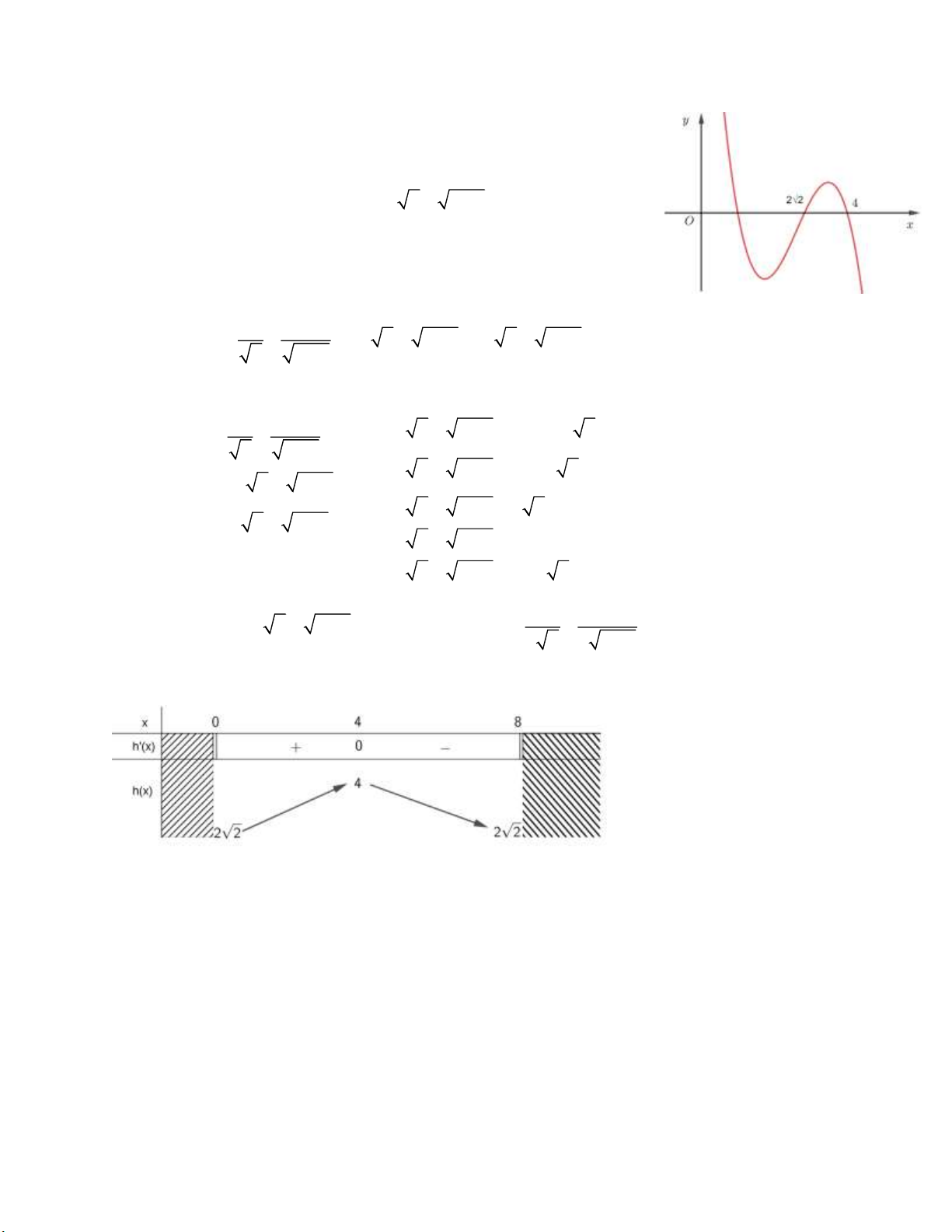
a, Cho hàm số bậc ba y = f (x) có đồ thị như hình bên. Tìm số
điểm cực trị của hàm số g x =  f  ( x + − x ) 2 ( ) 8   Giải:
Điều kiện: 0  x  8   Ta có: 1 1 g '(x) = − f ' 
 ( x + 8 − x ). f ( x + 8 − x )  x 8 − x  x = 4   1 1  − =
x + 8 − x = a   (0;2 2)(1) 0    x 8 − x     + − =   g x =
f ( x + − x ) x 8 x b (2 2;4)(2) '( ) 0 ' 8 = 0      + − = f  ( x + − x ) x 8 x 2 2(3) 8 = 0 
x + 8 − x = 4(4)  
 x + 8 − x = t  2 2(5) Xét hàm số ( h x) =
x + 8 − x trên 0;  8 có 1 1 h '(x) = −
; h '(x) = 0  x = 4 2 x 2 8 − x Bảng biến thiên
Dựa vào bảng biến thiên ta có
+)Phương trình (1); (5) vô nghiệm  =  +) (2) x c (0; 4)  
x = d (4;8)  = +) (3) x 0   x = 8
+) (4)  x = 4(kep)
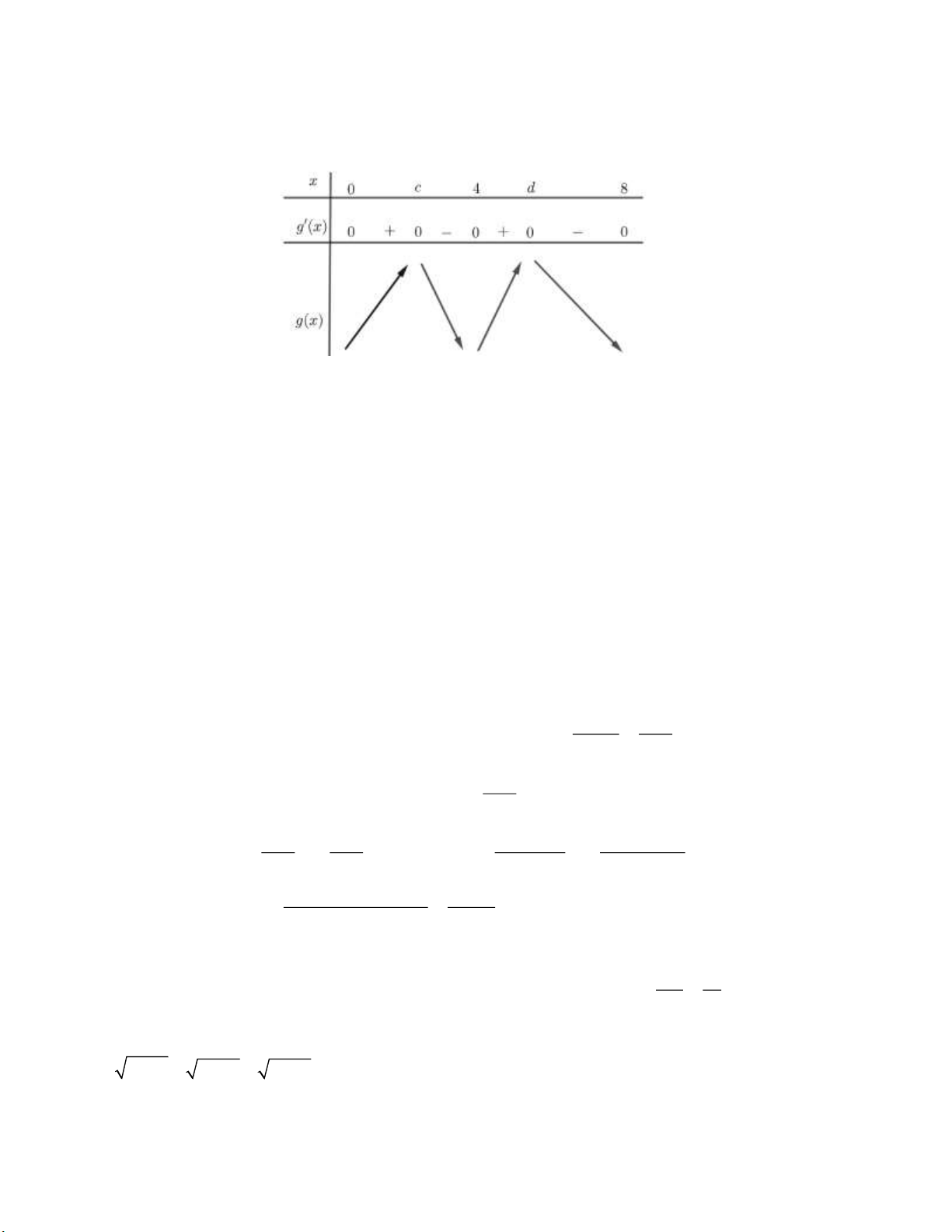
Bảng biến thiên của hàm số g(x) với 0  x  8
Vậy hàm số g(x) có 3 điểm cực trị
b, Trong quá trình truy vết lịch sử tiếp xúc của bệnh nhân Covid-19 ở một trường học,
trung tâm y tế xác định được 3 giáo viên và một số học sinh có sự liên quan đến bệnh
nhân đó. Người ta chọn ngẫu nhiên 10 người trong số các giáo viên và học sinh liên quan
để làm xét nghiệm gộp. Biết rằng xác suất để trong 10 người được chọn có 3 giáo viên
bằng 6 lần xác suất trong 10 người được chọn đều là học sinh. Tính xác suất để trong 10
người được chọn làm xét nghiệm có nhiều nhất 2 giáo viên. Giải:
Gọi số học sinh liên quan đến bệnh nhân Covid -19 là n(n 10) Ta có: n () 10 = C n+3 3 7 7 C .C C
Xác suất để chọn 10 người trong đó có 3 giáo viên bằng 3 n n = 10 10 C C n+3 n+3 10 C
Xác suất để chọn 10 người đều là học sinh là n 10 Cn+3 7 10 C C n! n! n n 7 10 = 6.  C = 6.C  = 6. 10 10 n n C C 7!(n − 7)! 10!(n −10)! n+3 n+3 1 6 Theo bài ra ta có:  =
 (n − 7)(n − 8)(n − 9) = 120 = 6.5.4
(n − 7)(n − 8)(n − 9) 8.9.10  n = 13 7 C 11
Vậy xác suất để trong 10 người có nhiều nhất 2 giáo viên là 13 P = 1− = 10 C 14 16
Câu 3:(1,5 điểm) Cho a, ,
b c là các số thực không âm thay đổi thỏa mãn điều kiện 2
1+ a + 1+ 2b + 1+ 2c = 5 . Tìm giá trị lớn nhất của biểu thức 3 3 3
P = 2a + b + c Giải:
Trước tiên, ta xét bài toán phụ sau:
Cho hai số thực x, y không âm. Chứng minh 1+ 2x + 1+ 2 y  1+ 1+ 2(x + y)
• Chứng minh: Vì x, y không âm nên ta có: xy  0
 (1+ 2x)(1+ 2y) 1+ 2(x + y)  (1+ 2x) + (1+ 2y) + 2 (1+ 2x)(1+ 2y) 1+ 2(x + y) + 2 1+ 2(x + y) +1
 ( 1+ 2x + 1+ 2y )2  (1+ 1+ 2(x + y))2
 1+ 2x + 1+ 2y 1+ 1+ 2(x + y)  = Dấu bằng xảy ra x 0    y = 0
Quay trở lại bài toán, ta có: 2
5 = 1+ a + ( 1+ 2b + 1+ 2c ) 2
 1+ a +1+ 1+ 2(b + c) 2 2
 4  1+ a + 1+ 2(b + c) 1+ 1+ a + 2(b + c) 2 8 − a 2
a + 2b + 2c  8  b + c  2 2 − Vì 8 a b + c  0 
 0  0  a  2 2 2 Ta có: 3 3 3 3
b + c = (b + c) − 3bc(b + c)  (b + c) vì bc  0 3 2  8 − a  3 3 3
P  2a + (b + c)  2a +    2  3 2  −  Xét hàm số 8 a 3
f (a) = 2a +   trên 0;2 2    có: 2  2 2  a  3 3 2 3 2 f (
a) = 6a − 3a4 −  = a(a − 2)(−a − 2a +12a +32) = a(a − 2) a  ( 2 12 − a ) 2 + 2(16 − a )  2  4 4 a = 0  f (
a) = 0  a = 2 a( 2 12 − a ) 2 + 2(16 − a ) = 0 2 2
a  0; 2 2   a(12 − a ) + 2(16 − a )  0   Vì  a = 0
f (a) = 0  a = 2
Hàm số f (a) liên tục trên 0;2 2 
 , đồng thời f (0) = 64; f (2) = 24; f (2 2) = 32 2
Suy ra max f (a) = f (0) = 64 a [  0;2 2 ]
Vậy giá trị lớn nhất của P bằng 64. Dấu bằng xảy ra khi a = b = 0;c = 4 hoặc
a = c = 0;b = 4
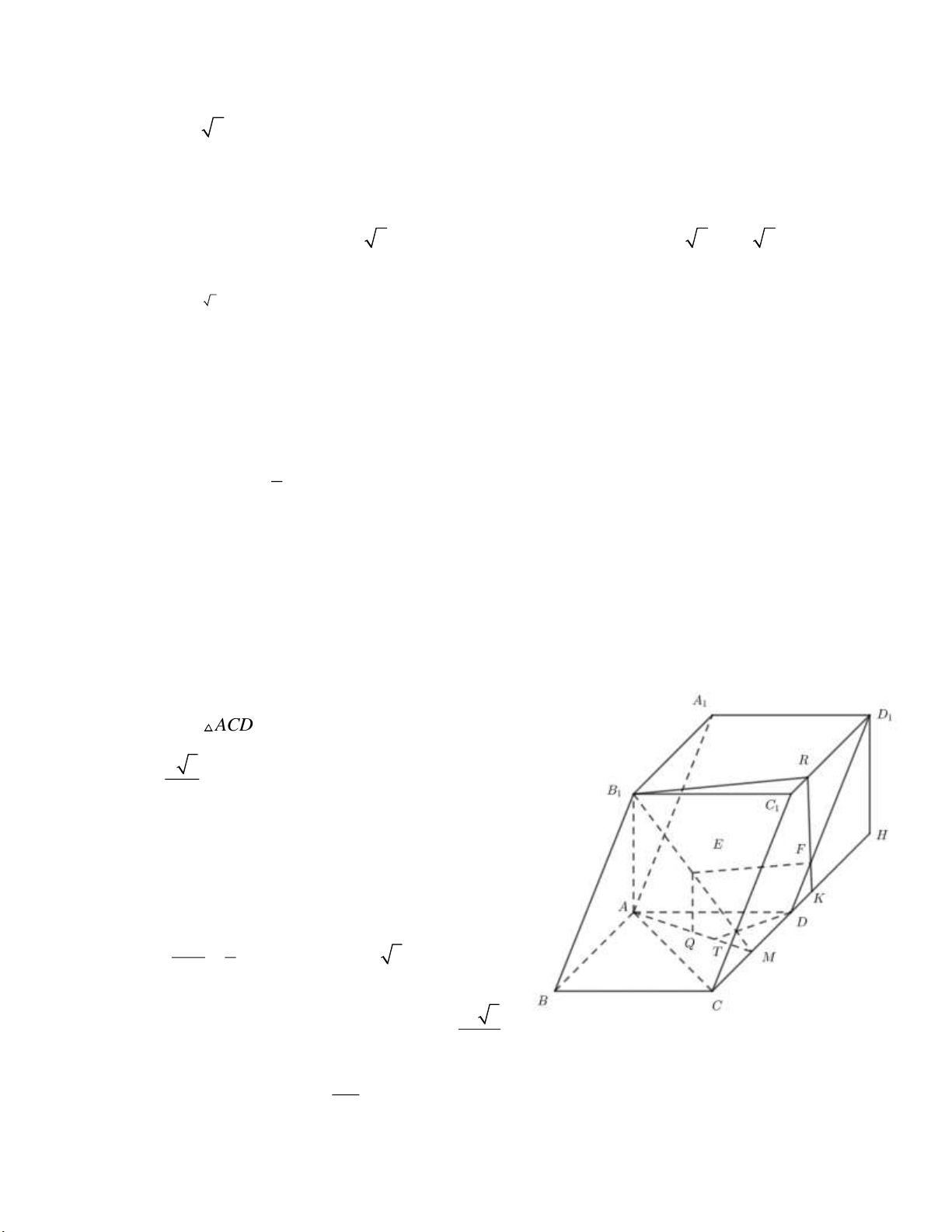
Câu 4: (6,0 điểm) Cho hình hộp ABC .
D A B C D có đáy ABCD là hình thoi cạnh bằng 1 1 1 1 a, A
BC = 60 và B A ⊥ (ABCD) . Biết góc giữa hai mặt phẳng (B CD và ( A B C D 1 1 1 1 ) 1 ) 1 bằng  với 1 cot  =
. Gọi M là trung điểm của C ,
D E là trung điểm của B M 2 1
a) Tính thể tích khối hộp ABC . D A B C D 1 1 1 1
b) Gọi F là điểm thuộc đường thẳng DD sao cho EF ⊥ AC . Tính độ dài đoạn EF và 1
cosin góc giữa hai mặt phẳng (AEM ) và ( AEF ) Giải:
a) Dễ thấy ACD đều suy ra AM ⊥ CD và a 3 AM = . Khi đó ta có: 2 CD  ⊥ B A 1 
CD ⊥ (B AM   = AMB 1 ) 1 CD  ⊥ AM
Xét tam giác vuông AMB có : 1 AM 1 cot  =
=  AB = 2AM = a 3 1 AB 2 1 2 Ta cũng có a 3 S = 2S = . BA BC.sin 60 = ABCD ABC 2 3 3aV = AB .S = ABCD. 1 A 1 B 1 C 1 D 1 ABCD 2 b)
- Từ AB = a 3  BA A = 60 ;  AAB =120 1 1 1 1
Kẻ D H ⊥ (ABCD); FK / /D H FK ⊥ (ABCD)  FK ⊥ AC 1 1  ⊥ Ta có: FK AC
AC ⊥ (EFK)  AC ⊥ EK EF ⊥ AC
Gọi Q là trung điểm của AM
EQ / /B A EQ ⊥ (ABCD)  EQ ⊥ AC 1  ⊥ Ta có: EK AC
AC ⊥ (EQK)  AC ⊥ QK EQ ⊥ AC
Dễ thấy AH / /BD AH ⊥ AC QK / / AH
Suy ra K là trung điểm của MH 1 1 a
DK = MK − MD = MH − MD = (MD + DH ) − MD = 2 2 4 DK 1 DF 1 1 1 1 a 2 2  = 
=  DF = DD = AA = B A + B A = 1 1 1 1 1 DH 4 DD 4 4 4 4 2 1  a 3 2 2
FM = FD + DM − 2 . FD DM .cos120 =  Ta cũng có: 2   a 15 2 2 B M = B A + AM = 1 1  2
Kẻ FR ⊥ ( A B C D FR / /C D 1 1 1 1 ) 1  FR D F 3 3 3 3a 3 1  =
=  FR = C D = B A = 1 1 C D DD 4 4 4 4 1 1   C R DF 1 C D a  1 1 1 = =  C R = = 1 C D DD 4 4 4  1 1 1 a 21 2 2
B R = B C + C R − 2.C . R B C .cos120 = 1 1 1 1 1 1 1 4 2 2
B F = B R + RF = a 3 1 1
Áp dụng công thức đường trung tuyến trong tam giác B FM ta có: 1 2( 2 2 B F + FM ) 2 − B M 1 1 a 15 EF = = 2 4
- Gọi  là góc giữa hai mặt phẳng (AEM ) và ( AEF )
d ( F;(AEM )) Ta có: sin  = d (F; AE)
+) Ta có: d (F;(AEM )) = d (F;(AB M ) = d K;(AB M ) 1 ) ( 1 )
d ( K;( AB M ) KM KD 3 1 ) = = + = d ( 1 ; D ( AB M ) DM DM 2 1 )  d ( 3 K; ( AB M ) = d ; D ( AB M ) 1 ) ( 1 ) 2
Kẻ DT ⊥ AM DT ⊥ (B AM d ;
D (B AM ) = DT 1 ) ( 1 )
Ta có: DT.AM = A .
D DM .sin 60(= 2S ADM ) . AD DM .sin 60 a  = =  ( a DT d ; D (B AM ) = 1 ) AM 2 2  ( 3a d K; (B AM ) = 1 ) 4 2 +)  HD a 6 2 2 2 2 1 AF = AK + KF =
AD + DK − 2A . D DK.cos120 + =    4  2 Xét tam giác 3a
AEF cân tại E . Kẻ EE ⊥ AF EE = 1 1 4
Kẻ FF ⊥ AE d(F; AE) = FF 1 1 Ta có: EE AF a a
FF .EA = EE .AF (= 2SFF = =  d F AE = EAF ) . 3 3 1 ( ; ) 1 1 1 EA 10 10
d ( F;(AEM )) Suy ra 10 6 sin  = =  cos  = d (F; AE) 4 4
Câu 5: (1,5 điểm) Cho tứ diện ABCD và điểm M nằm trong tứ diện. Qua M dựng các mặt phẳng / / BCD , / / ACD , / / ABD và / / ABC . Biết cắt AB tại E, cắt BC tại F, cắt CD tại P, cắt AD tại Q. EA FB PC QD Chứng minh 4 3. EB FC PD A Q Giải: Gọi A AM BCD , B AM ACD , 1 1 C AM ABD , D AM ABC 1 1
+) Trong mặt phẳng ABA kẻ đường thẳng qua M 1 song song với EA MA A B cắt AB tại E . 1 EB MA1 +) Tương tự ta cũng có: FB MB PC MC QD MD , , . FC MB PD MC QA MD 1 1 1 Khi đó: EA FB PC QD MA MB MC MD EB FC PD QA MA MB MC MD 1 1 1 1 Đặt V V, V V , V V , V V , V V . ABCD MBCD a MACD b MABD c MABC d V d M; BCD .S d M; BCD Khi đó BCD MA a 1 V d A; BCD .S d A; BCD AA BCD 1 MA AA MA AA V V V 3 V V V 3 V V V 1 1 1 a 1 1 b c d b c d (1) MA MA MA V V V V 1 1 1 a a a a 3 3 3 MB 3 V V V MC 3 V V V MD 3 V V V Tương tự ta có: a c d a b d a b c ; ; . (2) MB V MC V MD V 1 b 1 c 1 d MA MB MC MD Từ (1), (2) suy ra . . . . 81 MA MB MC MD 1 1 1 1 Khi đó MA MB MC MD MA MB MC MD 4 4 . . . 4 3 MA MB MC MD MA MB MC MD 1 1 1 1 1 1 1 1 Đẳ MA MB MC MD
ng thức xảy ra khi và chỉ khi
3 hay M là trọng tâm tứ diện. MA MB MC MD 1 1 1 1
Document Outline

  • de-thi-chon-hoc-sinh-gioi-tinh-toan-12-nam-2021-2022-so-gddt-nghe-an_Page_1-đã chuyển đổi
  • LỜI-GIẢI-THAM-KHẢO-ĐỀ-THI-HSG-TỈNH-NGHỆ-AN-NĂM-2021