Đề thi chọn học sinh giỏi tỉnh Toán THPT năm 2021 sở GD&ĐT Quảng Ninh

Thứ Ba ngày 21 tháng 12 năm 2021, sở Giáo dục và Đào tạo tỉnh Quảng Ninh tổ chức kỳ thi chọn học sinh giỏi cấp tỉnh THPT môn Toán năm học 2021 – 2022.

21 11 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 12

Môn: Toán 12

Thông tin:

16 trang 8 tháng trước

Tác giả:

Profile Nguyễn Vân
Trang 1/7 - WordToan
SỞ GIÁO DỤC VÀ ĐÀO TẠO
QUẢNG NINH
ĐỀ THI CHỌN HỌC SINH GIỎI LỚP 12
NĂM HỌC 2021 – 2022
MÔN THI: TOÁN(BẢNG A)
Thời gian: 90 phút (Không kể thời gian phát đề)
LỜI GIẢI CHI TIẾT
Lời giải được thực hiện bởi tập thể quý thầy cô: Trường Giang, Quỳnh Hương, Trần Xuân Thiện, Ký
Tống, Đường Ngọc Lan và Anh Tuấn.
Câu 1. a) Cho hàm số
2
2 1 4 4 2 5 7 4y x x m x m
có đồ thị là
m
C
, với
m
là tham số. Cho
đường thẳng
: 2 6d y x
và điểm
3;4I
. Tìm
m
để
d
cắt
m
C
tại ba điểm phân biệt
1;4A
,
B
,
C
sao cho tam giác
IBC
có diện tích bằng
4
.
Lời giải
Phương trình hoành độ giao điểm của đường thẳng
d
và đồ thị
m
C
:
2
2 1 4 4 2 5 7 4 2 6x x m x m x
2
2 1 4 4 2 5 7 2 1 0x x m x m x
2
2 1 4 4 2 5 6 0x x m x m
2
1
4 4 2 5 6 0 *
x
x m x m
.
Đường thẳng
d
cắt đồ thị
m
C
tại ba điểm phân biệt
*
có hai nghiệm phân biệt khác
1
2
2 2 4 5 6 0
4 4 2 5 6 0
m m
m m
2
; 1 2;
2 0
2
2
m
m m
m
m

.
Gọi
1
x
,
2
x
là nghiệm của phương trình (*).
Theo định lý Viét ta có
1 2
1 2
2
5 6
4
x x m
m
x x
.
Ta có tọa độ
1 1
;2 6B x x
,
2 2
;2 6C x x
. Suy ra
2 1 2 1
;2BC x x x x

.
Khi đó
2 2
2 1 2 1
4BC BC x x x x
.
Theo đề bài diện tích
IBC
bằng
4
, nên suy ra
2 2
2 1 2 1
2
2. 3 4 6
1 1
. .d , 4 . 4 .
2 2
2 1
IBC
S BC I BC x x x x
2 2
2 1 2 1 1 2
2 5 5 2 4x x x x x x
2
2
2 2 5 6 2 2m m m m
2
2
6 0
3
m
m m
m
.
Vậy
3m
thỏa mãn yêu cầu bài toán.
b) Một đại lý xăng dầu cần tìm một cái bồn chứa dầu hình trụ có thể tích bằng
3
125
4
m
. Tìm bán
kính đáy cùa bồn chứa dầu sao cho bồn chứa dầu được làm ra tốn ít nguyên vật liệu nhất.
Lời giải
b) Gọi bán kính đáy và chiều cao của bồn chứa dầu lần lượt là
x
,
( )h m
,
0, 0x h
.
Ta có:
2 2
2
125 125
4 4
V R h x h h
x
.
Để bồn chứa ít tốn nguyên vật liệu nhất thì diện tích toàn phần phải nhỏ nhất.
Trang 2/7 – Diễn đàn giáo viên Toán
Mà
2 2 2 2
125 125 125 125
2 2 2 2 2
2 2 4 4
p
S Rh R x x x
x x x x
.
Áp dụng BĐT AM-GM cho 3 số không âm
125
4x
,
125
4x
và
2
2x
, ta được:
2
3
125 125 75
3 2
4 4 2
p
S x
x x
.
Dấu " =" xảy ra khi và chỉ khi
2 3
125 5
2 8 125
4 2
x x x
x
(thỏa mãn).
Vậy để bồn chứa dầu ít tốn nguyên vật liệu thì bán kính đáy bằng
5
( )
2
m
.
Câu 2. a) Cho hàm số
3
( ) 3 2f x x x và hai số thực
a
,
b
thỏa mãn các điều kiện:
2022
log
2021 1
b
a
;
2021 2022
(log ) 2 (log )f a f b
. Tính
2022
log ( )a b
.
b) Cho tam giác
ABC
có các góc thỏa mãn điều kiện
3 2tan
tan
2 3tan
C
B
C
. Chứng minh ∆𝐴𝐵𝐶 có
một góc tù và tính diện tích hình tròn ngoại tiếp tam giác
ABC
, biết rằng
6BC
.
Lời giải
a) Xét hàm:
3 2
( ) 3 2 ( ) 3 3f x x x f x x
.
( ) 0 1f x x
.
Bảng biến thiên
Đặt
2021 2022
log , logu a v b .
Vì
2022
log
2021
b
a
nên
2021 2022
log log 0 0a b u v .
Lại có :
2021 2022
log 2 logf a f b
.
Nên
2f u f v f v f u
với mọi
0u v
.
Do đó :
, 0;1u v
. Khi đó từ
1
2
0
u
f v f u
v
.
Suy ra
2021a
và
1b
. Vậy
2022
log 1a b
.
b) Ta có:
3 2 tan sin 3cos 2sin
tan
2 3tan cos 2cos 3sin
2sin cos 3sin sin 3cos cos 2cos sin
2sin( ) 3cos( )
2sin 3cos .
C B C C
B
C B C C
B C B C B C B C
B C B C
A A
Vì sin A > 0 nên cosA < 0 suy ra góc A tù.
Ta có :
2 2
2 2
4sin 9cos 0
3
sin
13
sin cos 1
A A
A
A A
.
Áp dụng định lý Sin ta có
13
2sin
BC
R
A
.
Vậy diện tích hình tròn ngoại tiếp tam giác ABC là 13π.
Tổng hợp: Trần Minh Vũ Trang 3/7
Câu 3. a) Một hộp đựng
10
quả cầu được đánh số từ
1
đến
10
. Lấy ra
n
quả cầu từ
10
quả cầu
đó, biết xác suất lấy được ít nhất một quả cầu mà ghi số trên đó chia hết cho
5
trong
n
quả cầu
được lấy ra là
2
3
. Tìm
n
.
b) Tính giới hạn
3 2
2
2
9 4 2 7 6 1
lim
x
x x x x
I
x x x
.
Lời giải
a) Ta có
*
10
, 10
n
n C n n
.
Gọi
A
là biến cố lấy được ít nhất một quả cầu mà ghi số trên đó chia hết cho
5
trong
n
quả cầu đã
cho
1 1 2 2
2 8 2 8
. .
n n
n A C C C C
Ta có:
2
3
P A
1 1 2 2
2 8 2 8
10
. .
2
3
n n
n
C C C C
C
2.8! 8! 10!
3 2
1 ! 9 ! 2 ! 10 ! ! 10 !
n n n n n n
6 3 60
1 10 1 10
n n n n n
2
19 60 0
n n
4
15
n
n
.
Vậy
4
n
.
b) Ta có
3 2
3 2
2
2
2 2
9 4 1 2 7 6
9 4 2 7 6 1
lim lim
12 15 3 14 13
12 15 3 3 14 16
x x
x x x x
x x x x
I
x x x
x x x
2 2
8 4 4
2 2 3 2 3
9 4 1 9 4 1
lim lim
12 24 12
2 3 8 3 8
12 15 3 12 15 3
x x
x
x x x x x
x x
x
x x x
x x
=
2
2
2 2
2
8
2 1
4
2 2 3 2
9 4 1
9
9 4 1
lim lim
12 24
7
2 3 6 3
12 15 3
12 15 3
x x
x
x x
x
x
x
x
x
.
Câu 4. Cho hình chóp .
S ABC
có đáy
ABC
là tam giác vuông tại
A
, góc
0
90 , 6, 3
SBA SCA AB a AC a
, khoảng cách từ
C
đến
SAB
bằng
12a
7
.
a) Tính thể tích khối chóp .
S ABC
.
b) Gọi
,
O M
lần lượt là trung điểm của
,
BC SC
;
P
là mặt phẳng chứa
BM
và song song với
AO
. Gọi góc giữa
SB
và
P
là
. Tính
sin
.
c) Tính bán kính mặt cầu ngoại tiếp hình chóp
.
M ABC
.
Lời giải
Trang 4/7 – Diễn đàn giáo viên Toán
a) Gọi
D
là hình chiếu của
S
trên
mp ABC
. Ta có:
AB SB
AB SBD AB BD
AB SD
.
AC SC
AC SCD AC CD
AC SD
.
ABDC
là hình chữ nhật.
Kẻ đường cao
DH
của tam giác. Ta có:
12a
, ,
7
DH SB
DH SAB DH d D SAB d C SAB
DH AB
.
Trong
SBD
vuông tại
D
, ta có:
2 2 2 2 2 2
1 1 1 49 1 1
12
144 3
SD a
DH SD BD a SD a
.
Vậy:
3
.
1 1 1 1 1
. . . . . .12 . 3. 6 6 2
3 3 2 3 2
S ABC ABC
V SD S SD AC AB a a a a
.
b) Gọi
I
là giao điểm của
SO
và
BM I P SAD P SAD EF
, với
EF
đi qua
I
và song song
AD
,
,E SA F SD
.
Gọi
K
là trung điểm của
/ /CD MK SD MK ABDC
.
2
6
. . . . . 3 . 6 0
2
a
BK AD BD DK AB AC BD AB BD AC DK AB DK AC a a
 
BK AD AD BMK AD BM
, mà
/ /EF AD EF BM
.
Ta có:
2 2 2 2
3a 3a; D 7 3 ;BC AB AC AD SB S BD a
2 2 2
2 2
9 2
D 5 6
2 4 2
SB BC SC a
SC S DC BM
Do
I
là trọng tâm
SBC
nên
2
2a
3
EF AD
.
Tổng hợp: Trần Minh Vũ Trang 5/7
Vậy
2
1 1 9 2 9 2
. .2a. .
2 2 2 2
BEMF
S EF BM a a
Ta có:
.
. . .
.
2 2 1
. . V V V ;
9 9 9
S MEF
S MEF S CAD S ABDC
S CAD
V
SM SE SF
V SC SA SD
.
. . .
.
4 4 2
.
9 9 9
S BEF
S BEF S BAD S ABDC
S BAD
V
SE SF
V V V
V SA SD
3
.
. . . . .
3
1 2 8
4 2 ;
3 3 3
S BEMF
S BEMF S MEF S BEF S ABDC S ABC
BEMF
V
a
V V V V V a d S BEMF
S
.
Vậy:
;
8 3
sin
63
d S BEMF
SB
.
c) Do
ABDC
là hình chữ nhật nên mặt cầu ngoại tiếp hình chóp .
M ABC
cũng là mặt cầu ngoại
tiếp hình chóp .
M ABDC
.
Xét tam giác
DMC
có
5 6
2 2
SC
DM MC a MDC
cân tại
M
.
Gọi
P
là tâm đường tròn ngoại tiếp
MDC P
thuộc đường thẳng
MK
.
Gọi
r
là bán kính đường tròn ngoại tiếp
MDC
, ta có:
2 2 2
23 4 6 25
sin
2 . 25 25 8
2sin
MD MC DC DC a
cosDMC DMC r
MD MC
DMC
Dựng đường thẳng
d
đi qua
P
và vuông góc với
DMC d
là trục đường tròn ngoại tiếp
MDC
.
Dựng đường thẳng
đi qua
O
và vuông góc với
ABC
là trục đường tròn ngoại tiếp
ABC
.
Gọi
Q
là giao điểm của
d
và
Q
là tâm mặt cầu ngoại tiếp hình chóp .
M ABC
.
Gọi
R
là bán kính mặt cầu ngoại tiếp hình chóp .
M ABC
, ta có:
2
2
2 2 2 2
25 3 673
8 2 8
a a
R MP PQ MP OK a
.
Câu 5. Giải hệ phương trình
3
3
1 1
1 1
3
2
3 3 3 6
3 48 2 6 24 4 6
x
y
x y
x y x
.
Lời giải
Điều kiện
6
4
x
y
.
Trang 6/7 – Diễn đàn giáo viên Toán
Ta có
3
3
1 1
1 1
3
3 3 3 6
x
y
x y
3
3
1 1
1 1
3
3 3 1 3 3 1
3
x
y
x
y
1 1
3
x
f f y
,
với
3
1
3 3
t
f t t
.
Hàm số
3
1
3 3
t
f t t
đồng biến trên
0;

.
Khi đó
1 1 1 1 3 6
3 3
x x
f f y y x y
.
Thay
3 6
x y
vào phương trình
2
3 48 2 2 12 4 6
x x x
.
Điều kiện của phương trình
6 6
x
2 2
3 48 2 2 12 4 6 3 48 2 2 12 2 6
x x x x x x
2 2 2 2
6 6 6 6
3 48 8 144 16 72 2 16 72 2 3 8 96
x x
x x x x x x
2
2
4 3
2 2
6 6,3 8 96 0
6 6,3 8 96 0
9 48 1536 9216 0
16 72 2 3 8 96
x x x
x x x
x x x
x x x
2
2
2
2 2
2
6 6,3 8 96 0
6 6,3 8 96 0
3 96 0
3 96 3 16 96 0
3 16 96 0
x x x
x x x
x
x x x
x x vn
2
6 6,3 8 96 0
4 2
4 2
4 2
x x x
x
x
x
Thay
4 2
x vào (3) ta được
4 2 6
3
y
. Hệ phương trình có nghiệm là
4 2 6
; 4 2;
3
x y
.
Câu 6. Cho
, , 0
a b c
thỏa mãn
1, ( ) 3
ab c a b c
. Tìm giá trị nhỏ nhất của
2 2
6ln 2
1 1
b c a c
P a b c
a b
.
Lời giải
Ta có:
2 2
2 1 1 6ln 2
1 1
b c a c
P a b c
a b
2 1 2 1
6ln 2
1 1
a b c a b c
a b c
a b
1 1
2 1 6ln 2
1 1
a b c a b c
a b
.
Ta lại có:
1 1 1 1
1 1
1 1
a b
ab ab
1 1 1 1
ab a ab b
a ab b ab
Tổng hợp: Trần Minh Vũ Trang 7/7
1 1
1
b a a b
a b
ab
.
1 1
1
a b ab a b
b a
a b
ab
2
1
0, , 0; 1
1 1 1
a b ab
do a b ab
ab a b
1 1 2 2 4 4 4
1
1 1 3
1
1
2
ab
a b ab ab c a b c a c b c
ab
2 1 2 1
2 6ln 2
1 1
a b c a b c
P a b c
a b
.
1 1
2 1 6ln 2
1 1
a b c a b c
a b
.
Đặt
2 0t a b c
ta có
2
16 1
2 6ln
t
P t
t
.
Xét hàm số
2
16 1
6ln
t
f t t
t
2
3
6 16 32
0 4
t t
f t f t t
t
.
4 5 6ln 4f
3 6ln 4 min 3 6ln 4.P P
Dấu bằng xảy ra khi
1a b c
.
HẾT
SỞ GIÁO DỤC VÀ ĐÀO TẠO
QUẢNG NINH
ĐỀ THI CHỌN HỌC SINH GIỎI LỚP 12
NĂM HỌC 2021 – 2022
MÔN THI: TOÁN(BẢNG B)
Thời gian: 90 phút (Không kể thời gian phát đề)
Câu 1. [HSG-QUẢNG NINH-B 2021-2022] a) Cho hàm số
2
2 1 4 4 2 5 7 4y x x m x m
có
đồ thị là
m
C
, với
m
là tham số và đường thẳng
: 2 6d y x
. Tìm
m
để
d
cắt
m
C
tại 3 điểm
phân biệt
1;4A
,
,B C
sao cho 2 5BC .
Lời giải
Xét phương trình hoành độ giao điểm:
2
2
2
2 1 4 4 2 5 7 4 2 6
2 1 4 4 2 5 7 2 1 0
2 1 4 4 2 5 5 0
2 1 0 *
x x m x m x
x x m x m x
x x m x m
x g x
Để
d
cắt
m
C
tại 3 điểm phân biệt
1;4A
,
,B C
thì phương trình
2
4 4 2 5 5 0x m x m
phải có hai nghiệm phân biệt ,
B C
x x khác
1
. Điều kiện đó tương đương với
2
1 5
2
4 0
1 5
4 1 0
2
1 1 0
1
m
a
m m m
g m
m
.
Khi đó toạ độ 2 giao điểm
,B C
là
;2 6 , ;2 6
B B C C
B x x C x x
với
2
5 1
4
B C
B C
x x m
m
x x
.
Theo giả thiết
2
2
2 5 20 5 20
C B
BC BC x x
2 2 2
4 4 4 2 5 1 4
C B C B C B
x x x x x x m m
2
1 21
2
5 0
1 21
2
m
m m
m
thoả mãn điều kiện.
Câu 1. [HSG-QUẢNG NINH-B 2021-2022] b) Một đại lý xăng dầu cần làm một cái bồn chứa dầu hình trụ
có thể tích bằng
3
125
4
m
. Tính bán kính đáy của bồn chứa dầu sao cho bồn chứa dầu được làm ra
tốn ít nguyên liệu nhất?
Lời giải
Gọi
,r h m
lần lượt là bán kính đáy và chiều cao của chiếc bồn
, 0r h
.
Theo giả thiết ta có:
2
125 125
4 4
V r h h
r
.
Để bồn chứa dầu được làm ra tốn ít nguyên liệu nhất thì diện tích toàn phần của chiếc bồn hình trụ
phải nhỏ nhất.
Tacó diện tích toàn phần của chiếc bồn là:
2 2
125 125
2 2 2
4 4
tp
S r r r
r r
.
Xét hàm số
2
125
2
4
f r r
r
trên khoảng
0;
.
Ta có
3
2
125 8 5
2 ; 0 0;
4 2
r
f r f r r
r
.
Ta tính được giá trị nhỏ nhất của hàm số
2
125
2
4
f r r
r
ứng với
5
2
r m
.
Câu 2. [HSG-QUẢNG NINH-B 2021-2022]
a) Cho
, ,
a b c
là các số thực dương khác 1 thỏa mãn:
6
2022
1
log 3;log 2;log
3
a c
a b b
. Tính
4
9
2022
log
abc
.
b) Cho tam giác
ABC
có các góc thỏa mãn điều kiện
3 2tan
tan
2 3tan
C
B
C
. Chứng minh
ABC
có một
góc tù và tính diện tích hình tròn ngoại tiếp tam giác
ABC
, biết rằng
6
BC
.
Lời giải
a)
3
2022
4
4
4 12 21
9
9
2022 2022
6
6
log 3
2022
28
log 2 2022 log log 2022
3
1
2022
log
3
a
c
a
a
b b a abc
c b
b
.
b) Vì
, ,
A B C
là ba góc của một tam giác nên
0 , , 180
A B A C
. Với điều kiện này ta có:
3
tan
3 2tan
2
tan tan
3
2 3tan
1 tan
2
C
C
B A C
C
C
tan tan
A C C
, (với
3
tan
2
)
tan tan
A
3
tan 0
2
A
suy ra góc
A
tù hay
ABC
có một góc tù (đpcm).
2
3 2 1 13 3 13
tan cot sin
2 3 sin 9 13
A A A
A
.
Gọi
R
là bán kính đường tròn ngoại tiếp tam giác
ABC
ta có
3 13 9 13
2 sin 6.
13 13
R BC A R
.
Diện tích hình tròn ngoại tiếp tam giác
ABC
là:
2
81
13
S R
.
Câu 3. [HSG-QUẢNG NINH-B 2021-2022]
a) Cho đa thức
3 5
2
n
P x x
biết
n
thỏa mãn
2 3
3 5 2
n n
A C n
,
n
. Tìm hệ số của
7
x
trong
khai triển của
P x
.
b) Tính giới hạn
2
2
2 3 9 4 3
lim
12 15 2 7
x
x x x x
I
x x
.
Lời giải
a) Ta có
2 3
! !
3 5 2 3 5 2
2 ! 3! 3 !
n n
n n
A C n n
n n
2
5
3 1 1 2 2
6
18 1 5 1 2 12
5 33 40 0
5
8
.
5
n n n n n n
n n n
n n
n
n
Do đó
20
2
P x x
.
Số hạng tổng quát:
20
20
2
k
k k
C x
,
k
k n
.
Theo yêu cầu bài toán:
20 7 13
k k
.
Vậy hệ số của
7
x
trong khai triển là
13
13
20
2
C
.
b) Ta có
2
2
2
2
2
2 2
2 3 9 4 3
lim
12 15 2 7
2 3 9 4 1 6
lim
12 15 2 7
2 3 9 4 1
6
lim lim .
12 15 2 7 12 15 2 7
x
x
x x
x x x x
I
x x
x x x x
x x
x x
x x
x x x x
Ta tính
1
2
2
2
2
2
2
2
2 3 9 4 1
lim
12 15 2 7
2 3 9 4 1 12 15 2 7
lim
9 4 1 12 15 4 28 49
4 2 3 2 12 15 2 7
lim
9 4 1 4 40 64
4 2 3 2 12 15 2 7
lim
4 9 4 1 2 8
2 3 12 15 2 7
lim
9 4 1 8
1
.
2
x
x
x
x
x
x x
I
x x
x x x x
x x x x
x x x x
x x x
x x x x
x x x
x x x
x x
2
2
2
2 2
2 2
2 3 12 15 2 7
6
lim lim
4 40 64
12 15 2 7
2 3 12 15 2 7 3 12 15 2 7
lim lim
4 8 2 4 8
5
.
4
x x
x x
x x x x
x x
I
x x
x x
x x x x x x x
x x x
Vậy
1 5 3
2 4 4
I
.
Câu 4. [HSG-QUẢNG NINH-B 2021-2022] Cho hình chóp
.S ABC
có đáy
ABC
là tam giác vuông tại
A
,
góc
90SBA SCA
,
6AB a
,
3AC a
, khoảng cách từ
C
đến
SAB
bằng
12
7
a
.
a) Tính thể tích khối chóp
.S ABC
.
b) Gọi
O
,
M
lần lượt là trung điểm của
BC
,
SC
;
P
là mặt phẳng chứa
BM
và song song với
AO
. Tính khoảng cách từ điểm
S
đến mặt phẳng
P
.
c) Tính bán kính mặt cầu ngoại tiếp hình chóp
.M ABC
.
Lời giải
a) Dựng hình chữ nhật
ABDC SD ABCD
.
Do
1
AC CD
AC SCD SD AC
AC SC
.
Tương tự:
2SD AB
.
Từ (1) và (2) suy ra
SD ABCD
.
Đặt
, 0SD x x
.
Kẻ
,DH SB H SB DH SAB
.
Suy ra
d ,D SAB
2 2 2 2
. 3.
3
BD SD a x
DH
BD SD a x
.
Do
2 2
12 3.
/ / d , d ,
7
3
a a x
CD AB C SAB D SAB
a x
2 2
12 3 7 3.a x x
2 2
12 3 7 3.a x x
2 2 2
144 3 147a x x
2 2
144 12a x x a
.
Suy ra
12SD a
.
Vậy thể tích khối chóp
.S ABC
là
3
1 1 1
. . .12 . . 6. 3 6 2
3 3 2
ABC
V SD S a a a a
(đvtt).
b)
Gọi
BM SO I
.
Khi đó
I
là trọng tâm
SBC
.
Kẻ đường thẳng đi qua
I
và song song với
AD
, lần lượt cắt
SA
và
SD
tại
N
và
Q
.
Do
/ / 2
SI SQ
IQ OD
IO QD
.
Mặt khác
.
3
. .
.
1 2 1 1 1 1 1
. . . . . . .12 . 3. 6 2 2
2 3 3 3 3 6 18
S MQB
S MQB S CDB
S CDB
V
SM SQ
V V SD DB DC a a a a
V SC SD
Ta có
2
2 2 2 2 2
1
.12 3 19 19
3
BQ QD BD a a a BK a
.
Mặt khác
2 2 2 2 2 2
144 3 147 147SB SD DB a a a SB a ;
2 2 2 2 2 2
144 6 150 5 6SC SD DC a a a SC a ;
2 2 2 2
6 3 3BC AB AC a a a
.
Áp dụng công thức đường trung tuyến vào
SBC
ta có
2 2 2 2 2 2 2
2
147 9 150 81 9 2
2 4 2 4 2 2
SB BC SC a a a
MB MB a
.
Áp dụng định lý cosin vào
SMQ
ta có
2 2 2 2 2
2. . .cos 2. . .cosMQ SM SQ SM SQ MSQ SM SQ SM SQ MSQ
2 2
2. . .
SD
SM SQ SM SQ
SC
2 2
1 4 1 2
2. . . . .
4 9 2 3
SD
SC SH SC SD
SC
2
2 2 2 2 2 2 2
1 4 2 1 2 1 2 11 22
. . .150 .144
4 9 3 4 9 4 9 2 2
a a
SC SD SD SC SD a a MQ
.
Áp dụng hệ quả định lý cosin vào
MBQ
ta có
2 2
2
2 2 2
81 11
19
3 38 19
2 2
cos sin
2. . 19 19
9 2
2. . 19
2
a a
a
MB BQ MQ
MBQ MBQ
MB BQ
a a
.
Diện tích
MBQ
là
2
1 1 9 2 19 9 2
. . .sin . . 19.
2 2 2 19 4
MBQ
a
S MB BQ MBQ a a
(đvdt).
Vậy
3
.
2
3
3.2 2 8
d , d ,
3
9 2
4
S MBQ
MBQ
V
a a
S P S MBK
S
a
.
c) Dựng đường thẳng
d
đi qua
O
và song song với
SD
.
Khi đó
d
là trục đường tròn ngoại tiếp
ABC
.
Suy ra tâm mặt cầu ngoại tiếp hình chóp
.M ABC
là điểm
G d
.
Gọi
N
là hình chiếu vuông góc của
M
trên
CD
. Suy ra
/ /GO MN
và
1
6
2
MN SD a
.
Ta có
2 2
2 2 2
R GB GM GO OB GO ON NM
  
2 2 2 2 2
2. . 2. . . .GO OB GOOB GO ON NM GO ON GO NM ON NM
2 2 2 2 2
2. .GO OB GO ON NM GO NM
Do
, ,GO OB GO ON ON NM
.
Suy ra
2
2
2
2 2 2 2
1 3 1 69
2. . .9 .12
4 2 2 2
a a
GO NM OB ON NM a a

2
2 2
69 23 673
2. .6 .cos180
2 8 8
a a a
GO a GO R GO OB
.
Câu 5. [HSG-QUẢNG NINH-B 2021-2022] Giải hệ phương trình
3 8
2
2
2 2 3 6
3 13 6 24 2 6 5
y
x
x y
x y x
.
Lời giải
Điều kiện
2 6
8
3
x
y
.
Ta có
3 8
2
2 2 3 6
y
x
x y
3 8
2
2 2 2 3 8
y
x
x y
2 3 8
f x f y
,
với
2
t
f t t
.
Do
1
2 . .ln 1 0, 0
2
t
f t t t
t
suy ra hàm số hàm số
2
t
f t t
đồng biến trên
0;

.
Khi đó
2 3 8 2 3 8 3 6
f x f y x y y x
.
Thay
3 6
y x
vào phương trình
2
3 13 6 24 2 6 5
x y x
ta được
2
3 13 2 12 2 6 5
x x x
2
3 13 5 2 12 2 6 0
x x x
2
3 13 5 2 12 2 6 0
x x x
2
2
2 12 4 6
3 12
0
2 12 2 6
3 13 5
x x
x
x x
x
2
3 6 6
2 0
2 12 2 6
3 13 5
x
x
x x
x
2
2
3 6 6
0( )
2 12 2 6
3 13 5
x
x
vn
x x
x
.
Với
4
2
3
x y
.
Vậy hệ phương trình đã cho có nghiệm
2
4
3
x
y
.
Câu 6. [HSG-QUẢNG NINH-B 2021-2022] Cho
, , 0
a b c
thỏa mãn
1, ( ) 3
ab c a b c
. Tìm giá trị nhỏ
nhất của
3 2
2 2
1 1 2
a b c
b c a c
P
a b
.
Lời giải
Ta có:
2 2 3
2 1 1 2
1 1 2
b c a c
P a b c
a b
2 1 2 1 3
2
1 1 2
a b c a b c
a b c
a b
1 1 3
2 1 2
1 1 2
a b c a b c
a b
.
Ta lại có:
1 1 1 1
1 1
1 1
a b
ab ab
1 1 1 1
ab a ab b
a ab b ab
1 1
1
b a a b
a b
ab
.
1 1
1
a b ab a b
b a
a b
ab
2
1
0, , 0; 1
1 1 1
a b ab
do a b ab
ab a b
1 1 2 2 4 4 4
1
1 1 3
1
1
2
ab
a b ab ab c a b c a c b c
ab
2 2
4 16
2
2
a b c
a c b c
.
Suy ra:
2
16 2 1
3
2 2
2
2
a b c
P a b c
a b c
.
Đặt
2 0
t a b c t
.
Do
1, ( ) 3 4
ab c a b c ab c a b c
4
a c b c
2
2
4 4
2 4
a c b c t
a c b c t
.
Khi đó:
2 2
16 1
3 16 16
2 2
2 4 4
t
t t
P t t
t t t
2
16 16
2 . 3 . . 2 9
4 4
t t
t
t t
.
Vậy:
min 9
P
khi
1.
a b c
HẾT
| 1/16
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI CHỌN HỌC SINH GIỎI LỚP 12 QUẢNG NINH NĂM HỌC 2021 – 2022 MÔN THI: TOÁN(BẢNG A)
Thời gian: 90 phút (Không kể thời gian phát đề) LỜI GIẢI CHI TIẾT
Lời giải được thực hiện bởi tập thể quý thầy cô: Trường Giang, Quỳnh Hương, Trần Xuân Thiện, Ký
Tống, Đường Ngọc Lan và Anh Tuấn. Câu 1.
a) Cho hàm số y  x   2 2
1 4x  4 m  2 x  5m  7  4  
có đồ thị là C , với m là tham số. Cho m 
đường thẳng d  : y  2x  6 và điểm I 3;4 . Tìm m để d  cắt C tại ba điểm phân biệt m 
A1;4, B , C sao cho tam giác IBC có diện tích bằng 4 . Lời giải
Phương trình hoành độ giao điểm của đường thẳng d  và đồ thị C : m  x   2 2
1 4x  4m  2 x  5m  7  4  2x  6     x   2 2
1 4x  4 m  2 x  5m  7  2 x 1  0   x  1   x   2 2
1 4x  4 m  2 x  5m  6  0     . 2 4x  4 
m  2 x 5m  6  0 *
Đường thẳng d  cắt đồ thị C tại ba điểm phân biệt  * có hai nghiệm phân biệt khác 1  m 
   m   2 2 2   4  5m  6  0 2 m  m  2  0 m ;    1  2;        . 4  4 
m  2  5m  6  0 m  2  m  2 
Gọi x , x là nghiệm của phương trình (*). 1 2 x  x  m  2 1 2 
Theo định lý Viét ta có  5m  6 . x x   1 2  4 
Ta có tọa độ B  x ;2x  6 , C  x ;2x  6 . Suy ra BC  x  x ;2 x  x . 2 1  2 1 2 2  1 1  
Khi đó BC  BC  x  x 2  4x  x 2 . 2 1 2 1
Theo đề bài diện tích IBC bằng 4 , nên suy ra 1    S  BC I BC   x  x  x  x I  BC   1 . .d , 4 .  2. 3 4 6 4 . 2 1 2  2 12  2 2 2 2 1
 2 5  5 x  x 2  2  x  x 2  4x x   m  2 2 2
2  5m  6  2  m  m  2 2 1 2 1 1 2 m  2  2
 m  m  6  0   . m  3
Vậy m  3 thỏa mãn yêu cầu bài toán. 125
b) Một đại lý xăng dầu cần tìm một cái bồn chứa dầu hình trụ có thể tích bằng  3 m  . Tìm bán 4
kính đáy cùa bồn chứa dầu sao cho bồn chứa dầu được làm ra tốn ít nguyên vật liệu nhất. Lời giải
b) Gọi bán kính đáy và chiều cao của bồn chứa dầu lần lượt là x , h ( ) m ,  x  0, h  0. 125 125 Ta có: 2 2 V   R h    x h  h  . 2 4 4x
Để bồn chứa ít tốn nguyên vật liệu nhất thì diện tích toàn phần phải nhỏ nhất. Trang 1/7 - WordToan 125 125  125 125  Mà 2 2 2 2
S  2 Rh  2 R    2 x    2x     2x . p     2x  2x   4x 4x  125 125
Áp dụng BĐT AM-GM cho 3 số không âm , và 2 2x , ta được: 4x 4x 125 125 75 2 3 S   3   2x  . p 4x 4x 2 125 5
Dấu " =" xảy ra khi và chỉ khi 2 3
 2x  8x  125  x  (thỏa mãn). 4x 2 5
Vậy để bồn chứa dầu ít tốn nguyên vật liệu thì bán kính đáy bằng (m) . 2 Câu 2. a) Cho hàm số 3
f (x)  x  3x  2 và hai số thực a , b thỏa mãn các điều kiện: log2022 2021 b a  1; f (log a)  2  f (log b) . Tính log (a  b) . 2021 2022 2022 3  2 tan C
b) Cho tam giác ABC có các góc thỏa mãn điều kiện tan B 
. Chứng minh ∆𝐴𝐵𝐶 có 2  3tan C
một góc tù và tính diện tích hình tròn ngoại tiếp tam giác ABC , biết rằng BC  6 . Lời giải a) Xét hàm: 3 2
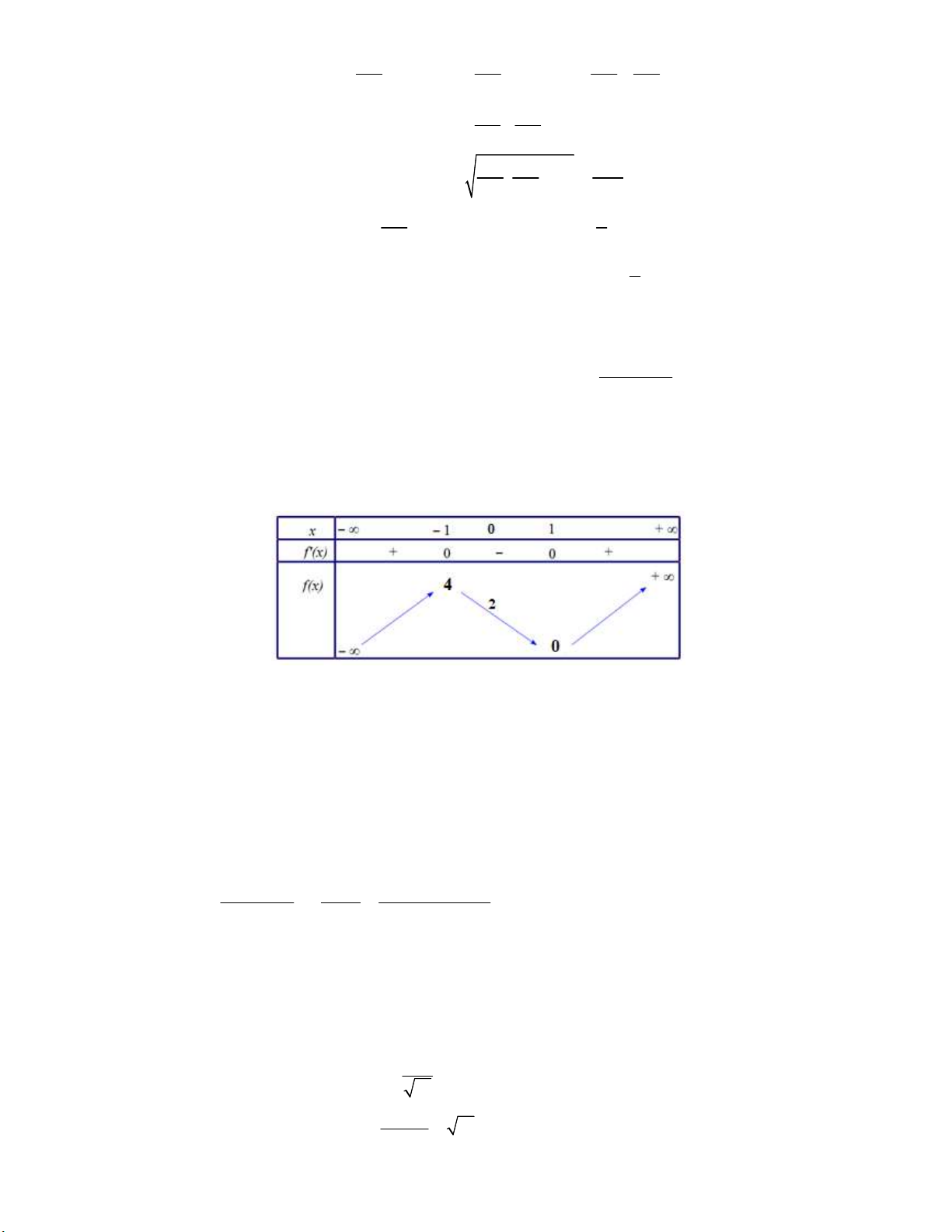
f (x)  x  3x  2  f (  x)  3x  3. f (  x)  0  x  1  . Bảng biến thiên Đặt u  log a, v  log b . 2021 2022 Vì log2022 2021 b a  nên log a  log b  0  u  v  0 . 2021 2022 Lại có : f log a  2  f log b . 2021   2022 
Nên f u  2  f v  f v  f u  với mọi u  v  0 . u  Do đó : u,v 0; 
1 . Khi đó từ f v  f u 1  2   . v  0
Suy ra a  2021 và b  1 . Vậy log a  b  1. 2022   b) Ta có: 3  2 tan C sin B 3cosC  2sin C tan B    2  3 tan C cos B 2cos C  3sin C
 2sin B cosC  3sin B sin C  3cos B cosC  2cos B sin C
 2sin(B  C)  3cos(B  C)  2sin A  3cos . A
Vì sin A > 0 nên cosA < 0 suy ra góc A tù. Ta có : 2 2 4sin A9cos A  0 3   sin A  . 2 2 s  in A cos A 1 13 BC
Áp dụng định lý Sin ta có R   13 . 2sin A
Vậy diện tích hình tròn ngoại tiếp tam giác ABC là 13π.
Trang 2/7 – Diễn đàn giáo viên Toán Câu 3.
a) Một hộp đựng 10 quả cầu được đánh số từ 1 đến 10 . Lấy ra n quả cầu từ 10 quả cầu
đó, biết xác suất lấy được ít nhất một quả cầu mà ghi số trên đó chia hết cho 5 trong n quả cầu 2
được lấy ra là . Tìm n . 3 3 2
9  4x  2x  7x  6x 1
b) Tính giới hạn I  lim . 2 x2 12x 15  3x 14x 13 Lời giải a) Ta có  n n  C  * n   , n 10 . 10 
Gọi A là biến cố lấy được ít nhất một quả cầu mà ghi số trên đó chia hết cho 5 trong n quả cầu đã cho n  A 1 n 1  2 n2  C .C  C .C 2 8 2 8 1 n 1  2 n2 C .C  C .C 2 Ta có: P  A 2  2 8 2 8   3 n C 3 10  2.8! 8!  10!  3    n     n n    n 2 1 ! 9 ! 2 ! 10 ! n  !10 n! 6 3 60 n  4    2  n 19n  60  0  . n 1 10  n n n   1 10  n  n  15 Vậy n  4 . b) Ta có       94x   3 2 3 2 1  2x  7x  6 9 4 2 7 6 1 x x x x x I  lim  lim 2 x2 x2 12x 15  3x 14x 13  12x15 3 2  3x 14x 16 8  4x 
 x x   x   4 2 2 3  x 2x  3 9  4x 1 9  4x 1  lim  lim x2 12x  24    x   x   x 2 12 2 3 8  3x  8 12x 15  3 12x 15  3 8  4  x   2   2 1 2 2x  3x  2 9 4 1  94x x    2 1 9 = lim  lim  . x2 12      x   x 2 24 7 2 3 6  12x 15  3  12x15 3 3 2
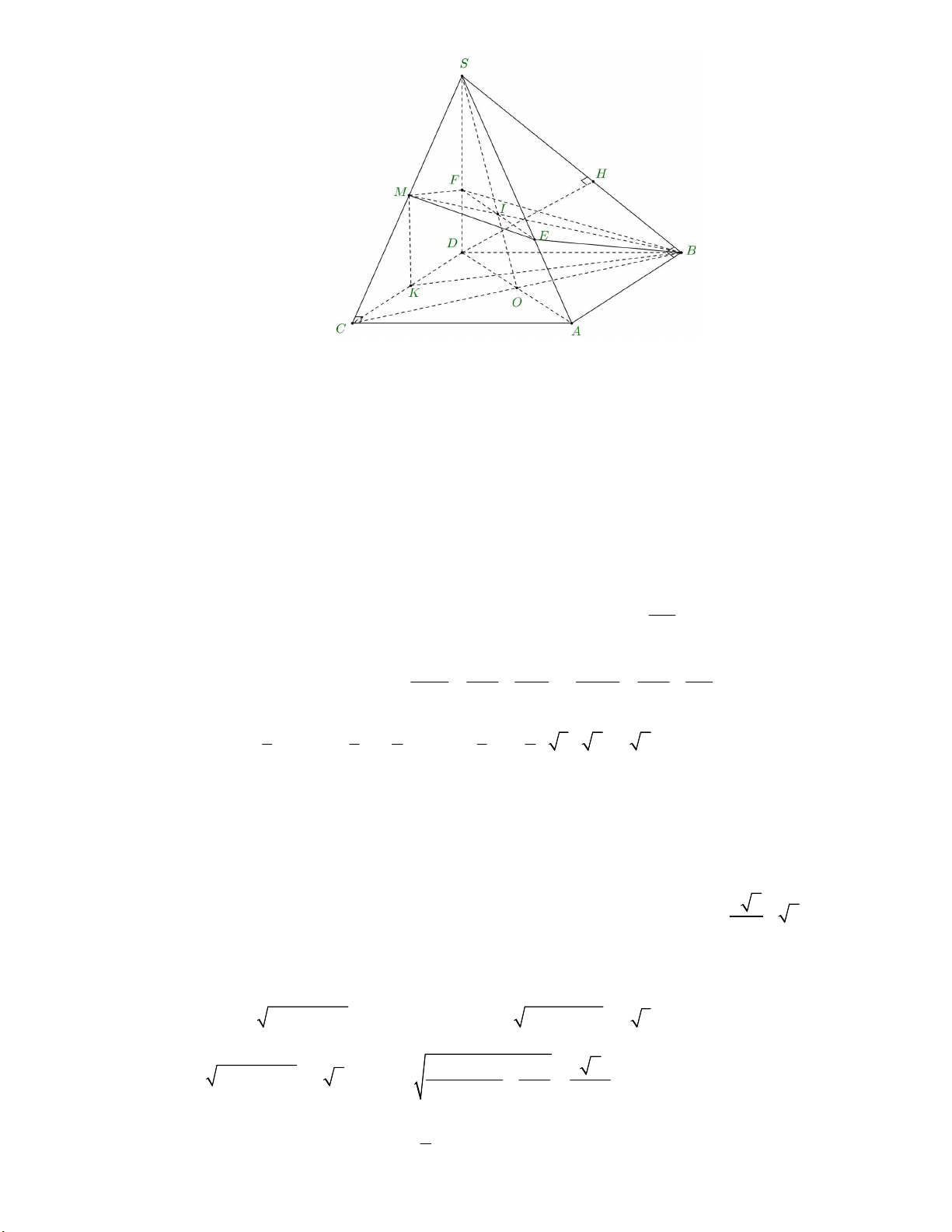
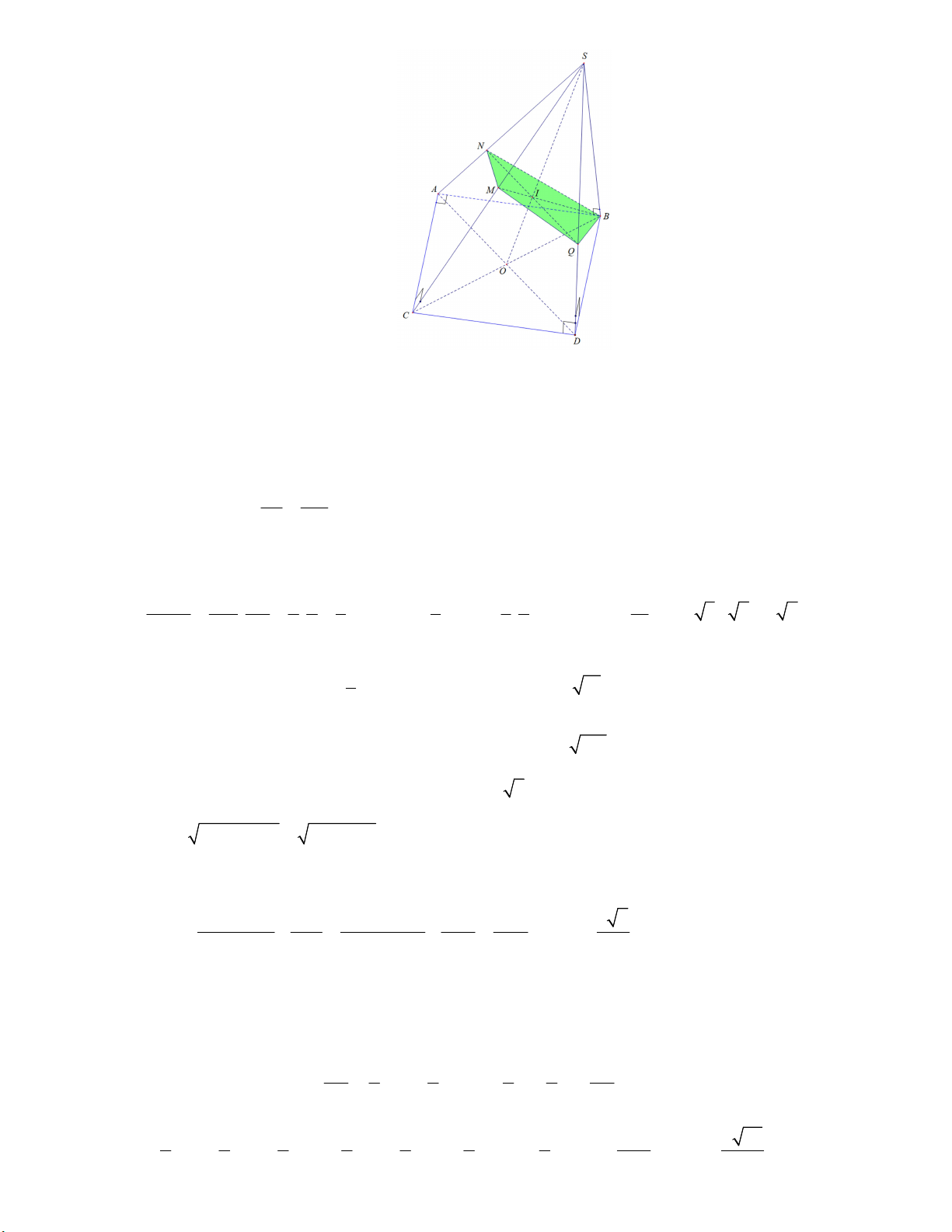
Câu 4. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A , góc  12a SBA   0
SCA  90 , AB  a 6, AC  a 3 , khoảng cách từ C đến SAB bằng . 7
a) Tính thể tích khối chóp S.ABC .
b) Gọi O, M lần lượt là trung điểm của BC, SC ; P là mặt phẳng chứa BM và song song với AO
. Gọi góc giữa SB và P là  . Tính sin .
c) Tính bán kính mặt cầu ngoại tiếp hình chóp M.ABC . Lời giải Tổng hợp: Trần Minh Vũ Trang 3/7
a) Gọi D là hình chiếu của S trên mp  ABC  . Ta có: AB  SB  
 AB  SBD  AB  BD . AB  SD AC  SC  
 AC  SCD  AC  CD . AC  SD
 ABDC là hình chữ nhật.
Kẻ đường cao DH của tam giác. Ta có: DH  SB 
 DH  SAB  DH  d D SAB  d C SAB 12a , ,  . DH  AB 7 1 1 1 49 1 1 Trong S
 BD vuông tại D , ta có:       SD  12a . 2 2 2 2 2 2 DH SD BD 144a SD 3a 1 1 1 1 1 Vậy: 3 V  . SD S  .S . D .AC.AB  .12 . a a 3.a 6  6 2a . S .ABC 3 ABC 3 2 3 2
b) Gọi I là giao điểm của SO và BM  I P  SAD  P SAD  EF , với EF đi qua I và song song AD , E  S , A F  SD .
Gọi K là trung điểm của CD  MK / /SD  MK   ABDC  .  
            a
BK.AD  BD  DK AB  AC  6 2  B . D AB  B .
D AC  DK.AB  DK.AC  3a  .a 6  0 2
 BK  AD  AD  BMK   AD  BM , mà EF / / AD  EF  BM . Ta có: 2 2 2 2
BC  AB  AC  3a  AD  3a; SB  D S  BD  7 3 ; a 2 2 2 SB  BC SC 9 2a 2 2
SC  SD  DC  5 6  BM    2 4 2 2 Do I là trọng tâm S
 BC nên EF  AD  2a . 3
Trang 4/7 – Diễn đàn giáo viên Toán 1 1 9 2 9 2 Vậy 2 S  EF.BM  .2a. a  a . BEMF 2 2 2 2 V SM SE SF 2 2 1 Ta có: S.MEF  . .   V  V  V ; S .MEF S .CAD S . V SC SA SD 9 9 9 ABDC S .CAD V SE SF 4 4 2 S .BEF  .   V  V  V S .BEF S .BAD S . V SA SD 9 9 9 ABDC S .BAD 1 2 3V 3 a  V  V V  V  V  4 2a  d S BEMF   . BEMF S MEF S BEF S ABDC S ABC  ;  8 S.BEMF S . . . . . 3 3 S 3 BEMF d S;BEMF  8 3 Vậy: sin   . SB 63
c) Do ABDC là hình chữ nhật nên mặt cầu ngoại tiếp hình chóp M.ABC cũng là mặt cầu ngoại tiếp hình chóp M.ABDC . SC 5 6
Xét tam giác DMC có DM  MC   a  MDC cân tại M . 2 2
Gọi P là tâm đường tròn ngoại tiếp M
 DC  P thuộc đường thẳng MK .
Gọi r là bán kính đường tròn ngoại tiếp M  DC , ta có: 2 2 2 MD  MC  DC 23 4 6 DC 25a cos  DMC    sin  DMC   r   2 . MD MC 25 25 2sin  DMC 8
Dựng đường thẳng d đi qua P và vuông góc với  DMC   d là trục đường tròn ngoại tiếp M  DC .
Dựng đường thẳng  đi qua O và vuông góc với  ABC    là trục đường tròn ngoại tiếp A  BC .
Gọi Q là giao điểm của d và   Q là tâm mặt cầu ngoại tiếp hình chóp M.ABC .
Gọi R là bán kính mặt cầu ngoại tiếp hình chóp M.ABC , ta có: 2 2  25a   a 3  673 2 2 2 2
R  MP  PQ  MP  OK        a . 8  2    8   x  3 1 1 3 3 y 1  1  
Câu 5. Giải hệ phương trình 3  3  x  3y  6  . 2
 3x  48  2 6y  24  4 6  x  Lời giải x  6 Điều kiện  .  y  4 Tổng hợp: Trần Minh Vũ Trang 5/7 x x 3 1  1  3 1  1   x   x  Ta có 3 3 y 1  1 3 3    x  3y  6 3 3 y 1  1  3  3 1  3   3 y     1  f 1  f  y     1 ,  3   3  với f t 3 t 1 3    3t . Hàm số f t 3 t 1 3  
 3t đồng biến trên 0; .  x  x Khi đó f 1  f    y  
1  1  y 1  x  3y  6 .  3  3
Thay x  3y  6 vào phương trình 2
3x  48  2 2x 12  4 6  x .
Điều kiện của phương trình 6   x  6 2 2
3x  48  2 2x 12  4 6  x  3x  48  2 2x 12  2 6  x   6   x  6  6   x  6       2 2 2 2 3x  48  8  x 144 16 72  2x 16  72  2x  3x  8x  96 2 2
6  x  6,3x  8x  96  0 
6  x  6,3x 8x 96  0     2 2 4 3 16  72  2x  3x  8x  96 9
 x  48x 1536x  9216  0 2
6  x  6,3x  8x  96  0 2
6  x  6,3x  8x  96  0       x  
3x  963x 16x  96 2 3 96 0 2 2  0  2 3x 16x  96  0  vn 2  6
  x  6,3x  8x  96  0   x  4 2  x  4 2   x  4 2 4 2  6   
Thay x  4 2 vào (3) ta được y 
. Hệ phương trình có nghiệm là  x y 4 2 6 ;  4 2;  3  3    . Câu 6. Cho a, ,
b c  0 thỏa mãn ab  1,c(a  b  c)  3 . Tìm giá trị nhỏ nhất của b  2c a  2c P    6ln a  b  2c. 1 a 1 b Lời giải  b  2c   a  2c  Ta có: P  2  1  1  6ln     a  b  2c  1 a   1 b 
a  b  2c 1 a  b  2c 1    6ln a  b  2c a 1 b 1     a  b  c   1 1 2 1   6ln   a  b  2c. 1 a 1 b   1 1   1 1  Ta lại có:     1 a    
1 ab  1 b 1 ab  ab  a ab  b  
1 a1 ab 1b1 ab
Trang 6/7 – Diễn đàn giáo viên Toán b  a  a b      1 ab 1 a 1 b      a  b  ab   a  b b a   . 1 ab 1 a1b  a  b2 ab  1    do a b  ab  1 ab  0, , 0; 1 1 a1b 1 1 2 2 4 4 4        1 a 1 b  ab 1 1 ab ab  3
ab  c a  b  c a  cb  c 1 2
a  b  2c 1 a  b  2c 1 P  2    6ln a  b  2c . 1 a 1 b     a  b  c   1 1 2 1   6ln   a  b  2c. 1 a 1 b  16t   1
Đặt t  a  b  2c  0 ta có P  2   6ln t . 2 t 16 t 1 2 6t 16t  32 Xét hàm số f t     6ln t  f t 
 f  t  0  t  4 . 3   2 t t
f 4  5  6ln 4  P  3 6ln 4  minP  3 6ln 4. Dấu bằng xảy ra khi a  b  c 1. HẾT Tổng hợp: Trần Minh Vũ Trang 7/7
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI CHỌN HỌC SINH GIỎI LỚP 12 QUẢNG NINH NĂM HỌC 2021 – 2022 MÔN THI: TOÁN(BẢNG B)
Thời gian: 90 phút (Không kể thời gian phát đề)
Câu 1. [HSG-QUẢNG NINH-B 2021-2022] a) Cho hàm số y  x   2 2
1 4x  4 m  2 x  5m  7  4   có
đồ thị là C , với m là tham số và đường thẳng d  : y  2x  6 . Tìm m để d  cắt C tại 3 điểm m  m 
phân biệt A1;4, B,C sao cho BC  2 5 . Lời giải
Xét phương trình hoành độ giao điểm: 2 x   2 1 4x  4 
m  2 x 5m  7  4  2x  6   2x   2 1 4x  4 
m  2 x 5m  7  2  x 1  0  2x   2 1 4x  4 
m  2 x 5m 5  0   2x   1 g x  0 *
Để d  cắt C tại 3 điểm phân biệt A1;4, B,C thì phương trình 2
4x  4m  2 x  5m  5  0 m 
phải có hai nghiệm phân biệt x , x khác 1
 . Điều kiện đó tương đương với B C  1 5 m  2 a  4  0       4 1 5 2 m  m   1  0  m  . 2   g    1  m 1  0 m  1    x  x   m  B C  2 
Khi đó toạ độ 2 giao điểm B,C là B  x ;2x  6,C  x ;2x  6 với . B B C C   5m   1 x x  B C  4 Theo giả thiết BC   BC   x  x 2 2 2 5 20 5  20 C B
  x  x 2   x  x 2  x x   m  2 4 4 4 2  5 m 1  4 C B C B C B  1 21 m  2 2
 m  m  5  0   thoả mãn điều kiện.  1 21 m   2
Câu 1. [HSG-QUẢNG NINH-B 2021-2022] b) Một đại lý xăng dầu cần làm một cái bồn chứa dầu hình trụ 125 có thể tích bằng  3
m  . Tính bán kính đáy của bồn chứa dầu sao cho bồn chứa dầu được làm ra 4
tốn ít nguyên liệu nhất? Lời giải
Gọi r, h m lần lượt là bán kính đáy và chiều cao của chiếc bồn r, h  0. 125 125 Theo giả thiết ta có: 2 V   r h   h  . 4 4r
Để bồn chứa dầu được làm ra tốn ít nguyên liệu nhất thì diện tích toàn phần của chiếc bồn hình trụ phải nhỏ nhất. 125 125
Tacó diện tích toàn phần của chiếc bồn là: 2 2 S 2 r 2 r 2       r . tp   4r  4r  125 Xét hàm số f r 2 2     r 
 trên khoảng 0;   .  4r  3  12  5  8r  5 Ta có f r  2 ; f  r  
 0  r   0;  . 2      4r  2 125 5
Ta tính được giá trị nhỏ nhất của hàm số f r 2 2     r 
 ứng với r  m .  4r  2
Câu 2. [HSG-QUẢNG NINH-B 2021-2022] 1 a) Cho a, ,
b c là các số thực dương khác 1 thỏa mãn: 6 log a  3;log b  2;log b  . Tính 2022 a c 3 log abc4 9 . 2022 3  2 tan C
b) Cho tam giác ABC có các góc thỏa mãn điều kiện tan B 
. Chứng minh ABC có một 2  3tan C
góc tù và tính diện tích hình tròn ngoại tiếp tam giác ABC , biết rằng BC  6 . Lời giải  3 log a  3   2022 a 2022   4 4 28 a) 4 12 log b  2  b   a  2022  log abc   . a   log  21 9 9 2022 2022 2022  3   6 1 6 c  b  2022 log b   c  3 b) Vì ,
A B,C là ba góc của một tam giác nên 0  , A ,
B A  C 180 . Với điều kiện này ta có: 3  tan 3  2 tan C C B     AC 2 tan tan  2  3tan C 3 1 tan C 2  3
tan A  C   tan   C  , (với tan  ) 2  tan A  tan 3
 tan A    0 suy ra góc A tù hay ABC có một góc tù (đpcm). 2 3 2 1 13 3 13
tan A    cot A      sin A  . 2 2 3 sin A 9 13 3 13 9 13
Gọi R là bán kính đường tròn ngoại tiếp tam giác ABC ta có 2R  BC sin A  6.  R  . 13 13 81
Diện tích hình tròn ngoại tiếp tam giác ABC là: 2 S   R  . 13
Câu 3. [HSG-QUẢNG NINH-B 2021-2022] a) Cho đa thức    3 5 2 n P x x    biết n thỏa mãn 2 3 3A  5C  2n , n 
 . Tìm hệ số của 7 x trong n n
khai triển của P  x . 2x 3 2 9  4x  x  x  3
b) Tính giới hạn I  lim . x2 12x 15  2x  7 Lời giải a) Ta có n! n! 2 3 3A  5C  2n  3   n n n n   5 n   2 2 ! 3! 3 !  nn   5 3 1  nn   1 n  2  2n 6  18n   1  5n   1 n  2  12 2  5  n  33n  40  0 n  5   8 n  .  5
Do đó P  x   x  20 2 . k    Số hạng tổng quát: 20 2 k k k C x   , . 20   k n
Theo yêu cầu bài toán: 20  k  7  k  13. Vậy hệ số của 7
x trong khai triển là C 213 13 . 20 b) Ta có 2x 3 2 9  4x  x  x  3 I  lim x2 12x 15  2x  7
2x 3 94x   2 1  x  x  6  lim x2 12x 15  2x  7
2x 3 94x  1 2 x  x  6  lim  lim . x2 x2 12x 15  2x  7 12x 15  2x  7 Ta tính
2x 3 94x  1 I  lim 1 x2 12x 15  2x  7
2x 39 4x  1 12x15 2x7  lim x2  9  4x   1  2
12x 15  4x  28x  49
42x  32  x 12x 15  2x  7  lim x2  94x  1 2 4x  40x  64
42x  32  x 12x 15  2x  7  lim x2 4   9 4x   1  x  2 x 8
2x 3 12x15 2x 7  lim x2  94x  1x8 1   . 2 2 x  x 
x  2x 3 12x 15 2x 7 6  I  lim  lim 2 2 x2 x2 12x 15  2x  7 4x  40x  64
x  2x  3 12x15 2x 7
x  3 12x15 2x 7  lim  lim x2 4  x 8x  2 x2 4x 8 5  . 4 1  5 3 Vậy I    . 2 4 4
Câu 4. [HSG-QUẢNG NINH-B 2021-2022] Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A , 12a góc  SBA  
SCA  90 , AB  a 6 , AC  a 3 , khoảng cách từ C đến SAB bằng . 7
a) Tính thể tích khối chóp S.ABC .
b) Gọi O , M lần lượt là trung điểm của BC , SC ; P là mặt phẳng chứa BM và song song với
AO . Tính khoảng cách từ điểm S đến mặt phẳng P .
c) Tính bán kính mặt cầu ngoại tiếp hình chóp M .ABC . Lời giải
a) Dựng hình chữ nhật ABDC  SD   ABCD . AC  CD Do
 AC  SCD  SD  AC   1 . AC  SC
Tương tự: SD  AB 2 .
Từ (1) và (2) suy ra SD   ABCD . Đặt SD  x, x  0 .
Kẻ DH  SB, H  SB  DH  SAB . B . D SD a 3.x
Suy ra d D,SAB  DH   . 2 2 2 2 BD  SD 3a  x 12a a 3.x
Do CD / / AB  d C,SAB  d D,SAB   2 2  12 3a  x  7 3.x 2 2 7 3a  x 2 2  12 3a  x  7 3.x   2 2 a  x  2 144 3  147x 2 2  144a  x  x  12a . Suy ra SD  12a . 1 1 1
Vậy thể tích khối chóp S.ABC là 3 V  .S . D S  .12 . a .a 6.a 3  6 2a (đvtt). 3 ABC 3 2 b) Gọi BM  SO  I . Khi đó I là trọng tâm S  BC .
Kẻ đường thẳng đi qua I và song song với AD , lần lượt cắt SA và SD tại N và Q . SI SQ Do IQ / / OD    2 . IO QD Mặt khác VS.MQB SM SQ 1 2 1 1 1 1 1 3  .  .   V  V  . . . SD D . B DC  .12 . a a 3.a 6  2 2a S.MQB S. V SC SD 2 3 3 3 CDB 3 6 18 S.CDB 2  1  Ta có 2 2 2 2 2 BQ  QD  BD 
.12a  3a 19a  BK  a 19   .  3  Mặt khác 2 2 2 2 2 2
SB  SD  DB  144a  3a  147a  SB  a 147 ; 2 2 2 2 2 2
SC  SD  DC  144a  6a  150a  SC  5 6a ; 2 2 2 2
BC  AB  AC  6a  3a  3a .
Áp dụng công thức đường trung tuyến vào S  BC ta có 2 2 2 2 2 2 2   2 SB BC SC 147a 9a 150 81a 9 2 MB       MB  a . 2 4 2 4 2 2
Áp dụng định lý cosin vào SMQ ta có 2 2 2 MQ  SM  SQ  SM SQ  2 2 2. .
.cos MSQ  SM  SQ  2.SM .S . Q cos  MSQ 2 2 SD  1 4 1 2 SD SM  SQ  2.SM . . SQ 2 2  SC  SH  2. .SC. . . SD SC 4 9 2 3 SC 2 1 4 2 1 2 1 2 11a a 22 2 2 2 2 2 2 2
 SC  SD  .SD  SC  .SD  .150a  .144a   MQ  . 4 9 3 4 9 4 9 2 2
Áp dụng hệ quả định lý cosin vào MBQ ta có 2 2 81a 2 11a 19a   2 2 2 MB  BQ  MQ 3 38 MBQ      19 2 2 cos sin MBQ  . 2.M . B BQ 9 2 19 19 2. . a a 19 2 1 1 9 2a 19 9 2 Diện tích MBQ là S  .M . B B . Q sin  2 MBQ  . .a 19.  a (đvdt). M  BQ 2 2 2 19 4 3VS MBQ 3.2 2a 8a
Vậy d S,P  dS,MBK  3 .    . S M  BQ 9 2 3 2 a 4
c) Dựng đường thẳng d đi qua O và song song với SD .
Khi đó d là trục đường tròn ngoại tiếp A  BC .
Suy ra tâm mặt cầu ngoại tiếp hình chóp M .ABC là điểm G  d . 1
Gọi N là hình chiếu vuông góc của M trên CD . Suy ra GO / / MN và MN  SD  6a . 2   2
   2 Ta có 2 2 2
R  GB  GM  GO  OB  GO  ON  NM   
      2 2 2 2 2  GO  OB  2.G .
O OB  GO  ON  NM  2.G . O ON  G . O NM  ON.NM    2 2 2 2 2
 GO  OB  GO  ON  NM  2.G . O NM
Do GO  OB, GO  ON , ON  NM . 2 2 2   1  a 3   1  69a Suy ra 2 2 2 2 2.G .
O NM  OB  ON  NM  .9a     .12a       4 2    2  2 2 69a 23a 2 2 a 673  2.G . O 6 . a cos180    GO   R  GO  OB  . 2 8 8 x2 3 y8 2  2  x  3y  6 Câu 5.
[HSG-QUẢNG NINH-B 2021-2022] Giải hệ phương trình  . 2
 3x 13  6y  24  2 6  x  5  Lời giải 2  x  6  Điều kiện  8 . y    3 Ta có x2 3 y8 2  2  x  3y  6 x2 3 y8  2  x  2  2
 3y  8  f x  2  f 3y  8 , với    2 t f t  t . Do f t t 1  2 . .ln t 1  0, t
  0 suy ra hàm số hàm số    2 t f t
 t đồng biến trên 0; . 2 t
Khi đó f  x  2  f 3y  8  x  2  3y  8  3y  x  6 .
Thay 3y  x  6 vào phương trình 2
3x 13  6 y  24  2 6  x  5 ta được 2
3x 13  2x 12  2 6  x  5 2
 3x 13  5  2x 12  2 6  x  0 2
 3x 13  5  2x 12  2 6  x  0 2 3x 12 2x 12  46  x    0 2 3x 13  5 2x 12  2 6  x      x   3x 6 6 2     0 2  3x 13  5 2x 12  2 6  x  x  2   3x  6 6  .   0(vn) 2  3x 13  5 2x 12  2 6  x 4 Với x  2  y   . 3 x  2 
Vậy hệ phương trình đã cho có nghiệm  4 . y    3
Câu 6. [HSG-QUẢNG NINH-B 2021-2022] Cho a, ,
b c  0 thỏa mãn ab  1,c(a  b  c)  3 . Tìm giá trị nhỏ nhất của
b  2c a  2c 3a  b  2c P    . 1 a 1 b 2 Lời giải  b  2c   a  2c  3 Ta có: P  2  1  1      a  b  2c  1 a   1 b  2
a  b  2c 1 a  b  2c 1 3    a  b  2c a 1 b 1 2     a  b  c   1 1 3 2 1     a b  2c. 1 a 1 b  2  1 1   1 1  Ta lại có:     1 a    
1 ab  1 b 1 ab  ab  a ab  b  
1 a1 ab 1b1 ab b  a  a b      1 ab 1 a 1 b      a  b  ab   a  b b a   . 1 ab 1 a1b  a  b2 ab  1       ab  0,do a,b 0;ab  1 1 1 a1b 1 1 2 2 4 4 4        1 a 1 b  ab 1 1 ab ab  3
ab  c a  b  c a  cb  c 1 2 4 16   . 2  a  c  b  c  a  b  2c2    2  16a  b  2c   1 3 Suy ra: P  2   a  b  2c . 2   a b  2c 2
Đặt t  a  b  2c t  0 .
Do ab  1,c(a  b  c)  3  ab  c a  b  c  4
 a  cb  c  4 2 2  a  c  b  c  t
 4  a  cb  c    t  4   .  2  4 16t   1 3 16  16 t t  Khi đó: P   t  2   t     2 2    2  t 2  t   t 4 4  16 16 t t  2 .t  3 . .  2  9 . 2 t t 4 4
Vậy: min P  9 khi a  b  c  1. HẾT
Document Outline

  • DDGVT05-HSG-QUẢNG-NINH BẢNG-A-NĂM-2021-2022
  • de-thi-chon-hoc-sinh-gioi-tinh-toan-thpt-nam-2021-so-gddt-quang-ninh
    • de-thi-chon-hoc-sinh-gioi-tinh-toan-thpt-nam-2021-so-gddt-quang-ninh
    • DDGVT04-HSG-QUẢNG-NINHBẢNG-B-NĂM-2021-2022