Đề thi chọn học sinh giỏi Toán 12 cấp trường năm 2017 – 2018 trường Lý Thái Tổ – Bắc Ninh

SỞ GIÁO DỤC VÀ ĐÀO TẠO BẮC NINH
ĐỀ THI CHỌN HỌC SINH GIỎI CẤP TRƯỜNG
TRƯỜNG THPT LÝ THÁI TỔ NĂM HỌC 2017 – 2018
Môn thi: Toán – Lớp 12
Thời gian làm bài: 180 phút (không kể thời gian giao đề) ĐỀ CHÍNH THỨC
Ngày thi: 16 tháng 09 năm 2017
(Đề gồm 01 trang)
Câu I. (4,0 điểm) x - 2
1) Cho hàm số y =
có đồ thị là C và M là điểm thuộc C . Tiếp tuyến của C tại M cắt hai x + 1
đường tiệm cận của C tại A và B. Gọi I là giao điểm của hai tiệm cận. Tìm tọa độ điểm M sao cho bán kính
đường tròn nội tiếp tam giác IAB lớn nhất. 1
2) Tìm tất cả các giá trị của tham số m để hàm số 3
y = x -(m - ) 2 1 x -(m - 3) 2
x + 5m + 1 đồng 3
biến trên khoảng (0; 3) .
Câu II. (4,0 điểm)
1) Tính tổng các nghiệm thuộc é0; 2018pù êë úû của phương trình: 2
2 sin x + 3 sin 2x = 3 3 sin x + 3 cos x - 1 2) Tính tổng: 1 2 2 2 3 3 4 2016 2017 S = C - 2 C + 3.2 C - 4.2 C + ... + 2017.2 C . 2017 2017 2017 2017 2017
Câu III. (4,0 điểm) 1
1) Giải bất phương trình: log ( 2 x - 4x + 4 + log
x + 2 > log 4 - x 4 ) ( ) 2 2 ( ) 2 (ìïï17 - 3x ï
) 5 - x + (3y -14) 4 -y = 0
2) Giải hệ phương trình: í
(x,y Î ) ï 3
ï4 2x + 8 + (x - y + 2) x + 3y - 5 = 2x + 14 ïî
Câu IV. (6,0 điểm)
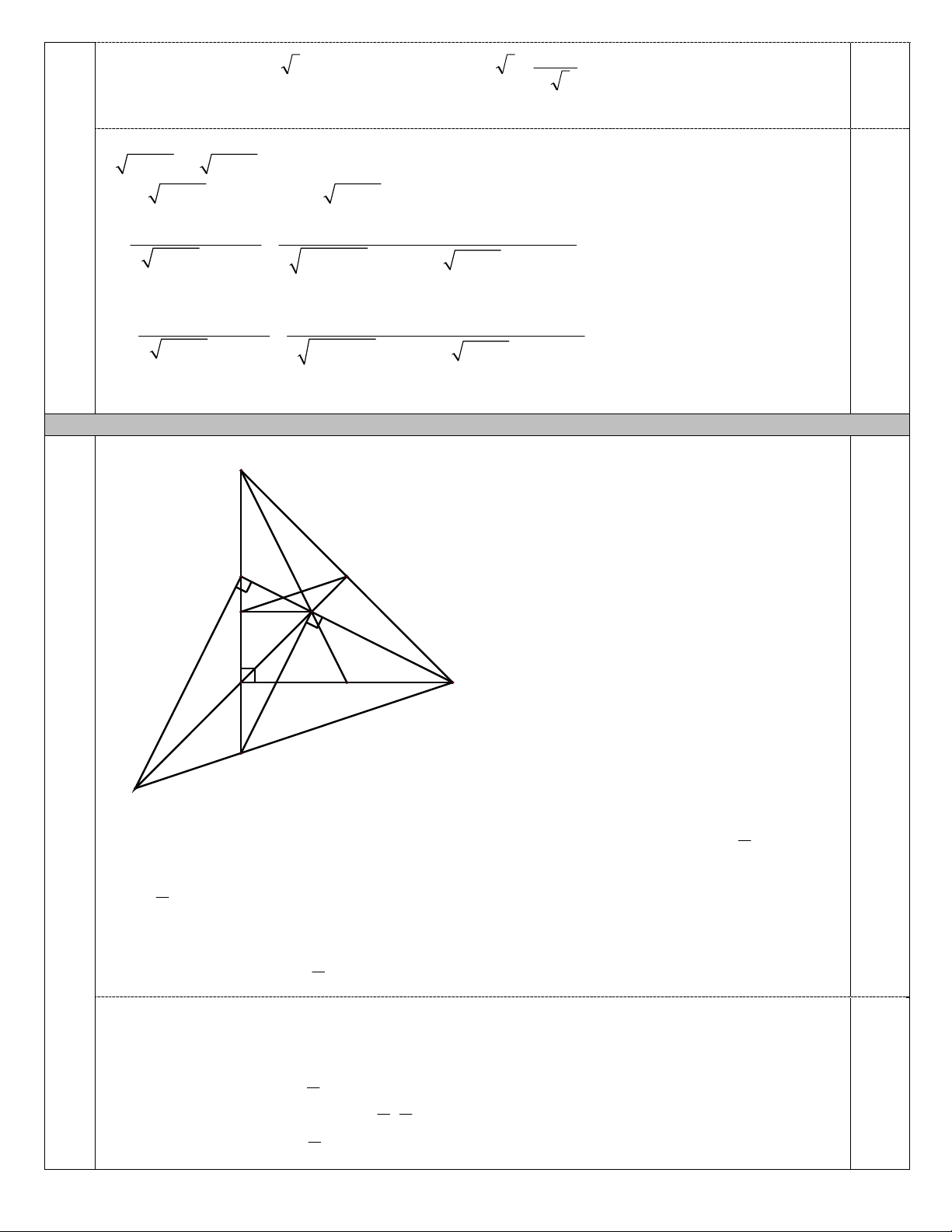
1) Cho tam giác ABC vuông cân tại A, có trọng tâm G. Gọi E, H lần lượt là trung điểm của các cạnh AB,
BC; D là điểm đối xứng với H qua A, I là giao điểm của đường thẳng AB và đường thẳng CD. Biết điểm D (-1;- )
1 , đường thẳng IG có phương trình 6x - 3y - 7 = 0 và điểm E có hoành độ bằng 1. Tìm tọa độ các
đỉnh của tam giác ABC.
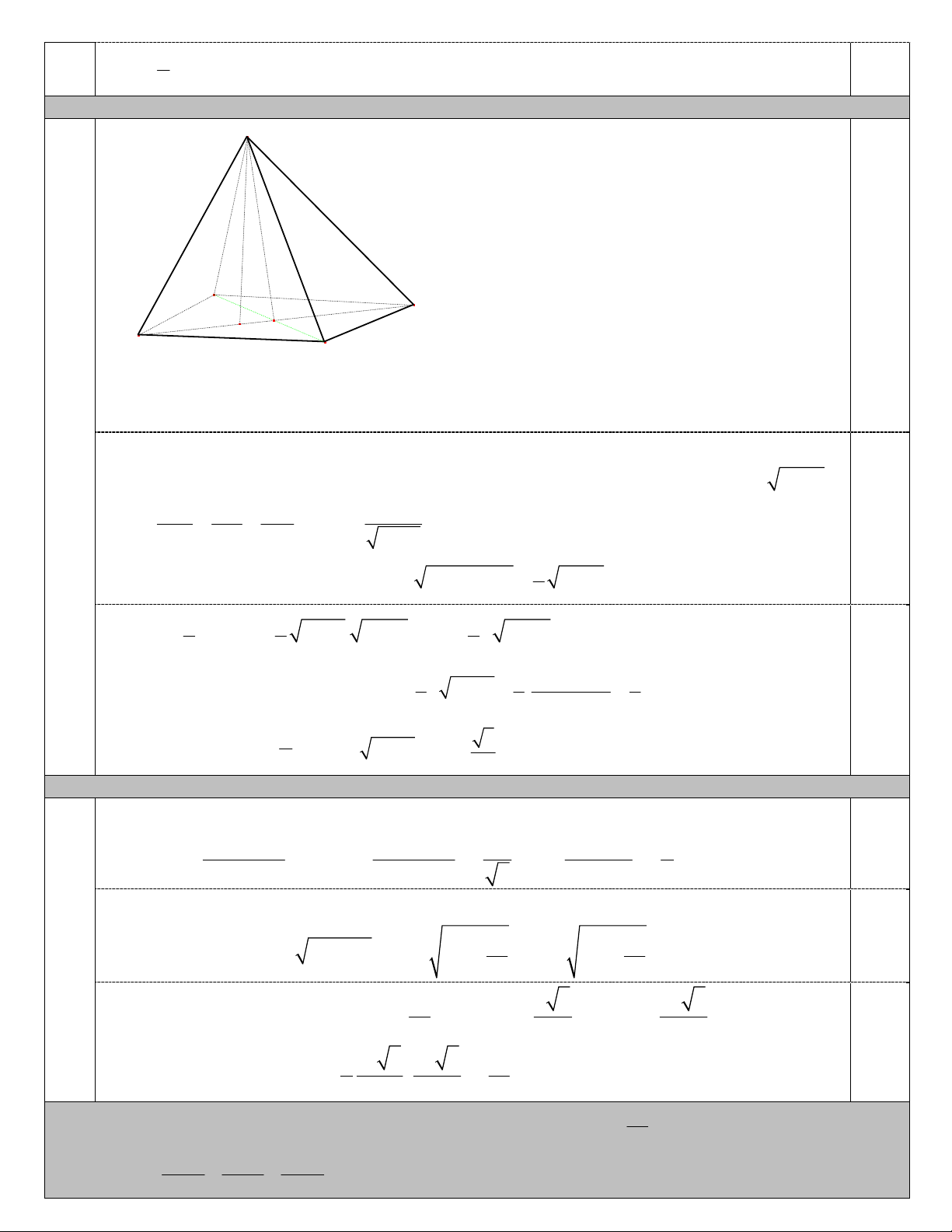
2) Cho hình chóp S.ABCD có SA = x, tất cả các cạnh còn lại bằng 1. Tính thể tích khối chóp đó theo
x và tìm x để thể tích đó là lớn nhất.
3) Cho hình chóp S.ABC có mặt đáy là tam giác đều cạnh a và hình chiếu của S lên mặt phẳng
(ABC ) là điểm H nằm trong tam giác ABC sao cho  0  0  0
AHB = 150 ,BHC = 120 ,CHA = 90 .Biết tổng diện 31
tích các mặt cầu ngoại tiếp các hình chóp S.HAB, S.HBC , S.HAC bằng 2 a
p . Tính theo a thể tích khối 3 chóp S.ABC . 1
Câu V. (2,0 điểm)Cho a,b,c là các số thực dương thoả mãn abc = 1 và 3 3 a b + b a +
= ab + 2 . Tìm giá trị ab 1 1 3
lớn nhất của biểu thức: P = + - . 2 2 1 + a 1 + b 1 + 2c
---------------Hết----------------
Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm.
Họ và tên thí sinh:……….………..…….................…….….….; Số báo danh:……….....……….
SỞ GIÁO DỤC VÀ ĐÀO TẠO BẮC NINH HƯỚNG DẪN CHẤM
TRƯỜNG THPT LÝ THÁI TỔ
THI CHỌN HỌC SINH GIỎI CẤP TRƯỜNG NĂM HỌC 2017 - 2018
Môn: Toán – Lớp 12 Câu
Lời giải sơ lược Điểm 1.1 (2,0 điểm)  x  2  Gọi M 0  x ; 0  (C) x 1  0  3 x  2
Phương trình tiếp tuyến tại M: 0 y  (x  x )  1,0 2 0 (x 1) x 1 0 0 Khi đó: A  x  5  0  1;  B(2x0+1; 2) ; I(-1; 1) x  1  0  1 1 6
*Ta có: SIAB = . IA. IB = 
2 x 1  2.3  6 (đvdt) 2 0 2 x 1 0  S S . p r  r   r  p IAB max min p 6 x  1   3
Chu vi tam giác IAB nhỏ nhất khi IA = IB hay 0  2 x 1   1,0 0 x 1 0 x  1   3  0
*Vậy có 2 điểm thoả mãn M1( 1   3;1 3 ) M2( 1   3;1 3 ) 1.2 (2,0 điểm) TXĐ:  2
y '  x  2m  
1 x  m  3 1,0
Do phương trình y '  0 có nhiều nhất hai nghiệm trên  , nên để hàm số đã cho đồng biến trên
khoảng 0;3  y'  0, x  0;3 2 x  2x  3   , m x  0;3 . 2x 1 2 x  2x  3
Xét hàm số g  x  trên khoảng 0;3 2x 1 0,5 2 x  x  x  g ' x 2 2 4 1 
; g ' x  0  2     2x   1 x  2   loai
Từ BBT, g  x  , m x
 0;3  m  2 0,5
Vậy, m  2 thì hàm số đã cho đồng biến trên khoảng 0;3 2.1 (2 điểm) 2
2sin x  3 sin 2x  3 3 sin x  3cos x 1 . (1) (1) 2 2
 3sin x  2 3 sin x cos x  cos x  3 3sinx  cos x 0,5    x2 3 sinx cos
 3( 3 sinx  cos x) 1,0
 3 sinx  cos x  0
  3sinxcosx 3(VN)  
Giải ra ta được nghiệm của phương trình là x 
 k ;k  Z 6 Do x é0;2018pù Î
 k Î {1;2;...;2018}  êë úû
.phương trình có 2018 nghiệm.
Các nghiệm này lập thành cấp số cộng với 0,5 5p 2018 æ 5p ö ç ÷ 6110504p x =
,d = p  S = 2 ç . + 2017p÷ = 1 2018 6 2 çè 6 ÷÷ø 3
2.2 (2 điểm). Ta có (1 - x )2017 0 1 2 2 3 3 2017 2017 = C -C x + C x -C x + ... -C x 2017 2017 2017 2017 2017
Lấy đạo hàm 2 vế ta được: 1,0 -2017 (1 - x )2016 1 2 3 2 2017 2016 = C - + 2C x - 3C x + ... - 2017C x 2017 2017 2017 2017 1 2 3 2 2017 2016
x = 2  -2017 = C - + 2C 2 - 3C 2 + ... - 2017C 2 2017 2017 2017 2017 1,0 Vậy S =2017 3.1 (2 điểm) 2
x  4x  4  0  x  2
+ ĐK : x  2  0   0,5   2   x  4 4  x  0  1
+ Bất phương trình đã cho tương đương với 2
log (x  2)  log (x  2)  log (4  x) 2 1 2 2 2 2 2
 log x  2  log (x  2)  log (4  x) 2 2 2 0,5
 log x  2 (x  2)  log (4  x) 2   2
 x  2 (x  2)  4  x (1) +) TH1: Với x  ( 2
 ;2)thì (1)  (2  x)(x  2)  4  x  x (0;1). Kết hợp với ĐK trong
trường hợp này ta được x  (0;1)
+) TH2: Với x (2;4) thì 1   33 1   33
(1)  (x  2)(x  2)  4  x  x  ( ;  )  (
;) . Kết hợp với ĐK trong 2 2 1,0 1   33
trường hợp này ta được x  ( ;4) 2 1   33
* Vậy bất phương trình có tập nghiệm là x  (0;1)  ( ;4) 2 (ìïï17 - 3x ï
) 5 - x + (3y -14) 4 -y = 0
3.1 (2 điểm) Giải hệ phương trình: í
(x,y Î ) ï 3
ï4 2x + 8 + (x - y + 2) x + 3y - 5 = 2x + 14 ïî ìï-4 £ x £ 5 Điều kiện ïí 0,5 y ï £ 4 ïî
Phương trình (1) tương đương với  5 (
3  x)  2 5  x   (
3 4  y)  2 4  y (3) 0,5 3t  2 Xét hàm f t ( )  t 3 (  )
2 t với t  0 , ta có f '(t)  3 t   ; 0 t  .
0 ra suy ra f(t) đbiến trên 2 t é0;+¥ ê ) ë
Kết hợp với (3) ta có f 5
(  x)  f (4  x)  5  x  4  y  y  x  . 1
Thay vào phương trình (2) của hệ ta được 3
4 2x  8  3 4x  8  2x 14  0
 4 2x  8  x 12 3
  3 4x 8  (x  2)  0     2 2 (x  4) (x  4) (x 14)    0 3 2 3 2
4 2x  8  x 12 9 (4x 8)  3(x  2) 4x 8  (x  2) 1,0 2
(x  4)  0  x  4(tm)  y  3(tm)   1 (x 14)    0(4)  3 2 3 2
4 2x  8  x 12 9 (4x  8)  3(x  2) 4x 8  (x  2) 
Nhận xét: Với x  4
 ,vế trái của phương trình (4) luôn dương , nên (4) vô nghiệm
Vậy hệ phương trình có nghiệm ( 4;3) 4.1 (2 điểm) B E H G K A C F 0,5 I D 1
Gọi K là trung điểm của BI, suy ra HK / /CD  A là trung điểm của KI, HK  DI  IC ; 2 1
AK  BK  GK / / AC  GK  AB  GB  GI  GC hay G là tâm đường tròn đi qua ba 2
điểm C, I, B.    1 2  90o CGI IBC
, ID  IC  DE / /IG . 2
Phương trình đường thẳng DE: 2x  y 1  0  E 1;3
CE  IG , suy ra phương trình CE :x  2 y  7  0 . Tọa độ của G là nghiệm của hệ phương trình  7 x  1,0
x  2y  7  0  3  7 7      G ;    C 5;  1
6x  3y  7  0 7   3 3  y   3  5 
DG  AG  A1; 
1  B 1;5 . Vậy, A1; 
1 , B1;5 và C 5;  1 . 0,5 2 4.2 (2 điểm) S 0,5 B A O H C D
Gọi H là hình chiếu của S trên (ABCD)
Do SB = SC = SD nên HB = HC = HD, suy ra H là tâm đường tròn ngoại tiếp tam giác BCD.
Mặt khác, tam giác BCD cân tại C nên H thuộc CO, với O là giao của AC và BD.
Lại có, CBD  ABD   SBD 
 OC  OA  OS nên SAC  vuông tại S 2
 AC  x 1 Ta có, 1 1 1 x    SH  0,5 2 2 2 2 SH SA SC x 1 ABCD là hình thoi 2 2 1 2
 AC  BD  OB  AB  AO  3  x 2 + 1 1 2 2 1 2 S  AC.BD 
x 1. 3  x  V  x 3  x ABCD 2 2 6 2 2
+ Áp dụng bất đẳng thức Cô si ta có, 1   2 1 x 3 x 1
V  x 3  x  .  1,0 6 6 2 4 1
V có giá trị lớn nhất là khi 2 6
x  3  x  x  4 2 3.1 (2 điểm)
Gọi r , r , r lần lượt là bán kính đường tròn ngoại tiếp DHAB, DHBC , DHAC 1 2 3 a a a a a 0,5 Khi đó r = = a;r = = , r = = 1 0 2 0 3 0 2 sin 150 2 sin 120 3 2sin90 2
Gọi R , R , R lần lượt là bán kính các mặt cầu ngoại tiếp các hình chóp . S , HAB . S H , BC . S HAC 1 2 3 2 2 a a 0,5 Đặt 2 2 2 2
SH = 2x  R = x + a , R = x + , R = x + 1 2 3 3 4 31 a 3 2a 3 Ta có 2 2 2 2 S = 4 R p + 4 R p + 4 R p = a p  x =  SH = 1 2 3 3 3 3 1,0 2 3 1 a 3 2a 3 a
Vậy thể tích khối chóp là V = . = 3 4 3 6 1
5 (2 điểm) Cho a,b,c là các số thực dương và a.b.c=1, thỏa mãn: 3 3 a b  b a 
 ab  2. Tìm giá trị lớn nhất của ab 1 1 3 biểu thức P    2 2 1 a 1 b 1 2c 1 Theo BĐT Cô–si ta có: 3 3 2 2 2 2
a b  ab  2a b  ab  2  2a b  ab 0,5 1 1 Đặt t=a.b>0 2 3 2
 t  2  2t   2t  t  2t 1  0   t 1 t 2 1 1 2
Với a,b  0; ab  1 ta chứng minh   (*) 2 2 1 a 1 b 1 ab 1 1 1 1 Thật vậy: (*)  (  )  (  )  0 2 2 1 a 1 ab 1 b 1 ab
a(b  a)
b(a  b) 2  
 0  (a  b) (ab 1)  0 (đúng) 0,5 2 2
(1 a )(1 ab) (1 b )(1 ab) 2 3 2 3t  P     1 ab 2 1 t t  2 1 ab 1  2 3t 2 6 Xét t 
;1 ; f t  
; f 't     0   2  1 t t  2
1t2 t  22 1   1  11
Từ đó f t nghịch biến trên
;1  Max f t  f      1,0  2   2  15 1 1 1
Dấu “=” xảy ra khi t   a  ;b  ;c  2 2 2 2
1. Hướng dẫn chấm này chỉ trình bày sơ lược một cách giải. Bài làm của học sinh phải chi tiết, lập luận chặt
chẽ, tính toán chính xác mới được tính điểm tối đa.
2. Với các cách giải đúng nhưng khác đáp án, tổ chấm trao đổi và thống nhất điểm chi tiết nhưng không
được vượt quá số điểm dành cho bài hoặc phần đó. Mọi vấn đề phát sinh trong quá trình chấm phải được
trao đổi trong tổ chấm và chỉ cho điểm theo sự thống nhất của cả tổ.
3. Điểm toàn bài là tổng số điểm của các phần đã chấm, không làm tròn điểm