Đề thi chọn học sinh giỏi Toán 12 năm 2019 – 2020 sở GD&ĐT Quảng Trị

SỞ GIÁO DỤC VÀ ĐÀO TẠO KỲ THI CHỌN HỌC SINH GIỎI VĂN HÓA LỚP 12 THPT QUẢNG TRỊ
Khóa ngày 02 tháng 10 năm 2019 Môn thi: TOÁN
ĐỀ CHÍNH THỨC Thời gian làm bài: 180 phút (không kể thời gian giao đề) Câu 1. (5,0 điểm)
1. Tìm giá trị lớn nhất của hàm số 2 y  x  5x. 2. Cho bất phương trình 2
1 x  8  x  8  7x  x  .
m Tìm tất cả các giá trị thực của tham số m để bất
phương trình nghiệm dùng với mọi x [1;8]. Câu 2. (5,0 điểm) 2 x  x  5
(x  5 x 1)(x 1) 1. Giải phương trình:  . x 1 1 x  2
2. Có hai dãy ghế đối diện nhau, mỗi dãy có bốn ghế. Xếp ngẫu nhiên 8 học sinh, gồm 4 nam và 4 nữ, ngồi
vào hai dãy ghế đó sao cho mỗi ghế có đúng một học sinh ngồi. Tính xác suất để mỗi học sinh nam đều
ngồi đối diện với một học sinh nữ. Câu 3. (6,0 điểm)
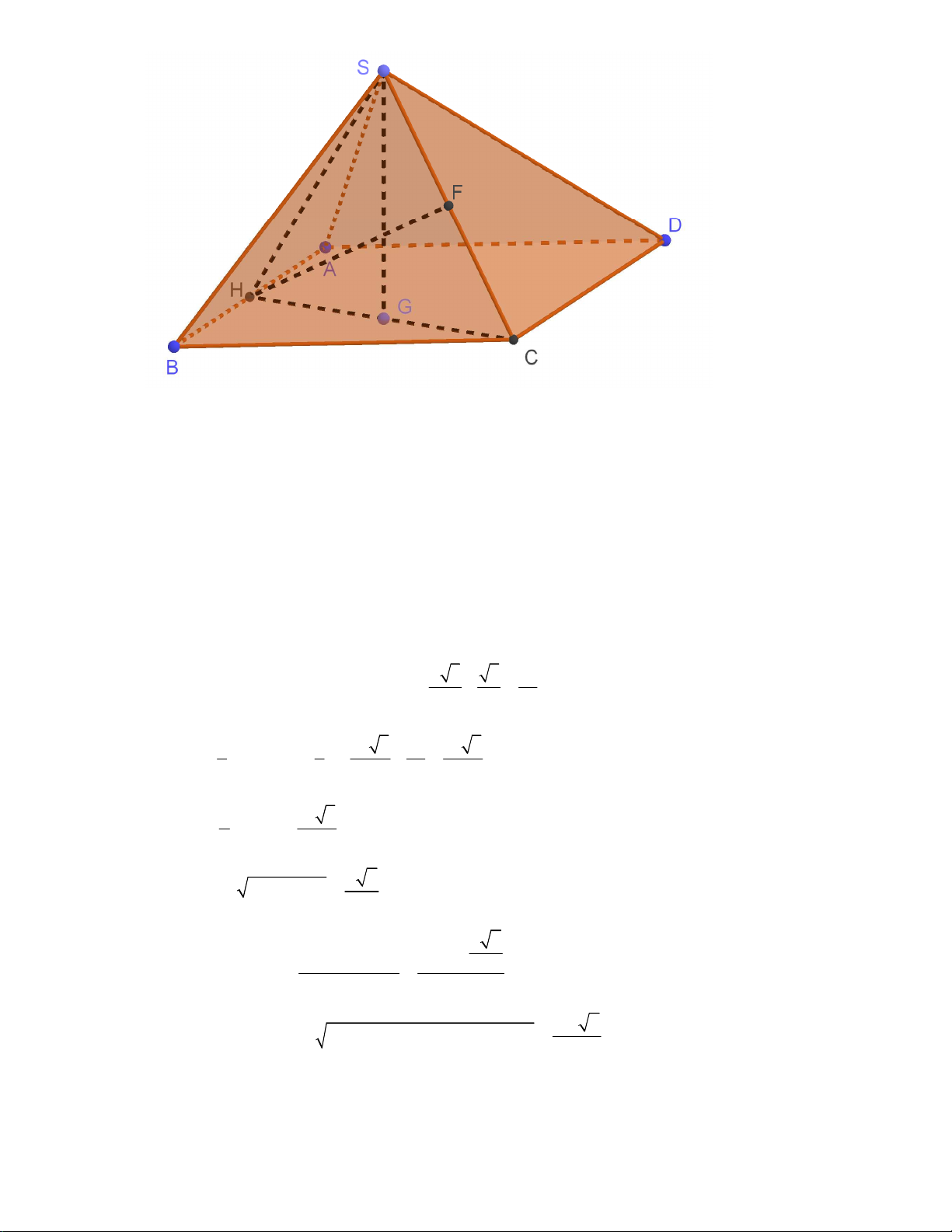
1. Cho hình chóp S.ABCD có đáy ABCD là hình thoi với  0
ABC  60 , BC  .
a Biết tam giác SAB đều, tam
giác SCD vuông tại C và nằm trong mặt phẳng hợp với mặt phẳng đáy một góc 0
60 . Tính thể tích khối chóp
S.ABCD và khoảng cách từ B đến mặt phẳng (SAD) theo a.
2. Cho tam giác nhọn ABC (AB < AC) có các đường cao AD, BE và CF đồng quy tại H. Gọi G là giao điểm
BH và DF, L là giao điểm của BC và EF, O là tâm đường tròn ngoại tiếp tam giác BCH, K là trung điểm
của BC. Chứng minh H là trực tâm tam giác AKL và LG vuông góc AO. Câu 4. (2,0 điểm)
Cho dãy số  x thỏa mãn: n  x  3 1  2  . 5x  3 x 16 n n x  ( n   , n  1) n 1   4
Tìm số hạng tổng quát của  x và tính giới hạn của dãy số  n x n . n  Câu 5. (2,0 điểm) a b c
Cho ba số thực a, b, c  0 thoả mãn    5. b c a 17 a b c Chứng minh rằng     1 4 2. 4 c a b
--------------- HẾT ---------------
(Thí sinh không được sử dụng tài liệu và máy tính cầm tay) HDG
Câu 1. (5 điểm) Thầy Tâm Nguyễn
1. Tìm giá trị lớn nhất của hàm số 2
y = −x + 5x Lời giải Hàm số có nghĩa khi: 2
−x + 5x ≥ 0 ⇔ x ∈[0;5] −2x + 5 −2x + 5 5 / y = , cho / y = 0 ⇔ = 0 ⇔ x = ∈[0;5] 2 −x + 5x 2 2 −x + 5x   f (0) = 0  5
Ta có:  f (5) = 0 ⇒ max y = . [0;5] 2   5  5  f   =   2  2
2. Cho bất phương trình 2
1+ x + 8 − x + 8 + 7x − x ≤ m . Tìm tất cả các giá trị thực của
tham số m để bất phương trình có nghiệm đúng với mọi x ∈[ 1 − ;8] Lời giải 2
1+ x + 8 − x + 8 + 7x − x ≤ m (1)
Đặt t = 1+ x + 8− x ; với điều kiện 1 − ≤ x ≤ 8 7 − 2x / ⇒ t =
2. (1+ x)(8 − x) ( 8− x + 1+ x ) 7 /
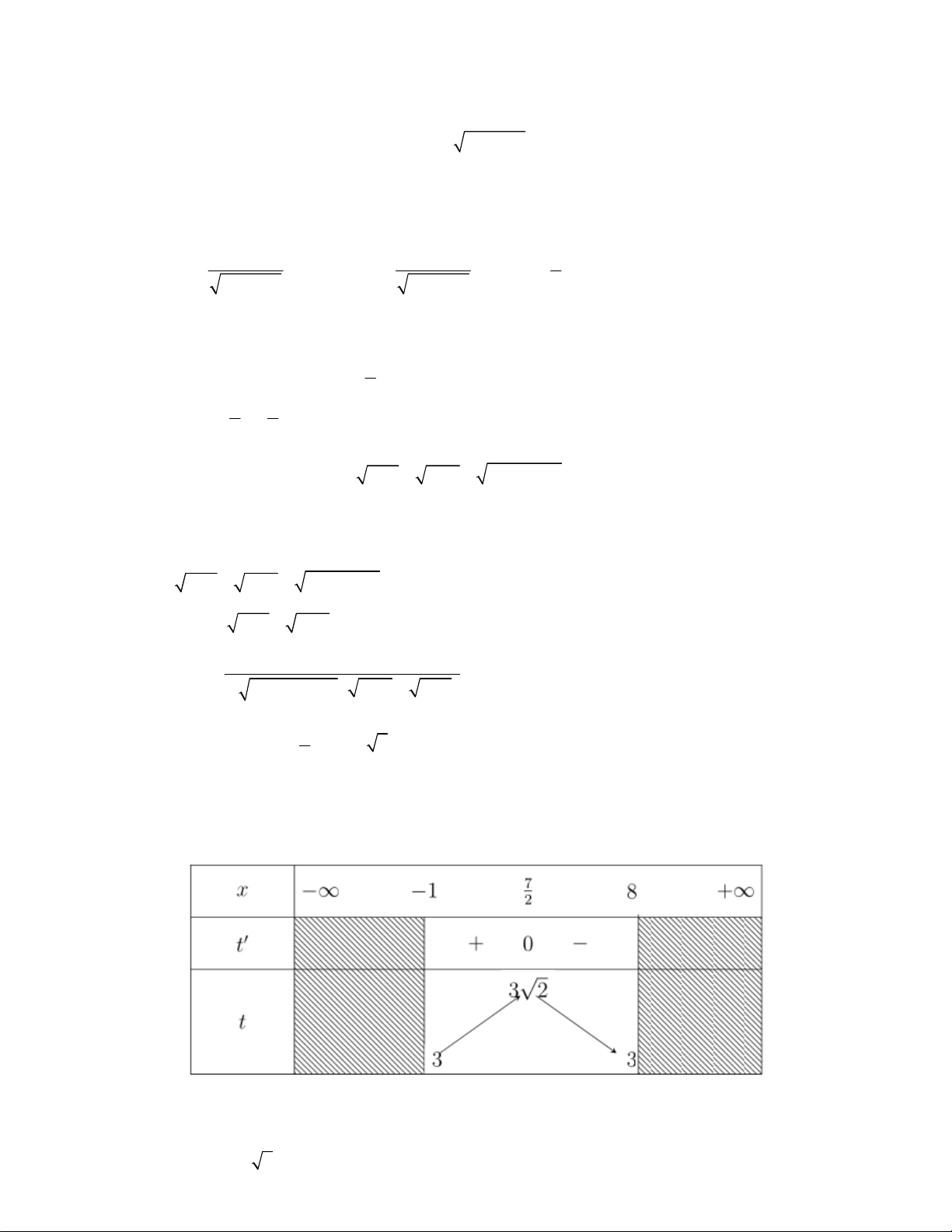
Cho t = 0 ⇔ x = ⇒ t = 3 2 2 t( 1 − ) = t(8) = 3 Bảng biến thiên
Dựa vào bảng biến thiên ⇒ 3 ≤ t ≤ 3 2 2 (1) t − 9
Khi đó ⇒ m ≥ t + t  ∀ ∈ 3;3 2   2 2 t − 9 / f (t) t f (t) t 1 0 t 3;3 2 = + ⇒ = + ≥ ∀ ∈   2
Suy ra f(t) đồng biến trên 3;3 2    9 + 6 2
m ≥ max f (t) = f (3 2) = . 3;3 2 2  
Câu 2. (5,0 điểm) Thầy Cao Văn Kiên – Trương Đức Thịnh 2
(x+5 x−1)(x x x − + − )1 5
1) Giải phương trình = . x −1 −1 x − 2 Lời giải x ≥ 1 Điều kiện:  . x ≠ 2 2
(x+5 x−1)(x x x − + − )1 5 Ta có = x −1 −1 x − 2 2 + −
(x+5 x−1)(x− x x )1 5 ⇔ =
(vì x −1 +1 > 0 ) x − 2
(x −2)( x−1+ )1
(x+5 x−1)(x− )1 2
⇒ x + x − 5 = x −1 +1 2 x + x − 5 x + 5 x −1 ⇒ =
(Do x = 1 không là nghiệm của phương trình) x −1 x −1 +1
(x − ) + (x − )+ ( x − )2 2 1 + 5 x −1 +1 2 5 2 1 ⇒ ( = (*) x − 2) +1 x −1 +1 2 t + 5t +1
Xét hàm số f (t ) = , t ∈ (−1;+∞). t +1 t + 2t + 4 (t + )2 2 1 + 3 Có f ′(t ) = = > 0, t ∀ ∈ 1 − ;+∞ . 2 2 ( ) (t + )1 (t + )1
⇒ f (t) đồng biến trên ( 1 − ;+∞).  ≥
( ) ⇔ f (x − ) = f ( x− ) x 2 * 2
1 ⇔ x − 2 = x −1 ⇔ 
( x − 2)2 = x −1 x ≥ 2 x ≥ 2  5 + 5 ⇔  ⇔  ⇒ x = ±
(Thỏa mãn điều kiện). 2 5 5
x − 5x + 5 = 0 x = 2  2 5 5  +  Kết luận: S =  .  2 
Bài toán phát triển 2 3
x − x − 2 2x +1
Giải phương trình x +1 = . 3 2x +1−3 Lời giải 2 3 2
x − x − 2 2x +1 x − x − 6 Ta có x +1 = ⇔ x +1 + 2 = 3 3 2x +1 −3 2x +1 −3 (x −3)(x + 2)
( x +1 + 2)( x +1− 2)(x + 2) ⇔ x +1 + 2 = = 3 3 2x +1−3 2x +1−3
( x +1− 2)(x + 2) ⇔ 1= 3 2x +1−3 3
⇔ 2x +1−3 = ( x +1− 2)(x + 2) 3 3
⇔ 2x +1+ 2x +1 = (x +1) + x +1 Xét hàm số 3 2
f (t) = t + t ⇒ f ′(t) = 3t +1> 0, ∀t ∈ ℝ.
Hàm số f (t)đồng biến, phương trình trở thành 3
f ( 2x +1) = f ( x +1) 3 ⇔ 2x +1 = x +1 3 2
⇔ x − x − x = 0  x = 0(l)    1− 5 1+ 5 ⇔ x = (l) ⇔ x = .  2 2   1+ 5 x = (t / m)  2 1  + 5 Kết luận: S   =  .  2   
2) Có hai dãy ghế ngồi đối diện nhau, mỗi dãy có 4 ghế. Xếp ngẫu nhiên 8 học sinh gồm
4 nam và 4 nữ ngồi vào hai dãy ghế đó sao cho mỗi ghế có đúng một học sinh ngồi. Tính
xác suất để mỗi học sinh nam đều ngồi đối diện với một học sinh nữ. Lời giải
Ta có không gian mẫu là n(Ω) = 8!
Gọi A là biến cố “ Mỗi học sinh nam ngồi đối diện với học sinh nữ”.
Trước hết ta xếp các bạn nam vào một bên, xếp các bạn nữ vào một bên sau đó đổi chỗ các
bạn ngỗi đối diện, theo quy tắc nhân ta có n ( A) 4 = 4!.4!.2 Vậy P ( A) 4 4!.4!.2 8 = = . 8! 35
Bài tập tương tự :
Câu 1: Có hai dãy ghế ngồi đối diện nhau, mỗi dãy có 4 ghế. Xếp ngẫu nhiên 8 học sinh gồm 4
nam và 4 nữ ngồi vào hai dãy ghế đó sao cho mỗi ghế có đúng một học sinh ngồi. Tính xác
suất để ít nhất có một cặp học sinh nam và nữ ngồi đối diện với nhau. Lời giải
Ta có không gian mẫu là n(Ω) = 8!
Gọi A là biến cố “ ít nhất có một cặp học sinh nam và nữ ngồi đối diện với nhau”. Suy ra
A là biến cố “ không có một cặp học sinh nam và nữ ngồi đối diện với nhau”.
tức là nam ngồi đối diện nhau và nữ ngồi đối diện nhau.
Trước hết ta chọn 2 trong 4 cặp ghế để xếp các học sinh nam sau đó xếp các bạn nữ vào 4
ghế còn lại, theo quy tắc nhân ta có n ( A) 2 = C .4!.4! 4 2 C .4!.4! 3 32 Do đó P ( A) 4 = = ⇒ P ( A) = 8! 35 35
Câu 2: Trong cuộc gặp mặt dặn dò trước khi lên đường tham gia kì thi HSG có 10 bạn trong đội
tuyển gồm 2 bạn đến từ lớp 12A1, 3 bạn từ 12A2, 5 bạn còn lại đến từ các lớp khác nhau.
Thầy giáo xếp ngẫu nhiên các bạn kể trên ngồi vào một bàn dài mà mỗi bên có 5 ghế xếp
đối diện nhau. Tính xác suất sao cho không có học sinh nào cùng lớp ngồi đối diện nhau. 73 38 5 53 A. . B. . C. . D. . 126 63 9 126 Lời giải Chọn B
Ta có không gian mẫu là n(Ω) =10!
Gọi A là biến cố “ không có học sinh nào cùng lớp ngồi đối diện nhau”
A là biến cố “ có học sinh nào cùng lớp ngồi đối diện nhau”
A là biến cố “ học sinh A ngồi đối diện nhau”; A là biến cố “ học sinh A ngồi đối diện 1 1 2 1 nhau”. Khi đó n (
A ) = n( A + n A − n A ∩ A . 1 ) ( 2) ( 1 2)
Xét biến cố A : Trước hết chon 1 trong 5 cặp ghế để xếp 2 hs A ngồi, đổi chỗ 2 bạn này 1 1
có 2! cách., 8 người còn lại có 8!. Theo quy tăc nhân có n ( A ) 1 = C .2!.8! 1 5 Tương tự n ( A ) 1 2
= C .A .8!; n( A ∩ A = A .2!.A .6! thay vào ta được 1 2 ) 2 2 2 5 3 5 3 P ( A ) 25 = ⇒ P ( A) 38 = . 63 63
Câu 3. (6,0 điểm) Thầy Lục Minh Tân
1. Cho hình chóp S.ABCD có đáy ABCD là hình thoi với 0
ABC = 60 , BC = .
a Biết tam giác SAB
đều, tam giác SCD vuông tại C và nằm trong mặt phẳng hợp với mặt phẳng đáy một góc 0 60 .
Tính thể tích khối chóp S.ABCD và khoảng cách từ B đến mặt phẳng (SAD) theo a Lời giải
Gọi H , F lần lượt là trung điểm của AB, SC . Kẻ SG ⊥ HC (G ∈ HC) Ta có:
⇒ ( ABCD) ⊥ (SHC) 
 AB ⊥ SC ( AB / /DC, DC ⊥ SC)  
⇒ AB ⊥ (SHC) ( ABCD) ∩(SHC) = HC ⇒ SG ⊥ ( ABCD)  AB ⊥ CH  SG ⊥ CH 
Hay SG là đường cao hình chóp
* Ta có: ((SCD) ( ABCD)) = (HC SC ) 0 , , = SCG = 60 SH = HC ⇒ S
∆ HC cân tại H và 0
SCH = 60 nên ∆SCH đều.   ⇒ a 3 3 3a
G là trung điểm của CH và SG =  . =    2  2 4 2 3 1 1
 a 3  3a a 3 * V S SG ABCD = . . ABCD = .2 . =   3 3  4  4 8 3 1 a 3 * V V S ABD = S ABCD = . . 2 16 7 Ta có: 2 2 = + = a SD SC CD 2 a 7 a + a +
SA + AD + SD Chu vi ∆SAD là 2 p = = 2 2
Diện tích ∆SAD là S =
p ( p − SA)( p − SD)( p − AD) 2 3a 7 = 16
Khoảng cách từ B đến SAD là: 3 a 3 3. 1 3V a 21 16 V d B SAD S d B SAD B SAD = , . ⇒ , SAD = = = . ( ( )) ( ( )) 2 3 S a SAD 3 7 7 16
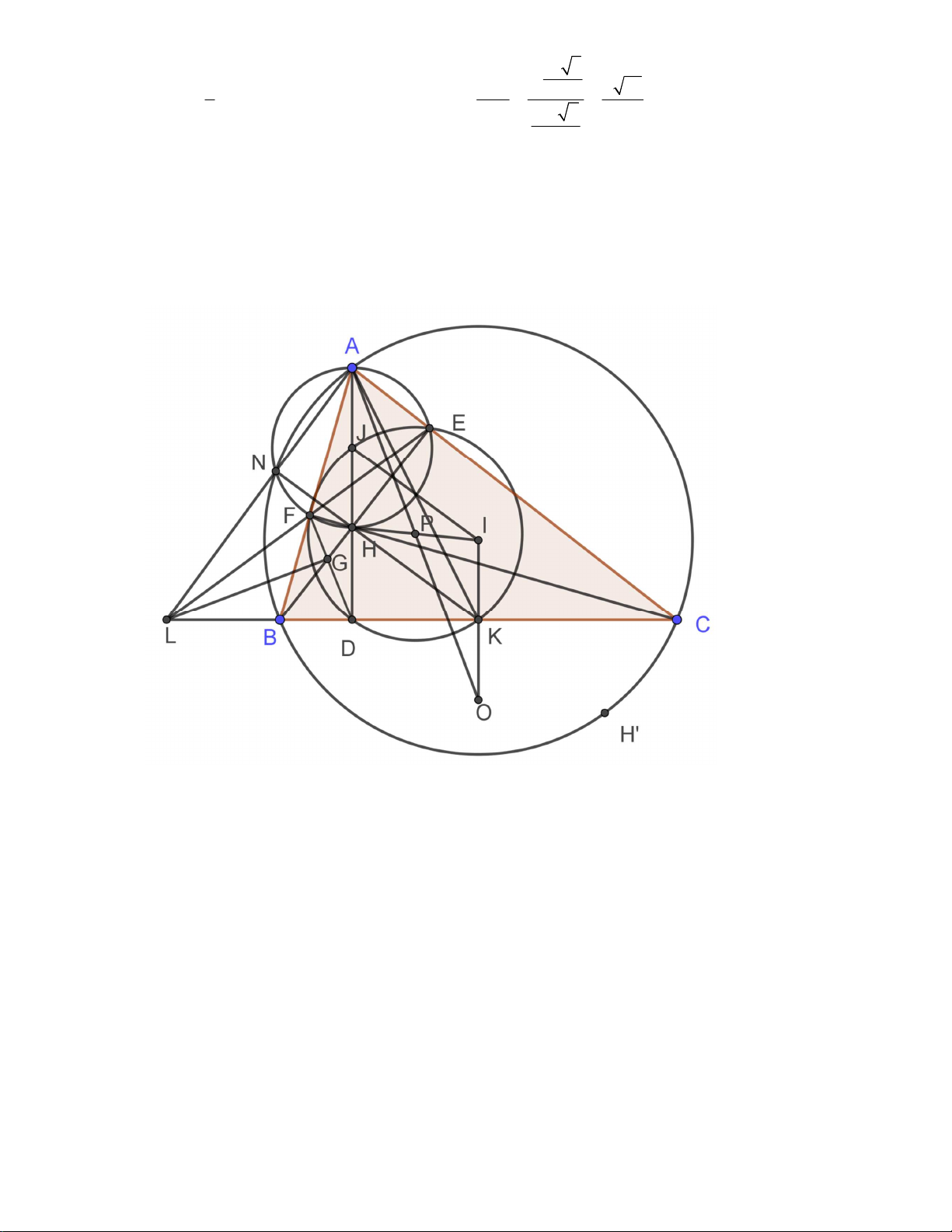
2. Cho tam giác nhọn ABC ( AB < AC) có các đường cao AD, BE,CF đồng quy tại H. Gọi G là
giao điểm của BH và DF , I là giao điểm của BC và FE ; O là tâm đường tròn ngoại tiếp tam
giác BCH ; K là trung điểm của BC. Chứng minh H là trực tâm của tam giác AKL và LG vuông góc với A . O Lời giải
* Gọi J là trung điểm của AH và I là tâm đường tròn ngoại tiếp A ∆ BC
Ta có: AEH = AFH ⇒ AFHE nội tiếp đường tròn tâm J , với J là trung điểm của AH.
⇒ HN ⊥ AN (1)
* Gọi N là giao điểm của đường tròn ( J , JA) và đường thẳng AL( N ≠ A)
Ta có: LN.LA = LF.LE
Mặt khác: BFEC nội tiếp đường tròn tâm K ⇒ L .
B LC = LF.LE
⇒ LN.LA = L . B LC ⇒ ,
A N , B, C nội tiếp đường tròn tâm I
* Đường tròn ( J, JA) và (I, IA) có trục đẳng phương là AN ⇒ JI ⊥ AN
Mà JI / /HK ⇒ HK ⊥ AN (2) Từ ( )
1 ,(2) ⇒ N, H, K thẳng hàng và KN ⊥ AN
* Xét ∆AKL có AD, KN lần lượt là đường cao và đồng quy tại H
⇒ H là trực tâm của AKL
b. Gọi P là tâm của đường tròn Ơle của tam giác ABC ⇒ I ∈ AO * L . B LC = L . E LF ⇒ P = P L/(P) L/(O) G .
D GF = GH.GB ⇒ P = P G /(P) G /(O)
⇒ LG ⊥ OI ⇒ LG ⊥ AO Câu 4. (2,0 điểm) x = 3, 1 
Cho dãy số ( x thỏa mãn 2  n ) 5x + 3 x +16 n n x = ( n ∀ ∈ ℕ,n ≥1). n 1 +  4
Tìm số hạng tổng quát của ( x và tìm giới hạn dãy số ( n x n ). n )
Cách 1: Cô Nguyễn Thị Hồng Gấm 2 2 −1 1 4 15 2 −1 1
Từ giả thiết ta tính được 2 x = 3 = = 2 − ; 3 x = = = 2 − ; 1 0 0 2 2 2 2 2 2 6 63 2 −1 1 n+ 1 4 x = = = 2 − , do vậy ta dự doán 1 x = 2 − 1 , n ∀ ∈ ℕ,n ≥1 . n n 1 − ( ) ( ) 3 2 2 4 2 2 2
Ta sẽ chứng minh công thức ( ) 1 đúng bằng qui nạp. Hiển nhiên ( )
1 đúng với n = 1, n = 2, n = 3 . k + 1 Giả sử ( )
1 đúng với n = k (k ≥1, k ∈ ℕ) tức là ta có 1 x = 2 − k k 1 2 − Xét 2 2         k + 1 k + 1 k + 1 k + 1 1 1 1 1 5 2 −  + 3  2 −  +16 5 2 −  + 3  2 +  2 k 1 − k 1 − k 1 − k 1 5x + 3 x +16 −         k k 2 2 2 2 x = = = k 1 + 4 4 4 k 1 + 2 8.2 − k 1− k + + 1 2 1 1 = = 2 − . Vậy ( )
1 cũng đúng với n = k +1. k 1 + 1 4 2 −
Theo giả thiết quy nạp ta được ( )
1 đúng ∀n ∈ ℕ, n ≥ 1. 1 1 Khi đó ta có * 2 n
< x < 2.2n ,∀n ∈ ℕ đồng thời lim 2.2n = 2 nên theo nguyên lý kẹp ta có n lim ( n x = . n ) 2
Cách 2: Thầy Ngô Thanh Tòng 2 5x + 3 x +16 2 Ta có n n x = ⇔ x − x = x + 2 2
⇔ 2x − 5x .x + 2x = 18 . n+ (4 5 n+ n ) 9 ( 2 16 1 1 n ) + + 4 n 1 n 1 n n 2 2
2x − 5x .x + 2x −18 = 0 + + Vậy n 1 n 1 n n 
, ∀n ≥ 1 nên x , x +
là hai nghiệm của phương trình 2 2  n 2 n 2x
− 5x .x + 2x −18 = 0 n+2 n+2 n 1 + n 1 + 2 2
2x − 5x .x + 2x −18 = 0 . n 1 + n 1 + 5x Theo Vi-et ta có n 1 x + x + =
⇔ 2x − 5x + 2x = 0 n+2 n + + 2 n 2 n 1 n 1 1 3 ⇔ x − 2x = x − 2x = ... = x − 2x = , n ∀ ≥1. n+2 n 1 + ( n 1+ n ) n ( 2 1 ) n 1 2 2 2 + 1 −
(ý tưởng sử lí: 2x
− 5x + 2x = 0 ⇔ x + ax = x + ax ) n+2 n 1 + n n+2 n 1 + ( n 1+ n ) 2a 3 1  1    n− 1 Do đó 1 n+2 x − 2x = ⇔ x + = 2 x +  = ... = 2  x +  = 2 . n 1 + n n n 1 + n n n 1 − 2 2 2  2   2  3 a  a 
(ý tưởng sử lí: x − 2x = ⇔ x + = 2 x +  ) n 1 + n n n 1 + n 1 2 2 + n  2n  n+ 1 Vậy 1 x = 2 − , ∀n ≥ 1. n n 1 2 −
*) Tìm giới hạn dãy số ( n x . n ) 1 1 n+ 1 Ta có 1 + n n n n n n x = 2 − nên dễ thấy 1 2 n
< x < 2 , hay 2 n
< x < 2.2n . Mà lim 2n = 2 nên n n 1 2 − n n
theo định lý kẹp thì lim n x = 2 . n Cách 3: Thầy Aki Le
Từ hệ thức truy hồi, ta suy ra dãy số dương, dãy tăng. Hơn nữa, với * n ∈ ℕ , ta có (4x −5x = + ⇔ − + = + )2 9( 5 2 x 16 x x x x n n n ) 2 2 9 1 n 1 + n 1 + 2 n n Do đó,  5 2 2 x  + x = 9 + x x n 1 + n n 1 +  2 n 5 5 2 2  ⇒ x − x = x x
− x ⇒ x + x = x . n+2 n n 1 + ( n+2 n ) n+2 n n 1 + 5 2 2  2 2 x + x = 9 + x x n+2 n 1 + n+2 n 1 +  2
Vì thế, dãy truy hồi cấp một “phi tuyến” trên chính là dãy truy hội tuyến tính cấp hai:  15 x  = 3, x = , 1 2  2  5
x − x + x = 0, n ∀ ≥1. n+2 n 1 +  2 n
Dãy truy hồi được viết lại 5 1
Vì phương trình đặc trưng 2
λ − λ +1 = 0 có hai nghiệm λ = và λ = 2 nên 2 1 2 2 a n * x = + .
b 2 , ∀n ∈ ℕ . n 2n 15 1 Do x = 3, x = nên n 1 + * x = − + 2 , n ∀ ∈ ℕ . 1 2 2 n n 1 2 − Suy ra 1/ n * 2 n
< x < 2.2 , n ∀ ∈ ℕ . n Và 1/
lim 2.2 n = 2 = lim 2.Vì thế, theo định lý kẹp, dãy ( n x hội tụ về 2. n ) n→∞ n→∞ Bình luận.  15 x  = 3, x = , 1 2 •  2
Dãy truy hồi tuyến ( x : 
có thể giải nhờ vào cấp số n ) 5
x − x + x = 0, n ∀ ≥1, n+2 n 1 +  2 n
nhân (ý tưởng của thầy Ngô Thanh Tòng). Ta có 1 x − 2x = x − 2x , n ∀ ≥1. Do đó n+2 n 1 + ( n 1+ n ) 2 1 3 x − 2x = ⋅ x − 2x = , n ∀ ≥ 0. n+2 n 1 + n ( 2 1 ) n 1 2 2 + 3 Từ x − 2x = , n ∀ ≥ 1, ta thu được n 1 + n 2n 1  1    n− 1 1 n+2 x + = 2⋅ x +  = 2  x +  = 2 , n ∀ ≥ 1. n 1 + n n n 1 − 2 2  2   2  1 Vì thế, n 1 x 2 + = − + . n 2n
• Ngoài ra, việc tìm công thức công thức tổng quát của dãy (x có thể tiếp cận n )
theo 3 cách khác: (i) dự đoán quy luật số hạng tổng quát của dãy rồi dùng phương
pháp qui nạp của cô Nguyễn Thị Hồng Gấm; (ii) Sử dụng dãy số phụ thông qua  1 
ý tưởng “thoát căn” của thầy SongMinh Nguyễn: x = 2 a − ; (iii) sử dụng n n  a  n 3
hàm sinhyperbolic (một hình thức khác của cách ii)), xét α :sinh α = . Khi 1 ( 1) 4 x − x − đ e e ó, u = sinh α với α = + ≥ = +
α α, n 1. (Hàm sinh (x) . ) n ( n ) n 1 n 2 a b c
Câu 5. (2,0 điểm) Cho ba số thực a,b, c > 0 thỏa mãn + + = 5 . b c a 17 a b c Chứng minh rằng ≤ + + ≤1+ 4 2 . 4 c a b Lời giải
Cách 1: Thầy Nguyễn Bá Trinh
 x, y, z > 0
 x, y, z > 0    Đặ a b c 1 t x = , y = , z = . Ta có  xyz = 1 ⇔  yz = b c a   x
x + y + z = 5
y + z = 5 − x 2 2 4
Suy ra 0 < x < 5 và ( y + z) ≥ 4 yz ⇔ (5 − x) 3 2
≥ ⇔ x −10x + 25x − 4 ≥ 0 x
3 − 2 2 ≤ x ≤ 4 ⇔ ( x − 4)( 2 x − 6x + ) 1 ≥ 0 ⇔ 
⇔ 3− 2 2 ≤ x ≤ 4  x > 3 + 2 2 a b c 1 1 1 1 1 Khi đó P =
+ + = + + = xy + yz + zx = x(5− x) 2
+ = −x + 5x + . c a b x y z x x 1
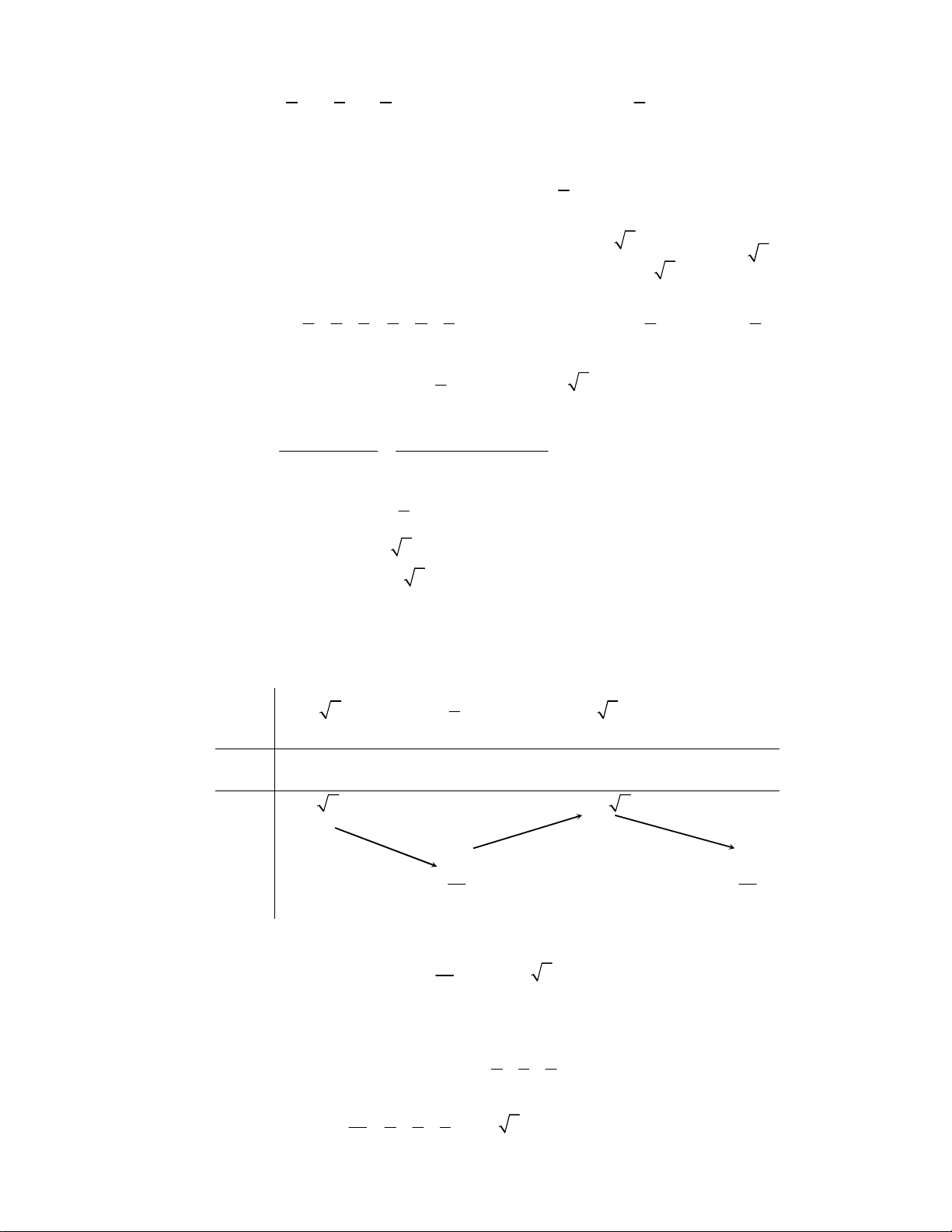
Xét hàm số f ( x) 2
= −x + 5x + trên đoạn 3 2 2;4 −   . x 2 x x x f ′( x) 3 2 − x + x − (2 )1( 2 )1 2 5 1 − − + + = = 2 2 x x  1  x = 2 
⇒ f ′( x) = 0 ⇔ x =1− 2 < 0   x = 1+ 2  Bảng biến thiên x 1 3 − 2 2 1+ 2 4 2
f ′( x) − 0 + 0 − 1 + 4 2 1 + 4 2 f ( x) 17 17 4 4 17
Dựa vào bảng biến thiên ta có ≤ P ≤ 1+ 4 2 . 4
Cách 2 : Thầy Đào Văn Tiến a b c
Cho ba số thực dương a, , b c thoả mãn + + = 5 . b c a 17 a b c Chứng minh rằng ≤ + + ≤1+ 4 2 . 4 c a b Lời giải Đặ a b c t x = ; y = ; z = với , x y, z > 0 . b c a xyz = 1 Ta có  .
x + y + z = 5 Vì 2 2  y + z   5 − x 
x + y + z = 5 ⇒ x < 5, xyz = 1 ⇒ 1 = xyz ≤ x ⇒   1 ≤ x 
 ⇔ 3 − 2 2 ≤ x ≤ 4.  2   2  a b c Khi đó P =
+ + = xy + yz + zx . Vậy theo định lý viet ta có x, y, z là nghiệm dương c a b 1 của phương trình 3 2 2
t − 5t + Pt −1 = 0 ⇔ P = t − + 5t + t 1
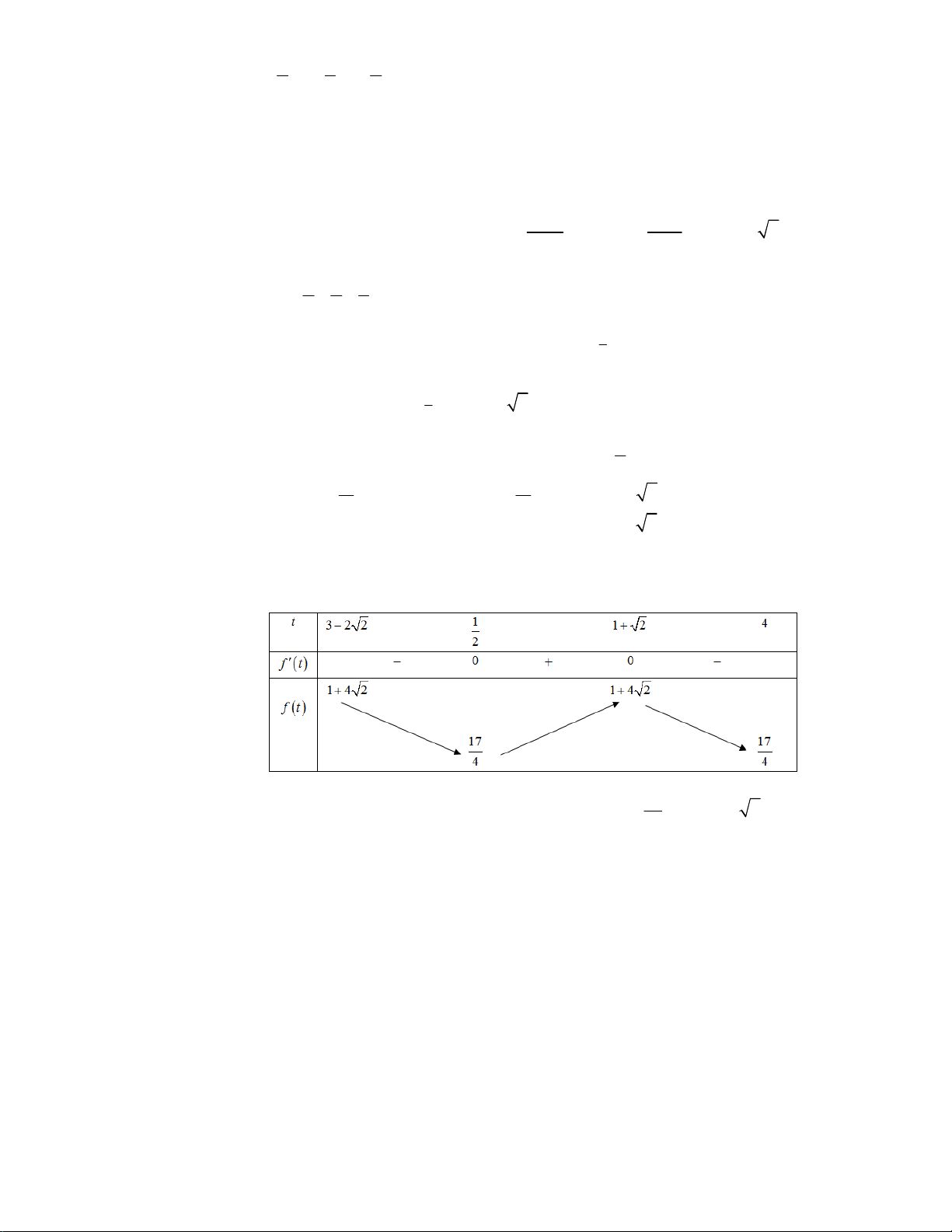
Xét hàm số f (t) 2 t 5t , t 3 2 2;4 = − + + ∈ − .   ta có t  1 t  = 2  f ′(t) 1 1 = 2
− t + 5 − , f ′ t = 0 ⇔ 2
− t + 5 − = 0 ⇔ t =1+ 2 . 2 ( ) 2 t t  t = 1− 2  BBT: 17
Quan sát bảng biến thiên ta thấy để có ba nghiệm dương thì ≤ P ≤1+ 4 2 . 4
Document Outline