Đề thi chọn học sinh giỏi Toán 12 THPT năm 2021 – 2022 sở GD&ĐT Hà Nội

SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI CHỌN HỌC SINH GIỎI LỚP 12 HÀ NỘI NĂM HỌC 2021 – 2022 MÔN THI: TOÁN
Thời gian: 90 phút (Không kể thời gian phát đề) 2 x  mx 1
Câu 1. [HSG-HÀ NỘI 2021-2022] Chứng minh rằng với mọi m  2 hàm số f (x) = có đúng 4 2 x  2x  3 cực trị. Lời giải 2 x  mx 1 g(x).g (  x) Cách 1. Đặt g(x) =  y  g(x)  y  . 2 x  2x  3 g(x)
Số điểm cực trị của hàm số y  g(x) là số nghiệm của phương trình: g(x).g (  x)  0 . Xét 2
g(x)  0  x  mx 1  0. Ta thấy ac  1   0, m
  g(x)  0 luôn có 2 nghiệm bội lẻ (1). Xét g (  x)  0. 2 2 2  (2x  )
m (x  2x  3)  (2x  2)(x  mx 1)  0  (2  ) m x 8x  3m  2  0 m  2  Do  2 2 2 32
 ' 16  (2  m)(3m  2)  3m  4m 12  3(m  )   0  3 3
nên g '(x)  0 cũng có 2 nghiệm bội lẻ (2). 2 x  mx 1
Từ (1) và (2) ta có hàm số y=
có đúng 4 điểm cực trị (ĐPCM) 2 x  2x  3 2 x  mx 1 g(x).g (  x) Cách 2. Đặt g(x) =  y  g(x)  y  . 2 x  2x  3 g(x)
Số điểm cực trị của hàm số y  g(x) là số nghiệm của phương trình: g(x).g '(x)  0 Xét 2
g(x)  0  x  mx 1  0. Ta thấy ac  1   0, m
  g(x)  0 luôn có 2 nghiệm bội lẻ (1).
Nhận xét: g '(x) cũng bậc 2, nếu g '(x) không đổi dấu thì g(x)  0 chỉ có tối đa 1 nghiệm. (loại)
Do đó: g '(x) phải đổi dấu, tức là g '(x) phải có 2 nghiệm phân biệt.
Vậy hàm số luôn có đúng 4 cực trị.
Câu 2. [HSG-HÀ NỘI 2021-2022] a) Giải phương trình x 1  3x  2x  2  2x 1 . Lời giải x 1 0    x  1  3   x  0  1 Điều kiện:   x  0  x  . 2x  2  0 2   1 2x 1 0 x    2 2 2
 Ta có x 1  3x  2x  2  2x 1   x 1  3x    2x  2  2x 1
 4x 1 2 3xx  
1  4x 1 2 2x  22x   1  3x  x  
1  2x  22x   1 Trang 1/6 - WordToan x  1  lo¹i 2   2 2
 3x  3x  4x  2x  2  x  x  2  0   . x  2
Vậy phương trình đã cho có nghiệm duy nhất x  2 . 2 2
x  5x  4  4 x 1  y 3y  4 y
Câu 2. [HSG-HÀ NỘI 2021-2022] b) Giải hệ phương trình  . 2 2 x  y  25  Lời giải 1   x  5 Điều kiện:  . 0  y  5  Ta có 2 2 2 2
x  5x  4  4 x 1  y  3y  4 y  x  2x 1 3 3x  4 x 1  y  3y  4 y
  x  2  x   2 1 3
1  4 x 1  y  3y  4 y * .  Xét hàm số f t 4 2
 t  3t  4t với t  0 . Ta có f t 3
 4t  6t  4 ; f  t 2 12t  6 .   Khi đó f  t 2 2 1 2 2
 0  12t  6  0  t   t   f    4  2 2  0 . 2 2  2    Suy ra f t 3  4t  6t  4  0, t   0 . Vậy hàm số f t 4 2
 t  3t  4t đồng biến với mọi t  0 .
 Ta có *  f  x 1  f  y   x 1  y  y  x 1.
Thay y  x 1 vào phương trình 2 2 x  y  25 ta được     x   x   x 4 y 3 2 2 2
1  25  x  x 12  0   . x  3   lo¹i
Kết luận: Vậy hệ phương trình đã cho có nghiệm duy nhất  ; x y  4;3 .
Câu 3. [HSG-HÀ NỘI 2021-2022] Chọn ngẫu nhiên một số từ tập các số tự nhiên có 8 chữ số. Tính xác
suất để chọn được số chia hết cho 9 và chứa nhiều nhất một chữ số 9. Lời giải
Số phần tử của không gian mẫu: n 7  9.10 .
Gọi biến cố: A:"chọn được số chia hết cho 9 và chứa nhiều nhất một chữ số 9 ".
Gọi số cần lập có dạng: a a a a a a a a a  0 . 1 2 3 4 5 6 7 8  1  TH1: a  9,i  1,8 . i Chọn a có 8 cách chọn. 1 Chọn a a a a a a có 6 9 cách. 2 3 4 5 6 7
Chọn a , có 1 cách chọn. 8 Vậy có: 6 8.9 số.
TH2: a  9 và các chữ số còn lại khác 9. 1
Trang 2/6 – Diễn đàn giáo viên Toán Chọn a có 1 cách. 1 Chọn a a a a a a có 6 9 cách. 2 3 4 5 6 7
Chọn a , có 1 cách chọn. 8 Vậy có: 6 9 số.
TH3: Chữ số 9 không ở vị trí a . 1 Chọn a , có 8 cách. 1
Chọn vị trí cho chữ số 9, có 7 cách chọn. Giả sử a  9 . 2 Chọn a a a a a , có 5 9 cách. 3 4 5 6 7
Chọn a , có 1 cách chọn. 8 Vậy có: 5 8.7.9 số. n  A 6 6 5  8.9  9  56.9 . n A 898857
* Xác suất của biến cố A là P  A     . n 7 10 3u 1
Câu 4. [HSG-HÀ NỘI 2021-2022] Cho dãy số u xác định bởi u  3; n u  ; n 1, 2,3,... n  1 n 1  u  3 n 1) Chứng minh dãy số u là dãy số giảm. n  1 1 1 2) Tính tổng S    ... u 1 u 1 u 1 1 2 100 Lời giải 1) Ta có u  3  0 . 1 2u  n 1 Giả sử u  1, ta có u 1   0 . n n 1  u  3 n
Theo nguyên lí quy nạp thì u  1 với mọi số nguyên dương n . n 2 3u 1 1 u Xét hiệu n n u  u   u   0 . n 1  n u  3 n u n n3 Suy ra * u  u , n
   . Vậy u là dãy giảm. n  n 1  n 2u  3u 1 4 u  n  n 1 n 1 2) Ta có u 1  và u 1  1  n 1  u  3 n 1  u  3 u  3 n n n u 1 u 1 u  n n n 1 Suy ra 1 1 n 1  2  ...  2  2  u 1 u 1 u 1 n 1  n 1 1 n 1 Vì vậy:  2  u 1 2 n 1  Ta có: Tổng hợp: Trần Minh Vũ Trang 3/6 1 1 1 S    ... u 1 u 1 u 1 1 2 100  1   1   1 0 1 99   2   2  ... 2         2   2   2  100 100  2 1 50  2  51.
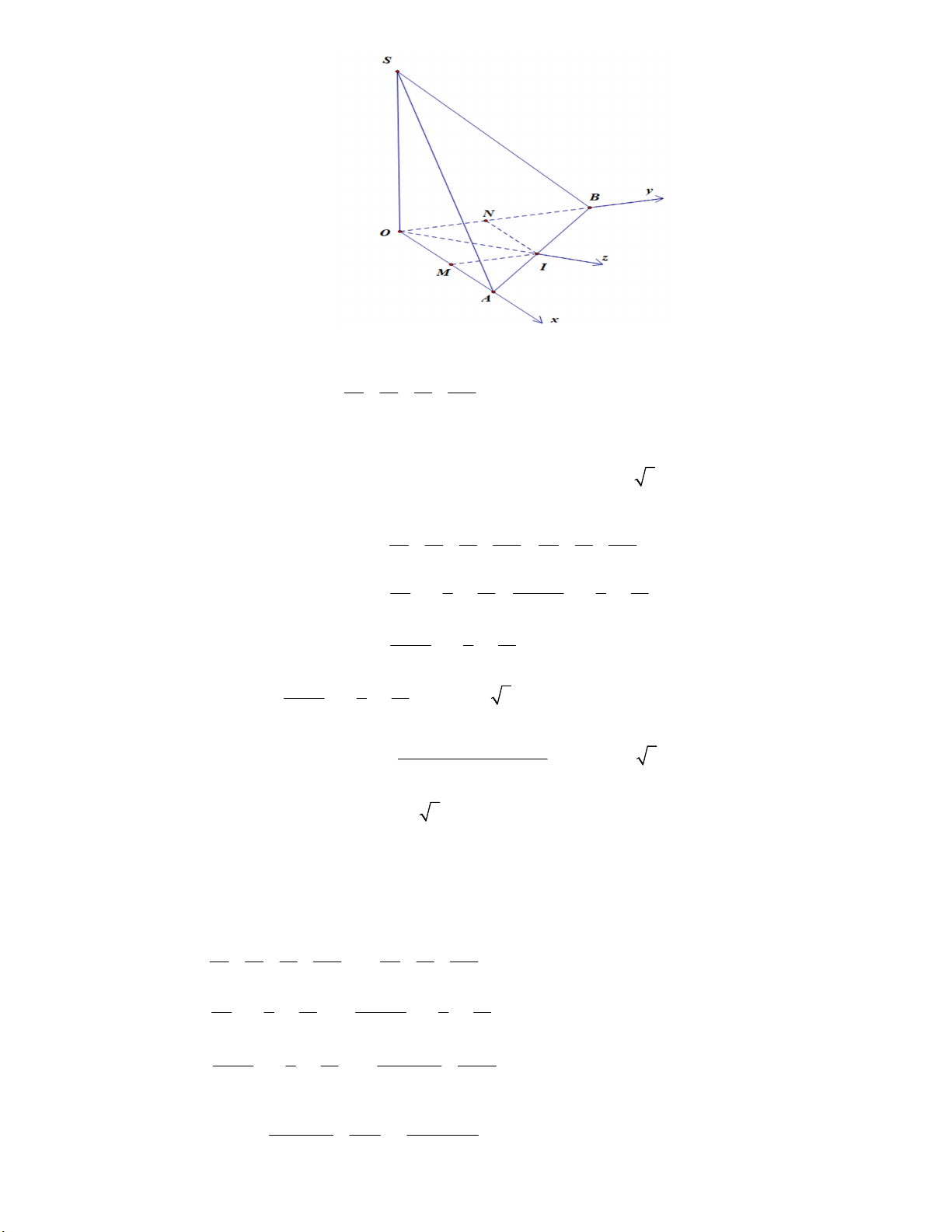
Câu 5. [HSG-HÀ NỘI 2021-2022] Trong mặt phẳng P cho góc  0
xOy  90 và tia Oz thỏa mãn  0 xOz  30 ;  0
zOy  60 . Trên tia Oz lấy điểm I sao cho OI  2a . Trên đường thẳng d đi qua O và vuông góc
với P lấy điểm S sao cho OS  a . Mặt phẳng Q thay đổi đi qua SI và cắt các tia Ox,Oy lần lượt tại ,
A B ( A khác O và B khác O ). 1)
Tính góc giữa P và Q khi I là trung điểm của AB . 2)
Tìm giá trị nhỏ nhất của thể tích khối chóp S.OAB . Lời giải
Đặt OA  x,OB  y (x, y  0) . 1)
Khi I là trung điểm của AB suy ra AB  2AI  2BI  2OI  4a nên  0 OAI  30 ,  0 OBI  60 .
Khi đó x  2a 3, y  2a nên nếu gọi E là chân đường vuông góc hạ từ O xuống AB ta có góc giữa
P,Q bằng góc  SEO . O . A OB SO 1 Lại có OE   a 3 suy ra tan  SEO     0 SEO  30 . AB OE 3 2)
M , N lần lượt là hình chiếu của I lên Ox, Oy suy ra OM  a 3, ON  a và do đó
   a 3  a  OI  OM  ON  OA  OB . Vì ,
A I , B thẳng hàng nên ta có x y a 3 a 3 x  2a 3 2   1 2a
 xy  4 3a và dấu bằng xảy ra khi  x y xy y  2a 3 1 2 3a 3 2 3a Suy ra V  axy 
. Vậy thể tích khối chóp S.OAB nhỏ nhất V  . S .OAB 6 3 min 3
Câu 6. [HSG-HÀ NỘI 2021-2022] Với a, ,
b c là các số thực dương thỏa mãn 2 2 2
a  b  c  3. Tìm giá trị 1 1 1 2
nhỏ nhất của biểu thức: P     . 2 2 2 a b c abc Lời giải Cách 1.
Không mất tính tổng quát giả sử rằng c  maxa, , b  c , khi đó 1  c  3 .
Áp dụng bất đẳng thức AM-GM ta có: 1 1 1 2 2 1 2 P        2 2 2 2 a b c abc ab c abc 2  1  1 4  1  1  1   1    2 2 2   2 ab  c  c a  b  c  c 4  1  1  1  . 2   2 3  c  c  c 4  1  1 Xét hàm số f c  1  với c  1  ; 3  , có: 2   2 3  c  c  c 6 2 c   1  2 c  2c  3 f c   0, c   1  ; 3 . 2   3 c  2 3  c 
Do đó hàm số f c đồng biến trên 1  ; 3 
, suy ra f c f  11.
Từ đó ta có min P  1, đẳng thức xảy ra khi a  b  c 1. Cách 2.
Không mất tính tổng quát giả sử rằng c  maxa, , b  c , khi đó 2 c  3. Ta có: 1 1 1 2 2 1 2 P 1     1   1 2 2 2 2 a b c abc ab c abc 2  1  1 4  1  1  1  1  1  1   2 2 2   2 ab  c  c a  b  c  c 4  1  1 4c   2 1 1 c  1  1   2   2 3  c  c  c c  2 3  c  2 c  4 c 1  c 1  c   3 2 1        c   c c c 3 2 3  c  2 2 c  c   2 3  c    c  2 1  2 c  c  3   0. 2 c  2 3  c 
Đẳng thức xảy ra khi a  b  c 1. Vậy min P  1. HẾT
Trang 6/6 – Diễn đàn giáo viên Toán
Document Outline

• de-thi-chon-hoc-sinh-gioi-toan-12-thpt-nam-2021-2022-so-gddt-ha-noi
• DDGVT06-HSG-HÀ-NỘI-NĂM-2021-2022