

Preview text:
PHÒNG GD&ĐT THỌ XUÂN
ĐỀ THI CHỌN HỌC SINH GIỎI LỚP 8 Môn: Toán
Thời gian: 150 phút (không kể thời gian giao đề) 2 2 x x (x − ) 1 ( x − ) 3
Bài 1: Cho biểu thức: K = + . 2 2 4 2 x − 5x + 6 x − 3x + 2 x + x + 1 a) Rút gọn K
b) Tìm giá trị lớn nhất của K
Bài 2: a) Tìm tất cả các số nguyên tố x, y sao cho: x2 – 6y2 = 1.
b) Cho p và p + 2 là các số nguyên tố (p > 3). Chứng minh rằng p + 1 6.
Bài 3: a) Chứng minh rằng A = 7.52n + 12.6n chia hết cho 19
b) Giải phương trình nghiệm nguyên: 4 4 3
(x + 2) −x = y (1)
Bài 4: Cho hình chữ nhật ABCD, điểm P thuộc đường chéo BD ( P khác B và D), Gọi M là
điểm đối xứng của C qua P
a. Chứng minh AM song song với BD
b. Gọi E, F lần lượt là hình chiếu của M trên AD và AB.
Chứng mỉnh ba điểm E, F, P thẳng hàng
c. Chứng minh tỉ số độ dài hai đoạn thẳng MF và FA không phụ thuộc vào vị trí của P 2 2 2 2 4x y x y
Bài 5: Cho hai số thực x, y 0,CMR : + + 3(1) 2 2 2 2 2 (x + y ) y x Hết Bài 1 a, ĐKXĐ: x 1;2;3 2 2 x x (x − ) 1 (x − ) 3 K = ( + x − ) 3 (x − ) 2
(x−2)(x− ) . 4 2 1 x + x + 1 2 2x (x − ) 1 (x − ) 3 2 2x = K = = K = 4 2 ( x − ) 1 (x − ) . 4 2 3 x + x + 1 x + x + 1
b, Nếu x = 0 = K = 0 2 2 2 2
Nếu x 0 = K = =
, vậy K lớn nhất bằng khi x= - 1 2 1 2 3 1 3 x 1 + + 2 x − + 3 x x Bài 2 a) HD: Trang 1 2 2 2 2 2 Ta ã
c : x − 6y = 1 x −1 = 6y (x −1)(x + 1) = 6y 2
Do 6y 2 (x −1)(x + 1) 2
Mµ x - 1 + x + 1 = 2x x - 1 vµ x + 1 cã cï ng tÝnh ch½n lÎ .
x - 1 vµ x + 1 lµ hai sè ch½n liªn tiÕp 2 2
(x −1)(x +1) 8 6y 83y 4 2
y 2 y 2 y = 2 x = 5
b) HD: Vì p là số nguyên tố và p > 3, nên số nguyên tố p có 1 trong 2 dạng: 3k + 1, 3k + 2 với k N*.
- Nếu p = 3k + 1 thì p + 2 = 3k + 3 = 3(k + 1) p + 2 3 và p + 2 > 3. Do đó
p + 2 là hợp số ( Trái với đề bài p + 2 là số nguyên tố).
- Nếu p = 3k + 2 thì p + 1 = 3k + 3 = 3(k + 1) (1).
Do p là số nguyên tố và p > 3 p lẻ k lẻ k + 1 chẵn k + 1 2 (2) Từ (1) và (2) p + 1 6.
Bài 3 Chứng minh rằng A = 7.52n + 12.6n chia hết cho 19 HDa:
Ta có A = A = 7.52n + 12.6n = A = 7.25n + 12.6n
Vì 25 ≡ 6 (mod 19) => 25n ≡ 6n (mod 19)
=>7.25n ≡ 7.6n (mod 19) => 7.25n + 12.6n ≡ 7.6n + 12.6n ≡ 19.6n ≡ 0 (mod 19) . Điều
này chứng tỏ A chia hết cho 19. HD b: 3 2 3 3 3 2 3
(1) 8x + 24x + 32x +16 = y → y 2 → y 2 → y = 2z(z Z ) → x = 3x + 4x + 2 = z Ta chứng minh được: 3 3 2 3 2 3 3 2
x z (x + 2) → x z x + 2 → z = x +1 → x + 3x + 4x + 2 = (x +1) = x + 3x + 3x +1 → x = 1
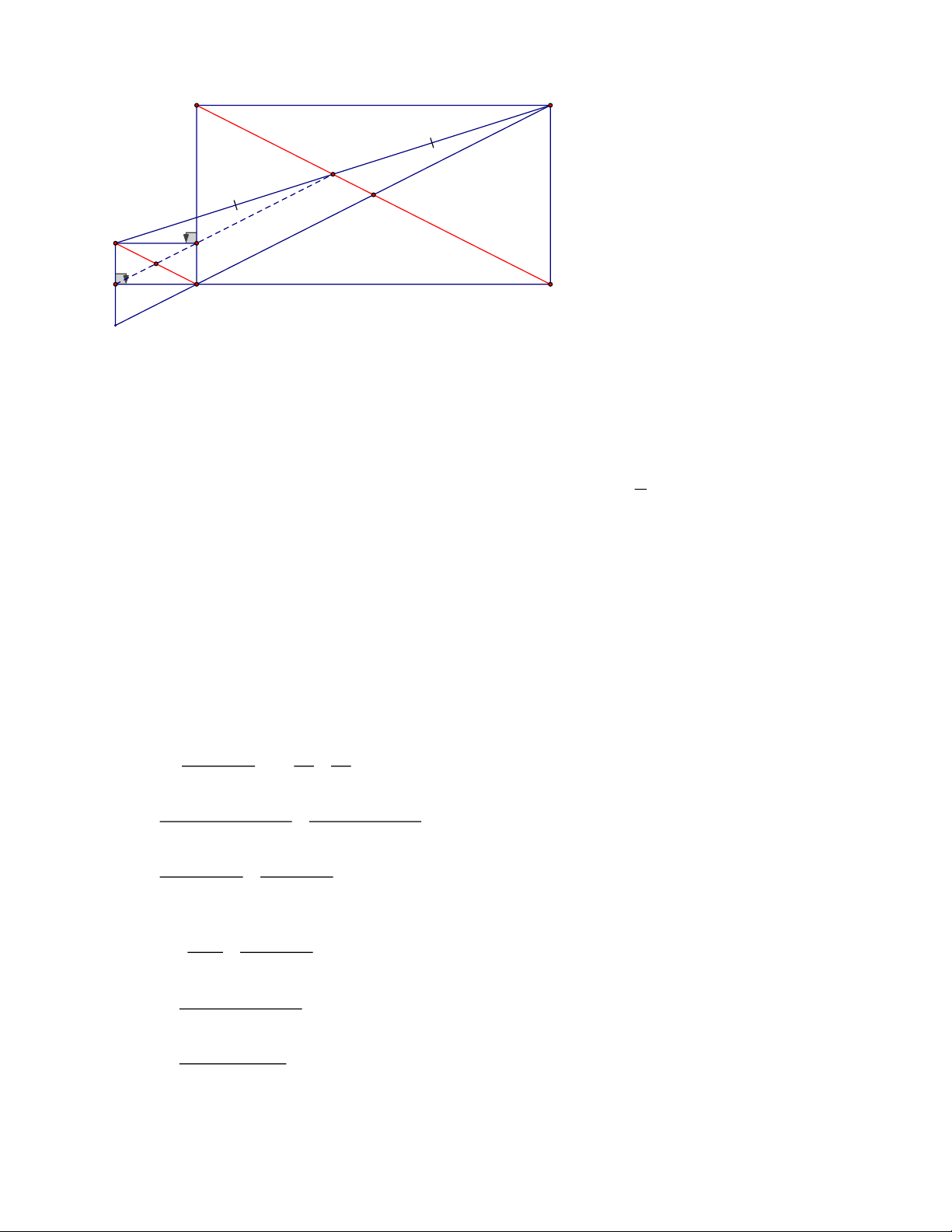
− → z = 0 → y = 0 → ( , x y) = ( 1 − ,0) Bài 4: Trang 2 B C P O M I F E A D K
a, Ta có: O là trung điểm của AC (ABCD là hình chữ nhật)
P là trung điểm của CM ( Vì M đối xứng với C qua P)
Nên Op là đường trung bình của ACM, do đó: OP//AM=> AM//BD b, Vì OP là đườ 1
ng trunh bình của ACM nên OP//AM và OP= AM 2
Do đó: OP//AI và OP=AI=> tứ giác AIPO là hình bình hành=> PI//AC (1)
Kẻ ME//AB cắt AC tại K, ta có: KAE = EAM (= KD ) A
Nên AE là phân giác KAM . Mặt khác: AE ⊥ KM = A KM cân E là trung điểm của KM,
do đó EI là đường trung bình của AMK=> EI//OA=>EI//AC (2)
Ta lại có : E, I, F thẳng hàng (3)
Từ (1), (2) và (3) ta có: E, F, P thẳng hàng. B5.HD: 2 2 2 2 4x y x y (1) −1+ + − 2 0 2 2 2 2 2 (x + y ) y x 2 2 2 2 2 4 4 2 2
4x y − (x + y )
x + y − 2x y + 0 2 2 2 2 2 (x + y ) x y 2 2 2 2 2 2 −(x − y ) (x − y ) + 0 2 2 2 2 2 (x + y ) x y 1 1 2 2 2 (x − y ) . − 0 2 2 2 2 2 x y (x + y ) 2 2 2 2 2
(x + y ) − x y 2 2 2 (x − y ) . 0 2 2 2 2 2
x y (x + y ) 4 4 2 2
x + y + x y 2 2 2 (x − y ) . 0 2 2 2 2 2
x y (x + y ) x = y Trang 3




