SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI CHỌN HỌC SINH GIỎI NAM ĐỊNH NĂM HỌC 2022 - 2023
Môn: Toán – Lớp: 8 THCS.
Thời gian làm bài: 120 Phút. Đề thi gồm: 01 trang. Câu 1. (4,0 điểm)
1) Tìm điều kiện xác định và rút gọn biểu thức: 2  2  1  1  1  2x − 3x − 5 A =  . −1 + . +1  : −     1. 3 2 2 2 4 3 2
 x − 3x + 3x −1  x
 x − 2x +1  x
 2x − x −10x
2) Cho các số thực x, y, z thoả mãn 1 1 1 1
+ + = và x + y + z = 3. Tính giá trị của biểu thức: x y z 3 2023 2023 2023 2023 2023 2023 P = (x + y ).(y + z ).(z + x ) . Câu 2. (4,0 điểm)
1) Biết rằng đa thức f (x) chia cho x − 2 dư 11, chia cho x + 2 dư ( ) 1 − , chia cho 2 x − 4 được
thương là 3x và còn dư. Tính f (2023) + f ( 2023 − ) .
2) Tìm tất cả giá trị của số tự nhiên n để biểu thức 6 4 3 2
B = n − n − 2n + 2n có giá trị là một số chính phương. Câu 3. (3,0 điểm)
1) Tìm tất cả các nghiệm nguyên của phương trình: x( 2 x + x + ) 3 2 4 = y − 3. 2 2 2
2) Giải phương trình:  x + 3   x − 3  63− 7 + 6 x + =     0 . 2  x − 2   x + 2  x − 4 Câu 4. (7,0 điểm)
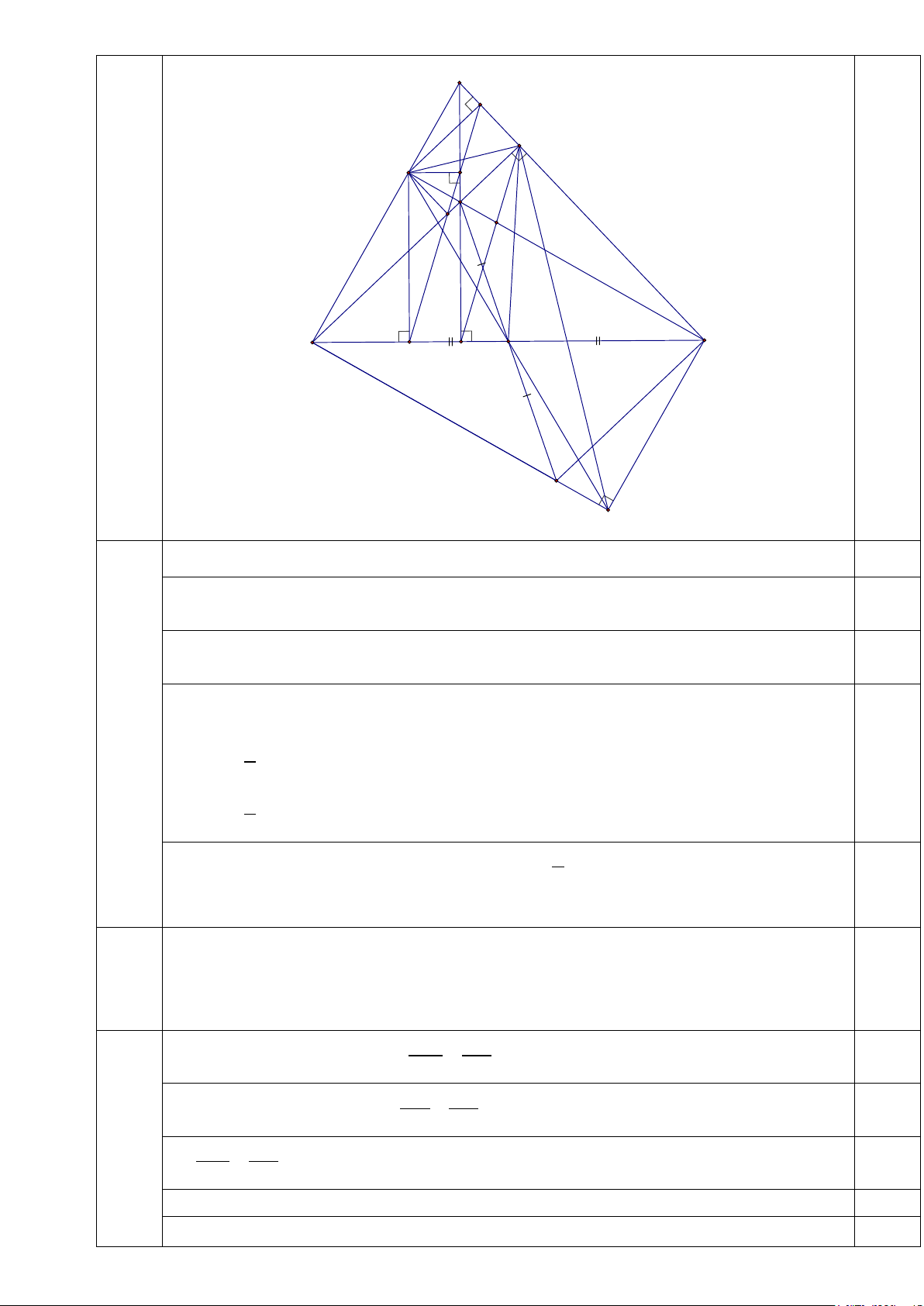
Cho tam giác ABC nhọn ( AB < AC) . Các đường cao AD, BM , CN của tam giác ABC cắt
nhau tại H . Gọi O là tr
ung điểm của đoạn thẳng BC, E là điểm đối xứng của H qua O. Kẻ CF
vuông góc với đường thẳng BE tại F. 1) Tính số đo  FMN.
2) Gọi K, L, R lần lượt là chân các đường vuông góc kẻ từ N đến các đường thẳng AC, AD, BC. Gọi
giao điểm của DM và CN là S. Chứng minh rằng:
a) Ba điểm K, L, R thẳng hàng.
b) HN.CS = NC.SH . 3) Tia phân giác của 
BAC cắt BC tại I, kẻ đường thẳng đi qua C và vuông góc với đường thẳng
AI tại P, đường thẳng CP cắt đường thẳng AO tại Q . Gọi G là trung điểm của đoạn thẳng . IQ Chứng
minh đường thẳng PG đi qua trung điểm của đoạn thẳng AC . Câu 5. (2,0 điểm)
1) Xét x, y là hai số thực dương thay đổi thoả mãn điều kiện .xy =1. Tìm giá trị lớn nhất của biểu 2( 3 3 x + y ) thức A = ( . 4 2 x + y )( 2 4 x + y )
2) Một chiếc hộp đựng 99 chiếc thẻ màu vàng, 100 chiếc thẻ màu đỏ và 101 chiếc thẻ màu xanh.
Người ta tiến hành trò chơi rút thẻ như sau: mỗi lần rút thẻ người ta lấy ra hai chiếc thẻ khác màu và
thay vào đó bằng hai chiếc thẻ có màu còn lại, quá trình này diễn ra liên tục. Hỏi đến một lúc nào đó
người ta có thể nhận được trong hộp tất cả các thẻ có cùng một màu hay không? Hãy giải thích vì sao?
....................Hết....................
Họ tên thí sinh:..................................................... . Số báo danh:........................................................ ......
Họ, tên và chữ ký của GT1:................................... Họ, tên và chữ ký của GT2:........................................ Câu Đáp án Điểm
Tìm điều kiện xác định và rút gọn biểu thức 2  2  1  1  1  2x − 3x − 5 A =  . −1 + . +1  : −     1. (2,0) 3 2 2 2 4 3 2
 x − 3x + 3x −1  x
 x − 2x +1  x
 2x − x −10x Điều kiện xác định x ≠ 0  3 2
x − 3x + 3x −1 ≠ 0   2
x − 2x +1 ≠ 0 0,25  2
2x − 3x − 5 ≠ 0  4 3 2
2x − x −10x ≠  0
Tìm đúng điều kiện và kết luận 5
x ≠ 0; x ≠ 1; x ≠ 1; − x ≠ 2 − ; x ≠ 0,25 1.1 2 (2,0 đ)  2 2 1− x 1
1+ x  (2x − 5).(x + ) 1 A =  . + .  : −1 0,5 (x − )3 1 x (x − )2 2 2 1
x  x (2x −5).(x + 2)   2 2 1 x  − + x +1 A =  +  : −1 0,25  x  ( x − )2 2 1 x (x − )2 2 1  x (x + 2)  2 2 − x +1+ x x +1 A = : −1 0,25 2 x (x − )2 2 1 x (x + 2) (x − )2 2 1 x (x + 2) x + 2 1 A = . −1 = −1 = 0,25 2 x (x − )2 1 x +1 x +1 x +1 Vậy với 5
x ≠ 0; x ≠ 1; x ≠ 1; − x ≠ 2 − ; x ≠ thì 1 A = 0,25 2 x +1
Cho các số thực x, y, z thoả mãn 1 1 1 1 + + =
và x + y + z = 3. Tính giá trị của biểu x y z 3 (2,0) thức: 2023 2023 2023 2023 2023 2023 P = (x + y ).(y + z ).(z + x ) . Kết hợp 1 1 1 1 + + =
và x + y + z = 3 ta được 1 1 1 1 + + = x y z 3
x y z x + y + z 0,25 1 1 1 1  1 1   1 1  ⇔ + + − = 0 ⇔ + + − =     0
x y z x + y + z 0,25
 x y   z x + y + z  x + y x + y 1.2 ⇔ +
= ⇔ z (x + y)(x + y + z) + xy(x + y) = 0 0,25 xy
z (x + y + z) 0
(2,0đ) ⇔(x+ y)( 2
xz + yz + z + xy) = 0 ⇔ (x + y)(x + z)( y + z) = 0 0,25 x + y = 0  ⇔ x + z = 0  0,25  y + z =  0
Nếu x + y = 0 thì 2023 2023 2023 2023
x = −y ⇒ x = −y ⇒ x + y = 0 0,25 2023 2023 2023 2023 2023 2023 P = (x + y ).(y + z ).(z + x ) = 0 0,25 + = + =
Tương tự nếu y z 0 hoặc z x 0 thì P = 0 0,25
Vậy với x, y, z thoả mãn 1 1 1 1 + + =
và x + y + z = 3 thì P = 0 x y z 3
Biết rằng đa thức f (x) chia cho x − 2 dư 11, chia cho x + 2 dư 1 − , chia cho 2
x − 4 được (2,0)
thương là 3x và còn dư. Tính f (2023) + f ( 2023 − ) .
f (x) chia cho x − 2 dư 11 ⇒ f (x) = (x − 2).P(x) +11 ⇒ f (2) =11 0,25
f (x) chia cho x + 2 dư 1
− ⇒ f (x) = (x + 2).Q(x) −1 ⇒ f ( 2) − = 1 − 0,25 f (x) chia cho 2
x − 4 được thương là 3x và còn dư 0,25 ⇒ f x = ( 2 ( )
x − 4).3x + ax + b (1) 2.1
(2,0đ) Từ (1) ⇒ f (2) = 2a + , b f ( 2) − = 2 − a + b 0,25 2a + b =11
⇒  2−a+b = 1− 0,25
tìm được a = 3, b = 5 Suy ra f x = ( 2 x − ) 3 ( )
4 .3x + 3x + 5 = 3x − 9x + 5 0,25 3 3
f (2023) + f ( 2023 −
) = 3.2023 − 9.2023+ 5 + 3.( 2023 − ) − 9.( 2023 − ) + 5 0,25
⇒ f (2023) + f ( 2023 − ) =10 0,25
Tìm tất cả giá trị của số tự nhiên n để biểu thức 6 4 3 2
B = n − n − 2n + 2n có giá trị là một số (2,0) chính phương. 6 4 3 2 2
B = n − n − 2n + 2n = n ( 4 2
n − n − 2n + 2) 0,25 2 2 2 (*)
= n (n −1) .(n + 2n + 2) 0,25
- Xét n = 0 thì B = 0 là số chính phương 0,25
- Xét n =1 thì B = 0 là số chính phương 0,25
2.2 - Xét n ≥ 2 ta thấy 2 2
n (n −1) là số chính phương, 2 2 2
n + 2n + 2 > n + 2n +1 = (n +1) (2,0đ) 0,25 2 2 2
n + 2n + 2 < n + 4n + 4 = (n + 2) Suy ra 2 2 2
(n +1) < n + 2n + 2 < (n + 2) 0,25 Mà 2 (n +1) và 2
(n + 2) là 2 số chính phương liên tiếp 2
⇒ n + 2n + 2 không phải là số chính 0,25 phương (**).
Từ (*) và (**) suy ra B không là số chính phương với n ≥ 2 0,25
Vậy n = 0 hoặc n =1 thì B có giá trị là số chính phương.
Tìm tất cả các nghiệm nguyên của phương trình x( 2 x + x + ) 3 2 4 = y − 3. (1,5 ) x( 2 x + x + ) 3 3 3 2 (*) 2
4 = y − 3 ⇔ y = x + 2x + 4x + 3 0,25 2
Ta có 2x + 4x + 3 = 2.(x + )2
1 +1 > 0 với mọi x 3 3
⇒ y > x (1) 3.1 3 3 2
y = x + 2x + 4x + 3 = (x + 2)3 − 4(x + )2
1 −1< (x + 2)3 với mọi x (2) 0,25 (1,5đ) 3 3
Từ (1) và (2) suy ra x < y < (x + 2)3 0,25
Mà x, y nguyên nên y = x +1
Thay y = x +1 vào (*) ta được: 3 2 3 2
x + 2x + 4x + 3 = x + 3x + 3x +1 0,25 2
⇔ x − x − 2 = 0 x = 1 − 0,25 ⇔ x = 2 Với x = 1 − thì y = 0
Với x = 2 thì y = 3 0,25
Vậy phương trình đã cho có 2 nghiệm nguyên là ( ; x y) = ( 1; − 0) ; ( ; x y) = (2;3) . 2 2 2  x + 3   x − 3  63− 7 (1,5đ) Giải phương trình + 6 x + =     0 . 2  x − 2   x + 2  x − 4
Điều kiện xác định x ≠ 2, x ≠ 2 − 0,25
Phương trình được viết lại 2 2 2 2 2  x + 3   x − 3  x − 9  x + 3   x − 3  (x −3)(x +3) + 6 − 7 = 0 ⇔ + 6 − 7 =         0 2 0,25  x − 2   x + 2  x − 4  x − 2   x + 2  (x − 2)(x + 2) + − Đặt x 3 x 3 u = ; v = , 3.2 x − 2 x + 2 (1,5đ) u = v Phương trình trở thành 2 2
u − 7uv + 6v = 0 ⇔ (u − v)(u − 6v) ⇔ 0,25  u = 6v TH1: + −
u = v ⇔ x 3 x 3 = 2 2
⇔ x + 5x + 6 = x − 5x + 6 ⇔ x = 0(T ĐK M ) x − 2 x + 2 0,25 TH2: u = 6v x + 3 x − 3 ⇔ = 6. 2 2
⇔ 6x − 30x + 36 = x + 5x + 6 x − 2 x + 2 x =1(TMĐK) 0,25 2
⇔ x − 7x + 6 = 0 ⇔ (x − ) 1 (x − 6) = 0 ⇔  x = 6(T ĐK M )
Vậy phương trình đã cho có tập nghiệm là S = {0;1; } 6 0,25
Cho tam giác ABC nhọn ( AB < AC) . Các đường cao AD, BM , CN của tam giác
ABC cắt nhau tại H . G
ọi O là trung điểm của đoạn thẳng BC, E là điểm đối xứng của
H qua O . Kẻ CF vuông góc với đường thẳng BE tại F. 1) Tính số đo  FMN.
2) Gọi K, L, R lần lượt là chân các đường vuông góc kẻ từ N đến các đường thẳng
AC, AD, BC. Gọi giao điểm của DM và CN là S. Chứng minh rằng: 4 (7,0)
a) Ba điểm K, L, R thẳng hàng.
b) HN.CS = NC.SH.
3) Tia phân giác của 
BAC cắt BC tại I, kẻ đường thẳng đi qua C và vuông góc với
đường thẳng AI tại P, đường thẳng CP cắt đường thẳng AO tại Q . Gọi G là trung điểm của đoạn thẳng .
IQ Chứng minh đường thẳng PG đi qua trung điểm của đoạn thẳng AC . A K M N L H S V C B R D O E F Tính số đo  FMN . 2,0
Vì E đối xứng với H qua O nên O là trung điểm của EH . 0,25
Chứng minh được tứ giác BHCE là hình bình hành ⇒ CH //EB . 0,25
Chứng minh được tứ giác BNCF là hình chữ nhật 0,25
⇒ O là trung điểm của NF và BC = NF. 0,25 4.1
BM là đường cao của A
∆ BC ⇒ BM ⊥ AC ⇒ B
∆ MC vuông tại M .
(2,0đ) Vì MO là đường trung tuyến ứng với cạnh huyền của tam giác vuông BMC 1 ⇒ MO = BC 0,25 2 1 ⇒ MO = NF 0,25 2 . Xét MN ∆
F có MO là đường trung tuyến và 1
MO = NF ⇒ MN ∆
F vuông tại M 0,25 2 ⇒  0 FMN = 90 . 0,25
Gọi K, L, R lần lượt là chân các đường vuông góc kẻ từ N đến các đường thẳng 4.2
AC, AD, BC. Gọi giao điểm của DM và CN là S. Chứng minh rằng: 3,0
(3,0đ) a) Ba điểm K, L, R thẳng hàng.
b) HN.CS = NC.SH . Chứng minh được // AK AN NK BM ⇒ = . AM AB 0,25 Chứng minh được // AN AL NL BC ⇒ = . 4.2a AB AD 0,25 (1,25đ) AK AL ⇒ = ⇒ KL//DM. AM AD (1) 0,25
Chứng minh tương tự ta được KR//DM. (2) 0,25
Từ (1) và (2) suy ra 3 điểm K, L, R thẳng hàng. 0,25
Gọi V là giao điểm của KR và BM . Chứng minh được //AD BN BR NR ⇒ = . (3) 0,25 BA BD Vì //MD BR BV KR ⇒ = . (4) 0,25 BD BM Từ (3) và (4) BN BV ⇒ = ⇒ NV //AC . 0,25 BA BM
4.2b Chứng minh được tứ giác MKNV là hình chữ nhật, suy ra được  =  NMH KVM. (1,75đ) 0,25
Vì KR//DM nên  =  SMH KVM ⇒  = 
SMH NMH ⇒ MH là tia phân giác của  NMS. Xét N
∆ MS có MH là đường phân giác ⇒ HN MN = . (5) HS MS 0,25
Chứng minh được MC là đường phân giác góc ngoài của N ∆ MS ⇒ CN MN = . (6) 0,25 CS MS
Từ (5) và (6) ⇒ HN CN =
⇒ HN.CS = NC.SH. 0,25 HS CS
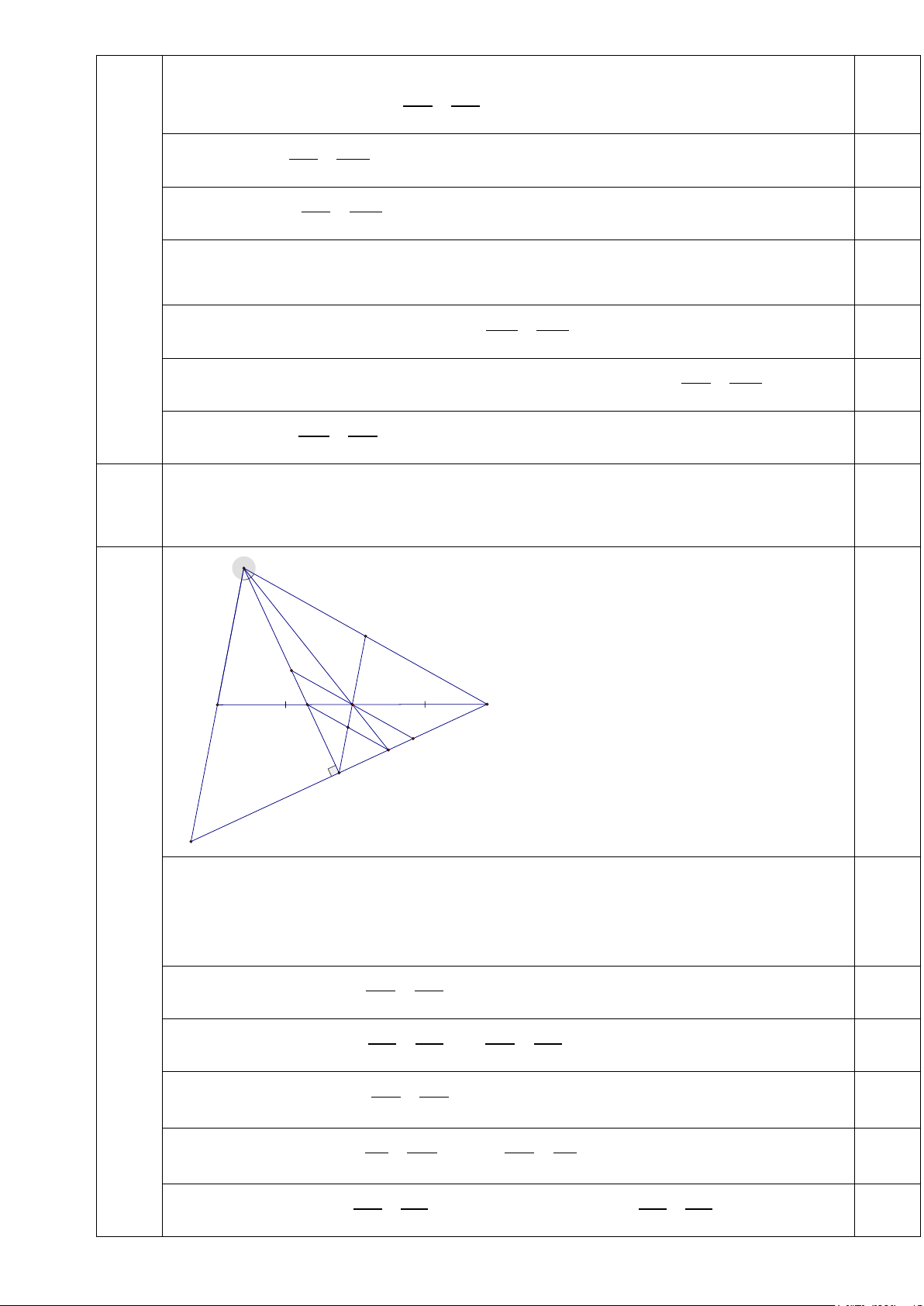
4.3 Tia phân giác của 
BAC cắt BC tại I, kẻ đường thẳng đi qua C và vuông góc với đường
(2,0đ) thẳng AI tại P, đường thẳng CP cắt đường thẳng AO tại Q , gọi G là trung điểm của 2,0
đoạn thẳng IQ . Chứng minh đường thẳng PG đi qua trung điểm của đoạn thẳng AC . A T X O B C I J G Y Q P U
Gọi giao điểm của CP với AB là U, giao điểm của PO với IQ và AC lần lượt là J và T
. Kẻ đường thẳng đi qua O và song song với AC cắt AI và CP lần lượt tại X và Y Chứng minh được A
∆ UC cân tại A ⇒ P là trung điểm của UC 0,25
⇒ OP//BU ⇒ T là trung điểm của AC 0,25 Xét P ∆ TAcó // OX PO OX AT ⇒ = 0,25 TA PT Xét P ∆ TC có // OY PO OY CT ⇒ = OX OY ⇒ = ⇒ OX = OY 0,25 TC PT TA TC Xét A ∆ QC có // QO OY OY AC ⇒ = QA AC 0,25 Xét A ∆ IC có // IO OX OX AC ⇒ = Suy ra QO IO = ⇒ IQ//AC IC AC QA IC 0,25 Xét A ∆ PT có IJ IJ// PJ AT ⇒ = 0,25 ∆ có QJ QJ// PJ CT ⇒ = AT PT , Xét CPT CT PT IJ QJ ⇒ =
⇒ IJ = QJ ⇒ J AT CT
là trung điểm của IQ ⇒ J trùng với G ⇒ PG đi qua trung điểm của AC . 0,25
Xét x, y là hai số thực dương thay đổi thoả mãn điều kiện .xy =1. Tìm giá trị lớn nhất của 2( 3 3 x + y ) biểu thức A = ( . 1,0 4 2 x + y )( 2 4 x + y ) 2( 3 3 x + y ) 3 3
x + y + x + y x + y +1.( 3 3 3 3 3 3 x + y ) A = ( = = 4 2 x + y )( 2 4 x + y ) ( 4 2 x + y )( 2 4 x + y ) ( 4 2 x + y )( 2 4 x + y ) 0,25 3 3
x + y + x . y ( 3 3 x + y ) . y ( 4 2
x + y ) + .x( 2 4 x + y ) x y ( = = + 4 2 x + y )( 2 4 x + y ) ( 4 2 x + y )( 2 4 x + y ) 4 2 2 4 x + y x + y 5.1 (1,0đ) Ta có ( x x 1 1 x − y)2 2 4 2 2 ≥ 0 x ∀ ,
y ⇒ x + y ≥ 2x y x ∀ , y ⇒ ≤ =
= (do x, y > 0 ) 4 2 2 0,25 x + y 2x y 2xy 2 Chứng minh tương tự y 1 ≤ ⇒ A ≤1 2 4 x + y 2 0,25 2 x = y  Dấu “=” xảy ra khi 2
x = y ⇔ x = y = 1. Vậy giá trị lớn nhất của A = 1 khi x = y = 1 0,25 xy =1 
Một chiếc hộp đựng 99 chiếc thẻ màu vàng, 100 chiếc thẻ màu đỏ và 101 chiếc thẻ màu
xanh. Người ta tiến hành trò chơi rút thẻ như sau: mỗi lần rút thẻ người ta lấy ra hai chiếc
thẻ khác màu và thay vào đó bằng hai chiếc thẻ có màu còn lại, quá trình này diễn ra liên 1,0
tục. Hỏi đến một lúc nào đó người ta có thể nhận được trong hộp tất cả các thẻ có cùng một
màu hay không? Hãy giải thích vì sao?
Ta thấy 99 chia cho 3 dư 0, 100 chia cho 3 dư 1, 101 chia cho 3 dư 2, do đó số lượng thẻ 0,25
mỗi loại khi chia cho 3 được các số dư khác nhau là 0, 1, 2.
5.2 Sau mỗi lần rút thẻ, số lượng thẻ mỗi loại trong hộp giảm đi 1 hoặc tăng thêm 2. Khi đó số
(1,0đ) dư của chúng khi chia cho 3 thay đổi như sau:
Số thẻ chia cho 3 dư 0 sau mỗi lần rút sẽ chia cho 3 dư 2. 0,25
Số thẻ chia cho 3 dư 1 sau mỗi lần rút sẽ chia cho 3 dư 0.
Số thẻ chia cho 3 dư 2 sau mỗi lần rút sẽ chia cho 3 dư 1.
Do đó sau mỗi lần rút thẻ, số thẻ mỗi loại trong hộp khi chia cho 3 vẫn có số dư khác nhau
là 0, 1, 2. Giả sử đến một lúc nào đó người ta có thể nhận được trong hộp tất cả các thẻ có
cùng một màu thì số thẻ 2 màu còn lại bằng 0, số dư của chúng khi chia cho 3 bằng 0, điều
này mâu thuẫn với kết luận trên. 0,25
Vậy không thể nhận được các thẻ trong hộp có cùng một màu. 0,25 Chú ý:
- Nếu thí sinh làm đúng mà cách giải khác với đáp án và phù hợp kiến thức của chương trình THCS thì
tổ chấm thống nhất cho điểm thành phần đảm bảo tổng điểm như hướng dẫn quy định.
- Tổng điểm toàn bài không làm tròn.
------------------Hết----------------
Document Outline

• ĐỀ THI CHỌN HỌC SINH GIỎI
• SỞ GIÁO DỤC VÀ ĐÀO TẠO
• NAM ĐỊNH
• NĂM HỌC 2022 - 2023
• Môn: Toán – Lớp: 8 THCS.
• Thời gian làm bài: 120 Phút.