Đề thi chọn học sinh giỏi vòng trường môn Toán trường THPT Chu Văn An – Gia Lai

SỞ GIÁO DỤC ĐÀO TẠO GIA LAI
ĐỀ THI CHỌN HỌC SINH GIỎI VÒNG TRƯỜNG
TRƯỜNG THPT CHU VĂN AN MÔN: TOÁN Thời gian: 180 phút
Câu 1(4 điểm). Cho hàm số 3 2
y  x  3x  mx  2 (m là tham số) có đồ thị là (Cm). Xác
định m để (Cm) có các điểm cực đại và cực tiểu cách đều đường thẳng y  x 1. Câu 2(4 điểm). æ pö
1)Giải phương trình cos x + cos 3x = 1 + 2 sin 2 çç x ÷ + ÷ ç çè 4 ÷÷ø 2)Giải phương trình 2 2
x  4  x  2  x 4  x Câu 3(4 điểm).  2 y  2 3  y  2 
1)Giải hệ phương trình x  2  x  2 3x   2  y  u  1 1 2)Cho dãy số  (u ) xác định như sau  1 
(1). Chứng minh dãy số (u ) có n u  , n   2  n n 3  u  n 1
giới hạn hữu hạn khi n  
Câu 4(2 điểm). Trong mặt phẳng với hệ tọa độ Oxy cho tam giác ABC cân tại A , có đỉnh (
A 1; 4) và các điểm B, C thuộc đường thẳng  : x  y  4  0 . Xác định tọa độ điểm B
và C, biết diện tích tam giác ABC bằng 18. Câu 5(3 điểm). 1) Chứng minh rằng 0 2 4 2014 2013 3C  5C  7C  ...  2017C  1010.2 . 2014 2014 2014 2014
2) Cho tập A 1;2;3;4;5;6;7;8; 
9 . Lập ngẫu nhiên một số có 3 chữ số khác nhau với các
chữ số chọn từ tập A. Tính xác suất để số lập được chia hết cho 6. Câu 6(3 điểm). Cho hình chóp S.ABCD , đáy ABCD là hình chữ nhật có
AB  a, BC  b , SA  SB  SC  SD  c . K là hình chiếu vuông góc của P xuống AC .
a/ Tính độ dài đoạn vuông góc chung của SA và BK .
b/ Gọi M , N lần lượt là trung điểm của đoạn thẳng AK và CD . Chứng minh: Các đường
thẳng BM và MN vuông góc nhau ………Hết………
(Giám thị coi thi không giải thích gì thêm. Học sinh không được sử dụng tài liệu)
SỞ GIÁO DỤC ĐÀO TẠO GIA LAI
ĐAP ÁN ĐỀ THI CHỌN HỌC SINH GIỎI
TRƯỜNG THPT CHU VĂN AN VÒNG TRƯỜNG 2017 MÔN: TOÁN Thời gian: 180 phút Câ Nội dung Điể u m 1. Ta có: 2
y '  3x  6x  m . Hàm số có CĐ, CT 2
 y '  3x  6x  m  0 có 2 nghiệm phân biệt x ; x 1 2
  '  9  3m  0  m  3  (*) 1,0
Gọi hai điểm cực trị là A x ; y ; B x ; y 1 1   2 2   1 1   2m   m 
Thực hiện phép chia y cho y ta được: y  x  y '  2 x  2         3 3   3   3   2m   m   2m   m 
 y  y x    2 x  2 
; y  y x    2 x  2  1  1   1   2  2   2    3   3   3   3 
 Phương trình đường thẳng đi qua 2 điểm cực trị là 1,0   2m   m  : y    2 x  2       3   3  Các
điểm cực trị cách đều đường thẳng y  x 1  xảy ra 1 trong 2 trường hợp:
TH1: Đường thẳng đi qua 2 điểm cực trị song song hoặc trùng với đường thẳng y  x 1  2m  3 1,0    2 1  m     (thỏa mãn)  3  2 TH2: Trung
điểm I của AB nằm trên đường thẳng y  x 1 y  y x  x  2m   m  1 2 1 2
 y  x 1   1    2 x x x x I I     2 2     2 1 2     1 2  2 2  3   3   2m  2   m 3 .2  6   m  0    3  3  3
Vậy các giá trị cần tìm của m là: m  0;  1,0  2 2.
1) PT  2 cos 2x cos x = 1 + sin 2x + cos 2x
 cos 2x(2 cos x - 1) = 1 + 2 sin x cos x 2 2 2 0,5
 (cos x - sin x)(2 cos x - 1) = (cos x + sin x)
écosx + sinx = 0 (1) ê  (cos ê
x - sin x)(2 cos x - 1) = cos x + sin x (2) êë æ pö ç ÷ p p 0,5 (1)  2 sin x ç + ÷ = 0  x +
= kp  x = - + kp ç çè 4 ÷÷ø 4 4 cos x = 0 é é p ê ê x = + kp ê ê  - - =  æ ö 2 (2) 2 cos x(cos x sin x 1) 0 p  ê ç ÷ ê (k Î ) 2 cos x ç + ÷ = 1 ê ç ÷ ê p p ç ê è 4 ÷ x + =  + k2p ø ê ë ë 4 4 p p 0,5
Vậy pt có nghiệm là x = - + kp , x = + k ,
p x = k2p (k Î ). 4 2
2) Điều kiện 2  x  2 PT 2 2 2 2
 (x 2)  (x 1) 4  x  (x 2)  (x 1) (4  x ) 1,0 2
 x(x 2)(x  2)  0  x  0,x  2,x   2
Thử lại điều kiện thỏa mãn 0,5 3 1) ĐK: xy  0 2 2 3
 x y  y  2 (1) Hệ  
. Trừ vế hai phương trình ta được 2 2 3
 y x  x  2 (2) x  y  0 2 2 2 2
3x y  3xy  y  x  3xy(x  y)  (x  y)(x  y)  0  1,0 
3xy  x  y  0
TH 1. x  y  0  y  x thế vào (1) ta được 3 2
3x  x  2  0  x  1 2 y  2 2 x  2
TH 2. 3xy  x  y  0. Từ 3y 
 y  0 , 3x   x  0 2 x 2 y
 3xy  x  y  0 . Do đó TH 2 không xảy ra.
Vậy hệ phương trình có nghiệm duy nhất (1 ; 1) 1,0
2)Chứng minh bằng phương pháp qui nạp được 3   5 u  với mọi n = 1,2,… n 2
Chứng minh được dãy (u ) giảm n 0,5 Do đó  
(u ) tồn tại giới hạn. Giả sử lim u  a thì 3 5 a  n n n  2 0,5
Chuyển qua giới hạn hệ thức (1) ta được 1 3   5 2 a  
 a  3a  1  0  a  3  a 2 Vậy 3  5 lim u  1,0 n n  2 4.
Gọi H là hình chiếu của A trên  , suy ra H là trung điểm BC. Khi đó: 9 AH  d( , A BC)  2 1 S
 BC.AH  BC  4 2 AB  C 2 2 BC 97 2
AB  AC  AH   4 2
Suy ra B và C thuộc đường tròn tâm A và bán kính 97 R  1,5 2
Do đó B và C là giao điểm của  và đường tròn nên tọa độ điểm B và C là  97 2 2     
nghiệm của hệ: (x 1) ( y 4)  2 
x  y  4  0 Giải được: 11 3 3 5
B  ( ; ),C  ( ;  ) hoặc 3 5 11 3
B  ( ;  ),C  ( ; ) 1,5 2 2 2 2 2 2 2 2 5. 0 2 4 2014 A  3C  5C  7C ... 2017C 1) 2014 2014 2014 2014   2 4 2014 2C  4C  ... 2014C 3 0 2 4 2014 C  C  C ... C 2014 2014 2014 2014 2014 2014 2014  0,5 Tính được 0 2 4 2014 2013 C  C  C ... C  2 2014 2014 2014 2014 Chứng minh k k 1 kC 2014C   , k
 ,n  ,0  k  . n 2014 2013 Suy ra, 2 4 2014 2C  4C ... 2014C  2014 1 3 2013 C  C ... C  2012  2014.2 2014 2014 2014 2013 2013 2013 0,5 Vậy 2012 2013 2013 A  2014.2  3.2 1010.2 . 0,5
2) - Số chia hết cho 6 là số chia hết cho 3 và số đó là số chẵn.
- Số chia hết cho 3 là số a a a có tổng ba chữ số (a  a  a ) chia hết cho 3. 1 2 3 1 2 3
- Số chẵn là số chó chữ số tận cùng chia hết cho 2.
Để lập được số có 3 chữ số khác nhau từ tập A sao cho số đó chia hết cho 6 ta chia làm hai giai đoạn.
1/ chọn bộ ba chữ số khác nhau từ tạp A sao cho tổng 3 chữ số cộng lại chia hết cho 3 và
trong ba chữ số đó có ít nhất 1 chữ số chẵn.
2/ Xếp mỗi bộ chọn được thành số có 3 chữ số sao cho số tận cùng phảit là số chẵn.
Để chọn và xếp khoa học ta nên chia ra ba trường hợp nhỏ như sau:
TH1: trong 3 chữ số chỉ có một chữ số chẵn, gồm có các bộ số sau: 1;2;  3 , 1;2;  9 , 1;3;  8 , 1;4;  7 , 1;5;  6 , 2;3;  7 , 2;7;  9 , 3;4;  5 , 3;6;  9 , 3;7;  8 , 4;5;  9 , 5;6;  7 , 7;8;  9 .
Với trường hợp này: số cách chọn và xếp là: 1 N  C *1* 2 *1 = 26 TH1 13
TH2: trong 3 chữ số chỉ có hai chữ số chẵn, gồm có các bộ số sau:  1; 2;  6 , 1;6;  8 , 2;3;  4 , 2;4;  9 , 2;5;  8 , 2;6;  7 , 3;4;  8 , 4;5;  6 , 4;8;  9 6;7;  8
Với trường hợp này số ccáh chọn và xếp là: 1 N  C * 2 * 2*1 = 40 TH 2 10 0,5
TH3: trong 3 chữ số chọn được đề là chữ số chẵn, gồm có các bộ số sau: 2;4;  6 , 4;6;  8
Với trường hợp này số ccáh chọn và xếp là: 1 N  C *3! = 12 TH 3 2
Số cách chọn số có 3 chữ số khác nhau sao cho số đó chia hết cho 6 là: N  N  N = 78 TH1 TH 2 TH 3 0,5
Phép thử: lập số có 3 chữ số khác nhau từ A  n  3  A  504 9
A: là biến cố lập được số có ba chữ số khác nhau sao cho số đó chia hết cho 6. N ( ) A  N  N  N TH1 TH 2 TH 3 N ( ) A 78
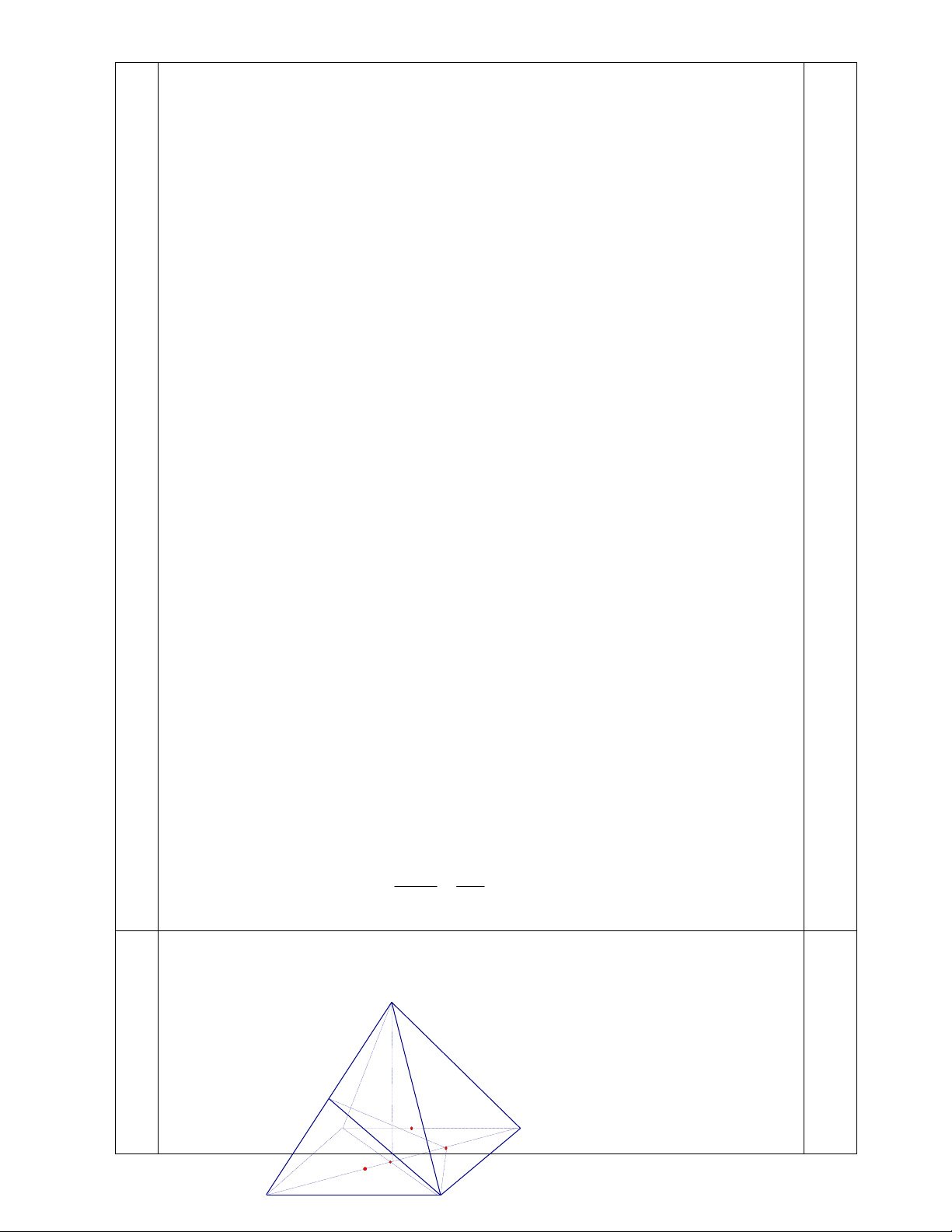
Xác suất của biến cố A: P( ) A    0.155 N () 504 0,5 6. _S _D _N _C _K _M _O _A _B
a) + Theo giả thiết ta được: SO   ABCD  SAC   ABCD .
Mà BK  SAC và B BK  AC  BK  SA .
+ Gọi H là hình chiếu của K xuống SA
 HK  SA và HK  BK ( vì HK  SAC)
 HK là đoạn vuông góc chung của SA và BK .
Suy ra được: BH  SA và HBK vuông tại K . 1,0 2 2 1 1 1 a b + Do A
 BC vuông đỉnh A nên: 2    BK  . 2 2 2 2 2 BK AB BC a  b 2 2 a c  .a SI.AB + SAB 
cân đỉnh S , BH là đường cao nên 4 HB   SA c
+ Do HBK vuông tại K nên: 2 2 2 2 2 (4c  a )a a b 2 2 2 HK  HB  BK   2 2 2 4c a  b 2 2 2 4 2 2 2 2 (4c  a  b )a a (4c  a  b ) 2 HK   HK  2 2 2 2 2 4c (a  b ) 2c (a  b )
  
b) + 2BM  BA  BK ( vì M là trung điểm của AK ) 1,0
    1    1 
+ MN  MB  BC  CN  (AB  KB)  BC  BA 2 2  1   + MN  KB  BC . 2 + Do đó:
 
   
4BM.MN  (BA  BK).(KB  2BC)  
     
= BA.KB  2BA.BC  BK.KB  2BK.BC
      = BA.KB  BK.KB  2BK.BC  
    = KB.(BA  BK  2.BC)
    
= KB.(BA  BC  BK  BC)
  
   
= KB.(CA  CK)  KB.CA  KB.CK  0
Vậy: BK  MN . 1,0