Đề thi chọn HSG cấp tỉnh Toán 12 năm 2018 – 2019 sở GD và ĐT Bình Thuận (Vòng 1)

Đề thi chọn HSG cấp tỉnh Toán 12 năm 2018 – 2019 sở GD và ĐT Bình Thuận (Vòng 1) gồm 1 trang với 4 bài toán tự luận, thời gian làm bài 180 phút , kỳ thi được diễn ra vào ngày 18 tháng 10 năm 2018, đề thi có lời giải chi tiết và thang chấm điểm.

13 7 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 12

Môn: Toán 12

Thông tin:

4 trang 8 tháng trước

Tác giả:

Profile Nguyễn Vân
SỞ GIÁO DỤC VÀ ĐÀO TẠO
BÌNH THUẬN
ĐỀ CHÍNH THỨC
(Đề này có 01 trang)
KÌ THI CHỌN HSG CẤP TỈNH LỚP 12 THPT
NĂM HỌC 2018 – 2019
Ngày thi: 18/10/2018
Môn: Toán
Thời gian làm bài: 180 phút (không kể thời gian giao đề)
Bài 1 (6,0 điểm).
a) Cho
x
và
y
là các số thực thỏa mãn
2 0.x y
Tìm giá trị lớn nhất và giá trị
nhỏ nhất của biểu thức
2
2
2
2
.
x xy y
P
x xy y
b) Tìm tất cả các giá trị thực của tham số
m
để đồ thị hàm số
3 2
3 3
y x x mx m
có hai điểm cực trị nằm khác phía đối với trục hoành.
Bài 2 (5,0 điểm).
a) Tìm số hạng tổng quát của dãy số
n
u
biết
1
2u
và
1
n
n
*
.n
b) Cho dãy số
n
v
thỏa mãn
1
1
,
2018
v
1
2
2
,
1 2018
n
n
n
v
v
v
*
.
n
Chứng minh
rằng
*
1
, .
n
n
v v n
Bài 3 (4,0 điểm). Giải hệ phương trình
2 2
2 2 2 2
2 1
.
1 1
xy x y x y
x y y x x y x
Bài 4 (5,0 điểm). Cho tam giác
ABC
nhọn có
AB AC
và hai đường cao
,BE CF
cắt
nhau tại
.H
Các đường tròn
1
,O
2
O
cùng đi qua
A
và theo thứ tự tiếp xúc với
BC
tại
, .B C
Gọi
D
là giao điểm thứ hai của
1
O
và
2
.O
a) Chứng minh đường thẳng
AD
đi qua trung điểm của cạnh
;BC
b) Chứng minh ba đường thẳng
,EF
,BC
HD
đồng quy.
-------------- HẾT -------------
Học sinh không được sử dụng máy tính cầm tay.
Cán bộ coi thi không được giải thích gì thêm.
Họ và tên thí sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Số báo danh: . . . . . . . . . . . . . . . .
HƯỚNG DẪN CHẤM
Bài Nội dung Điểm
1
6,0
a
Ta có
2
2
1
,
1
t t
P
t t
với
1
.
2
x
t
y
Xét hàm số
2
2
1
( )
1
t t
f t
t t
với
1
.
2
t
Tính được
2
2 2
2 2
(t) ,
( 1)
t
f
t t
( ) 0
1.
1
2
f t
t
t
Bảng biến thiên
Suy ra giá trị nhỏ nhất của
P
bằng
1
3
, không có giá trị lớn nhất.
0,5
0,5
1,0
0,5
0,5
b
Tập xác định
D
2
' 3 6 3y x x m
Yêu cầu bài toán
Phương trình
' 0
y
có hai nghiệm phân biệt
1 2
,x x
thỏa mãn
1 2
. 0.
y x y x
Phương trình
0
y
có hai nghiệm phân biệt
1 0
m
(*)
Khi đó đồ thị hàm số đã cho có hai điểm cực trị là
1 1 2 2
; , ; .A x y B x y
Ta có
1
. 2 1
3 3
x
y y m x
Do đó
1 1 1
2 1y y x m x
2 2 2
2 1y y x m x
2
1 2 1 2
. 0 4 1 . 0
y x y x m x x
1 2
. 0 0 0
x x m m
Kết hợp với điều kiện (*) ta có
0
m
thỏa mãn bài toán
0,25
0,5
0,25
0,25
0,25
0,25
0,5
0,5
0,25
2
5,0
a
*
,
n
ta có
1 1
2 5 5 2 5
n n n n
u u u u
Đặt
*
5, .
n n
w u n
Khi đó
*
1
2 , .
n n
w w n
Do đó
n
w
là cấp số nhân có
1 1
5 7,
w u
công bội
2.
q
Suy ra
1 1 *
1
. 7.2 , .
n n
n
w w q n
Vậy
1 *
7.2 5, .
n
n
u n
0,5
0,5
0,5
0,5
0,5
b
Chứng minh được
*
0, .
n
v n
Khi đó
*
1
2
2 2
1
, .
1 2108
2 2018. 2018
n n
n
n
n
v v
v n
v
v
(1)
Mặt khác,
*
,
n
ta có
2
3
1
2 2 2
1 2018
2 2018
0
1 2018 1 2018 1 2018
n n
n n n
n n n
n n n
v v
v v v
v v v
v v v
0,5
1,0
1,0
3
2 2
2 2 2 2
2 1 (1)
.
1 1 (2)
xy x y x y
x y y x x y x
4,0
Điều kiện
0
xy
Ta có
2
1 0,x x x
nên
0
y
không thỏa mãn (2). Do đó
0.
y
Suy ra
0
x
không thỏa mãn (1).
Nếu
,x y
cùng âm thì (1) vô lí. Do đó
,x y
cùng dương.
Suy ra
2 2
2
1
(2) 1 1 1
x x y y
x
2
2
1 1 1
1 1
y y y
x x x
(3)
Xét hàm số
2
( ) 1f t t t t
trên khoảng
0; .
Ta có
2
2
2
( ) 1 1 0, 0
1
t
f t t t
t
Suy ra
( )f t
đồng biến trên
0;

Do đó
1 1
(3) 1f f y y xy
x x
Thay
1xy
vào phương trình (1) ta được
2 2
2 2
2 1 1 1 0 1x y x y x y x y
Vậy hệ phương trình đã cho có nghiệm duy nhất
; 1;1
x y
0,25
0,5
0,25
0,5
0,25
0,5
0,5
0,5
0,5
0,25
4
5,0
a Gọi
I
là giao điểm của
AD
và
.BC
Ta có
2 2
. .IB IA ID IC
Suy ra
.IB IC
Do đó
I
là trung điểm của
.BC
Hay đường thẳng
AD
đi qua trung
điểm
I
của
.BC
0,25
0,75
0,25
0,25
b
Chứng minh được
.BHC BDC
Suy ra tứ giác
BHDC
nội tiếp.
Chứng minh
AFHD
nội tiếp
Chứng minh
, ,
EF BC HD
đồng qui
1,0
1,0
1,5
A
B C
E
F
H
D
I
K
| 1/4
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KÌ THI CHỌN HSG CẤP TỈNH LỚP 12 THPT BÌNH THUẬN NĂM HỌC 2018 – 2019 Ngày thi: 18/10/2018 ĐỀ CHÍNH THỨC Môn: Toán
(Đề này có 01 trang)
Thời gian làm bài: 180 phút (không kể thời gian giao đề) Bài 1 (6,0 điểm).
a) Cho x và y là các số thực thỏa mãn 2x y  0. Tìm giá trị lớn nhất và giá trị 2 2
x xy y
nhỏ nhất của biểu thức P  . 2 2
x xy y
b) Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số 3 2
y x  3x  3mx m có hai điểm cực trị nằm khác phía đối với trục hoành. Bài 2 (5,0 điểm).
a) Tìm số hạng tổng quát của dãy số u biết u  2 và * n   . n u  2u  5, 1 n 1  n 1 2v
b) Cho dãy số v thỏa mãn v  , n v  , * n   Chứng minh n  . 1 2018 n 1  2 1 2018vn rằng * vv , n    . n 1  n
Bài 3 (4,0 điểm). Giải hệ phương trình 2 xy      x y  2 2 1 x y  . 2 2 2 2
x y y 1  x 1  x y x
Bài 4 (5,0 điểm). Cho tam giác ABC nhọn có AB AC và hai đường cao BE, CF cắt
nhau tại H. Các đường tròn O , O cùng đi qua A và theo thứ tự tiếp xúc với 2  1 
BC tại B, C. Gọi D là giao điểm thứ hai của O và O . 2  1 
a) Chứng minh đường thẳng AD đi qua trung điểm của cạnh BC;
b) Chứng minh ba đường thẳng EF, BC, HD đồng quy.
-------------- HẾT -------------
Học sinh không được sử dụng máy tính cầm tay.
Cán bộ coi thi không được giải thích gì thêm.
Họ và tên thí sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Số báo danh: . . . . . . . . . . . . . . . . HƯỚNG DẪN CHẤM Bài Nội dung Điểm 1 6,0 a 2 t t 1 x 1 Ta có P  , với t   . 2 t t 1 y 2 0,5 2 t t 1 1
Xét hàm số f (t)  với t  . 2 t t 1 2 0,5  f (  t)  0 2 2t  2  1,0 Tính được f (  t)  ,  1  t  1. 2 2 (t t 1) t    2 0,5 Bảng biến thiên 1 0,5
Suy ra giá trị nhỏ nhất của P bằng , không có giá trị lớn nhất. 3 b
Tập xác định D   2
y '  3x  6x  3m 0,25
Yêu cầu bài toán  Phương trình y '  0 có hai nghiệm phân biệt 0,5
x , x thỏa mãn y x .y x  0. 1   2  1 2
Phương trình y  0 có hai nghiệm phân biệt  1 m  0 (*) 0,25
Khi đó đồ thị hàm số đã cho có hai điểm cực trị là
A x ; y , B x ; y . 1 1   2 2  0,25  x 1  Ta có y  
.y  2 m     1 x  3 3  0,25
Do đó y y x  2 m 1 x 1  1   1 0,25 y y x
 2 m  1 x 2  2    2 0,5
y x .y x   0  4m  2 1 x .x  0 1 2 1 2 0,5
x .x  0  m  0  m  0 1 2 0,25
Kết hợp với điều kiện (*) ta có m  0 thỏa mãn bài toán 2 5,0 a * n    , ta có u
 2u  5  u  5  2 u  5 0,5 n 1  n n 1   n  Đặt *
w u  5, n   . n n Khi đó * w
 2w , n   . 0,5 n 1  n
Do đó w là cấp số nhân có w u  5  7, công bội q  2. 0,5 n  1 1 Suy ra n 1  n 1  *
w w .q  7.2 , n    . 0,5 n 1 Vậy n 1  * u  7.2  5, n   . 0,5 n b Chứng minh được * v  0, n    . 0,5 n 2v 2v 1 Khi đó n n * v    , n    . (1) 1,0 n 1  2 1 2108v v n 2 2018. 2018 n Mặt khác, * n    , ta có vv v v v n  2 3 1 2018 2 2018 n n n n vv   v    0 n 1  n 2 n 2 2 1 2018v 1 2018v 1 2018v n n n 1,0 3 2 xy 4,0 
x y   2 2 1  x y (1)  . 2 2 2 2
x y y 1  x 1  x y x (2) 
Điều kiện xy  0 0,25 Ta có 2
x 1  x  0, x
   nên y  0 không thỏa mãn (2). Do đó
y  0. Suy ra x  0 không thỏa mãn (1). 0,5
Nếu x, y cùng âm thì (1) vô lí. Do đó x, y cùng dương. 0,25 1 Suy ra (2) 
 2x 1 x  y 2y 11 2  x 1 1 1 2  1 
y y 1  y (3) 0,5 2 x x x Xét hàm số 2
f (t)  t t 1  t trên khoảng 0; . 0,25 2 t Ta có 2 f (
t)  t 1  1  0, t   0 0,5 2 t 1
Suy ra f (t) đồng biến trên 0;  0,5  1  1 Do đó (3)  ff  
y   y xy  1 0,5  x x
Thay xy  1 vào phương trình (1) ta được 2 2
x y   2 2 2
1  x y   x   1   y   1
 0  x y  1 0,5
Vậy hệ phương trình đã cho có nghiệm duy nhất  ; x y  1;  1 0,25 4 5,0 a
Gọi I là giao điểm của AD và BC. 0,25 Ta có 2 2 IB  . IA ID IC . 0,75
Suy ra IB IC. 0,25
Do đó I là trung điểm của B .
C Hay đường thẳng AD đi qua trung 0,25
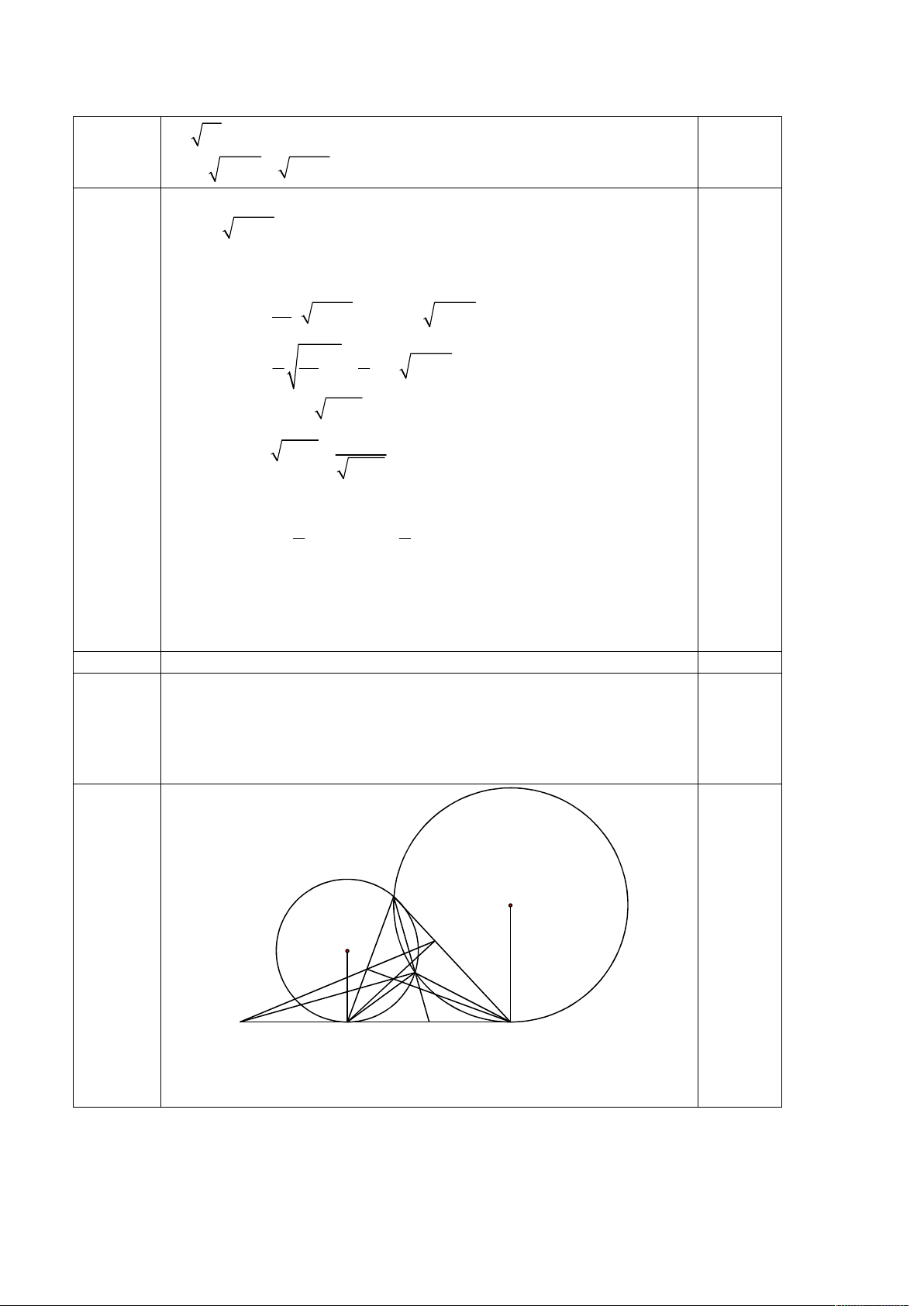
điểm I của BC. b A E F H D K B I C Chứng minh được  
BHC BDC. Suy ra tứ giác BHDC nội tiếp. 1,0
Chứng minh AFHD nội tiếp 1,0
Chứng minh EF , BC, HD đồng qui 1,5