Đề thi chọn HSG cấp tỉnh Toán 12 THPT năm 2018 – 2019 sở GD&ĐT Lâm Đồng

NHÓM TOÁN VD – VDC
SỞ GD&ĐT LÂM ĐỒNG
KỲ THI CHỌN HSG CẤP TỈNH LỚP 12 ĐỀ CHÍNH THỨC NĂM HỌC 2018 - 2019 (Đề thi có 01 trang)
MÔN: TOÁN – Hệ : THPT N Ngày thi : 18/01/2019 Thời gian: 180 phút H Ó M
Họ và tên: ...................................................................................... SBD: ............................................... . T O
Câu 1: (2,0 điểm) ÁN
Tìm tất cả các giá trị của tham số m để hàm số 3 2
y  x  x   2 m   2 3 3
1 x  3m 1 có hai điểm V D
cực trị x , x thỏa x  4x  0 . 1 2 1 2 –
Câu 2: (4,0 điểm) VD
2.1. Cho a  log 6 và b  log 12 . Tính log 60 theo a và b 5 6 3 C 2 x
2.2. Giải phương trình 1 x  1 x  2  . 4
Câu 3: (2,0 điểm)
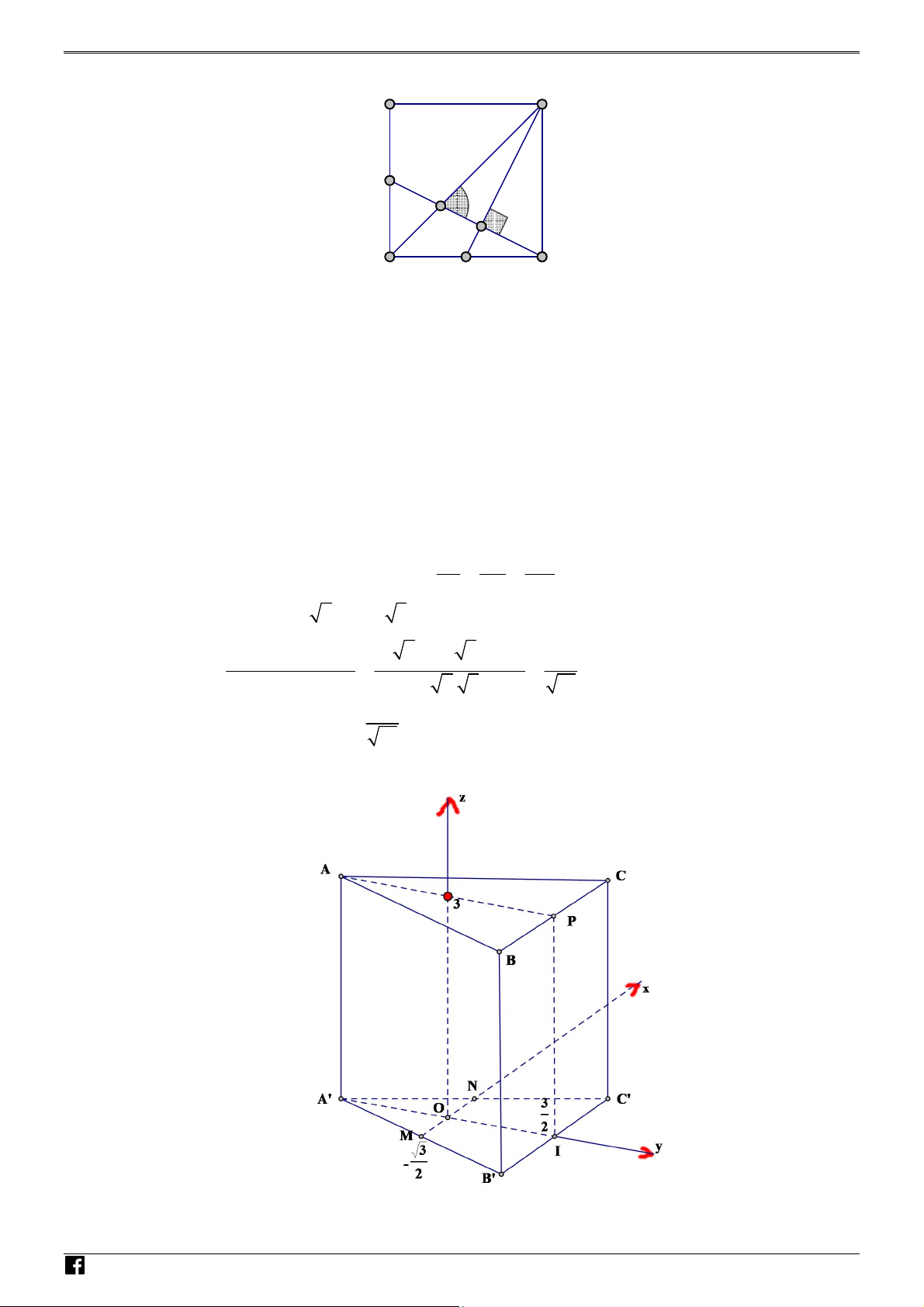
Một biển quảng cáo có dạng hình chữ nhật ABCD được sơn trang
trí như hình bên. Chi phí để sơn phần tô đậm là 250.000 đồng/ 2 m
và phần còn lại là 160.000 đồng/ 2
m . Hỏi số tiền để sơn biển
quảng cáo theo cách trên là bao nhiêu?
Biết AD  4m , DC  3m và AE  EF  FB .
Câu 4: (2,0 điểm)
Trong không gian với hệ tọa độ Oxyz cho ba điểm A1;0;3 , B  3
 ;1;3 , C 1;5  ;1 . Tìm tọa độ   
điểm M thuộc mặt phẳng Oxy sao cho biểu thức T  2 | MA |  | MB  MC | có giá trị nhỏ nhất.
Câu 5: (2,0 điểm) N 2 2 2 3 k 2 k 2 2019 H
Tính tổng S  2 C  3 C  ...  1  k C  ...  2019 C . 2019 2019   2019 2019 Ó
Câu 6: (4,0 điểm) M T
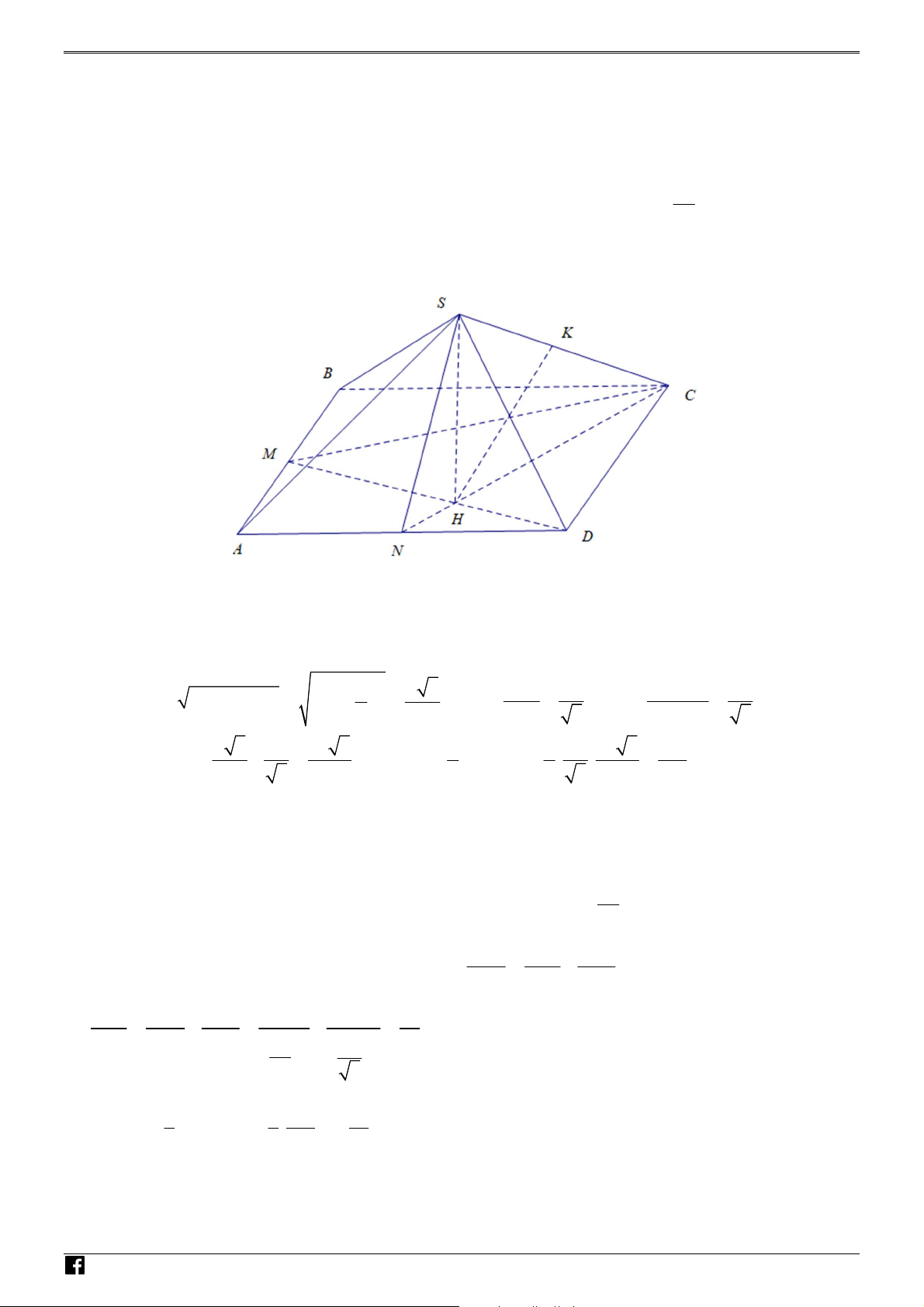
6.1. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a . Gọi M , N lần lượt là trung O
điểm của các cạnh AB, AD và H là giao điểm của CN và DM . Biết SH vuông góc với mặt ÁN 2a V
phẳng ( ABCD) và khoảng cách giữa hai đường thẳng DM và SC bằng . Tính theo a thể D 3
tích khối tứ diện SHMC . – V
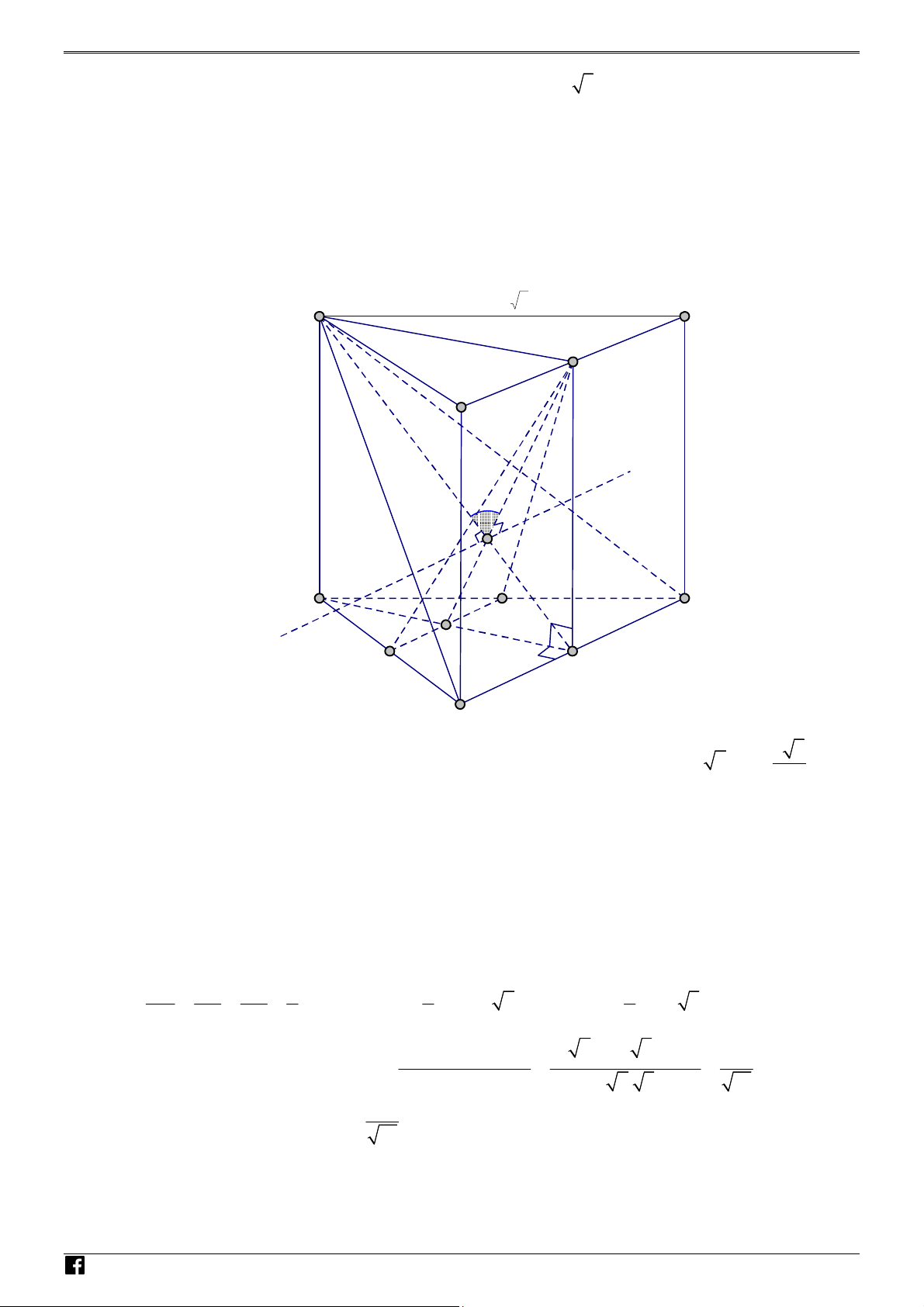
6.2. Cho hình lăng trụ tam giác đều ABCA ' B 'C ' có AB  2 3 , AA '  3 . Gọi M , N, P lần lượt là D C
trung điểm của các cạnh A' B ', A'C ', và BC . Tính côsin của góc tạo bởi hai mặt phẳng  AB 'C ' và  MNP .
Câu 7: (2,0 điểm)
Tìm tất cả giá trị của tham số m để hệ phương trình
x  y  4  2xy  
2x y  m   2 2 x  y 
x  x  y  y  5   có nghiệm  ;
x y  thỏa mãn x  1, y  1 .
Câu 8: (2,0 điểm)
Cho x, y, z là các số thực thỏa mãn x  y  z và 2 2 2
x  y  z  2 . Tìm giá trị nhỏ nhất của biểu thức
P  (x  y)( y  z)(z  x)(xy  yz  zx). ----- HẾT -----
https://www.facebook.com/groups/toanvd.vdc Trang 1 NHÓM TOÁN VD – VDC
SỞ GD&ĐT LÂM ĐỒNG HƯỚNG DẪN GIẢI ĐỀ CHÍNH THỨC N H
Câu 1: (2,0 điểm) Ó M
Tìm tất cả các giá trị của tham số m để hàm số 3 2
y  x  x   2 m   2 3 3
1 x  3m 1 có hai điểm T O
cực trị x , x thỏa x  4x  0 . 1 2 1 2 ÁN V Lời giải D –
Tập xác định: D   . VD 2 2 C
y  3x  6x  3m   1 .  x  1 m y  0   x  1 m 
Hàm số có hai điểm cực trị  y  0 có hai nghiệm phân biệt  m  0 . x  1 m +) TH1: 1  x  1 m  2 5
Khi đó x  4x  0  1 m  4 1 m  0  m   (TM). 1 2 3 x  1 m +) TH2: 1  , x  1 m N  2 H Ó 5 M
Khi đó x  4x  0  1 m  41 m  0  m  (TM). 1 2 T 3 O Á 5 N Vậy m  
là các giá trị cần tìm. V 3 D –
Câu 2: (4,0 điểm) V
2.1. Cho a  log 6 và b  log 12 . Tính log 60 theo a và b D 5 6 3 C 2 x
2.2. Giải phương trình 1 x  1 x  2  . 4 Lời giải
2.1. Cho a  log 6 và b  log 12 . Tính log 60 theo a và b . 5 6 3 log 6  a 5  log 6  a log 2  b1   5 6  Ta có:     . log 12  b log 12  . a b  6 5
log 2a b1  5    log 60 1 log 12 1 ab 1 ab 5 5 log 60     . 3 log 3 log 6 log 2 a  a b 1  a 2b 5 5 5    
https://www.facebook.com/groups/toanvd.vdc Trang 2 NHÓM TOÁN VD – VDC 2 x
2.2. Giải phương trình 1 x  1 x  2  . 4
Điều kiện: 1 x 1. N H 2 t  2 Ó
Đặt t  1 x  1 x 2 
 1 x , với 2  t  2 . M 2 T O 2 2    Á t 2     N 7    2  V 2
Phương trình theo t có dạng: t   t 2  2 t  4t   8  0  t  2 D 4 – V 2 D
 1 x  1 x  2  1 x 1 x  0 . C
Vậy phương trình có nghiệm x  0 .
Câu 3: (2,0 điểm)
Một biển quảng cáo có dạng hình chữ nhật ABCD được sơn trang
trí như hình bên. Chi phí để sơn phần tô đậm là 250.000 đồng/ 2 m
và phần còn lại là 160.000 đồng/ 2
m . Hỏi số tiền để sơn biển
quảng cáo theo cách trên là bao nhiêu?
Biết AD  4m , DC  3m và AE  EF  FB . Lời giải
Gọi H , K lần lượt là trung điểm của AB và CD ; I là
giao điểm của CE và DF .  1 N EH  EF H   2 1 1 Ó Ta có:   EH  KC  IH  HK  1 (m) , M 2 3  4 EF  KC T   3 O IK  3 (m) . ÁN V Ta có: S  3.4  12 2 (m ) . ABCD D 1 2 – S  S  .1.4  2 (m ) . ADE BCF V 2 D 1 1 1 C 2 S  IH .EF  .1.1  (m ) . IEF 2 2 2 1 1 9 2 S  IK.CD  .3.3  (m ) . ICD 2 2 2
Gọi S là diện tích phần tô đậm và S là diện tích phần còn lại. 1 2 Ta có: 2 S  S  S  S  S  9 (m ) . 2 ADE BCF IEF ICD Suy ra: 2 S  S
 S  3 (m ) . 1 ABCD 2
Vậy tổng số tiền để làm là: T  3.250 000  9.160 000  2190 000 (đồng).
Câu 4: (2,0 điểm)
Trong không gian với hệ tọa độ Oxyz cho ba điểm A1;0;3 , B  3
 ;1;3 , C 1;5  ;1 . Tìm tọa độ   
điểm M thuộc mặt phẳng Oxy sao cho biểu thức T  2 | MA |  | MB  MC | có giá trị nhỏ nhất. Lời giải
https://www.facebook.com/groups/toanvd.vdc Trang 3 NHÓM TOÁN VD – VDC N H Ó M T O ÁN VD – V    D
Gọi K là trung điểm của BC , ta có: K  1
 ;3; 2 và MB  MC  2MK . Suy ra: C  
T  2 | MA | 2 | MK |  2MA MK  .
Nhận xét: A, K nằm khác phía so với mặt phẳng Oxy . Gọi A' là điểm đối xứng của điểm A qua mặt
phẳng Oxy . Khi đó: T  2 MA  MK   2 MA  MK  Suy ra : T
 MA  MK   A ,
 M , K thẳng hàng hay M là giao điểm của A' K với mặt phẳng min min Oxy . 
Ta có: H 1;0;0  A1;0;3  AK  2;3;5 . Do đó: Phương trình tham số của A' K là
x 12t   1 9  y  3t  M   ; ;0     5 5 
z 35t 
Câu 5: (2,0 điểm) N k Tính tổng 2 2 2 3  2  3  ...  1 k S C C  k C  ...  2019 C . 2019 2019   2 2 2019 H 2019 2019 Ó Lời giải M T
- Trước hết ta chứng minh đẳng thức: 2 k k C  n n 
C   nC    1 2 k , n k, n       . n   k 2 k 1 1 O n 2 n 1  ÁN 2 k k k V
Thật vậy: do k C  k k 
C  kC 2 . n   1 n n D – n n  n  k ! 1 ! 1 !     k 1  V Mà: kC  k.  . n  . n  nC 3 n n 1  D
k !.n  k ! k  
1 !.n  k ! k   1 !.n   1  k   1 ! C
Áp dụng (3) hai lần ta được: k   1 k kC  k 
nC   n k 
C   n n  C  4 n   k 1 1 . n   k 1 1 n   k 2 1 1 1 n2
Từ 2 , 3 , 4 ta được   1 . - Áp dụng   1 ta được: 2019 2019
S    k 2 k 1 k k C     1 . k 2 k 1 2019.2018.C  2019.C  2019 2017 2018  k 2 k 2 2017 2018 k k  2018.2019. k C . 1   2019 k C 1   2017    2018   k 0 k 1     2017    2018 2018.2019. 1 1 2019 1 1   1  2019 .
https://www.facebook.com/groups/toanvd.vdc Trang 4 NHÓM TOÁN VD – VDC Vậy S  2019 .
Câu 6: (4,0 điểm)
6.1. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a . Gọi M , N lần lượt là trung N
điểm của các cạnh AB, AD và H là giao điểm của CN và DM . Biết SH vuông góc với mặt H 2a Ó
phẳng ( ABCD) và khoảng cách giữa hai đường thẳng DM và SC bằng . Tính theo a thể M 3 T
tích khối tứ diện SHMC . O Lời giải ÁN VD – VDC
Theo giả thiết ABCD là hình vuông, suy ra A
 DM  DCN (c.g.c) Từ đó suy ra  
ADH  DCN  DM  CN 2 2  a  a 5 CD 2a DC.DN a Vậy có: 2 2 2 NC  DC  DN  a   ; HC   ; HD   ; N    2  2 CN 5 NC 5 H Ó a 5 a 3a 5 2 1 1 2a 3a 5 3a M
HM  MD  HD    và S  HC.HM  . .  H  MC T 2 5 10 2 2 5 10 10 O Á
Mặt khác, ta có SH  (ABCD)  SH  DM N V D
Theo chứng minh trên DM  CN , suy ra DM  (SCN ) . – V 2a D
Kẻ HK  SC thì HK là khoảng cách giữa DM và SC . Suy ra HK  . C 3 1 1 1
Tam giác SHC vuông tại H , đường cao HK suy ra   2 2 2 HK SH HC 1 1 1 1 1 1        SH  a 2 2 2 2 2 2 SH HK HC  2a   2 a a    3      5  2 3 1 1 3a a Vậy V  S .SH  . .a  SHMC 3 H  MC 3 10 10
https://www.facebook.com/groups/toanvd.vdc Trang 5 NHÓM TOÁN VD – VDC
6.2. Cho hình lăng trụ tam giác đều ABCA ' B 'C ' có AB  2 3 , AA '  3 . Gọi M , N, P lần lượt là
trung điểm của các cạnh A' B ', A'C ', và BC . Tính côsin của góc tạo bởi hai mặt phẳng  AB 'C ' và  MNP . N Lời giải H Ó  Cách 1: M T O ÁN V A 2 3 C D – P VDC B 3 Δ G A' C' N I M Q N B' H Ó M 3 5
Gọi I,Q lần lượt là trung điểm của các cạnh MN và B 'C ' , khi đó AQ  3 2, PI  . T 2 O
Giả sử PI  AQ  G .  G  AB 'C '  MNP . Á       N V 
MN   MNP  , B 'C '   AB 'C ' D Hơn nữa 
nên giao tuyến của mặt phẳng  AB 'C ' và  MNP MN B 'C ' –   V
là đường thẳng  đi qua G và song song với MN và B 'C ' . D C
Ta có B 'C '   AA 'QP  AG   . Chứng minh tương tự ta có PG   .
Do đó  AB C  MNP   AG PG  ' ' , ,
. Mặt khác IQ  AP , theo định lý Ta-lét có GQ GI IQ 1 2 2   
 GA  2GQ 
AQ  2 2 ; GP  2GI  PI  5 . GA GP AP 2 3 3 2 2 2 2 2 2 2 2  5  3
GA  GP  AP 1
Xét tam giác AGP có      cos AGP    2G . A GP 2 2. 5 10
Vậy cos  AB C  MNP  1 ' ' ,  . 10  Cách 2
https://www.facebook.com/groups/toanvd.vdc Trang 6 NHÓM TOÁN VD – VDC 3 A P N X H T 3 Ó M T O A' Á I Q N V D – Gọi I , ,
Q X lần lượt là trung điểm của các cạnh MN, B 'C ' và AA' . V  0 D
Ta có AP  PQ  QA'  A' A  3 và A' AP  90  tứ giác APQA ' là hình vuông. C I
 PQ  XQA'c  g  c  
 IPQ  XQA '  PI  QX   1
Ta có B 'C '   APQA '  B 'C '  QX , mà MN  B 'C '  MN  QX 2 Từ  
1 và 2  QX  MNP .
Chứng minh tương tự ta có A ' P   AB 'C ' .
Do đó  AB C  MNP   A P QX   ' ' , ' , . TP TQ PQ
Ta có XA  PQ , theo định lý Ta-lét có    2 . TA TX AX
Từ đó ta được TP  2 2, XQ  5 . Xét tam giác PTQ , theo định lý côsin ta có 2 2 2  2 2 2
TP  TQ  PQ 2 2  5 3 1 cosPTQ    2T . P TQ 2 2. 5 10 N H
Vậy cos  AB C  MNP  1 ' ' ,  . Ó 10 M  Cách 3 T O ÁN VD – VDC Gọi I , ,
O J lần lượt là trung điểm của các cạnh B 'C ', MN và AP . Ta có MN  B 'C ' và
A ' I  B 'C '  MN  A ' I . Đặt hình lăng tru tam giác đều ABC.A ' B 'C ' trong hệ trục tọa độ
https://www.facebook.com/groups/toanvd.vdc Trang 7 NHÓM TOÁN VD – VDC
Oxyz với gốc tọa độ O 0;0;0 , chiều dương Ox trùng với tia ON, chiều dương Oy trùng với
tia OI , chiều dương Oz trùng với tia OJ . Khi đó ta có : 3 3 3 3  3           3 
A 0;  ;3 , B '  3; ; 0 , C '
3; ;0 , M  ; 0; 0 , N          ; 0;0  , P 0; ;0   N 2 2 2 2  2           2    H   Ó
Gọi n , n lần lượt là véctơ pháp tuyển của mặt phẳng  AB 'C ' và  MNP . M 1 2 
     T
Ta có n   AB ', AC '  0; 2; 2 , n  MN , MP  0; 2  ;1 . 1   1   O     ÁN
Gọi  là góc tạo bởi hai mặt phẳng  AB 'C ' và  MNP . V   D 0  4  2 1
Khi đó cos  cos n , n   .  1 2  – 2 2 2 2 2 2 10
0  2  2 . 0  2 1 VDC
Vậy cos  AB C  MNP  .   1 ' ' , 10
Câu 7: (2,0 điểm)
Tìm tất cả giá trị của tham số m để hệ phương trình
x  y  4  2xy  
2x y  m   2 2 x  y 
x  x  y  y  5   có nghiệm  ;
x y  thỏa mãn x  1, y  1 . Lời giải
x  y  4  2xy   1  Xét hệ 
(với x, y  1)
2x y  m   2 2 x  y 
x  x  y  y  5  2  Từ  
1 ta có x  y  2xy  4 N H Ó
Thế vào 2 ta được x y  m 2 2 2
x  y  x  2xy  y 1 M T O x  y   Á 
 m x  y   x  y2 2 1  N     V D  x  y2 –
Đặt t  x  y  2 và x  y  4  2xy 
 x  y  4  t  4 . V 2 D C
Do x  1, y  1 nên  x   1  y  
1  0  xy  x  y  1  0  xy  x  y 1  2xy  2 x  y  2
 x  y  4  2  x  y  2  x  y  6 . Do đó  t   m  2 2 t  t 1 t  m   2 2
t 1  t  .
Hệ đã cho có nghiệm  ;
x y  thỏa mãn x  1, y  1 khi và chỉ khi phương trình t  m   2 2
t 1  t  có
nghiệm t 4;6 .   t 1 Xét hàm số   t f t   2 2
t 1  t  với 4  t  6 . Có f t  2  2t 1 tln 2   . 2  t  1 
https://www.facebook.com/groups/toanvd.vdc Trang 8 NHÓM TOÁN VD – VDC 1 Mà 2
t 1  t  t và 2 t 1  1  
 1 nên f t  0 với 4  t  6 . 2 t 1
Suy ra f t  là hàm số đồng biến. Do đó f 4  m  f 6  16 17  4  64 37  6. N H Ó
Câu 8: (2,0 điểm) M
Cho x, y, z là các số thực thỏa mãn x  y  z và 2 2 2
x  y  z  2 . Tìm giá trị nhỏ nhất của biểu thức T O
P  (x  y)( y  z)(z  x)(xy  yz  zx). Á Lời giải N V Cách 1 D –
Đặt Q  (x  y)( y  z)(x  z)(xy  yz  zx) ta có Q   . P VDC
+ xy  yz  zx  0 ta có Q  0.
+ xy  yz  zx  0 đặt t  xy  yz  zx  0. 2 3
 x  y  y  z  (x  z)
Áp dụng BĐT Côsi ta có (x  y)( y  z)(x  z)  (x  z)    (1)  2  4 Mà  2 2 2
x  y  z  xy  yz  zx 2 2 2 4
 2(x  z)  2(x  y)  2( y  z)  x  z
  x  y  y  z 2 2 2 2( ) ( ) ( )
 3(x  z) hay   t  2 4 5
 3(x  z)  0 (2)  t  5 3 1  4  2 3 Từ (1) và (2) suy ra 2 3 Q  t. (5  t)  t (5  t) .   N 4  5  9 H Ó M Xét hàm số 2 3
f (t)  t (5  t) trên 0  t  5 ta có 2 f (
 t)  t(5  t) (10  5 t), f (
 t)  0  t  2 hoặc t  5 T O Á
f (0)  0, f (5)  0, f (0)  0, f (2)  108. N V D
Do đó Q  4 nên GTLN của Q là 4 khi x  2, y  1, z  0. – VD
Suy ra P  4 nên GTNN của P là 4
 khi x  2, y  1, z  0. C Cách 2: Đặt 2 2 2
t  xy  yz  zx  x  y  z  t  5 . 2 2 2 2 2 2 Giả thiết: 2 2 2
10  2x  2 y  2z   x  y   y  z    z  x  2t   x  y   y  z    z  x  10  2t 1 3  z  x2 2 2 2 2 2 2 5  t
Mà  x  y   y  z    z  x   x  y  y  z   z  x   z  x   2 2 4 3 2
 x  y  y  z   x  z2 2 2  x  z4 2  5  t  
x  y  y  z  
  x  y  y  z         2  4 16  3 
https://www.facebook.com/groups/toanvd.vdc Trang 9 NHÓM TOÁN VD – VDC 2 2 2 2 2
 5  t  20  4t 4 3 Ta có: 2
P   x  y  y  z  z  x . xy  yz  zx 2  .t    5  t  2 t .  3  3 27 Xét hàm số suy ra 2
P  16  min P  4
 tại t  2   ; x ;
y z   2;1;0 . N H Ó M T O ÁN VD – VD C N H Ó M T O ÁN VD – VDC
https://www.facebook.com/groups/toanvd.vdc Trang 10
Document Outline