Đề thi chọn HSG THPT năm học 2017 – 2018 môn Toán 12 sở GD và ĐT Hà Nam

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI THPT HÀ NAM
NĂM HỌC: 2017 - 2018 ĐỀ CHÍNH THỨC
Môn: Toán – Lớp 12
(Đề thi có 01 trang)
Thời gian làm bài: 180 phút. Câu 1. (5,0 điểm) 1. Cho hàm số 3 2 2 3 2
y  x  3mx  3(1 m )x  m  m , với m là tham số thực. Chứng minh rằng m
∀ ∈ hàm số trên luôn có hai điểm cực trị. Tìm tọa độ điểm M thuộc đồ thị hàm số trên thỏa
mãn điều kiện điểm M vừa là điểm cực đại của đồ thị hàm số ứng với giá trị này của m đồng thời
điểm M vừa là điểm cực tiểu của đồ thị ứng với giá trị khác của m . x + 2. Cho hàm số 2 1 y =
C , điểm I (3;3) và đường thẳng d : y = −x + m . Tìm m x + có đồ thị ( ) 1
để đường thẳng d cắt đồ thị (C) tại hai điểm phân biệt ,
A B sao cho diện tích tứ giác OAIB bằng 6
( O là gốc tọa độ). Câu 2. (4,0 điểm)
1. Giải bất phương trình sau trên tập số thực  2     2 16x 96x 208  x  9  log         2 2 3x 4 6x 3 5x 9 .
 12x 16  45x 81  y 2x 1  x 2.4 1 2  2log2( )  y 
2. Giải hệ phương trình sau trên tập số thực  . 2 3 2 
x  x  2 4 y 1  x  1   3 2x  13  2 2 x
Câu 3. (2,0 điểm) Tính tích phân I  . dx  2 2
(x 1) cos x 1 x sin 2x  4 Câu 4. (5,0 điểm)
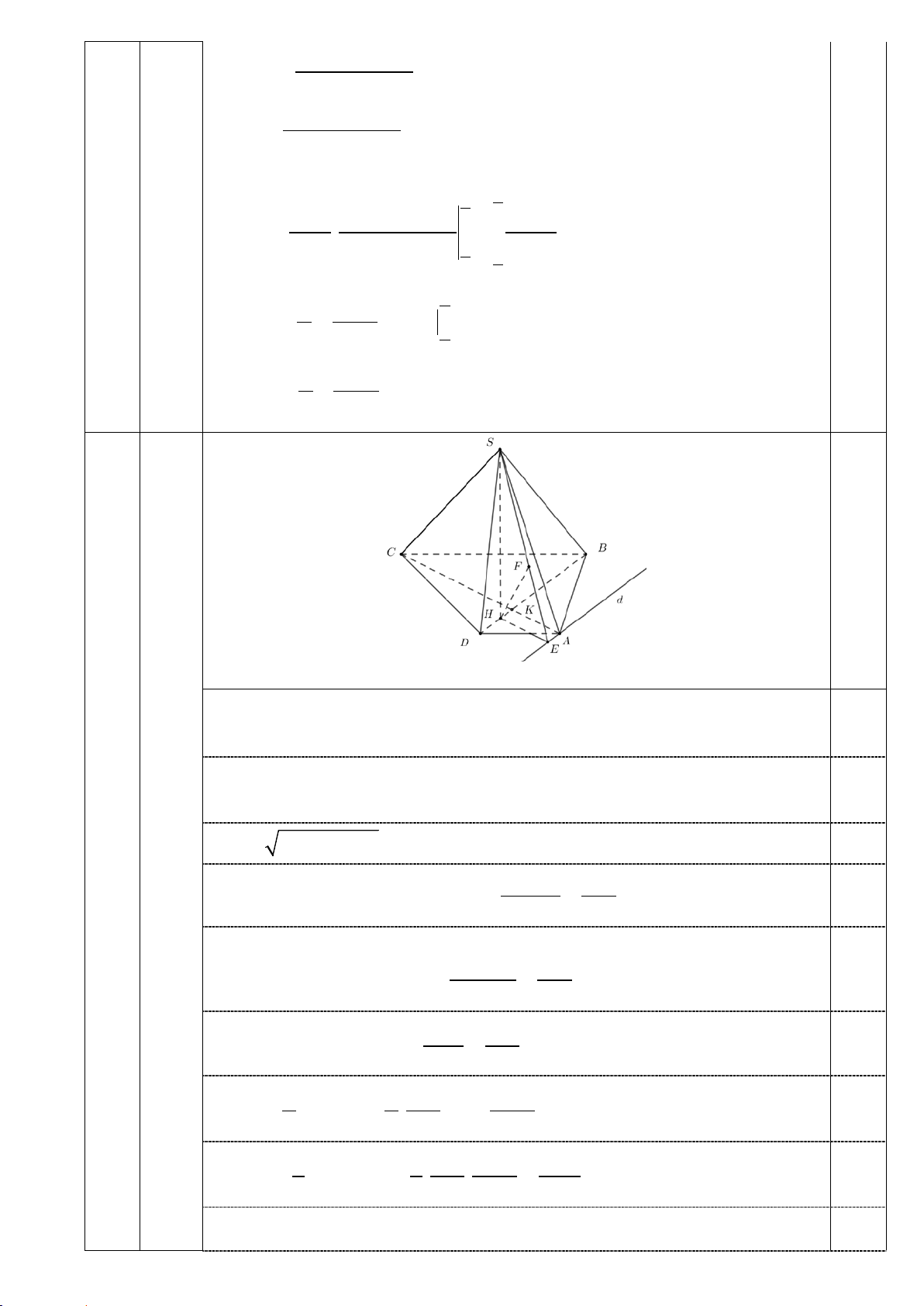
1. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B. Biết AB=SD=3a,
AD=SB=4a, đường chéo AC vuông góc với mặt phẳng (SBD). Tính theo a thể tích khối chóp
S.ABCD và khoảng cách giữa hai đường thẳng BD và SA.
2. Cho mặt cầu có tâm O và bán kính R. Từ một điểm S bất kỳ trên mặt cầu ta dựng ba cát tuyến
bằng nhau, cắt mặt cầu tại các điểm A, B, C ( khác với S) và  ASB   BSC  
CSA   . Tính thể tích
khối chóp S.ABC theo R và α . Khi α thay đổi, tìm α để thể tích khối chóp S.ABC lớn nhất.
Câu 5. (2,0 điểm) Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S ) đi qua điểm ( A 2; 2; − 5) và
tiếp xúc với các mặt phẳng (α) : x =1;(β ) : y = 1
− ;(γ ) : z = 1. Viết phương trình mặt cầu (S) .
Câu 6. (2,0 điểm) Cho a,b,c là các số thực dương thỏa mãn ab ≥ 1 và c(a + b + c) ≥ 3. b  2c a  2c
Tìm giá trị nhỏ nhất của biểu thức: P  
 6ln(a  b  2c) . 1 a 1 b ---HẾT---
Họ và tên thí sinh……………………………….Số báo danh………………………..........................
Người coi thi số 1……………………………….Người coi thi số 2.………………...........................
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KÌ THI CHỌN HỌC SINH GIỎI THPT HÀ NAM NĂM HỌC 2017 - 2018
(Hướng dẫn chấm có 07 trang)
Hướng dẫn chấm môn: Môn Toán – Lớp 12 Câu ý Nội dung Điểm Câu 1. TXĐ: D   1 (2,5đ) 2 0,25
y   x  mx   2 ' 3 6 3 1 m  5,0đ x = m −1 y ' = 0 ⇔ 
Hàm số luôn có hai điểm cực trị 0,25 x = m +1 2
x = m −1 ⇒ y = −m + 3m − 2 . 0,25
Điểm cực tiểu của đồ thị 2
(m −1;−m + 3m − 2) 0,25 2
x = m + 1 ⇒ y = −m + 3m + 2 . 0,25
Điểm cực đại của đồ thị 2
(m + 1;−m + 3m + 2) 0,25
Quỹ tích điểm cực tiểu của đồ thị là (P): 2
y = −x + x 0,25
Quỹ tích điểm cực đại của đồ thị là (P’): 2
y = −x + 5x − 2 0,25
Điểm M vừa là điểm cực đại ứng với giá trị này của m, vừa là điểm cực tiểu ứng
với giá trị khác của m nên tọa độ điểm M là nghiệm của hệ  1 = 2 x
y = −x + x  2  ⇔  2
y = −x + 5x − 2 1  0,25 y =  4 Vậy 1 1 M ( ; ) 0,25 2 4 2.
TXĐ: D   \   1 2,5đ + Phương trình hoành độ 2x 1 giao điểm : = −x + m x + . 1 0,25 0,25 2
⇔ x + (3 − m)x +1− m = 0 . 2
∆ = m − 2m + 5 > 0 m ∀ . Đườ 0,25
ng thẳng d luôn cắt (P) tại hai điểm phân biệt A, B Gọi (
A x ;−x + m), B(x ;−x + m) 1 1 2 2
Theo Vi-ét x + x = m − 3; x x = 1 − m 1 2 1 2 0,25 2 2 2 ⇒
AB = 2(x − x ) = 2[(x + x ) − 4x x ] = 2(m − 2m + 5) 2 1 1 2 1 2 0,25 0,25 OI = 3 2
Tứ giác OAIB có OI ⊥ AB 0,25 1 1 2 S
= OI.AB = .3 2. 2(m − 2m + 5) . OAIB 0,25 2 2 0,25 2
= 3 m − 2m + 5 1 2  S
 6  m  2m  5  2  m 1 O  AIB 0,25 1. 2,0đ ĐK: 4 x ≥ − 3 2 16(x + 6x + 13) BPT 2 ⇔ x + 9 + log
≤ 2 3x + 4 − 6x + 3 5x + 9 2
2 3x + 4 + 3 5x + 9 0,25 2 2
x  6x 13  log           0,25 2 ( x 6x 13) 2 3x 4 3 5x 9 log2 (2 3x 4 3 5x 9)
Xét hàm số f t log  , với      2 t t
t  0 có f t 1 ' 1 0, t 0 . t ln 2
Do đó hàm số f t đồng biến trên 0;. 0,25 Câu 2 BPT có dạng 2
f (x  6x 13)  f (2 3x  4  3 5x  9) 0,25 4,0đ 2
 x  6x 13  2 3x  4 3 4x 5 0,25 2
 x  x  2(x  2 3x  4) 3(x 3 5x 9)  0 0,25 2 2 2(x + x) 3(x + x) 2 ⇔ (x + x) + + ≤ 0 x + 2 + 3x + 4 x + 3 + 5x + 9 2 3 2 ⇔ (x + x)(1+ + ) ≤ 0 0,25 x + 2 + 3x + 4 x + 3 + 5x + 9 2
⇔ x + x ≤ 0 ⇔ x∈[ −1;0] 0,25  y 2x 1  x 2.4 1 2  2log2( ) (1)  y  .  2 3 2 
x  x  2 4 y 1  x  1  (2)  3 2x  13    ĐK: 0 x 13 y0  y 1 2 (1) ⇔ 4 + = 2 x + log x − log y 2 2 2 x 2. x y 2 ⇔ 4 + log 2 + log y = 2 + log 2 2. 2 2 2 2 2,0đ x 2. x 2 y 2 ⇔ 2 + log 2.y = 2 + log ( 2. ) 2 2 2 0,25 t t 1 2 2
f (t) = 2 + log ( 2.t) ⇒ f '(t) = 2.2 .ln 2 + > 0 t ∀ > 0 2 t ln 2 0,25
Hàm số f(t) đồng biến với t>0 x x 2
PT ⇔ f ( y) = f ( ) ⇔ y = ⇔ 2y = x 0,25 2 2 Với 2
2 y  x thay vào PT(2) ta có: 2 3 2
x  x  2 2x 1 x  x  6 x 1   x 1  2  3 3 2x 1 3 2x 1 3 0,25 2 (x − 3)(x + 2)
( x + 1 + 2)( x + 1 − 2)(x + 2) ⇔ x +1 + 2 = = 3 3 2x + 1 − 3 2x + 1 − 3
( x + 1 − 2)(x + 2) ⇔ 1 = 3 2x +1 − 3 3 ⇔
2x + 1 − 3 = ( x + 1 − 2)(x + 2) 3 3
⇔ 2x +1+ 2x +1 = (x +1) + x +1 0,25 Xét hàm số 3 2
g(u) = u + u ⇒ g '(u) = 3u + 1 > 0 u ∀
Hàm số g(u)đồng biến, phương trình trở thành 3
g( 2x + 1) = g( x + 1) 3 ⇔ 2x +1 = x +1 3 2
⇔ x − x − x = 0 0,25  x = 0(l)   1 − 5 ⇔ x = (l)  2   1 + 5 x = (t / m)  2 0,25 1 + 5 1 + 5 + + x = ⇒ y =
. Hệ phương trình có nghiệm 1 5 1 5 ( ; ) 0,25 2 2 2 2  2 2 x I  dx  2
(x cos x  sin x)  0,25 4 π 2 x x sin xdx = . ∫ Câu 0,25 2
π sin x (x cos x − sin x) 3 4 2,0đ  x u    Đặt sin x   x sin x dv  dx  2 
(x cos x  sin x)  0,25   x u    sin x    d
 (xcos x sin x) dv   2 
(x cos x  sin x)  0,25 3 
sin x − x cos x du = dx  2  sin x ⇒  1  v = 
x cos x − sin x 0,25 π π 2 2 x 1 dx ⇒ I = . + ∫ 2
sin x x cos x − sin x π π sin x 0,25 4 4   2 2 I    cot x 0,25 2   4  4   Vậy 2 I    1 0,25 2   4 Câu 1. 4 3,0đ 5,0đ AC ⊥ (SBD) ⇒ ⊥ (SBD) ( ABCD) 0,25
(SBD) ∩ ( ABCD) = BD Kẻ
SH ⊥ BD tại H ⇒ SH ⊥ ( ABCD) 0,25 2 2 0,25 BD =
AB + AD = 5a
Tam giác SBD vuông tại S nên: . SB SD 12a SH = = 0,25 BD 5
Gọi K là giao điểm của AC và BD. Ta có A . B AD 12a
AK.BD = A . B AD ⇔ AK = = 0,25 BD 5 2 AB 15a 2
AK.AC = AB ⇔ AC = = 0,25 AK 4 2 1 1 15a 75a = = = S AC.BD . .5a 0,25 ABCD 2 2 4 8 2 3 1 1 12a 75a 15a V = SH.S = . . = 0,25 S . ABCD 3 ABCD 3 5 8 2 4
Kẻ đường thẳng d đi qua A và song song với BD Kẻ HE // KA, E thuộc d 0,25
(SHE) ⊥ (SA,d); (SHE) ∩ ( , SA d ) = SE
Kẻ HF vuông góc với SE tại F thì HF vuông góc với (SA,d)
BD//(SA,d) nên d(BD,SA)=d(BD,(SA,d))=d(H, (SA,d))=HF 0,25 1 1 1 25 25 25 = + = + = Trong tam giác SHF ta có 0,25 2 2 2 2 2 2 HF SH HE 144a 144a 72a 6 2a 6 2a HF =
⇒ d(BD,S ) A = 0,25 5 5 2 2,0đ
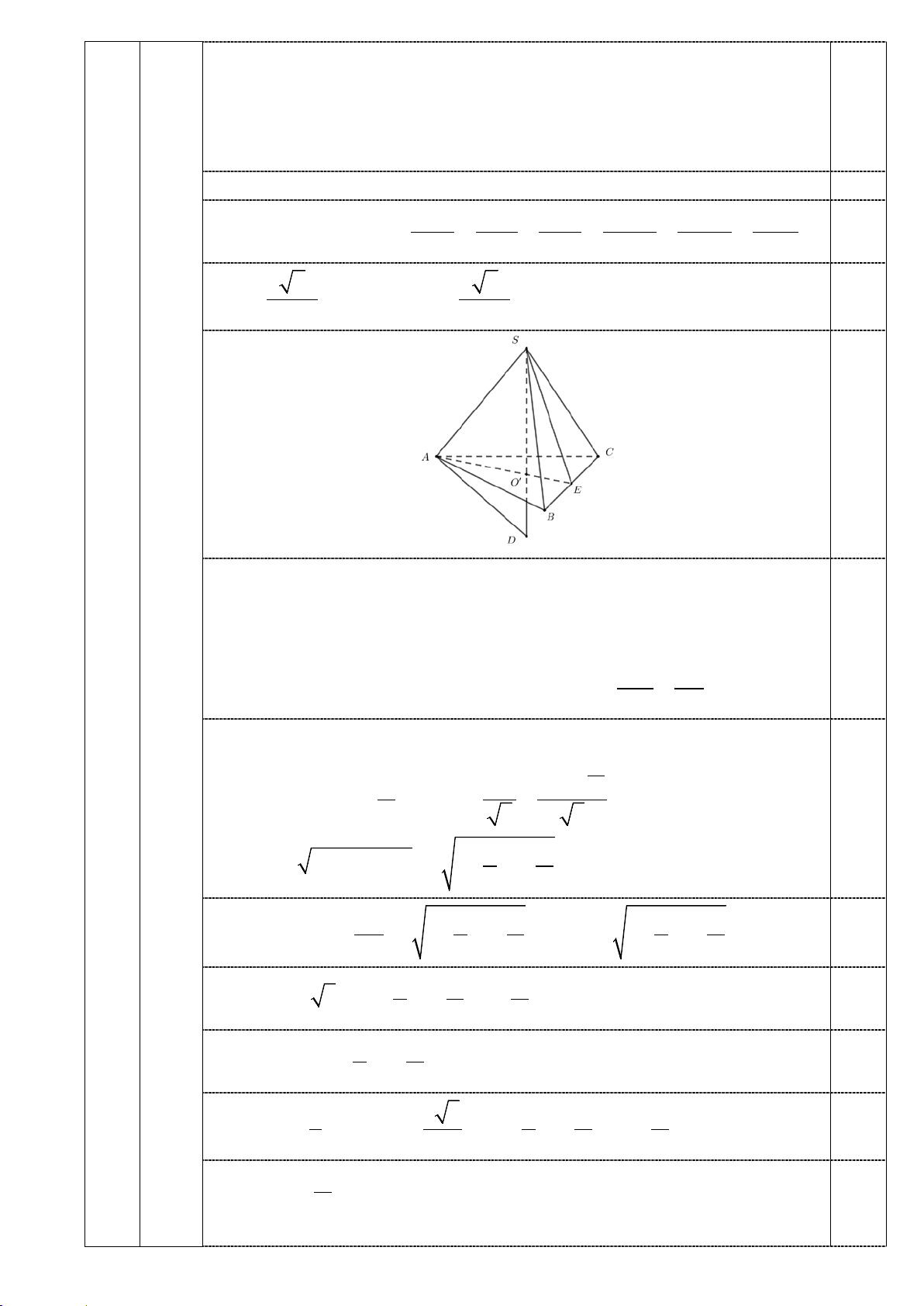
Tam giác ABC đều, kẻ SO’ vuông góc với (ABC) thì O’ là tâm đường tròn ngoại
tiếp tam giác ABC và O’ thuộc SO.
Giả sử SO’ cắt mặt cầu tại D thì tam giác SAD vuông tại A Gọi SA=SB=SC=l 2 2 SA l Trong tam giác SAD ta có 2
SO '.SD = SA ⇒ SO ' = = (1) SD 2R 0,25
Gọi E trung điểm BC ta có α 2l sin α BC 2
BC = 2BE = 2l sin ⇒ AO' = = 2 3 3 4 α 2 2 2
⇒ SO' = SA − O' A = l 1− sin (2) 0,25 3 2 2 l 4 α 4 α 2 2 Từ (1) và (2) ta có = l 1− sin
⇔ l = 2R 1− sin 0,25 2R 3 2 3 2 4 α α 2 2 2 ⇒ = − S 4 3R (1 sin )sin ABC 0,25 3 2 2 4 α 2
⇒ SO' = 2R(1− sin ) 0,25 3 2 α α 1 8 3 4 3 2 2 2 ⇒ V = SO'.S = R (1 − sin ) .sin 0,25 S . ABC 3 ABC 3 3 2 2 α Đặt 2 x = sin ⇒ 0 < x <1 2 5 Xét hàm số 4 1 2 3 2 = − = − + y x(1 x) (16x 24x 9x) 3 9  1 x =  1 4 2
⇒ y ' = (16x −16x + 3) ⇒ y ' = 0 ⇔  3 3  x =  4 x 0 ¼ ¾ 1 y’ + 0 - 0 + 1/9 y 0,25 3 8 3R 1 α 1
Thể tích S.ABC lớn nhất là khi 0 x = ⇔ sin = ⇔ α = 60 0,25 27 4 2 2
Gọi mặt cầu tâm I (a; ;
b c) , bán kính R 0,25
Mặt cầu tiếp xúc với các mặt (α ) : x =1;(β ) : y = 1 − ;(γ ) : z =1 0,25
nên R = a − 1 = b + 1 = c − 1 Điểm ( A 2; 2;
− 5) thuộc miền thỏa mãn : x >1; y < 1 − ; z >1 0,25
Mặt cầu có tâm I và đi qua A nên a >1;b < 1 − ;c >1 Câu  = + 5 a R 1 2,0đ 
Vậy R = a −1 = b
− −1 = c −1⇒ b  = −R −1 c = R +1 0,25  0,25 2 2
⇒ I(R +1;−R −1;R +1) ⇒ IA = R ⇔ IA = R 2 2 2 2
⇔ (R −1) + (−R +1) + (R − 4) = R 2
⇔ 2R −12R +18 = 0 ⇔ R = 3 0,25
Vậy mặt cầu (S) có tâm I (4; 4;
− 4) , bán kính R = 3 0,25 Phương trình mặt cầu : 2 2 2
(x − 4) + ( y + 4) + (z − 4) = 9 0,25
a + b + 2c + 1
a + b + 2c + 1 + = + + + + P 2 6ln(a b 2c) 1 + a 1 + b 1 1 =
(a + b + 2c + 1)( +
) + 6ln(a + b + 2c) 1 + a 1 + b 0,25 Ta chứng minh BĐT sau Câu 1 1 2 6 + ≥
(a,b > 0;ab ≥ 1) 2,0đ + + 1 a 1 b 1 + ab Thật vậy 1 1 2 2 + ≥
⇔ ( a − b) ( ab −1) ≥ 0 (luôn đúng vì ab ≥1) 0,25 1 + a 1 + b 1 + ab 6 Lại có ab +1 ab ≤ 2 1 1 2 4 4 4 16 + ≥ ≥ ≥ = ≥ 2 2
1+ a 1+ b 1+ ab 3 + ab
c + ab + bc + ca
(a + c)(b + c)
(a + b + 2c) 0,25
16(a + b + 2c + 1) ⇒ P + 2 ≥
+ 6ln(a + b + 2c) 2 (a + b + 2c) 0,25 + Đặt 16(t 1)
t = a + b + 2c > 0 ta có P + 2 ≥ + 6lnt 0,25 2 t Xét hàm số 2 16(t + 1) 6t −16t − 32 f (t) =
+ 6lnt ⇒ f '(t) =
⇒ f '(t) = 0 ⇔ t = 4 0,25 2 3 t t t 0 4 + ∞ f’(t) - 0 + f(t) f (4) = 5 + 6ln 4 0,25
⇒ P ≥ 3 + 6ln 4 ⇒ MinP = 3 + 6ln 4 khi a = b = c =1 0,25
Lưu ý: Các cách giải khác, nếu đúng thì cho điểm tương đương theo từng phần như hướng dẫn chấm. ------ HẾT------ 7
Document Outline

• DE TOAN 12(17-18) - CTHUC
• ĐA TOAN 12(17-18) - CTHUC