Đề thi chọn HSG tỉnh Toán 12 năm 2017 – 2018 sở GD&ĐT Quảng Bình

SỞ GD&ĐT QUẢNG BÌNH KỲ THI CHỌN HSG TỈNH NĂM HỌC 2017-2018
Khóa ngày 22 tháng 3 năm 2018 ĐỀ CHÍNH THỨC Môn thi: TOÁN
Họ và tên:………………….. LỚP 12 THPT
Thời gian: 180 phút (không kể thời gian giao đề)
SỐ BÁO DANH:……………
Đề gồm có 01 trang Câu 1 (2.0 điểm) x
Viết phương trình tiếp tuyến với đồ thị C  : y 
, biết rằng khoảng cách từ tâm x 1
đối xứng của đồ thị C  đến tiếp tuyến là lớn nhất. Câu 2 (2.0 điểm) x
Cho các số thực dương x, y thỏa mãn: 3 3 x  x  log
 8 y  2 y  1. 2 y
Tìm giá trị nhỏ nhất của biểu thức 3 2 4 2 2
P  x  x  4 y  y  2xy  2xy  4 . Câu 3 (2.0 điểm) e a. Cho n * I  ln . x dx (n  ) I
 e  n  1 I n 
 , chứng minh rằng: n 1   n 1  4
b. Tính tích phân sau: I  ln 1  tan x dx  0 Câu 4 (3.0 điểm)
Cho hình chóp S.ABCD có đáy ABCD là một hình bình hành. Gọi K là trung điểm
của SC . Giả sử  P  là mặt phẳng đi qua hai điểm A , K và luôn cắt các cạnh SB, SD lần
lượt tại M , N ( M , N không trùng S ). SB SD a. Chứng minh rằng:   3 . SM SN
b. Gọi V và V theo thứ tự là thể tích của khối chóp S.AMKN và S.ABCD . 1 V
Xác định vị trí của mặt phẳng  P  để tỷ số 1 đạt giá trị lớn nhất. V Câu 5 (1.0 điểm) Cho a, ,
b c là các số thực không âm, thỏa mãn a  b  c  3 . Chứng minh rằng: 2 2 2 a b c 3    2 2 2 b  1 c  1 a  1 2
-------------------hÕt-------------------
SỞ GD&ĐT QUẢNG BÌNH KỲ THI CHỌN HSG TỈNH NĂM HỌC 2017-2018
Khóa ngày 22 tháng 3 năm 2018 HƯỚNG DẪN CHẤM Môn thi: TOÁN LỚP 12 THPT
Đáp án này gồm có 05 trang YÊU CẦU CHUNG
* Đáp án chỉ trình bày một lời giải cho mỗi bài. Trong bài làm của học sinh yêu cầu
phải lập luận lôgic chặt chẽ, đầy đủ, chi tiết và rõ ràng.
* Trong mỗi bài, nếu học sinh giải sai ở bước giải trước thì cho điểm 0 đối với
những bước giải sau có liên quan. Ở câu 4 nếu học sinh không vẽ hình hoặc vẽ hình sai thì cho điểm 0.
* Điểm thành phần của mỗi bài nói chung phân chia đến 0,25 điểm. Đối với điểm
thành phần là 0,5 điểm thì tuỳ tổ giám khảo thống nhất để chiết thành từng 0,25 điểm.
* Học sinh có lời giải khác đáp án (nếu đúng) vẫn cho điểm tối đa tuỳ theo mức điểm của từng bài.
* Điểm của toàn bài là tổng (không làm tròn số) của điểm tất cả các bài. Câu Nội dung Điểm x
Viết phương trình tiếp tuyến với đồ thị C  : y  , biết rằng x 1 2,0
khoảng cách từ tâm đối xứng của đồ thị C  đến tiếp tuyến là lớn nhất.  x  Gọi 0 M x ; , x  1 
là tiếp điểm của tiếp tuyến và đồ thị C  , tiếp 0  0 x 1  0   x 
tuyến của C  tại 0 M x ;  là : 0  x 1  0  0,50 1 x y   x  x 
 x  x 1 y  x  0 () 2   0 0  0 2 2  x   0 1 x 1 0 0
Và tâm đối xứng của C  là I 1;  1 . Khi đó: 1 2 2 (2,0 điểm)
1   x 1  x 0  2 x 1 d  I; 0 0   1   x  4 1 1   x  4 1 0 0 0,50 2  1  x 1 2  0 2  x 1 0  1 2 Mà  x 1
 2  d I;  2 2  0     x 1 0  0,50 1  x  0
Dấu ‘‘=’’ xảy ra khi và chi khi
 x 1   x  2 0 1  1  0 0  x 1 x  2 0  0
Với x  0 tiếp tuyến cần tìm là: y  x 0 0,50
Với x  2 tiếp tuyến cần tìm là: y  x  4 0 x
Cho các số thực dương x, y thỏa mãn: 3 3 x  x  log
 8 y  2 y  1. 2 y 2,0
Tìm giá trị nhỏ nhất của biểu thức 3 2 4 2 2
P  x  x  4 y  y  2xy  2xy  4 . x Ta có: 3 3 x  x  log
 8 y  2 y  1 2 y 3 0,25 3
 x  x  log x  2 y
 2 y  log 2 y * 2   2     Xét hàm số: 3
f (t)  t  t  log t, t   0 , ta có: 2 1 2
f '(t)  3t  1   0, t   0 t ln 2 0,5
Do đó f (t) là hàm đồng biến trên (0; ) .
Khi đó  *   f  x   f  2 y   x  2 y . Khi đó, ta có: 3 2 4 2 2
P  x  x  4 y  y  2xy  2xy  4 3 2 4 2 3 2 0,25 2
 8 y  4 y  4 y  y  4 y  4 y  4 (2,0 điểm) 4 3 2
 4 y 12 y  9 y  4 Xét hàm số 4 3 2
P( y)  4 y 12 y  9 y  4, y   0 , ta có: 3 2
P '( y)  16 y  36 y  18y 0,25 3 3 3 2
P '( y)  0  16 y  36 y  18y  0  y  0, y  , y  4 2 Bảng biến thiên y 3 3 0  4 2 P  ' y + 0  0 + 0,5 337  64 P y 4 4
Dựa vào bảng biến thiên, ta có: 3
min P  4, khi x  3, y  0,25 x, y0 2 e a. Cho n * I  ln . x dx (n  ) I
 e  n  1 I 1,0 n 
 , chứng minh rằng: n 1   n 1 e e Ta có: n * n 1 I  ln .
x dx (n   )  I  ln  .
x dx (n  Z  ) 0,25 n  n 1   1 1 Đặt: 3 n 1  1 n (2,0 điểm) u  ln
x  du  n   1 ln . x dx 0,25 x
dv  dx  v  x e e e Khi đó: n 1  n 1 I  ln . x dx  .
x ln  x  n  1 lnn . x dx n 1      1 0,5 1 1
 e  n   1 I n  4
b. Tính tích phân sau: I  ln 1  tan x dx  1,0 0    C Đặt x 
 t  dx  dt . Đổi cận: x  0  t  , x   t  0 0,25 4 4 4   4 4     
Khi đó: I  ln 1  tan x dx  ln 1  tan  t dt      4      0 0 0,25   4 4  1  tan t   2   ln 1  dt  ln dt        1  tan t   1  tan t  0 0    4 4 4 
 ln 2dt  ln 1  tan t dt 
ln 2  ln 1  tan x dx   4  0,25 0 0 0  4 
Vậy I  ln 1  tan x dx  ln 2  0,25 8 0
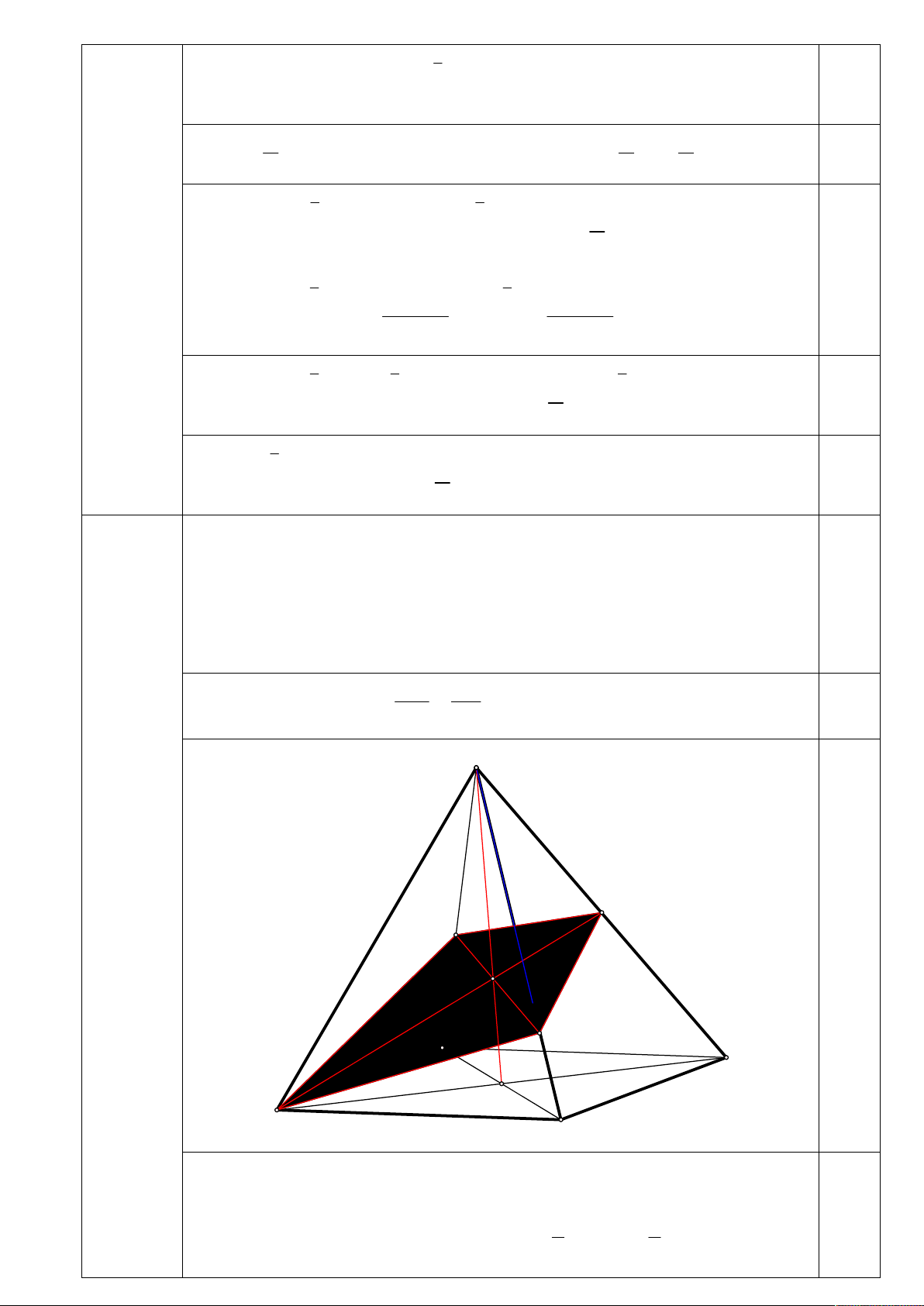
Cho hình chóp S.ABCD có đáy ABCD là một hình bình hành. Gọi
K là trung điểm của SC . Giả sử  P  là mặt phẳng đi qua hai 3,0
điểm A , K và luôn cắt các cạnh SB, SD lần lượt tại M , N ( M , N không trùng S ). SB SD a. Chứng minh rằng:   3 . SM SN 1,5 S 4 K (3,0 điểm) N 0,5 I M D C O A B
Gọi O  AC  BD, I  SO  AK . Qua I dựng đường thẳng d sao
cho d luôn cắt các cạnh SB, SD lần lượt tại M , N . 1 1 Ta có: V  V  V  V  V  V S . ADC S . ABC S . ABD S .CBD S . 2 ABCD 2 V SN SK 1 SN 1 SN SN
Khi đó: S.ANK  .  .  V  . .V  V S . ANK S . V SD SC 2 SD 2 ADC SD 4SD 0,5 S . ADC Tương tự SM SM SN V SM SN V V  V , V  . . , V  . . S . AMK 4SB S . AMN SB SD 2 S .MNK SB SD 4 Do đó: V  V  V  V  V S . AMKN S . ANK S . AMK S . AMN S .KMN SN SM SM SN V SM SN V SM SN 3V  V  V  . .  . .  . . 0.5 4SD 4SB SB SD 2 SB SD 4 SB SD 4 SB SD SM SN V    3 (Chia cả 2 vế cho . . ) SM SN SB SD 4
b. Gọi V và V theo thứ tự là thể tích của khối chóp S.AMKN và 1 V
S.ABCD . Xác định vị trí của mặt phẳng  P  để tỷ số 1 đạt giá trị V 1,5 lớn nhất. SM SN Đặt  x,
 y; 0  x, y  1 SB SD  x  y  3xy
Theo câu a ta có: V  V 
V  x  y  3xy 1 4 4 x 1  y   x  (do y  0 ) 3x  1 3 0,5 SN x 1 và y   1 
 1  2x  1  0 (do 3x  1  0 ) suy ra x  SD 3x  1 2 1 Do đó  x  1 2 2 V 3xy 3x 2 3x  1  Ta có 1  
. Đặt f (x)  ; x   ;1 V 4 4 3x  1 4 3x  1  2  0,5 2 3(3x  2x) 2
Tính được f '(x) 
; f '(x)  0  x  0; x  2 4(3x  1) 3 Bảng biến thiên: 1 2 x 1 2 3 f  ' x  0  3 3 8 8 f x 1 0,5 8
Dựa vào bảng biến thiên, ta có: V 3
 x  1  M  B
1 có giá trị lớn nhất là khi  1 SM 1 V 8 x     2 SB 2
Vậy mặt phẳng  P  trùng với mặt phẳng  ABK  hoặc mặt phẳng
 P  đi qua AK và trung điểm của SB . Cho a, ,
b c là các số thực không âm, thỏa mãn a  b  c  3 . Chứng 2 2 2 a b c 3 1,0 minh rằng:    2 2 2 b  1 c  1 a  1 2 Ta có : 2 2 +) 2 2 2 2 2
9  (a  b  c)  3(a  b  c )  a  b  c  3 2 2 +)  2 2
a  b  c    2 2 2 2 2 2
3 a b  b c  c a  0,25 a b c
 a  b  c 2 2 2 2 +)    ; , m , n p  0 m n p
m  n  p Khi đó: 2 2 2 4 4 4 a b c a b c S       2 2 2 2 b  c  a  a  2 b   2 b  2 c   2 c  2 1 1 1 1 1 a  1 5 Nên (1,0 điểm)
 a  b  c 2
 a  b  c 2 2 2 2 2 2 2 S   2 2 2 2 2 2 2 2 2
a b  b c  c a  a  b  c 1 0,25
 a  b  c 2 2 2 2 2 2 2
 a  b  c 3 Đặt 2 2 2
t  a  b  c  3 ta được: 2 t 3t S  
 f (t), t    3;  1 2 t  3 t  t 3 9 Do f '(t)   0, t    3;  2 (t  3) 0,25
suy ra hàm số đồng biến trên t    3;  3
Từ đây: S  f (t)  f (3)  2
Dấu “=” xảy ra khi và chỉ khi t  3 hay a  b  c  1 0,25