Đề thi chọn HSG tỉnh Toán 12 năm 2018 – 2019 sở GD&ĐT Quảng Bình

SỞ GD&ĐT QUẢNG BÌNH KỲ THI CHỌN HSG TỈNH NĂM HỌC 2018-2019
Khóa ngày 14 tháng 3 năm 2019 ĐỀ CHÍNH THỨC Môn thi: TOÁN
Họ tên: …………………… LỚP 12 THPT
Thời gian: 180 phút (không kể thời gian giao đề)
SBD: ………………………
Đề gồm có 01 trang
Câu 1 (2.0 điểm) a. Cho hàm số 1 y æ ö
= có đồ thị là đường cong C và điểm 5 5 I ç- ; . Viết phương x ( ) ÷ ç 6 4÷ è ø
trình đường thẳng d đi qua I và cắt (C) tại hai điểm M, N sao cho I là trung điểm của MN . b. Cho hàm số 2
y = x + x - 2x + m , với m là tham số. Tìm m để hàm số có cực đại.
Câu 2 (2.0 điểm)
a. Giải phương trình sau trên tập số thực  : 3 2
x  7x  9x 12   x  3x  2  5 x  3 x  3   1 .
b. Cho sáu thẻ, mỗi thẻ ghi một trong các số của tập E = {1;2;3;4;6; } 8 (các thẻ
khác nhau ghi các số khác nhau). Rút ngẫu nhiên ba thẻ, tính xác suất để rút được ba
thẻ ghi ba số là số đo ba cạnh của một tam giác có góc tù. t
Câu 3 (2.0 điểm). Cho tích phân I t    xsin x2 dx . 0
a. Tính I (t) khi t =p .
b. Chứng minh rằng I (t)+ I (-t)= 0, t " Î  .
Câu 4 (3.0 điểm)
Cho khối tứ diện SABC và hai điểm M, N lần lượt thuộc các cạnh SA, SB sao cho SM 1 SN = ,
= 2 . Gọi (P) là mặt phẳng đi qua hai điểm M, N và song song với đường MA 2 NB thẳng SC.
a. Trong trường hợp SABC là tứ diện đều cạnh a, xác định và tính theo a diện tích
thiết diện của khối tứ diện SABC với mặt phẳng (P).
b. Trong trường hợp bất kì, mặt phẳng (P) chia tứ diện SABC thành hai phần. Tính
tỉ số thể tích của hai phần đó.
Câu 5 (1.0 điểm)
Chứng minh rằng với mọi số nguyên dương n >1 ta luôn có: log (n+ ) 1 > log (n+2) n n 1 +
-------------------HẾT------------------- 1
LỜI GIẢI CHI TIẾT
Câu 1 (2.0 điểm). 1  5 5  a. Cho hàm số y 
có đồ thị là đường cong C và điểm I  ;   . Viết phương trình x  6 4 
đường thẳng d đi qua I và cắt C tại hai điểm M , N sao cho I là trung điểm của MN . Lời giải Cách 1:  5 5 
+ Gọi d đi qua điểm I  ; 
 và có hệ số góc k có phương trình là:  6 4   5  5
12kx 10k 15 y  k x      y  .  6  4 12
+ Xét phương trình hoành độ giao điểm của C và d : 1
12kx 10k 15 x  0     x 12 g   x 2
 12kx  10k 15 x 12  0 *
+ Đường cong C cắt d tại hai điểm M , N khi và chỉ khi phương trình * có hai
nghiệm phân biệt khác 0 . k  0     k  0 k 0     219   84 6      k 0    10k 152 2
 4.12 .k  0     1 50 .     g  0  0 1  2  0   219  84 6 k   50
+ Với k thỏa mãn  
1 , gọi x ; x lần lượt là hoành độ của hai điểm M , N , với x ; x là hai 1 2 1 2
nghiệm của phương trình * . 5  2k  3
+ Theo định lý Vi-et ta có: x  x  . 1 2 12k
+ I là trung điểm của MN khi và chỉ khi: 5  2k  3 5
x  x  2x    3
 2k  3  4k  k  (thỏa mãn   1 ). 1 2 I 12k 3 2 3 + Với k 
ta có phương trình đường thẳng d là: 3x  2y  5  0 . 2 Cách 2:  1  + M ; m  
 C , I là trung điểm của MN nên ta có:  m      5
  3m 5m  2 
N  x  x y  y   m   ; I M I M  5 5 1 2 ; 2 ;      3 2 m   3 2m   5  5m  2 3  m  0; m 
+ Vì N C suy ra    3 2m 5  3m   5m  2   5
  3m  6m  5  m  2 
 m  0;m     3  1  .  2 m 3
 m 5m2  0  3  1    1 
+ Với m  2 ta có M 2  ; ; N ;3    .  2   3  1  1   1   + Với m  ta có M ;3 ; N 2  ;    . 3  3   2   7 7  7
+ Đường thẳng d đi qua hai điểm M , nhận MN  ;   
2;3 làm vecto chỉ phương,  3 2  6
hay nhận n  3; 2 làm vecto pháp tuyến :    x   1 3 2  2 y   0  
 3x  2y  5  0.  2 
Vậy phương trình đường thẳng d cần tìm là: 3x  2y  5  0 . b. Cho hàm số 2
y  x  x  2x  m , với m là tham số. Tìm m để hàm số có cực đại. Lời giải Hàm số 2
y  x  x  2x  m . TXĐ: .
Trƣờng hợp 1: m  1 2
 x  2x  m  0 với x   . + 2 2
y  x  x  2x  m  x  x  m , hàm số này có đồ thị là một Parabol nên chỉ có cực tiểu,
suy ra m  1 không thỏa mãn.
Trƣờng hợp 2: m  1 2
x  x  m khi x   ;1
  1 m   1   1 m;    + 2
y  x  x  2x  m   . 2
x  3x  m khi x  
1 1m;1 1m
2x 1 khi x ;1
  1 m 1 1 m;   + y   .  2
 x  3 khi x  
1 1m;1 1m 1 1 1 3
+) 2x 1  0  x 
. Dễ thấy 1 1 m 
với mọi m  1 và 1 1 m   m  . 2 2 2 4 3 3 3 3 +) 2
 x  3  0  x  . Dễ thấy 1 1 m 
với mọi m  1 và  1 1 m  m  . 2 2 2 4 3 +) Với m 
, ta có bảng xét dấu của y : 4 3
Hàm số đạt cực đại tại x  . 2 3 +) Với
 m  1, ta có bảng biến thiên 4
Hàm số không có cực đại. 3 Dễ thấy khi m 
hàm số không có cực đại. 4 3
Vậy hàm số có cực đại với m  . 4
Câu 2 (2.0 điểm)
a. Giải phương trình sau trên tập số thực : 3 2
x  7x  9x 12   x  3x  2  5 x  3 x  3   1 . Lời giải Cách 1: 3 2
x  7x  9x 12   x  3x  2  5 x  3 x  3  
1 (điều kiện x  3 )  
 x  x  x    x x  x  x 4 2 4 3 3 3 2 5 3 x  3 1 x  4  0  2 
x  5x  6  5 . x
x  3 15 x  3  2
x  3x  3   x  3 1 x  4Nhan   .
 2x 8x 12 x 3  92x   1 Giải   1 :  2
x  8x 12 x  3  9  2x .
Đặt t  x  3  0 . Phương trình   1 trở thành: 5 3 2
t  2t  2t  3t  3  0 2 .
(Phân tích phương trình 2 như sau: VT   2
t  at  b  3 2
. t  ct  dt  e . Đồng nhất hệ số ). 2 
t  t   2 :  1 0 2 t  t   1  3 2
t  t  3  0   . 3 2
t  t  3  0  vo nghiem do t  0  1 5 t  Nhan 2 1 5 9  5    x  3   x  Nhan .   t     2 2 1 5 0 Loai  2  9  5 
Vậy tập nghiệm của phương trình đã cho là S  4;  .  2  
Cách 2: Điều kiện: x  3 .
Phương trình đã cho tương đương với: 2  x  x   x  x  x  4 5 6 5 3 3 2
x  3x  3    x 4 x  3 1 x  4 Nhan  2  
x  5x  6  5 x  3 x  3 2  
x  3x  3     1  x  3 1 Giải (1): 2
x  5x  6  5 x  3 x  3 2  
x  3x  3   0 x  3 1   2
x  x   x    2 3 3
3 1  x  5x  6  5 x  3 x  3  0   x   2 9 2
x  8x 12 x  3  0 3 2
 x  x  x    2 12 46 57
x  8x 12x  4  x  3  0
 x   2 x  x   2 3 9 19
x  8x 12x  4  x  3  0
 x  x   x  x   x   2 3 4 3 4 3
x  8x 12x  4  x  3  0
 x   x  x   
x  x  2 4 3 3 4 3
x  8x 12  0 
 x 3  x  4 2
 x  4 x 33 x x 3  x  0  
 3x x3x0 3 x  4     9  5 x 4 x  9  5 *Giải (2):
x  3  x  4      x  . 2 2
x  9x 19  0  2  9 5 x   2 *Giải 3 :
3 x x 3  x  0  x  3 3
 x  0 (vô nghiệm do x  3)  9  5 
Vậy phương trình đã cho có tập nghiệm S  4;  .  2  
Cách 3: Phương trình đã cho tương đương với:  x  x  4 4 2
x  3x  3   x  3x  2  5 x  3 x 3 1 x  4 Nhan   1  . 2
x  3x  3   x  3 x  2  5 x  3   1  x  3 1 Giải (1):
x  2  5 x  3 2 x  3x  3
x  2  5 x  3 2
x  3x  3   x  3   x  3 1 x  3 x  3 1 x  2 4
 5(x  4) 1 x  3  5 x  3 1    . x  4 1 x  3 1 t  t 
Xét hàm số f t  2 5 1  ,t  0 t  . 1   t  t  f t  2 t 2t 4      
, suy ra hàm số f t  2 5
1 đồng biến trên 0; . t   0, t 0 2 1 t 1 x  4    x  4     x  4 9 5 x  9  5
Suy ra x  3  x  4       2  x  . x  3   x  42 2
x  9x 19  0   2  9  5 x   2  9  5 
Vậy phương trình đã cho có tập nghiệm S  4;  .  2  
b). Cho sáu thẻ, mỗi thẻ ghi một trong các số của tập E  1;2;3;4;6; 
8 (các thẻ khác nhau
ghi các số khác nhau). Rút ngẫu nhiên ba thẻ, tính xác suất để rút được ba thẻ ghi ba số là
số đo ba cạnh của một tam giác có góc tù. Lời giải
Lấy ba thẻ từ 6 thẻ có số cách lấy là 3
C , nên số phần tử của không gian mẫu là 6 3   C  20 . 6
Gọi biến cố A : ‚rút được ba thẻ ghi ba số là số đo ba cạnh của một tam giác có góc tù‛.
Giả sử rút được bộ ba số là  ; a ;
b c , với a  b  c , do đó 4  c , nên c 4;6;  8 .
a , b , c là ba cạnh của tam giác ABC , với BC  a , CA  b , AB  c có góc C tù 2 2 2 
a  b  c cosC   0 2 2 2     a b c  2 2 2ab  
 a  b  c  a  b , với c4;6;  8 . 
4  c  a  b
4  c  a  b
+Xét c  4 thì có bộ  ;
a b  2;3 thỏa mãn.
+Xét c  6 , do a  b  c , 6  c  a  b  2b , nên b  4 và a  3. Suy ra có bộ  ; a b  3;4 thỏa mãn.
+Xét c  8 , do a  b  c , 8  c  a  b  2b , nên b  6 và a  3 hoặc a  4 . Suy ra có hai bộ
 ;ab  3;6hoặc  ;ab  4;6 thỏa mãn.
Suy ra số phần tử của biến cố A là   4 . A A 4 1
Nên xác suất cần tìm là p    .  20 5 t
Câu 3 (2.0 điểm). Cho tích phân I t   xsin x2 dx . 0
a. Tính I t khi t   . Lời giải
a. Khi t   , ta có:     1 3 1 x 1 3  1 + I   2 2 2
 x sin x dx  x 
 1cos2xdx 2  . 
x cos 2x dx    .J . 2 2 3 2 6 2 0 0 0 0    du 2 d x x 2 u   x  + Với 2
J  x cos 2x dx  . Đặt    1 .
dv  cos 2x dx v  sin 2x 0  2  du  dx 2   x 1 u   x  + Ta có J 
sin 2x  x sin 2x dx   x sin 2x dx   . Đặt 1    1  2
dv  sin 2x dx  v  cos 2x 0 0 0 1  1  2     x 1      x
J     cos 2x  cos 2x dx    1  cos 2x  sin 2x    . 2 2   2 4  2 0  0        + Vậy I   3 3 3 1 1   J   .   . 6 2 6 2 2 6 4
b. Chứng minh rằng: I t  I  t    0 Lời giải t + Xét 2 I ( t
 )  (xsin x) dx 
. Đặt x  u
 , suy ra dx  du . 0
Đổi cận: x  0  u  0 ; x  t
  u  t . t t Khi đó: I ( t  )    u  sin( u  )2 du   
xsin x2 dx. 0 0 t t Vậy 2 2
I (t)  I ( t
 )  (xsin x) dx  (xsin x) dx  0   (đpcm). 0 0
Nhận xét: Nếu làm trắc nghiệm thì có thể làm nhanh hơn. 0 t Do hàm số 2
y  (x sin x) là hàm chẵn nên ta có tính chất: 2 2
(x sin x) dx  (x sin x) dx   . t 0 t t t 0 Khi đó: 2 2
I (t)  I ( t
 )  (xsin x) dx  (xsin x) dx   2 2
 (xsin x) dx  (xsin x) dx  0   0 0 0 t
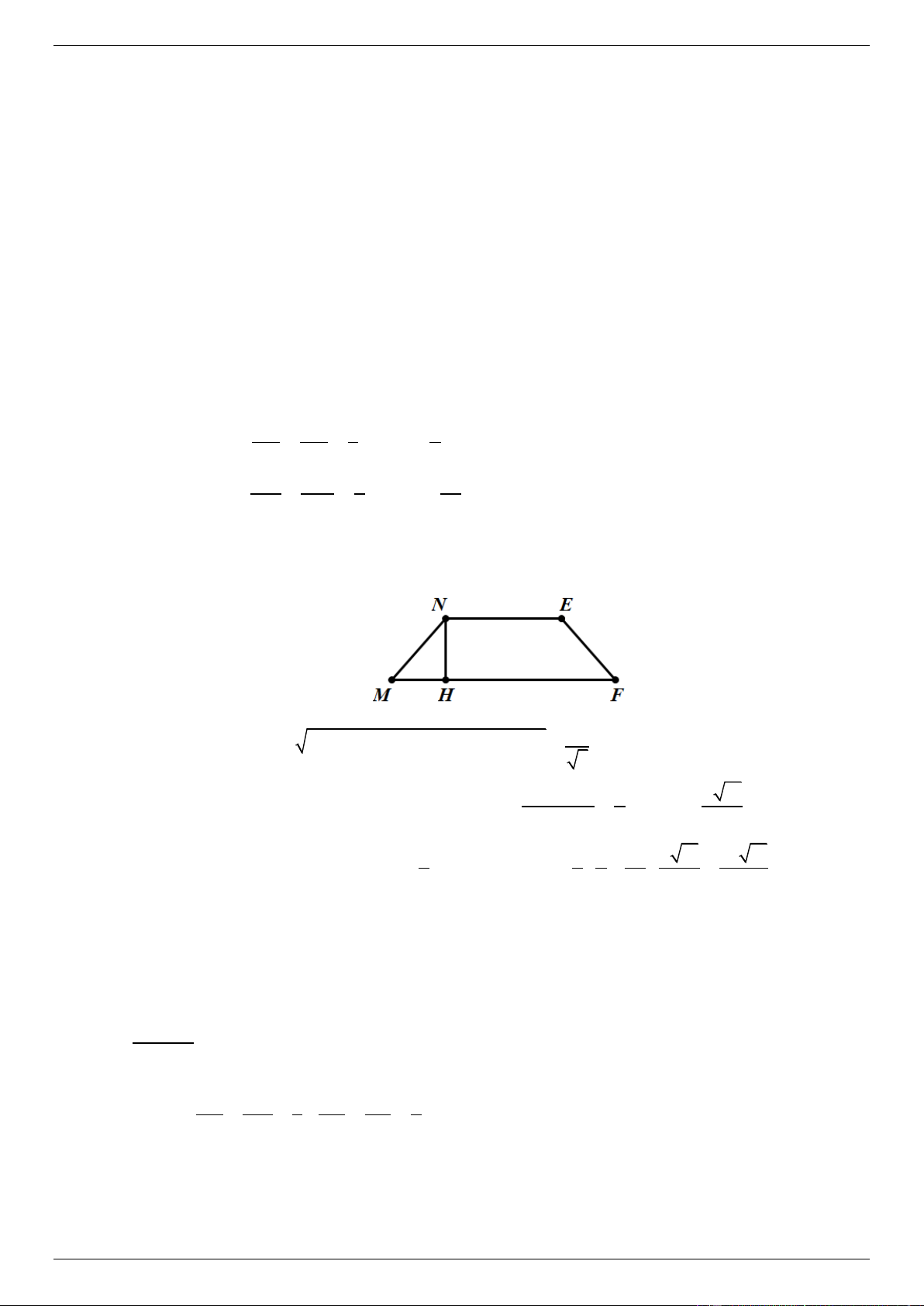
Câu 4 (3.0 điểm) Cho khối tứ diện SABC và hai điểm M , N lần lượt thuộc các cạnh SA , SB sao SM 1 SN cho  ,
 2. Gọi P là mặt phẳng đi qua hai điểm M , N và song song với MA 2 NB đường thẳng SC .
a. Trong trường hợp SABC là tứ diện đều cạnh a , xác định và tính theo a diện tích thiết
diện của khối tứ diện S.ABC với mặt phẳng P . Lời giải
*) Xác định thiết diện
SC / / P 
Ta có: SC  SAC 
 PSAC  MF MF / /SC;F  AC .
M P  SAC
SC / / P 
Ta có: SC  SBC 
 PSBC  NE NE / /SC;E BC.
N P  SBC
 Thiết diện là tứ giác MNEF . Mặt khác ta có:
+) NE / /MF / / SC . +) S  MN  CF 
E  MN  FE . NE BN 1 a +) NE / /SC     NE  . SC BS 3 3 MF AM 2 2a +) MF / /SC     MF  . SC AS 3 3
Vậy thiết diện MNEF là hình thang cân.
*) Tính diện tích thiết diện a Xét SMN có 2 2 MN 
SM  SN  2.SM .SN.cosMSN  . 3 MF  NE a a
Kẻ NH  MF, MNEF là hình thang cân  MH   11  NH  2 6 6 .  a a  a a
Vậy diện tích thiết diện là: S  NE  MF NH    . MNEF   2 1 1 2 11 11 .   2 2  3 3  6 12
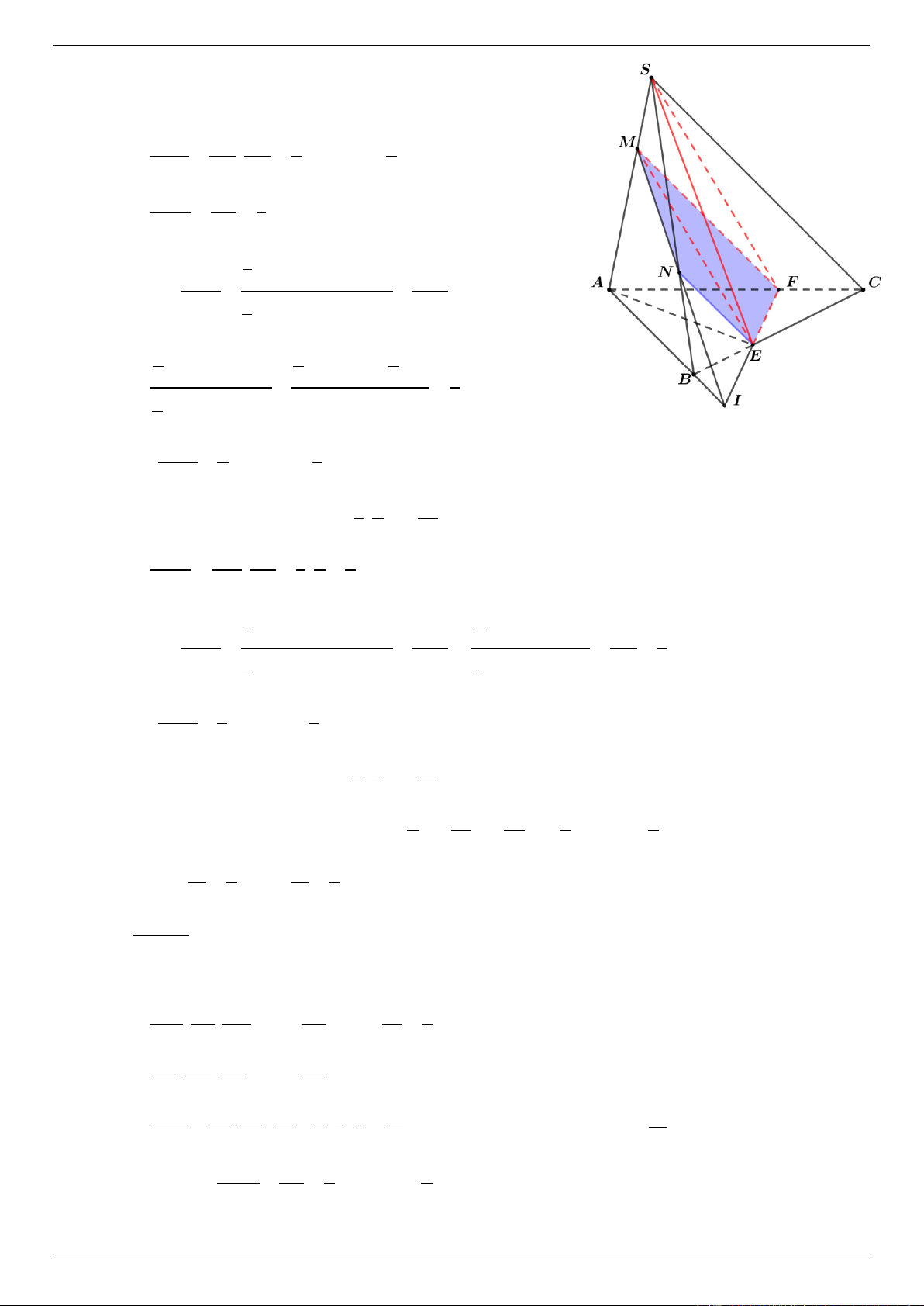
b. Trong trường hợp bất kì, mặt phẳng P chia tứ diện SABC thành hai phần. Tính tỉ số
thể tích của hai phần đó. Lời giải
Cách 1: Vì mp P đi qua M , N và song song với SC nên:
PSAC  MF,F  AC,MF / /SC; PSBC  NE,EBC,NE / /SC . CF SM 1 CE SN 2 Khi đó   ;   . CA SA 3 CB SB 3
Mặt phẳng P chia khối tứ diện SABC thành hai khối: MNEFSC và MNEFAB . + Gọi V V, V V , V V . SABC MNEFSC 1 MNEFAB 2 + Ta có V  V V V V . 1 MNEFSC CSEF SFME SMNE V CE CF 2 2 + CSEF  .   V  V . V CB CA 9 CSEF 9 CSBA V SN 1 + SFME     1 . V SA 3 SFAE
1 d S,AEF.SAEF V S + Mà SFAE 3 AEF   V 1 S SABC
d S, ABC . ABC S 3 ABC
1 d E, AF 2 .FA
d  B, AC  2 . AC 4 2 3 3    . 1 d B AC
d  B, AC .AC 9 , .AC 2 V 4 4 SFAE    V  V 2. V 9 SFAE 9 SABC 1 4 4
Từ (1) và (2) suy ra V  . V  V . SFME 3 9 27 V SM SN 1 2 2 + SMNE  .  .    3 . V SA SB 3 3 9 SABE 1 1
d S, ABE.S d  , A BE .BE ABE V S BE 1 + Mà SABE 3 ABE   2    . V 1 S 1 BC 3 SABC
d S, ABC . ABC S d  , A BC .BC 3 ABC 2 V 1 1 SABE    V  V 4. V 3 SABE 3 SABC 2 1 2
Từ (1) và (2) suy ra V  . V  V . SABE 9 3 27 2 4 2 4 5
+ Do đó V  V V V  V  V  V 
V  V  V . 1 CSEF SFME SMNE 9 27 27 9 2 9 V 4 V 5 + Vậy 1  hoặc 2  . V 5 V 4 2 1
Cách 2: Vì MF / / NE / /SC nên tứ giác MNEF là hình thang.
Gọi I  FE  MN  I  AB .
Theo định lý Mennelaus, ta có SM AI BN AI IB + . . 1  1 4   . AM BI SN BI IA 4 AB IE FC IE + . . 1
1  E là trung điểm của FI . IB FE AC FE V IB IN IE 1 1 1 1 15 + IBNE  . .  . .   V  V  V V  V . V IA IM IF 4 2 2 16 2 MNEFAB IAMF IBNE 6 IAMF IAMF V IA 4 Mặt khác IAMF   4  V  V . V BA 3 IAMF 3 BAMF BAMF 2 AM 2 + S  S ;  4  V  V . ABF 3 ABC AS 3 BAMF 9 SABC 15 4 4 5  4 V  . . V
 V  V  V . 2 16 3 9 SABC 9 1 9 V 4 V 5 + Vậy 1  hoặc 2  . V 5 V 4 2 1
Câu 5 (1.0 điểm) Chứng minh rằng với mọi số nguyên dương n  1 ta luôn có: log n   1  log n  2 n n 1    Lời giải Cách 1 log n  2 n 1    + Xét A   n n    log n  . n   log .log 2 n 1 n 1   1
+ Áp dụng bất đẳng thức AM  GM cho hai số dương log n log n  2 ta được: n 1  và n 1    log n  log n  2 log n n  2 n 1      log . n log n  2 n n   . n 1  n 1    1 1   2 2 + Mà 2 2
n  2n  n  2n 1 nên n  n  n  2 2 2 1 . log n  n    n n n n  2 2  log   2 1 logn n   2 2 1 1 1     1. 2 2 2 log n  2   log . n log n  2  1 n  1  log n  2  log n 1 n 1  n 1    1    log n  . n   n 1   n   1 C h 2
+ Với mọi số nguyên dương n  1 ta có: ln n   1 ln n  2 log n   1  log n  2   . n n 1    ln n ln n   1 ln  x   1 + Xét hàm số y  với x  1 . ln x ln x ln  x   1 
x ln x   x   1 ln  x    1 + Ta có: x 1 x y    . ln x2 x  x   1 ln x2 + Với x
  1 thì x 1  x 1; lnx  
1  ln x  0  x ln x   x   1 ln  x   1  0 .
 y  0, x  1.
Suy ra hàm số nghịch biến trên 1; .
+ Do đó với mọi số nguyên dương n  1 thì y n  y n   1 . Vậy log n   1  log n  2 . n n 1   
-------------------- HẾT --------------------
Document Outline

• de-thi-chon-hsg-tinh-toan-12-nam-2018-2019-so-gddt-quang-binh.pdf