Đề thi chọn HSG tỉnh Toán 12 năm 2020 – 2021 sở GD&ĐT Quảng Bình

SỞ GD&ĐT QUẢNG BÌNH
KỲ THI CHỌN HSG TỈNH NĂM HỌC 2020-2021
Khóa ngày 08 tháng 12 năm 2020 ĐỀ CHÍNH THỨC Môn thi: TOÁN LỚP 12 THPT
SỐ BÁO DANH:……………
Thời gian: 180 phút (không kể thời gian giao đề)
Đề gồm có 01 trang và 05 câu. Câu 1 (2,0 điểm). x  2 a. Cho hàm số y  có đồ thị (C) . Gọi ,
A B là các giao điểm của (C) với các trục tọa x 1
độ. Tìm trên (C) các điểm M có tọa độ nguyên sao cho tam giác MAB có diện tích bằng 8 (đvdt). 1 1
b. Tìm m để giá trị lớn nhất của hàm số 2 y  sin 3x  o
c s x  sinx  m bằng 1. 12 4 Câu 2 (2,0 điểm).
a. Cho dãy số u thỏa mãn 3 logu logu  logu logu 3  3 và u  u 2, n  19 1 19 1 n 1   n
với mọi n   *. Tìm n sao cho 2020 ( 2) n u  4 . x  1   2   2020  b. Cho f  x 2020  . Tính tổng S  f  f  f .       2020x  2020  2021  2021  2021 Câu 3 (2,0 điểm).
a. Cho đa giác đều A A ... A
nội tiếp đường tròn (O), chọn ngẫu nhiên 3 đỉnh bất kỳ của 1 2 2020
đa giác đó. Tính xác suất để nhận được một tam giác tù. 2 2 2 2 b. Chứng minh rằng  1 C   2 2C   3 3C  ... 2020 2020C  2 2019  2020 C . 2020 2020 2020 2020 4038 Câu 4 (3,0 điểm).
Cho tứ diện ABCD và hai điểm M, N lần lượt thuộc các cạnh AB, AC sao cho
2 AM  BM , 2CN  AN. Mặt phẳng P đi qua hai điểm M, N và song song với cạnh A , D cắt
các cạnh BD và CD lần lượt tại K và L.
a. Gọi V là thể tích của khối tứ diện ABCD . Tính thể tích khối đa diện BCMNLK theo V .
b. Giả sử tứ diện ABCD có BC  x 0  x  3, tất cả các cạnh còn lại đều bằng 1. Tìm x để
thể tích khối tứ diện ABCD đạt giá trị lớn nhất. Câu 5 (1,0 điểm).
Chứng minh rằng với mọi số nguyên dương n lớn hơn 1, ta luôn có n 1 1 1 1 n 1 ln
   .......   log . 2 2 2 3 n 2
-------------HẾT------------- SỞ GD&ĐT QUẢNG BÌNH
KỲ THI CHỌN HSG TỈNH NĂM HỌC 2020-2021
Khóa ngày 08 tháng 12 năm 2020 HƯỚNG DẪN CHẤM Môn thi: TOÁN LỚP 12 THPT
Đáp án này gồm có 06 trang YÊU CẦU CHUNG
* Đáp án chỉ trình bày một lời giải cho mỗi câu. Trong bài làm của học sinh yêu cầu phải lập
luận lôgic chặt chẽ, đầy đủ, chi tiết và rõ ràng.
* Trong mỗi câu, nếu học sinh giải sai ở bước giải trước thì cho điểm 0 đối với những bước
giải sau có liên quan. Ở câu 4 nếu học sinh không vẽ hình hoặc vẽ hình sai thì cho điểm 0.
* Điểm thành phần của mỗi câu nói chung phân chia đến 0,25 điểm. Đối với điểm thành phần
là 0,5 điểm thì tuỳ tổ giám khảo thống nhất để chiết thành từng 0,25 điểm.
* Học sinh có lời giải khác đáp án (nếu đúng) vẫn cho điểm tối đa tuỳ theo mức điểm của từng câu.
* Điểm của toàn bài là tổng (không làm tròn số) của điểm tất cả các câu. Câu Nội dung x  2 a. Cho hàm số y  có đồ thị (C) . Gọi ,
A B là các giao điểm của x 1
(C) với các trục tọa độ. Tìm trên (C) các điểm M có tọa độ nguyên sao 2,0 1
cho tam giác MAB có diện tích bằng 8 (đvdt). điểm
b. Tìm m để giá trị lớn nhất của hàm số 1 2 1 y 
sin 3x  cos x  sinx  m bằng 1. 12 4
Giao điểm của (C) với trục hoành là A(-2; 0) , với trục tung là B(0; -2) 0,25
Phương trình đường thẳng AB là x  y  2  0, AB  2 2. x  2 Gọi 0 M(x ; ) với x  1. Ta có 0 x 1 0 0 x  2 0 x   2 0,25 0 2 x 1 x  2x 0 0 0 d(M; AB) =  2 2 x 1 0 1a 2 1 1 x  2x 0 0 S  8  .A . B d(M, AB) = 8  .2 2.  8 0,25 MAB 2 2 2 x 1 0 x  2 0  2 x  4 x  6x  8  0 0 2 0 0  x  2x  8 x  1    0 0 0 2 x  10x  8  0 x  5   33 0,25 0 0 0  x  5   33 0
Vậy có hai điểm M thỏa mãn bài ra là M (2; 4), M(4; 2). 3 3 3sin x  4sin x sinx sin x 1b 2 2 y  1 sin x   m   sin x  m 1 12 4 3 0.25
Đáp án Toán 12 năm học 2020-2021 Trang 1 3 t Đặt t  sinx, t  1  ;  1 , ta có hàm số 2 y 
 t  m 1 với t  1  ;  1 3 3 t Xét 2 g(t) 
 t  m 1 với t  1  ;  1 3 t  0 2 g (
 t)  t  2t  0   t  2 (L) 1 1 g( 1
 )  m  ; g(0)  m1, g(1)  m  3 3 3 1 1 t Ta có 2 2 max
sin 3x  cos x  sinx  m  max  t  m 1 x t   1;1 12 4    3  0.25 1 1   1 
 max  m 1 , m  , m    max  m 1, m   3 3 3      1 
Đặt A   m 1 , m  , ta có các trường hợp:  3    7  A  1   ,  m  2  3 + TH1 : m 1  1     m  0   1 0.25 A  1   ,    3
Ta thấy chỉ có m  0 thỏa mãn yêu cầu bài toán.  2  1  m  A    ,1 1  3 3  +TH2: m   1     3 4   7 m     A    ,1   3  3  0.25 2
Ta thấy chỉ có m  thỏa mãn yêu cầu bài toán. 3 2 Kết luận : m  0; m = 3
a. Cho dãy số u thỏa mãn 3 logu logu  logu logu  3  3 n  19 1 19 1 và u  u 2, với mọi * n   .Tìm n ( 2) n u  n 1   n sao cho 2020 4 . x 2,0 2 b. Cho f  x 2020  . 2020x  2020 điểm  1   2   2020  Tính tổng S  f  f  f .        2021  2021  2021 u   0,u  0 Điều kiện 1 19  . logu logu 30 19 1  2a  0,25 3 a   logu logu Đặt 19 1  3 2   a b  3  . b   logu  logu 3  0 19 1  
Đáp án Toán 12 năm học 2020-2021 Trang 2
Ta được hệ phương trình a  b  3 b   3a a     1       (thỏa mãn). 0,25 3 2 a  b  3   a  1   2a 60 b2  Do u u 2
u là cấp số cộng với công sai d  2 n 1    nên  n n u u 18d u 36. 19 1 1 Với a  1 suy ra 0,25 u19 log u  logu 1  log
1  u 10u  u 36 10u  u  4. 19 1 19 1 1 1 1 u1
Số hạng tổng quát của u là u  u  n1 d  4 2 n 1  2n 2. n 1     n  Do đó 0,25 2020 2n 2  2020 ( 2) nu  4  ( 2)  4  n  4039 Kết luận : n  4039 2020 Ta có f (1 x)  0,25 2020x  2020  f (x)  f (1 x) 1 0,25 2b  1   2   2020  S  f  f  f        2021  2021  2021 0,5  1   2020  2   2 0 19  1010   1011  f  f  f  f ...  f  f 1010              2021  2021  2021  2021  2021  2021
a. Cho đa giác đều A A ... A
nội tiếp đường tròn (O). Chọn ngẫu 1 2 2020
nhiên 3 đỉnh bất kỳ của đa giác đều. Tính xác suất để nhận được một tam 2,0 3 giác tù. b. Chứng minh rằng điểm
C 2 2C 2 3C 2 ...2020C 2 1 2 3 2020 2 2019  2020 .C . 2020 2020 2020 2020 4038 Ta có 3   C 2020 0,25
Gọi A là biến cố : ‘ Chọn được 3 đỉnh từ đa giác để tạo thành tam giác tù’. Xét đường chéo A A
của đa giác đều là đường kính của đường tròn O 1 1011
ngoại tiếp đa giác đều, chia đường tròn ra làm hai phần, mỗi phần có 1009 điểm: từ A đến A và A đến A . 2 1010 1012 2020 0,25
Khi đó, mỗi tam giác có dạng A A A là tam giác tù nếu A và A cùng nằm 1 i j i j
trong nửa đường tròn O
Chọn nửa đường tròn: có 2 cách chọn 3a
Chọn hai điểm A , A là hai điểm tùy ý được lấy từ 1009 điểm A , A ,..., A i j 2 3 1010 0,25 có 2 C cách chọn. 1009
Giả sử A nằm giữa A và A thì tam giác A A A tù tại đỉnh A . i 1 j 1 i j i
Mà A A A  A A A nên kết quả bị lặp hai lần. j i 1 1 i j 2 2.C .2020
Có 2020 cách chọn đỉnh., do đó 1009 2    2020C . 0,25 A 1009 2 2 A 2020C 504 Vậy 1009 p(A)    . 3  C 673 2020
Đáp án Toán 12 năm học 2020-2021 Trang 3 Ta có k k 1
kC  nC  , với 1 k  n n n 1  1 0 C   2020C 2020 2019  2 1 2  C  2020C 2020 2019 
Áp dụng công thức trên ta có 3 2 3  C   2020C . 0,25 2020 2019
........................  2020 2019 2  020C  2020C 2020 2019 
 C 2 2C 2 3C 2 ...2020C 2 1 2 3 2020 2020 2020 2020 2020 3b 0,25 2020 . C 
2 C 2 C 2 ... C 2 2 0 1 2 2019       (1) 2019 2019 2019 2019    Ta có, hệ số chứa 2019 x
trong khai triển đa thức   x2019  x  2019 1 1 là
C 2 C 2 C 2 ...C 2 0 1 2 2019 và hệ số chứa 2019 x trong khai triển 0,25 2019 2019 2019 2019 đa thức   4038 1 x là 2019 C 4038 2 2 2 2 Do đó  0 C   1C   2 C  ... 2019 C  2019  C . (2) 2019 2019 2019 2019 4038 Từ (1) và (2) suy ra 0,25
C 2 2C 2 3C 2 ...2020C 2 1 2 3 2020 2 2019  2020 .C . 2020 2020 2020 2020 4038
Cho tứ diện ABCD và hai điểm M, N lần lượt thuộc các cạnh AB, AC
sao cho 2 AM  BM , 2CN  AN.Mặt phẳng P đi qua hai điểm M, N và song song với cạnh A ,
D cắt các cạnh BD và CD lần lượt tại K và L. 3,0 4
a. Gọi V là thể tích của khối tứ diện ABCD . Tính thể tích khối đa diện BCMNLK theo điểm V .
b. Giả sử tứ diện ABCD có BC  x 0  x  3,tất cả các cạnh còn lại
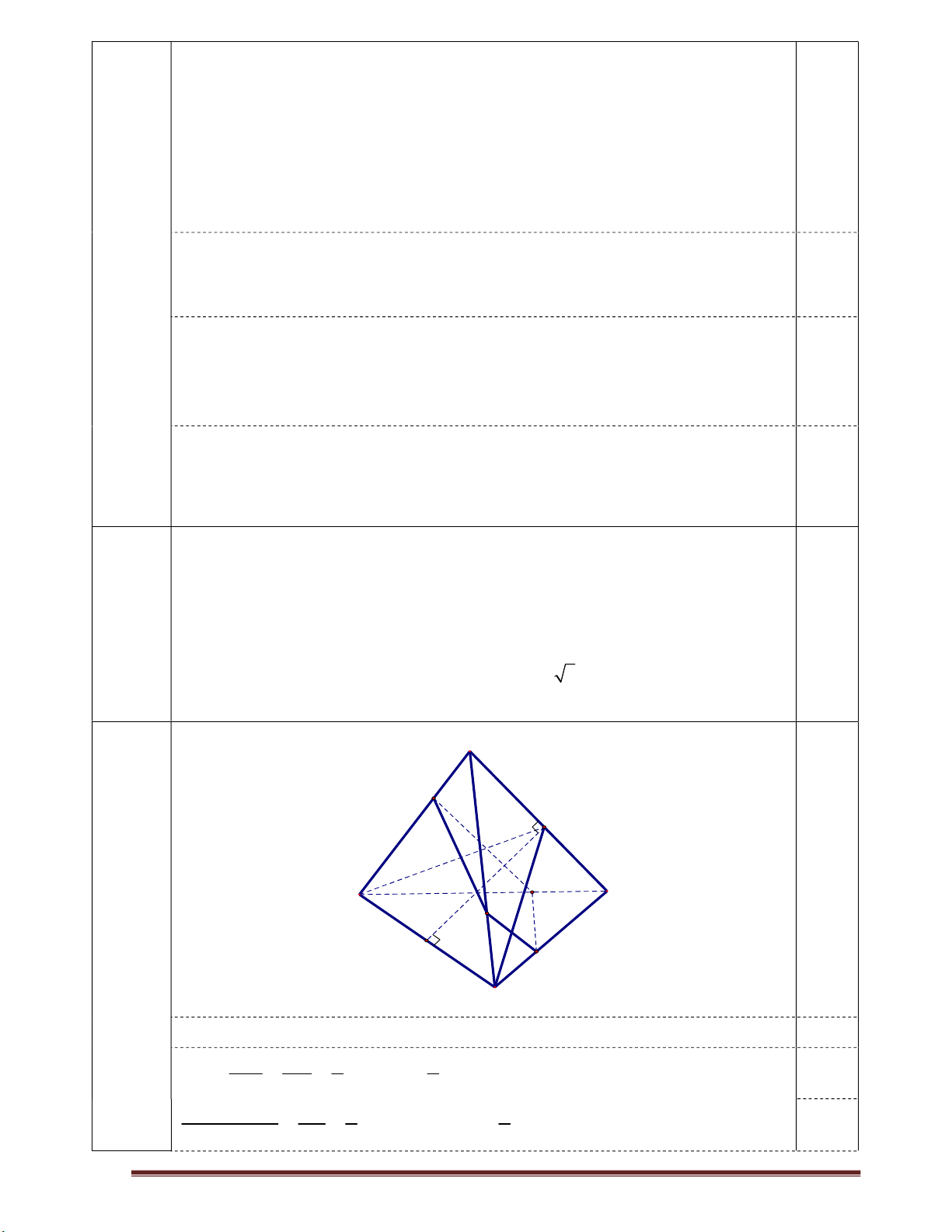
đều bằng 1.Tìm x để thể tích khối tứ diện ABCD đạt giá trị lớn nhất. A M F 0,25 B D K N 4a E L C Kẻ MK / / AD (K  B ) D , NL / / AD(L C ) D 0,25 BM BK 2 4 Ta có    S  S 0,25 BA BD 3 BMK 9 BAD d(N;(ABD)) NA 2 2 
  d(N;(ABD))  d(C;(ABD)) 0,25 d(C;(ABD)) CA 3 3
Đáp án Toán 12 năm học 2020-2021 Trang 4 8 Suy ra V  V N .BMK 27 1
Tương tự, ta có d(N;(BCD))  d(A;(BCD)) 3 0,25 DK 1 DL 2 Từ  ,  DB 3 DC 3 2 7  S  S  S  S DKL 0,25 9 DBC BCLK 9 DBC 7 Suy ra V  V N .BCLK 27 0,25 15 5 Do đó V  V V  V  V BCMNLK N .BMK N .BCLK 27 9
Gọi E, F lần lượt là trung điểm của BC và AD 0,25
Ta có EF  BC, EF  AD và AD  (FBC)
Tam giác FBC cân tại F nên 2 2 2 2  2 2 BC 2 AD BC 3 x EF  BF   AB    4 4 4 4 0,25 2 3  x suy ra EF  2 4b 1 1 Do đó 2 V  A . D S  . x 3  x ABCD 0,25 3 FBC 12 2 2 x  3  x 1   0,25 24 8 6
Đẳng thức xảy ra khi và chỉ khi x  . 2 0,25 6 Kết luận : x  . 2
Chứng minh rằng với mọi số nguyên dương n lớn hơn 1, ta luôn có 1,0 5 n 1 1 1 1 n 1 ln    .......  log . điểm 2 2 2 3 n 2
Theo bất đẳng thức Cauchy với k  2, k  N:     k  k 2 1 1 .... 1 1 2  2.1.1......1   k   
(Dấu bằng không xảy ra). k k k 1  so 1 3 Do đó: 2  2 0,25 4 3 2  3 ............. n  n 1 2  n n  n 3 4 5 1
Nhân vế theo vế các bất đẳng thức ta có: 3 4 2. 2. 2..... 2  . . ...... 0,25 2 3 4 n
Đáp án Toán 12 năm học 2020-2021 Trang 5 1 1 1  ....... n 1 Hay 2 3 2 n 
, logarit cơ số 2 hai vế ta có : 2 1 1 1 n 1   .......  log ĐPCM 2   2 3 n 2
+ Trước hết ta chứng minh bất đẳng thức với x  0, thì ln(x 1)  x 1 x
Thật vậy, xét hàm số f (x)  ln(x 1)  x , có f (  x)  1   0 với x 1 x 1 x  0 . Do đó f ( )
x nghịch biến nên với x  0 thì f (x)  f(0)  0. Do đó ln(x 1)  . x
+ Áp dụng bất đẳng thức trên ta có : 1 1 0,25 ln(1 )  2 2 1 1 ln(1 )  3 3 .................... 1 1 ln(1 )  n n Cộng vế theo vế ta có: 1 1 1 1 1 1
ln(1 ) + ln(1 ) +…..+ ln(1 ) <   .......  2 3 n 2 3 n 1 1 1 1 1 1
 ln(1 )(1 )......(1 )    ....... 2 3 n 2 3 n 0,25 3 4 n 1 1 1 1  ln( . ...... )    .......  2 3 n 2 3 n n 1 1 1 1  ln    ....... Đ C P M  2 2 3 n
Đáp án Toán 12 năm học 2020-2021 Trang 6
Document Outline

• de
• da