Đề thi chọn HSG tỉnh Toán 12 năm 2020 – 2021 sở GD&ĐT Thừa Thiên Huế

NHÓM TOÁN VDC&HSG THPT
ĐỀ THI HỌC SINH GIỎI 2020 - 2021
ĐỀ THI HỌC SINH GIỎI – THỪA THIÊN HUẾ
NĂM HỌC 2020 – 2021 Môn: Toán 12
HỌC HỎI - CHIA SẺ KIẾN THỨC
Thời gian: 180 phút (Không kể thời gian phát đề)
LINK NHÓM: ht ps://www.facebook.com/groups/1916660125164699 Câu 1. (4,0 điểm) Cho hàm số 3 2
y = f (x) = x + 3x + mx − 3 (1) có đồ thị (C m) , m là tham số.
a) Tìm giá trị của m để hàm số y = f (x) (1) có hai điểm cực trị âm.
b) Tìm các giá trị của tham số m để đường thẳng d : y = x − m cắt đồ thị (Cm ) tại ba điểm
phân biệt có hoành độ lần lượt là x x x
1 , 2 , 3 sao cho biểu thức 2 2 2 2 2 2
T = x + x + x + 4x x x − 7 1 2 3 1 2 3
đạt giá trị nhỏ nhất. Câu 2. (4,0 điểm)
1. Giải phương trình lượng giác (sin x + cos x)2 2 − 2sin x 2   π   π  = sin − x − sin −    3x 2 1 cot x 2  4 4  +     2   4(1+ 1+ 4 1 x x )
2. Giải phương trình  −  = .   2  x x +1
x + x + 3x + 2 +1 Câu 3. (4,0 điểm) 3 9
 y + y = x 3x −  1 ( ) 1
1. Giải hệ phương trình:  . 2
 9y + 7 + 3x + 6 = 8  (2)
2. Gọi S là tập hợp các số tự nhiên có 4 chữ số đôi một khác nhau được lập từ các chữ số
0,1,2,3,4,5 . Chọn ngẫu nhiên một số từ tập S . Tính xác suất để số được chọn là một số chẵn. Câu 4. (3,0 điểm)
Cho phương trình (2 + 3)16x − (4 − 2)4x m m + 3m − 8 = 0 ( )
1 , m là tham số thực.
a) Giải phương trình khi m = 3 .
b) Tìm các giá trị của tham số m để phương trình ( )
1 có hai nghiệm trái dấu. Câu 5. (3,0 điểm)
Cho hình chóp S.ABCD có cạnh SA = x , tất cả các cạnh còn lại có độ dài bằng 1. Gọi H là
hình chiếu của S lên mặt phẳng đáy ABCD .
a) Chứng minh rằng SA ⊥ SC .
b) Tính diện tích đáy ABCD theo x của hình chóp S.ABCD .
c) Xác định x để khối chóp S.ABCD có thể tích lớn nhất. Tính giá trị thể tích lớn nhất đó. Câu 6. (3,0 điểm)
TÀI LIỆU ÔN THI HỌC SINH GIỎI Trang 1
NHÓM TOÁN VDC&HSG THPT
ĐỀ THI HỌC SINH GIỎI 2020 - 2021 Cho 2 2
2x + y − 2xy =1. Tìm giá trị lớn nhất của biểu thức f (x y) 4 4 2 2
, = 4x + y − 2x y + 2018.
------------------------HẾT------------------------ Trang 2
TÀI LIỆU ÔN THU THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT
ĐỀ THI HỌC SINH GIỎI 2020 - 2021 HƯỚNG DẪN GIẢI Câu 1. (4,0 điểm)
Cho hàm số y = f ( x) 3 2
= x + 3x + mx − 3 ( )
1 có đồ thị (C m ), m là tham số.
a) Tìm giá trị của m để hàm số y = f (x) ( )
1 có hai điểm cực trị âm.
b) Tìm các giá trị của tham số m để đường thẳng d : y = x − m cắt đồ thị (Cm ) tại ba điểm
phân biệt có hoành độ lần lượt là x x x
1 , 2 , 3 sao cho biểu thức 2 2 2 2 2 2
T = x + x + x + 4x x x − 7 1 2 3 1 2 3
đạt giá trị nhỏ nhất. Lời giải a)
 Ta có: f ′( x) 2
= 3x + 6x + m
 Để hàm số y = f ( x) có hai điểm cực trị âm thì phương trình f ′( x) = 0 có hai nghiệm âm phân biệt 2
⇔ 3x + 6x + m = 0 có hai nghiệm âm phân biệt ∆ ' > 0 9  − 3m > 0  
⇔ S < 0 ⇔  2 − < 0 ⇔ 0 < m < 3. P > 0   m > 0
b) Xét phương trình hoành độ giao điểm: 3 2 3 2
x + 3x + mx −3= x − m ⇔ x + 3x − x(1− m) −3+ m = 0 . x = 1 − ⇔  2x .
+ 2x − 3 + m = 0  (*)
 Để đường thẳng d : y = x − m cắt đồ thị (Cm ) tại ba điểm phân biệt có hoành độ lần lượt là x x x
1 , 2 , 3 thì phương trình (*) có hai nghiệm phân biệt khác 1
− . Điều này tương đương với:
∆′ = 1+ 3 − m = 4 − m > 0 m < 4  ⇔  ⇔ m < 4 . 1
 − 2 − 3 + m ≠ 0 m ≠ 4  Khi đó: x = 1 − x + x = 2 − x x = 3 − + m 1 ; 2 3 ; 2 3 . 2 2 2 2 2 2
T = x + x + x + 4x x x − 7 = 1+ x + x − 2x x + 4 x x − 7 1 2 3 1 2 3 ( 2 3 )2 2 3 ( 2 3 )2 2  
= + (− )2 − (m − ) + (m − )2 2 13 9 9 1 2 2 3 4
3 − 7 = 4m − 26m + 40 = 4 m − − ≥ −  . 4    4 4 9 13  Vậy T = − m = min khi
( thỏa mãn điều kiện của m ). 4 4 Câu 2. (4,0 điểm)
1. Giải phương trình lượng giác (sin x + cos x)2 2 − 2sin x 2   π   π  = sin − x − sin −    3x 2 1 cot x 2  4 4  +     2   4(1+ 1+ 4 1 x x )
2. Giải phương trình  −  = .   2  x x +1
x + x + 3x + 2 +1 Lời giải 1.
TÀI LIỆU ÔN THI HỌC SINH GIỎI Trang 3
NHÓM TOÁN VDC&HSG THPT
ĐỀ THI HỌC SINH GIỎI 2020 - 2021
 ĐKXĐ: x ≠ kπ , k ∈ . (sin x + cos x)2 2 − 2sin x 2   π   π   Phương trình: = sin − x − sin −    3x 2 1 cot x 2  4 4  +     π π π π 2 − x + − 3x − x − + 3 1+ sin 2 − 2sin 2 x x x 4 4 4 4 ⇔ = .2cos .sin 1 2 2 2 2 sin x ( x x)  π 2 cos 2 sin 2 .sin x 2 cos 2  ⇔ + = −  x.sin x  4   π   π 2 2 cos 2x .sin x 2 cos 2  ⇔ − = −    x.sin x  4   4   π 2 cos 2  ⇔
− x .sin x(sin x − ) 1 =   0  4    π cos −  2x =  0  π π 4 x = − − m     8 2  ⇔ sin x = 0 ⇔ x = nπ ( , m , n p ∈). sin x 1 0  − = π  x = + p2π    2
Đối chiếu với đkxđ của phương trình ta có nghiệm của phương trình là: π π π
x = − − m ; x = + p2π với , m p ∈ . 8 2 2 2.
 Điều kiện: x > 0.
 Phương trình đã cho tương đương với 4 1 (1+ 1+4x) x +1+ (x + ) 1 (x + 2) = ⇔
= 4x + 4x 1+ 4x x(x + )2 1
x + x + 3x + 2 +1 (x + )2 2 1 1 1 x + 2 1 1 1 ⇔ +
= 4x + 4x 1+ 4x ⇔ + 1+
= 4x + 4x 1+ 4x (*).
x +1 x +1 x +1 x +1 x +1 x +1
 Xét hàm số f (t) = t + t 1+ t với t > 0, ta có ′( ) =1+ 1 t f t + t + > 0, t ∀ > 0 2 1+ t
Suy ra hàm số f (t) luôn đồng biến trên (0;+∞)  1  1 1 − ± 2  Từ (*) suy ra f = f (4x) 2 ⇔
= 4x ⇔ 4x + 4x −1 = 0 ⇔ x =   .  x +1 x +1 2
Kết hợp với điều kiện, ta nhận 1 2 x − + = . 2 − + 
 Vậy tập nghiệm của phương trình đã cho là 1 2 S =  .  2   Câu 3. (4,0 điểm) 3 9
 y + y = x 3x −  1 ( ) 1
1. Giải hệ phương trình:  . 2
 9y + 7 + 3x + 6 = 8  (2) Trang 4
TÀI LIỆU ÔN THU THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT
ĐỀ THI HỌC SINH GIỎI 2020 - 2021
2. Gọi S là tập hợp các số tự nhiên có 4 chữ số đôi một khác nhau được lập từ các chữ số
0,1,2,3,4,5 . Chọn ngẫu nhiên một số từ tập S . Tính xác suất để số được chọn là một số chẵn. Lời giải 1.  Điều kiện: 1 x ≥ . 3  Ta có: ( ) 3
1 ⇔ 27y + 3y = 3x 3x −1 ⇔ ( y) + y = ( x − )3 3 3 3 3 1 + 3x −1 .  Xét hàm số : ( ) 3
f x = x + x , có f ′(x) 2
= 3x +1 > 0, x
∀ ∈  ⇒ f (x) đồng biến trên  . ( )
1 ⇔ f (3y) = f ( 3x −1) ⇔ 3y = 3x −1 .
(2) ⇔ 3x + 6 + 3x + 6 = 8 ⇔ 3x + 6 = 4 ⇔ 3x + 6 =16 10 ⇔ x = . 3 Với 10 x = ⇒ y =1. 3  
 Vậy hệ có nghiệm duy nhất ( x y) 10 ; =  ;1 . 3    2.
 Số các số tự nhiên có 4 chữ số đôi một khác nhau được lập từ các chữ số 0,1, 2,3, 4,5 là 5.5.4.3 = 300.
 Số các số tự nhiên chẵn có 4 chữ số đôi một khác nhau được lập từ các chữ số 0,1, 2,3, 4,5 là 3 A + 2.4.4.3 =156. 5
Vậy xác suất để số được chọn là số chẵn là 156 13 = . 300 25 Câu 4. (3,0 điểm)
Cho phương trình (2 + 3)16x − (4 − 2)4x m m + 3m − 8 = 0 ( )
1 , m là tham số thực.
a) Giải phương trình khi m = 3 .
b) Tìm các giá trị của tham số m để phương trình ( )
1 có hai nghiệm trái dấu. Lời giải
a) Với m = 3 , phương trình ( ) 1 trở thành 4x =1 x = 0 9.16x 10.4x 1 0   − + = ⇔ ⇔  . x 1 1 4 = x = log = −log 3 4 2  9  9 b)  Đặt 4x
t = , phương trình ( )
1 trở thành ( m + ) 2 2
3 t − (4m − 2)t + 3m −8 = 0 (2) .
 Phương trình (1) có hai nghiệm trái dấu khi phương trình (2) có hai nghiệm t ,t thỏa 1 2
mãn 0 < t <1< t . 1 2 3 − t − 2t + 8
 Ta có (2) ⇔ m(2t − 4t + 3) 2 2 2
+ 3t + 2t − 8 = 0 ⇔ m = . 2 2t − 4t + 3
TÀI LIỆU ÔN THI HỌC SINH GIỎI Trang 5
NHÓM TOÁN VDC&HSG THPT
ĐỀ THI HỌC SINH GIỎI 2020 - 2021 2 3 − t − 2t + 8
 Xét hàm số f (t) = với t ∈(0;+∞) . 2 2t − 4t + 3 2 16t − 50t + 26
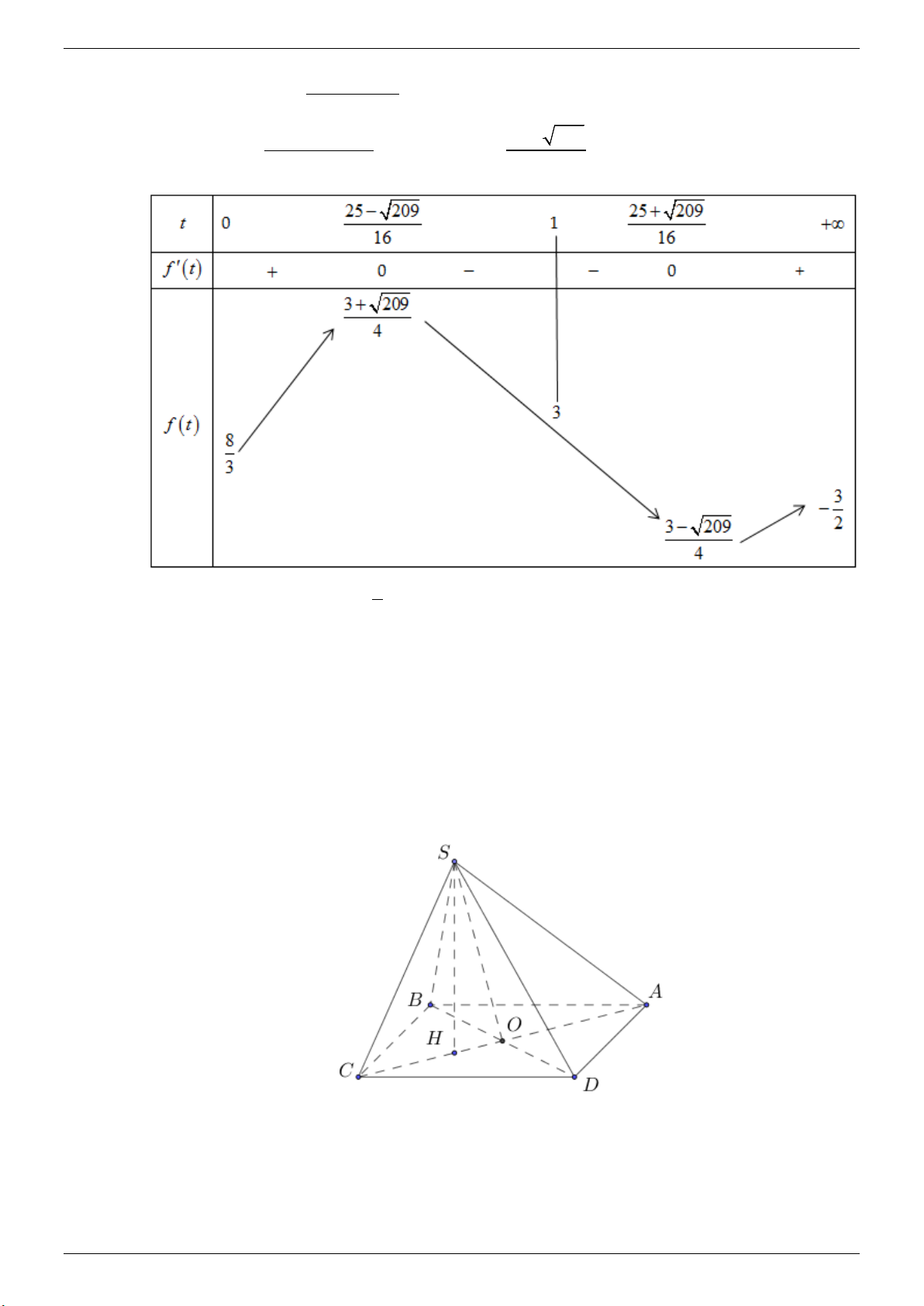
 Ta có f ′(t) = ( , f (t) 25 209 0 t ± ′ = ⇔ = . Bảng biến thiên 2t − 4t + 3)2 2 16
 Từ bảng biến thiên, suy ra 8 < m < 3. 3 Câu 4. (3,0 điểm)
Cho hình chóp S.ABCD có cạnh SA = x , tất cả các cạnh còn lại có độ dài bằng 1. Gọi H là
hình chiếu của S lên mặt phẳng đáy ABCD .
a) Chứng minh rằng SA ⊥ SC .
b) Tính diện tích đáy ABCD theo x của hình chóp S.ABCD .
c) Xác định x để khối chóp S.ABCD có thể tích lớn nhất. Tính giá trị thể tích lớn nhất đó. Lời giải
a) Chứng minh rằng SA ⊥ SC .
 Gọi O = AC ∩ BD .
 Ta có AB = AD = CB = CD = SB = SD = 1 ⇒ C ∆ BD = S ∆ BD = A ∆ BD (c.c.c.)
 Mà O là trung điểm của BD ⇒ OC = OS = OA ⇒ S
∆ AC vuông tại S hay SA ⊥ SC (đpcm). Trang 6
TÀI LIỆU ÔN THU THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT
ĐỀ THI HỌC SINH GIỎI 2020 - 2021
b) Tính diện tích đáy ABCD theo x của hình chóp S.ABCD .
 Tam giác SAC vuông tại 2 2 2
S ⇒ AC = SA + SC = x +1 .
 Ta có ABCD là hình thoi ⇒ AC ⊥ BD ⇒ OC ⊥ OD 2 2 x x
 Tam giác OCD vuông tại 2 2 1 3 O OD CD OC + − ⇒ = − = 1− = (với 4 2 1 OC = AC ) 2 2
⇒ BD = 2OD = 3− x . 1 1  Vậy S = AC BD = x +
− x (với 0 < x < 3 ). ABCD . ( 2 )1( 2 3 ) 2 2
c) Xác định x để khối chóp S.ABCD có thể tích lớn nhất. Tính giá trị thể tích lớn nhất đó.
 Gọi H là tâm đường tròn ngoại tiếp tam giác BCD ⇒ H ∈ AC .
 Vì SB = SC = SD = 1⇒ SH ⊥ ( ABCD) . . SA SC x
 Tam giác SAC vuông tại S ⇒ SH = = . 2 AC x +1 1 1 2 1 2 ⇒ V = S
SH = x − x = x − x ≤ . S ABCD ABCD ( 2 1 . 3 3 . ) 3 6 6 4
 Dấu bằng xảy ra khi và chỉ khi 2 2 6
x = 3− x ⇔ x = . 2  Vậy 6 x =
thì thể tích khối chóp S.ABCD đạt giá trị lớn nhất bằng 1 . 2 4 Câu 6. (3,0 điểm) Cho 2 2
2x + y − 2xy =1. Tìm giá trị lớn nhất của biểu thức f (x y) 4 4 2 2
, = 4x + y − 2x y + 2018. Lời giải  Ta có :
x + y − xy = ⇔ ( x + y − xy)2 2 2 2 2 4 4 2 2 2 2 3 3 2 2 1 2 2
= 1 ⇔ 4x + y + 4x y + 4x y −8x y − 4xy =1 4 4 2 2
⇔ x + y + x y − xy ( 2 2 x + y ) 4 4 2 2 4 8 4 2
= 1 ⇔ 4x + y + 8x y − 4xy (1+ 2xy) =1 4 4 4 4
⇔ 4x + y − 4xy =1 ⇔ 4x + y =1+ 4xy .
 Thay vào biểu thức f ( x y) 4 4 2 2
, = 4x + y − 2x y + 2018 ta có: f (x y) 2 2 , = 2
− x y + 4xy + 2019 = 2 − (xy − )2 1 + 2021.
 Vậy f ( x, y) ≤ 2021 với mọi x, y ∈  .
TÀI LIỆU ÔN THI HỌC SINH GIỎI Trang 7
NHÓM TOÁN VDC&HSG THPT
ĐỀ THI HỌC SINH GIỎI 2020 - 2021  1 xy =1 y =   1  y =  Dấu bằng xảy ra khi x  ⇔ ⇔  x 2 2 
2x + y − 2xy = 1  2 1 2x + − 3 = 0  4 2
2x − 3x +1 = 0 2  x x =1  y = 1 x = 1 −  1  y =  = −  y 1 x     2 ⇔  2
x =1 ⇔ x =   2   2 1 x =   y = 2  2   2 x = −  2  y = − 2
 Vậy giá trị lớn nhất của f ( ; x y) bằng 2021 khi (      x y) (  ) ( ) 2 2 ; 1;1 ; 1; 1 ; ; 2 ; ; 2  ∈ − − − −  . 2 2          
------------------------HẾT------------------------ Trang 8
TÀI LIỆU ÔN THU THPT QUỐC GIA
Document Outline

• de-thi-chon-hsg-tinh-toan-12-nam-2020-2021-so-gddt-thua-thien-hue
• TOÁN-VDC&-HSG3-HSG-TOÁN-12-THỪA-THIÊN-HUẾ-2020-2021-HOÀN-THIỆN