Đề thi chọn HSG tỉnh Toán 12 năm học 2017 – 2018 sở GD và ĐT Hải Dương

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KÌ THI CHỌN HỌC SINH GIỎI TỈNH HẢI DƯƠNG
LỚP 12 THPT NĂM HỌC 2017 – 2018 MÔN THI : TOÁN
Thời gian làm bài: 180 phút
(Đề thi gồm 01 trang) Câu 1 (2 điểm) x 1 1. Cho hàm số y =
có đồ thị là (C). Viết phương trình tiếp tuyến của x +1
đồ thị (C) sao cho khoảng cách từ tâm đối xứng của (C) đến tiếp tuyến là lớn nhất.
2. Tìm m để phương trình sau có nghiệm thực ; 1 1 1 4 2 x   (x  )  x   m 4 2 x x x Câu 2 (2 điểm) 2 1. Giải phương trình: 2017 2018 x sin x  cos x   cos x . 2 20  6 x 1
 7 5 y 3x 6 x 3y 5 y  0   1
2. Giải hệ phương trình:   ,x y   2 2
 2x y 5 3 3x2y 11  x 6x13   2 Câu 3 (2 điểm)
1. Môn bóng đá nam SE GAME có 10 đội bóng tham dự trong đó có Việt
Nam và Thái Lan. Chia 10 đội bóng này thành 2 bảng A, B. Mỗi bảng có 5 đội.
Tính xác suất sao cho Việt Nam và Thái Lan ở cùng một bảng. 2. 6  2 Cho d·y sè (u u  
n) tho¶ m·n ®iÒu kiÖn: , u
2  u víi mäi n=1, 2, .... 1 2 n1 n
Chøng minh r»ng d·y sè (u n 
n) cã giíi h¹n vμ t×m Lim 2 . 2 u . n Câu 4 (3 điểm)
1. Cho tứ diện ABCD có AB  CD  ,
c AC  BD  ,
b AD  BC  a .
a.Tính góc giữa hai đường thẳng AB, CD.
b.Chứng minh rằng trọng tâm của tứ diện ABCD cách đều tất cả các mặt của tứ diện.
2. Cho hình chóp S.ABCD có SA = x , tất cả các cạnh còn lại có độ dài bằng 1. Tính
thể tích khối chóp đó theo x và tìm x để thể tích đó là lớn nhất.
Câu 5 (1 điểm). Cho các số thực a, b, c sao cho a  0, b  0, 0  c  1
và a2 + b2 + c2 = 3. Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức sau: P = 2ab + 3bc + 3ca + 6
a  b  c
…………………Hết………………….
Họ và tên thí sinh:………………Số báo danh:…………………………
Chữ ký của giám thị 1:…………Chữ ký của giám thị 2:………………
ĐÁP ÁN VÀ HƯỚNG DẪN CHẤM MÔN TOÁN
KÌ THI CHỌN HỌC SINH GIỎI TỈNH
LỚP 12 THPT NĂM HỌC 2017 – 2018 Câu Ý Nội dung Điểm
Viết phương trình tiếp tuyến của đồ thị (C) sao cho khoảng cách từ I
1 tâm đối xứng của (C) đến tiếp tuyến là lớn nhất. 1,00
Tâm đối xứng của đồ thị là I(–1; 1)
Gọi N(x0,y0) là tiếp điểm của tiếp tuyến và đồ thị, khi đó tiếp
tuyến của (C) tại M có phương trình: 0,25   x  1  2 x 1 y  x  x    2  0  0 x  1 x 1 2 2
2x  (x 1) y  x  2x 1  0 0  0 0 0 0
Gọi d là khoảng cách từ I đến tiếp tuyến trên ta có: 4 x 1 0 d  ; x  1  , 0 4 4  (x 1) 0,25 0
Áp dụng bất đẳng thức côsi ta có 4 4 2
4  (x 1)  2 4.(x 1)  4(x 1) 0 0 0 4
 4  (x 1)  2 x 1 0 0 4 x 1 0  d   2 0,25 4 4  (x 1) 0 x  1   2 dấu '=" 4 0
 4  (x 1)   0 x  1   2  0
Vậy ứng với hai giá trị đó ta có hai tiếp tuyến sau: y  x  (2  2) ;
y  x  (2  2) ; 0,25
Tìm m để phương trình sau có nghiệm thực ; 2 1 1 1 4 2 x   (x  )  x   m 1,00 4 2 x x x ĐK: x  0 Đặt t= 1
x  ( ĐK t  2 ) x 2 1  1 2  2 x   x   2  t  2 2   x  x  Ta có 2  1   1 4 2  4 2 x   x 
 2  t  4t  2  4   2   x   x  0,25
Phương trình đã cho trở thành: 4 2
t  t    2 4 2
t  2  t  m 4 2
 t  5t  t  4  m Xét hàm số 4 2
f (t)  t  5t  t  4 với t  ;  2  2; 0,25 ta có 3
f '(t)  4t 10t 1 2
f '(t) 12t 10  0 t  ;  2  2; t  -2 2  f ''(t) + -11  f '(t)  13   0,25 f (t) -2 2
Từ bảng biến thiên suy ra: m  2
 thì phương trình đã cho có nghiệm. 0,25 2 II
1 Giải phương trình: 2017 2018 x sin x  cos x   cos x . 1,00 2 2 x Xét hàm số: f(x)=  cos x trên R 2 Ta có f '(x)  x  sin x f '(x)  1 cos x  0 x   R
Do đó hàm số f'(x) đồng biến trên R Vậy x
 0;  f '(x)  f '(0)  0 0,25 x   ;
 0  f '(x)  f '(0)  0 Bảng biến thiên: x  0  f'(x) - 0 + f(x) 1 2 x
Từ bảng biến thiên suy ra VF   cos x 1 x  R 2 0,25 Ta có 2017 2018 2 2 VT  sin x  cos x  sin x  cos x  1
Do đó phương trình (*) tương đương 0,25 x  0 VT  1  2017 2   sin  x  sin x  x  0 0,25 VF  1  2018 2 cos x  cos x 
Giải hệ phương trình :
2 20 6 x 17 5 y 3x 6 x 3y 5 y  0   1 1,00 
x, y 2
2 2x  y  5  3 3x  2y 11  x  6x 13  2
Điều kiện: x  6; y  5;2x  y  5  0; 3x  2y 11 0
203x 6 x  17 3y 5 y
 36  x  2 6  x  35 y  2 5 y 3 0,25
Xét hàm số f t   3t  2 t với t  0 , ta có t  f t 3 2 '  3 t   0, t   0 0,25 2 t
Kết hợp với 3 ta có f 6  x  f 5  y  6  x  5  y  y  x 1
Thay vào phương trình 2 của hệ, ta được 4 2
2 3x  4  3 5x  9  x  6x 13 , với x   . 3
 2 3x  4 x  23 5x 9 x 3 2  x  x 2
 xx   1 3
 xx   1 2    x  x
3x  4   x  2
5x  9   x  3 0,25  
 xx   2 3 1       x x  x x  1 0 3 4 2 5 9 3           2 3 x  0; x  1  (vì 
  với mọi x thuộc
x    x  
x    x   1 1 3 4 2 5 9 3 TXĐ)
Với x  0  y  1  Với x  1   y  2 
Thử lại ta thấy nghiệm của hệ phương trình đã cho là 0,25
x; y 0; 1;1;2 III 1 1,00 n 5 5  C .C 10 5
Gọi A là biến cố: “ Việt Nam và Thái Lan ở cùng một bảng” 0,25
TH 1: “ Việt Nam và Thái Lan ở cùng một bảng A” Trường hợp này có 2 3 5
C .C .C cách chia. 2 8 5 0,25
TH 1: “ Việt Nam và Thái Lan ở cùng một bảng B”
Trường hợp này có 2 3 5
C .C .C cách chia. 2 8 5
Suy ra: n A 2 3 5
 2C .C .C 2 8 5 0,25 2 3 5 n( ) A 2C .C .C 4 2 8 5 P( ) A    0,25 5 5 n() C .C 9 10 5 2 1,00     5  Ta cã u  2 sin 1    2cos  . 12   12  0,25
Tõ hÖ thøc truy håi b»ng ph¬ng ph¸p chøng minh quy n¹p ta cã ®îc 0,25  5  u  2cos n   , n = 1, 2,....  n 6.2 
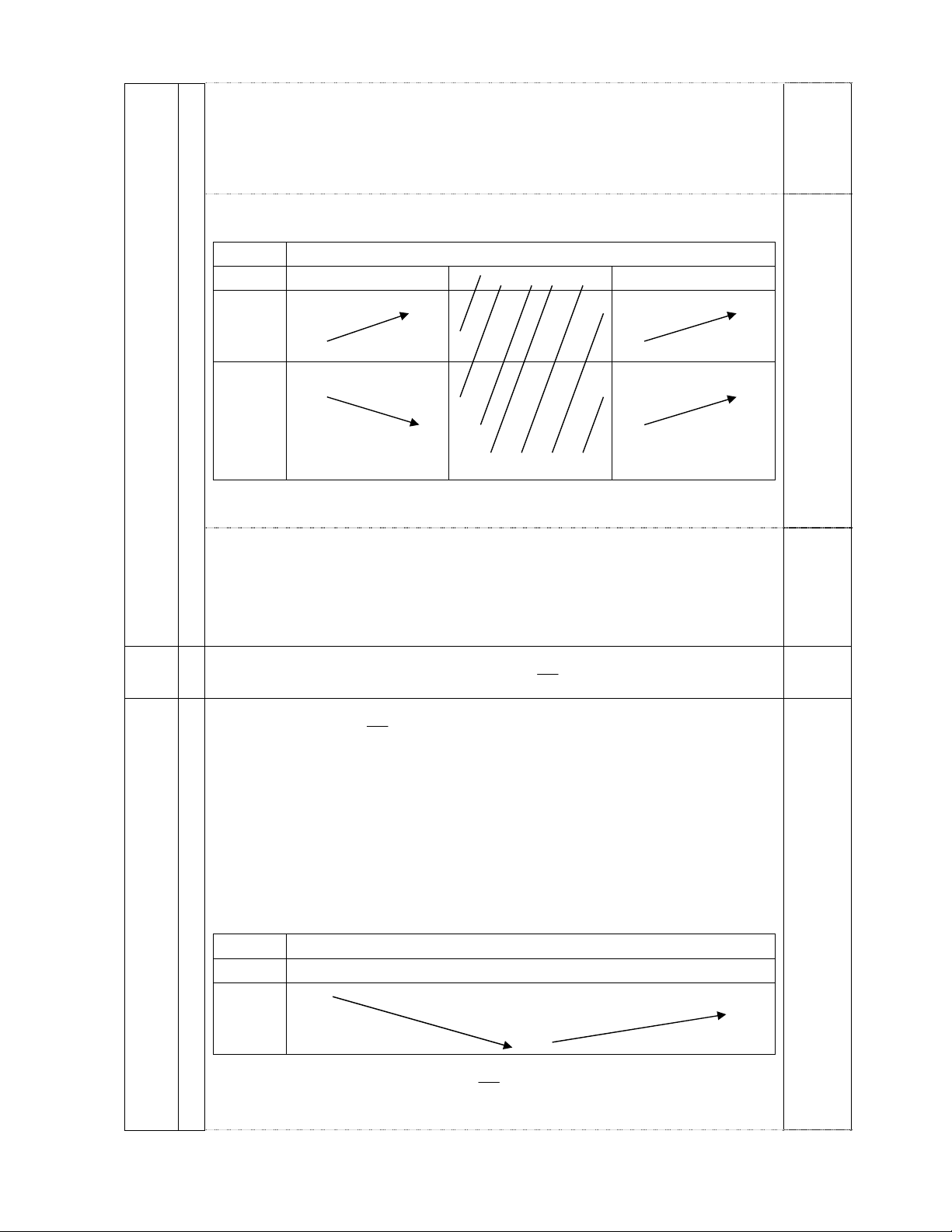
Tõ c«ng thøc x¸c ®Þnh sè h¹ng tæng qu¸t cña d·y, ta dÔ dμng chøng minh d·y sè       n 5 n 5  0,25 cã giíi h¹n. 1 Lim2 2  2cos  Lim2 sin   n   n 1   6.2   6.2    5  sin  n 1   5 5 6.2  Lim    5 0,25 6 6   n 1  6.2   IV 1 1,50 A I B D G C a) Ta có
    
    .
AB CD  AB(AD  AC)  . AB AD  . AB AC 2 2 2 2 2 2
AB  AD  BD
AB  AC  BC 2 2    a  b 0,5 2 2       a  b Lại có, . AB CD  .
AB CD cos AB,CD  cos AB,CD 2 2  2 c
Gọi  là góc giữa hai đường thẳng AB, CD ta có:   a  b a  b 0,5
cos  cos AB,CD 2 2 2 2     arccos 2 2 c c b)
Gọi I, G lần lượt là trọng tâm của tứ diện ABCD và tam giác BCD 1 1
Ta có IG  AG  V  V 4 IBCD 4 ABCD 0,5 1 Tương tự, V V V  V IABC IABD IACD 4 ABCD Vậy, V  V  V  V IABC IABD IACD IBCD Mặt khác, A  BC  BAD   C  DA  D
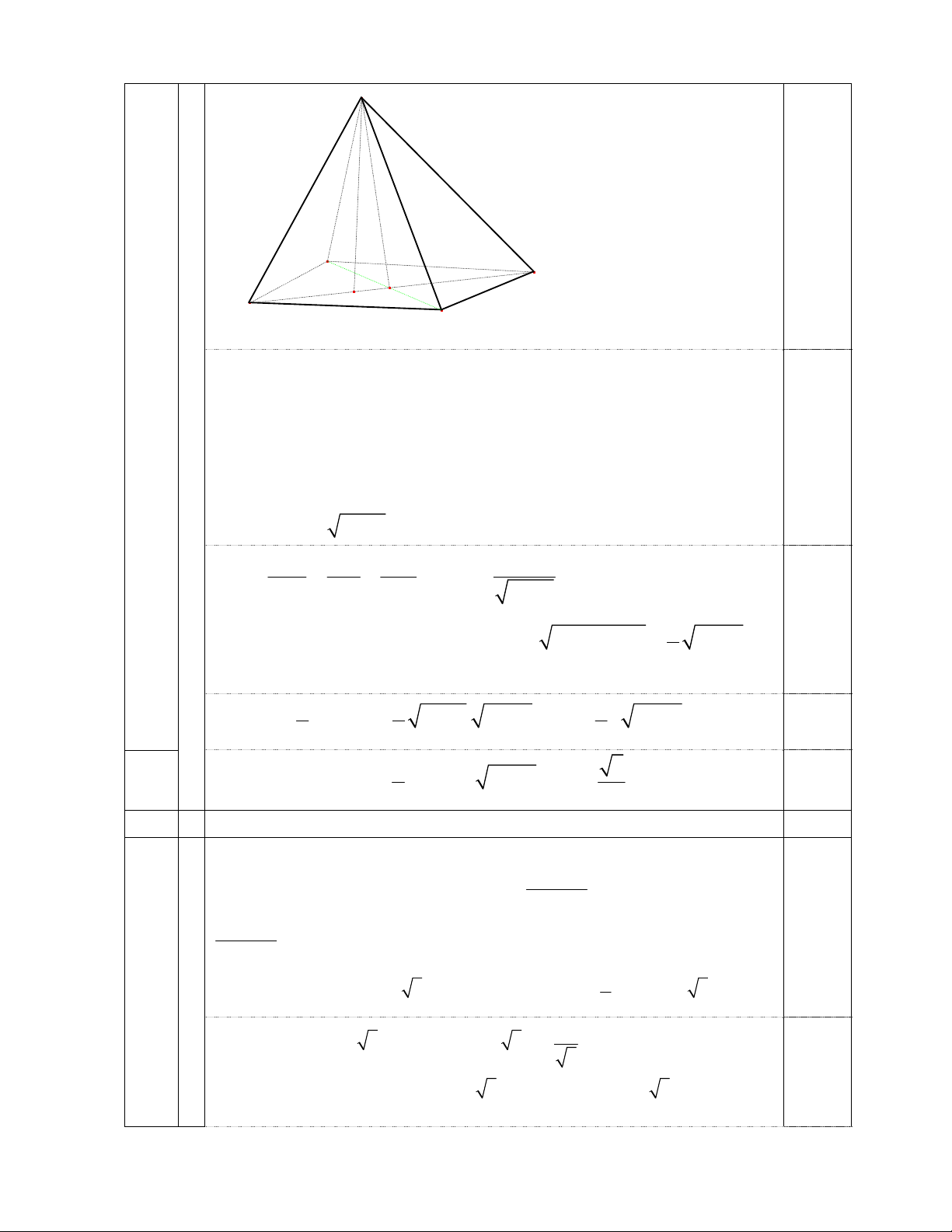
 CB(c  c  c) 0,5 Do đó, d  d  d  d I,(ABC) I,(ABD) I,(ACD) I,(BCD) 2 1,50 S B A O H C D
Gọi H là hình chiếu của S trên (ABCD)
Do SB = SC = SD nên HB = HC = HD, suy ra H là tâm đường tròn ngoại tiếp tam giác BCD.
Mặt khác, tam giác BCD cân tại C nên H thuộc CO, với O là giao của AC 0,25 và BD. Lại có, C  BD  ABD   SBD 
 OC  OA  OS nên SAC  vuông tại S 2
 AC  x 1 1 1 1 x Ta có,    SH  2 2 2 2 SH SA SC x 1 1 0,25 ABCD là hình thoi 2 2 2
 AC  BD  OB  AB  AO  3  x 2 1 1 1 + 2 2 2 S  AC.BD 
x 1. 3  x  V  x 3  x 0,25 ABCD 2 2 6 1 6
V có giá trị lớn nhất là khi 2
x  3  x  x  0,25 4 2 V
Tìm giá trị lớn nhất và nhỏ nhất..... 1,00 Ta có: 6
P = (a + b + c)2 – a2 – b2 - c2 + bc + ca +  (a + b + c)2 - 3 +
a  b  c 6 0,25
a  b  c 6
Đặt t = a + b + c => t [ 3 ; 3]. Xét f(t) = t2 – 3 + , với t [ 3 ; 3]. t 6
Vì f’(t) > 0 ,  t[ 3 ; 3] => f(t)  f( 3 ) = . 3
Dấu bằng xảy ra khi a =c = 0, b = 3 hoặc b =c = 0, a = 3 0,25 6 Vậy Pmin =
khi a =c = 0, b = 3 hoặc b =c = 0, a = 3 3 Ta có: 6
P = (a + b + c)2 – a2 – b2 - c2 + bc + ca +
a  b  c 2 2 2
a  b  2c 6  (a + b + c)2 - 3 + + 2
a  b  c 6  (a + b + c)2 - 1 +
a  b  c 0,25 6
Đặt t = a + b + c => t [ 3 ; 3]. Xét g(t) = t2 – 1 + , với t [ 3 ; 3]. t
Vì g’(t) > 0 ,  t[ 3 ; 3] => g(t)  g(3) =10.
Dấu bằng xảy ra khi a = b = c = 1.
Vậy Pmax = 10 khi a = b = c = 1. 0,25
Chú ý: Nếu học sinh làm theo cách khác mà đúng thì cho điểm tối đa.