Đề thi chọn HSG Toán 12 cấp cơ sở năm học 2018 – 2019 sở GD và ĐT Điện Biên

ĐỀ VÀ HDG HỌC SINH GIỎI 12 ĐIỆN BIÊN 2018-2019 Câu 1: (6,0 điểm) 1. 2x −3 Cho hàm số y =
(C) và đường thẳng d : x − y −1 = 0 . Viết phương trình tiếp tuyến x −1
của đồ thị (C) biết tiếp tuyến đó song song với d.
2. Tìm m để hàm số 3 2
y = x − mx + ( 2 3 3 m − )
1 x + m + 2 đồng biến trên khoảng (2;+ ) ∞ . Câu 2: (4,0 điểm) 2 1. 2 sin x
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số f (x) = . x x 4 4 sin + cos 2 2 3 3
x − y −  ( 2 2
3 2x − y + 2 y)+15x −10 = 0
2. Giải hệ phương trình  ( ; x y ∈ ℝ) . 
2 − y + 3− x = 2x − 2  Câu 3: (4,0 điểm)
1. Gọi S là tập hợp tất cả các số tự nhiên có 5 chữ số khác nhau được chọn từ các số
0;1; 2;3; 4;5; 6; 7;8;9 . Xác định số phần tử của S . Chọn ngẫu nhiên một số từ S ,
tính xác suất để số được chọn là số chẵn.
2. Trong mặt phẳng tọa độ Oxy cho hai điểm A(0; ) 9 , B(3; )
6 . Gọi D là miền nghiệm của hệ
2x − y + a ≤ 0 phương trình  
. Tìm tất cả các giá trị của a để AB ⊂ D . 6
 x + 3y + 5a ≥ 0  Câu 4: (4,0 điểm)
1. Cho hình chóp SABC . Trên các đoạn thẳng S ,
A SB, SC lần lượt lấy các điểm A ', B ', C ' khác V SA SB SC
với điểm S . Chứng minh rằng: S . ABC = . . V
SA ' SB ' SC '
S .A' B 'C '
2. Cho hình chóp tứ giác đều S.ABCD , có AB = a, SA = a 3 . Gọi O là giao điểm của AC và
BD , G là trọng tâm tam giác SCD .
a) Tính thể tích khối chóp S.OGC.
b) Tính khoảng cách từ G đến mặt phẳng (SBC).
c) Tính cosin góc giữa hai đường thẳng SA và BG . Câu 5: (2,0 điểm)
1. Cho phương trình (m+ ) x( 2 x + ) 2 2 1 − x +(m− ) 6 x −1= 0 ( )
1 . Tìm các giá trị của m để phương trình ( ) 1 có nghiệm thực.
2. Cho đa thức f (x) 4 3 2
= x + ax +bx + ax +1 có nghiệm thực. Chứng minh rằng 2 2
a + b − 4b +1> 0 . HDG Câu 1: (6,0 điểm) 1. 2x −3 Cho hàm số y =
(C) và đường thẳng d : x − y −1 = 0 . Viết phương trình tiếp tuyến x −1
của đồ thị (C) biết tiếp tuyến đó song song với d.
2. Tìm m để hàm số 3 2
y = x − mx + ( 2 3 3 m − )
1 x + m + 2 đồng biến trên khoảng (2;+ ) ∞ . Tập xác định: . ℝ Lời giải
1. d : x − y −1= 0 ⇒ d : y = x −1⇒ d có hệ số góc k =1. d 2x −3
Xét hàm số y = f (x) = : x −1
+ Tập xác định D = ℝ \ { } 1 . 1 + / f (x) = , ∀x ≠ 1. (x − )2 1  2x 3 − 2x −3
Gọi ∆ là tiếp tuyến của   (C) tại 0 M x ;  thì ∆ : / 0
y = f (x )(x − x ) + 0    x −1  0 0 x −1 0 0 1 x = 0
+ Giả sử ∆ / /d ta được / 0
f (x ) = k ⇔ = 1 ⇔  . 0 d (x − )2 1 x = 2 0 0  + Thử lại:
i x = 0 ⇒ ∆ : y = x + 3 thỏa mãn ∆ / /d . 0
i x = 2 ⇒ ∆ : y = x −1⇒ ∆ ≡ d. Trường hợp này không thỏa mãn. 0
Vậy có đúng một tiếp tuyến của (C) thỏa đề, đó là ∆ : y = x + 3. 2. / 2 2
y = 3x − 6mx + 3(m −1), ∀x ∈ ℝ x = m −1 / y = 0 ⇔ 
: Hai nghiệm phân biệt với mọi . m x = m−1  Bảng biến thiên x -∞ m-1 m+1 +∞ y' + _ 0 0 + +∞ y y1 y2 -∞
Hàm số đồng biến trên (2;+ )
∞ ⇔ (2;+∞)⊂(m +1;+ )
∞ ⇔ m +1≤ 2 ⇔ m ≤1.
Vậy m cần tìm là m ≤1. Câu 2: (4,0 điểm) 2 1. 2 sin x
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số f (x) = . 4 x 4 x sin + cos 2 2 3 3
x − y −  ( 2 2
3 2x − y + 2 y)+15x −10 = 0
2. Giải hệ phương trình  ( ; x y ∈ ℝ) . 
2 − y + 3− x = 2x − 2  Lời giải 2 1. x x x x 1 2 −sin x Ta có 4 4 2 2 2 sin + cos =1− 2sin cos =1− sin x = ≠ 0, ∀ . x 2 2 2 2 2 2 Cách 1: 2 4 sin x 8 Khi đó f (x) = = − 4 . 2 2 2 −sin x 2 −sin x 8 Vì 2 2
0 ≤ sin x ≤1⇒1≤ 2−sin x ≤ 2 nên 4 ≤
≤ 8 . Do đó 0 ≤ f (x)≤ 4 . 2 2 −sin x Ta có f (x) 2
= 0 ⇔ sin x = 0 ⇔ sin x = 0 ⇔ x = kπ(k ∈ ℤ), π f (x) 2
= 4 ⇔ sin x =1 ⇔ sin x = ±1 ⇔ x = ± + 2kπ(k ∈ ℤ). 2
Vậy giá trị nhỏ nhất của f (x) là 0 đạt được khi x = kπ(k ∈ ℤ), π
giá trị lớn nhất của f (x) là 4 đạt được khi x = ± + 2kπ(k ∈ ℤ). 2 Cách 2: Đặt 2
sin x = t , Điều kiện t ∈[0; ] 1  x ≤ 3
2. Điều kiện:  .  y ≤ 2 
Phương trình thứ nhất của hệ tương đương với:
(x − )3 + (x − )= ( y − )3 2 3 2 1 + 3( y − ) 1 ( ) 1
Xét hàm số f (t) 3
= t + 3t,t ∈ ℝ . Khi đó ta có ' f (t) 2
= 3t + 3> 0, ∀t ∈ ℝ . Do đó f (t) là hàm đồng biến trên ℝ . Nên phương trình ( )
1 trở thành f (x − ) 2 = f ( y − )
1 ⇔ x − 2 = y −1 ⇔ y = x −1 .
Thay y = x −1 vào phương trình thứ hai ta được:
2 3− x = 2x − 2 ⇔ 3− x = x −1 x ≥1 x ≥1    ⇔  
⇔  x = 2 ⇔ x = 2 2 3
 − x = x −2x +1    x = −1 
Với x = 2 thì y =1 (thỏa mãn).
Vậy hệ phương trình đã cho có nghiệm là ( ; x y) = (2; ) 1 . Câu 3: (4,0 điểm)
1. Gọi S là tập hợp tất cả các số tự nhiên có 5 chữ số khác nhau được chọn từ các số
0;1; 2;3; 4;5; 6; 7;8;9 . Xác định số phần tử của S . Chọn ngẫu nhiên một số từ S , tính xác suất
để số được chọn là số chẵn.
2. Trong mặt phẳng tọa độ Oxy cho hai điểm A(0; ) 9 , B(3; )
6 . Gọi D là miền nghiệm của hệ
2x − y + a ≤ 0 phương trình  
. Tìm tất cả các giá trị của a để AB ⊂ D . 6
 x + 3y + 5a ≥ 0  Lời giải
1. Số phần tử của tập S là n(S)= 9.9.8.7.6 = 27216.
Gọi số chẵn thuộc tập S có dạng abcde (a ≠ 0). Nếu e ∈ {2; 4;6; }
8 , trường hợp này ta có: 8.8.7.6.4 =10752 số.
Nếu e = 0 , trường hợp này ta có: 9.8.7.6 = 3024 số. 10752 + 3024 13776 41
Vậy xác suất cần tìm là: P = = = . 27216 27216 81
2. Phương trình đường thẳng AB : x + y −9 = 0.
Trường hợp 1: Nếu AB là đường thẳng.
a ≤−2x + y Xét hệ   . 5
 a ≥−6x −3  y a ≤ −12 a ≤ −12  
Dễ thấy điểm C (2; 7)∈ AB nhưng C ∉ D vì    33 ⇔  33 ⇔ a ∈ . φ 5  a ≥ − a ≥ −    2  10
a ≤ −2x + y
Trường hợp 2: Nếu AB là đoạn thẳng. Ta thay y = 9− x (x ∈[0; ] 3 ) vào hệ 5
 a ≥ −6x −3  y
a ≤ 9−3x  −3x − 27 ta được   −3x − 27 ⇒
≤ a ≤ 9 −3x ( ) * a ≥ 5  5 ( ) 27
* đúng với ∀x ∈[0; ] 3 ⇔ − ≤ a ≤ 0 . 5 27 Vậy −
≤ a ≤ 0 thỏa mãn yêu cầu bài toán. 5 Câu 4: (4,0 điểm)
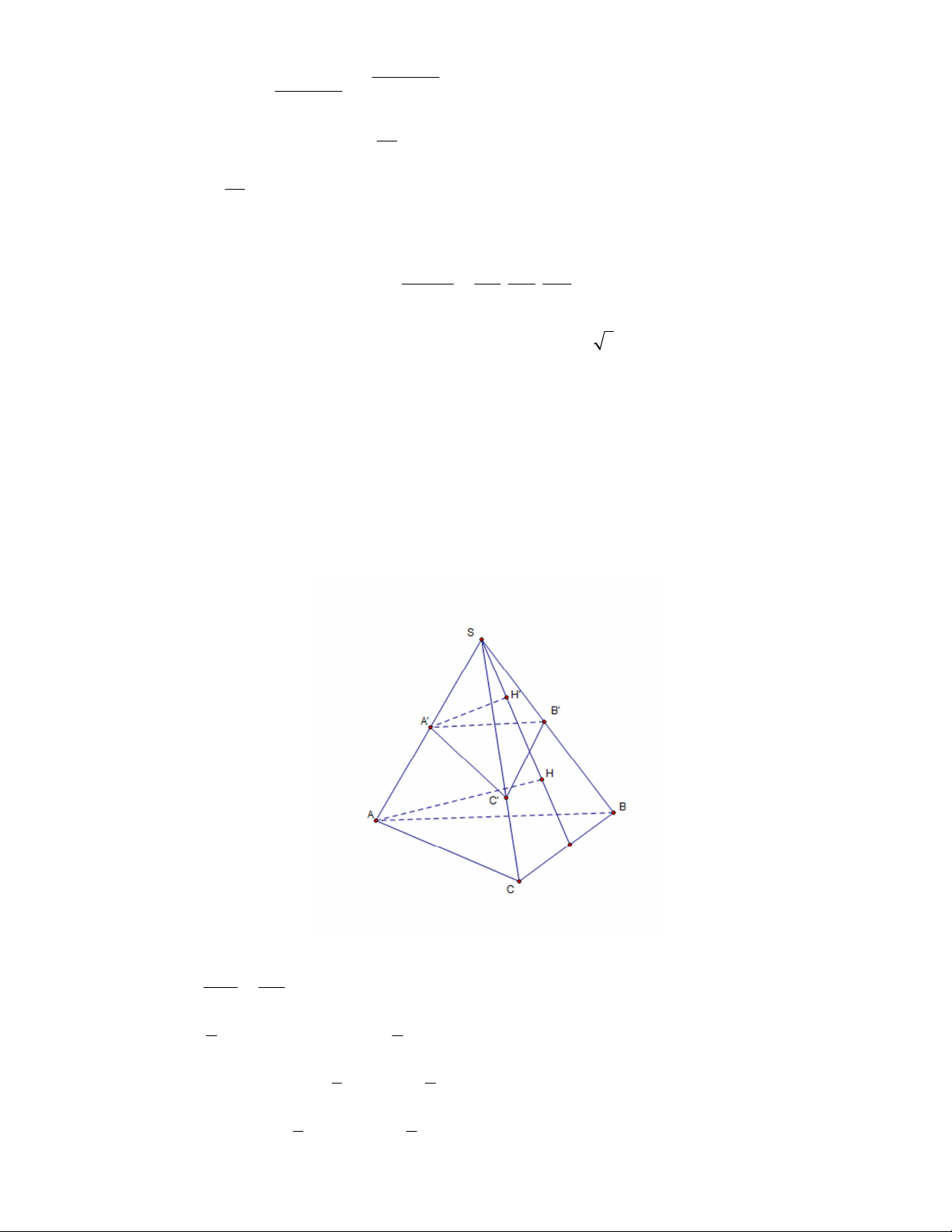
1. Cho hình chóp SABC . Trên các đoạn thẳng S ,
A SB, SC lần lượt lấy các điểm A ', B ', C ' khác V SA SB SC
với điểm S . Chứng minh rằng: S . ABC = . . V
SA ' SB ' SC '
S . A' B 'C '
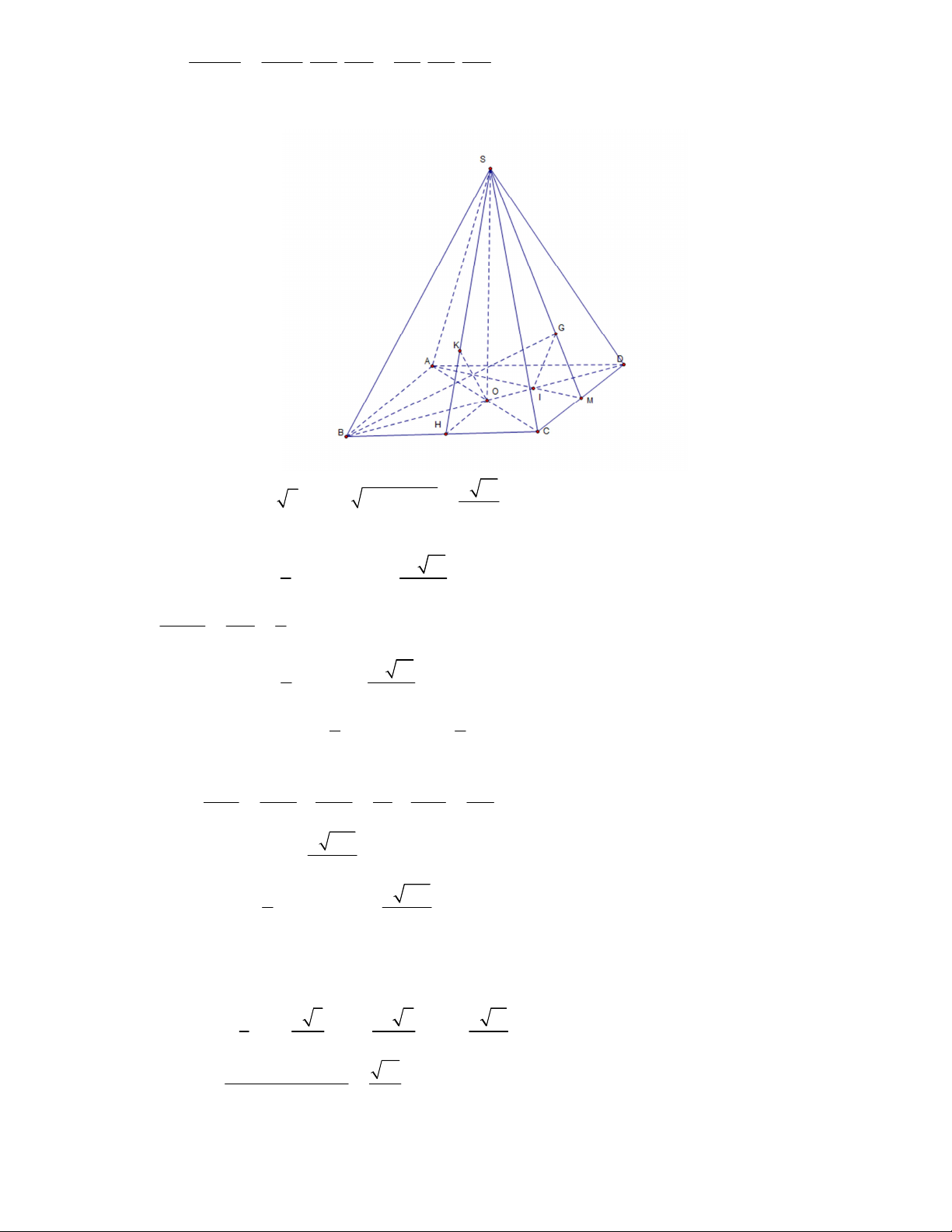
2. Cho hình chóp tứ giác đều S.ABCD , có AB = a, SA = a 3 . Gọi O là giao điểm của AC và
BD , G là trọng tâm tam giác SCD .
a) Tính thể tích khối chóp S.OGC.
b) Tính khoảng cách từ G đến mặt phẳng (SBC) .
c) Tính cosin góc giữa hai đường thẳng SA và BG . Lời giải 1.
Gọi H , H ' lần lượt là hình chiếu vuông góc của ,
A A ' trên (SBC) . AH SA Ta có = AH ' SA ' 1 1 S = S .
B SC.sin BSC ; S =
SB '.SC '.sin BSC SBC SB 'C ' 2 2 1 1 Khi đó V = V = AH .S = AH .S . B SC.sin BSC S . ABC A.SBC 3 SBC 6 1 1 V = V = A ' H '.S =
A ' H '.SB '.SC '.sin BSC
S . A' B 'C '
A'.SB 'C ' SB 'C ' 3 6 V AH SB SC SA SB SC Vậy S . ABC = . . = . . V
A ' H ' SB ' SC '
SA ' SB ' SC '
S .A' B 'C ' 2. a 10
a) Ta có AC = a 2 ; 2 2
SO = SA −OA = 2
Gọi M là trung điểm CD 3 1 a 10 Khi đó V = S . O OM .MC = S .OCM 6 48 V SG 2 S .OCG = = V SM 3 S.OCM 3 2 a 10 Suy ra S.OGC = S.OMC = . 3 72 2 2
b) Ta có d (G, (SBC)) =
d (M , (SBC)) =
d (O, (SBC)) 3 3
Gọi H là trung điểm BC , K là hình chiếu vuông góc của O trên SH . 1 1 1 4 4 22 Ta có = + = + = 2 2 2 2 2 2 OK OH OH a 10a 5a a 110
d (O, (SBC)) = OK = 22 2 a 110
d (G, (SBC)) =
d (O, (SBC)) = 3 33
c) Gọi I là giao điểm của BD và AM , I là trong tam tam giác ADC .
Suy ra IG / /SA nên góc giữa hai đường thẳng SA và BG bằng góc giữa hai đường thẳng IG và BG 1 a 3 2a 2 a 11 Ta có IG = SA = ; BI = ; BG = 3 3 3 3 2 2 2
BG + IG − BI 33 cosIGB = = 2.B . G IG 11
Ta có thể tọa độ hóa. Câu 5: (2,0 điểm)
1. Cho phương trình (m+ ) x( 2 x + ) 2 2 1 − x +(m− ) 6 x −1= 0 ( )
1 . Tìm các giá trị của m để phương trình ( ) 1 có nghiệm thực.
2. Cho đa thức f (x) 4 3 2
= x + ax + bx + ax +1 có nghiệm thực. Chứng minh rằng 2 2
a + b − 4b +1> 0 . Lời giải
1. Điều kiện: x ≥ 0.
- Với x = 0 thì phương trình vô nghiệm. x + x +
- Với x > 0 , phương trình ( ) ⇔ (m + ) 2 2 1 1 1 2 − + m − 6 = 0 . x x t  ≥ 2 2 +  Đặ x 1 t 2 t = ⇒  x +1 ; 2 x t  =  x 2 t − 2t + 6
Ta được phương trình mới theo ẩn phụ: (m + 2) 2
t − t + m − 6 = 0 ⇔ = m (2). t +1
Yêu cầu bài toán ⇔ (2) có nghiệm trên  2; +∞  ). 2 2 t 2t 6 t 2t 8  − + + − t = 4 − (l)
Xét hàm số f (t) = ⇒ f ′(t) = = ⇔  . t +1 (t + ) 0 2 1 t = 2 Bảng biến thiên x – ∞ -4 2 + ∞ y' + 0 – – 0 + + ∞ y 2
Vậy phương trình có nghiệm ⇔ m ≥ 2 .
2. Giả sử đa thức đã cho có nghiệm trong trường hợp 2 2
a + b − 4b +1≤ 0 .
a + b − b + ≤ ⇔ a +(b − )2 2 2 2 4 1 0 2 ≤ 3 ( ) 1 .
Vì x = 0 không phải là nghiệm của phương trình f (x) = 0 nên 2  1   1  1  1  4 3 2 2
x + ax + bx + ax +1 = 0 ⇔   x +  + a  x +  + b = 0 ⇔   x +   + a  x +  + b − 2 = 0 . 2          x   x   x   x  Đặ 1 t t = x +
thì phương trình trên có nghiệm khi và chỉ khi 2
t + at + b − 2 = 0 có nghiệm x thoả mãn t ≥ 2 .
Xét hàm số g (t) 2
= t + at +b−2 −a −a
g′(t) = 2t + a ; g′(t)= 0 ⇔ t = . Như (1) trên thì ∉ (−2;2) 2 2
Do đó ta có bảng biến thiên:
−2a + b + 2 ≤ 0 (2)
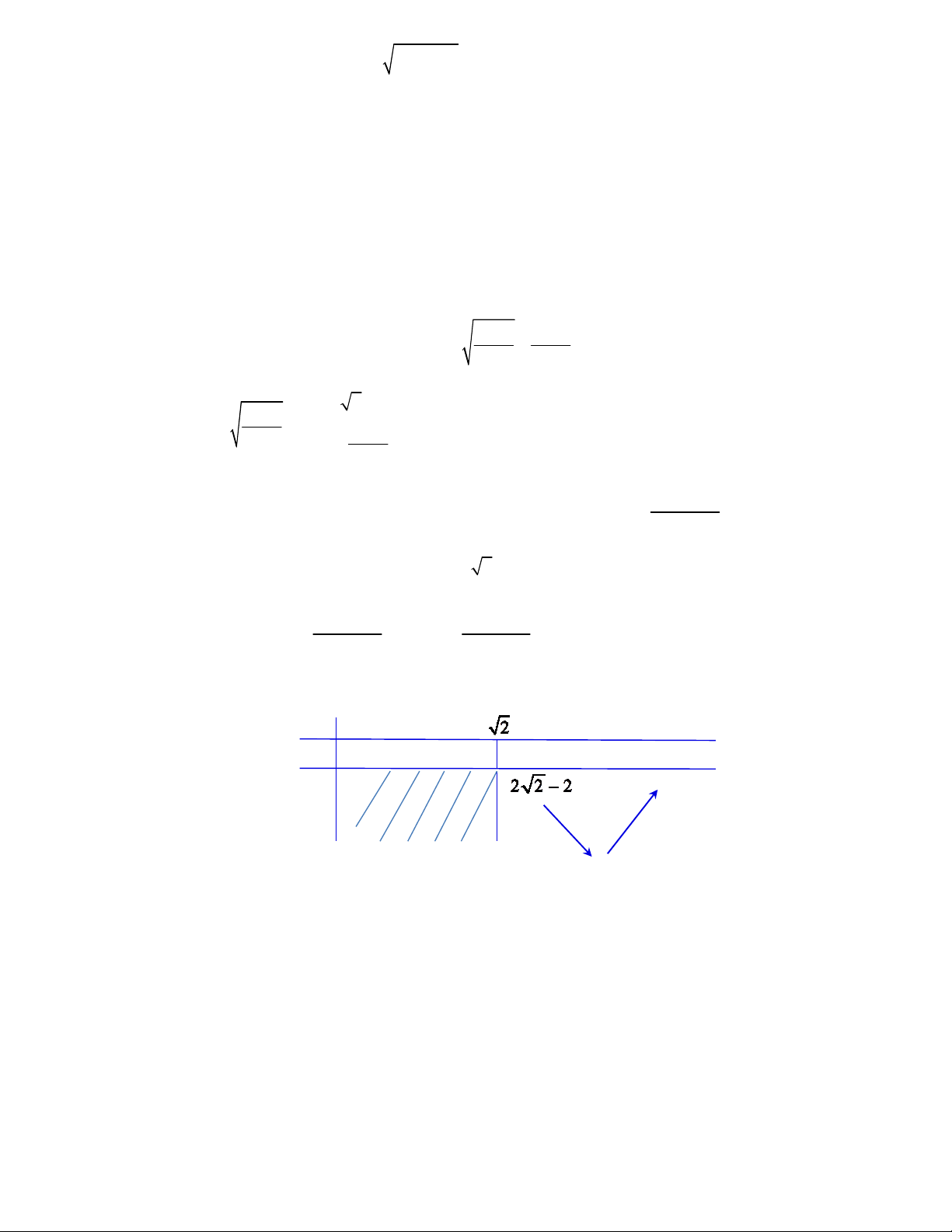
Phương trình có nghiệm thì 2a+b+2≤0  ( ) 3  Những điểm M ( ;
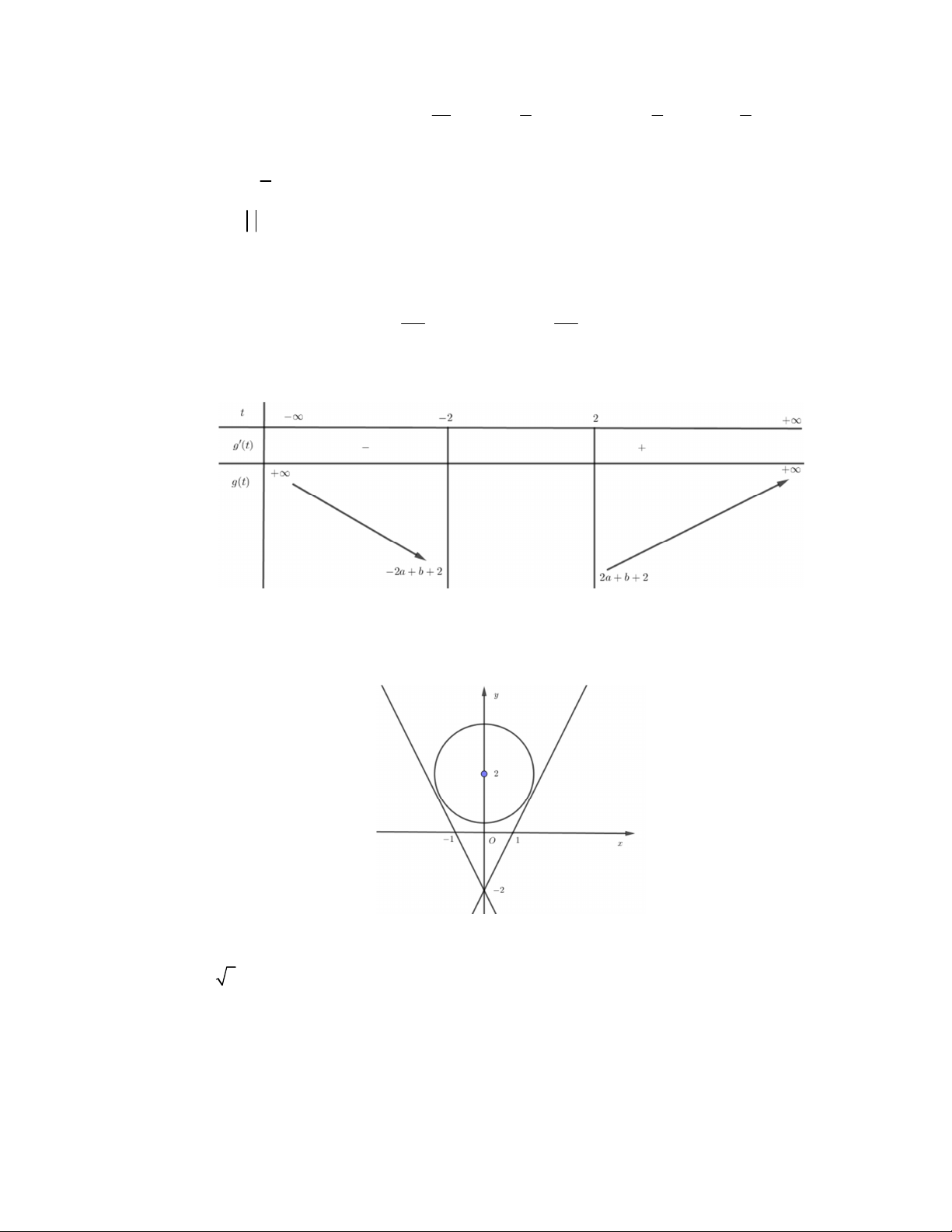
a b) thoả (1) thì nằm bên trong hoặc biên đường tròn tâm I (0; 2) và bán kính bằng 3 . Những điểm N ( ;
a b) thoả mãn (2) và (3) là những điểm thuộc phần không chứa gốc tạo độ của
−2x + y + 2 = 0 các đường thẳng  .
2x + y + 2 = 0 
Những phần đó theo hình vẽ là không có điểm chung, vì vậy ta có mâu thuẫn.
Ta có điều phải chứng minh: Nếu đã thức đã cho có nghiệm thì 2 2
a + b − 4b +1> 0 .
Chú ý: Bài có thể giải nhanh như sau: 2 2 2
t + at + b − 2 = 0 ⇔ 2
t = −at + 2 − b 4 t ( at b) 2 a (b )  ⇒ = − + − ≤ + − ( 2 2 2 1+   t )   4 t −1
⇒ a +(b − 2)2 2 2 > = t −1≥ 3 2 2
⇒ a + b − 4b +1> 0 2 . t +1