SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI THPT CẤP TỈNH VÒNG 2 LONG AN NĂM HỌC: 2018-2019 Môn thi: TOÁN ĐỀ CHÍNH THỨC
Ngày thi: 20/9/2018 (Buổi thi thứ nhất)
(Đề thi có 01 trang, gồm 04 câu)
Thời gian: 180 phút (không kể thời gian phát đề)
Câu 1 (5,0 điểm):
 2x y x y  1 
Giải hệ phương trình sau trên tập số thực:  . 
 2x  y  4x  y  2  Câu 2 (5,0 điểm): Cho hàm số 4 2
y  x  2mx  3 (m là tham số thực) có đồ thị C . Tìm tất cả các m 
giá trị của m sao cho trên đồ thị C tồn tại duy nhất một điểm mà tiếp tuyến của C tại m  m 
điểm đó vuông góc với đường thẳng x  8y  2018  0 . Câu 3 (5,0 điểm):
Cho tam giác ABC có ba góc nhọn, không cân và nội tiếp đường tròn O. Gọi H
là chân đường cao kẻ từ A và I là tâm đường tròn nội tiếp của tam giác ABC . Đường
thẳng AI cắt đường tròn O tại điểm thứ hai M (M khác A ). Gọi AA' là đường kính
của O. Đường thẳng MA' cắt các đường thẳng AH, BC theo thứ tự tại N và K . Chứng  minh 0 NIK  90 . Câu 4 (5,0 điểm):
Cho K là tập hợp các số tự nhiên có bốn chữ số. Chọn ngẫu nhiên một số từ K . Tính
xác suất để số được chọn có tổng các chữ số là bội của 4.
---------- HẾT ----------
(Thí sinh không được sử dụng tài liệu – Cán bộ coi thi không giải thích gì thêm)
Họ và tên thí sinh: …………………………………………… Số báo danh: …………………………………
Cán bộ coi thi 1 (ký, ghi rõ họ và tên)
Cán bộ coi thi 2 (ký, ghi rõ họ và tên)
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI THPT CẤP TỈNH VÒNG 2 LONG AN NĂM HỌC: 2018-2019 Môn thi: TOÁN ĐỀ CHÍNH THỨC
Ngày thi: 21/9/2018 (Buổi thi thứ hai)
(Đề thi có 01 trang, gồm 03 câu)
Thời gian: 180 phút (không kể thời gian phát đề)
Câu 5 (6,0 điểm):
Cho hàm số f :    thỏa f xf y  f f x  f y  yf x  f x  f y, x  ,y   .
a) Chứng minh rằng: “Nếu tồn tại a   sao cho f a  0 thì f là đơn ánh”.
b) Tìm tất cả các hàm số f . Câu 6 (7,0 điểm): u   2020  1 
Cho dãy số (u ) được xác định như sau:  2018n  2 . n u   (u 1), n   1,2,3,...  n 1   2019n  2 n
Chứng minh rằng dãy số đã cho có giới hạn hữu hạn và tìm giới hạn đó. Câu 7 (7,0 điểm):
Có bao nhiêu số tự nhiên có 2018 chữ số, trong mỗi số đó các chữ số đều lớn hơn 1 và
không có hai chữ số khác nhau cùng nhỏ hơn 7 đứng liền nhau?
---------- HẾT ----------
(Thí sinh không được sử dụng tài liệu – Cán bộ coi thi không giải thích gì thêm)
Họ và tên thí sinh: …………………………………………… Số báo danh: …………………………………
Cán bộ coi thi 1 (ký, ghi rõ họ và tên)
Cán bộ coi thi 2 (ký, ghi rõ họ và tên)
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI THPT CẤP TỈNH VÒNG 2 LONG AN NĂM HỌC: 2018-2019 Môn thi: TOÁN
Ngày thi: 20/9/2018 (Buổi thi thứ nhất)
Thời gian: 180 phút (không kể thời gian phát đề) HƯỚNG DẪN CHẤM
Cách giải khác nếu đúng thì giám khảo vẫn cho đủ số điểm. NỘI DUNG ĐIỂM Câu 1 ( 5,0 điểm):
 2x y x y  1 (1) 
Giải hệ phương trình sau trên tập số thực:  . 
 2x  y  4x  y  2 (2)  2
 x  y  0   u   2x  y  Điều kiện  . Đặt  ( , u v  0) 4
 x  y  0 0,5    v   4x  y   2 2 u
 v  2x 2  x  Ta có:   u  1,0 u   v  2 2  2  x 2  x 3 Thay u  vào (1) , ta có:
 x  y  1  y  x 1,0 2 2 2 3 7 1 Thay y  x vào (1), ta có:
x  x  1  14x  2  x 1,0 2 2 2 x   2    x   9  77   x  9  77  1,0   x  9  77  3      27 3 77 
y  9  77. So điều kiện, hệ có nghiệm 9   77;    0,5 2  2    Câu 2 (5,0 điểm): Cho hàm số 4 2
y  x  2mx  3 (m là tham số thực) có đồ thị C . Tìm tất cả các giá trị m 
của m sao cho trên đồ thị C C
m  tồn tại duy nhất một điểm mà tiếp tuyến của  m  tại điểm đó
vuông góc với đường thẳng x  8y  2018  0 .
Tiếp tuyến có hệ số góc bằng 8  0,5 3 Gọi x x
x  mx  2  0 (1)
0 là hoành độ tiếp điểm thì 0 là nghiệm của phương trình 1,0
Để thỏa yêu cầu bài toán thì (1) có nghiệm duy nhất. 1,0 Trang 1/ 3
Vì x  0 không là nghiệm của (1) nên 2 2 (1)  m  x   x 3 2 2 2 2  x  2
Xét hàm số: f (x)  x
  ; f '(x)  2  x   0,5 2 2 x x x Bảng biến thiên x  0 1  f '(x)   0  1,0  3  f (x)   
Từ bảng biến thiên, (1) có nghiệm duy nhất khi và chỉ khi m  3 . 1,0
Vậy m  3 thỏa yêu cầu bài toán. Câu 3 (5,0 điểm):
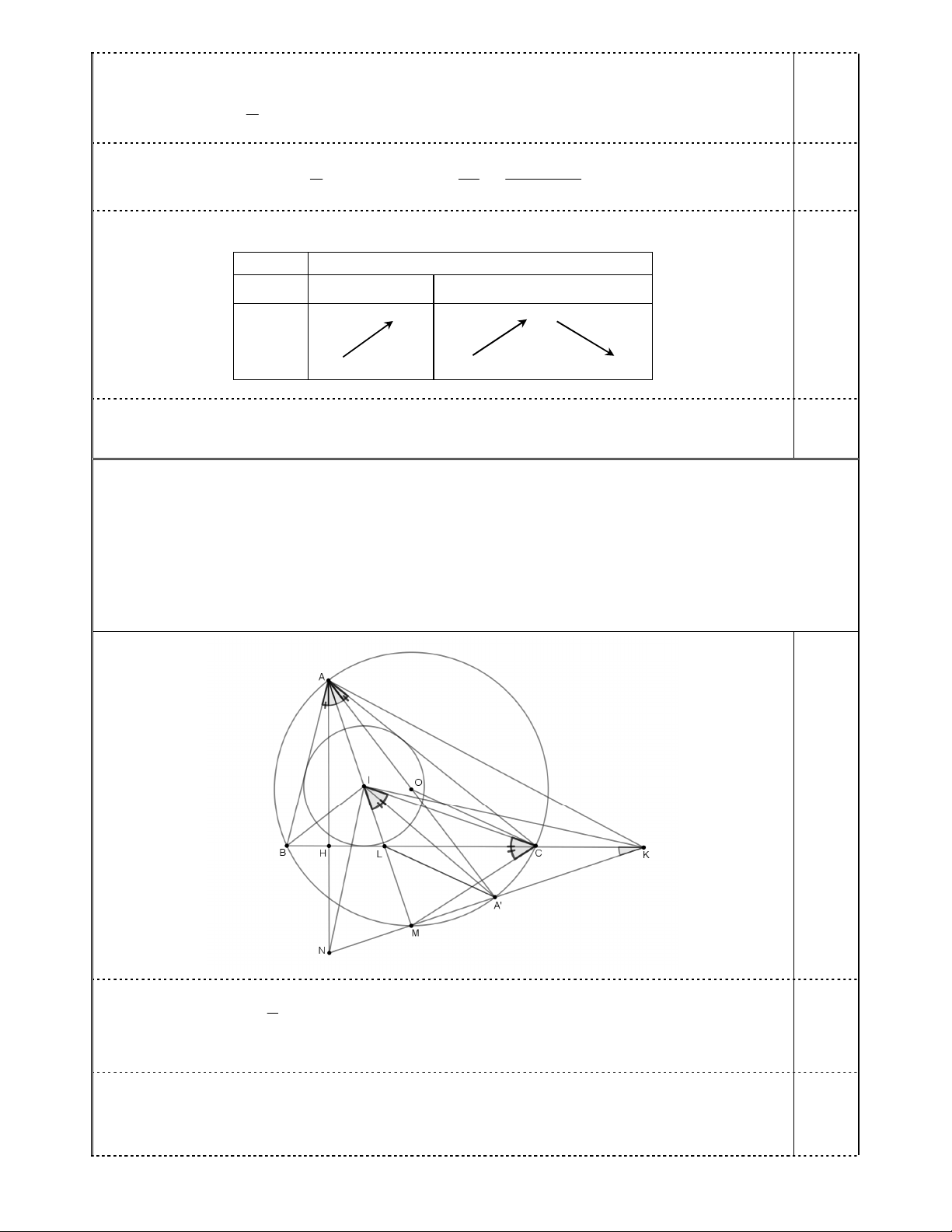
Cho tam giác ABC có ba góc nhọn, không cân và nội tiếp đường tròn O. Gọi H là chân
đường cao kẻ từ A và I là tâm đường tròn nội tiếp của tam giác ABC . Đường thẳng AI cắt đường
tròn O tại điểm thứ hai M (M khác A). Gọi AA ' là đường kính của O. Đường thẳng MA '  0
cắt các đường thẳng AH, BC theo thứ tự tại N và K . Chứng minh NIK  90 .  0 1  0   Ta có OAC  90 
AOC  90  ABC  BAH mà AI là phân giác góc A nên 2 1,0  
HAI  OAI . Suy ra tam giác ANA' cân tại A.
Gọi L là giao điểm của MA và BC.  0   
Ta có HKN  90  HNK  HAM  LAA ' . Suy ra, tứ giác ALA'K nội tiếp. 1,0
Do đó MA ' .MK  M .
L MA  MN.MK  M . L MA. (1) Trang 2/ 3    
Vì MAC  MCB hay MAC  MCL nên hai tam giác MCL và MAC đồng dạng. 1,0 Suy ra 2 .
ML MA  MC . (2) Do ,
IA IC là các tia phân giác trong của tam giác ABC nên ta có:   1 1    1 1   
MIC   sñ AB  sñ MC         và MCI sñ AB sñ MB  . 1,0 2 2  2 2     
Do đó, MIC  MCI nên tam giác MIC cân tại M . Suy ra, MI  MC . (3) 2  0
Từ (1), (2), (3) suy ra MN .MK  MI  NIK  90 . 1,0 Câu 4 (5,0 điểm):
Cho K là tập hợp các số tự nhiên có bốn chữ số. Chọn ngẫu nhiên một số từ K . Tính xác suất để
số được chọn có tổng các chữ số là bội của 4. 3
Ta có: K  9.10  9000 . 0,5
Gọi A là tập hợp các số tự nhiên có bốn chữ số mà tổng các chữ số của nó chia hết cho 4.
A  abcd   : a b c d 4.
Xét b  c  d  4k  r 0  r  3 . Nếu r  0;1; 
2 thì mỗi giá trị của r sẽ có hai giá 1,0
trị của a sao cho a  b  c  d 4 (đó là a  4 r, a  8 r ). Nếu r  3 thì mỗi giá
trị của r sẽ có ba giá trị của a sao cho a  b  c  d  4 (đó là a  1, a  5, a  9 ).
Gọi B  bcd   : 0  , b ,
c d  9, b  c  d  4k  r, 0  r   2 ,
C  bcd   : 0  ,b ,cd  9, b c d  4k   3 . 1,0 Khi đó, ta có: A 
B  C  B  C  3 2 3 2
 C  2.10  C .
Xét tập hợp C với c  d  4m  n . Nếu n  0; 
1 thì mỗi giá trị của n sẽ có hai giá trị
của b sao cho b  c  d  4k  3 . Nếu n  2; 
3 thì mỗi giá trị của n sẽ có ba giá trị của 1,0
b sao cho b  c  d  4k  3 .
Gọi D  cd   : 0  ,
c d  9,c d  4m  ,
n 0  n   1 ,
E  cd   : 0  ,cd  9, c d  4m  ,
n 2  n   3 . 1,0
Khi đó, ta có: C  D  E   D  E  2 2 3 2
 E  2.10  E , với E  25  24  49 . 3 2
Suy ra: A  2.10  2.10  49  2249 .
Gọi biến cố X : “Số được chọn có tổng các chữ số là bội của 4”. Khi đó, xác suất của biến 0,5
cố X là: P X  2249  . 9000
…….…HẾT…….… Trang 3/ 3
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI THPT CẤP TỈNH VÒNG 2 LONG AN NĂM HỌC: 2018-2019 Môn thi: TOÁN
Ngày thi: 21/9/2018 (Buổi thi thứ hai)
Thời gian: 180 phút (không kể thời gian phát đề) HƯỚNG DẪN CHẤM
Cách giải khác nếu đúng thì giám khảo vẫn cho đủ số điểm. NỘI DUNG ĐIỂM
Câu 5 (6,0 điểm):
Cho hàm số f :    thỏa f xf y  f f x  f y  yf x  f x  f y, với
mọi x,y   .
a) Chứng minh rằng: “Nếu tồn tại a   sao cho f a  0 thì f là đơn ánh”.
b) Tìm tất cả các hàm số f .
Lấy y ,y   f y  f y (1) 1 2 sao cho  1  2 .
Thế x bởi a và thế y lần lượt bởi y ,y 1 2 ta được: 1,0
f af y  f f a  f y  y f a  f a  f y (2) 1
    1 1     1
f af y
 f f a  f y
 y f a  f a  f y (3) 2 
    2 2     2
Từ (1), (2), (3) ta được: y f a  y f a  y  y f a  1   2   1 2 (vì   0 ). 1,0
Vậy f là một đơn ánh.
TH1: Nếu f x   0 với mọi x   . Thử lại ta thấy thỏa mãn. 1,0
TH2: Nếu tồn tại a sao cho f a  0 .
Thế x  0,y  1 vào đề bài ta được: f  
0  f f   0  f   1   f  
0  f f   1 . 1,0
Vì f là đơn ánh nên ta được: f   0  0 .
Mặt khác, thế y  0 vào đề bài ta được: f xf  
0   f f x  f  
0   0.f x  f x  f   0 , x   1,0 . Vì f  
0  0 nên f f x  f x, x
   hay f x  x, x   . 1,0
Vậy f x  0, x   hoặc f x  x, x   . Câu 6 (7,0 điểm): u   2020  1 
Cho dãy số (u ) được xác định như sau:  2018n  2 . n u   (u 1), n   1,2,3,...  n 1   2019n  2 n
Chứng minh rằng dãy số đã cho có giới hạn hữu hạn và tìm giới hạn đó. Trang 1/ 3
Ta có: u  0, n  1, 2... n 0,5
(2018n  2)(u  1)  (2019n  2)u
2018n  2  nu Xét hiệu: n n n u  u   n 1  n 1,0 2019n  2 2019n  2
Ta đi chứng minh: 2018n  2  nu  0  nu  2018n  2, n  2, 3, 4,... n n () 0,5
Khi n  1 , dễ thấy mệnh đề () đúng.
Giả sử: ku  2018k  2, k  2, 3, 4,... k 0,5 2018k  2 (k  1)u  (k  1) (u  1) k 1  2019k  2 k 1,0 k  1 
2018ku 2u 2018k   2 2019k  2 k k k 1  2018k 2    
2018(2018k  2)  2  2018k  2 2019k  2  k    (k 1)(2018k 2) 1   1,0  
(k  1)(2018k  2)  20  19  2   2019k  2  k  k 2
 2018k  2  2018 
 2018k  2020, k  2, 3, 4,... 1,0 k Vậy u
 u , n  2, 3, 4,... n 1  n 0,5 Mà (u )
n bị chặn dưới nên dãy số đã cho có giới hạn hữu hạn.
Gọi L  lim un . 2018 1,0 Ta có: L 
(L  1)  L  2018 2019
Câu 7 (7,0 điểm) Có bao nhiêu số tự nhiên có 2018 chữ số, trong mỗi số đó các chữ số đều lớn
hơn 1 và không có hai chữ số khác nhau cùng nhỏ hơn 7 đứng liền nhau?
Xét trường hợp tổng quát với số tự nhiên có n chữ số, với n là số nguyên dương. Gọi A , B n
n lần lượt là tập các số tự nhiên có n chữ số thỏa yêu cầu đề bài mà chữ số tận 0,5
cùng nhỏ hơn 7 và chữ số tận cùng lớn hơn 6.
Lấy một phần tử a thuộc An , có một cách thêm vào chữ số cuối cho a (thêm vào bên phải
chữ số cuối cùng của a ) để được một phần tử của An 1
 và có 3 cách thêm vào chữ số cuối 0,5
cho a để được một phần tử của Bn 1  .
Lấy một phần tử b thuộc Bn , có 5 cách thêm vào chữ số cuối cho b để được một phần tử 0,5 của A B n 1
 và có 3 cách thêm vào chữ số cuối cho b để được một phần tử của n 1  . Trang 2/ 3 A  A  5 B  n 1  n n Ta có:  . 1,0 B  3 A  3 B  n 1  n n  Khi đó: A  B
 4 A  8 B  4 A  B  4 B n 1  n 1  n n  n n  n . 1,0
 4A  B  4.3A  B  4 A  B  12 A  B ,n  2 n n n 1  n 1    n n   n 1 n 1   1,0
với A  5, B  3, A  20, B  24 1 1 2 2 Kí hiệu x  A  B x  4x  12x x  8,x  44 n n
n , ta được: n 2  n 1  n , trong đó 1 2 . 1,0 1  n n 
Sử dụng sai phân tuyến tính, ta được: x  5.6    n   2 . 1,0 4   1 2018 2018
Áp dụng cho n  2018 , ta có
5.6 2  số cần tìm. 0,5 4
…….…HẾT…….… Trang 3/ 3
Document Outline

• ĐỀ THỐNG NHẤT - NGÀY 1
• ĐỀ THỐNG NHẤT - NGÀY 2
• ĐÁP ÁN THỐNG NHẤT _NGÀY 1
• ĐÁP ÁN THỐNG NHẤT _NGÀY 2