Đề thi chọn HSG Toán 12 THPT năm 2018 – 2019 sở GD&ĐT Đồng Nai

Giới thiệu đến bạn đọc nội dung đề thi chọn HSG Toán 12 THPT năm 2018 – 2019 sở GD&ĐT Đồng Nai, kỳ thi được diễn ra vào ngày 18 tháng 01 năm 2019, đề thi được dành cho học sinh khối 12 theo học chương trình chuẩn hệ THPT, đề gồm 06 bài toán tự luận, thời gian làm bài 180 phút

24 12 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 12

Môn: Toán 12

Thông tin:

6 trang 7 tháng trước

Tác giả:

Profile Nguyễn Vân
GIẢI ĐỀ THI HỌC SINH GIỎI LỚP 12 TỈNH ĐỒNG NAI NĂM 2018 – 2019
Câu 1. (5,0 điểm) Cho hàm số
32
2 3( 3) 18 8y x m x mx
,
m
là tham số.
a) Tìm
m
để hàm số đã cho đồng biến trên .
b) Tìm
m
để đồ thị hàm số đã cho có hai điểm cực trị nằm vế hai phía của trục tung.
c) Tìm
m
để giá trị nhô nhất của hàm số đã cho trên đoän
[ 1;0]
bằng
24
Giải
a)
2
' 6 6( 3) 18y x m x m
,
Hàm số đồng biến trên
22
'
' 0 9( 3) 108 0 6 9 0 3
y
m m m m m
.
b) Đồ thị hàm số có hai điểm cực trị nằm về hai phía trục tung
0m
c)
+ Nếu
hàm số nghịch biến trên nên giá trị nhô nhất trên
[ 1;0]
là
(0) 8 24y
(vô lí)
+ Nếu
2
1 ' 6 12 1 8m y x x
thì trên
( 1;0)
hàm số nghịch biến nên giá trị nhô nhất trên
[ 1;0]
là
(0) 8 24y
(vô lí)
+ Nếu
2
0 ' 6 1 8m y x x
thì trên
( 1;0)
hàm số đồng biến nên giá trị nhô nhất trên
[ 1;0]
là
( 1) 3 21 24 1y m m
(loäi)
+ Nếu
3, 0, 1mmm
thì
'0y
luôn có hai nghiệm là
m
và
3
. Ta xét các trường hợp sau
Nếu
0m
thì trên
( 1;0)
hàm số đồng biến nên giá trị nhô nhất trên
[ 1;0]
là
( 1) 24y
1m
(nhận)
Nếu
10m
thì trên
( 1; )m
hàm số đồng biến và trên
( ;0)m
hàm số nghịch biến nên giá
trị nhô nhất trên
[ 1;0]
là
( 1)y
hoặc
(0)y
, mà
(0) 24y
(vô lí) và
( 1) 24 1ym
(loäi)
Nếu
1m
thì trên
[ 1;0]
hàm số nghịch biến nên giá trị nhô nhất trên
[ 1;0]
là
( 1)y
hoặc
(0)y
, mà
(0) 24y
(vô lí) và
( 1) 24 1ym
(loäi)
Vậy
1m
là giá trị cần tìm
Câu 2. (3,5 điểm)
1) Giâi phương trình
21
8.25 8.10 15.2 0
x x x
.
2) Giâi phương trình
(1 2sin4 )tan2 1xx
Giải
1)
2
21
55
55
22
8.25 8.10 15.2 0 8. 8. 30 0 1
22
53
22
x
xx
x x x
x
x







2) Điều kiện
42
xk
(1 2sin 4 )tan2 1 sin2 2sin4 .sin2 cos2 sin2 cos2 cos 6 cos2x x x x x x x x x x
2 6 2
2 16 4
sin2 cos 6 cos 2 cos 6
2
2 6 2
2 8 2
x x k x k
x x x x
x x k x k
(thôa đk)
Câu 3. (3,5 điểm) Cho tứ diện
ABCD
có
AB
vuông góc với mặt phẳng
()BCD
. Tam giác
BCD
là
tam giác đều,
,2AB a BC a
.
1) Tính góc giữa hai mặt phẳng
()ABC
và
()BCD
2) Tính theo
a
khoâng cách giữa hai đường
AC
và
BD
Giải
1) Có
()AB BCD
mà
( ) ( ) ( )AB ABC ABC BCD
.
Suy ra góc giữa hai mặt phẳng
()ABC
và
()BCD
là
0
90
2) Gọi
E
là trung điểm
BD
, dựng hình chữ nhật
BFCE
Gọi
H
là hình chiếu của
B
trên
AF
Ta có
()BD FC BD AFC
Suy ra
( , ) ( ,( )) ( ,( ))d BD AC d SB AFC d B AFC
(1)BH AF
CF
vuông góc
BF
và
AB
. Suy ra
(2)BH CF
Từ
(1)
và
(2) ( )BH AFC
.
Vậy
( ,( ) ( , )BH d B AFC d BD AC
Xét tam giác vuông
ABF
ta có :
2 2 2 2 2 2
. . 3. 3
2
3
BF AB CE AB a a a
BH
BF AB CE AB a a
Vậy
3
( , )
2
a
d BD AC
Câu 4. (3,0 điểm) Trong một tiết học môn Toán, giáo viên mời ba học sinh
,,A B C
thực hiện trò chơi
chơi như sau : Mỗi bän
,,A B C
chọn ngẫu nhiên một số nguyên khác
0
thuộc khoâng
( 6;6)
và lần
lượt thế vào ba tham số của hàm số
42
y ax bx c
; nếu đồ thị hàm số thu được có ba điểm cực trị
đều nằm phía trên trục hoành thì được nhận thưởng. Tính xác suất để ba học sinh
,,A B C
được nhận
thưởng.
Giải
3
( ) 10n
Hàm số có ba cực trị
0ab
32
0
' 4 2 0 2 (2 ) 0
2
x
y ax bx x ax b
b
x
a
Đồ thị hàm số có ba điểm cực trị là
22
(0; ), ; , ;
2 4 2 4
b b b b
A c B c C c
a a a a
Trường hợp 1 :
Nếu
0a
thì
A
là điểm cực tiểu nên đồ thị hàm số có ba điểm cực trị đều nằm phía trên trục hoành
0 0 { 5; 4; 3; 2; 1}
0 0 {1;2;3;4;5}
0 0 {1;2;3;4;5}
A
a a a
b b b
y c c
có
5.5.5 125
(cách)
Trường hợp 2 :
Nếu
0a
thì
,BC
là điểm cực tiểu nên đồ thị hàm số có ba điểm cực trị đều nằm phía trên trục hoành
2
0
0
0
0
0
0
4
B
C
a
a
b
b
y
b
c
y
a
Dễ suy được
0c
và
4 {4;8;12;16;20}a
Ta có các khâ năng sau :
Với
2
11
4
b
c
a
,
1 {1;2;3;4;5}ba
có
5
(cách)
Với
2
11
4
b
c
a
,
2 {2;3;4;5}ba
có
4
(cách)
Với
2
11
4
b
c
a
,
3 {3;4;5}ba
có
3
(cách)
Với
2
11
4
b
c
a
,
4 {5}ba
có
1
(cách)
Với
2
22
4
b
c
a
,
1 {1;2;3;4;5}ba
có
5
(cách)
Với
2
22
4
b
c
a
,
2 {1;2;3;4;5}ba
có
5
(cách)
Với
2
22
4
b
c
a
,
3 {2;3;4;5}ba
có
4
(cách)
Với
2
22
4
b
c
a
,
4 {3;4;5}ba
có
3
(cách)
Với
2
22
4
b
c
a
,
5 {4;5}ba
có
2
(cách)
Với
2
33
4
b
c
a
,
1 {1;2;3;4;5}ba
có
5
(cách)
Với
2
33
4
b
c
a
,
2 {1;2;3;4;5}ba
có
5
(cách)
Với
2
33
4
b
c
a
,
3 {1;2;3;4;5}ba
có
5
(cách)
Với
2
33
4
b
c
a
,
4 {2;3;4;5}ba
có
4
(cách)
Với
2
33
4
b
c
a
,
5 {3;4;5}ba
có
3
(cách)
Với
2
44
4
b
c
a
,
1 {1;2;3;4;5}ba
có
5
(cách)
Với
2
44
4
b
c
a
,
2 {1;2;3;4;5}ba
có
5
(cách)
Với
2
44
4
b
c
a
,
3 {1;2;3;4;5}ba
có
5
(cách)
Với
2
44
4
b
c
a
,
4 {2;3;4;5}ba
có
4
(cách)
Với
2
44
4
b
c
a
,
5 {2;3;4;5}ba
có
4
(cách)
Với
2
55
4
b
c
a
,
1 {1;2;3;4;5}ba
có
5
(cách)
Với
2
55
4
b
c
a
,
2 {1;2;3;4;5}ba
có
5
(cách)
Với
2
55
4
b
c
a
,
3 {1;2;3;4;5}ba
có
5
(cách)
Với
2
55
4
b
c
a
,
4 {1;2;3;4;5}ba
có
5
(cách)
Với
2
55
4
b
c
a
,
5 {2;3;4;5}ba
có
4
(cách)
Trong trường hợp này có :
101
(cách)
Suy ra có tất câ
125 101 226
(cách chọn)
Vậy xác suất là
226 113
1000 500
Câu 5. (2,5 điểm) Giâi hệ phương trình
3 2 2
2
2 1 0 (1)
2 3 2 2 (2)
x x y y x
x x y y
Giải
Điều kiện:
2
0,
3
xy
3 2 2 3 2 2 2 2
2 1 0 ( ) ( ) ( ) (1 ) 0x x y y x x x y x x xy x xy x y
2
( 1) ( 1) ( 1) (1 )(1 ) 0x x y x x y x y y y
2
2
2
( 1) ( 1) ( 1)( 1) 0
( 1)( 1) 0
1
10
x x y x x y y x y
x y x x y
xy
x x y
Với
1xy
thay vào
(2)
ta được
22
1 3 3 2 2 3 2 1 (2 3) 0y y y y y y y y
35
23
22
(2 3)( 1) 0
1
3 2 1
1 0 ( )
3 2 1
yx
y
yy
yy
y VN
yy
Trường hợp này có nghiệm
53
;
22
Với
22
1 0 1x x y x x y
, vì
2
0 1 1 1x x x y
Kết hợp điều kiện ta được
2
1
3
y
Ta có
2
22
2
3 3 1 0
2 3 21
1 1 1 0 0,3
0
36
xx
x x y x x x
xx
3 21
0 0,3
6
x
(vì
0x
)
Xét vế trái của
(2)
:
( ) 2f x x x
với
3 21 7
0 ( ) 2
64
x f x
Xét vế phải ta có
2
( ) 3 2 2f y y y
với
2
1
3
y
Ta có
3
33
'( ) 4 0 8 3 2 3 192 128 9 0
4
2 3 2
f y y y y y y y
y
Suy ra
5
1 ( )
8
fy
nên phương trình vô nghiệm
Vậy hệ phương trình có nghiệm duy nhất
53
;
22
Câu 6. (2,5 điểm)
1) Cho ba số thực dương
,,a b c
. Tìm giá trị nhô nhất của
2 2 3 2 3
a b c
P
b c c a a b
2) Chứng minh rằng
3
n
n
C
chia hết cho
3
với mọi
n
nguyên dương
1) Đặt
1
( 6 9 4 )
35
23
1
2 3 (9 4 6 )
35
23
1
(4 6 9 )
35
a u v w
u b c
v c a b u v w
w a b
c u v w
1 6 9 4 4 6 9 9 4 6 1 9 4 4 9 9 4
18
35 35
u v w u v w u v w v w u w u v
P
u v w u u v v w w
1 4 4 4 4 4 4 5 5 5
18
35
v u w v w u v w u
u v v w u w u v w
13
( 18 2. 16 2 16 2. 16 3 125)
35 5
Vậy giá trị nhô nhất của
P
là
5
3
a b c
2)
1
3 3 1 3
(3 )! 1.2.3...(3 1).3 1.2.3...(3 1)
3. .3 3.
!.(2 )! 1.2.3... .(2 )! 1.2.3...( 1).(2 )!
n n n
n n n
n n n n
C C C
n n n n n n
chia hết cho
3
| 1/6
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

GIẢI ĐỀ THI HỌC SINH GIỎI LỚP 12 TỈNH ĐỒNG NAI NĂM 2018 – 2019
Câu 1. (5,0 điểm) Cho hàm số 3 2 y 2x 3(m 3)x 18mx 8 , m là tham số.
a) Tìm m để hàm số đã cho đồng biến trên .
b) Tìm m để đồ thị hàm số đã cho có hai điểm cực trị nằm vế hai phía của trục tung.
c) Tìm m để giá trị nhô nhất của hàm số đã cho trên đoän [ 1;0] bằng 24 Giải a) 2
y '  6x  6(m  3)x  18m ,
Hàm số đồng biến trên 2 2
  '  0  9(m  3)  108m  0  m  6m  9  0  m  3 . y '
b) Đồ thị hàm số có hai điểm cực trị nằm về hai phía trục tung m 0 c) + Nếu 2 m 3 y ' 6x 36x 54
hàm số nghịch biến trên nên giá trị nhô nhất trên [ 1;0] là ( y 0) 8 24 (vô lí) + Nếu 2 m 1 y ' 6x 12x
18 thì trên ( 1;0) hàm số nghịch biến nên giá trị nhô nhất trên [ 1;0] là ( y 0) 8 24 (vô lí) + Nếu 2 m 0 y ' 6x
18x thì trên ( 1;0) hàm số đồng biến nên giá trị nhô nhất trên [ 1;0] là ( y 1) 3 21m 24 m 1 (loäi) + Nếu m 3, m 0, m 1 thì y '
0 luôn có hai nghiệm là m và 3 . Ta xét các trường hợp sau  Nếu m
0 thì trên ( 1;0) hàm số đồng biến nên giá trị nhô nhất trên [ 1;0] là ( y 1) 24 m 1 (nhận)  Nếu 1 m
0 thì trên ( 1;m) hàm số đồng biến và trên ( ;
m 0) hàm số nghịch biến nên giá
trị nhô nhất trên [ 1;0] là y( 1) hoặc y(0), mà ( y 0) 24 (vô lí) và ( y 1) 24 m 1 (loäi)  Nếu m
1 thì trên [ 1;0] hàm số nghịch biến nên giá trị nhô nhất trên [ 1;0] là y( 1) hoặc y(0), mà ( y 0) 24 (vô lí) và ( y 1) 24 m 1 (loäi) Vậy m 1 là giá trị cần tìm Câu 2. (3,5 điểm)
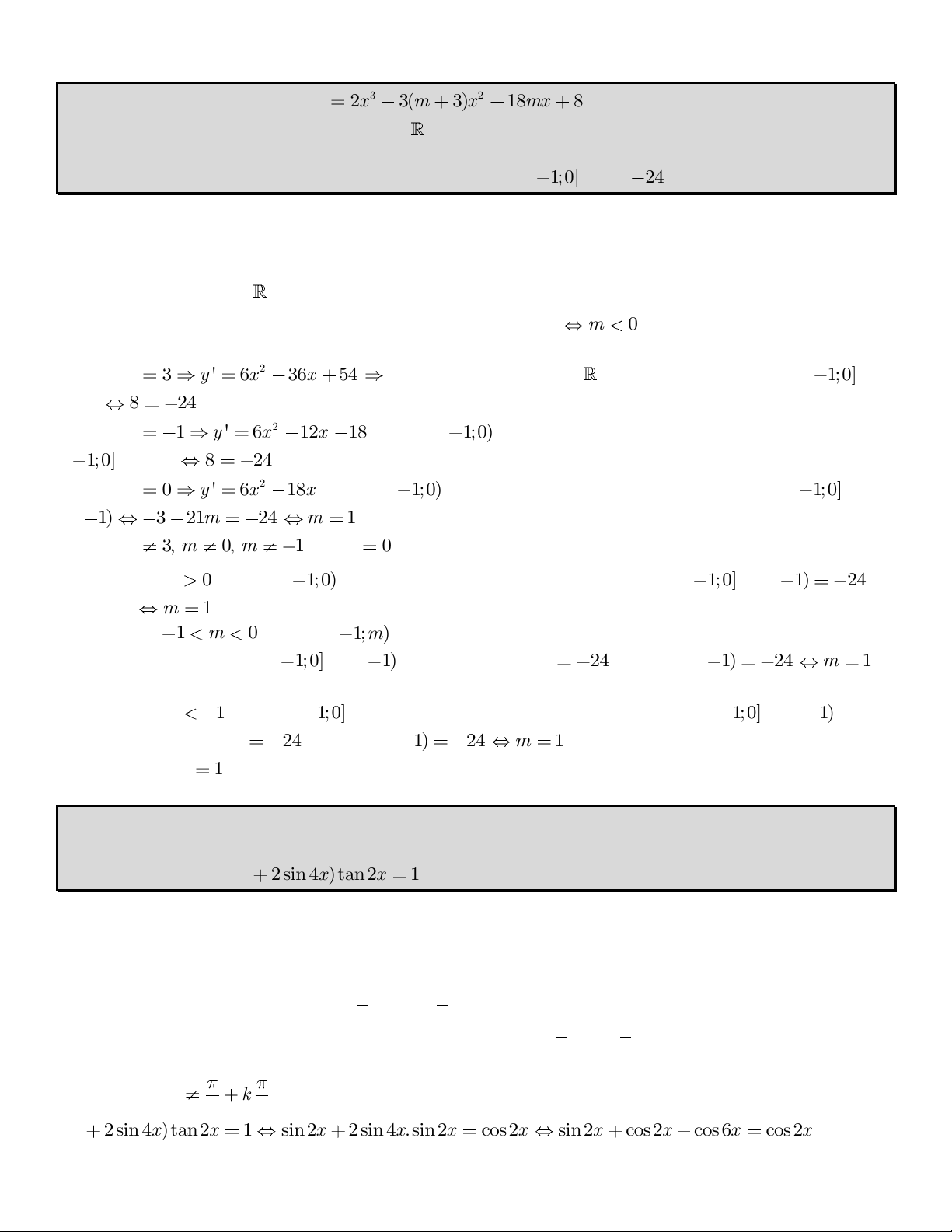
1) Giâi phương trình x x 2x 1 8.25 8.10 15.2     0 .
2) Giâi phương trình (1 2sin 4x)tan2x 1 Giải x  5  5  2x x        x x x  5 5  2 2 1) 2 1 8.25 8.10 15.2 0 8.  8.  30 0           x  1 2 2  x      5  3      2 2   2) Điều kiện x k 4 2 (1 2sin 4x)tan2x 1 sin2x 2sin 4x.sin2x cos2x sin2x cos2x cos 6x cos2x 2x 6x k2 x k 2 16 4 sin 2x cos 6x cos 2x cos 6x (thôa đk) 2 2x 6x k2 x k 2 8 2
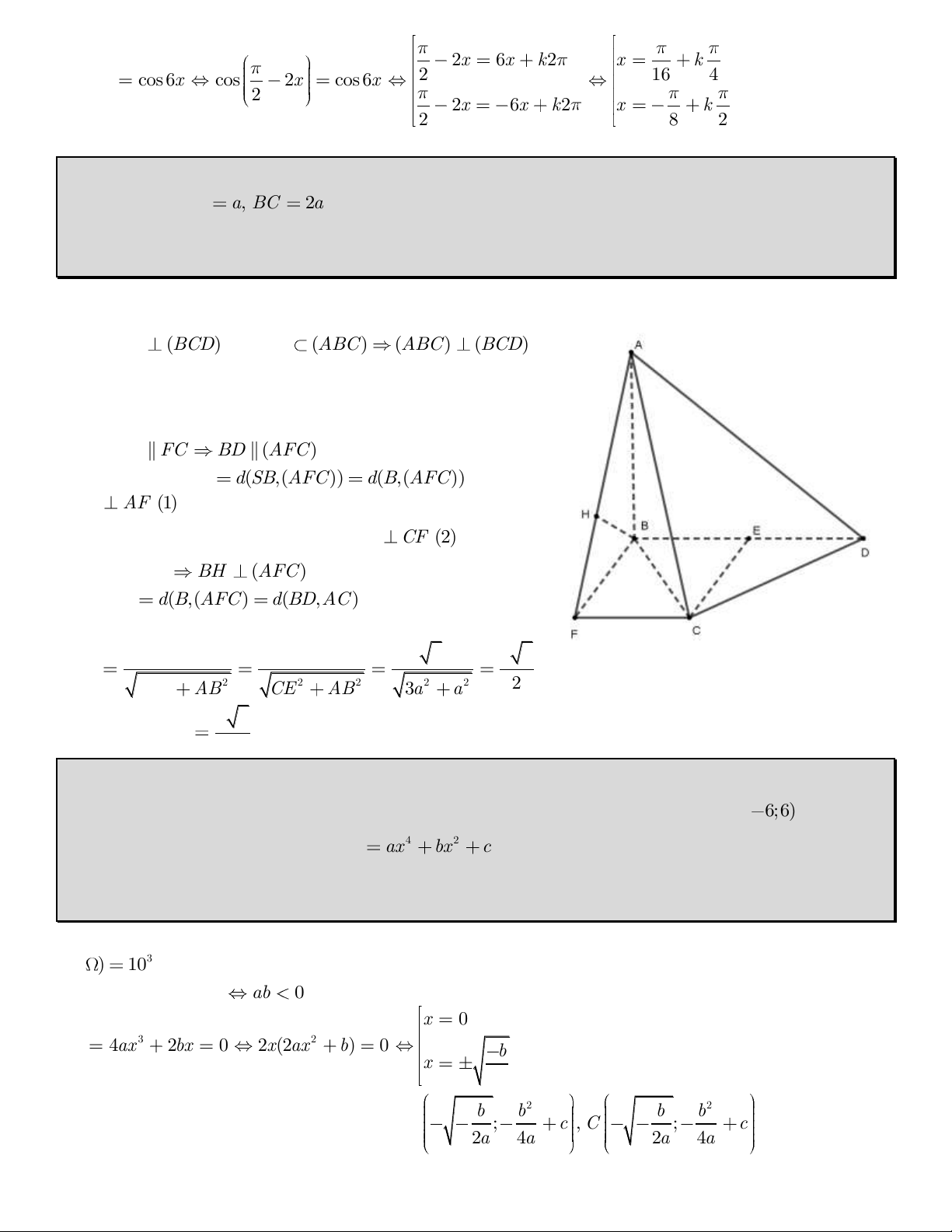
Câu 3. (3,5 điểm) Cho tứ diện ABCD có AB vuông góc với mặt phẳng (BCD) . Tam giác BCD là tam giác đều, AB , a BC 2a .
1) Tính góc giữa hai mặt phẳng (ABC) và (BCD)
2) Tính theo a khoâng cách giữa hai đường AC và BD Giải 1) Có AB (BCD) mà AB (ABC) (ABC) (BC ) D .
Suy ra góc giữa hai mặt phẳng (ABC) và (BCD) là 0 90
2) Gọi E là trung điểm BD , dựng hình chữ nhật BFCE
Gọi H là hình chiếu của B trên AF Ta có BD FC BD (AFC) Suy ra d(B , D AC) d(S , B (AFC)) d( , B (AFC)) BH AF (1)
CF vuông góc BF và AB . Suy ra BH CF (2) Từ (1) và (2) BH (AFC). Vậy BH d( , B (AFC) d(B , D AC )
Xét tam giác vuông ABF ta có : BF.AB CE.AB a 3.a a 3 BH 2 2 2 2 2 2 2 BF AB CE AB 3a a a 3 Vậy d(B , D AC ) 2
Câu 4. (3,0 điểm) Trong một tiết học môn Toán, giáo viên mời ba học sinh , A ,
B C thực hiện trò chơi chơi như sau : Mỗi bän , A ,
B C chọn ngẫu nhiên một số nguyên khác 0 thuộc khoâng ( 6;6) và lần
lượt thế vào ba tham số của hàm số 4 2 y ax bx
c ; nếu đồ thị hàm số thu được có ba điểm cực trị
đều nằm phía trên trục hoành thì được nhận thưởng. Tính xác suất để ba học sinh , A , B C được nhận thưởng. Giải 3 ( n ) 10 Hàm số có ba cực trị ab 0 x 0 3 2 y ' 4ax 2bx 0 2x(2ax b) 0 b x 2a 2 2 b b b b
Đồ thị hàm số có ba điểm cực trị là ( A 0;c), B ; c , C ; c 2a 4a 2a 4a Trường hợp 1 : Nếu a
0 thì A là điểm cực tiểu nên đồ thị hàm số có ba điểm cực trị đều nằm phía trên trục hoành a 0 a 0 a { 5; 4; 3; 2; 1} b 0 b 0 b {1;2;3;4;5} có 5.5.5 125 (cách) y 0 c 0 c {1;2;3;4;5} A Trường hợp 2 : Nếu a 0 thì ,
B C là điểm cực tiểu nên đồ thị hàm số có ba điểm cực trị đều nằm phía trên trục hoành a 0 a 0 b 0 b 0 y 0 B 2 b y 0 c C 4a Dễ suy được c 0 và 4a {4;8;12;16;20} Ta có các khâ năng sau : 2 b Với c 1 1, b 1 a {1;2;3;4;5} có 5 (cách) 4a 2 b Với c 1 1, b 2 a {2;3;4;5} có 4 (cách) 4a 2 b Với c 1 1, b 3 a {3;4;5} có 3 (cách) 4a 2 b Với c 1 1, b 4 a {5} có 1 (cách) 4a 2 b Với c 2 2 , b 1 a {1;2;3;4;5} có 5 (cách) 4a 2 b Với c 2 2 , b 2 a {1;2;3;4;5} có 5 (cách) 4a 2 b Với c 2 2 , b 3 a {2;3;4;5} có 4 (cách) 4a 2 b Với c 2 2 , b 4 a {3;4;5} có 3 (cách) 4a 2 b Với c 2 2 , b 5 a {4;5} có 2 (cách) 4a 2 b Với c 3 3 , b 1 a {1;2;3;4;5} có 5 (cách) 4a 2 b Với c 3 3 , b 2 a {1;2;3;4;5} có 5 (cách) 4a 2 b Với c 3 3 , b 3 a {1;2;3;4;5} có 5 (cách) 4a 2 b Với c 3 3 , b 4 a {2;3;4;5} có 4 (cách) 4a 2 b Với c 3 3 , b 5 a {3;4;5} có 3 (cách) 4a 2 b Với c 4 4 , b 1 a {1;2;3;4;5} có 5 (cách) 4a 2 b Với c 4 4 , b 2 a {1;2;3;4;5} có 5 (cách) 4a 2 b Với c 4 4 , b 3 a {1;2;3;4;5} có 5 (cách) 4a 2 b Với c 4 4 , b 4 a {2;3;4;5} có 4 (cách) 4a 2 b Với c 4 4 , b 5 a {2;3;4;5} có 4 (cách) 4a 2 b Với c 5 5 , b 1 a {1;2;3;4;5} có 5 (cách) 4a 2 b Với c 5 5 , b 2 a {1;2;3;4;5} có 5 (cách) 4a 2 b Với c 5 5 , b 3 a {1;2;3;4;5} có 5 (cách) 4a 2 b Với c 5 5 , b 4 a {1;2;3;4;5} có 5 (cách) 4a 2 b Với c 5 5 , b 5 a {2;3;4;5} có 4 (cách) 4a
Trong trường hợp này có : 101 (cách) Suy ra có tất câ 125 101 226 (cách chọn) 226 113 Vậy xác suất là 1000 500 3 2 2 x x y y 2x 1 0 (1)
Câu 5. (2,5 điểm) Giâi hệ phương trình 2 x x 2 3y 2 2y (2) Giải 2
Điều kiện: x 0, y 3 3 2 2 3 2 2 2 2 x x y y 2x 1 0 (x x y x ) (x xy x) (xy x) (1 y ) 0 2 x (x y 1) x(x y 1) x(y 1) (1 y)(1 y) 0 2 x (x y 1) x(x y 1) (y 1)(x y 1) 0 2 (x y 1)(x x y 1) 0 x y 1 2 x x y 1 0 Với x y 1 thay vào (2) ta được 2 2 y 1 y 3 3y 2 2y 3y 2 y 1 (2y y 3) 0 3 5 y x 2y 3 2 2 (2y 3)(y 1) 0 1 3y 2 y 1 y 1 0 (VN ) 3y 2 y 1 5 3
Trường hợp này có nghiệm ; 2 2 Với 2 2 x x y 1 0 1 x x y , vì 2 x 0 1 x x 1 y 1 2
Kết hợp điều kiện ta được y 1 3 2 2 3x 3x 1 0 3 21 Ta có 2 2 x x 1 y x x 1 1 0 x 0, 3 2 3 x x 0 6 3 21 0 x 0, 3 (vì x 0) 6 3 21 7
Xét vế trái của (2) : f (x) x x 2 với 0 x f (x) 2 6 4 2 Xét vế phải ta có 2 f (y) 3y 2 2y với y 1 3 3 3 Ta có 3 f '(y) 4y 0 8y 3y 2 3 192y 128y 9 0 y 2 3y 2 4 5 Suy ra 1 f (y)
nên phương trình vô nghiệm 8 5 3
Vậy hệ phương trình có nghiệm duy nhất ; 2 2 Câu 6. (2,5 điểm) a b c
1) Cho ba số thực dương , a ,
b c . Tìm giá trị nhô nhất củaP 2b c 2c 3a 2a 3b
2) Chứng minh rằng n
C chia hết cho 3 với mọi n nguyên dương 3n 1 a ( 6u 9v 4w) u 2b 3c 35 1 1) Đặt v 2c 3a b (9u 4v 6w) 35 w 2a 3b 1 c (4u 6v 9w) 35 1 6u 9v 4w 4u 6v 9w 9u 4v 6w 1 9v 4w 4u 9w 9u 4v P 18 35 u v w 35 u u v v w w 1 4v 4u 4w 4v 4w 4u 5v 5w 5u 18 35 u v v w u w u v w 1 3 ( 18 2. 16 2 16 2. 16 3 125) 35 5 5
Vậy giá trị nhô nhất của P là a b c 3 n n n n n (3 )! 1.2.3...(3 1).3 1.2.3...(3 1) 2) n 1 C 3. .3 3. n C C chia hết cho 3 3n 3n 1 3 n !.(2n)! 1.2.3...n.(2n)! 1.2.3...(n 1).(2n)! n