Đề thi chọn HSG Toán 12 THPT năm học 2018 – 2019 sở GD và ĐT Hà Nội

LỜI GIẢI ĐỀ THI CHỌN HỌC SINH GIỎI LỚP 12, THÀNH PHỐ HÀ NỘI NĂM HỌC 2018-2019 −x
Câu 1: (4 điểm) Cho hàm số y = C = + 2
có đồ thị ( ) và đường thẳng d có phương trình y x m , x +1
m là tham số. Tìm m để d cắt (C) tại hai điểm phân biệt A và B sao cho tổng hệ số góc của
các tiếp tuyến với (C) tại A và B là lớn nhất. Lời giải  1  1 −
Tập xác định D = ℝ \ − y′ = 2 . Ta có đạo hàm .   (2x+ )2 1 −x 2
Phương trình hoành độ giao điểm
= x + m ⇔ g(x) = 2x + 2(m + ) 1 x + m = 0 2 . x +1 2 2
∆′ = m + 2m +1− 2m = m +1 > 0, m ∀  Ta có   1  1
nên đường thẳng d luôn cắt đồ thị (C) tại hai g   −  = − ≠ 0, m ∀   2  2
điểm phân biệt A , B với mọi giá trị thực m . S = −(m + ) 1  Gọi x x
1 , 2 là hoành độ của điểm A và B khi đó  m . P =  2  1 1  2
4S −8P + 4S + 2 2 Suy ra K   = − + = − = −(4m + 2) ≤ 2 − . (2  2 x + )2 1 (2x +  )2 1 4P + 2S +1 1 2  ( )
Vậy tổng hệ số góc lớn nhất của các tiếp tuyến với (C) tại A và B bằng 2 − đạt được khi m = 0 .
Câu 2: (5 điểm) a) Giải phương trình 2 cos x = 1− x Lời giải Xét hàm số 2
f (x) = cos x + x −1 với x ∈ ℝ .Ta có f '(x) = −sin x + 2x ;
f ' (x) = −cos x + 2 .Vì f ' (x) > 0 ∀x ∈ ℝ ⇒ f '(x) đồng biến trên ℝ . Mà f '(0) = 0 suy ra
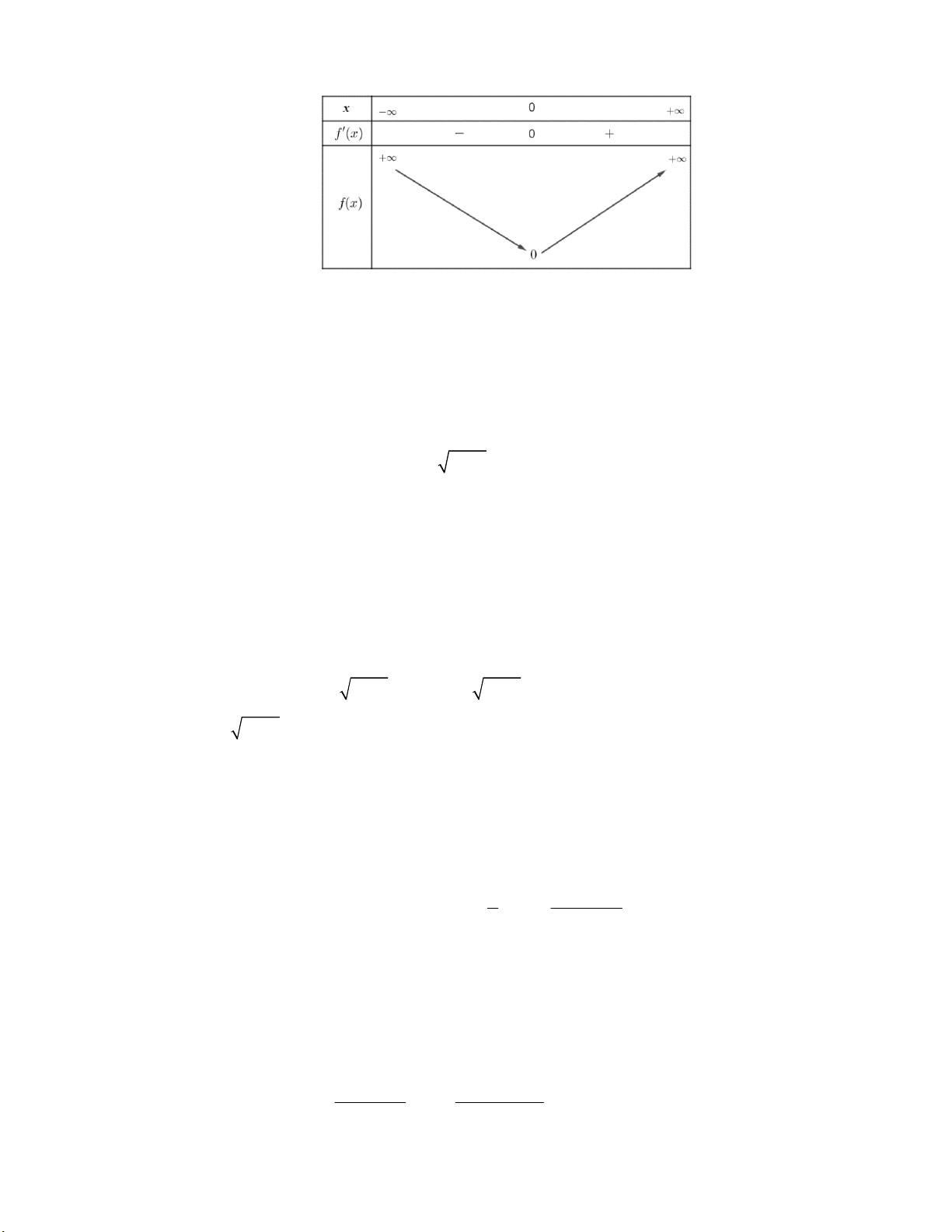
phương trình f '(x) = 0 có nghiệm duy nhất x = 0 . Bảng biến thiên: 1
Từ bảng biến thiên suy ra f (x) = 0 ⇔ x = 0 .
Vậy phương trình đã cho có nghiệm là x = 0 . 2 2
x + 3y + 2xy −6x − 2y + 3 = 0
b) Giải hệ phương trình   2 x 
− y + 5 = 2x y + 3  Lời giải Ta có: 2 2
x + 3y + 2xy − 6x − 2 y + 3 = 0
⇔ x + ( y − ) x +( y − )2 2 2 2 3
3 + 2 y + 4 y − 6 = 0 2
⇒ 2 y + 4 y −6 ≤ 0 ⇔ 1≤ y ≤ 3 ( ) 1 . Lại có: 2
x − y + 5 = 2x y + 3 2
⇔ x − 2x y + 3 + y + 3+ 2(1− y) = 0 ⇔ (x− y + )2 3
+ 2(1− y) = 0 ⇒ 2(1− y)≤ 0 ⇔ y ≥1 ( ) 2 . Từ ( ) 1 và ( )
2 ⇒ y = 1.Thay y = 1 vào hệ được x = 2 . x = 2
Vậy hệ có nghiệm là   .  y =1  2 Câu 3: 1 a
(3 điểm) Cho dãy số (a xác định bởi a = , n a = ; n = 1, 2,... n ) 1 n 1 + 2 2 a − a +1 n n
a) Chứng minh dãy số (a là dãy số giảm. n )
b) Với mỗi số nguyên dương n, đặt b = a + a + ... + a . Tính lim b . n 1 2 n n n→+∞ Lời giải a −a a − n n ( n )2 2 1 a) Xét hiệu a − a = − a = . n 1 + n 2 n 2 a − a +1 a − a +1 n n n n 2
Từ cách xác định dãy số ta có a > 0∀n và 2 *
a − a +1 > 0 ⇒ a − a < 0 n ∀ ∈ N n n n n 1 + n
Vậy (a là dãy số giảm. n ) 2
a − a +1+ a −1 a −1 b) Ta có n n n a = =1 n + n 1 + 2 2 a − a +1 a − a +1 n n n n 2 a −1 1 a − a +1 1 ⇒ a −1 n n n = ⇒ = = a + n 1 + 2 a − a +1 a −1 a −1 n a −1 n n n 1 + n n 1 1 ⇒ a = − n a −1 a −1 n 1 + n 1 1 1
Suy ra b = a + a + ... + a = − = + 2 (1) n 1 2 n a
−1 a −1 a −1 n 1 + 1 n 1 +
Lại có: Dãy số (a là dãy số giảm, bị chặn dưới bởi 0 nên có giới hạn, giả sử n ) 2 a
lim a = a ⇒ lim a = a ⇒ a = ⇒ a = 0 a = (2) n n 1 + 2 n n→+∞ n→+∞ a − a + hay lim 0 1 n→+∞
Từ (1) và (2) ta có lim b = 1. n n→+∞
Câu 4: (6 điểm)
1) Trong mặt phẳng tọa độ Oxy , cho tam giác ABC nội tiếp đường tròn tâm I , đường cao AH .
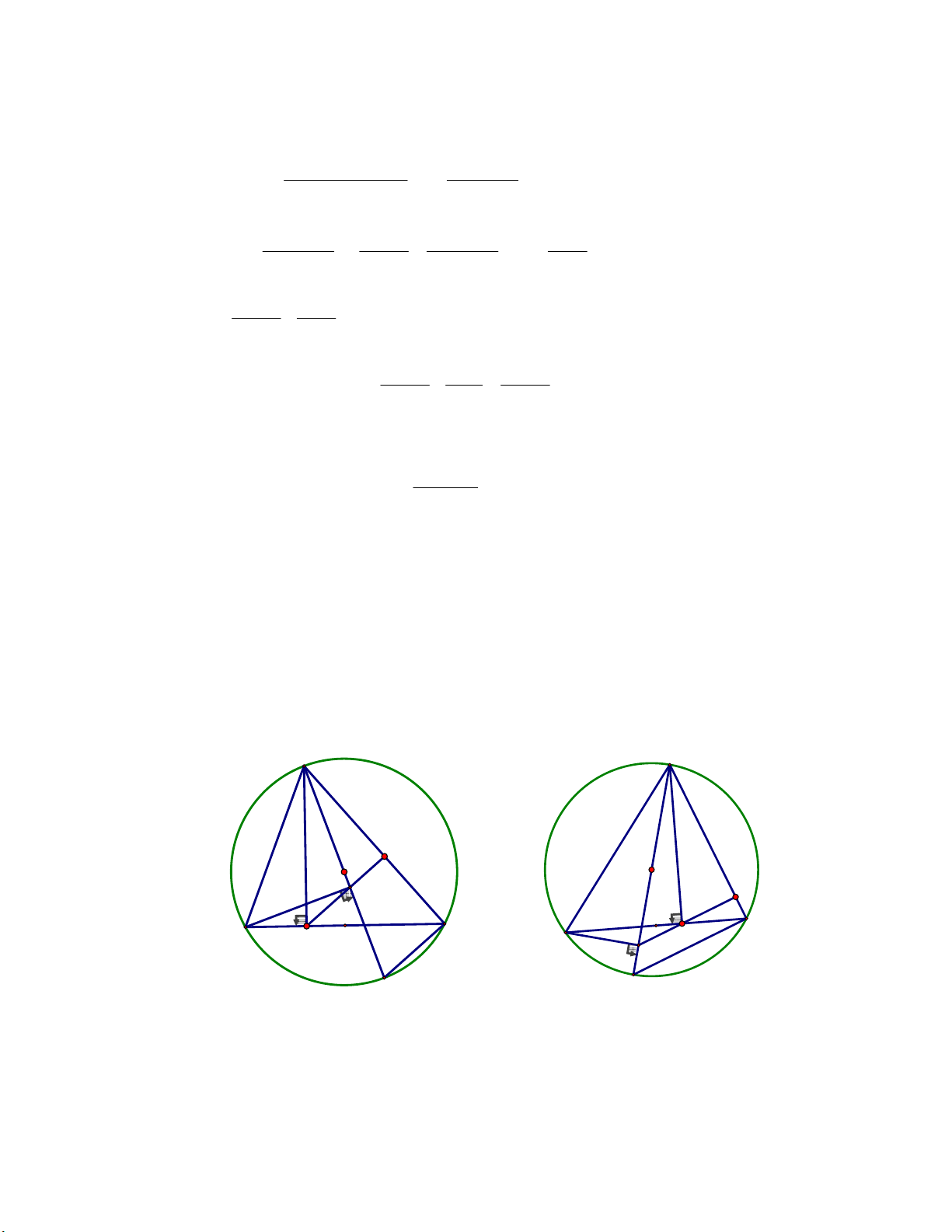
Gọi E là hình chiếu của B trên AI , HE cắt AC tại P . Gọi M là trung điểm của BC . Biết H (6; 4 − ) ; P(11; ) 1 và M (10; 4 − ) . Lời giải A A P I I E P M C C B H M H B E F F Hình 1 Hình 2
H không trùng M nên tam giác ABC không cân.
Vẽ đường kính AF của đường tròn ( I ) . 3
Ta có AHB = AEB = 90° nên bốn điểm ,
A E, H , B cùng thuộc một đường tròn.
Từ đó ta có ABH = HEF = AFC (với hình 1) hoặc ABH = AEH = AFC (với hình 2).
nên HP//CF , lại có AC ⊥ CF suy ra HP ⊥ AC . Ta có HP (5;5)
Do vậy đường thẳng AC qua P (11; ) 1 có vtpt là n (1; )
1 có phương trình x + y –12 = 0
Đường thẳng BC qua H (6; 4
− ) và M (10; 4
− ) có phương trình y = 4 − .
C là giao điểm của AC và BC , tọa độ điểm C là nghiệm của hệ phương trình
x + y –12 = 0 x = 16  ⇔   y = 4 −  y = 4 − Vậy C (16; 4 − ) và do M (10; 4
− ) là trung điểm của BC nên B(4; 4 − ).
Đường thẳng AH vuông góc với BC và qua H (6; 4
− ) có phương trình x = 6 .
x + y –12 = 0 x = 6
A là giao điểm của AH và AC nên tọa độ là nghiệm của hệ  ⇔  x = 6  y = 6
Vậy A(6;6); B(4; 4 − );C (16; 4 − ). 2)
a) Theo quy tắc hình hộp ta có: AC ' AB AD AA '
AC ' = AB + AD + AA ' ⇒ AQ = AM + AN + AP . AQ AM AN AP AC ' AB AD AA ' 3 1 1 1
Mà M, N, P, Q đồng phẳng nên = + + ⇒ = + + . ( Vì AC’ AQ AM AN AP AQ AM AN AP 1
là đường chéo hình lập phương ABCDA’B’C’D’ nên AB = AD = AA' = AC ' ). 3 1 1 1 1
b) Dễ dàng chứng minh kết quả quen thuộc của tứ diện vuông là: = + + . 2 2 2 2 AH AM AN AP 2 1 1 1  1 1 1  Mà + + <  + +  2 2 2 AM AN AP  AM AN AP  1 1 1 1 3 ⇒ < + + = ⇒ AQ < 3AH AH AM AN AP AQ
Câu 5: (2 điểm) Cho a,b,c là các số thực không âm thỏa mãn 2 2 2
a + b + c = 1 . Tìm giá trị lớn nhất của 4
biểu thức P = a + b + c − 4abc . Lời giải 1
Không mất tính tổng quát giả sử a ≥ b ≥ c thì từ 2 2 2
1 = a + b + c 2 2
⇒ 1 ≤ 3a ⇒ a ≥ . 3 Mặt khác: 2 2 2
2bc ≤ b + c = 1− 1 2
a ⇒ 0 ≤ 2bc ≤ 1− = 1 ⇒ 0 ≤ bc ≤ . 3 3 3 Ta có: 2 2
P = a ( − bc) + (b + c) 2 2 1 4 .1         2 ≤ a +
= (1+ 2bc) (1− 4bc)2 
(b +c) (1−4bc) +1 +1 a Dấu bằng xảy ra khi = b + c(*) 1 − bc Đặ 1
t t = bc ⇒ 0 ≤ t ≤ , suy ra được 2 P ≤ ( + t )( 2 t − t + ) 3 1 2 16 8
2 = 32t − 4t + 2 3  6 t =  1  12
Xét hàm số f (t ) 3
= 32t − 4t + 2, t ∈ 0;    ; f ′(t ) 2 = 96t − 4 = 0 ⇔ .  3   − 6 t = (l)  12     f ( ) 1 50 6 0 = 2, f   = , f   ≈ 1, 4556   .  3  27  12   1 a  = c = b = 0 ( )* 2
Suy ra GTLN f (t) = 2 khi t = 0 ⇒   ⇒ . c = 0  1 a = b =  2  1 a = b =
Kết luận: max P = 2 , đạt được khi 
2 , hoặc các hoán vị của nó.  c = 0
Tập thể thầy cô trên Nhóm Toán VD -VDC giải bài: 1. Thầy Binh Nguyen 2. Thầy Khải Nguyễn
3. Cô Trang Nguyễn Thị Thu
4. 1. Thầy Lê Thanh Bình – 2. Thầy Huỳnh Đức Vũ 5. Thầy Trần Minh Ngọc
Tổng hợp : Thầy Lê Tài Thắng 5
Document Outline

• [toanmath.com] - Đề thi chọn HSG Toán 12 THPT năm học 2018 – 2019 sở GD và ĐT Hà Nội
• LG - HSGHaNoi2018