Đề thi chọn HSG Toán 12 THPT năm học 2018 – 2019 sở GD và ĐT Vĩnh Phúc

Nhóm toán VD-VDC
ĐỀ VÀ HDG HỌC SINH GIỎI 12 VĨNH PHÚC 2018-2019 Câu 1. Cho hàm số 4 2
y = x − 14x + 20x + 4 có đồ thị (C) . Viết phương trình tiếp tuyến của (C) biết
tiếp tuyến song song với đường thẳng ∆ : y = −4x + 15.
Câu 2. Giải phương trình (2cos x − )
1 (2sin x + cos x) + sin x = sin 2x 4 3
Câu 3. Tìm tất cả các giái trị thực của tham số 3 2 2
m để hàm số y = x + (m + )
1 x + 3mx − m đồng 3 2
biến trên khoảng (−1;+∞) .
Câu 4. Tìm tất cả các giá trị thực của tham số m để hàm số 3 2
y = x − 3x + m − 2 có đúng năm điểm cực trị.  1  Câu 5.
Cho dãy số (u có số hạng tổng quát u = ln 1  −  , ( *
n ∈ ℕ ) . Tính giá trị của biểu n ) n  (n + )2 1  thức 1 u 2 u 2018
H = 2019.e .e ... u e
Câu 6: Xếp mười học sinh gồm bốn học sinh lớp 12 , ba học sinh lớp 11 và ba học sinh lớp 10 ngồi
vào một hàng ngang gồm 10 ghế được đánh số từ 1 đến 10 . Tính xác suất để không có hai học
sinh lớp 12 ngồi cạnh nhau.
Câu 7: Cho hai đường thẳng Ax, By chéo nhau, vuông góc và nhận đoạn AB làm đoạn vuông góc
chung. Hai điểm M , N lần lượt di động trên Ax, By sao cho AM + BN = MN . Gọi O là trung
điển của đoạn AB . Chứng minh tam giác OMN là tam giác tù và khoảng cách từ O đến
đường thẳng MN không đổi khi M , N khi di động trên Ax, By .
Câu 8: Cho tứ diện ABCD và các điểm M , N, P lần lượt thuộc các cạnh BD, BC, AC sao cho
BD = 2BM , BC = 4BN , AC = 3AP . Mặt phẳng (MNP) cắt AD tại Q . Tính tỷ số thể tích hai
phần của khối tứ diện ABCD được chia bởi(MNP) .
Câu 9: Trong mặt phẳng với hệ trục tọa độ Oxy , cho hình vuông ABCD , điểm G (3;3) là trọng tâm
tam giác ABD . Đường thẳng đi qua A vuông góc với BG và cắt BD tại điểm E (1;3). Tìm
tọa độ các đỉnh của hình vuông ABCD biết rằng đỉnh A có tung độ lớn hơn 1.  2  3  4 
Câu 10: Cho các số thực x, y, z thuộc khoảng (0;3) thỏa mãn  −1 −1 −1 =1. Tìm giá trị  x  y  z  2 2 2
nhỏ nhất của biểu thức x y z P = + + . 4 9 16 HẾT 1 Nhóm toán VD-VDC HƯỚNG DẪN GIẢI Câu 1. Cho hàm số 4 2
y = x − 14x + 20x + 4 có đồ thị (C) . Viết phương trình tiếp tuyến của (C) biết
tiếp tuyến song song với đường thẳng ∆ : y = −4x +15. Lời giải Tập xác định R . Ta có ' 3
y = 4x − 28x + 20 . Gọi M ( 4 2
a; a − 14a + 20a + 4) là điểm thuộc đồ thị (C) mà tiếp tuyến song song với đường
thẳng ∆ : y = −4x +15. Khi đó ta có: a = 1 '  y (a) 3
= −4 ⇔ 4a − 28a + 20 = −4 ⇔ (a − ) 1 ( 2
a + a − 6) = 0 ⇔ a = −3  . a = 2
Với a = 1 ta có M (1; 1 )
1 ∈ ∆ khi đó tiếp tuyến tại M chính là ∆ nên loại. Với a = 3
− ta có M (3; −10 )
1 , phương trình tiếp tuyến tại M là: y = 4 − (x + ) 3 −101 = 4 − x −113 .
Với a = 2 ta có M (2; 4) , phương trình tiếp tuyến tại M là: y = 4 − (x − 2) + 4 = 4 − x +12 .
Vậy có hai tiếp tuyến cần tìm lần lượt có phương trình là:
y = −4x − 113; y = −4x + 12 .
Câu 2. Giải phương trình (2cos x − )
1 (2sin x + cos x) + sin x = sin 2x Lời giải Ta có
(2cos x − )1(2sin x + cos x)+sin x = sin 2x ⇔ (2cos x − )
1 (2sin x + cos x) = sin x(2cos x − ) 1 ⇔ (2cos x − )
1 (sin x + cos x) = 0  π x = + k2  π 3  1  cos x =   π ⇔ 2
⇔ x = − + k2π   3
sin x = − cos x  π x = − + kπ  4 2 Nhóm toán VD-VDC 4 3
Câu 3. Tìm tất cả các giái trị thực của tham số 3 2 2
m để hàm số y = x + (m + )
1 x + 3mx − m đồng 3 2
biến trên khoảng (−1;+∞) . Lời giải
+Tập xác định: D = ℝ . + 2
y ' = 4x + 3(m + )
1 x + 3m .Hàm số đồng biến trên khoảng (−1;+∞) khi và chỉ khi y ' ≥ 0
∀x ∈(−1;+∞) và phương trình y ' = 0 chỉ có một số hữu hạn nghiệm trên khoảng (−1;+∞) 2 ⇔ 4x + 3 2 x 4x + 3(m + )
1 x + 3m ≥ 0 ∀x ∈(−1;+∞) ⇔ 3 − m ≤ ∀x ∈(−1;+∞) ( ) 1 . x +1 2 4x + 3 2 4x + 8x + 3 +Xét hàm số ( ) x f x =
với x ∈(−1;+∞) .Ta có f '(x) = ∀x ∈(−1;+∞); x +1 (x + )2 1 1  1 
f '(x) = 0 ⇔ x = − ; f  −  = −1; lim f (x) = +∞ ; lim f (x) = +∞ .Do đó 2  2  x→+∞ x 1+ →−  1 
min f (x) = f  −  = 1 − . ( 1 − ;+∞)  2  1 + ( ) 1 ⇔ 3 − m ≤ 1
min f (x) ⇔ m ≥ .Vậy đáp số cần tìm là m ≥ . (−1;+∞) 3 3
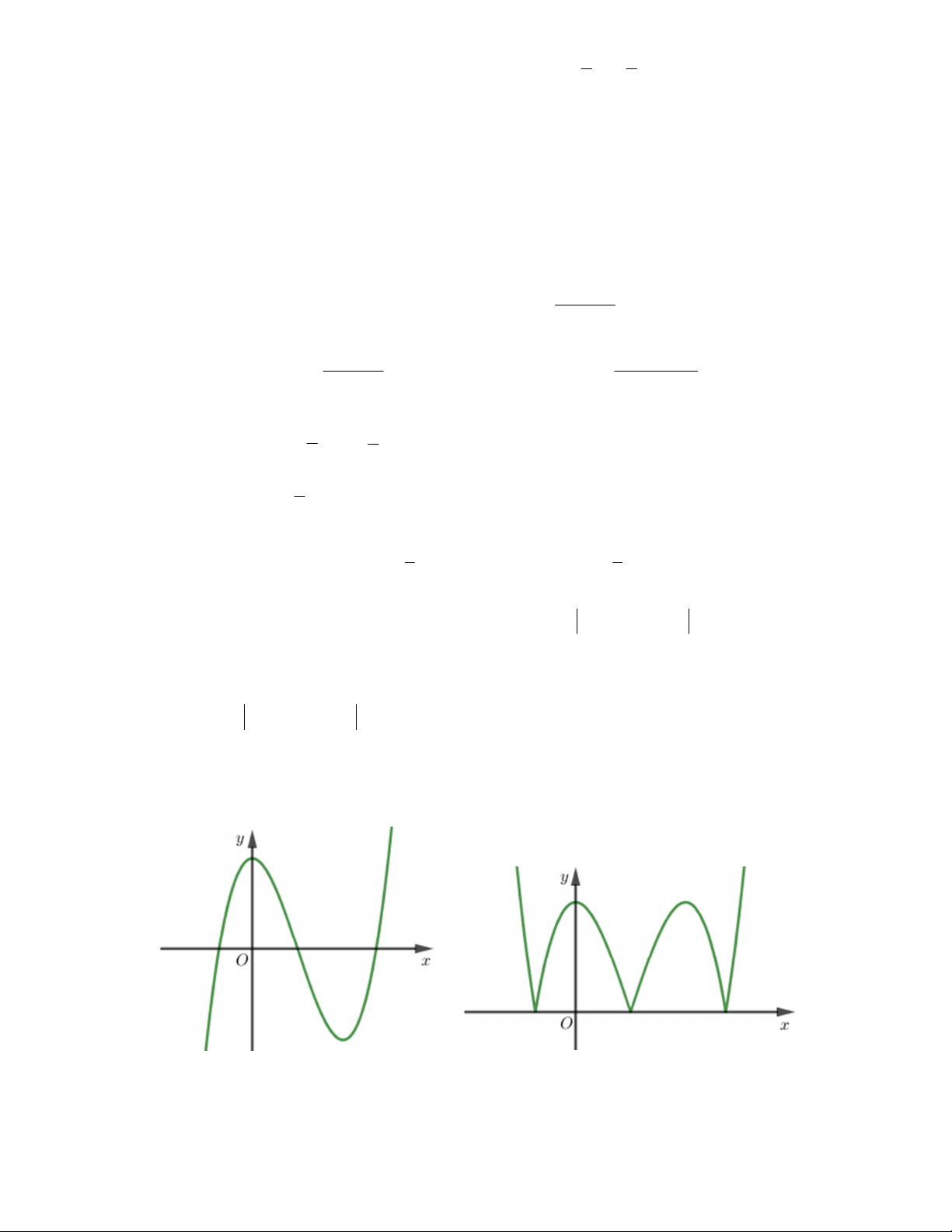
Câu 4. Tìm tất cả các giá trị thực của tham số m để hàm số 3 2
y = x − 3x + m − 2 có đúng năm điểm cực trị. Lời giải Hàm số 3 2
y = x − 3x + m − 2 có đúng năm điểm cực trị khi và chỉ khi hàm số 3 2
y = x − 3x + m − 2 cắt trục hoành tại 3 điểm phân biệt khi và chỉ khi phương trình 3 2
x − 3x + m − 2 = 0 ( )
1 có 3 nghiệm phân biệt. Ta có ( ) 3 2
1 ⇔ x − 3x = 2 − m 3 Nhóm toán VD-VDC x = 0
Xét hàm số f (x) 3 2
= x − 3x ta có f ′(x) 2
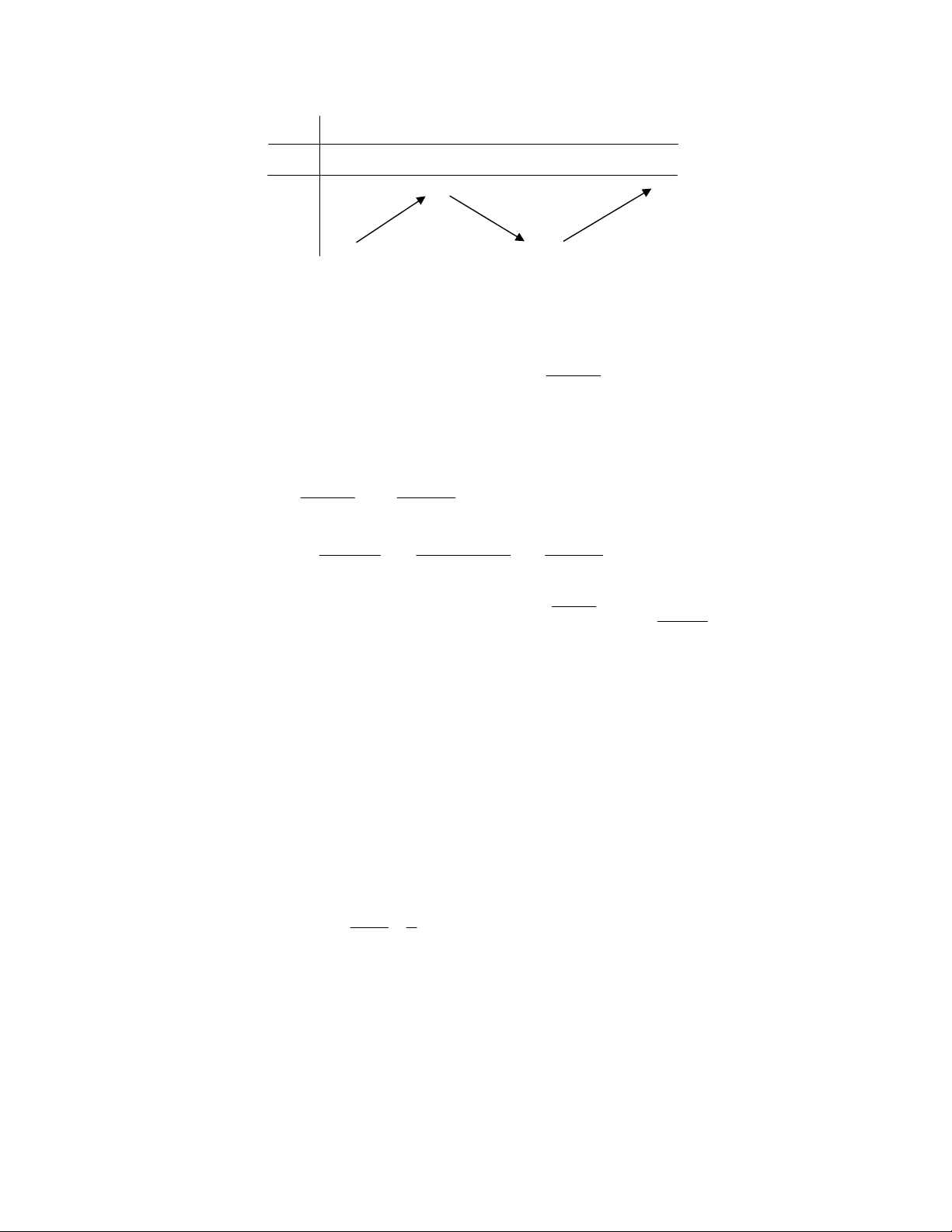
= 3x − 6x = 0 ⇔  . x = 2 x −∞ 0 2 +∞ y′ + 0 − 0 + 0 +∞ y −∞ 4 −
Từ bảng biến thiên ta có phương trình ( )
1 có 3 nghiệm phân biệt khi và chỉ khi 4
− < 2 − m < 0 ⇔ 2 < m < 6.  1 
Câu 5. Cho dãy số (u có số hạng tổng quát u = ln 1  −  , ( *
n ∈ ℕ ) . Tính giá trị của biểu n ) n  (n + )2 1  thức 1 u 2 u 2018
H = 2019.e .e ... u e Lời giải  1  n (n + ) 1 Ta có u = ln 1  −  = . n  (n + ) ln 2 1  (n + )2 1 n n k (k + 2) n! n + 2 ! n + 2 Do đó ∑u = ln ∏ ( ) = ln = ln . k + 2  n  +1 ! .2! 2 n +1 k = k = (k )2 1 1 1 ( )  ( ) 2018 2018+2 ∑ ku ln 2 2018 1 + 2020 k 1 = ( ) Suy ra 1 u 2 u 2018
H = 2019.e .e ... u e = 2019.e = 2019.e = 2019. = 1010 . 2.2019
Câu 6: Xếp mười học sinh gồm bốn học sinh lớp 12 , ba học sinh lớp 11 và ba học sinh lớp 10 ngồi
vào một hàng ngang gồm 10 ghế được đánh số từ 1 đến 10 . Tính xác suất để không có hai học
sinh lớp 12 ngồi cạnh nhau. Lời giải
+ Có 10! cách xếp bất kỳ 10 học sinh.
+ Có 6! cách xếp 6 học sinh lớp 11 và lớp 10; 6 học sinh đó tạo thành 7 chỗ trống (tính cả vị
trí hai đầu). Chọn 4 vị trí và xếp 4 học sinh lớp 12 có 47 A cách. Suy ra có 4
A .6! cách xếp 10 học sinh sao cho không có hai học sinh lớp 12 ngồi cạnh nhau. 7 4 A .6! 1 Xác suất cần tìm là: 7 P = = . 10! 6
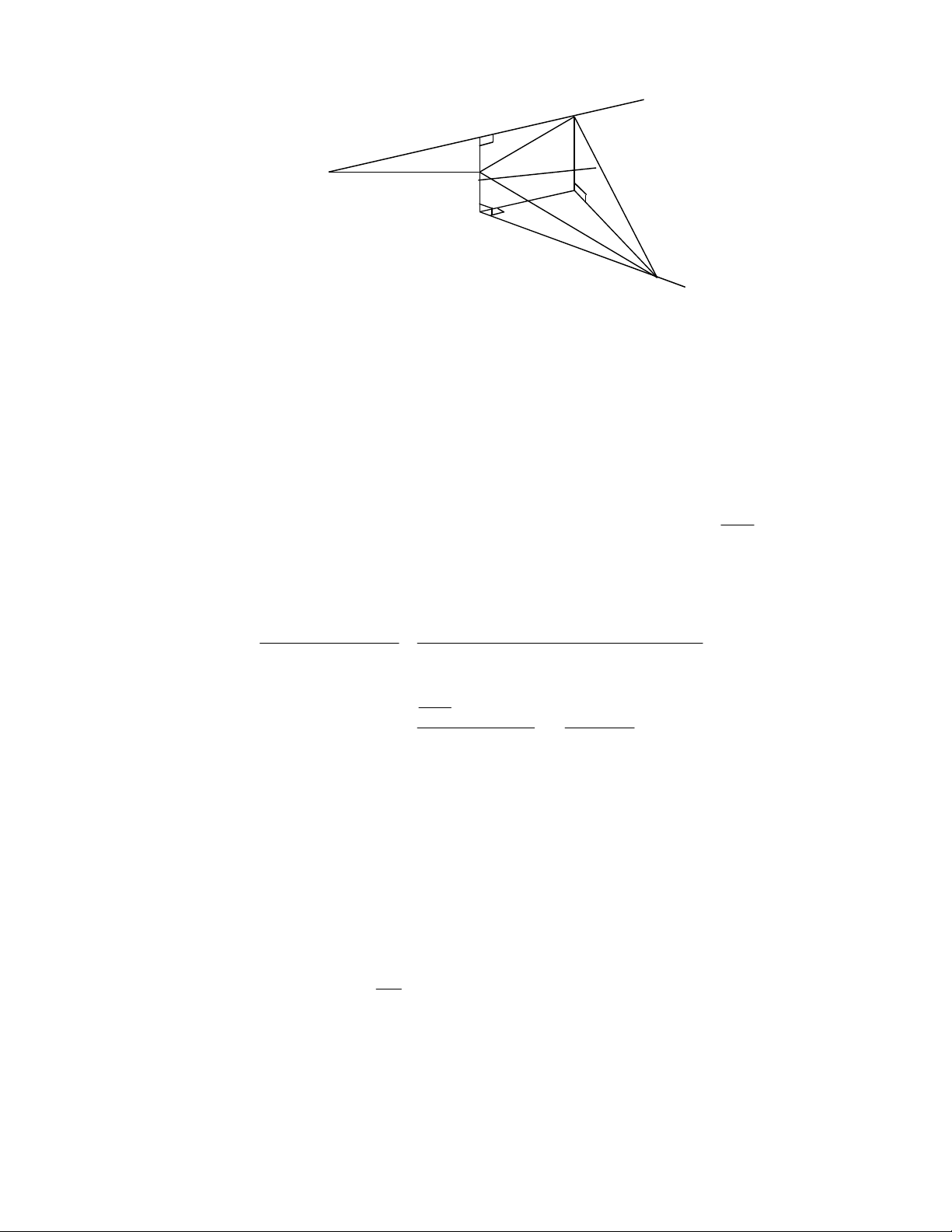
Câu 7: Cho hai đường thẳng Ax, By chéo nhau, vuông góc và nhận đoạn AB làm đoạn vuông góc
chung. Hai điểm M , N lần lượt di động trên Ax, By sao cho AM + BN = MN . Gọi O là trung
điển của đoạn AB . Chứng minh tam giác OMN là tam giác tù và khoảng cách từ O đến
đường thẳng MN không đổi khi M , N khi di động trên Ax, By . Lời giải 4 Nhóm toán VD-VDC x M A Q H O P A B y N
Dựng hình bình hành ABPM . Ta có (B ;
P BN ) = ( AM; BN ) = 90° .
AB ⊥ (PBN ) ⇒ MP ⊥ PN . Suy ra 2 2 2 2 2 2 2 2 2  2
MN = MP + PN = MP + BP + BN = AB + AM + BN  ⇒ AM . AB = . MN  = ( AM + BN ) BN 2 2 2
Xét tam giác OMN . Ta có 2 2 2
OM + ON − MN
OA + AM + OB + BN − ( AM + BN )2 2 2 2 2 cos MON = = 2OM .ON 2OM .ON 2
AB − 2AM.BN 2 2 AB = = − < 0 2OM .ON 4OM .ON
Như vậy tam giác OMN là tam giác tù.
Lấy điểm Q trên tia đối của tia Ax sao cho AQ = BN và gọi H là hình chiếu vuông góc của
O trên đường thẳng MN . Ta có O ∆ AQ = O
∆ BN ( .cg.c) ⇒ OQ = ON . O ∆ MQ = O
∆ MN ( .c .cc) ⇒ OA = OH . AB Như vậy d ( ; O MN ) = OH = không đổi. 2
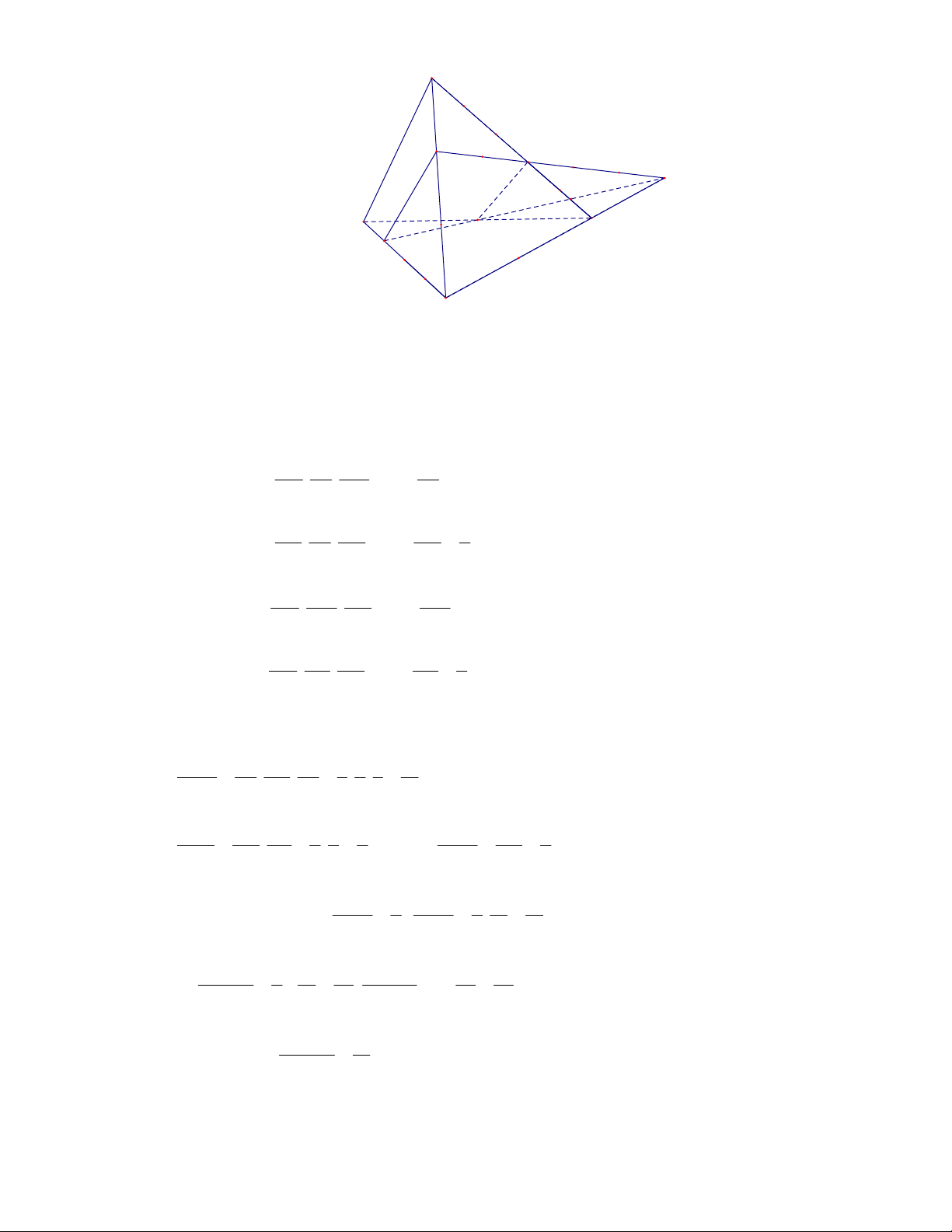
Câu 8: Cho tứ diện ABCD và các điểm M , N, P lần lượt thuộc các cạnh BD, BC, AC sao cho
BD = 2BM , BC = 4BN , AC = 3AP . Mặt phẳng (MNP) cắt AD tại Q . Tính tỷ số thể tích hai
phần của khối tứ diện ABCD được chia bởi(MNP) . Lời giải 5 Nhóm toán VD-VDC A P Q I B M D N C
Trong (BCD) , gọi I = MN ∩CD. Khi đó Q = IP ∩ AD chính là giao điểm của (MNP) và AD .
Kết hợp giả thiết và áp dụng định lí Mê-nê-la-uýt trong các tam giác sau ta có: - Với ∆
: NB . IC . MD = 1⇒ IC BCD = 3. NC ID MB ID PA IC QD QD 2 - Với ∆ACD : . . =1⇒ = . PC ID QA QA 3 - Với ∆
: DC . MI . BN = 1⇒ MI ICN = 2 . DI MN BC MN DC QI AP QI 3 - Với ∆IPC : . . =1⇒ = . DI QP AC QP 2
Áp dụng công thức tỉ số thể tích ta có: VIMQD IQ IM ID 3 2 1 2 = . . = . . = ( )1 V IP IN IC 5 3 3 15 INPC V CN CP 3 2 1 V CI 3 INPC = . = . = (2) ; ABCI = = (3) V CP CA 4 3 2 V CD 2 ABCI ABCD V 3 VIMQD 3 2 1 Từ ( )
1 ,(2) và (3) ⇒ INPC = , = . = . V 4 V 4 15 10 ABCD ABCD V V CDMNPQ 3 1 13 ABMNPQ 13 7 ⇒ = − = , =1− = . V 4 10 20 V 20 20 ABCD ABCD VABMNPQ 7 Do vậy ta có: = . V 13 CDMNPQ 6 Nhóm toán VD-VDC
Câu 9: Trong mặt phẳng với hệ trục tọa độ Oxy , cho hình vuông ABCD , điểm G (3;3) là trọng tâm
tam giác ABD . Đường thẳng đi qua A vuông góc với BG và cắt BD tại điểm E (1;3). Tìm
tọa độ các đỉnh của hình vuông ABCD biết rằng đỉnh A có tung độ lớn hơn 1. Lời giải Cách 1: A K B G M H E D C
Gọi M là trung điểm của cạnh AD , H = AE ∩ BM , K = GE ∩ AB .
Vì AG ⊥ BE và BG ⊥ AE nên G là trực tâm tam giác ABE ⇒ GE ⊥ AB , GE//AD . Có KG BG = và GE BG = KG GE ⇒ =
mà AM = MD ⇒ KG = GE ⇒ G là trung điểm AM BM MD BM AM MD
x = 2x − x của K G E KE ⇒  ⇒ K (5;3) .
 y = 2.y − y K G E
AB đi qua K (5;3) và có một vectơ pháp tuyến EG = (2;0) ⇒ AB : x − 5 = 0 .
Vì A∈ AB ⇒ A(5;a) với a >1. Vì KAG = 45° ⇒ A
∆ KG vuông cân nên KA = KG ⇒ (  = a − )2 a 5 3 = 4 ⇒ 
. Vì a > 1 ⇒ A(5;5) . a = 1 x − 5 = −6 Ta có: AC = 3AG C ⇒  ⇒ C ( 1 − ;− ) 1 .  y − 5 = −6 C x − 5 = −6 Có AD = 3 D GE ⇒  ⇒ D (−1;5) .  y − 5 = 0 D x − 5 = 0 Vì B AB = DC ⇒  ⇒ B (5;− ) 1 .  y − 5 = 6 − B Cách 2: 7 Nhóm toán VD-VDC A B G M H I E D C
Gọi M là trung điểm của cạnh AD , H = AE ∩ BM , I là tâm của hình vuông ABCD và a 5 2 a
AB = a . Ta có: 2 2 BM = AM + AB = mà BG = 5 BM ⇒ BG = . 2 3 3 2 AB 2 5
Xét tam giác ABM ta có: 2
BH .BM = AB ⇒ BH = = a . BM 5 Vì ∆ BH BE BH BG BHE # ∆BIG ⇒ = . 2 2 ⇒ BE = =
a ⇒ EI = BE − 2 2 2 BI = a − a BI BG BI 3 3 2 2 2 2 =  1   1  a
a . Xét tam giác IGE có: 2 2
GE = GI + EI =  .a 2  +  .a 2  = . 6  6   6  3 Mà a
G (3;3) và E (1;3) nên GE = 2 . Do đó = 2 ⇒ a = 6 . 3
Xét tam giác ABE có: 2 2 2
AE = AB + BE − 2 A . B BE.cos 45° 2 2  2 2  2 2 2 5 a 5 2 = +   − 2. . . a a a a a =  ⇒ AE = = 2 5 . 3  3 2 9   3
Gọi A(x; y) với y > 1.  a 2 2 2   AG = = 2 2
(3− x) +(3− y) = 8 Ta có: 2 2  3 ⇒ 
⇒ (1− x) − (3− x) = 12  (1
 − x)2 + (3 − y)2 = 20  AE = 2 5  y = 1
⇒ x = 5 ⇒ + ( − y)2 4 3 = 8 ⇒ ( − y)2 3 = 4 ⇒  ⇒ A(5;5).  y = 5 x − 5 = −6 Vì AC = 3AG C ⇒  ⇒ C ( 1 − ;− ) 1 .  y − 5 = −6 C a 2 1 1 Có EI =
= DI mà IG = IA (tính chất trọng tâm) nên GE // AD và 6 3 3 x − 5 = 6 − AD = 3 D GE ⇒  ⇒ D (−1;5) .  y − 5 = 0 D 8 Nhóm toán VD-VDC x − 5 = 0 Vì B AB = DC ⇒  ⇒ B (5;− ) 1 .  y − 5 = −6 B  2  3  4 
Câu 10: Cho các số thực x, y, z thuộc khoảng (0;3) thỏa mãn  −1 −1 −1 =1. Tìm giá trị  x  y  z  2 2 2
nhỏ nhất của biểu thức x y z P = + + . 4 9 16 Lời giải  x  3 = a 0 < a <  2  2    y 0 < b < 1  = b  Đặt  3 ⇒  3 ; Áp dụng BĐT  0 < c < z 4  = c  4  13 0 < t <
a + b + c = t  4 ( + + )
(a +b +c)3 3 3 ≥ 27 t a b c abc ⇔ abc ≤ = 27 27 Từ điều kiện ta có:  1   1   1 
 −1  −1  −1 = 1 ⇔ (ab + bc + ca) = 2abc + (a + b + c) −1  a   b   c  . 2 4 − 3
⇒ ab + bc + ca ≤ t + t −1 ⇒ 2
− (ab + bc + ca) 3 ≥ t − 2t + 2 27 27 4
Mà P = (a + b + c)2 − 2(ab + bc + ca) 3 2 ≥ −
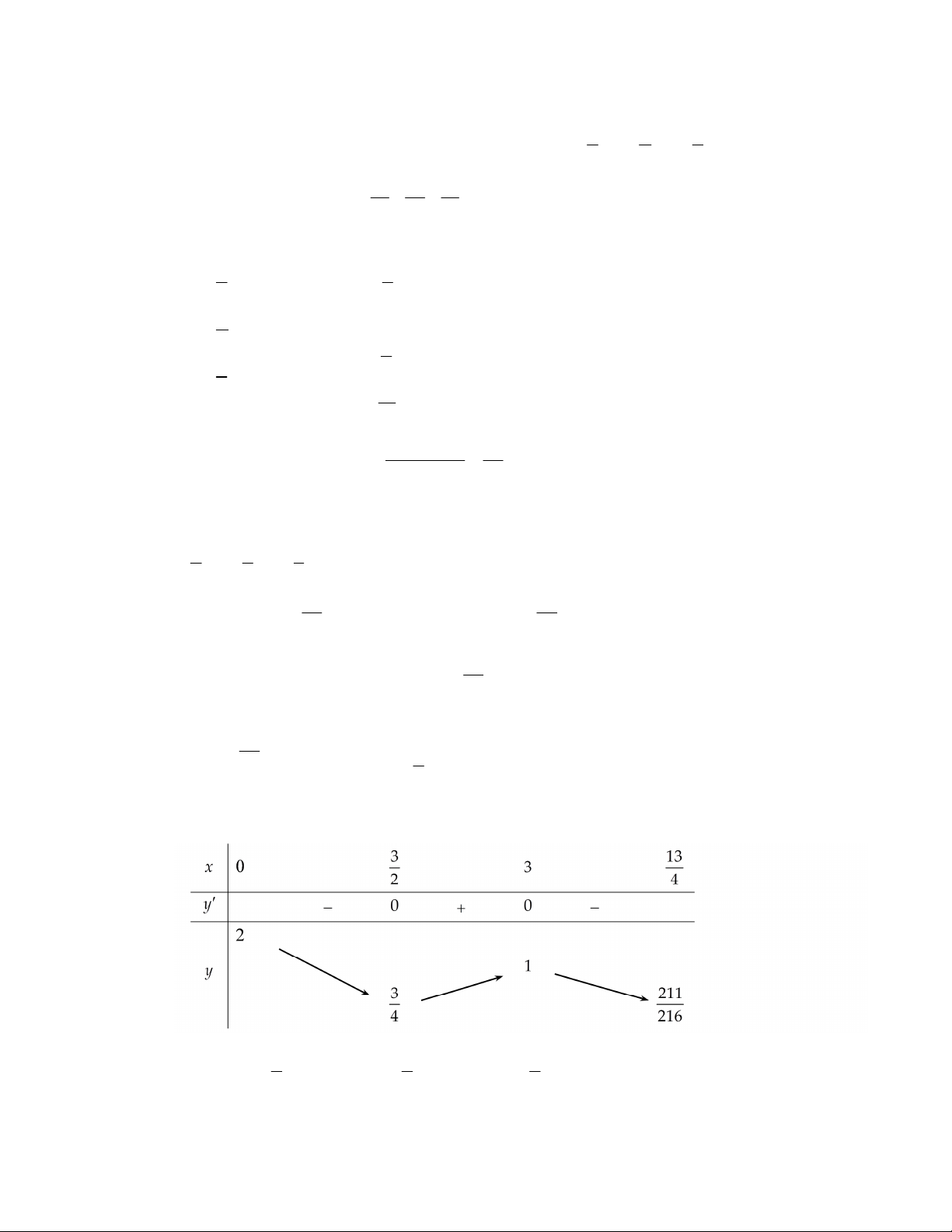
t + t − 2t + 2 . Coi P là hàm số theo biến t 27 t = 3 4 − Thì 2  P′ =
t + 2t − 2 = 0 ⇔ 3 . 9 t =  2 BBT 3 1  3 
Vậy min P = khi a = b = c = ⇒ ( ;
x y; z ) = 1; ; 2 . 4 2  2  9