UBND THÀNH PHỐ BẮC NINH
ĐỀ THI CHỌN HSG CẤP THÀNH PHỐ
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO NĂM HỌC 2023-2024 Môn thi: Toán 7 ĐỀ CHÍN H THỨC Ngày thi: 10/04/2024
Thời gian làm bài: 120 phút, Không kể thời gian phát đề (Đề gồm 01 trang)
Bài 1. (4,0 điểm) Tính giá trị các biểu thức sau: 3 3    7 5 7 12 3  0 0,375 0,3 1) A  .  .  ; 11 12 B  . 23 17 17 23 23 5 5 0,625  0,5   11 12
2) C  x  3y  2z, biết x  y  5; y  z  8  . Bài 2. (4,0 điểm) 11 3 1) Tìm x biết : 2  x  . 2 2
3x 1 7 y  4 3x  7 y 5 2) Tìm x, y thỏa mãn:   . 4 5 3x Bài 3. (3,0 điểm) 3    1) Cho 2 2 12a 3b 5c  a b  a ; c c  bd ( a, ,
b c, d khác 0). Chứng minh rằng:    .  12b  3c  5d  d 2) Cho a, ,
b c,d là các số nguyên dương thỏa mãn 2 2 2 2 2023 a  b  c  d  2024 . Chứng minh rằng
a  b  c  d là hợp số. Bài 4. (7,0 điểm)
1) Cho tam giác ABC vuông tại , A  B  2
C kẻ AH vuông góc với BC tại H. Trên tia HC lấy điểm
D sao cho HD  HB . Từ C kẻ đường thẳng vuông góc với đường thẳng AD tại E .
a) Tam giác ABD là tam giác gì? Vì sao?
b) Chứng minh rằng DE  DH; HE//AC.
c) Gọi K là giao điểm của AH và CE, lấy điểm I bất kỳ thuộc đoạn thẳng HE I  H, I  E. 3AC Chứng minh rằng  IA  IK  IC. 2 2) Cho tam giác ABC có  BAC  15 ,  
ABC  45 . Trên tia đối của tia CB lấy điểm D sao cho CD 2CB . Tính số đo  ADC . Bài 5. (2,0 điểm)
1) Một số nguyên dương được gọi là số may mắn nếu số đó gấp 99 lần tổng tất cả các chữ số của nó.
Tìm số may mắn có bốn chữ số.
2) Cho tam giác ABC vuông tại A, độ dài cạnh huyền bằng 2015. Trong tam giác ABC lấy 2031121
điểm phân biệt bất kỳ. Chứng minh rằng tồn tại ít nhất hai điểm có khoảng cách không lớn hơn 1. Hết
Họ và tên thí sinh…………………………SBD………………………………
(Giám thị coi thi không giải thích gì thêm) UBND THÀNH PHỐ BẮC NINH
HDC ĐỀ THI CHỌN HSG CẤP THÀNH PHỐ
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO NĂM HỌC 2023-2024 Môn : Toán 7 Câu Đáp án Điểm 7 5 7 12 30 1 A  .  .  23 17 17 23 23 1,5 7 5 7 12 3  0 7  5 12  3  0 A  .  .   .     23 17 17 23 23 23 17 17  23 0,75 7 30 2  3  .1   1  . 23 23 23 0,75 3 3 0,375  0,3   11 12 B  5 5 1,5 0,625  0,5   11 12 3 3 3 3 3 3 0,375  0,3      11 12 8 10 11 12 B   5 5 5 5 5 5 0,625  0,5      11 12 8 10 11 12 0,75  1 1 1 1  3.       8 10 11 12  3    1 1 1 1  5 0,75 5.       8 10 11 12 
C  x  3y  2z, biết x  y  5; y  z  8. 1,0
Ta có C  x  3y  2z   x  y  2 y  z 0,5
Thay x  y  5; y  z  8 vào C ta được: C  5  2. 8    1  1 0,5 11 3 2.1 Tìm x biết : 2  x  . 2 2 2,0 11 3 2   x  11 3 2  2 2  x    2 2 11 3 2   x    2 2 11 3 TH1: 2 2
 x   x  4  x  2 2 2 11 3 TH2: 2 2  x   x  7  x   7 2 2 Vậy x  2  ; 7
3x 1 7 y  4 3x  7 y  5 2.2 Tìm x, y thỏa mãn:   4 5 3x 2,0  1 x  3  x 1  0 
+ Nếu 3x  7y  5  0 thì 3    7 y  4  0 4 y  0,5  7
+ Nếu 3x  7y  5  0 thì áp dụng tính chất của dãy tỉ số bằng nhau ta có: 3x 1 7 y  4 3x  7 y  5     0,75   3x 7 y 5 3x 7 y 5    0  x  3 4 5 9 9 3x 3.3 1 7 y  4 Từ (1)    y  2 4 5 0,75  1 4   Vậy x, y ; ,   3;2  3 7   3  12a  3b  5c  a 3.1 Cho 2 2 b  a ;
c c  bd ( a, b, c, d khác 0). Chứng minh rằng:    .  12b  3c  5d  d 1,5 Từ 2 b  ac suy ra a b  ; b c Từ 2 c  bd suy ra b c  . c d 0,5 Do đó: a b c   b c d
Áp dụng tính chất dãy tỉ số bằng nhau, ta có: a b c a  b  c 0,5 12 3 5    b c d 12b  3c  5d 3 3      Suy ra a 12a 3b 5c        b   12b  3c  5d  3    Hay a b c 12a 3b 5c  . .    b c d 12b  3c  5d  0,5 3    Vậy a 12a 3b 5c     d  12b  3c  5d 
Cho a,b,c,d là các số nguyên dương thỏa mãn 2 2 2 2 2023 a  b  c  d  2024 . Chứng minh
3.2 rằng a  b  c  d là hợp số. 1,5 Xét hiệu  2 2 2 2
a  b  c  d   a  b  c  d  2 2 2 2
 a  a  b  b  c  c  d  d 0,5  aa   1  bb   1  cc   1  d d   1
Chứng minh được: aa   1 2  ;bb   1 2;cc   1 2  ;d d   1 2  0,5 Do đó :  2 2 2 2
a  b  c  d   a  b  c  d 2 mà 2 2 2 2 2023 a  b  c  d  2024 2  a  b  c  d 2
 , lại có a,b,c, d là các số nguyên dương nên a  b  c  d  2 0,5
Suy ra: a  b  c  d là hợp số.
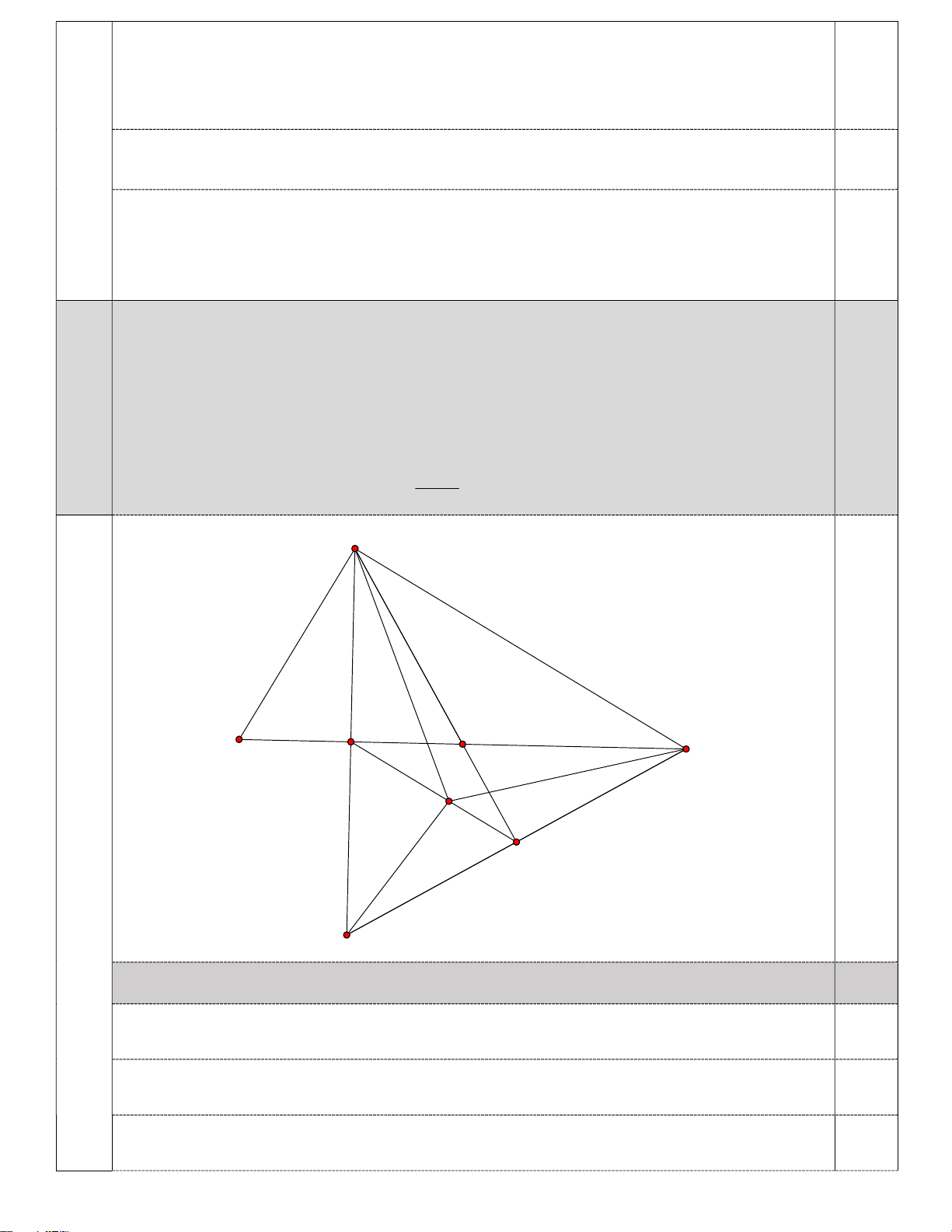
Cho tam giác ABC vuông tại , A  B  2
C kẻ AH vuông góc với BC tại H. Trên
tia HC lấy điểm D sao cho HD  HB . Từ C kẻ đường thẳng vuông góc với đường thẳng AD tại E.
a) Tam giác ABD là tam giác gì? Vì sao? 4.1 5,0
b) Chứng minh rằng DE  DH; HE//AC.
c) Gọi K là giao điểm của AH và CE, lấy điểm I bất kỳ thuộc đoạn thẳng HE  3AC
I  H , I  E  . Chứng minh rằng  IA  IK  IC. 2 A 1 D 1 0,5 B H 1 C 2 1 I 1 E K
1) Tam giác ABD là tam giác gì? Vì sao? 1,5 Ta có: A  BC vuông tại , A suy ra 𝐵 + 𝐶 = 90 0,5
Mà 𝐵 = 2𝐶 nên 𝐶 = 30 ; 𝐵 = 60 Chứng minh A  HB  A  HD( . c g.c)  AB  AD  nên ABD cân tại A 0,5
Mà 𝐵 = 60 ⇒ 𝛥𝐴𝐵𝐷 là tam giác đều. 0,5
2) Chứng minh rằng DE  DH; HE//AC. 2,0 * Chứng minh: DH  DE Chứng minh A  HD  C
 ED (cạnh huyền – góc nhọn) 0,75 Suy ra DH  DE * Chứng minh: HE//AC. Ta có: A
 BD là tam giác đều (cmt);suy ra 𝐵𝐴𝐷 = 60 , 𝐴𝐵 = 𝐴𝐷 = 𝐵𝐷
Suy ra 𝐴 = 𝐵𝐴𝐶 − 𝐵𝐴𝐷 = 90 − 60 = 30 0,75 A
 DC có 𝐴 = 𝐶 = 30 nên A
 DC cân tại D, suy ra AD  CD
và 𝐷 = 180 − 2𝐶 = 180 − 2.30 = 120 Suy ra 𝐷 = 𝐷 = 120 Do H
 DE cân tại D⇒ 𝐻 = 𝐸 = = = 30 0,75
Suy ra 𝐴 = 𝐸 = 30 ⇒ 𝐻𝐸//𝐴𝐶 3AC 3) Chứng minh rằng  IA  IK  IC. 1,0 2 A  EC  A  EK(g. . c g)  AC  AK  A  CK cân tại A
Ta có: 𝐶𝐴𝐾 = 𝐴 + 𝐷𝐴𝐻 = 30 + 30 = 60 nên A  CK là tam giác đều 0,5
Suy ra: AC  CK  AK  3AC  AC  CK  AK (3)
Áp dụng BĐT tam giác vào các tam giác AIC,CIK, KIA có:
AC  IA  IC;CK  IC  IK; AK  IA  IK
AC  CK  AK  2IA  IC  IK  4 0,5 AC
Từ (3) và (4) suy ra : AC  IA  IC  IK  3 3 2   IA  IC  IK 2 Cho tam giác ABC có  BAC  15 ,  
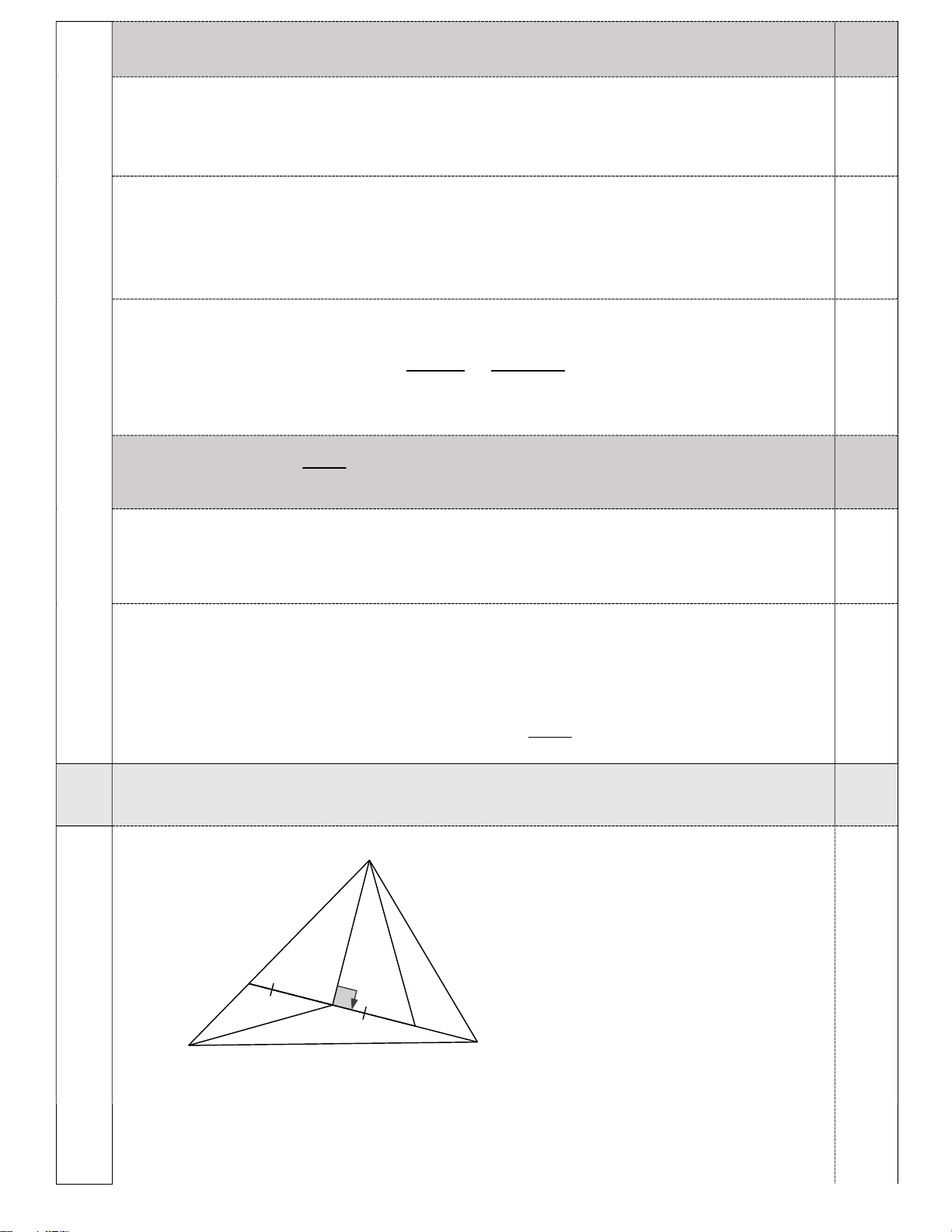
ABC  45 . Trên tia đối của tia CB lấy điểm D 4.2 2,0
sao cho CD 2CB . Tính số đo  ADC . D C E F A B Kẻ DE  CA 0,75 Xét A  BC , có  0 0 0 0
ACB  180  45 15  120   0 ACD  60 hay  0 ECD    0 60 EDC  30
Trên tia đối của tia EC lấy điểm F sao cho EC  EF . Ta chứng minh được D  CF đều  1 CE  CD  CE  CB 2   CBE   0 CEB  30   EDC  E  BD cân tại E . 0,75  0 CBE  30   EBA   CBA   0 0 0 CBE  45  30  15  B  EA cân tại E.  EA  EB  ED  A  ED vuông cân   0 ADE  45 0,5 Vậy  ADC   ADE   0 EDC  75
5.1 Một số nguyên dương được gọi là số may mắn nếu số đó gấp 99 lần tổng tất cả các chữ 1,0
số của nó. Tìm số may mắn có bốn chữ số.
Giả sử số cần tìm là 𝑎 𝑎 … 𝑎 => 𝑎 𝑎 … 𝑎 = 99(𝑎 + 𝑎 + ⋯ + 𝑎 )
Suy ra 1000. 𝑎 + 100. 𝑎 + 10. 𝑎 + 𝑎 = 99(𝑎 + 𝑎 + 𝑎 + 𝑎 ) 0,25
hay 901𝑎 + 𝑎 = 89𝑎 + 98𝑎
do 89𝑎 + 98𝑎 ≤ (89 + 98). 9 = 1683 nên a1 = 1. 0,25 Khi đó 𝑎 = 10 − 𝑎 +
Giải thích được 11 + 𝑎 − 9𝑎 = 0 và tìm được a2 = 7, a4 = 2, a3 = 8 và a1 = 1.
Vậy số cần tìm là 1782. 0,5
Cho tam giác ABC vuông tại A, độ dài cạnh huyền bằng 2015. Trong tam
5.2 giác ABC lấy 2031121 điểm phân biệt bất kỳ. Chứng minh rằng tồn tại ít nhất hai điểm 1,0
có khoảng cách không lớn hơn 1.
Chia cạnh huyền BC thành 2015 đoạn thẳng bằng nhau. Từ các điểm chia đó vẽ
các đường thẳng song song với hai cạnh AB và AC ta được 2015 tam giác vuông 0,5
cân có cạnh huyền bằng 1 và (2014 + 2013 + …+ 1) hình vuông có đường chéo bằng 1.
Do đó trong tam giác ABC có tất cả 2015 + (2014x2015)/2 = 2031120 hình (vừa
hình vuông có đường chéo bằng 1 vừa tam giác vuông cân có cạnh huyền bằng 1).
Như vây trong 2031121 điểm sẽ tồn tại ít nhất hai điểm nằm trong một hình nào 0,5 đó.
Với hai điểm đó thì khoảng cách của nó không lớn hơn 1 (đpcm)
------------------------------- HẾT -----------------------------