Đề Thi Chọn HSG Toán 8 Huyện Gia Viễn 2025-2026 Có Đáp Án

PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI CHỌN HSG LỚP 8 THCS HUYỆN GIA VIỄN NĂM HỌC 2025-2026 Môn: Toán Ngày thi: 30/3/2025
ĐỀ THI CHÍNH THỨC
Thời gian làm bài:150 phút (không kể thời gian giao đề)
Họ và tên thí sinh :..............................................................Số báo danh .......................................
Họ và tên, chữ ký: Giám thị thứ nhất: ............................................................................................
Giám thị thứ hai:...............................................................................................
Câu 1 (4,5 điểm) 2 2 æ + - ö æ - ö Cho biểu thức 2x x 6 1 2 x 6 A ç = ç + - : ÷ ç ÷ çx + 2 ÷ + ÷ với x  2. 2 çè x - 4 x- 2 x + 2÷ ÷ ç ø è 2- x ÷ ÷ ø
a) Rút gọn biểu thức A.
b) Tìm giá trị của x để A nhận giá trị âm.
c) Tìm giá trị nguyên của x để biểu thức A nhận giá trị nguyên.
Câu 2 (4,0 điểm)
a) Phân tích đa thức sau thành nhân tử: ( x − y − z)2 2 2
− y + 2yz − z .
b) Cho 3 số nguyên dương a ;a ;a có tổng bằng 2023 2022 . Chứng minh rằng: 1 2 3 3 3 3
a + a + a chia hết cho 3. 1 2 3
Câu 3 (4,5 điểm) 1 1 1 3 −
a) Giải các phương trình sau: + + = . 2 2 2
x + 7x +12 x + 9x + 20 x +11x + 30 2
b) Tính giá trị của biểu thức: y 5y − 4x B = +
. Biết 2x − y = 6. x − 3 x − 5
c) Tìm tất cả các cặp số nguyên (x;y) thoả mãn: 2 2
x + 5y + 4xy = 2023.
Câu 4 (5,0 điểm)
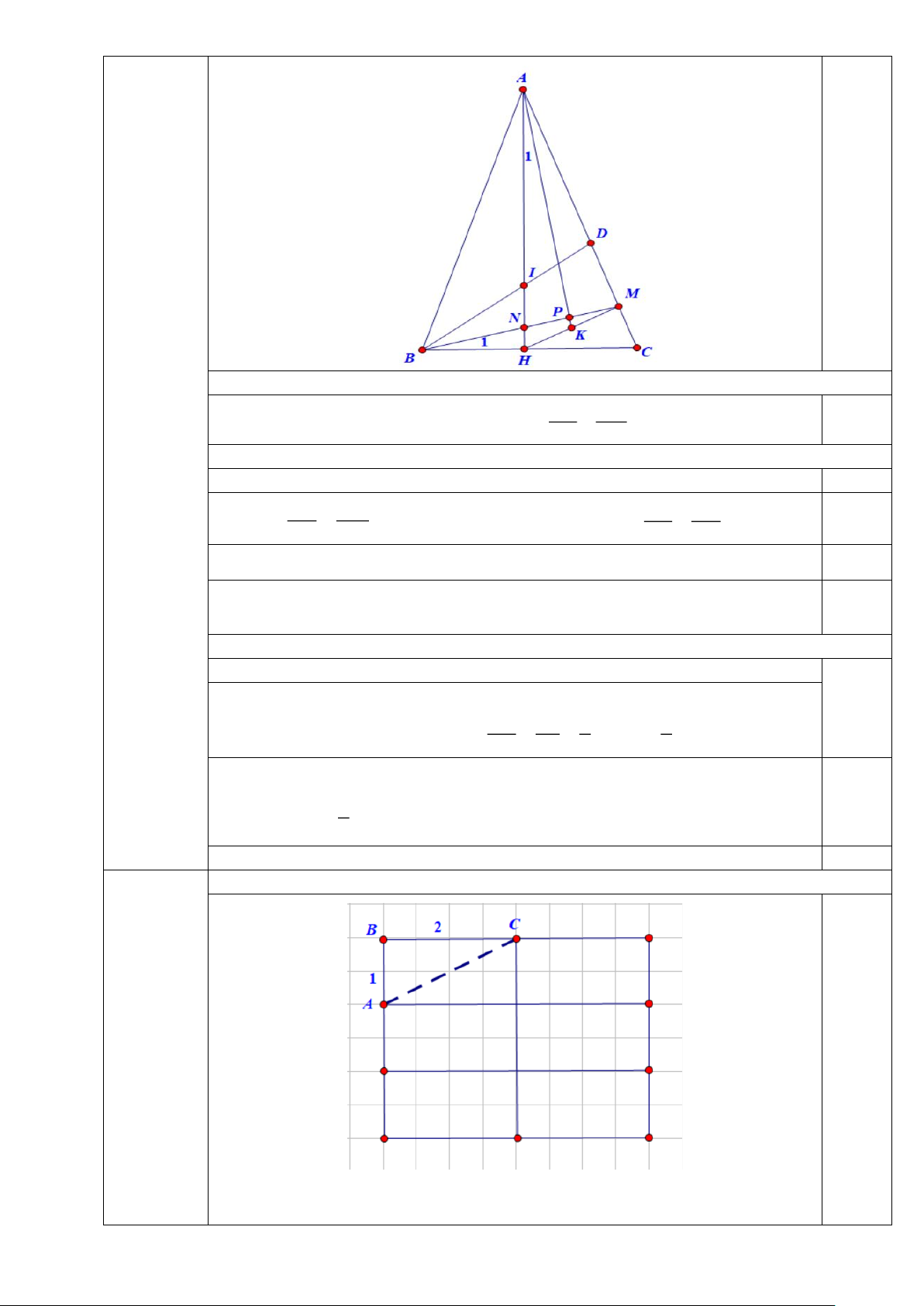
Cho tam giác ABC cân tại A (góc A nhọn), đường cao AH cắt tia phân giác BD tại
điểm I. Gọi M là hình chiếu của điểm H trên cạnh AC, K là trung điểm của HM. a) Chứng minh AH HM = . HC CM
b) Chứng minh AK vuông góc với BM.
c) Biết AI = 5cm, HI = 4cm. Tính độ dài cạnh BC.
Câu 5 (2,0 điểm)
a) Xét hình chữ nhật kích thước 3cm x 4 cm. Chứng minh rằng với 7 điểm bất kì
nằm trong hình chữ nhật, luôn có thể chọn ra hai điểm có khoảng cách nhỏ hơn 3. b) Cho hai số thực ,
x y thỏa mãn x  −1; y > 1 và x + y = 1. Tìm giá trị nhỏ nhất 2 2 æ ö æ ö của biểu thức 1 1 P = çx + 1 ÷ ç + ç ÷ + çy - 1 ÷ + ÷ . çè x + 1÷ ø çè y - 1÷ ÷ ø --------Hết.--------
Thí sinh không được sử dụng tài liệu. Giám thị không giải thích gì thêm. Trang 1
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO HƯỚNG DẪN CHẤM HUYỆN GIA VIỄN
ĐỀ THI CHỌN HSG LỚP 8 THCS NĂM HỌC 2025-2026 Môn: Toán Ngày thi 30/3/2023
(Hướng dẫn chấm này gồm 04 trang) Câu Đáp án Điểm
a) (2,0 điểm) 2 2 2 æ x + x- 6 1 2 ö æ x - 6ö A ç = ç + - : ÷ ç ÷ çx + 2 ÷ + ÷ với x  2. 2 ç ÷ çè - - + ÷ ç ÷ x 4 x 2 x 2ø çè 2- x ÷ ø æ 2 ç 2x + x- 6 x + 2 (x- ) ö 2 2 2 2 ÷ x æ - 4 x - 6ö A = ç + - : ÷ ç ÷ 0,5 ç ÷ ç - ÷ ( çè x- ) 2 (x + ) 2 (x- ) 2 (x + ) 2 (x- ) 2 (x + ) 2 ÷ ç ø è x- 2 x- 2 ÷ ÷ ø 2 2x 2 A = : 0,75 (x- ) 2 (x + ) 2 x- 2 2 2 2x x - 2 x A = . = ( 0,75 x- ) 2 (x + ) 2 2 x + 2 b) (1,5 điểm) Câu 1 2 x 2 x
4,5 điểm) Ta có: A = ( x  2) < 0 x + 2
nhận giá trị âm thì A < 0 nên x+ 2 0,5
 x + 2  0 (vì x2  0 với mọi x  2)  x  −2 (thỏa mãn đk) 0,75
Vậy x  −2 thì A nhận giá trị âm. 0,25 c) (1,5 điểm) 2 2 x x - 4 4 4 0,5 Ta có: A = = + = x- 2+
với x Z, x  2. x + 2 x + 2 x + 2 x + 2 4
Để A nhận giá trị là số nguyên thì
Î Z Þ x + 2 Î Ư(4) 0,25 x + 2
Þ x + 2 Î {1;- 1;2;- 2;4;- }
4 Þ x Î {- 1;- 3;0;- 4;2;- } 6 0,5
x Z, x  2   x 1 − ; 3 − ;0; 4 − ;−  6 0,25 Vậy x 1 − ; 3 − ;0; 4 − ;− 
6 thì A nhận giá trị là số nguyên. a) (2,0 điểm)
(x − y − z)2 2 2
− y + 2yz − z 1,0
= (x − y − z)2 −( y − yz + z ) = (x − y − z)2 −( y − z)2 2 2 2
= (x − y − z + y − z)(x − y − z − y + z) 0,5
= (x − 2z)(x − 2y) 0,5 Câu 2 b) (2,0 điểm) (4,0 điểm) Ta có: 2023 2022 3; 2023
a + a + a = 2022
nên a + a + a 3. M 0,5 1 2 3 1 2 3 Với n  Z thì 3
n − n = n( 2
n − ) = (n− )n(n+ ) 3 1 1 1 3 M  n − n 3 M 0,5
(vì n – 1; n; n + 1 là ba số nguyên liên tiếp nên tích chia hết cho 3). Trang 2 Do đó: ( 3 a − a ) 3; M ( 3 a − a ) 3; M ( 3 a − a 3 M 1 1 2 2 3 3 )  ( 3 a − a ) + ( 3 a − a ) + ( 3 a − a 3. M  ( 3 3 3
a + a + a − a + a + a 3 M 0,5 1 2 3 ) ( 1 2 3) 1 1 2 2 3 3 )
Mà a + a + a 3 M nên 3 3 3
a + a + a 3. M 0,5 1 2 3 1 2 3 a) (1,5 điểm) 1 1 1 3 + + = − . (1) 0,25 2 2 2
x + 7x +12 x + 9x + 20 x +11x + 30 2 ĐK: x  3 − ; x  4 − ; x  5 − ; x  6 − (1) 0,25 1 1 1 1 1 1 3  − + − + − = − .
x + 3 x + 4 x + 4 x + 5 x + 5 x + 6 2 1 1 3 3 3 0,5  − = −  = − x + 3 x + 6 2 (x +3)(x +6) 2  (x + )(x + ) 2 3 6 = 2
−  x + 9x + 20 = 0  (x + 4)(x + 5) = 0 0,25 x = 4 −  
(không tmđk). Vậy phương trình đã cho vô nghiệm. 0,25 x = 5 − b) (1,5 điểm) y 5y − 4x Ta có: B = +
. ( x  3; x  5); 2x − y = 6  y = 2x − 6 . Câu 3 x − 3 x − 5 0,5 (4,5 điểm)
2x − 6 5.(2x − 6) − 4x Khi đó: B = + . x − 3 x − 5 2(x − ) 3 6x − 30 6(x − ) 5 B = + = 2+ = 2+ 6 = 8. 1,0 x − 3 x − 5 x − 5 c) (1,5 điểm) Ta có: 2 2
x + 5y + 4xy = 2023. (1) (x,y  Z)  ( x + y)2 2 2 + y = 2023. 0,25 Với n  Z thì 2
n  0;1;2;3 (mod 4)  n  0;1(mod 4)
Vậy x,y  Z thì (x + y)2 2  0;1 (mod 4) và 2 y  0;1 (mod 4) 0,5 nên (x + y)2 2 2
+ y  0;1;2 (mod 4) mà 2023  3 (mod 4) 0,5
Do đó, phương trình ( x + y)2 2 2
+ y = 2023, không có nghiệm nguyên. 0,25
Vậy không có số nguyên x, y nào thỏa mãn yêu cầu đề bài. Trang 3 a) (2,0 điểm) 
Chứng minh AHM ∽ HCM (g-g) AH HM  = 2,0 HC CM b) 1,5 điểm)
Gọi N, P lần lượt là giao điểm của BM và AH, AK. Câu 4: AH HM
(5,0 điểm) - Ta có: =
mà HM = 2HK, BC = 2CH nên AH HK = 0,5 HC CM BC CM
- Chứng minh AHK ∽ BMC (c-g-c) µ µ  A = B 0,5 1 1
- Chứng minh NAP ∽ NBH (g-g) · · 0,5
 APN = BHN , mà · 0 · 0
BHN = 90  APN = 90  AK ⊥ BM c) (1,5 điểm)
Ta có: AH = AI + HI = 5 + 4 = 9 (cm)
Vì BD là tia phân giác của ABC nên 0,5 BH HI 4 5
BI là tia phân giác của ABH  = =  AB = .BH AB AI 5 4
Xét ABH vuông tại H, có: 2 2 2
AH + BH = AB 2  5  2 2  9 + BH = .BH 
  BH = 12 (c ) m 0,5  4 
ABC cân tại A, có BC = 2.BH = 2.12 = 24 (cm) 0,5
a) (1,0 điểm) Câu 5 0,25 (2,0 điểm)
Chia hình chữ nhật kích thước 3cm x4 cm thành 6 hình chữ nhật nhật
kích thước 1 cm x 2 cm (hình vẽ). Trang 4
Theo nguyên lý Dirichlet, trong 7 điểm bất kì nằm trong hình chữ nhật
kích thước 3cm x4 cm (hay nằm trong 6 hình chữ nhật nhật kích thước 1
cm x 2 cm) thì luôn tồn tại 2 điểm cùng thuộc một chữ nhật nhật kích 0,5
thước 1 cm x 2 cm và khoảng cách giữa hai điểm này luôn nhỏ hơn độ dài đường chéo AC = 2 2 1 + 2 = 5  3.
Vậy với 7 điểm bất kì nằm trong hình chữ nhật kích thước 3cm x4 cm, 0,25
luôn có thể chọn ra hai điểm có khoảng cách nhỏ hơn 3. b) (1,0 điểm)
x  −1; y > 1 thì x +1 0; y - 1 0 ; x + y = 1 (x + ) 1 + (y − ) 1 = 1 Đặt ( x + ) 1 = ; a (y − ) 1 = b ( ,
a b  0)  a+ b = 1 2 2 2 2 0,25 æ 1 ö æ 1 ö æ 1ö æ 1ö P = çx + 1 ÷ ç + ç ÷ + çy - 1 ÷ + ÷ = a ç ÷ + ç ÷ è + ø ç ÷ ç ÷ + b ç ÷ + ç ÷ x 1 çè y - 1÷ ç ø è a÷ ø çè b÷ ø
Áp dụng bất đẳng thức Bunhiacopxki, có: 0,25 2 2 2 é 1 1 ù æ ö æ ö æ ö êa ç ÷ + ç ÷ + b ç ÷ ú + ê ç ÷ ( 1 1 2 2 . 1 + 1 )³ a ç + b ÷ + + ç ÷ è ø ç ÷ ú ç ÷ a è bø çè a b÷ ø êë úû 1 1 4 0,25 Mà ,
a b  0, a + b = 1, + ³ = 4 nên Þ P ³ ( + )2 25 2. 1 4 Þ P ³ a b a + b 2 Dấu “=” xảy ra khi 1 - a = b = 1 3 Þ x = ; y = . 2 2 2 Vậy 25 - P = khi 1 3 x = ; y = . 0,25 min 2 2 2 Lưu ý:
- Lời giải chỉ trình bày tóm tắt, học sinh trình bày hoàn chỉnh, lý luận chặt chẽ mới cho điểm tối đa.
- Học sinh có thể trình bày nhiều cách giải khác nhau nếu đúng thì cho điểm tương ứng./. Trang 5