UBND THÀNH PHỐ BẮC NINH
ĐỀ THI CHỌN HSG CẤP THÀNH PHỐ
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO NĂM HỌC 2023-2024
Môn thi: Toán 8 Ngày thi: 10/4/2024 ĐỀ CHÍNH THỨC
Thời gian làm bài: 150 phút, không kể thời gian phát đề (Đề gồm 01 trang)
Câu 1. (4,0 điểm) 2 2  2x  8 x  2x  3
x  x  6  1
1. Cho biểu thức H    : 
với x  1; x  2; x  3 . 2 2 2  x  3x  2 x  5x  6 x  4x  3 x 1  
a. Rút gọn H . H
b. Tìm tất cả các giá trị của x để biểu thức
nhận giá trị là số tự nhiên. x  2 2. Cho a, ,
b c là các số thực khác 0 thỏa mãn: 2 2 2 2 2 2
a  c  c;c  b  ;
b b  a  a . Tính giá trị
biểu thức T  (a  b)(b  c)(c  a) .
Câu 2. (4,0 điểm)
1. Cho hai đa thức P(x),Q(x) có bậc khác 0 và có hệ số cao nhất đều bằng 1, thỏa mãn
P(Q(x))  P(x).Q(x) x
 . Tính Q(2024)  P(2023).
2. Chọn ngẫu nhiên một số tự nhiên có 4 chữ số. Tính xác suất để số được chọn là số có 4 chữ
số thỏa mãn chữ số đứng sau lớn hơn chữ số đứng trước. Câu 3. (4,0 điểm)
1. Tìm tất cả các số nguyên tố m, n, p thỏa mãn 2 2 2
m  3n  5 p  8mn . p
2. Trong mặt phẳng tọa độ Oxy , cho 3 đường thẳng (d ) :y  2x  2
m  1,(d ) :y  x  2 m  m 1 2
và (d ) : y  3x  2
m  m  2 . Biết (d ) cắt (d ) và (d ) lần lượt tại A x ;y và B x ;y . 2 2  1 1  3 1 2 3 2 2
Tìm m để x  x y y 320 . 1 2     1 2  
Câu 4. (6,0 điểm)
1. Cho tam giác ABC nhọn (AB < AC), đường cao AD, CF cắt nhau tại H. Gọi M là điểm
thuộc đoạn thẳng DC sao cho BM < 2BD. Qua A vẽ đường thẳng vuông góc với AM cắt CH tại K.
a. Chứng minh rằng: K  AH ∽ A  B M .
b. Lấy G đối xứng với H qua K. Gọi P là trung điểm của BM. Chứng minh: AG  AP .
c. Khi BM = 2MC, gọi N là giao điểm của AG và BH. Chứng minh: AG = 2AN.
2. Cho hình vuông ABCD có cạnh bằng 8. Trên cạnh BC , lấy điểm M sao cho BM  5 . Gọi
N là giao điểm của đường thẳng CD và đường thẳng vuông góc với AM tại A . Gọi I là
trung điểm của MN . Hãy tính độ dài đoạn thẳng DI .
Câu 5. (2,0 điểm)
1. Cho ba số nguyên dương a, ,
b c thỏa mãn a  b  c  10. Tìm giá trị nhỏ nhất của biểu thức: a  b b  c c  a K    . c a b
2. Cho số 884 số nguyên tố phân biệt. Chứng minh rằng tồn tại hai số nguyên tố p, q trong
các số đã cho thỏa mãn p  q2024.
   HẾT   
Họ và tên thí sinh:………………………………………………………SBD………………...…
(Giám thị coi thi không giải thích gì thêm) 1 UBND THÀNH PHỐ BẮC NINH HƯỚNG DẪN CHẤM
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI CHỌN HSG CẤP THÀNH PHỐ NĂM HỌC 2023-2024
(HDC gồm 07 trang)
Môn thi: Toán 8, ngày thi: 10/4/2024 2 2  2x −8 x − 2x − 3
x − x − 6  1 =  + −
Câu Cho biểu thức H  : với 2 2 2
 x − 3x + 2 x − 5x + 6 x − 4x + 3  x −1 2.5 1.1 điểm
x  1; x  2; x  3.
1.1a Rút gọn H . 1.5 2 2  2x −8 x − 2x − 3
x − x − 6  1 có H =  + −  :
(Đk: x  1; x  2; x  3) 2 2 2
 x − 3x + 2 x − 5x + 6 x − 4x + 3  x −1 0.5  2x − 8 (x +1)(x − 3)
(x + 2)(x − 3)  1 = + − :  
(x −1)(x − 2) (x − 2)(x − 3) (x − 3)(x −1)  x −1  2x − 8 x +1 x + 2  1 = + − :   0.25  − − − −  − (x 1)(x 2) x 2 x 1 x 1
2x − 8 + (x +1)(x −1) − (x + 2)(x − 2) = .(x −1)
(x −1)(x − 2) 0.5 2 2
2x − 8 + x −1− x + 4 2x − 5 = = x − 2 x − 2 2x − 5 Vậy H =
với x  1; x  2; x  3 0.25 x − 2 H
1.1b Tìm tất cả các giá trị của x để biểu thức
nhận giá trị là số tự nhiên. 1.0 x − 2 H 2x − 5 2(x − 2) −1 2 1  1 2 có = = = − = 1− −1  1 2 2 2   x − 2 (x − 2) (x − 2) x − 2 (x − 2)  x − 2  0.25 H H mà
nhận giá trị là số tự nhiên nên {0;1} x − 2 x − 2 2 2 H  1   1  +) = 0  1− −1 = 0  −1 = 1     x − 2  x − 2   x − 2   1  1 5 −1 = 1 = 2  x = (t / m)   0.25 x − 2 x − 2 2     1 1   − 1 = 1 − = 0 (L)  x − 2  x − 2 2 2 H  1   1  +) = 1 1− −1 = 1  −1 = 0     x − 2  x − 2   x − 2  0.25 1 
−1 = 0  x − 2 = 1  x = 3 (L) x − 2 2 Vậy 5 H x = thì
nhận giá trị là số tự nhiên. 0.25 2 x − 2 Câu Cho a, ,
b c là các số thực khác 0 thỏa mãn: 2 2 2 2 2 2 a − c = ; c c − b = ;
b b − a = a . 1.5 1.2
Tính giá trị biểu thức T = (a − b)(b − c)(c − a) . điểm Có: 2 2 2 2 2 2
a − c = c (1);
c − b = b (2)
b − a = a (3)
Cộng vế với vế của (1),(2),(3), ta được: 0.5
a + b + c = 0  a + b = −c,b + c = −a,c + a = b − (3)
Nhân vế với vế của (1), (2), (3) ta được:
(a − c)(a + c)(c − b)(c + b)(b − a)(b + a) = abc 0.5 (4) (3), (4) => 0.25
(a − c)( b
− )(c − b)(−a)(b − a)( c
− ) = abc  abc(a − b)(b − c)(c − a) = abc
=> T = 1 (do abc  0 ) 0.25
Câu Cho hai đa thức P(x),Q(x) có bậc khác 0 và có hệ số cao nhất đều bằng 1, 2.0 2.1
thỏa mãn P(Q(x)) = P(x).Q(x) x
 . Tính Q(2024) − P(2023). điểm
Gọi p, q lần lượt là bậc của đa thức P(x),Q(x) . * p, q 
=> P(Q(x)) có bậc p.q ; P(x).Q(x) có bậc p + q
Từ giả thiết P(Q(x)) = P(x).Q(x) , ta có: .
p q = p + q  ( p −1)(q −1) = 1 0.5 mà * p, q 
 p −1 0;q −1 0
 p −1= q −1=1 p = q = 2 .
=> P(x),Q(x) là các đa thức bậc 2 và có hệ số cao nhất là 1. Đặt 2
P(x) = x + ax + b và 2
Q(x) = x + cx + d .
Từ P(Q(x)) = P(x).Q(x) suy ra 2 2 2 2 2
(x + cx + d ) + a(x + cx + d ) + b = (x + ax + )
b (x + cx + d ) 4 3 2 2 2
 x + 2cx + (c + 2d + a)x + (2cd + ac)x + d + ad + b 4 3 2
= x + (a + c)x + (b + d + ac)x + (ad + bc)x + bd 0.5
2c = a + c  2
c + a + 2d = b + d + ac
Đồng nhất hệ số, ta có: 
2cd + ac = ad + bc   2
d + ad + b = bd c = a c = a   c = a 2 2
a + a + 2d = b + d + a
d + a = b     
 d = b − a = −a 0.5 2 2
2ad + a = ad + ab
ad + a = ab   b = 0   2 
d + ad + b = bd
d(d + a) + b = bd Vậy 2 2
P(x) = x + a ,
x Q(x) = x + ax − a . 0.5 Do đó: 2 2
Q(2024) − P(2023) = 2024 + 2024a − a − (2023 + 2023a) = 4027
Câu Chọn ngẫu nhiên một số tự nhiên có 4 chữ số. Tính xác suất để số được chọn 2.0 2.2
là số có 4 chữ số thỏa mãn chữ số đứng sau lớn hơn chữ số đứng trước. điểm
Gọi abcd là số tự nhiên có 4 chữ số thỏa mãn chữ số đứng sau lớn hơn chữ số 0.5 3
đứng trước => a, , b ,
c d  ;0  a  b  c  d  9
=> Mỗi số abcd tương ứng với một cách chọn 4 số khác nhau (không tính
đến thứ tự sắp xếp của các số) từ tập {1;2;3;4;5;6;7;8;9}
Số cách chọn 4 số từ tập 9 số (không tính đến thứ tự sắp xếp của các số) là 9! 9! 6.7.8.9 = = = 7.2.9 = 126 (cách chọn) 0.5 4!(9 − 4)! 4!5! 2.3.4
=> có 126 số tự nhiên có 4 chữ số thỏa mãn yêu cầu bài toán 0.25
Số các số tự nhiên có 4 chữ số là: 9999 −1000 +1 = 9000 (số) 0.25
Xác suất số được chọn là số tự nhiên có 4 chữ số thỏa mãn đề bài là: 126 7 0.5 P = = 9000 500 Câu 2.0
Tìm tất cả các số nguyên tố ,
m n, p thỏa mãn 2 2 2
m + 3n + 5 p = 8mn . p 3.1 điểm Có: 2 2 2
m + 3n + 5 p = 8mnp (*) Vì 8mnp chẵn nên 2 2 2
m + 3n + 5 p chẵn, suy ra ba số ,
m n, p hoặc cùng chẵn 0.5
hoặc có đúng 1 số chẵn, hai số còn lại lẻ. Nếu ,
m n, p cùng chẵn thì m = n = p = 2 (không thỏa mãn (*)) – loại Do đó, trong ba số ,
m n, p có đúng 1 số chẵn, hai số còn lại lẻ.
Trường hợp 1. m = 2 , n, p lẻ. Ta có phương trình: 2 2
3n + 5 p + 4 = 16np (1) 0.5
Vì n, p là số nguyên tố lẻ nên 2 2
n , p  1 (mod 8)
VT(1)  3.1+ 5.1+ 4  4 (mod 8) mà VP(1) =16np  0 (mod 8) => mâu thuẫn.
Trường hợp 2. n = 2, m, p lẻ. Ta có phương trình: 2 2
m + 5 p +12 = 16mp (2)
Vì m, p là số nguyên tố lẻ nên 2 2
n , p  1 (mod 8) 0.25
VT(2) 1+ 5.1+12  2 (mod 8) mà VP(2) =16np  0 (mod 8) => mâu thuẫn.
Trường hợp 3. p = 2 , m, n lẻ. Ta có phương trình: 2 2 2 2
m + 3n + 20 = 16mn  (m − 8n) − 61n = 2 − 0 (3) Suy ra 2 2 2 2
(m − 8n) − 61n  1(mod 3)  (m − 8n) − n  1(mod 3) 0.5 mà 2 2
(m − 8n)  0,1(mod 3); n  0,1(mod 3) nên 2 2
(m − 8n)  1(mod 3); n  0(mod 3) suy ra n = 3
Thay n = 3 vào (3) suy ra m = 47
Vậy có duy nhất một bộ ( ; m ;
n p) = (47;3; 2) thỏa mãn yêu cầu đề bài. 0.25
Trong mặt phẳng tọa độ Oxy , cho 3 đường thẳng (d ) :y = 2x − 2 m + 1, 1
(d ) :y = x − 2
m − m và (d ) : y = 3x − 2
m − m + 2 . Biết (d ) cắt (d ) và Câu 2 3 1 2 2.0 3.2 (d ) lần lượt tại
A(x ;y và B (x ;y . Tìm m để điểm 2 2 ) 1 1 ) 3 (x −x y y 320 . 1 2 )2 + ( − 1 2 )2 = 4
Xét phương trình hoành độ giao điểm của (d :y 2x m 1 và 1 ) = − 2 +
(d :y x m m là: 2 2
2x − m +1 = x − m − m  x = −m −1 2 ) = − 2 − Với 2 2 x = 1
− − m  y = m
− −1− m − m = m − − 2m−1 0.5 x = 1 − − m
=> đường thẳng (d cắt (d tại A( 2 1 − − ;
m −m − 2m − ) 1 hay 1  2 ) 1 ) 2
y = −m − 2m −1  1
Xét phương trình hoành độ giao điểm của (d :y 2x m 1 và 1 ) = − 2 +
(d :y 3x m m 2 là: 2 2
2x − m +1 = 3x − m − m + 2  x = m −1 3 ) = − 2 − + 0.5 Với 2 2
x = m −1 y = 2(m −1) − m +1 = m − + 2m−1 x = m −1
=> đường thẳng (d cắt (d tại B ( 2
m −1; −m + 2m − ) 1 hay 2  3 ) 1 ) 2
y = −m + 2m −1  2 Từ giả thiết ( 2 2
x − x )2 + ( y − y )2 = 320 suy ra ( 2 − m) + ( 4 − m) = 320 1 2 1 2 2 2  1.0
20m = 320  m =16  m = 4  . Vậy m = 4
 là giá trị cần tìm.
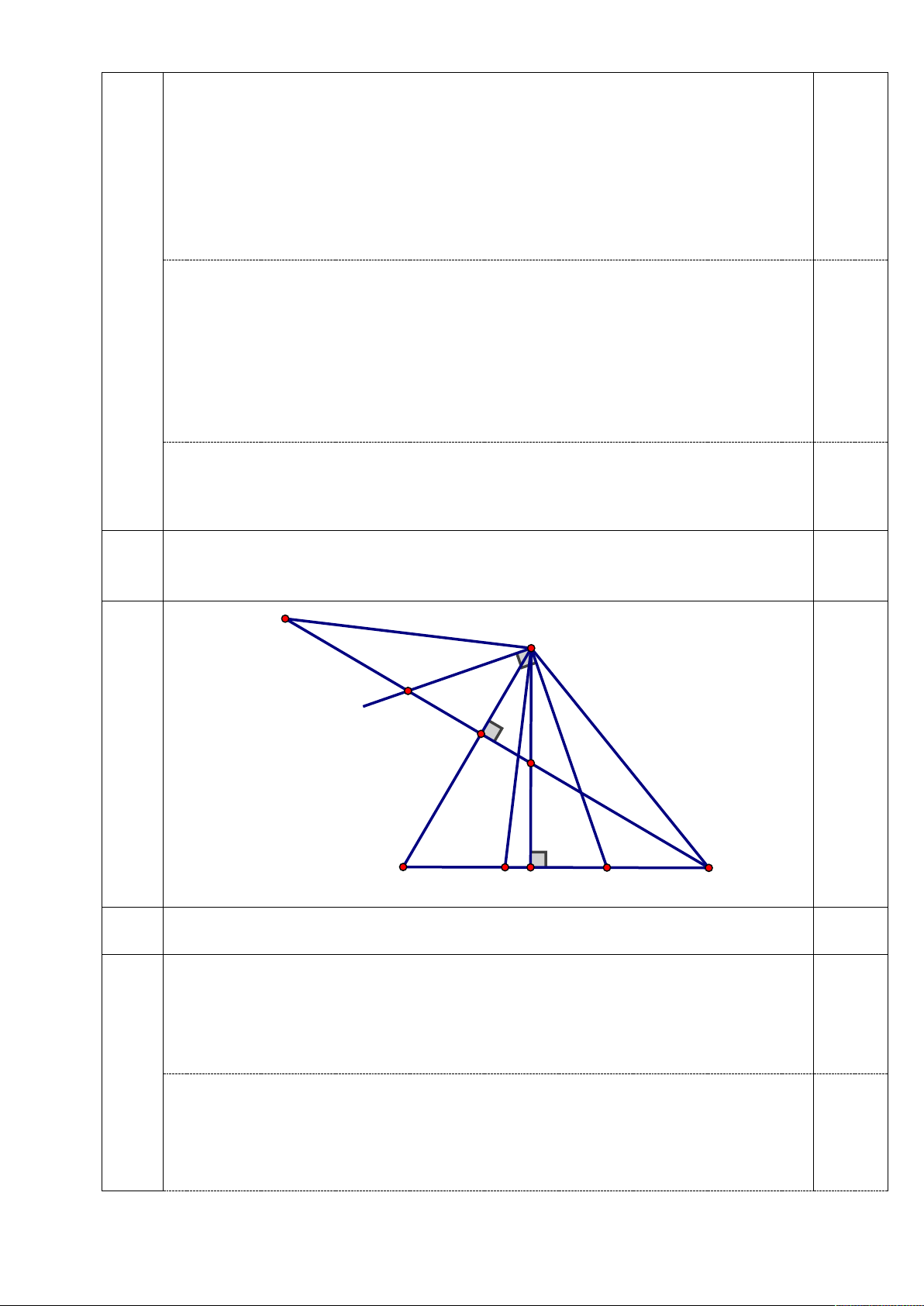
Cho tam giác ABC nhọn (AB < AC), đường cao AD, CF cắt nhau tại H. Gọi Câu 4.5
M là điểm thuộc đoạn thẳng DC sao cho BM < 2BD. Qua A vẽ đường thẳng 4.1 điểm
vuông góc với AM cắt CH tại K. G A K Hình F vẽ H 0.5 B P D M C 1.5
4.1a Chứng minh rằng: K  AH ∽  B AM . điểm
Có AHF vuông tại F => 0
FHA + FAH = 90 hay 0 KHA + BAD = 90 Có ABD  vuông tại D => 0
ABD + BAD = 90 hay 0 ABM + BAD = 90 0.5
=> KHA = ABM
có ADM vuông tại D => 0
AMD + DAM = 90 hay 0 AMB + DAM = 90
mà KAH + DAM = KAM = 90 0.5
=> KAH = AMB 5 Xét KAH 
và AMB có: KAH = AMB ; KHA = ABM  K  AH ∽  B AM (g.g). 0.5
Lấy G đối xứng với H qua K. Gọi P là trung điểm của BM. Chứng minh 1.5 4.1b AG ⊥ AP . điểm có K  AH ∽  B
AM (ý a)  KH AH = (cạnh tương ứng) 0.25 AB MB 1
mà G đối xứng với H qua K => KH = GH 2
P là trung điểm của BM => BM = 2PB 0.5 1 GH 2 AH GH AH  =  = AB 2PB AB PB GH AH Xét A
 GH và PAB có: =
và AHG = ABP ( cmt) AB PB 0.25  A  GH ∽ B PA (c.g.c)
 GAH = APB  APB = GAP + PAD
mà APB = ADP + PAD = 90 + PAD (Tính chất góc ngoài) 0.5
 GAP = 90  AG ⊥ AP 1.0
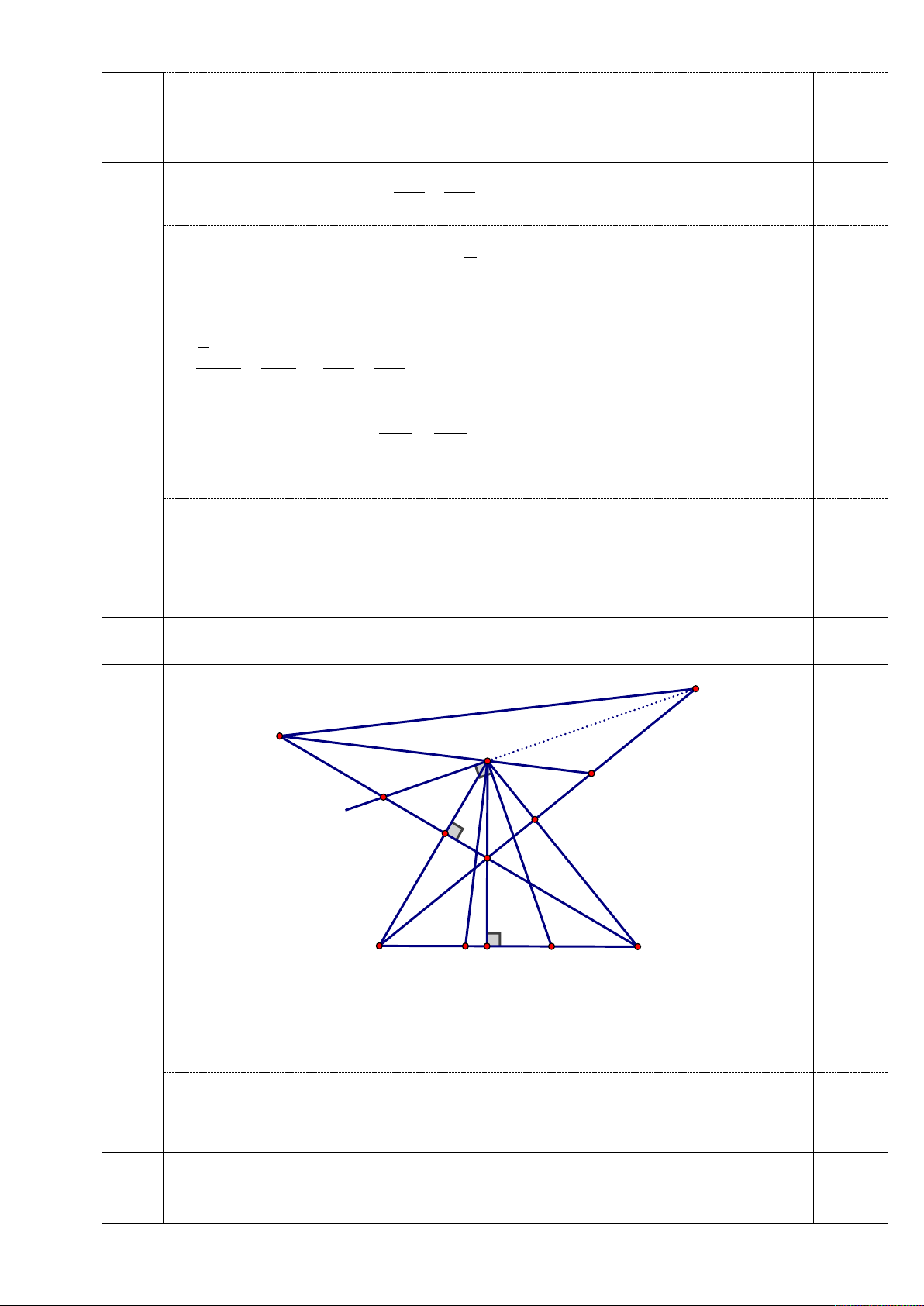
4.1c Khi BM = 2MC, gọi N là giao điểm của AG và BH. Chứng minh AG = 2AN. điểm Q G A K N F H B P D M C
Lấy Q đối xứng với H qua N .
Ta có: BM = 2MC và P là trung điểm của BM nên M là trung điểm của PC. 0.5
Chứng minh tương tự ý a và b, ta có AQ ⊥ AM
mà AK ⊥ AM (giả thiết) => Ba điểm K, A , Q thẳng hàng. Xét GHQ 
có GN và QK là các đường trung tuyến và QK  GN =   A
=> A là trọng tâm của GHQ  0.5  AG = 2AN
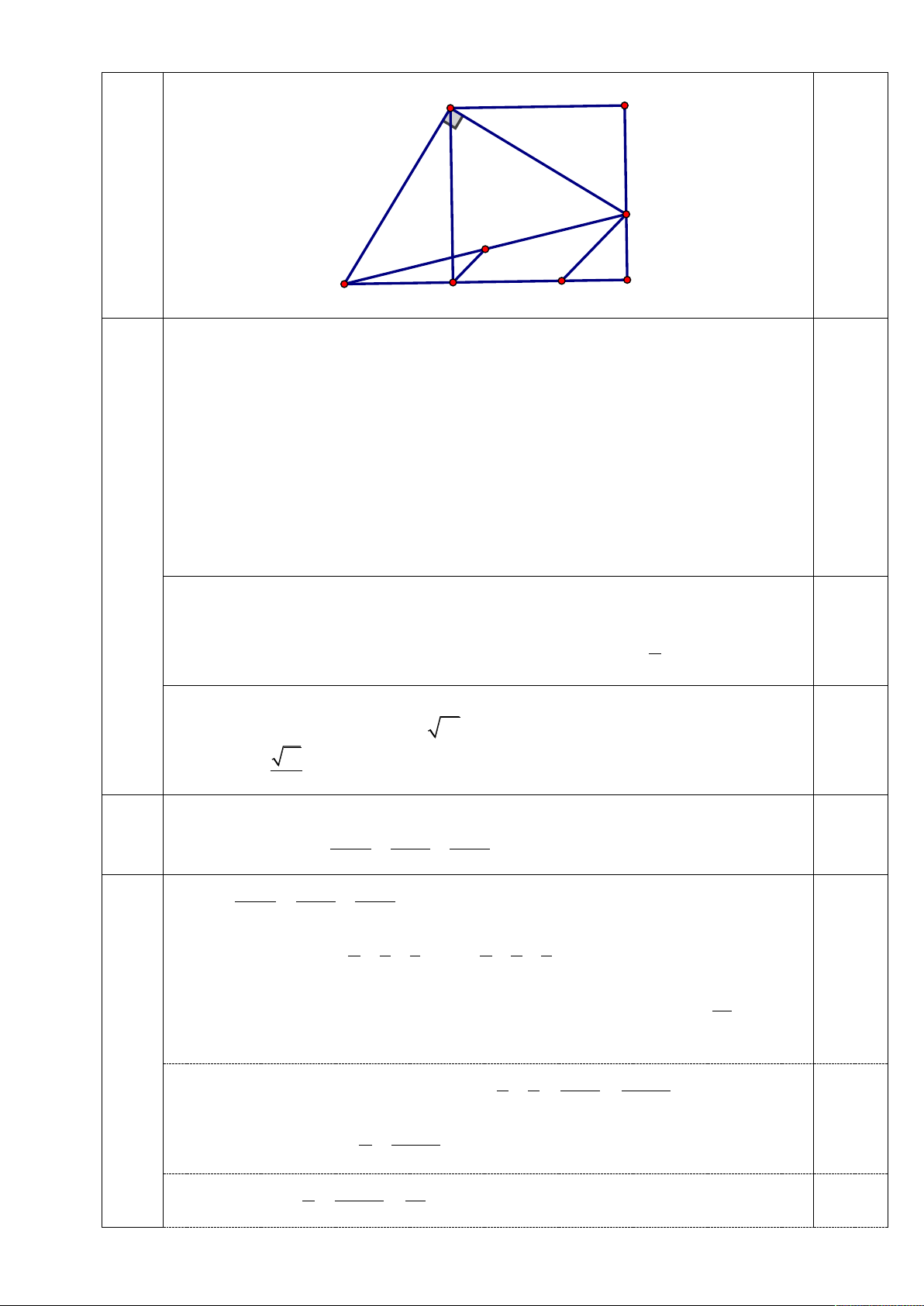
Cho hình vuông ABCD có cạnh bằng 8. Trên cạnh BC , lấy điểm M sao cho Câu 1.5
BM = 5 . Gọi N là giao điểm của đường thẳng CD và đường thẳng vuông góc 4.2 điểm
với AM tại A . Gọi I là trung điểm của MN . Hãy tính độ dài đoạn thẳng DI . 6 A B 3 2 1 Hình vẽ M I N D E C
BC = CD = AD = 8 (cm). 
Tứ giác ABCD là hình vuông =>  0
ABC = BAD = ADC = BCD = 90 0 A + A = 90   Có: 1 2   A = A 1 3 0 A + A = 90  2 3  0.5
Xét ABM và A  DN , có: 0
ABM = ADN = 90  
AB = AD (cmt)   A  BM = A  DN(g. .
c g) => BM = DN = 5 (c ) m (1). 
A = A (cmt) 3 1 
Lấy E trên cạnh DC sao cho DE = DN = 5cm => EC = MC = 3cm Xét M  NE , có: IN = IM  0.5
 => DI là đường trung bình của M  1 NE  DI = ME DN = DE  2 Xét C
 ME vuông tại C, có: 2 2 2
EM = EC + MC (định lý Pythagore) 2 2 2
 EM = 3 + 3 =18  EC = 18 (cm). 0.5 Do đó 18 DI = (cm) . 2
Cho ba số nguyên dương a,b,c thỏa mãn a + b + c = 10. Tìm giá trị nhỏ nhất Câu 1.0 a + b b + c c + a 5.1
của biểu thức: K = + + . điểm c a b a + b b + c c + a có K = + + c a b  1 1 1   1 1 1 
 K + 3 = (a + b + c) + + =10 + +     (1)  a b c   a b c  0.25
Không mất tổng quát, giả sử a  b  10
c  3a  a + b + c = 10  a  3 mà *
a  N nên a  4 . 1 1 4 4
Áp dụng bất đẳng thức cộng mẫu ta có, +  = b c b + c 10 − (2) a  0.25 1 4 
Từ (1),(2) => K  10 +   (3)
 a 10 − a  1 4 11 Ta chứng minh +  a  (*) 0.25 a 10 − với 4 a 12 7
Thật vậy, bất đẳng thức (*)  12(10 − a) + 48a  11a(10 − a)
 11a − 74a +120  0  (a − 4)(11a − 30)  0 (luôn đúng với a  4) 11 37
Từ (3), (*)  K + 3  10.  K  . 12 6 b  = c 
Dấu “=” xảy ra khi và chỉ khi a + b + c = 10  a = 4;b = c = 3 0.25 a = 4  37
Vậy biểu thức đạt giá trị nhỏ nhất K =
tại a = 4,b = c = 3 và các hoán vị. 6
Câu Cho số 884 số nguyên tố phân biệt. Chứng minh rằng tồn tại hai số nguyên tố 1.0 5.2
p, q trong các số đã cho thỏa mãn p − q 2024. điểm Có 3 2024 = 2 .11.23
Trong 884 số nguyên tố phân biệt đã cho thì có ít nhất 881 số nguyên tố 0.25
phân biệt khác 2;11 và 23.
Vì một số nguyên tố khác 23 khi chia cho 23 thì có dư thuộc tập có 22 phần
tử {1; 2; 3; ...; 22}, mà 881=22.40+1 nên theo nguyên lý Dirichlet, trong 881
số nguyên tố trên tồn tại ít nhất 40+1=41 số nguyên tố phân biệt có cùng số 0.25 dư khi chia cho 23.
Vì một số nguyên tố khác 11 khi chia cho 11 thì có dư thuộc tập có 10 phần
tử {1; 2; 3; ...; 10}, mà 41=10.4+1 nên theo nguyên lý Dirichlet, trong 41 số
nguyên tố trên tồn tại ít nhất 4+1=5 số nguyên tố phân biệt có cùng số dư khi 0.25 chia cho 11.
Vì một số nguyên tố khác 2 khi chia cho 8 thì có dư thuộc tập có 4 phần tử {1;
3; 5; 7}, mà 5=4.1+1 nên theo nguyên lý Dirichlet thì trong 5 số nguyên tố
trên tồn tại ít nhất 1+1=2 số nguyên tố phân biệt có cùng số dư khi chia cho 8.
Giả sử hai số đó là p, q . 0.25
Khi đó p, q có cùng số dư khi chia cho 8; 11 và 23 mà ba số này đôi một
nguyên tố cùng nhau nên p − q 2024. (đpcm) Tổng 20 điểm
………………………………..HẾT……………………………..
Họ, tên giám khảo……………………………..Đơn vị công tác:……………………………….
Document Outline

• Toán 8
• HDC Toán 8