Đề thi chọn HSG Toán THPT cấp tỉnh năm học 2017 – 2018 sở GD và ĐT Hưng Yên

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI THPT CẤP TỈNH HƯNG YÊN NĂM HỌC 2017 - 2018 Môn thi: TOÁN ĐỀ CHÍNH THỨC
Thời gian làm bài: 180 phút, không kể thời gian phát đề
Câu I (5,0 điểm) x − 1. Cho hàm số 2 1 y =
có đồ thị (C ) . Viết phương trình tiếp tuyến của (C ) tại giao x −1
điểm của nó và đường thẳng y = 2x +1. 2. Cho hàm số 3 2
y = x − 3x + (m + )
1 x − 4 , m là tham số. Tìm các giá trị của m để đồ thị hàm số có 2 điểm  7 
cực trị và khoảng cách từ điểm A ;1 
 đến đường thẳng đi qua hai  2 
điểm cực trị đó lớn nhất.
Câu II (4,0 điểm) x + x + x 1 (3 )1log 3 1 4 ( )
1. Tìm nghiệm dương của phương trình 4 − 2x −1 = log . 2 2 x   3x π   x π   1
2. Giải phương trình 2 2 2 cos − cos −
+ sin x = sin 2x + sin x       .   2 8   2 8   2
Câu III (4,0 điểm)
1. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = a, AD = 2a . Mặt bên
(SAB) là tam giác cân tại S và vuông góc với mặt phẳng đáy. Khoảng cách từ B đến mặt phẳng ( a SAC ) bằng
6 . Tính thể tích khối chóp S.ABCD theo a. 3
2. Cho hình lăng trụ tam giác đều ABC.A′B C
′ ′ có độ dài cạnh đáy bằng 2a , góc giữa mặt
phẳng ( A′BC) và mặt phẳng đáy bằng 0
60 . Gọi M , N lần lượt là trung điểm của các cạnh
BC và CC′ . Tính khoảng cách giữa hai đường thẳng A′M và AN theo a .
Câu IV (3,0 điểm) Giải hệ phương trình 2 2 3
 x − 2y − xy +12x −17y −15 = 0   2
 2 − x + 6 − x − x = y + 2y + 5 − y + 4. 
Câu V (2,0 điểm) Cho tam giác ABC nhọn. Tìm giá trị lớn nhất của biểu thức T = ( 2 A + A + )( 2 B + B + )( 2 cos cos 2 cos cos 2
cos C + cos C + 2 ).  1 x =  1  2
Câu VI (2,0 điểm) Cho dãy số ( x được xác định bởi  n ) 2 x 1  n 1 x − + = , n ∀ ≥ 2. n  2 2 1 1
1. Chứng minh rằng − ≤ x ≤
với mọi n ≥ 1. 8 n 2
2. Tìm giới hạn của dãy số ( x khi n → +∞ . n )
----------------- Hết -----------------
Thí sinh không được sử dụng tài liệu và máy tính cầm tay.
Cán bộ coi thi không giải thích gì thêm.
Họ và tên thí sinh: ........................................................... Số báo danh: .............................
Chữ kí của cán bộ coi thi: ....................................................................................................
SỞ GIÁO DỤC VÀ ĐÀO TẠO HƯỚNG DẪN CHẤM HƯNG YÊN
KÌ THI CHỌN HỌC SINH GIỎI THPT CẤP TỈNH NĂM HỌC 2017 - 2018
( Hướng dẫn chấm gồm 6 trang) Môn: TOÁN I. Hướng dẫn chung
1) Hướng dẫn chấm thi này chỉ trình bày các bước chính của lời giải hoặc nêu kết quả. Trong bài
làm, thí sinh phải trình bày lập luận đầy đủ.
2) Nếu thí sinh làm bài không theo cách nêu trong đáp án mà vẫn đúng thì cho đủ điểm từng phần
như hướng dẫn quy định.
3) Việc chi tiết hoá thang điểm (nếu có) so với thang điểm trong hướng dẫn phải đảm bảo không
sai lệch với hướng dẫn chấm và được thống nhất thực hiện trong tổ chấm thi. Các điểm thành phần và
điểm cộng toàn bài giữ nguyên không làm tròn.
II. Đáp án và thang điểm Câu Đáp án Điểm x − 1. Cho hàm số 2 1 y =
có đồ thị (C ) . Viết phương trình tiếp tuyến của (C ) tại x −1
Câu I.1 giao điểm của (C) và đường thẳng y = 2x +1. 2,0 điểm Xét hàm số 2x −1 1 − 0,25 y = . Với x
∀ ≠ 1, ta có y′ = x −1 (x − )2 1
Phương trình hoành độ giao điểm của (C) và đường thẳng: 0,5 2x −1 x ≠ 1 = 2x +1 ⇔  2 x −1 2x − 3x = 0 x = 0 0,25  ⇔ 3  x =  2
Với x = 0 tọa độ giao điểm A(0; ) 1 0,5
Phương trình tiếp tuyến của (C) tại A(0; )
1 là: y = −x +1 Với 3   0,5 x = tọa độ giao điểm 3 B ; 4   2  2 
Phương trình tiếp tuyến của (   C ) tại 3 B ; 4   là: y = 4 − x +10  2  2. Cho hàm số 3 2
y = x − 3x + (m + )
1 x − 4 , m là tham số. Tìm m để đồ thị hàm số  
Câu I.2 có 2 điểm cực trị và khoảng cách từ điểm 7 A ;1 
 đến đường thẳng đi qua hai 3,0 điểm  2 
điểm cực trị đó lớn nhất. Với x ∀ ∈  , ta có 2
y′ = 3x − 6x + m +1 0,25
Điều kiện để hàm số có hai cực trị là phương trình y′ = 0có hai nghiệm
phân biệt ⇔ phương trình 2
3x − 6x + m +1 = 0 có hai nghiệm phân biệt 0,25
⇔ ∆′ > 0 ⇔ m < 2 0,5   − − Khi đó, ta có 1 1 2m 4 m 11 y = y .′ x − + x +    0,5 3 3  3 3
Phương trình đường thẳng qua các điểm cực trị của đồ thị hàm số là 2m − 4 m −11 y = x + (d ). 3 3 Đường thẳng (   d ) đi qua điểm 1 M − ; 3 −   với mọi m .  0,5 2     2m − 4  Ta có: AM ( 4; − 4
− ) , đường thẳng (d ) có vtcp u 1;    3 
Dựng AH ⊥ d suy ra d ( ;
A d ) = AH ≤ AM 0,5
Dấu bằng xảy ra ⇔ H ≡ M ⇔ AM ⊥ d   1
⇔ AM .u = 0 ⇔ m = 2 0,5
Kết hợp điều kiện suy ra 1 m =
thỏa mãn điều kiện bài toán. 2 x + x + x 1 (3 ) 1 log 3 1 4 ( ) − − =
1. Tìm nghiệm dương của phương trình 4 2x 1 log 2 2 x
Câu II.1 Với x > 0, phương trình tương đương
2,0 điểm 4x − 2x −1= log 3x +1 + log log 3x +1  −log x 4 ( ) 4  4 ( ) 4 0,25
⇔ 4x + x + log x = 3x +1+ log 3x +1 + log log 3x +1  4 4 ( ) 4  4 ( )
Đặt log 3 +1 = ⇔ 3 +1 = 4y x y x 4 ( )
Phương trình trở thành: ⇔ 0,25 4x + + log = 4y x x + y + log y 1 4 4 ( ) Xét hàm số ( ) = 4t f t
+ t + log t trên (0;+∞) . 4 0,25
Hàm số f (t ) đồng biến trên (0;+∞) . Phương trình ( )
1 ⇔ f ( x) = f ( y) ⇔ x = y 0,25
Trở lại phép đặt ta được: 4x = 3 +1 ⇔ 4x x − 3x −1 = 0 0,25 Xét hàm số ( ) = 4x g x − 3x −1 trên . Chứng minh phương trình 0,25
g ( x) = 0 có nhiều nhất hai nghiệm trên  .
Có g (0) = g ( )
1 = 0 nên phương trình g ( x) = 0 có nghiệm x = 0; x = 1. 0,25
Kết hợp điều kiện, phương trình có nghiệm x =1. 0,25   3x π   x π   1 − − + = +
2. Giải phương trình 2 2 2 cos cos sin x sin 2x sin x       .   2 8   2 8   2 Câu II.2 2,0 điểm   3x π   x π   1 0,25 2 2 2 cos − cos −
+ sin x = sin 2x + sin x         2 8   2 8   2  3x π   x π  2 ⇔ 2 2 cos − cos −
+ 2 2 sin x = sin xcos x + sin x      2 8   2 8   π  0,25 2 ⇔ 2 cos 2x −
+ 2 cos x + 2 2 sin x = sin xcos x + sin x    4  ⇔ x + x + ( x + x) 2 cos 2 sin 2 2 cos 2sin
= sin xcos x + sin x 0,25 2 2
⇔ cos x + sin xcos x − 2sin x + 2 (cos x + 2sin x) = 0 0,25
⇔ (cos x − sin x)(cos x + 2sin x) + 2 (cos x + 2sin x) = 0 0,25
⇔ (cos x + 2sin x)(cos x −sin x + 2) = 0
cos x + 2sin x = 0 ( ) 1 ⇔  0,25
cos x − sin x + 2 = 0  (2) Giải (1): cot x = 2
− ⇔ x = acr cot ( 2 − ) + kπ 0,25 Giải (2):  π  3π 0,25
sin x − cos x = 2 ⇔ sin x − = 1 ⇔ x = + k2π    4  4
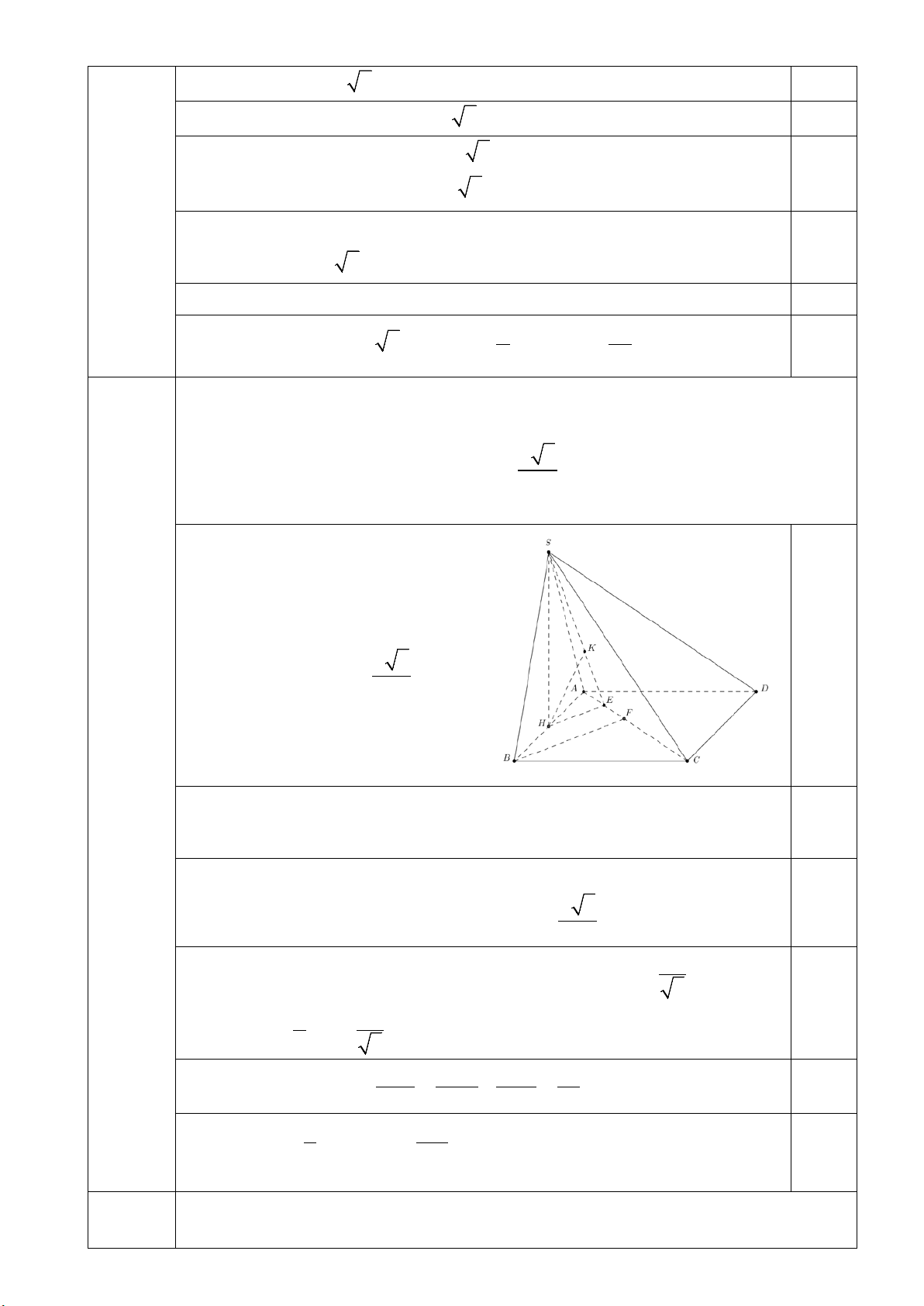
1. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = a, AD = 2a .
Mặt bên (SAB) là tam giác cân tại S và vuông góc với mặt phẳng đáy. Khoảng Câu III.1
2,0 điểm cách từ a
B đến mặt phẳng (SAC ) bằng
6 . Tính thể tích khối chóp S.ABCD 3 theo a .
Gọi H là trung điểm của AB suy ra
SH ⊥ AB . Mà (SAB) ⊥ ( ABCD) 0,5
nên SH ⊥ ( ABCD) . d ( ;
B (SAC )) = 2d ( H;(SAC )) a
Suy ra d ( H (SAC )) 6 ; = 6
Trong mặt phẳng ( ABCD) , dựng HE ⊥ AC
Chứng minh (SHE) ⊥ (SAC) 0,25
Trong mặt phẳng (SHE), dựng HK ⊥ SE 0,25 a
Suy ra HK ⊥ (SAC ) ⇒ HK = d ( H (SAC )) 6 ; = 6 Trong mặt phẳng ( 2a 0,5
ABCD) , dựng BF ⊥ AC . Tính BF = . 5 1 a Suy ra HE = BF = . 2 5 1 1 1 1 0,25
Xét tam giác SHE có = − = ⇒ SH = a . 2 2 2 2 SH HK HE a 3 Vậy 1 2a 0,25 V = SH.S = . S . ABCD 3 ABCD 3
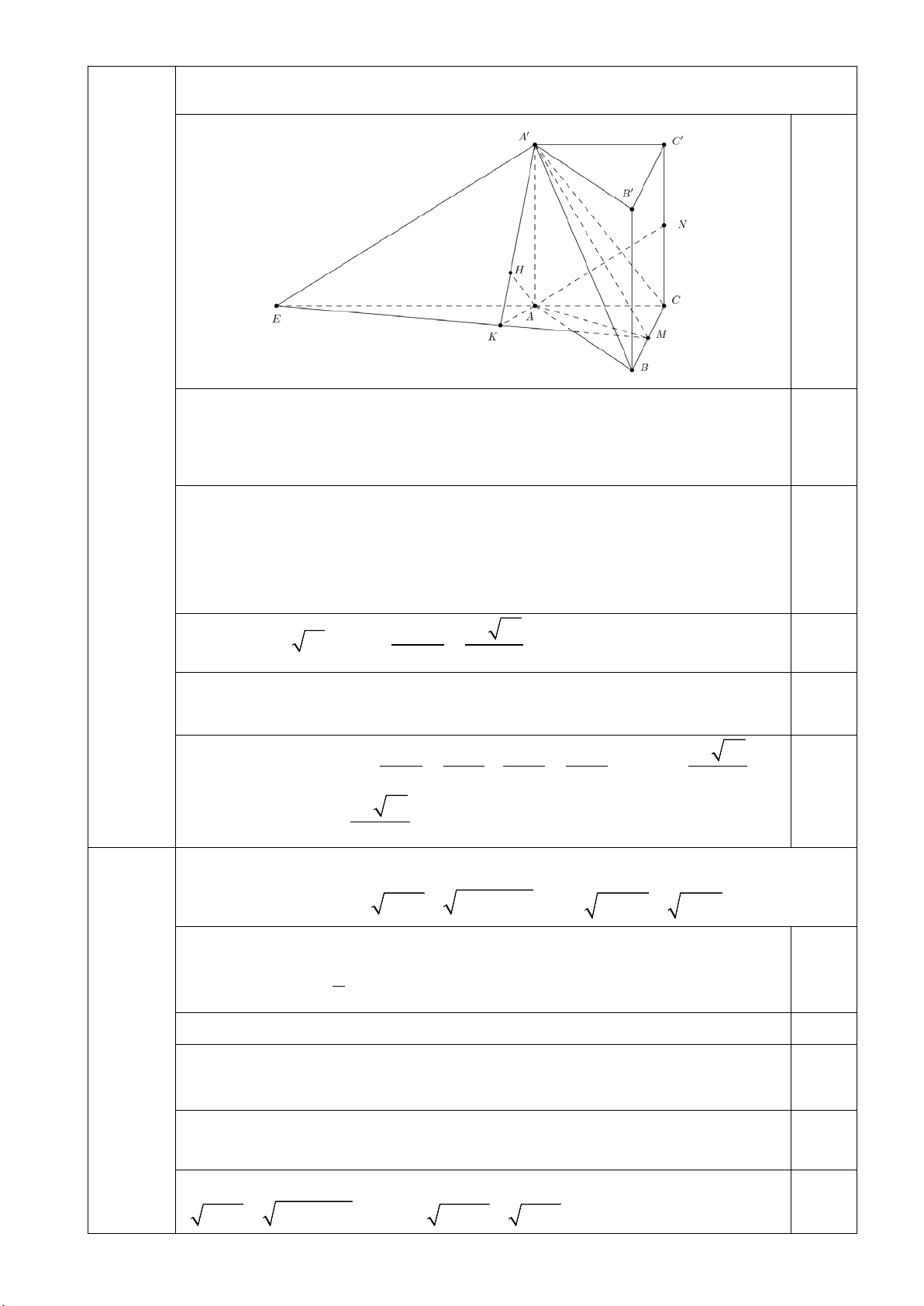
2. Cho hình lăng trụ tam giác đều ABC. ′
A B′C′ có độ dài cạnh đáy bằng 2a , góc giữa mặt phẳng ( ′
A BC ) và mặt phẳng đáy bằng 0
60 . Gọi M , N lần lượt là trung
Câu III.2 điểm của các cạnh BC và CC′ . Tính khoảng cách giữa hai đường thẳng ′ A M và
2,0 điểm AN theo a .
Trong mặt phẳng ( ACC A
′ ′), dựng A′E song song với AN (E ∈ AC) 0,5
Khi đó, AN song song với mặt phẳng ( A′ME)
suy ra d ( AN; A′M ) = d ( AN;( A′ME )) = d ( ;
A ( A′ME ))
Trong mặt phẳng ( ABC), dựng AK ⊥ EM 0,25
Chứng minh ( AA′K ) ⊥ ( A′ME).
Trong mặt phẳng ( AA′K ), dựng AH ⊥ A′K
Suy ra AH ⊥ ( A′ME ) ⇒ d ( ;
A ( A′ME )) = AH . 2S 2a 93 0,5
Tính ME = a 31 ; AME AK = = ME 31 Góc giữa ( ′
A BC ) và mặt phẳng đáy là  0 A′MA = 60 0,5 suy ra 0
AA′ = AM .tan 60 = 3a 1 1 1 97 6a 97 0,25
Xét tam giác AA′K , có = + = ⇒ AH = 2 2 2 2 AH AK AA′ 36a 97
Vậy d ( AN A′M ) 6a 97 ; = . 97 2 2 3
 x − 2y − xy +12x −17y −15 = 0  ( )1
Giải hệ phương trình  Câu IV 2
 2 − x + 6 − x − x = y + 2y + 5 − y + 4  (2) 3,0 điểm  3 − ≤ x ≤ 2 Điều kiện:  0,25 5 y ≥ −  2
( )1 ⇔ (x − y − )1(3x + 2y +15) = 0 0,5  y = x −1 0,25 ⇔ 
3x + 2y +15 = 0
TH 3x + 2 y +15 = 0 0,5
Từ điều kiện, 3x + 2 y +15 ≥ 9 − − 5 +15 > 0 (loại)
TH y = x −1, thay vào phương trình (2) ta được: 2 0,25
2 − x + 6 − x − x = x −1 + 2x + 3 − x + 3
⇔ 2 − x + 3 + x + (2 − x)(3 + x) = x −1+ 2x + 3 (ĐK: 3 − ≤ x ≤ 2 ) 2 Đặt − − x +
+ x = t ⇒ ( − x)( + x) 2 t 5 2 3 2 3 = 2 2 0,5 t − 5 (2x + 3) − Phương trình trở thành 5 t + = 2x + 3 + (3) 2 2 Xét hàm số − 0,25 f (u) 2 u 5 = u + trên (0;+∞) . 2
Hàm số f (u) đồng biến trên (0;+∞) .
Phương trình (3) ⇔ f (t) = f ( 2x + 3) ⇔ t = 2x + 3
Trở lại phép đặt: 2 − x + 3 + x = 2x + 3 2
⇔ 6 − x − x = x −1 0,25 x ≥ 1 1 + 41 ⇔  ⇔ x = 2
2x − x − 5 = 0 4 Với 1 + 41 3 − + 41 x = ⇒ y = (thỏa mãn). 4 4  + − +  0,25
Vậy hệ phương trình có nghiệm (x y) 1 41 3 41 ; =  ;  4 4  
Cho tam giác ABC nhọn. Tìm giá trị lớn nhất của biểu thức T = ( 2 A + A + )( 2 B + B + )( 2 cos cos 2 cos cos 2
cos C + cos C + 2 ) Câu V
2,0 điểm Đặt cos A = ;
x cos B = y, cos C = z . Ta có: 0 < x, y, z < 1 0,25
Biểu thức trở thành: T = ( 2 x + x + )( 2 y + y + )( 2 2 2 z + z + 2 ) Chứng minh: 3 0,5
x + y + z ≤ 2 0,25đ T = ( 2 x + x + 2 )( 2 y + y + 2 )( 2 z + z + 2 ) ⇔ lnT = ln ( 2 x + x + 2 ) + ln( 2 y + y + 2 ) + ln( 2 z + z + 2 ) Ta chứng minh 2 1 0,5đ : ln ( 2 x +
x + 2 ) ≤ x + ln 2 − với x ∈(0; ) 1 . 3 3 Tương tự: 2 1 ln ( 2 y +
y + 2 ) ≤ y + ln 2 − với y ∈(0; ) 1 . 3 3 2 1 ln ( 2 z +
z + 2 ) ≤ z + ln 2 − với z ∈(0; ) 1 . 3 3 2 0,25đ Suy ra ln T ≤
(x + y + z) + 3ln2 −1≤ 3ln2 ⇔ T ≤ 8. 3 Dấu bằng xảy ra khi 1 π 0,25đ
x = y = z =
⇔ A = B = C = . 2 3
Vậy maxT = 8 khi tam giác ABC đều.  1 = x  1  2
Câu VI Cho dãy số ( x
được xác định bởi  . n ) 2 x 1 2,0 điểm  n 1 x − + = , n ∀ ≥ 2 n  2 2 0,5
1. Ta chứng minh quy nạp 1 1
− ≤ x ≤ với mọi n ≥1. 8 n 2 2 x 1
2. Xét x là nghiệm của phương trình x + = với 1 1 − ≤ x ≤ . 2 2 8 2 0,25 2 2 Khi đó 1 x 1 x x − x = − − = − 1 2 2 2 2 n 0,5 1 1 − x − x = − x − x = x x + x x + x x + x n ( 2 2n− ) ( ) 2 ... 1 n ( 1 ) ( 2 ) ( n 1 − ) 2 2 1 0,5 Ta có x =
2 −1 , nên x + x ≤ x + x ≤ 2 −1 +
< 1 với mọi n ≥1. n n 2 1 Nên x − x ≤ với mọi n ≥ 1 n 2n 1 0,25 Có lim
= 0 do đó lim x = x = 2 −1. 2n n
---------------- Hết ----------------
Document Outline

• De Toan HSG 2017_2018 Chinh thuc
  • Cán bộ coi thi không giải thích gì thêm.
  • Họ và tên thí sinh: ........................................................... Số báo danh: .............................
  • Chữ kí của cán bộ coi thi: ....................................................................................................
• DA Toan HSG 2017_2018 Chinh thuc