Đề thi cuối HK1 Toán 11 năm 2022 – 2023 trường THPT Lương Văn Can – TP HCM

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 11 đề kiểm tra đánh giá chất lượng cuối học kỳ 1 môn Toán 11 năm học 2022 – 2023 trường THPT Lương Văn Can, quận 8, thành phố Hồ Chí Minh

19 10 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề HK1 Toán 11

Môn: Toán 11

Thông tin:

4 trang 8 tháng trước

Tác giả:

Profile Kim Oanh
SỞ GIÁO DỤC & ĐÀO TẠO TP. HCM
TRƯỜNG THPT LƯƠNG VĂN CAN
ĐỀ KIỂM TRA HỌC KỲ I
NĂM HỌC 2022 – 2023
Môn: TOÁN 11
Thời gian làm bài: 90 phút
Họ và tên thí sinh:............................................... Số báo danh: .............................
Câu 1: (3.0 điểm) Giải các phương trình sau:
a)
3
cos( )
4 2
x
b)
2
2sin sin 3 0x x
c)
2 2
2cos 3 sin cos sin 1x x x x
.
Câu 2: (1.0 điểm) Cho tập X={0,1,2,3,4,5,6,7}. Hỏi từ tập X có thể lập được bao nhiêu số tự nhiên
gồm 3 chữ số khác nhau và kết thúc là chữ số 3.
Câu 3: (1.0 điểm) Một tổ gồm 7 học sinh nam và 3 học sinh nữ, xếp thành một hàng ngang. Hỏi có
bao nhiêu cách xếp sao cho không có 2 học sinh nữ nào đứng cạnh nhau?
Câu 4: (1.0 điểm) Một lớp gồm 25 học sinh nam và 15 học sinh nữ. Chọn ngẫu nhiên 4 học sinh để
lập tốp ca. Tính xác suất để số học sinh được chọn có 2 nữ.
Câu 5: (1.0 điểm) Tìm hệ số của số hạng chứa x
3
trong khai triển
12
2
2
x
x
.
Câu 6: (3.0 điểm) Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N lần lượt
là trung điểm SA, CD.
a) Tìm giao tuyến của hai mặt phẳng (SAB) và (SCD).
b) Tìm giao điểm I của đường thẳng MN và mặt phẳng (SBD).
c) Chứng minh OI//(SAB).
Hết
SỞ GIÁO DỤC & ĐÀO TẠO TP. HCM
TRƯỜNG THPT LƯƠNG VĂN CAN
ĐỀ KIỂM TRA HỌC KỲ I
NĂM HỌC 2022 – 2023
Môn: TOÁN 11
Thời gian làm bài: 90 phút
Họ và tên thí sinh:............................................... Số báo danh: .............................
Câu 1: (3.0 điểm) Giải các phương trình sau:
a)
3
cos( )
4 2
x
b)
2
2sin sin 3 0x x
c)
2 2
2cos 3 sin cos sin 1x x x x
.
Câu 2: (1.0 điểm) Cho tập X={0,1,2,3,4,5,6,7}. Hỏi từ tập X có thể lập được bao nhiêu số tự nhiên
gồm 3 chữ số khác nhau và kết thúc là chữ số 3.
Câu 3: (1.0 điểm) Một tổ gồm 7 học sinh nam và 3 học sinh nữ, xếp thành một hàng ngang. Hỏi có
bao nhiêu cách xếp sao cho không có 2 học sinh nữ nào đứng cạnh nhau?
Câu 4: (1.0 điểm) Một lớp gồm 25 học sinh nam và 15 học sinh nữ. Chọn ngẫu nhiên 4 học sinh để
lập tốp ca. Tính xác suất để số học sinh được chọn có 2 nữ.
Câu 5: (1.0 điểm) Tìm hệ số của số hạng chứa x
3
trong khai triển
12
2
2
x
x
.
Câu 6: (3.0 điểm) Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N lần lượt
là trung điểm SA, CD.
a) Tìm giao tuyến của hai mặt phẳng (SAB) và (SCD).
b) Tìm giao điểm I của đường thẳng MN và mặt phẳng (SBD).
c) Chứng minh OI//(SAB).
Hết
ĐÁP ÁN KIỂM TRA HỌC KỲ I
NĂM HỌC 2022 – 2023
Môn: TOÁN 11
Câu
Đáp án
Câu 1
(3 điểm)
a) (1đ) Giải phương trình
3
cos( )
4 2
x
3
cos( ) cos
4 2 6
x

2
4 6
2
4 6
x k
x k
Vậy ng pt
2
12
5
2
12
x k
x k
,kZ.
0,25
0,25 x 3
b) (1đ) Giải phương trình
2
2sin sin 3 0x x
2
2sin sin 3 0x x
Đặt
sin , 1 1t x t
Pt
2
2 3 0t t
1 ( )
3
( )
2
t n
t l

1 sin 1 2
2
t x x k
Vậy nghiệm của phương trình là:
2
2
x k
(
k Z
).
0,25 x 4
Làm cách
khác cho
điểm tương
tự
c) (1đ) Giải phương trình
2 2
2cos 3 sin cos sin 1x x x x
.
xét
cos 0
x
pt
1 1
(đúng) nên nhận
,
2
x k k Z
xét
cos 0
x
1
tan tan( )
6
3
pt x

6
x k
.
Vậy nghiệm của phương trình là:
2
6
x k
x k
(
k Z
).
0,25
0,25
0,25
0,25
Câu 2
(1 điểm)
Cho tập X={0,1,2,3,4,5,6,7}. Hỏi từ tập X có thể lập được bao nhiêu số tự
nhiên gồm 3 chữ số khác nhau và kết thúc là chữ số 3.
Gọi
abc
Chọn c: 1 cách (c = 3)
Chọn a: 6 cách (a≠0, c)
Chọn b: 6 cách (b≠a,c)
Vậy số số tự nhiên cần tìm là: 1.6.6=36 (số)
0,25
0,25
0,25
0,25
Câu 3
(1 điểm)
Một tổ gồm 7 học sinh nam và 3 học sinh nữ, xếp thành một hàng ngang.
Hỏi có bao nhiêu cách xếp sao cho không có 2 học sinh nữ nào đứng cạnh
nhau?
Xếp 7nam : 7! Cách
Chọn 3 chỗ từ 8 chỗ ( ở 2 đầu hàng và 6 chỗ giữa 7 nam ):
3
8
A
cách.
Kết luận: 7!
3
8
A
=1693440.
0,5
0,25
Câu 4
(1 điểm)
Một lớp gồm 25 học sinh nam và 15 học sinh nữ. Chọn ngẫu nhiên 4 học
sinh để lập tốp ca. Tính xác suất để số học sinh được chọn có 2 nữ.
Xác định :chọn 4 học sinh từ lớp 40 học sinh n() =
4
40
C
=91390
Gọi A : “Chọn 2 nữ và 2 nam”
n(A) =
2 2
15 25
.C C
=31500
P(A) =
)(n
)A(n
=
31500
91390
0,25
0,25
Câu 5
(1 điểm)
Tìm hệ số của số hạng chứa x
3
trong khai triển
12
2
2
x
x
.
 Số hạng tổng quát
12
1 12
2
2
( )
k
k k
k
T C x
x
=
12 3
12
2
k k k
C x
Hệ số của số hạng chứa : 12-3k = 3 k = 3
Vậy hệ số x
3
:
3 3
12
2 .C
= 1760
0,25
0,25
0,5
Câu 6
(3 điểm)
a) (1đ) Tìm giao tuyến của hai mặt phẳng (SAB) và (SCD)
Hình vẽ
( ) ( )
( ) ( )
AB/ / CD
( ), ( )
S SAB SCD
d SAB SCD
AB SAB CD SCD
qua S và // AB//CD
0,25 X 4
b) (1đ) Tìm giao điểm I của đường thẳng MN và mặt phẳng (SBD).
Ta có(SAN) MN
( AN) (S )S S BD
(1)
Trong mp (ABCD), gọi
AN BD H
, ( AN) ( AN)
, (S ) (S )
( AN) (S ) (2)
H AN AN S H S
H BD BD BD H BD
H S BD
Từ (1) và (2)
( AN) (S )SH S BD
SH MN I
, ( ) ( )
I MN
I SH SH SBD I SBD
I = MN (SBD) .
0,5
0.25
0.25
c) (1đ) Chứng minh OI//(SAB).
Chứng minh H trọng tâm tam giác ACD ,
1
4
HO
HB
0,25
Chứng minh đúng :
1
4
HI
HS
1
4
HO HI
HB HS
OI / /SB, SB SAB OI / / (SAB)
0,25
0,25
0,25
| 1/4
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GIÁO DỤC & ĐÀO TẠO TP. HCM
ĐỀ KIỂM TRA HỌC KỲ I
TRƯỜNG THPT LƯƠNG VĂN CAN
NĂM HỌC 2022 – 2023 Môn: TOÁN 11
Thời gian làm bài: 90 phút
Họ và tên thí sinh:............................................... Số báo danh: .............................
Câu 1: (3.0 điểm) Giải các phương trình sau:  3 a) cos(x  )  b) 2 2
 sin x  sin x  3  0 4 2 c) 2 2
2 cos x  3 sin x cos x  sin x  1.
Câu 2: (1.0 điểm) Cho tập X={0,1,2,3,4,5,6,7}. Hỏi từ tập X có thể lập được bao nhiêu số tự nhiên
gồm 3 chữ số khác nhau và kết thúc là chữ số 3.
Câu 3: (1.0 điểm) Một tổ gồm 7 học sinh nam và 3 học sinh nữ, xếp thành một hàng ngang. Hỏi có
bao nhiêu cách xếp sao cho không có 2 học sinh nữ nào đứng cạnh nhau?
Câu 4: (1.0 điểm) Một lớp gồm 25 học sinh nam và 15 học sinh nữ. Chọn ngẫu nhiên 4 học sinh để
lập tốp ca. Tính xác suất để số học sinh được chọn có 2 nữ. 12  2 
Câu 5: (1.0 điểm) Tìm hệ số của số hạng chứa x3 trong khai triển x   . 2   x
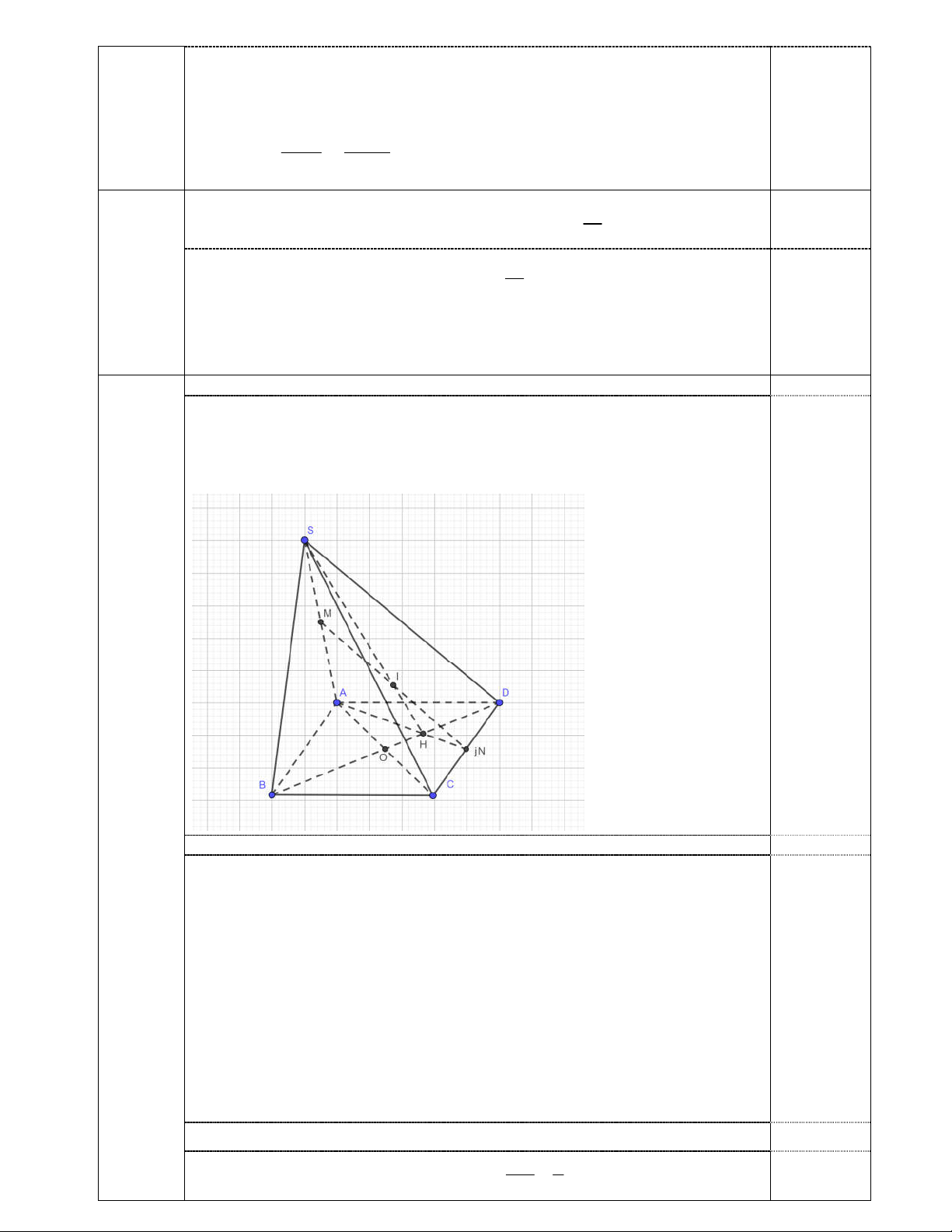
Câu 6: (3.0 điểm) Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N lần lượt là trung điểm SA, CD.
a) Tìm giao tuyến của hai mặt phẳng (SAB) và (SCD).
b) Tìm giao điểm I của đường thẳng MN và mặt phẳng (SBD). c) Chứng minh OI//(SAB). Hết
SỞ GIÁO DỤC & ĐÀO TẠO TP. HCM
ĐỀ KIỂM TRA HỌC KỲ I
TRƯỜNG THPT LƯƠNG VĂN CAN
NĂM HỌC 2022 – 2023 Môn: TOÁN 11
Thời gian làm bài: 90 phút
Họ và tên thí sinh:............................................... Số báo danh: .............................
Câu 1: (3.0 điểm) Giải các phương trình sau:  3 a) cos(x  )  b) 2 2
 sin x  sin x  3  0 4 2 c) 2 2
2 cos x  3 sin x cos x  sin x  1.
Câu 2: (1.0 điểm) Cho tập X={0,1,2,3,4,5,6,7}. Hỏi từ tập X có thể lập được bao nhiêu số tự nhiên
gồm 3 chữ số khác nhau và kết thúc là chữ số 3.
Câu 3: (1.0 điểm) Một tổ gồm 7 học sinh nam và 3 học sinh nữ, xếp thành một hàng ngang. Hỏi có
bao nhiêu cách xếp sao cho không có 2 học sinh nữ nào đứng cạnh nhau?
Câu 4: (1.0 điểm) Một lớp gồm 25 học sinh nam và 15 học sinh nữ. Chọn ngẫu nhiên 4 học sinh để
lập tốp ca. Tính xác suất để số học sinh được chọn có 2 nữ. 12  2 
Câu 5: (1.0 điểm) Tìm hệ số của số hạng chứa x3 trong khai triển x   . 2   x
Câu 6: (3.0 điểm) Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N lần lượt là trung điểm SA, CD.
a) Tìm giao tuyến của hai mặt phẳng (SAB) và (SCD).
b) Tìm giao điểm I của đường thẳng MN và mặt phẳng (SBD). c) Chứng minh OI//(SAB). Hết
ĐÁP ÁN KIỂM TRA HỌC KỲ I
NĂM HỌC 2022 – 2023 Môn: TOÁN 11 Câu Đáp án Điểm Câu 1  3
(3 điểm) a) (1đ) Giải phương trình cos(x  )  4 2  3   cos(x  )   cos 0,25 4 2 6      x    k 2  x    k 2 4 6  12 0,25 x 3     Vậy ng pt  ,kZ.    5 x     k 2 x    k 2  4 6  12
b) (1đ) Giải phương trình 2 2
 sin x  sin x  3  0 2 2
 sin x  sin x  3  0 0,25 x 4 Đặt t  sin ,
x 1  t  1 Làm cách
t  1 (n)  khác cho  Pt  2 2
t t  3  0   3  t  1   sin x  1   x    k 2 t  (l) 2 điểm tương  2 tự 
 Vậy nghiệm của phương trình là: x  
k 2 ( k Z ). 2
c) (1đ) Giải phương trình 2 2
2 cos x  3 sin x cos x  sin x  1. 
 xét cos x  0 pt  1  1 (đúng) nên nhận x
k , k Z 0,25 2 xét cos x  0 1   0,25
pt   tan x    tan( )  x    k . 3 6 6 0,25  x   k
 Vậy nghiệm của phương trình là: 2 ( k Z ).  x    k 0,25 6 Câu 2
Cho tập X={0,1,2,3,4,5,6,7}. Hỏi từ tập X có thể lập được bao nhiêu số tự (1 điểm)
nhiên gồm 3 chữ số khác nhau và kết thúc là chữ số 3. Gọi abc Chọn c: 1 cách (c = 3) 0,25 Chọn a: 6 cách (a≠0, c) 0,25 Chọn b: 6 cách (b≠a,c) 0,25
Vậy số số tự nhiên cần tìm là: 1.6.6=36 (số) 0,25 Câu 3
Một tổ gồm 7 học sinh nam và 3 học sinh nữ, xếp thành một hàng ngang. (1 điểm)
Hỏi có bao nhiêu cách xếp sao cho không có 2 học sinh nữ nào đứng cạnh nhau? Xếp 7nam : 7! Cách 0,25
Chọn 3 chỗ từ 8 chỗ ( ở 2 đầu hàng và 6 chỗ giữa 7 nam ): 3 A cách. 0,5 8 0,25 Kết luận: 7! 3 A =1693440. 8 Câu 4
Một lớp gồm 25 học sinh nam và 15 học sinh nữ. Chọn ngẫu nhiên 4 học (1 điểm)
sinh để lập tốp ca. Tính xác suất để số học sinh được chọn có 2 nữ.
 Xác định  :chọn 4 học sinh từ lớp 40 học sinh  n() = 4 C =91390 0,5 40
 Gọi A : “Chọn 2 nữ và 2 nam” 0,25   n(A) = 2 2 C .C =31500 15 25 n(A) 0,25 31500   P(A) = = n() 91390 Câu 5 12  2 (1 điểm)
Tìm hệ số của số hạng chứa x3 trong khai triển x   . 2   x k kk  2 
 Số hạng tổng quát 12 TC (x) = 12 3 2k k k C x   k 1  12  2  12  x  0,25
 Hệ số của số hạng chứa : 12-3k = 3  k = 3 0,25 Vậy hệ số x3 : 3 3 2 .C = 1760 12 0,5 Câu 6
a) (1đ) Tìm giao tuyến của hai mặt phẳng (SAB) và (SCD)
(3 điểm)  Hình vẽ 
S  (SAB)  (SCD)     AB/ / CD
 d  (SAB)  (SCD) qua S và // AB//CD 
AB  (SAB), CD  (SCD)  0,25 X 4
b) (1đ) Tìm giao điểm I của đường thẳng MN và mặt phẳng (SBD). Ta có(SAN)  MN
S  (S AN)  (S BD) (1)
Trong mp (ABCD), gọi AN BD H
H AN , AN  (S AN)  H  (S AN) 
H BD, BD  (S BD)  H  (S BD) 
H  (S AN)  (S BD) (2)
Từ (1) và (2) SH  (S AN)  (S BD) 0,5 0.25
SH MN I I MN
I SH , SH  (SBD)  I  (SBD)  0.25   I = MN (SBD) .
c) (1đ) Chứng minh OI//(SAB). HO 1
 Chứng minh H trọng tâm tam giác ACD ,  0,25 HB 4 HI 1  Chứng minh đúng :  0,25 HS 4 HO HI 1   
 OI / /SB, SB  SAB  OI / / (SAB) HB HS 4 0,25 0,25