Đề thi cuối học kì 1 Toán 10 năm 2019 – 2020 trường THPT Phước Long – TP HCM

TRƯỜNG THPT PHƯỚC LONG
ĐỀ THI HỌC KỲ I_NĂM HỌC 2019 – 2020 TỔ TOÁN Môn: Toán – Lớp 10 ĐỀ CHÍNH THỨC
Thời gian làm bài: 90 phút (Không kể thời gian phát đề)
Họ và tên học sinh:……………………………………………………………………………………………………...................................................
Số báo danh:……………………………………………………………………………………………………………………………………………………
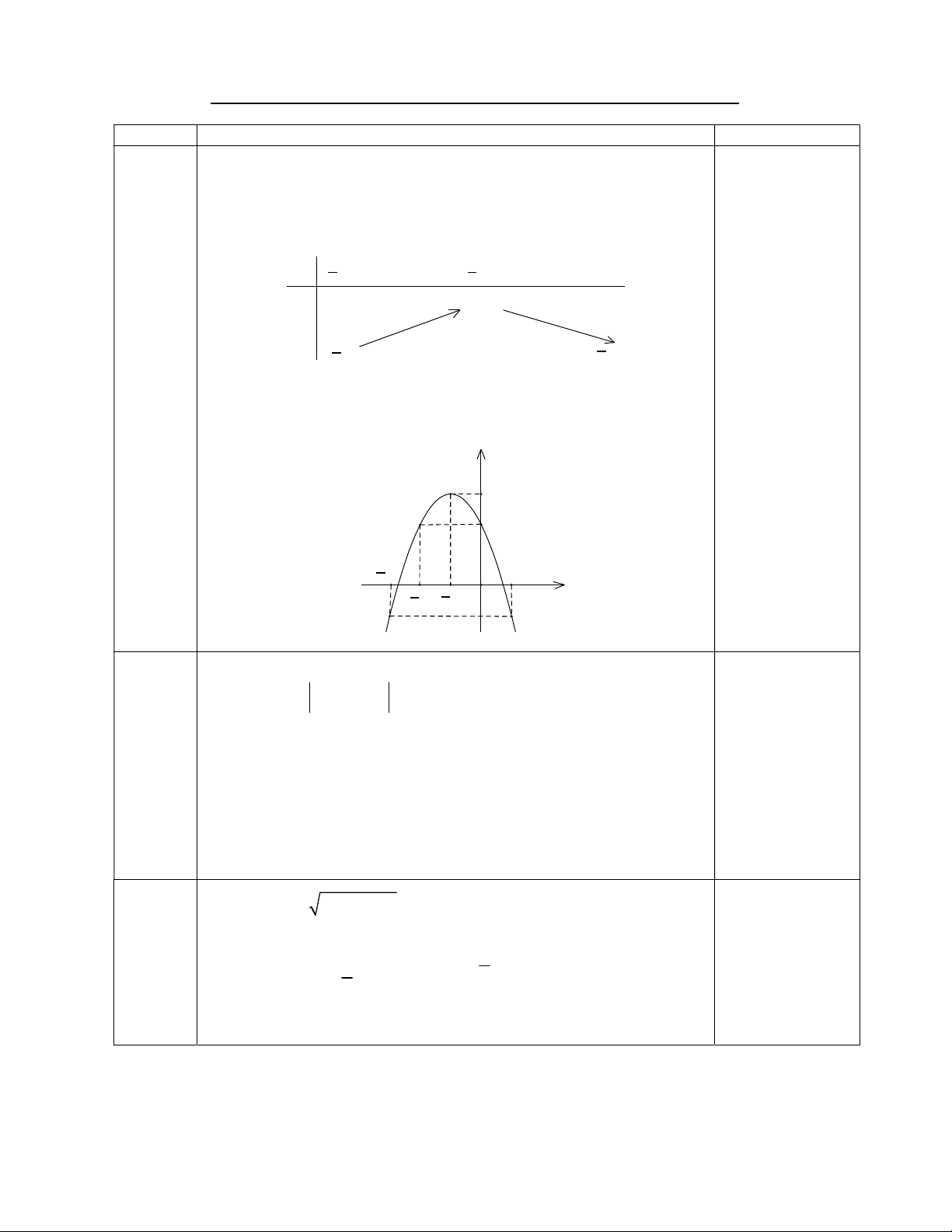
Câu 1 (1 điểm). Khảo sát sự biến thiên và vẽ đồ thị của hàm số 2 y  x  2x  2.
Câu 2 (3 điểm). Giải các phương trình sau: a) 2 x  2x  5  x 1. b) 2 5x  x  5  2x 1. c) 2
2x  5x  6  2 x 1  0 .
Câu 3 (2 điểm). Tìm tất cả các giá trị của tham số m để a) Phương trình 2
x  2(m 1)x  3m  2  0 có một nghiệm x  2  và tìm nghiệm
còn lại của phương trình nếu có. b) Phương trình 2 2
(3m  m )x  2mx 1  0 vô nghiệm.
Câu 4 (1 điểm). Cho phương trình 2 2
(x  2x  3)(x  2x  3m  2)  0 . Tìm tất cả các giá
trị của tham số m để phương trình đã cho có nghiệm kép.
Câu 5 (3 điểm). Trong mặt phẳng với hệ tọa độ Oxy cho ba điểm A(3;8), B( 1  ;2) và C(6;1) .
a) Chứng minh ba điểm A, B, C tạo thành một tam giác. Tìm tọa độ trọng tâm G của tam giác ABC.
b) Tìm tọa độ điểm E, biêt E nằm trên trục Oy và tam giác ACE vuông tại E.
c) Tìm tọa độ điểm H, biết rằng H thuộc đường thẳng d: y = x và độ dài đoạn BH bằng 5 . ----- Hết -----
ĐÁP ÁN ĐỀ THI HỌC KỲ I_NĂM HỌC 2019 – 2020 MÔN TOÁN 10 Câu Đáp án Thang điểm
Câu 1 Khảo sát sự biến thiên và vẽ đồ thị của hàm số 2 y  x  2x  2 . (1 đ). * TXĐ: D = R. * Đỉnh I( 1  ;3) * Bảng biến thiên: 0,25 x ∞ 1 +∞ 3 y 0,25 ∞ ∞
Hàm số đồng biến trên khoảng ( ;  1
 ) và nghịch biến trên khoảng 0,25 ( 1  ;) . * Đồ thị: y 3 2 0,25 3 1 2 1 O x Câu 2a x 1  0 (1 đ).  2 2
x  2x  5  x 1    x  2x  5  x 1  0,25  2 
x  2x  5  x 1 x  1 x  1 x  3      2 x 2  
 x  x  6  0   x  2  0,25+0,25+0,25      x  1 2 x  1  x  3x  4  0  x  4 Câu 2b 2x 1  0  (1 đ). 2
5x  x  5  2x 1   2 2 0,25 5
 x  x 5  4x  4x 1  1  1 x  x     2   2    x 1  0,25+0,25+0,25 x  1  2 x 5x 6 0      x  6 Câu 2c 2 2
2x  5x  6  2 x 1  0  2x  5x  6  2 x 1 (1 đ). x  1  x  1     2  2  0,25+0,25
2x  5x  6  4x  4 2x  x 10  0 x  1 x  2    x  2  0,25+0,25  5 x    2 Câu 3a phương trình 2
x  2(m 1)x  3m  2  0 có một nghiệm x  2  và (1 đ).
tìm nghiệm còn lại của phương trình nếu có. * PT có nghiệm x  2
  4  4(m 1)  3m  2  0  m  2  . 0,25+0,25
* Với m  2 ta có phương trình 2
x  2x  8  0  nghiệm còn lại 0,25+0,25 x  4 . Câu 3b Phương trình 2 2
(3m  m )x  2mx 1  0 vô nghiệm. (1 đ). 2 a  0  3  m  m  0   b   0 2m  0    ycbt c  0   1   0   0,25+0,25 a 0   2 3  m  m  0    ' 0     3  m  0 m  0 m  0     m  0 m  3  0,25+0,25  m  0  Câu 4 (1 đ). Cho phương trình 2 2
(x  2x  3)(x  2x  3m  2)  0 . Tìm tất cả các
giá trị của tham số m để phương trình đã cho có nghiệm kép. x 1  * PT  x  3  0,25  2 x
  2x  3m  2  0 (1)
* TH1: Phương trình (1) có nghiệm kép khác 1 và – 3  1 m  (L)   '  3m 1  0 3   2  1  1   2.1 3m  2  0  m  0,25 3  2  ( 3  )  2( 3  )  3m  2  0   17 m   3
* TH2: Phương trình (1) có hai nghiệm phân biệt và đồng thời có 1
nghiệm bằng 1 hoặc bằng – 3.  1 m   ' 3m 1 0      3 0,25   2  1 17   1   2.13m  2  0  m   m   3 3  2   ( 3
 )  2(3)  3m  2  0  17 m   3 17 Vậy m  . 3 0,25  Câu 5a AB  ( 4  ;6) (1 đ)  0,25 AC  (3; 9  ) 4  6   Ta có:  AB AC 3 9   ,
không cùng phương  ba điểm A, B, 0,25+0,25
C tạo thành một tam giác. 8
G là trọng tâm tam giác ABC  G( ;3) 3 0,25 Câu 5b E Oy  E(0; y) (1 đ)  AE  ( 3  ; y 8)  CE  (6; y 1) 0,25     AE  CE  AE.CE  0 0,25 0,25
 18  ( y 8)( y 1)  0  y  2  E(0; 2)   0,25  y  5  E(0;5) Câu 5c H  d : y  x  H ( ; x x) 0,25 (1 đ)  BH  (x 1; x  2) 2 2
BH  5  (x 1)  (x  2)  5 0,25 2  2x  2x  0 x  0  H  O(0;0)  0,25+0,25  x  1 H (1;1)