Đề thi cuối học kỳ 2 Thống kê ứng dụng | Trường Đại học Kinh tế – Luật, Đại học Quốc gia Thành phố Hồ Chí Minh

lOMoAR cPSD| 46663874
TRƯỜNG ĐẠI HỌC KINH TẾ LUẬT ĐỀ THI CUỐI KỲ
BỘ MÔN: Toán kinh tế Học kỳ I Năm học 2016 – 2017
(Được sử dụng tài liệu)
Môn: Thống kê ứng dụng.
Thời lượng: 60 phút Mã đề:202
Bài toán sau được dùng cho câu 1 và câu 2
Một thám tử xem xét tỉ lệ tội phạm trộm cắp ở hai khu vực khác nhau của thành phố.
Lấy mẫu ngẫu nhiên 1000 gia đình ở mỗi khu vực, phát hiện có 32 vụ trộm ở khu vực 1 và 14 vụ ở khu vực 2
Câu 1. Khoảng ước lượng với độ tin cậy 90% cho khác biệt về tỉ lệ phạm tội ở hai khu vực là: A. B. C. 0,018 ± 0,011 D.Đáp số khác
Câu 2. Giả sử thám tử tin rằng tỉ lệ hộ bị mất trộm trong khu vực 1 lớn hơn khu vực 2.
Kết quả kiểm định với mức ý nghĩa 5% cho thấy:
A. Có đủ chứng cứ để kết luận suy nghĩ của thám tử trên là đúng.
B. Không đủ chứng cứ để kết luận suy nghĩ của thám tử trên là đúng.
C. Có đủ chứng cứ để kết luận suy nghĩ của thám tử trên là sai.
D. Không đủ thông tin để đưa ra câu trả lời.
Câu 3 Để nghiên cứu ảnh hưởng của rượu đối với trí thông minh của trẻ em, người ta
đo chỉ số thông minh của 8 đứa trẻ mà mẹ của chúng uống rượu trong thời gian mang
thai (nhóm I), tìm được chỉ số thông minh trung bình của chúng là 78 và .
Một nhóm khác gồm 46 đứa trẻ có điều kiện kinh tế, xã hội giống như ở nhóm
trên, chỉ khác biệt duy nhất mẹ của chúng không hề uống rượu khi mang thai (nhóm
II). Kết quả đo được chỉ số thông minh trung bình của chúng là 99 và .
Với độ tin cậy 95% hãy ước lượng sự chênh lệch giữa chỉ số thông minh trung
bình (CSTMTB) của 2 nhóm trẻ trên (biết rằng chỉ số thông minh trung bình của các
nhóm trẻ tuân theo luật phân phối chuẩn, phương sai hai tổng thể chưa biết nhưng bằng nhau)
A. Với độ tin cậy 95%, CSTMTB của nhóm I = nhóm II.
B. Với độ tin cậy 95%, CSTMTB của nhóm I > nhóm II.
C. Với độ tin cậy 95%, CSTMTB của nhóm I < nhóm II. lOMoAR cPSD| 46663874
D. Đáp số khác..
Câu 4. Muốn đánh giá mức chi tiêu hàng tháng của sinh viên, người ta tiến hành điều
tra ngẫu nhiên một số sinh viên và thu được kết quả như sau Chi tiêu(triệu/tháng) 1.2-1.4 1.4-1.6 1.6-1.8 1.8-2.0 2.0-2.2 Số sinh viên 13 21 27 20 19
Với hệ số tin cậy 0,95, hãy ước lượng mức độ biến động chi tiêu hàng tháng (triệu
đồng/tháng) của sinh viên.
A. (0,052; 0,122) B. (0,228; 0,298) C. (0,091; 0,161) D. Đáp sô khác Câu 5. Doanh thu
bình quân hàng tháng của một đại lý bảo hiểm là 72000$. Để cải thiện doanh thu,
công ty đã triển khai một chương trình đào tạo mới. Mười đại lý được chọn tham gia
chương trình. Sau khi hoàn thành chương trình, doanh thu các đại lý trong tháng kế
tiếp được ghi nhận như sau ( đơn vị 1000$):
63 87 95 75 83 78 69 79 103 98
Với mức ý nghĩa 10%, có đủ chứng cứ để tin rằng chương trình đã thành công không?
A. Giá trị kiểm định t = 0,856, chương trình đã thành công.
B. Giá trị kiểm định t = 0,856, chương trình đã không thành công.
C. Giá trị kiểm định t = 2,71, chương trình đã không thành công.
D. Giá trị kiểm định t = 2,71, chương trình đã thành công.
Câu 6. Thời gian trung bình giữa nhiễm virus AIDS và phát triển AIDS đã được ước
tính là 10 năm với độ lệch chuẩn khoảng 3 năm. Kết luận này được đưa ra từ 1 nghiên
cứu có cỡ mẫu rất lớn, nên có thể xem là chuẩn. Bao nhiêu phần trăm người bị nhiễm
virus phát triển thành AIDS trong vòng 4 năm? A. 95% B. 5% C. 2,5% D. 35%
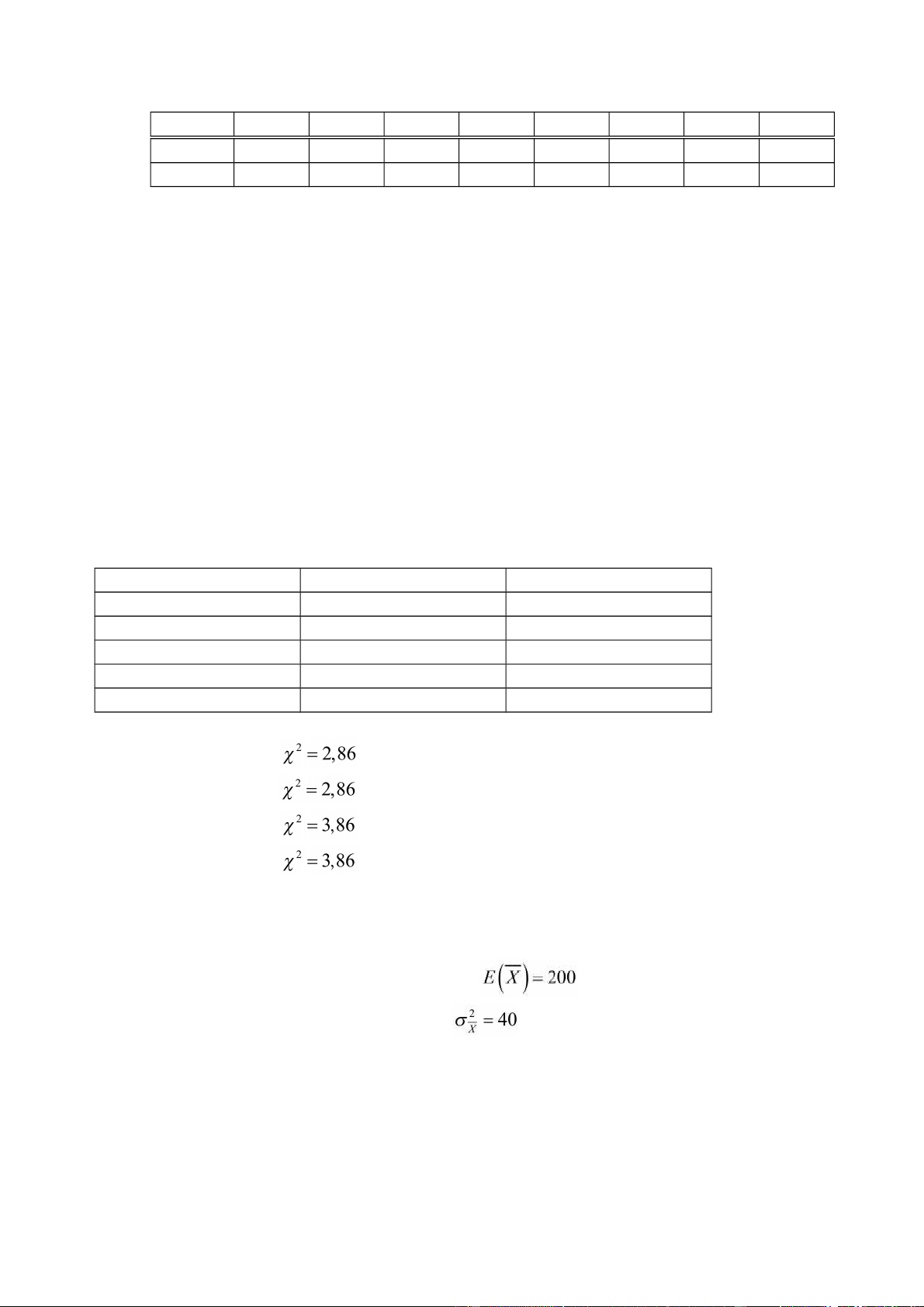
Câu 7. Một cuộc khảo sát về thu nhập (triệu đồng/tháng) của một nhóm sinh viên với kết quả như sau: lOMoAR cPSD| 46663874
Dựa vào bảng phân tích kết quả SPSS ở trên, thì trung bình mẫu (mean), độ lệch
chuẩn(Std.Deviation), độ xiên Skewnees và độ nhọn Kurtosis của bộ dữ liệu lần lượt là bao nhiêu?
A. 3,42; 3,347; 0,743; -0,084
B. 3,25; 1,82947; -0,084; 0.743
C. 3,25; 3,347; -0,084; 0,743
D. 3,42; 1,82947; 0,743; -0,084
Câu 8. Đối với bộ dữ liệu ở câu 7, dữ liệu có hình dạng như thế nào?
A. Phân phối cân đối
B. Phân phối lệch phải, do trung bình lớn hơn trung vị
C. Phân phối lệch trái, do trung bình nhỏ hơn trung vị
D. Không đủ thông tin để đưa ra kết luận
Câu 9. Có ý kiến cho rằng chất lượng của hai dây chuyền là như nhau. Người ta tiến
hành kiểm tra 100 sản phẩm do dây chuyền thứ nhất sản xuất ra thấy 12 phế phẩm và
kiểm tra 150 sản phẩm do dây chuyền thứ hai sản xuất ra thấy có 15 phế phẩm. Với
mức ý nghĩa 5%, hỏi ý kiến trên là đúng hay sai? (biết rằng chất lượng của 2 dây chuyền
tuân theo luật phân phối chuẩn). A. Giá trị kiểm định , Ý kiến trên là đúng. B. Giá trị kiểm
định , Ý kiến trên là sai. C. Giá trị kiểm định , Ý kiến trên là sai. D. Đáp số khác
Câu 10. Hai nhà hàng pizza cạnh tranh để phân phối nhanh nhất, tiến hành ghi thời gian
phân phối của 8 pizza cuối cùng từ nhà hàng A và 10 pizza từ nhà hàng B. Số liệu được cho trong bảng sau: Pizza A 11 15 16 17 18 18 21 23 lOMoAR cPSD| 46663874 Pizza B 12 15 16 19 22 23 23 26 29 32 Với
mức ý nghĩa 10% có thể kết luận rằng thời gian phân phối của hai nhà hàng pizza khác nhau hay không?
A. T = 112, thời gian phân phối của hai nhà hàng khác nhau.
B. T = 59, thời gian phân phối của hai nhà hàng như nhau.
C. T = 59, thời gian phân phối của hai nhà hàng khác nhau.
D. T = 112, thời gian phân phối của hai nhà hàng như nhau.
Câu 11. Một nhà cung cấp cà chua tin rằng tối thiểu 95% hạt giống cà chua sẽ nảy mầm
thành cây cà chua. Một nông dân kiểm định bằng một mẫu ngẫu nhiên 400 hạt giống
đem trồng. Sau hai tuần thấy có 368 cây cà chua. Có thể kết luận với mức ý nghĩa 1%
rằng niềm tin của nhà cung cấp là sai không?
A. Giá trị kiểm định Z = - 2,75, niềm tin của nhà cung cấp là chính xác.
B. Giá trị kiểm định Z = - 2,75, niềm tin của nhà cung cấp là sai.
C. Giá trị kiểm định Z = - 2, 21, niềm tin của nhà cung cấp là sai.
D. Giá trị kiểm định Z = - 2,21, niềm tin của nhà cung cấp là chính xác.
Bài toán sau được dùng cho câu 12 và câu 13
Mục tiêu nhằm so sánh sự thành công tương đối của 2 chuỗi cửa hiệu lớn, người ta đã
tiến hành đo doanh thu (triệu đồng) trên mỗi m2 . Lấy một mẫu 5 cửa hàng của mẫu 1
có số trung bình và phương sai lần lượt là 80,32 và 130,42; và 5 cửa hàng của mẫu 2 có
số trung bình và phương sai lần lượt là 70,10 và 53,67.
Câu 12. Với giả định các tổng thể lấy mẫu có phân phối chuẩn và phương sai hai tổng
thể chưa biết nhưng bằng nhau, trong bài toán kiểm định về sự sai khác giữa hai trung bình
tổng thể về doanh thu trên mỗi m2 của hai chuỗi cửa hiệu thì phương sai mẫu gộp nhận giá trị là A. B. C. D. Đáp số khác
Câu 13. Nếu lấy hai mẫu ngẫu nhiên với cỡ mẫu 50 từ mỗi tổng thể chuỗi cửa hiệu và
thu được số thống kê sau: . Với mức ý
nghĩa 10%, có thể kết luận gì từ dữ liệu này? A. Không đủ thông tin để đưa ra câu trả lời.
B. Không có đủ chứng cứ để kết luận rằng doanh thu bình quân/m2 của hai chuỗi cửa hiệu khác nhau
C. Doanh thu bình quân/m2 của chuỗi cửa hiệu thứ I thấp hơn của chuỗi cửa hiệu thứ hai.
D. Doanh thu bình quân/m2 của chuỗi cửa hiệu thứ I cao hơn của chuỗi cửa hiệu thứ hai.
Câu 14. Để khảo sát mức độ hài lòng của môn học Thống kê Ứng dụng ở 3 lớp K15A,
K15B, K15C người ta chọn một số SV ở 3 lớp với câu hỏi “ Bạn hãy đánh giá mức độ
hài lòng về môn học TKUD” (ghi rõ điểm số với 1. Hoàn toàn không hài lòng => 5.
Hoàn toàn rất hài lòng) thì thu được bảng số liệu sau: lOMoAR cPSD| 46663874 K15A 5 3 3 5 4 2 1 1 K15B 1 3 2 4 3 5 K15C 5 2 4 2 3 5 2
Hãy cho biết trong các kiểm định sau, kiểm định nào phù hợp để khẳng định về giả thiết
cho rằng không có sự khác biệt về mức độ hài lòng giữa 3 lớp. A. Phân tích ANOVA.
B. Kiểm định khi bình phương về tính độc lập.
C. Kiểm định Kruskall – Wallis.
D. Một kiểm định khác.
Câu 15. Giảng viên muốn ước lượng thời gian làm bài trung bình với sai số ước lượng
là 0,2 phút ở mức tin cậy 90% ( khoảng tin cậy dài bằng 4σ). Trong khảo sát sơ bộ, đã
quan sát thấy số giờ làm bài có giá trị từ 51,2 phút đến 55,6 phút. Với giả định tổng thể
số giờ làm bài có phân phối chuẩn, Giảng viên nên dùng cỡ mẫu là:
A. 9 B. 70 C. 82 D. Một đáp án khác Câu 16.
Để tìm hiểu chi tiết hơn về đặc trưng nhân khẩu học các độc giả, tạp chí MAGAZINE
tổ chức một cuộc khảo sát gồm 300 độc giả đăng kí, thiết lập được bảng tần số phân phối độ tuổi như sau: Tuổi Tần số n.Pi 15-25 30 29,04 25-35 78 71,04 35-45 96 99,84 45-55 62 71,04 55-65 34 29,04
Với mức ý nghĩa 10% có thể kết luận độ tuổi tuân theo phân bố chuẩn không? A.
Giá trị kiểm định , độ tuổi tuân theo phân bố chuẩn.
B. Giá trị kiểm định
, độ tuổi không tuân theo phân bố chuẩn.
C. Giá trị kiểm định
, độ tuổi không tuân theo phân bố chuẩn.
D. Giá trị kiểm định
, độ tuổi tuân theo phân bố chuẩn.
Câu 17. Một mẫu có cỡ n = 50 được chọn ngẫu nhiên từ một tổng thể có phân bố
chuẩn. Giả sử tổng thể có trị trung bình = 200 và độ lệch chuẩn σ = 40. Trong các
phát biểu sau đây có bao nhiêu phát biểu sai?
i) Giá trị kì vọng của trung bình mẫu ii) Phương sai của trung bình mẫu iii) Có gần như
toàn bộ số quan sát của .
tổng thể nằm trong khoảng ( 80; 320 ). iv) Để độ lệch chuẩn
của trung bình mẫu tối đa là 10, cỡ mẫu tối thiểu cần phải lấy là n = 16. A. 1 B. 2 C.3 D. 4
Bài toán sau được dùng cho câu 18 và câu 19 lOMoAR cPSD| 46663874
Hãng chế tạo máy tính đã nhận vô số than phiền liên quan tuổi thọ ngắn hạn của các ổ
đĩa, hầu hết cần sửa chữa trong vòng hai năm. Hãng quyết định kiểm định bốn loại ổ
đĩa hiện tại, để xác định có sự khác biệt về tuổi thọ giữa chúng hay không, đã lấy mẫu
ngẫu nhiên gồm 5 ổ đĩa mỗi loại và nối với máy vi tính. Số tuần lễ mà ổ đĩa bị hư
được ghi lại, từ đó thu được các trị trung bình lần lượt là:
và được bảng ANOVA như sau: Source of Df SS MS F Variation Between Groups X Y Z F Within Groups S 3423,2 T Total 5940,95
Câu 18. Hoàn tất bảng ANOVA trên, ta có:
A. X = 4; S = 16; Y = 2517,75; Z = 839,25; T = 213,95; F = 3,92.
B. X = 3; S = 16; Y = 2517,75; Z = 839,25; T = 213,95; F = 3,92.
C. X = 4; S = 20; Y = 2517,75; Z = 839,25; T = 213,95; F = 3,92.
D. X = 3; S = 20; Y = 2517,75; Z = 839,25; T = 213,95; F = 3,92.
Câu 19. Với mức ý nghĩa 5%, dữ liệu này cho phép kết luận rằng có sự khác biệt tuổi
thọ trung bình giữa các loại ổ đĩa không?
A. Không có đủ chứng cứ để kết luận rằng tuổi thọ trung bình của các loại ổ đĩa khác nhau B. ; C. D. ;
Câu 20. Trong bài toán kiểm định Chi bình phương về sự phụ thuộc giữa hai biến
định tính, tần số lý thuyết ( và cột thứ ) lần lư : ợt là
Thời gian học Dưới 8 (giờ/ngày) Trên 8 (giờ/ngày) Xếp loại Dưới Khá 100 50 Từ khá trở lên 200 250
A. 150 , 150, 150, 150 B. 225, 225, 75, 75 là ở vị trí hàng thứ
C. 75, 225, 75, 225 D. 75, 75, 225, 225