Đề thi cuối kỳ 1 Toán 10 năm 2020 – 2021 trường THPT Đông Hà – Quảng Trị

Đề thi cuối kỳ 1 Toán 10 năm 2020 – 2021 trường THPT Đông Hà – Quảng Trị được biên soạn theo hình thức 100% tự luận, đề gồm 01 trang với 08 bài toán, thời gian làm bài 90 phút, mời bạn đọc đón xem

19 10 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề HK1 Toán 10

Môn: Toán 10

Thông tin:

5 trang 8 tháng trước

Tác giả:

Profile Thanh Tâm
Trang 1
TRƯỜNG THPT ĐÔNG HÀ
TỔ: TOÁN
(Đề gồm 01 trang)
ĐỀ KIỂM TRA CUỐI KỲ I – NĂM HỌC 2020 - 2021
MÔN TOÁN – LỚP 10
Thời gian làm bài: 90 phút (Không kể thời gian giao đề)
Họ và tên:……………………………….. Lớp:…………. SBD:…………..
Câu 1: (2,5 điểm) Cho hàm số
2
23yx x
=−−
.
a) Khảo sát sự biến thiên và vẽ đồ thị (P) của hàm số.
b) Tìm tọa độ giao điểm của đồ thị (P) với đường thẳng
43yx= −
.
Câu 2: (1,0 điểm) Xét tính chẵn, lẻ của hàm số
() 3 1 3 1fx x x= −− +
.
Câu 3: (1,0 điểm) Giải và biện luận phương trình sau theo tham số m.
( )
2
322m mx m x− += −
.
Câu 4: (1,0 điểm) Cho phương trình
2
2 4 10x xm− − +=
. Tìm tất cả các giá trị của tham
số m để phương trình có hai nghiệm phân biệt
12
,xx
sao cho
Câu 5: (1,0 điểm) Giải hệ phương trình:
22
22
32 2
32 2
x yy
y xx
+= +
+= +
.
Câu 6: (0,5 điểm) Giải phương trình:
( ) ( )
2
6 7 1 2 4 26 0x x x x xx+ ++ + ++ − − =
.
Câu 7: (0,5 điểm)
Cho 4 điểm
,,,ABCD
. Chứng minh rằng:
AB DC AD BC−=−
   
.
Câu 8: (2,5 điểm) Trong mặt phẳng tọa độ Oxy, cho 3 điểm
( ) ( ) ( )
1; 3 , 1;1 , 2; 0AB C−
.
a) Chứng minh tam giác ABC cân. Tính diện tích của tam giác ABC.
b) Tính cosin của góc
ACB
.
c) Tìm tọa độ điểm M trên đường thẳng
: dy x=
sao cho vectơ
2u MA MB= +
 
có độ
dài nhỏ nhất.
………..
HẾT………
 HÀ

 - 2021
MÔN: TOÁN

Câu


Câu 1
(2,5 điểm)
P
2
23y x x
.
1,5
⦁ Tập xác định:
D
.
0,25
⦁ Tọa độ đỉnh
1; 4I
0,25
⦁ Bảng biến thiên
0,25
⦁ Bảng giá trị
x
1
0
1
2
3
y
0
3
4
3
0
0,25
⦁ Đồ thị
0,5

4 3.yx
1,0
Phương trình hoành độ giao điểm
2
2 3 4 3x x x
0,25
2
60xx
0
6
x
x
.
0,25
Với
03xy
Với
6 21.xy
0,25
Vậy (P) cắt d tại hai điểm
0; 3 , 6;21AB
.
0,25
Câu 2
(1,0 điểm)

( ) 3 1 3 1 .f x x x
1,0
TXĐ:
D
0,25
x D x D
0,25
3 1 3 1 3 1 3 1
3 1 3 1 3 1 3 1
f x x x x x
x x x x f x
0,25
Vậy hàm số
( ) 3 1 3 1f x x x
là hàm số lẻ.
0,25
Câu 3
(1,0 điểm)
m.
2
3 2 2m m x m x
.
1,0
2
3 2 2Pt m m x m
(1)
0,25
O
1
3
4
1
2
3
x
y
x

1

y

4

Câu


TH1:
2
1
3 2 0
2
m
mm
m
Với
1m
:
1 0. 1x
: Phương trình vô nghiệm.
0,25
Với
2m
:
1 0. 0x
: Phương trình có nghiệm đúng với
x
.
0,25
TH2:
2
1
3 2 0
2
m
mm
m
.
Phương trình có nghiệm duy nhất:
2
21
3 2 1
m
x
m m m

.
0,25

Với
1m
: Phương trình vô nghiệm.
Với
2m
: Phương trình có nghiệm đúng với
x
.
Với
1
2
m
m
. Phương trình có nghiệm duy nhất:
1
1
x
m
.
Câu 4
(1,0 điểm)

2
2 4 1 0x x m

m 
12
,xx
sao cho
22
1 2 1 2
3 9.x x x x
1,0
Phương trình có 2 nghiệm phân biệt khi và chỉ khi
' 0 1 4 1 0 0mm
0,25
Theo Định lý Viét ta có
12
12
2
41
xx
x x m

0,25
Với
0m
, phương trình có 2 nghiệm phân biệt
12
,xx
.
2
22
1 2 1 2 1 2 1 2
3 9 5 9x x x x x x x x
.
0,25
2
2 5 4 1 9m
1
2
m
(thỏa mãn điều kiện).
0,25
Câu 5
(1,0 điểm)

22
22
3 2 2 (1)
3 2 2 (2)
x y y
y x x
.
1,0
Lấy (1) trừ (2) vế theo vế ta được:
2 2 2 2 2 2
3 2 3 3 3 0x y y x y x x y x y
0,25
0
( )( 1) 0
1 0 1
x y x y
x y x y
x y x y



0,25
Với
xy
thế vào (1) ta có:
2 2 2
1
3 2 2 3 2 0
2
x
x x x x x
x
Trường hợp này hệ phương trình đã cho có 2 nghiệm
;xy
là
1;1 , 2;2
.
0,25
Với
1xy
thế vào (1) ta có:
2
22
1 3 2 2 1 0y y y y y
.
Phương trình vô nghiệm nên hệ vô nghiệm.
Vậy hệ phương trình đã cho có 2 nghiệm
;xy
là
1;1 , 2;2
.
0,25
Câu


Câu 6
(0,5 điểm)

2
6 7 1 2 4 26 0 (1)x x x x x x
.
0,5
Điều kiện:
2x 
.
2
1 6 7 3 1 2 2 6 0x x x x x x
6 2 1 2
2 3 0
7 3 2 2
x x x x
xx
xx
61
2 3 0
7 3 2 2
xx
xx
xx




2
61
3 0 (*)
7 3 2 2
x
xx
x
xx

0,25
Ta có
61
3
7 3 2 2
2 2 4 1
21
7 3 2 2 7 3 2 2
xx
x
xx
xx
x
x x x x


1 1 4 2 1
2 1 0 2
7 3 2 2 7 3 2 2
x
xx
x x x x




Do đó phương trình (*) vô nghiệm.
Vậy phương trình có nghiệm duy nhất
2x
.
0,25
Câu 7
(0,5 điểm)

, , ,A B C D
:
AB DC AD BC
.
0,5
Ta có
AB DC AD DB DC
0,25
AD CB AD BC
.
0,25
Câu 8
(2,5 điểm)
Oxy, c
1;3 , 1;1 , 2;0A B C
.
ABC ABC.
1,0
Ta có
2 2; 10; 10AB AC BC
10BC AC
nên tam giác ABC cân
tại C.
0,5
Gọi H là trung điểm AB. Vì tam giác ABC cân tại C nên CH là đường cao.
0;2H
;
22CH
.
0,25
Vậy
11
. .2 2.2 2 4
22
ABC
S CH AB
(đvdt).
0,25
b) Tính 
ACB
.
1,0
Ta có:
1;3CA 
,
0,25
3;1CB 
.
0,25
.
cos cos ,
.
CACB
ACB CA CB
CA CB

0,25
63
5
10. 10

.
0,25
     M   
: d y x
  
2u MA MB

0,5
Gọi
;M x x d
.
1 ;3MA x x
;
1 ;1MB x x
.
Câu


2 1 3 ;5 3u MA MB x x
0,25
22
2
2
2 1 3 5 3
18 24 26 2 3 2 18 3 2
u MA MB x x
x x x
u
nhỏ nhất bằng
32
tại
2
3
x
. Vậy tọa độ điểm M là
22
;
33
M



.
0,25
 Học sinh làm cách khác đúng thì vẫn được điểm tối đa cho câu đó.
----------  ----------
| 1/5
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

TRƯỜNG THPT ĐÔNG HÀ ĐỀ KIỂM TRA CUỐI KỲ I – NĂM HỌC 2020 - 2021 TỔ: TOÁN
MÔN TOÁN – LỚP 10
(Đề gồm 01 trang)
Thời gian làm bài: 90 phút (Không kể thời gian giao đề)
Họ và tên:……………………………….. Lớp:…………. SBD:…………..
Câu 1: (2,5 điểm) Cho hàm số 2
y = x − 2x − 3 .
a) Khảo sát sự biến thiên và vẽ đồ thị (P) của hàm số.
b) Tìm tọa độ giao điểm của đồ thị (P) với đường thẳng y = 4x −3.
Câu 2: (1,0 điểm) Xét tính chẵn, lẻ của hàm số f (x) = 3x −1 − 3x +1 .
Câu 3: (1,0 điểm) Giải và biện luận phương trình sau theo tham số m. ( 2
m − 3m) x + 2 = m − 2x .
Câu 4: (1,0 điểm) Cho phương trình 2
x − 2x − 4m +1 = 0 . Tìm tất cả các giá trị của tham
số m để phương trình có hai nghiệm phân biệt x , x sao cho 2 2
x + x − 3x x = 9. 1 2 1 2 1 2 2 2 
Câu 5: (1,0 điểm) Giải hệ phương trình: x + 3y = 2y + 2  . 2 2
y + 3x = 2x + 2
Câu 6: (0,5 điểm) Giải phương trình: (x + ) x + + (x + ) 2 6 7
1 x + 2 + x − 4x − 26 = 0 .
   
Câu 7: (0,5 điểm) Cho 4 điểm ,
A B, C, D . Chứng minh rằng: AB − DC = AD − BC .
Câu 8: (2,5 điểm) Trong mặt phẳng tọa độ Oxy, cho 3 điểm A(1;3), B( 1; − ) 1 ,C (2;0) .
a) Chứng minh tam giác ABC cân. Tính diện tích của tam giác ABC. b) Tính cosin của góc  ACB .   
c) Tìm tọa độ điểm M trên đường thẳng d: y = x sao cho vectơ u = MA+ 2MB có độ dài nhỏ nhất.
………..HẾT……… Trang 1
TRƯỜNG THPT ĐÔNG HÀ
ĐÁP ÁN ĐỀ KIỂM TRA HỌC KÌ I – NĂM HỌC 2020 - 2021 MÔN: TOÁN TỔ TOÁN LỚP: 10 Câu
Nội dung trả lời cần đạt được Điểm
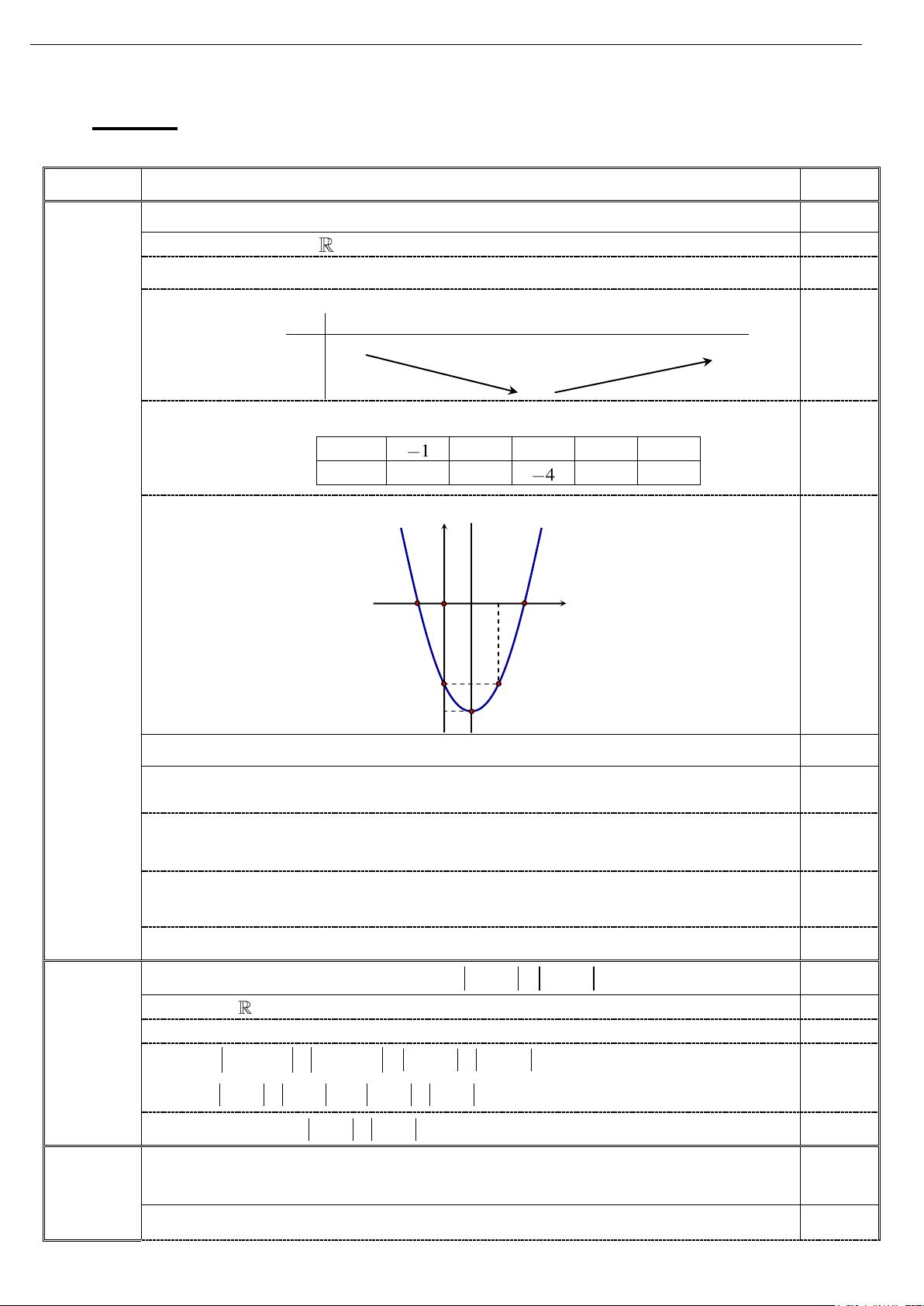
a) Khảo sát sự biến thiên và vẽ đồ thị (P) của hàm số 2
y x 2x 3 . 1,5
⦁ Tập xác định: D  . 0,25
⦁ Tọa độ đỉnh I 1;  4 0,25 ⦁ Bảng biến thiên x  1    0,25 y 4  ⦁ Bảng giá trị 0,25 x 1 0 1 2 3 y 0  3 4  3 0 ⦁ Đồ thị y Câu 1 (2,5 điểm) 1  O 1 2 3 x 0,5 3  4 
b) Tìm tọa độ giao điểm của đồ thị (P) với đường thẳng y 4x 3. 1,0
Phương trình hoành độ giao điểm 0,25 2
x  2x  3  4x  3 x  0,25 2  x  6x  0 0   . x  6
Với x  0  y  3  0,25
Với x  6  y  21.
Vậy (P) cắt d tại hai điểm A0; 3  , B6;2  1 . 0,25
Xét tính chẵn, lẻ của hàm số f (x) 3x 1 3x 1 . 1,0 TXĐ: D  0,25 x
 D  xD 0,25 Câu 2
f x  3x 1  3x        (1,0 điểm) 1 3x 1 3x 1 0,25
 3x 1  3x 1    3x 1  3x 1    f x
Vậy hàm số f (x)  3x 1  3x 1 là hàm số lẻ. 0,25
Giải và biện luận phương trình sau theo tham số m. Câu 3 2
m 3mx 2 m 2x . 1,0
(1,0 điểm) Pt   2
m  3m  2 x m  2 (1) 0,25 Câu
Nội dung trả lời cần đạt được Điểm m 1 TH1: 2
m  3m  2  0   m  2 0,25 Với m 1:   1  0.x  1
 : Phương trình vô nghiệm. Với m  2 :  
1  0.x  0 : Phương trình có nghiệm đúng với x   . 0,25 m  1 TH2: 2
m  3m  2  0   . m  2 0,25 
Phương trình có nghiệm duy nhất: m 2 1 x   . 2 m  3m  2 m 1 Kết luận:
Với m 1: Phương trình vô nghiệm.
Với m  2 : Phương trình có nghiệm đúng với x   . m  1 Với 
. Phương trình có nghiệm duy nhất: 1 x  . m  2 m 1 Cho phương trình 2
x 2x 4m 1 0 . Tìm tất cả các giá trị của tham số
m để phương trình có hai nghiệm phân biệt x , x sao cho 1 2 1,0 2 2
x x 3x x 9. 1 2 1 2
Phương trình có 2 nghiệm phân biệt khi và chỉ khi 0,25 Câu 4  '  0  1  4  m  
1  0  m  0 (1,0 điểm) x x  2
Theo Định lý Viét ta có 1 2  0,25 x x  4  m 1  1 2
Với m  0, phương trình có 2 nghiệm phân biệt x , x . 1 2 0,25
x x  3x x  9   x x 2 2 2 5x x  9 . 1 2 1 2 1 2 1 2  2 2 5 4  m   1  1 9  m
(thỏa mãn điều kiện). 0,25 2 2 2
x 3y 2y 2 (1)
Giải hệ phương trình: . 1,0 2 2     y 3x 2x 2 (2)
Lấy (1) trừ (2) vế theo vế ta được: 2 2 0,25
x y   y x   2 2 y x  2 2 3 2
 3x 3y 3x y  0 x y  0 x y Câu 5
 (x y)(x y 1)  0     0,25
x y 1  0 x 1 y
(1,0 điểm) Với x y thế vào (1) ta có: x 1 2 2 2
x  3x  2x  2  x  3x  2  0   x  2 0,25
Trường hợp này hệ phương trình đã cho có 2 nghiệm  ; x y là 1;  1 , 2;2 .
Với x 1 y thế vào (1) ta có:   y2 2 2 1
 3y  2y  2  y y 1 0 .
Phương trình vô nghiệm nên hệ vô nghiệm. 0,25
Vậy hệ phương trình đã cho có 2 nghiệm  ; x y là 1;  1 , 2;2 . Câu
Nội dung trả lời cần đạt được Điểm
Giải phương trình: x   x    x   2 6 7 1
x 2 x 4x 26 0 (1) . 0,5 Điều kiện: x  2  .  
1   x  6 x  7 3  x   1  x  2  2 2     x x 6 0
x 6x 2 x   1  x  2       x   
x   x 2x 3 0 7 3 2 2       x   x 6 x 1 2   x  3  0 0,25    x  7  3 x  2  2  x  2     x 6 x 1    x  3  0 (*) Câu 6  x  7  3 x  2  2
(0,5 điểm) Ta có x  6 x 1   x  3 x  7  3 x  2  2 x  2 x  2 4 1    x  2  1 x  7  3 x  2  2 x  7  3 x  2  2 0,25       x   1 1 4 x 2 1 2  1    0 x   2     x  7  3 x  2  2  x  7  3 x  2  2
Do đó phương trình (*) vô nghiệm.
Vậy phương trình có nghiệm duy nhất x  2 . Cho 4 điểm ,
A B, C, D . Chứng minh rằng: AB DC AD BC . 0,5 Câu 7
Ta có AB DC AD DB DC 0,25
(0,5 điểm) ADCB ADBC . 0,25
Trong m t phẳng tọa độ Oxy, cho 3 điểm A1;3, B1
;1,C 2;0. 1,0
a) Chứng minh tam giác ABC cân. Tính diện tích của tam giác ABC.
Ta có AB  2 2; AC  10; BC  10  BC AC  10 nên tam giác ABC cân 0,5 tại C.
Gọi H là trung điểm AB. Vì tam giác ABC cân tại C nên CH là đường cao. 0,25
H 0; 2 ; CH  2 2 . Vậy 1 1    S CH.AB .2 2.2 2 4 (đvdt). 0,25 ABC  2 2
b) Tính cosin của góc ACB . 1,0
Ta có: CA   1  ;3 , 0,25 CB   3  ;  1 . 0,25 Câu 8 (2,5 điểm) CA CB ACB  CA CB . cos cos ,  0,25 CA . CB 6 3   . 0,25 10. 10 5
c) Tìm tọa độ điểm M trên đường thẳng d: y x sao cho vectơ 0,5
u MA 2MB có độ dài nhỏ nhất. Gọi M  ;
x x d . MA  1 ;
x 3  x ; MB   1   ; x 1 x . Câu
Nội dung trả lời cần đạt được Điểm
u MA 2MB   1  3 ; x 5  3x 0,25
u MA  2MB   1
  3x2  53x2
 18x  24x  26  2 3x  22 2 18  3 2 0,25  2 2 
u nhỏ nhất bằng 3 2 tại 2 x
. Vậy tọa độ điểm M là M ;   . 3  3 3 
Lưu ý: Học sinh làm cách khác đúng thì vẫn được điểm tối đa cho câu đó.
---------- HẾT ----------
Document Outline

  • ĐỀ-CHÍNH-THỨC-TOÁN-10-HKI_2020-2021
  • DAP-AN-KIEM-TRA-HOC-KI-I-TOAN-10-2020-2021