Đề thi cuối kỳ 1 Toán 11 năm 2020 – 2021 trường Lương Đắc Bằng – Thanh Hóa

SỞ GD & ĐT THANH HÓA
ĐỀ KIỂM TRA CUỐI KỲ I KHỐI 11
TRƯỜNG THPT LƯƠNG ĐẮC BẰNG NĂM HỌC 2020 - 2021 Môn: TOÁN ĐỀ 1 Thời gian: 90 phút
(không kể thời gian giao đề)
Câu I (3.0 điểm) Giải các phương trình sau: 1) 2 2 sin x  sin x  3  0 2) cosx  3 sinx  2
3) 4 sin x cos2x  3  2 cos2x  2 3 s inx u  u  7
Câu II (1.0 điểm) Tìm công sai d và số hạng đầu u của cấp số cộng (u ) , biết: 2 3 1 n u u  10  1 5 Câu III (3.0 điểm) 1) Tìm hệ số của 15 x trong khai triển 3 10 (2x  3) .
2) Một hộp đựng 8 quả cầu màu đỏ, 7 quả cầu màu xanh và 6 quả cầu màu vàng (chúng chỉ
khác nhau về màu). Lấy ngẫu nhiên 4 quả cầu từ hộp. Tính xác suất để trong 4 quả cầu đó
phải có đủ 3 màu khác nhau?
3) Một nhóm học sinh gồm 18 nam và 6 nữ. Người ta muốn chọn từ nhóm ra 5 người để lập
thành một đội cờ đỏ sao cho phải có 1 đội trưởng nam, 1 đội phó nam và có ít nhất 1 nữ.
Hỏi có bao nhiêu cách lập đội cờ đỏ.
Câu IV (3.0 điểm) Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O . Gọi M là 1
điểm nằm trên cạnh SC sao cho SM  SC . 4
1) Tìm giao tuyến của hai mặt phẳng (MBD) và (SAC)
2) Gọi N là trung điểm của đoạn thẳng AO và  là mặt phẳng qua AM và song song
với BD và lần lượt cắt SB,SD tại E,F . Chứng minh rằng MN / /(ABE) S
3) Tính tỉ số diện tích S  EM S SBC ---Hết--- 1 SỞ GD & ĐT THANH HÓA
ĐỀ KIỂM TRA CUỐI KỲ I KHỐI 11
TRƯỜNG THPT LƯƠNG ĐẮC BẰNG NĂM HỌC 2020 - 2021 Môn: TOÁN ĐỀ 2 Thời gian: 90 phút
(không kể thời gian giao đề)
Câu I (3.0 điểm) Giải các phương trình sau: 1) 2 2 cos x  cosx  3  0 2) 3 sin x  cos x  1
3) 4 sin x cos2x  3  2 cos2x 2 3 s inx u  u  16
Câu II (1.0 điểm) Tìm công sai d và số hạng đầu u của cấp số cộng (u ) 1 n , biết: 1 5 u  u 19  3 4 Câu III (3.0 điểm) 1) Tìm hệ số của 12 x trong khai triển 3 12 (3x  2) .
2) Một hộp đựng 8 quả cầu màu đỏ, 6 quả cầu màu xanh và 5 quả cầu màu vàng (chúng chỉ
khác nhau về màu). Lấy ngẫu nhiên 4 quả cầu từ hộp. Tính xác suất để trong 4 quả cầu đó
phải có đủ 3 màu khác nhau?
3) Một nhóm học sinh gồm 17 nam và 7 nữ. Người ta muốn chọn từ nhóm ra 5 người để lập
thành một đội cờ đỏ sao cho phải có 1 đội trưởng nam, 1 đội phó nam và có ít nhất 1 nữ.
Hỏi có bao nhiêu cách lập đội cờ đỏ.
Câu IV (3.0 điểm) Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O . Gọi I là 1
điểm nằm trên cạnh SC sao cho SI  SC . 4
1) Tìm giao tuyến của hai mặt phẳng (IBD) và (SAC)
2) Gọi J là trung điểm của đoạn thẳng AO và  là mặt phẳng qua AI và song song
với BD và lần lượt cắt SB,SD tại P, .
Q Chứng minh rằng IJ / /(ADQ) S
3) Tính tỉ số diện tích SIQ S SCD ---Hết--- 2 SỞ GD & ĐT THANH HÓA
TRƯỜNG THPT LƯƠNG ĐẮC BẰNG HƯỚNG DẪN CHẤM
ĐỀ KIỂM TRA CUỐI KỲ I, NĂM HỌC 2020 -2021 Môn: Toán 11 ĐỀ 1 Câu Ý Nội dung Điểm Câu I sinx  1  2
2 sin x  sinx  3  0   3  sinx  (Loaï ) 0.5  i 1  2 
+) sinx  1  x   k2 ,  k   2 0.5 1 3 2 Pt  cosx  sin x    2  cosx.cos  sin x.sin  2 2 2 3 3 2 0.5     7   x    k2 x   k2   2     cos x      cos 3 4 12      ,k    3 4     x k 2      x   k2  3 4  12 7 
Vậy nghiệm của phương trình: x   k2 ,  x   k2 ,  k   12 12 0.5
Ta có phương trình tương đương với pt sau: 0.5
(2 cos 2x  3)(2 sin x 1)  0 3  1   5 sinx  x   k2 , x     k2 .  2      6 6  (k,l  )   3   cos2x= x=  l 0.5  2  12 Câu II
Gọi d và u lần lượt là công sai và số hạng đầu của CSC (u ) . Ta có: 1 n u  + u = -7 2  u +3d  7  u   1 2 3   1    1   1.0 u  + u = -10 2  u  4d  10 d   3 1 5   1   Câu III
Số hạng tổng quát trong khai triển nhị thức 3 10
(2x  3) là : k 10 k k 30 3 2 3  k C x 0.5 10 0.25 1 Hệ số của 15
x ứng với k thõa mãn: 30 3k  15  k  5 0.25 Vậy hệ số của 15 x là 5 5 5 C 2 3  1959552 10
 Số phần tử của không gian mẫu là 4 ( n )  C  5985 0.5 21
 Gọi A là biến cố “Chọn 4 quả cầu phải có đủ 3 màu khác nhau từ hộp đựng 8
quả cầu màu đỏ, 7 quả cầu màu xanh và 6 quả cầu màu vàng” ta có các 2 trường hợp sau:
+) Chọn được 1 quả cầu màu đỏ, 1 quả cầu màu xanh và 2 quả cầu màu
vàng có số cách chọn là: 3 1 1 2 C C C  840 (cách chọn) 0.25 8 7 6
+) Chọn được 1 quả cầu màu đỏ, 2 quả cầu màu xanh và 1 quả cầu màu
vàng có số cách chọn là: 1 2 1 C C C  1008 (cách chọn) 0.25 8 7 6
+) Chọn được 1 quả cầu màu đỏ, 2 quả cầu màu xanh và 1 quả cầu màu
vàng có số cách chọn là: 0.25 2 1 1 C C C  1176 (cách chọn) 8 7 6
Suy ra số phần tử của biến cố A là: ( n )
A  840 1008 1176  3024 3024 48
Vậy xác suất của biến cố A là P( ) A   0.25 5985 95
Vì trong 5 người được chọn phải có ít nhất 1 nữ và ít nhất phải có 2 nam nên
số học sinh nữ gồm 1 hoặc 2 hoặc 3 nên ta có các trường hợp sau:  Chọn 1 nữ và 4 nam.
+) Số cách chọn 1 nữ: 6 cách
+) Số cách chọn 2 nam 1 làm đội trưởng và 1 làm đội phó: 2 A 18
+) Số cách chọn 2 nam còn lại: 2 C 16 0.25 Suy ra có 2 2
6.A C cách chọn cho trường hợp này. 18 16  Chọn 2 nữ và 3 nam.
+) Số cách chọn 2 nữ: 2 C cách. 3 6
+) Số cách chọn 2 nam 1 làm đội trưởng và 1 làm đội phó: 2 A cách. 18
+) Số cách chọn 1 nam còn lại: 16 cách. Suy ra có 2 2
C A .16 cách chọn cho trường hợp này. 6 18  Chọn 3 nữ và 2 nam.
+) Số cách chọn 3 nữ: 3 C cách. 6 0.25
+) Số cách chọn 2 nam 1 làm đội trưởng và 1 làm đội phó: 2 A cách. 18 Suy ra có 3 2
C A cách chọn cho trường hợp 3. 6 18 Vậy có 2 2 2 2 3 2
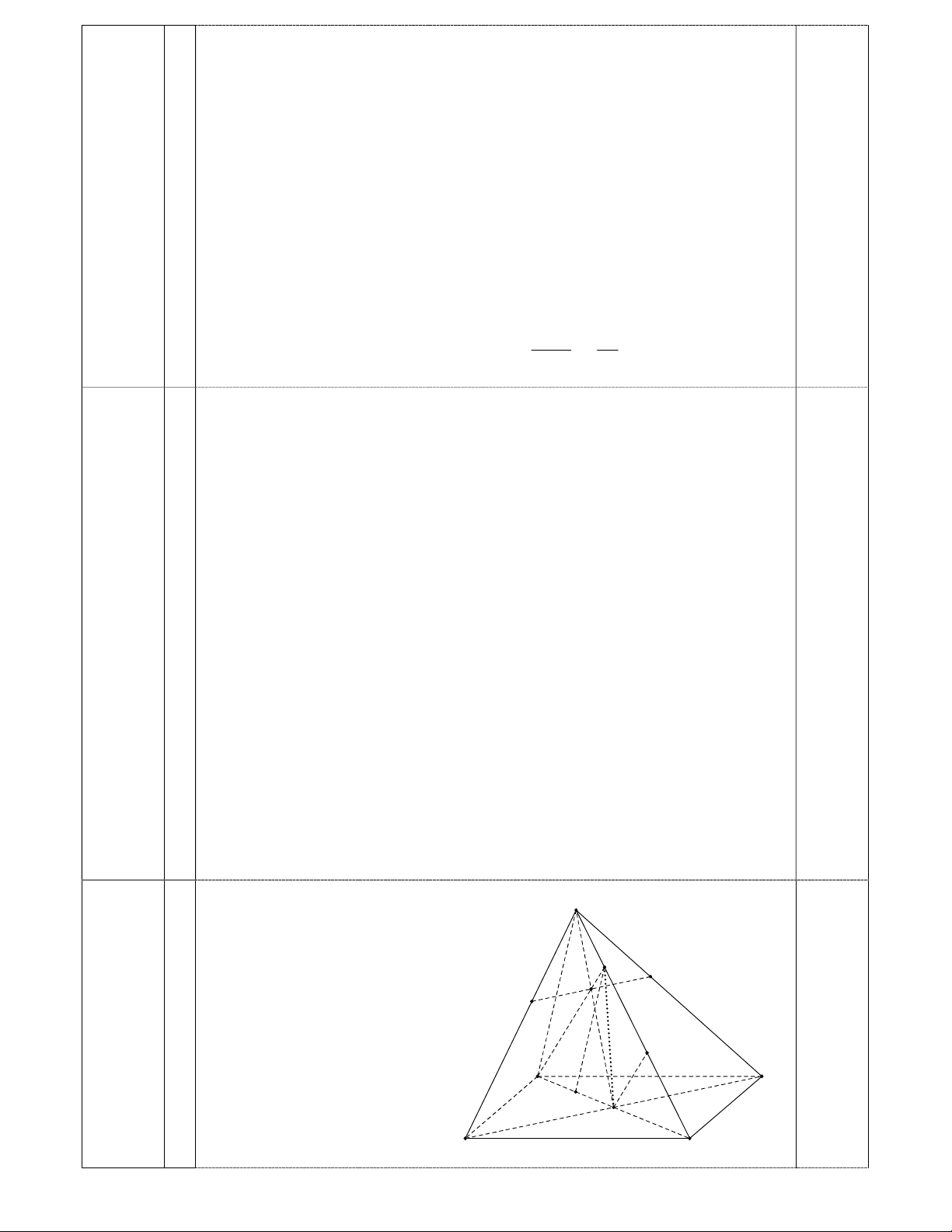
6.A C C A .16 C A  299880 cách. 18 16 6 18 6 18 Câu IV S M F K E 1 R A D N O B C 4
Ta có: M  SC  (SAC)  M  (SAC)  M  (MBD)(SAC)(1) 0.5 Lại có O  BD (MB ) D O (MB ) D 0.5
O  AC (SAC) O  (SAC) Suy ra O  (MB ) D (SAC)(2) 0.5
Từ (1) và (2), suy ra OM  (MB ) D (SAC) Trong tam giác SAC 1 CM 3 Ta có: SM  SC   (1) 4 CS 4 2 CN 3
Do N là trung điểm của AO nên suy ra  (2) CA 4 0.5 Từ (1) và (2) suy ra CM CN 
 MN / /SA mà SA  (ABE) CS CA 0.5  MN / /(ABE)
Gọi K là giao điểm của ( )
 với đường thẳng SO, Trong A  MC từ O
kẻ đường thẳng song song với AM cắt SC tại R. 1 SC SK SM 4 2 Ta có:    SO SR 5 5 0.25 SC 3 8 SE SF SK 2 Trong S  BD có EF / /BD     SB SD SO 5 1  SE.SM sinESM S SEM 2 SE SM 2 1 1 Vậy,    .  S 1 SB SC S  BC  5 4 10 SB.SC sinBSC 0.25 2 5 SỞ GD & ĐT THANH HÓA
TRƯỜNG THPT LƯƠNG ĐẮC BẰNG HƯỚNG DẪN CHẤM
ĐỀ KIỂM TRA CUỐI KỲ I, NĂM HỌC 2020 -2021 Môn: Toán 11 ĐỀ 2 Câu Ý Nội dung Điểm Câu I 1 cos x 1 2 
2cos x  cos x 3  0   cos x  3 0.5  (Loaïi)  2 +) cos x  1  x  k2 ,  (k  )  0.5 3 1 1 0.25 Pt  sinx  cosx    1
 sin x.cos  cos x.sin  2 2 2 6 6 2 x      k2   2     0.25  sin x        sin  x   k2  6 6      3 k    6 6 x        k2 x   k2 6 6    0.25
Vậy nghiệm của phương trình đã cho là x   k2 ,  x    k2 ,  k   3
Ta có phương trình tương đương với pt sau:
(2 cos 2x  3)(2 sin x 1)  0 3  1   5 0.5 sinx  x   k2 , x     k2 .  2      6 6  (k,l  )   3  5 cos2x= - x=  l  2  12 0.5 Câu II u  + u = 16 2  u + 4d = 16 u  = 2 Ta có: 1 5  1    1    u  + u = 19  2  u + 5d = 19 d  = 3 3 4  1   1.0 Câu III
Số hạng tổng quát trong khai triển nhị thức 3 12
(3x  2) là : k 12 k k 36 3 3 2  k C x 0.5 12 0.25 1 Hệ số của 12
x ứng với k thõa mãn: 36 3k  12  k  8 0.25 Vậy hệ số của 12 x là 8 4 8 C 3 2  10264320 12
 Số phần tử của không gian mẫu là 4 ( n )  C  3876 0.5 19
 Gọi A là biến cố “Chọn 4 quả cầu phải có đủ 3 màu khác nhau từ hộp đựng 8
quả cầu màu đỏ, 6 quả cầu màu xanh và 5 quả cầu màu vàng” ta có các trường hợp sau: 2
+) Chọn được 1 quả cầu màu đỏ, 1 quả cầu màu xanh và 2 quả cầu màu
vàng có số cách chọn là: 1 1 2 C C C  480 (cách chọn) 0.25 8 6 5 6
+) Chọn được 1 quả cầu màu đỏ, 2 quả cầu màu xanh và 1 quả cầu màu
vàng có số cách chọn là: 1 2 1 C C C  600 (cách chọn) 8 6 5 0.25
+) Chọn được 1 quả cầu màu đỏ, 2 quả cầu màu xanh và 1 quả cầu màu
vàng có số cách chọn là: 2 1 1 C C C  840 (cách chọn) 8 6 5 0.25
Suy ra số phần tử của biến cố A là: ( n )
A  480 600840 1920 1920 160
Vậy xác suất của biến cố A là P( ) A   3876 323 0.25
Vì trong 5 người được chọn phải có ít nhất 1 nữ và ít nhất phải có 2 nam nên
số học sinh nữ gồm 1 hoặc 2 hoặc 3 nên ta có các trường hợp sau:  Chọn 1 nữ và 4 nam.
+) Số cách chọn 1 nữ: 7 cách
+) Số cách chọn 2 nam 1 làm đội trưởng và 1 làm đội phó: 2 A 17
+) Số cách chọn 2 nam còn lại: 2 C 15 0.25 Suy ra có 2 2
7A .C cách chọn cho trường hợp này. 17 15  Chọn 2 nữ và 3 nam.
+) Số cách chọn 2 nữ: 2 C cách. 7
+) Số cách chọn 2 nam 1 làm đội trưởng và 1 làm đội phó: 2 A cách. 17
+) Số cách chọn 1 nam còn lại: 15 cách. Suy ra có 2 2
15C A cách chọn cho trường hợp này. 7 17  Chọn 3 nữ và 2 nam.
+) Số cách chọn 3 nữ: 3 C cách. 7 0.25
+) Số cách chọn 2 nam 1 làm đội trưởng và 1 làm đội phó: 2 A cách. 17 Suy ra có 3 2
C .A cách chọn cho trường hợp này. 5 17 Vậy có 2 2 2 2 3 2
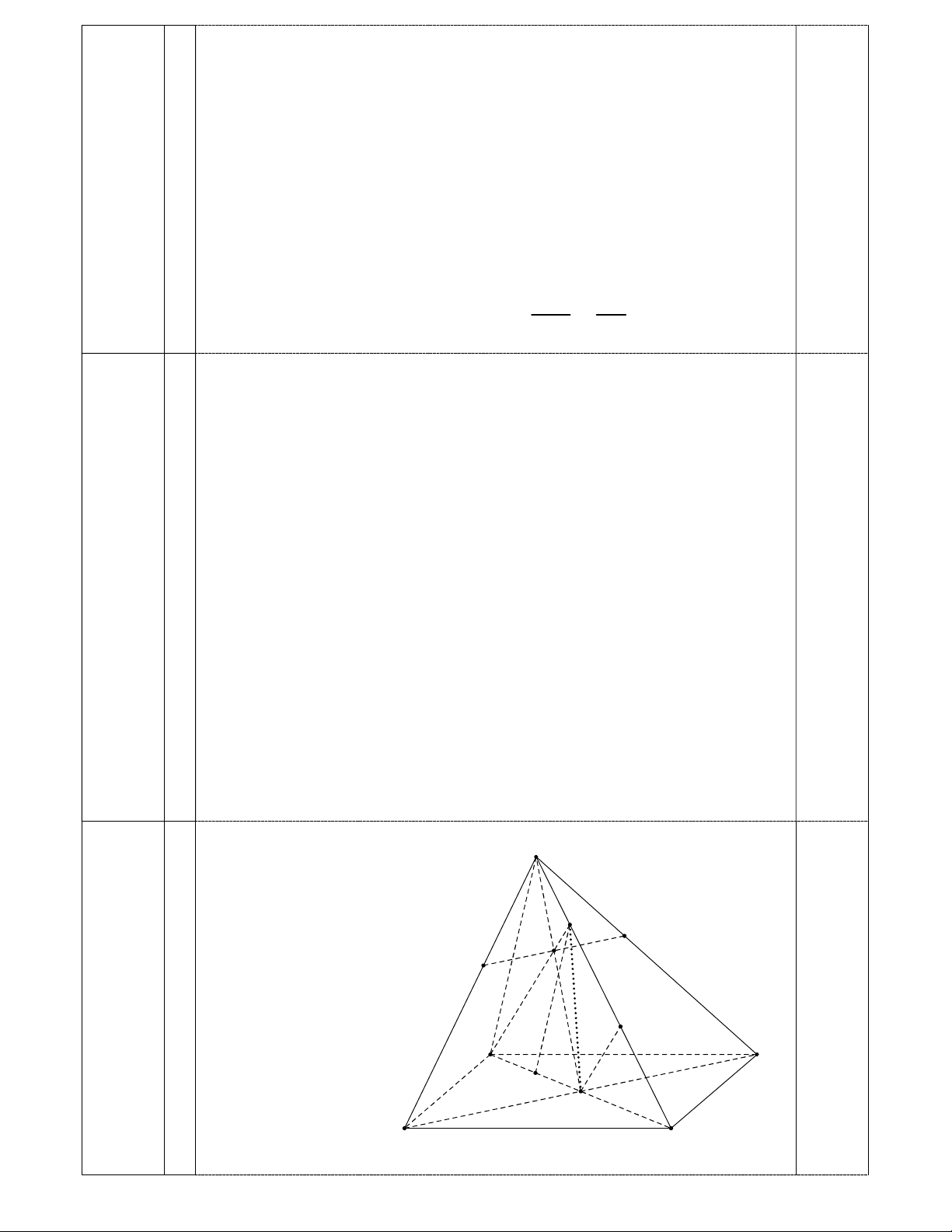
7A C  15C A C A .  295120 cách. 17 15 7 17 7 17 Câu IV S I Q K P 1 R A D J O B C 7
Ta có: I  SC  (SAC)  I  (SAC)  I  (IB ) D (SAC)(1) 0.5 Lại có O  BD (IB ) D O (IB ) D 0.5
O  AC (SAC) O  (SAC) Suy ra O  (IB ) D (SAC)(2)
Từ (1) và (2), suy ra OI  (IB ) D (SAC) 0.5 Trong tam giác SAC 1 CI 3 Ta có: SI  SC   (1) 4 CS 4 CJ 3
2 Do J là trung điểm của AO nên suy ra  (2) CA 4 0.5 CI CJ Từ (1) và (2) suy ra   IJ / /SA mà SA  (ADQ) CS CA  IJ / /(ADQ) 0.5
Gọi K là giao điểm của ( )
 với đường thẳng SO, Trong A  IC từ O
kẻ đường thẳng song song với AI cắt SC tại R. 1 SC SK SI 4 2 Ta có:    SO SR 5 5 0.25 SC 3 8 SP SQ SK 2 Trong S  BD có PQ / /BD     SB SD SO 5 1  SQ.SI sinISQ S SIQ 2 SQ SI 2 1 1 Vậy,    .  S 1 SD SC S  CD  5 4 10 SD.SC sinCSD 0.25 2 8