Đề thi cuối kỳ môn thống kê ứng dụng

lOMoARcPSD| 36207943
TRƯỜNG ĐẠI HỌC KINH TẾ LUẬT
ĐỀ THI CUỐI KỲ KHOA TOÁN KINH TẾ
Học kỳ I Năm học 2019 – 2020 _____________________
(Sinh viên ược sử dụng tài liệu bản quyền) _____________________
PHIẾU TRẢ LỜI TRẮC NGHIỆM
Môn: THỐNG KÊ ỨNG DỤNG Thời lượng: 75 phút Mã ề: 414
Tên SV : ………………………….......... MSSV: ………….......……...Mã lớp: ………...............
Chữ ký Giám t hị 1
Chữ ký Giám thị 2
Điểm (số) Điểm (chữ) Cán bộ c hấm thi 1 Cán bộ chấm thi 2
HƯỚNG DẪN TRẢ LỜI Chọn B
Bỏ B - Chọn C Bỏ C - Chọn lại B 1 1 1
A  A  A  B  B
C  B  C  D  D  C  D 
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
A                    
B                    
C                    
D                     lOMoARcPSD| 36207943
Lưu ý: Trong giờ làm bài, sinh viên chỉ ược phép sử dụng các tài liệu dưới ây 1. Giáo
trình Thống kê ứng dụng của UEL: bản in có bản quyền, không photocopy.
2. 1 tờ giấy A4 tóm tắt tiết kiến thức (viết tay).
Câu 1. Cho bảng thống kê mô tả sau về biến ộ tuổi (Age) Age Cumulative Frequency Percent Valid Percent Percent Valid 23-28 47 8.0 8.0 8.0 28-33 200 34.1 34.1 42.2 33-38 266 45.4 45.4 87.5 38-43 73 12.5 12.5 100.0 Total 586 100.0 100.0
Hãy cho biết các khẳng ịnh nào sau ây là SAI
A. Dữ liệu về ộ tuổi ược chia thành 4 khoảng
B. Cỡ mẫu iều tra là 586 mẫu
C. Có 87.5% số người có ộ tuổi trong khoảng 33-38 D. Số người trong ộ tuổi 28-33 chiếm 34.1%
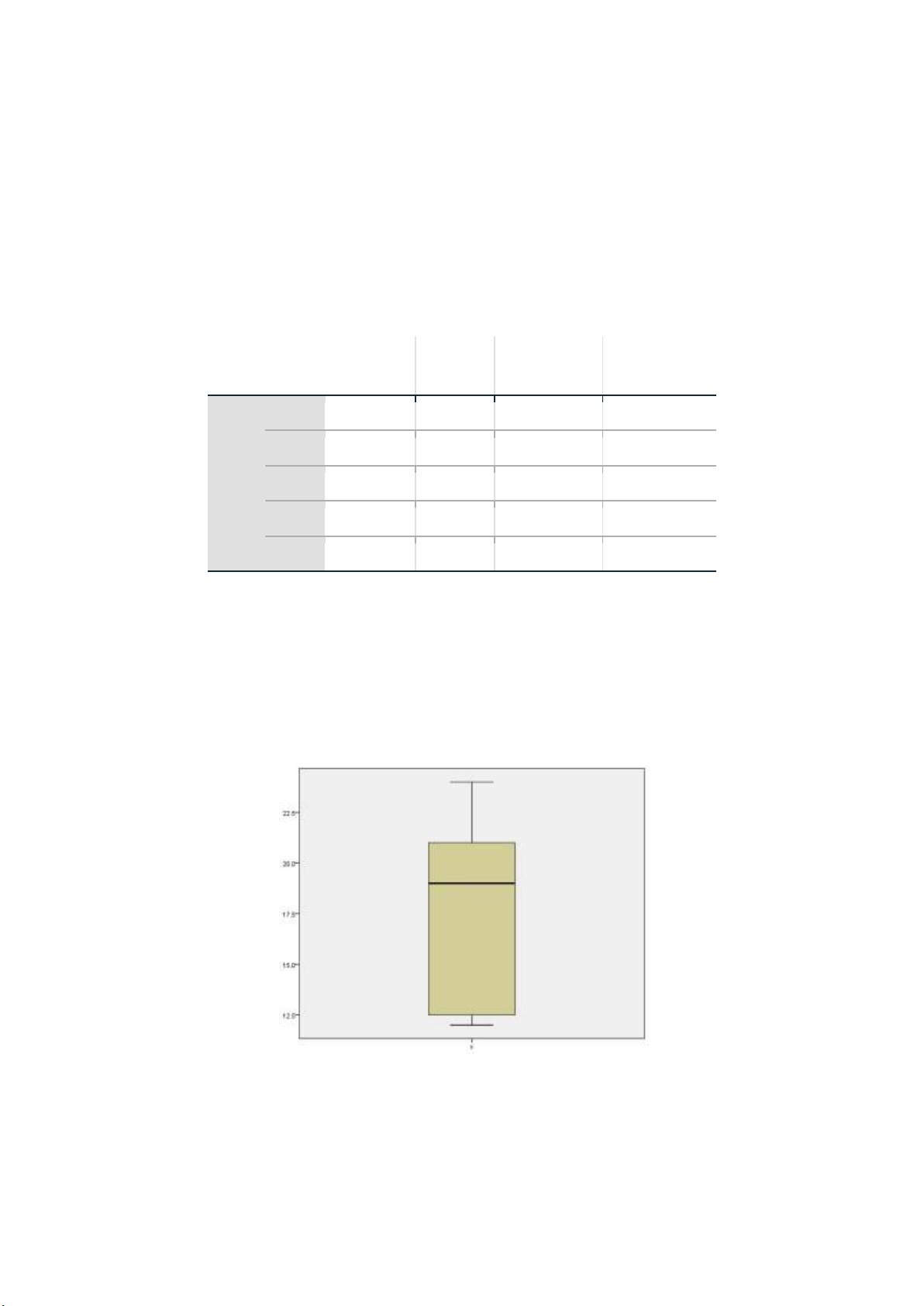
Câu 2. Dựa vào dữ liệu của biến X
A. Đồ thị của dữ liệu ối xứng
B. Đồ thị dữ liệu lệch trái
C. Đồ thị của dữ liệu lệch phải D. Chưa ủ thông tin ể kết luận lOMoARcPSD| 36207943
Câu 3. Bảng số liệu về iểm kiểm tra tiếng anh ầu vào (trước khi ôn tập) của một khóa gồm 80 sinh viên như sau: Truoc Frequency Percent Valid Percent Cumulative Percent 3.8 3.8 3.8 6.3 6.3 10.0 7.5 7.5 17.5 0 3 8.8 8.8 26.3 1 5 11.3 11.3 37.5 2 6 3 7 13.8 13.8 51.3 4 9 13.8 13.8 65.0 5 11 12.5 12.5 77.5 6 11 7 10 11.3 11.3 88.8 8 9 6.3 6.3 95.0 9 5 5.0 5.0 100.0 10 4 Valid Total 80 100.0 100.0
Các tham số ặc trưng của tổng thể nhận các giá trị 5.28; 5; 6.987 và 10 lần lượt là: A.
Trung vị, trung bình, phương sai mẫu hiệu chỉnh và khoảng biến thiên
B. Trung vị, trung bình, khoảng biến thiên và phương sai mẫu hiệu chỉnh C.
Trung bình, trung vị, phương sai mẫu hiệu chỉnh và khoảng biến thiên.
D. Trung bình, trung vị, khoảng biến thiên và phương sai mẫu hiệu chỉnh
Câu 4. Một dây chuyền sản xuất bánh ngọt ang kiểm tra xem trọng lượng gói bánh ược sản xuất ra có ổn
ịnh hay không. Người ta tiến hành lấy mẫu khảo sát gồm 400 gói bánh và thu ược kết quả sau: trọng
lượng trung bình của gói bánh là 4200 gr; ộ lệch chuẩn là 300 gr. Biết tổng thể lấy mẫu tuân theo quy luật
phân phối chuẩn, hãy cho biết có bao nhiêu phần trăm gói bánh có trọng lượng trong khoảng từ 3600 gr ến 4800 gr. A. 68% B. 95% C. 99% D. 100%
Câu 5. Phân tích thời gian hoạt ộng của 150 chuyến bay thu ược kết quả sau: lOMoARcPSD| 36207943 One-Sample Test Test Value = 0 t df Sig. (2-tailed) Mean Difference
95% Confidence Interval of the Difference Lower Upper Time 44.681 149 .000 ? 13.381 14.619
Biết tổng thể lấy mẫu tuân theo quy luật phân phối chuẩn, từ kết quả phân tích trên hãy tính giá trị trung
bình mẫu x và ộ lệch chuẩn mẫu S A. x =14; S= 3.8 B. x =14; S=3.7 C. x =14; S=3.9 D. x =12; S=3.6
Câu 6. Bảng số liệu về doanh thu (triệu ồng/ngày) của một cửa hàng trong 50 ngày ược tóm tắt trong bảng như sau: One-Sample Statistics N Mean
Std. Deviation Std. Error Mean Doanhthu 50 96.12 24.034 3.399
Giả sử tổng thể có phân phối chuẩn. Hãy ước lượng khoảng tin cậy 95% về trung bình của tổng thể A. (87.01; 105.23) B. (89.29; 102.95) C. (90.42; 101.82) D. (87.95; 104.29)
Câu 7. Một mẫu ngẫu nhiên có kích thước n = 100 thu ược từ một tổng thể có μ = 200 và σ = 30. Câu nào
sau ây mô tả úng nhất phân phối mẫu của X
về hình dạng, trung bình và ộ lệch chuẩn?
A. Phân phối mẫu của X xấp xỉ phân phối chuẩn với giá trị trung bình bằng 200 và ộ lệch chuẩn bằng 3.
B. Phân phối mẫu của X xấp xỉ phân phối chuẩn với giá trị trung bình bằng 200 và ộ lệch chuẩn bằng 30.
C. Phân phối mẫu của X xấp xỉ phân phối chuẩn với giá trị trung bình bằng 20 và ộ lệch chuẩn bằng 3.
D. Phân phối mẫu của X xấp xỉ phân phối chuẩn với giá trị trung bình bằng 30 và ộ lệch chuẩn bằng 2.
Câu 8. Chọn ngẫu nhiên 500 công dân của một nước ể thăm dò ý kiến về chương trình phát triển năng
lượng hạt nhân của chính phủ trong tương lai. Kết quả cho thấy 350 người không ủng hộ chương trình ó
của chính phủ. Biết tổng thể lấy mẫu tuân theo quy luật phân phối chuẩn, hãy tìm khoảng tin cậy 95% cho
tỷ lệ những người ủng hộ chương trình hạt nhân của chính phủ? lOMoARcPSD| 36207943 A. (0.2598; 0.3402) B. (0.2663; 0.3337) C. (0.2522; 0.3478) D. (0.6598; 0.7402)
Câu 9. Bảng số liệu iều tra về số lượng sản phẩm 𝑋 bán ược ( ơn vị tấn) tuân theo phân phối chuẩn, với hai nhóm 1: nhóm tặng kèm sản phẩm
và nhóm 2: nhóm tặng phiếu giảm giá. Ký hiệu 2 2
1, 2 lần lượt là trung bình của hai tổng thể trên. Ký hiệu
1 , 2 lần lượt là phương sai của hai
tổng thể. Trong các kết luận sau có bao nhiêu kết luận ĐÚNG: i. 12 22 ii. 1 2 0.11017;0.08417 iii. 1 2 0.10961;0.08361 iv.
Trọng lượng trung bình của nhóm 1 cao hơn trọng lượng trung bình của nhóm 2. A. 1 B. 2 C. 3 D. 4
Câu 10. Năm trước giá bán trung bình của xe ô tô cũ là 10000$. Năm nay do một số yếu tố ảnh hưởng ến
kinh tế nên người ta nghi ngờ giá bán xe trung bình không như năm trước. Khảo sát giá bán 50 chiếc xe
tại một số cửa hàng và phân tích ta thu ược kết quả sau One-Sample Statistics N Mean Std. Deviation Std. Error Mean Sale Price 50
9750.00 1399.999 197.990
Biết rằng tổng thể lấy mẫu có phân phối chuẩn, với mức ý ghĩa 5% có ủ kết luận về iều nghi ngờ trên hay không?
A. Giá trị kiểm ịnh Z=-1.263, không ủ kết luận về nghi ngờ trên
B. Giá trị kiểm ịnh Z=-1.263, ủ kết luận về nghi ngờ trên
C. Giá trị kiểm ịnh Z=197.990, không ủ kết luận về nghi ngờ trên D. Giá trị kiểm ịnh Z=49.244,
ủ kết luận về nghi ngờ trên lOMoARcPSD| 36207943
Câu 11. Một nghiên cứu ược thực hiện ể xác ịnh hiệu quả của phương pháp giảng dạy mới. Dữ liệu về
iểm trước và sau khi thực hiện phương pháp giảng dạy này của 8 học sinh ược hiển thị trong bảng sau. Sinh viên 1 2 3 4 5 6 7 8 Trước 44 55 25 54 63 38 31 34 Sau 55 68 40 55 75 52 49 48
Giả sử tổng thể các khác biệt theo phân phối chuẩn và ặt 𝜇𝑡𝑟ướ𝑐 − 𝜇𝑠𝑎𝑢 = 𝜇𝑑. Để xác ịnh liệu phương pháp
mới có hiệu quả hay không. Trong các khẳng ịnh sau có bao nhiêu khẳng ịnh ĐÚNG? H0 : d 0 i.
Cặp giả thuyết của bài toán kiểm ịnh này là: H 1 : d 0 ii.
Trung bình của các chênh lệch: 𝑑 = −12.25 iii.
Giá trị kiểm ịnh t = -6.920 iv.
Độ tự do của iá trị tới hạn của bài toán kiểm ịnh này là 7 A. 1 B. 2 C. 3 D. 4
Câu 12. Một tổ chức y tế khẳng ịnh rằng ở Mỹ tỷ lệ hút thuốc ở nam giới có ộ tuỗi từ 18 trở lên cao hơn
tỷ lệ hút thuốc ở nữ giới có ộ tuổi từ 18 trở lên. Một cuộc khảo sát ngẫu nhiên gồm 1.000 người Mỹ từ 18
tuổi trở lên, 129 trong số 516 nam giới ược hỏi tự nhận mình là người hút thuốc và 87 trong số 484 nữ
giới ược hỏi tự nhận mình là người hút thuốc. Đặt p1 là tỷ lệ thực sự của nam giới từ 18 tuổi trở lên có hút
thuốc và p2 là tỷ lệ thực sự của nữ giới từ 18 tuổi trở lên có hút thuốc, biết tổng thể lấy mẫu tuân theo quy
luật phân phối chuẩn. Để kiểm ịnh xem khẳng ịnh của tổ chức y tế có úng hay không, cặp giả thuyết nào sao ây là ĐÚNG? H 0 :p1 p2 A. H 1 :p1 p2 H 0 :p1 p2 B. H 1 :p1 p2 H 0 :p1 p2 C. H 1 :p1 p2 H 0 :p1 p2 D. 1 1 p2 H :p
Câu 13. Khảo sát giá trung bình của một mặt hàng ược bán tại 6 quốc gia Mỹ (US), Đức (DE), Anh Quôc
(GB), Brazil (BR), Nhật Bản (JP) và Trung Quốc (CN) ta thu ược kết quả phân tích sau: lOMoARcPSD| 36207943 ANOVA Product_price Sum of Squares df Mean Square F Sig. Between Groups ?????? 5 .066 ???? .689 Within Groups 179.027 1658 ???? Total 179.358 1663
Biết giá của mặt hàng này tại 6 quốc gia trên là tuân theo phân phối chuẩn, phương sai về giá của mặt
hàng này ở 6 quốc gia là bằng nhau và sai số ộc lập với nhau. Trong các khẳng ịnh sau có bao nhiêu khẳng ịnh ĐÚNG? i.
Cỡ mẫu của bộ dữ liệu này là 1663 ii. SSG = 0.331 iii. MSW = 0.108 iv. F = 0.614 A. 0 B. 1 C.2 D. 3
Câu 14. Để kiểm ịnh xem nghề nghiệp của mẹ (1: nội trợ; 2: kinh doanh; 3: công chức) có tác ộng ến
trọng lượng của trẻ sơ sinh hay không? Sử dụng kiểm ịnh hạng Kruskal-Wallis test ta thu ược kết quả sau: Ranks Test Statisticsa,b n_nghiep N Mean Rank tlsosinh tlsosinh 1.0 98 274.11 Kruskal-Wallis H 2.174 2.0 220 290.68 df 2 3.0 268 302.90 Asymp. Sig. .337 Total 586 a. Kruskal Wallis Test
b. Grouping Variable: n_nghiep
Trong các khẳng ịnh sau có bao nhiêu khẳng ịnh SAI i.
Giá trị kiểm ịnh 𝜒2 = 2.174 ii.
Giá trị tra bảng phân phối Chi bình phương với bậc tự do là 3 iii.
Có ít nhất hai tổng thể có mức ộ hài lòng khác nhau. A. 0 B. 1 C. 2 D. 3
Câu 15. Để ánh giá xem việc ến trung tâm ôn thi ể lấy chứng chỉ SAT có ảnh hưởng ến iểm số hay không,
ta tiến hành thu thập iểm số của một nhóm học sinh trước (no course) và sau (course) khi ến trung tâm ôn
thi, sau ó dùng kiểm ịnh Wicoxon ể so sánh Median giữa 2 nhóm cho kết quả kiểm ịnh như sau:
Wilcoxon Signed Ranks Test lOMoARcPSD| 36207943 Ranks Test Statisticsa N Mean Sum of No Course - Rank Ranks Course -2.842b Negative 18.79 488.50 Z 26a Ranks Asymp. Sig. (2-tailed) .004 Positive a. Wilcoxon Signed Ranks Test 9b 15.72 141.50 Ranks b. Based on positive ranks. Ties 0c No Course - Course Total 35 a. No Course < Course b. No Course > Course c. No Course = Course
Kết luận nào sau ây là ĐÚNG
A. Giá trị P-value=0.004 do ó việc ến trung tâm ôn thi ể lấy chứng chỉ SAT không có ảnh hưởng ến iểm số.
B. Giá trị kiểm ịnh Z= -2.84 do ó việc ến trung tâm ôn thi ể lấy chứng chỉ SAT có ảnh hưởng ến iểm số.
C. Số các 𝑑𝑖 mang dấu âm là 9 với 𝑑𝑖 = 𝑁𝑜 𝑐𝑜𝑢𝑟𝑠𝑒 − 𝐶𝑜𝑢𝑟𝑠𝑒
D. Cả 3 khẳng ịnh trên là sai
Câu 16. Có thông tin iều tra về màu sắc các ô tô trong một gian trưng bày sản phẩm như sau:
Có thể cho rằng tỷ lệ về màu sắc các ô tô là như nhau ược hay không, với mức ý nghĩa 5%:
A. Giá trị kiểm ịnh là 𝜒2 =2.2 và tỷ lệ màu sắc là như nhau
B. Giá trị kiểm ịnh là 𝜒2 =2.2 và tỷ lệ màu sắc là khác nhau
C. Giá trị kiểm inh là 𝜒2 =3 và tỷ lệ màu sắc là như nhau
D. Giá trị kiểm ịnh là 𝜒2 =3 và tỷ lệ màu sắc là khác nhau.
PHẦN 2. TỰ LUẬN ( 2 CÂU )
Câu 1. Môt trung tâm luyện thi IELTS tuyên bố các học viên vào học tại trung tâm sau 2 tháng sẽ tăng
ược ít nhất 0.5 iểm .Làm thế nào ể ánh giá tuyên bố trên có tin cậy không .
Câu 2. Trường ại học Kinh tế - Luật tuyển sinh vào trường từ 3 tổ hợp A00 ;A01;D01 của kỳ thi phổ
thông trung học quốc gia và kết quả kỳ thi ánh giá năng lực của ĐHQG thành phố HCM. Có số liệu về thí
sinh ăng kí nguyện vọng 1 các chuyên ngành trong trường . Người ta kết luận rằng tỉ lệ sinh viên ăng kí lOMoARcPSD| 36207943
nguyên vọng vào chuyên ngành toán kinh tế phụ thuộc vào các tổ hợp tuyển sinh.Có một mẫu 2000 thí
sinh ăng kí xét tuyển vào trường trong năm 2019 . Làm thế nào ể ánh giá ộ tin cậy của kết luận trên qua mẫu trên. ----------- HẾT ----------