Đề thi đánh giá chất lượng học kì II năm học 2025 – 2026 môn Toán lớp 9

NGÂN HÀNG ĐỀ THI RICHARD
KỲ THI ĐÁNH GIÁ CHẤT LƯỢNG HỌC TẬP
RICHARD SCHOOL – KHOA TOÁN
LẦN THỨ NHẤT – NĂM HỌC 2025 - 2026
BÀI THI: TOÁN – CTGD HỌC KÌ II
ĐỀ KIỂM TRA ĐỊNH KÌ LẦN 01
Ngày thi: 08 tháng 01 năm 2026
Đề thi gồm 06 câu trong 01 trang
Thời gian làm bài 40 phút, không kể thời gian phát đề
Họ và tên thí sinh: .....................................................................… Mã đề thi 000
Số báo danh: ..............................................................................…
ĐỀ THI CHÍNH THỨC – THỜI GIAN LÀM BÀI 40 PHÚT – MÃ ĐỀ THI 000 – ID ĐỀ : 0610
Câu 01: (1,0 điểm) Cho hàm số y = 5 2
x . Tính giá trị của y khi x = 2 và x = 3.
Câu 02: (1,0 điểm) Vẽ đồ thị của hàm số y = 2 2 x .
Câu 03: ( 2,0 điểm ) Trong mặt phẳng toạ độ Oxy, điểm
M (2; –1) thuộc đồ thị của hàm số y = a 2 x .
a) Tìm hệ số a.
b) Giả dụ nếu hệ số a là số nguyên dương thì đồ thị đó
nằm phía nào của trục hoành ?
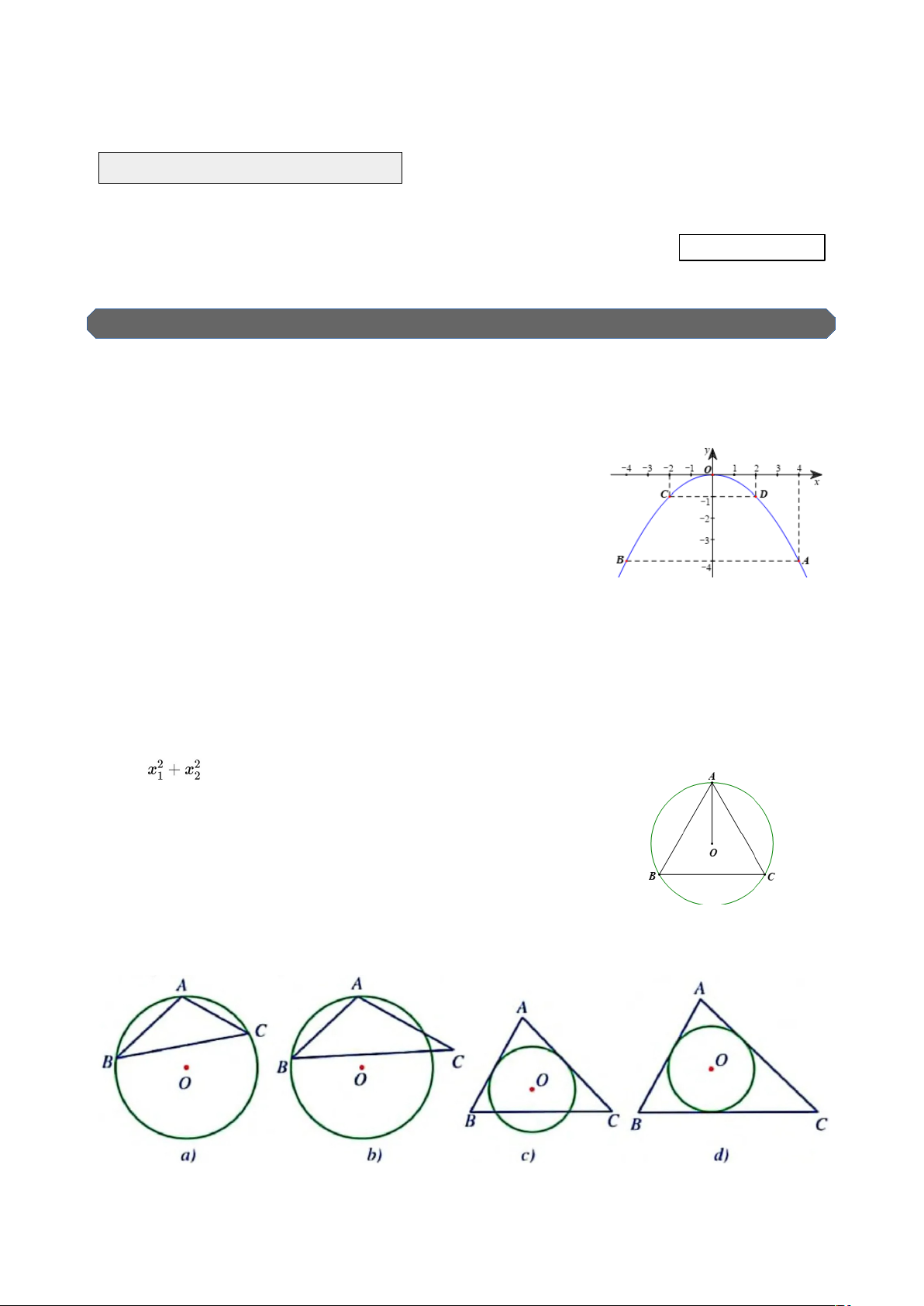
c) Quan sát đồ thị của hàm số bên, hãy xác định tọa độ
của các điểm A, B, C và D.
Câu 4: ( 2,0 điểm ) Giải các phương trình sau: 1) 2 2 2
x – x – 3 = 0
3) 9 x + 6 x + 1 = 0 2) – 3 2 2 x + x – 5 = 0
4) 4 x + 10 x + 15 = 0 Câu 5: ( 2
2,0 điểm ) Cho phương trình: 2 x – 3x – 6 = 0.
a) Chứng minh phương trình có hai nghiệm phân biệt x1, x2. b) Tính c) Tính | x 1 – x2 |.
Câu 06: ( 2,0 điểm )
a) Tam giác đều ABC nội tiếp đường tròn (O; 5 cm). Tính AB.
b) Quan sát các hình a, b, c, d, ở hình nào ta có đường tròn (O) là đường tròn ngoại tiếp tam giác
ABC ? Ở hình nào ta có đường tròn (O) là đường tròn nội tiếp tam giác ABC ? --- HẾT ĐỀ THI ---