Đề Thi Đề Xuất HSG Toán 8 Năm 2025-2026 Có Đáp Án-Đề 2

ĐỀ THI ĐỀ XUẤT CHỌN HỌC SINH GIỎI LỚP 8 Năm học 2025-2026 MÔN: TOÁN
Thời gian làm bài 150 phút
( Đề thi gồm 05 câu, 01 trang) Câu 1 (5,0 điểm) 2  6x +1
6x −1  x − 36
1. Cho biểu thức A = + .  2 2  2
 x − 6x x + 6x  12x +12
a) Tìm ĐKXĐ và rút gọn biểu thức A 1
b) Tính giá trị của biểu thức A với x = 9 + 4 5
2. Phân tích đa thức thành nhân tử: ( 2 + + )( 2 x x 1 x + x + 2) −12 Câu 2 (3,0 điểm)
1. Chứng minh rằng nếu a2 + b2 + c2 = ab + ac + bc thì a = b = c. 2. Cho đa thức 3 2
f(x) = x - 3x + 3x - 4 . Với giá trị nguyên nào của x thì giá trị của đa thức
f(x) chia hết cho giá trị của đa thức 2 x + 2 . Câu 3 (4,0 điểm)
1. Giải phương trình nghiệm nguyên: 4 2 6 3
5x +10x + 2y + 4y − 6 = 0 1 6y 2
2. Giải phương trình sau: = + 2 2 3y −10y + 3 9y −1 1− 3y
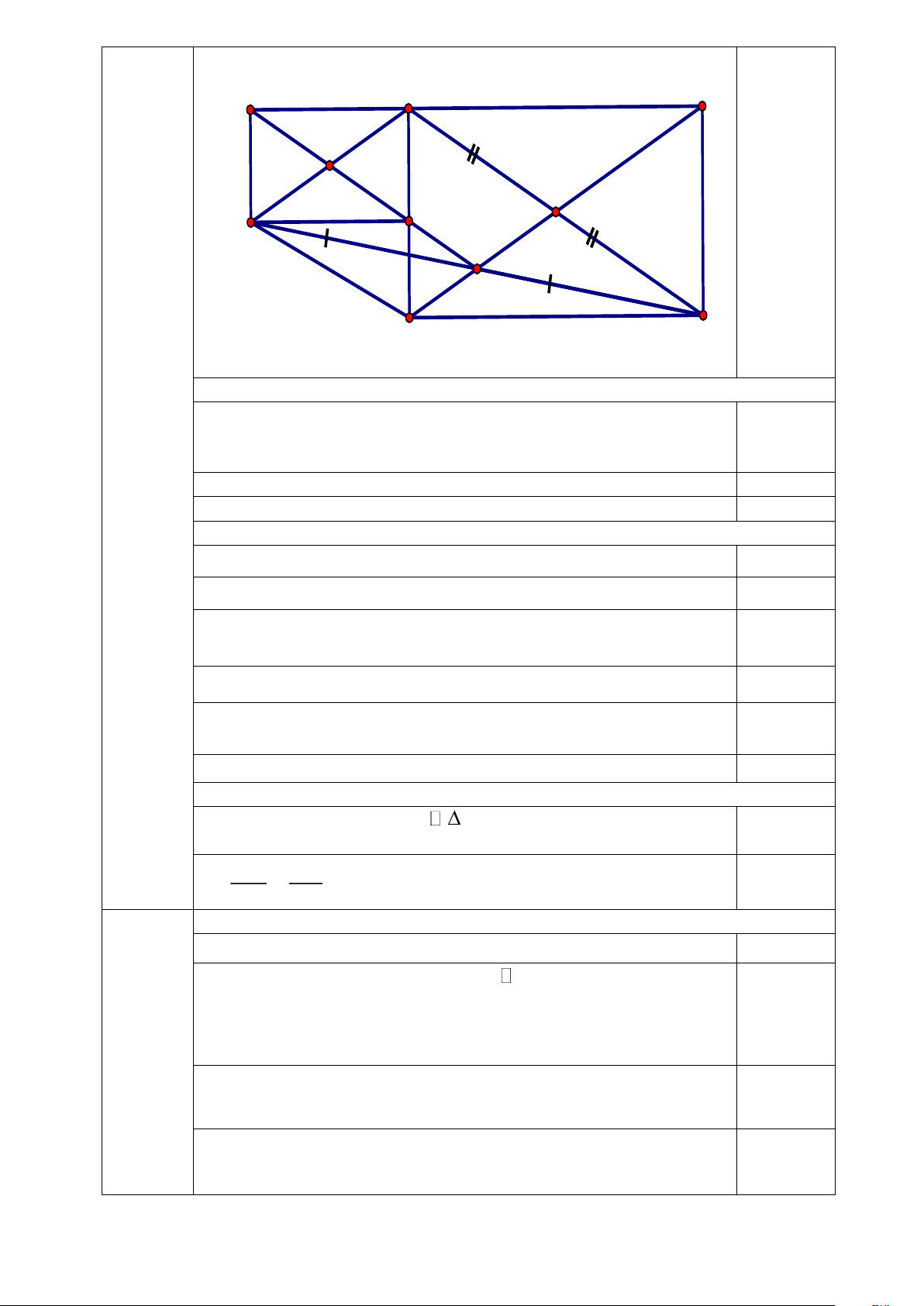
Câu 4 (6,0 điểm) Cho hình chữ nhật ABC .
D Trên đường chéo BD lấy điểm P, gọi M là
điểm đối xứng của C qua P.
a) Tứ giác AMDB là hình gì? Vì sao?
b) Gọi E, F lần lượt là hình chiếu của điểm M trên AD, A .
B Chứng minh EF / /AC và
ba điểm E, F, P thẳng hàng.
c) Chứng minh rằng tỉ số các cạnh của hình chữ nhật MEAF không phụ thuộc vào vị trí của điểm . P Câu 5 (2,0 điểm) 1. Chứng minh rằng 4 2
n + 7(7 + 2n ) chia hết cho 64 với mọi n là số nguyên lẻ.
2. Cho x, y, z là các số dương thỏa mãn x + y + z = 1. 1 1 1
Tìm giá trị nhỏ nhất của biểu thức: P = + + 16x 4y z ------------Hết---------- Trang 1 HƯỚNG DẪN CHẤM
ĐỀ THI ĐỀ XUẤT CHỌN HỌC SINH GIỎI LỚP 8 Năm học 2025-2026 MÔN: TOÁN
(Hướng dẫn chấm gồm 04 trang) Câu Đáp án Điểm 1. (3,0 điểm) a. (2,0 điểm)
a) ĐKXĐ: x  0; x  6 0,25 điểm  6x +1
6x −1  ( x + 6)( x − 6) 0,5 điểm A =  + 
x( x − ) x( x + ) . 6 6 12( 2 x +   )1 2 2
6x + 36x + x + 6 + 6x − 36x − x + 6 1 0,5 điểm = . x 12( 2 x + ) 1 12( 2 x + ) 1 1 0,5 điểm = . x 12( 2 x + ) 1 1 0,25 điểm = 1 x (5,0
b. (1,0 điểm) điểm) 1 0,25 điểm
x = 9+4 5 thỏa mãn ĐKXĐ 1 1 0,25 điểm A = = x 1 9 + 4 5 = 9 + 4 5 0,25 điểm = 2 + 5 0,25 điểm
2. (2,0 điểm ) Đặt ( 2 x + x + ) 1 = t ta có ( 2 x + x + 2) = t +1 0,5 điểm
Khi đó t(t+1) – 12 = (t-3)(t+4) 0,5 điểm
( 2 + + )( 2 + + )− = ( 2 + − )( 2 x x 1 x x 2 12 x x 2 x + x + 5) 0,5 điểm = ( − )( + )( 2 x 1 x 2 x + x + 5) 0,5 điểm 1. (1,5 điểm)
a2 + b2 + c2 = ab + ac + bc  2a2 + 2b2 + 2c2 = 2ab + 2ac + 2bc 0,25 điểm
 2a2 + 2b2 + 2c2 - 2ab - 2ac - 2bc = 0 0,25 điểm
 ( − )2 + ( − )2 + ( − )2 a b a c b c = 0 0,5 điểm
Vì (a − b)2  (a − c)2  (b − c)2 0, 0,  0 0,25 điểm 2 2 2 2
Nên (a − b) + (a − c) + (b − c) = 0 khi a = b = c 0,25 điểm Trang 2 (3,0 2. (1,5 điểm) điểm)
Chia f (x) cho 2
x + 2 được thương là x − 3 dư x + 2. 0,25 điểm
để f (x) chia hết cho 2
x + 2 thì x + 2 chia hết cho 2 x + 2 0,25 điểm
 (x + 2)(x − 2) chia hết cho 2 x + 2 2  x − 4 chia hết cho 2 x + 2 2
 x + 2 − 6 chia hết cho 2 x + 2 0,25 điểm  6 chia hết cho 2 x + 2 2  x +2 là ước của 6 mà 2 x + 2  2 0,5 điểm => 2 x + 23;  6 => x  1  ;  2
Thử lại ta thấy x = 1; x = −2 thỏa mãn 0,25 điểm Vậy với x = 1 ; x = 2
− thì f (x) chia hết cho 2 x + 2 1. (2,0 điểm) 4 2 6 3
5x +10x + 2y + 4y − 6 = 0  0,25 điểm ( 4 2 + + ) + ( 6 3 5x 10x 5 2y + 4y + 2) =13  4 2 6 3
5(x + 2x +1) + 2(y + 2y +1) = 13 0,5 điểm  2 2 3 2 5(x +1) + 2(y +1) = 13 2 x  Z x +1 Z 0,25 điểm Vì:    3 y  Z  y +1 Z  2 x +1 = 1 0,25 điểm  2 x = 0  x = 0  3 2 2(y +1) = 8  3 2 (y +1) = 4 0,25 điểm 3 3 y +1 = 2 3 y = 1 0,5 điểm (4,0     3 3 điểm) y +1 = −2 y = 3 − Vì y  Z nên 3 y = 1  y = 1
Vậy phương trình có một nghiệm nguyên (x; y) = (0; ) 1 2. (2,0 điểm) 1 0,25 điểm ĐKXĐ: y  3; y   3 (1)  1 6y 2 0,5 điểm ( = − 3y – ) 1 (y − 3) (3y – ) 1 (3y + ) 1 3y − 1
 3y +1 = 6y(y − 3) − 2(y − 3)(3y +1) 0,25 điểm 2 2
 3y +1 = 6y −18y − 6y +16y + 6 0,25 điểm  5y = 5 0,25 điểm
 y = 1(TMĐK) Vậy tập nghiệm của phương trình là S =   1 0,5 điểm Trang 3 0,5 điểm F A B I E O M P D C a. (2,0 điểm)
Gọi O là giao điểm của AC và BD 1,0 điểm
Ta có O là trung điểm của AC 4
P là trung điểm của MC (6,0
Hay PO là đường trung bình của ACM hay AM / /PO 0,5 điểm điểm)
Vậy BD / / AM hay tứ giác AMDB là hình thang. 0,5 điểm b. (2,0 điểm)
Do AM / /BD hay OBA = MAE (đồng vị) 0,25 điểm
Xét OAB cân ta có: OBA = OAB 0,25 điểm
Gọi I là giao điểm của MA và EF, ta thấy AEI cân ở I hay 0,25 điểm IAE = IEA
Suy ra FEA = OAB hay EF / / AC(1) 0,5 điểm
Mặt khác IP là đường trung bình của MAC suy ra 0,5 điểm IP / / AC(2)
Từ (1) và (2) suy ra: E, F, P thẳng hàng 0,25 điểm c. (1,5 điểm) a) Chứng minh M  AF D  ( BA g.g) 1,0 điểm MF AD 0,5 điểm  = không đổi. FA AB 1. (1,0 điểm) 4 2 4 2 2 2
n + 7(7 + 2n ) = n +14n + 49 = (n + 7) 0,25 điểm
Do n là số nguyên lẻ nên n = 2k +1 ( k  ) 0,25 điểm 2 2 Khi đó 2 2 2 + =  + +  =   ( 2 (n 7) (2k 1) 7 4k + 4k +1+ 7) 5 2 2 2 (2,0 = 4(k + k + 2) = 16   k(k +1) + 2
điểm) Vì k,k +1 là hai số nguyên liên tiếp  k(k +1) chia hết cho 2 0,25 điểm
  k(k +1) + 2chia hết cho 2 nên  + + 2 k(k 1) 2 chia hết cho 4  + + 2
16 k(k 1) 2 chia hết cho 64. 0,25 điểm Vậy 4 2
n + 7(7 + 2n ) chia hết cho 64 với mọi n là số nguyên lẻ. Trang 4 2. (1,0 điểm) 1 1 1 0,25 điểm + + = (        
x + y + z) 1 1 1 y x z x z y 21 P= + + = + + + + + +         16x 4y z
16x 4y z  16x 4y  16x z   4y z  16
Theo BĐT Cô Si ta có: y x 1 +
 dấu “=” khi y = 2x ; 0,25 điểm 16x 4y 4 Tương tự: z x 1 +  dấu “=” khi z y 0,25 điểm z = 4x ; + 1 dấu “=” 16x z 2 4y z khi z = 2y ;  49 0,25 điểm P  . Dấu “=” xảy ra khi 1 x = ; 2 y = ; 4 z = 16 7 7 7 Vậy Min 49 P = khi với 1 x = ; 2 y = ; 4 z = 16 7 7 7 -----------Hết----------- Trang 5