Đề thi định kỳ Toán 10 năm học 2018 – 2019 trường THPT chuyên Bắc Ninh lần 1

TRƯỜNG THPT CHUYÊN BẮC NINH
ĐỀ THI ĐỊNH KỲ LẦN I TỔ TOÁN TIN
NĂM HỌC 2018 – 2019
(Đề thi có 01 trang) Môn: Toán 10
Thời gian làm bài: 120 phút (không kể thời gian giao đề)
I. PHẦN CHUNG (7,0 điểm)
Câu 1 (2,0 điểm). Giải phương trình và hệ phương trình sau: 2x  3
(x 1)(y  2)  xy 1 1)  x 1  0 2)  x 1
(2x 1)(y  2)  2xy 1
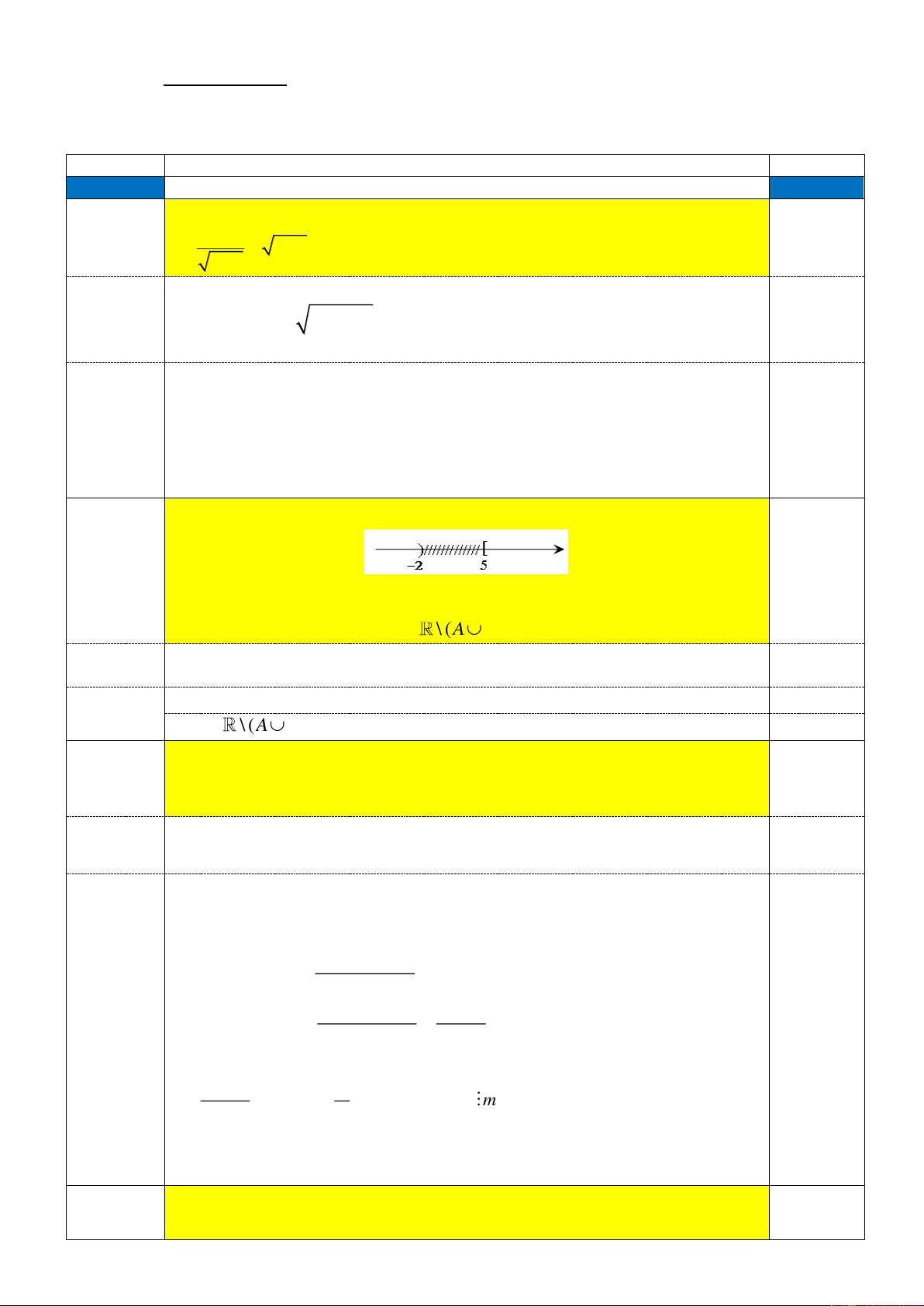
Câu 2 (1,5 điểm). Cho tập hợp A   ;  
1 3;6 và tập B được biểu diễn như hình vẽ sau:
1) Hãy viết tập B dưới dạng hợp của các khoảng, đoạn hoặc nửa khoảng.
2) Xác định các tập hợp sau dưới dạng hợp của các khoảng, đoạn hoặc nửa khoảng :
C  A  B và E  \ (A ) B
Câu 3 (1,0 điểm). Cho phương trình: 2
mx – 4m  2 x  3m – 2  0 (1) ( m là tham số).
1) Giải phương trình (1) khi m  2.
2) Tìm giá trị nguyên của tham số m để phương trình (1) có các nghiệm đều là số nguyên.
Câu 4 (1,0 điểm). Tìm tọa độ các giao điểm của đường Parabol 2
(P) : y  2x và đường thẳng (d) : y  3x 1.
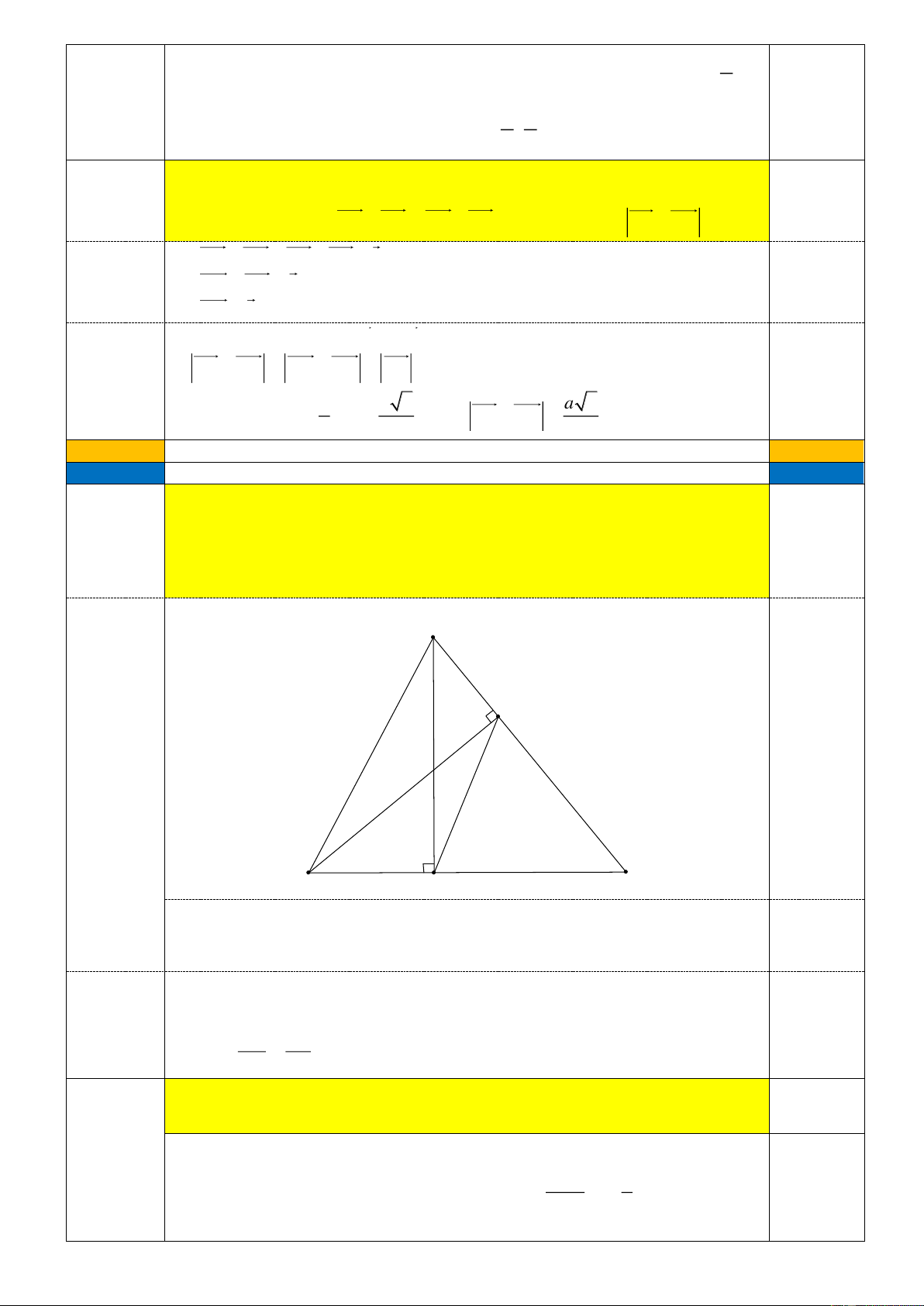
Câu 5 (1,5 điểm). Cho hình vuông ABCD có độ dài cạnh bằng a . Gọi O là giao điểm của AC và BD.
1) Chứng minh rằng: AC  BD  AD  BC
2) Tính AB  DO theo a .
II. PHẦN RIÊNG (3,0 điểm)
A. Phần dành cho thí sinh lớp 10: Anh1, Anh2, Văn, Cận2.
Câu 6a (2,0 điểm). Cho tam giác ABC có ba góc nhọn. Hai đường cao AE và BK của tam giác ABC
(với E thuộc BC, K thuộc AC ).
1) Chứng minh tứ giác ABEK nội tiếp được trong một đường tròn.
2) Chứng minh CE.CB  CK.CA .
Câu 7a (1,0 điểm). Cho các số x, y thỏa mãn x  0; y  0 và x  y 1 . Tìm giả trị lớn nhất và giá trị nhỏ nhất của biểu thức 2 2
A  x  y .
B. Phần dành cho thí sinh lớp 10: Lý, Hóa, Sinh, Tin, Cận1.
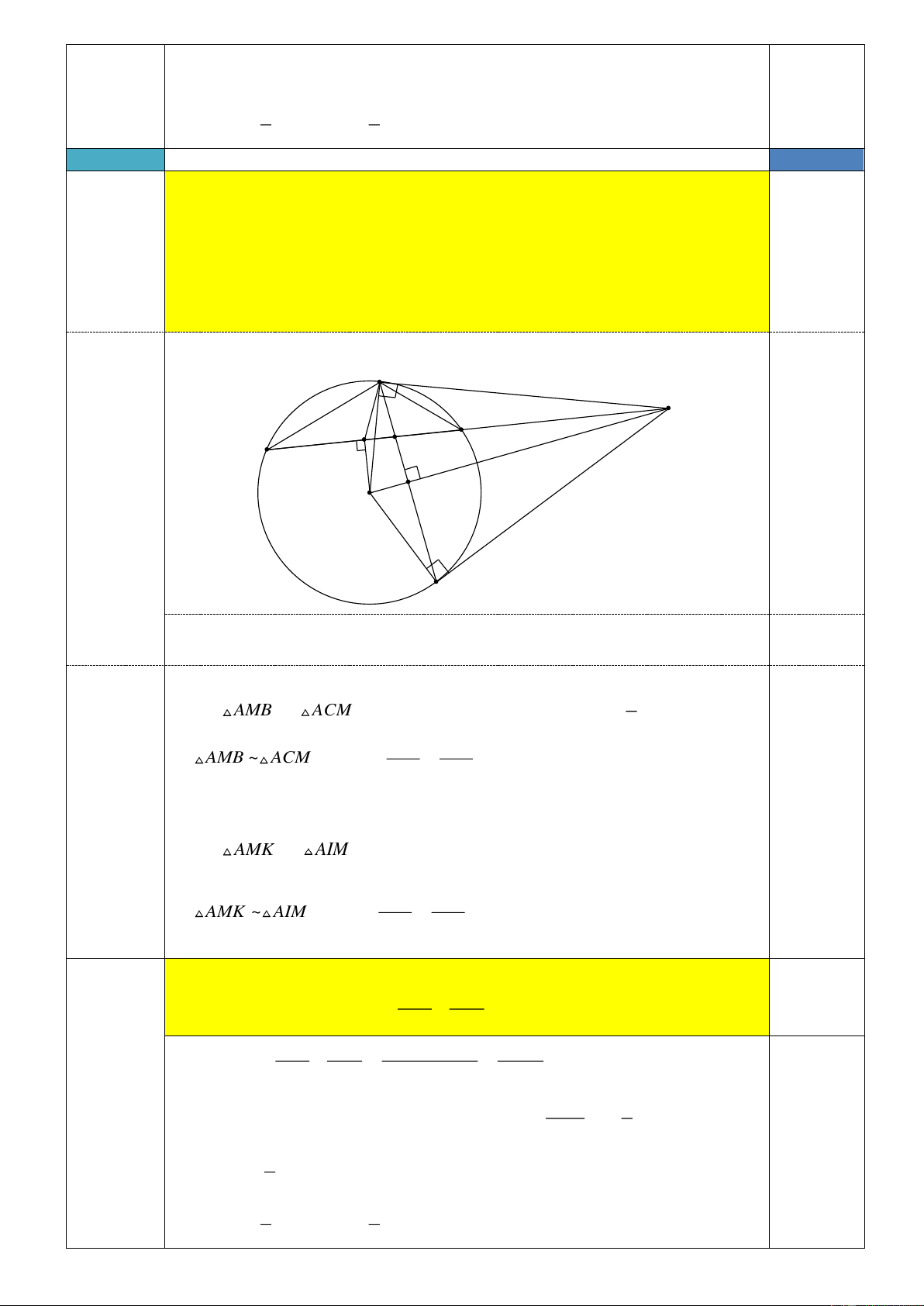
Câu 6b (2,0 điểm). Cho đường tròn tâm O . Từ A là một điểm nằm ngoài O kẻ các tiếp tuyến AM
và AN tới O ( M; N là các tiếp điểm ).
1) Chứng minh rằng tứ giác AMON nội tiếp được trong một đường tròn.
2) Đường thẳng qua A cắt đường tròn O tại B và C ( B nằm giữa A và C ). Gọi I là trung
điểm của BC , K là giao điểm của MN và BC . Chứng minh rằng: AK.AI  A . B AC .
Câu 7b (1,0 điểm). Cho các số x, y thỏa mãn x  0; y  0 và x  y  1. Tìm giả trị lớn nhất và giá trị nhỏ 1 1
nhất của biểu thức A   . x 1 y 1
-------------------------Hết--------------------------
(Thí sinh không được sử dụng tài liệu; Cán bộ coi thi không giải thích gì thêm)
Họ và tên thí sinh:.......................................................Số báo danh:...............................................................
TRƯỜNG THPT CHUYÊN BẮC NINH
HDC ĐỀ THI ĐỊNH KỲ LẦN I TỔ TOÁN TIN
NĂM HỌC 2018 – 2019 Môn: Toán 10 Câu Hướng dẫn Điểm
PHẦN CHUNG (7,0 điểm)
Giải phương trình và hệ phương trình sau: Câu 1 2x  3
(x 1)(y  2)  xy 1 (2,0 đ) 1)  x 1  0 2)  x 1
(2x 1)(y  2)  2xy 1 ĐK: x 1 0,25 Câu 1.1          (1,0 đ) x x x 0,5 Pt 2 2 3 ( 1) 0 ... 2 0 0,25 KL: x  2
xy  2x  y  2  xy 1
2x  y  3  Hệ     0,5          Câu 1.2 2xy 4x y 2 2xy 1 4x y 1 (1,0 đ) x  2  ...   , KL 0,5 y  7
Cho tập hợp A   ;  
1 3;6 và tập B được biểu diễn như hình vẽ sau: Câu 2 (1,5 đ)
1) Hãy viết tập B dưới dạng hợp của các khoảng, đoạn hoặc nửa khoảng.
2) Xác định các tập hợp sau dưới dạng hợp của các khoảng, đoạn hoặc nửa
khoảng : C  A  B và E  \ (A ) B Câu 2.1 (0,5 đ)     +) B  ( ; 2) [5; ) 0,5 Câu 2.2
+ C  A B  ( ;  2  ) [ 5;6) 0,5 (1,0 đ) + E  \ (A ) B  (1;3] 0,5 Cho phương trình: 2
mx – 4m  2 x  3m – 2  0 (1) ( m là tham số). Câu 3 (1,0 đ)
1) Giải phương trình (1) khi m  2.
2) Tìm giá trị của tham số m để pt (1) có các nghiệm đều là số nguyên. Câu 3.1
Thay m  2, ta được: 2 2
(1)  2x  6x  4  0  x  3x  2  0 0,25 (0,5 đ)
Ta thấy: 1 – 3 +2 = 0 nên pt có 2 nghiệm: x  1; x  2 0,25 1 2
* Nếu m  0 thì (1)  2x  2  0  x 1 nguyên 0,25
Suy ra: Với m  0 pt có nghiệm nguyên
* Nếu m  0 thì ph (1) là pt bậc 2 ẩn x . Từ ý 2 ta có: pt có 2 nghiệm: 
2m 1 m 1 x  1  1 m      Câu 3.2 2m 1 m 1 3m 2 x   (0,5 đ) 2   m m Để
pt (1) có nghiệm nguyên thì nghiệm x phải nguyên 2 3m  2 2 
 Z  3   Z (m  0) 2 m hay m là ước của 2 m m  m  2  ; 1  ;1;  2 0,25
Kết luận: Với m  { 1  ; 2
 ;0} thì pt có nghiệm nguyên Câu 4
Tìm tọa độ các giao điểm của đường Parabol 2
(P) : y  2x và đường thẳng (1,0 đ)
(d) : y  3x 1. 1
+ Phương trình hoành độ giao điểm: 2
2x  3x 1  ...  x  1; x  0,5 2  1 1 
+ KL: Tọa độ các giao điểm là: (1; 2) và ;    0,5 2 2 
Cho hình vuông ABCD có độ dài cạnh bằng a . Gọi O là giao điểm của AC Câu 5 và BD. (1,5 đ)
1) Chứng minh rằng: AC  BD  AD  BC
2) Tính AB  DO theo a
 AC  AD  BD  BC  0 0,25 Câu 5.1 (0,75đ)    0,25 DC CD 0
 DD  0 luôn đúng (đpcm) 0,25
+ Từ giả thiết ta được: AB  DC 0,25 Câu 5.2
+ AB  DO  DC  DO  OC  OC (0,75đ) 0,25 + Tính đượ 1 a 2 a 2 c OC  AC 
, KL: AB  DO  2 2 2 0,25
PHẦN RIÊNG (3,0 điểm)
A. Phần dành cho thí sinh lớp 10: Anh1, Anh2, Văn, Cận2.
Cho tam giác ABC có ba góc nhọn. Hai đường cao AE và BK của tam giác Câu 6a
ABC (với E thuộc BC, K thuộc AC ). (2,0 đ)
1) Chứng minh tứ giác ABEK nội tiếp được trong một đường tròn.
2) Chứng minh CE.CB  CK.CA .
Vẽ hình theo giả thiết: A E 0,25 Câu 6a.1 (1,0 đ) C B K + Ta có 0
AEB  AKB  90 . 0,5
Nên E và K cùng thuộc đường tròn đường kính AB.
+ Vậy tứ giác ABEK nội tiếp trong một đường tròn. 0,25 + Vì AE  B ;
C BK  AC nên 0
AEC  BKC  90 . 0,25 Câu 6a.2
+ Chỉ ra hai tam giác AEC và BKC đồng dạng (g-g). (1,0 đ) 0,5 CE CA Suy ra 
. Vậy CE.CB  CK.CA . CK CB 0,25
Cho các số x, y thỏa mãn x  0; y  0 và x  y  1 . Tìm giả trị lớn nhất và giá
trị nhỏ nhất của biểu thức 2 2
A  x  y . 2 +) Ta có 2 2
A  x  y  (x  y)  2xy  1 2xy 0,25 Câu 7a 2  x  y  1 (1,0đ)
+) Mà x  0; y  0 và x  y  1 ta được: 0  xy     0,25  2  4 0,25
x  0; y 1
+) max A  1 khi xy  0    0,25 x  1; y  0 1 1 +) min A  khi x  y  2 2
B. Phần dành cho thí sinh lớp 10: Lý, Hóa, Sinh, Tin, Cận1.
Cho đường tròn tâm O . Từ A là một điểm nằm ngoài O kẻ các tiếp tuyến
AM và AN tới O ( M; N là các tiếp điểm ). Câu 6b
1) Chứng minh rằng tứ giác AMON nội tiếp trong một đường tròn. (2,0 đ)
2) Đường thẳng qua A cắt đường tròn O tại B và C ( B
nằm giữa A và C ). Gọi I là trung điểm của BC , K là giao điểm của MN
và BC . Chứng minh rằng: AK.AI  A . B AC .
Vẽ hình theo giả thiết: M A B K I C 0,25 Câu 6b.1 E (1,0 đ) O N
Theo tính chất tiếp tuyến ta có :   90O AMO ANO 0,5
Vậy: Tứ giác AMNO nội tiếp đường tròn đường kính AO 0,25 Nối M với B, C. 1
+ Xét AMB và ACM có: MAC chung, MCB  AMB  sđ MB 2  AB AM 0,25
AMB ~ ACM (g.g) 2    A .
B AC  AM (1) AM AC Câu 6b.2
+ Vì I là trung điểm BC nên    90o OI BC OIA
nên I thuộc đường (1,0 đ) 0,25
tròn ngoại tiếp tứ giác AMNO .
+ Xét AMK và AIM có: MAK chung, AIM  AMK
(Vì: AIM  ANM cùng chắn AM và AMK  ANM ) 0,25  AK AM AMK ~ AIM (g.g) 2  
 AK.AI  AM (2) AM AI
Từ (1) và (2) ta có: AK.AI  A . B AC (đpcm) 0,25
Cho các số x, y thỏa mãn x  0; y  0 và x  y  1 . Tìm giả trị lớn nhất và giá 1 1
trị nhỏ nhất của biểu thức A   . x 1 y 1 1 1 x  y  2 3 +) Ta có A     x 1 y 1
xy  x  y 1 2  xy 0,25 Câu 7b 2 (1,0 đ)  x  y  1
+) Mà x  0; y  0 và x  y  1 ta được: 0  xy     0,25  2  4 3
x  0; y 1 0,25 +) max A  khi xy  0   2
x  1; y  0 4 1 +) min A  khi x  y  0,25 3 2
* Chú ý: Các cách giải toán khác phù hợp, giám khảo cho điểm tối đa theo thang điểm.