TRƯỜNG THPT CHUYÊN
ĐỀ THI GIỮA HỌC KÌ I HÀ NỘI - AMSTERDAM NĂM HỌC 2020 - 2021 MÔN TOÁN - LỚP 8 THCS.TOANMATH.com
Thời gian làm bài: 60 phút (không kể thời gian phát đề)
Câu 1. Phân tích các đa thức sau thành nhân tử: a) 2 (
A x)  x 3x  2 b) Bx y 2 2 ,
 x  4y 4xy 4 Câu 2. Tìm 3 3 3
x sao cho x  2 2x   1  9x   1  16 .
Câu 3. Cho a , b , c . là các số thực thỏa mãn 2 2 2
a  b  c  ab  bc  ca . Chứng minh rằng a  b  . c Câu 4. Cho A  BC vuông ở ,
A ( AB  AC) , đường cao AH , đường trung tuyến AM . Gọi
E , F lần lượt là hình chiếu vuông góc của H trên AB , AC . Trên tia đối của tia EH
lấy điểm P sao cho EP  EH , trên tia đối của tia FH lấy điểm Q sao cho FQ  FH .
a) Chứng minh ba điểm P , A , Q . thẳng hàng.
b) Chứng minh rằng tứ giác BPQC là hình thang vuông và BP  QC  BC .
c) Chứng minh AM vuông góc với EF
d) Gọi (d) là đường thẳng thay đổi, đi qua A , nhưng không cắt cạnh BC của tam giác ABC .
Gọi X , Y lần lượt là hình chiếu vuông góc của B , C trên (d) . Tìm vị trí của (d) để chu vi tứ
giác BXYC lớn nhất. Câu 5.
a) ( Dành cho các lớp 8B, 8C, 8D, 8E )
Cho a , b , c là các số thực đôi một khác nhau thỏa mãn 3 3 3
a  b  c  3abc . Tính giá trị của
biểu thức M  a bb  cc  a abc
b) ( Dành riêng cho lớp 8A)
Với a , b là các số thực thỏa mãn 3 3
a  b 3ab  18 . Chứng minh rằng 9  a  b 1 HẾT TRƯỜNG THPT CHUYÊN
ĐỀ THI GIỮA HỌC KÌ I HÀ NỘI - AMSTERDAM NĂM HỌC 2020 - 2021 MÔN TOÁN - LỚP 8 THCS.TOANMATH.com
Thời gian làm bài: 60 phút (không kể thời gian phát đề)
HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1. Phân tích các đa thức sau thành nhân tử: a) 2 (
A x)  x 3x  2 b) Bx y 2 2 ,
 x  4y 4xy 4 Lời giải a) 2 (
A x)  x 3x  2 2
 x  x 2x  2  xx  1  2x   1  x  1 x  2 b) 2 2
B(x, y)  x  4 y  4xy  4   2 2
x  4xy  4 y 4
 x y2 2 2 2
 x2y 2x2y  2 Câu 2. Tìm 3 3 3
x sao cho x  2 2x   1  9x   1  16 . Lời giải 3 3 3
Ta có x  2 2x   1  9x   1  16
 x  3  x  3 x  3  x  3 2 2 1 1 8 1  16
 x  3 x  3  x  3  x  3 2 1 2 1 8 1  16    
x  x   x  2 x  x  x  2  x  3 2 1 2 2 1 1 2 1 2x   1 3  16      
x   x   x  x   x   x    x  2  x   x   x  2 2 2 1 3 3 3 2 1 2 1 2 1 2 1 2 2 2 2  16      2
x  x    2 2 2 3 3 3 3
1 4x  4x 1 4x  6x  2  4x  8x   4 16  0 2
  x  x   2 9 9 9
12x 18x  716  0 2 2
 9x  9x 912x 18x 7 16  0 2
 21x 9x  0  3 . x 7x   3  0   x  0 x  0       3 7x  3  0  x    7  3   Vậy x  0;    .  7   
Câu 3. Cho a , b , c . là các số thực thỏa mãn 2 2 2
a  b  c  ab  bc  ca . Chứng minh rằng a  b  . c Lời giải 2 2 2
a  b  c  ab  bc  ca 2 2 2
 2a  2b  2c  2ab  2bc  2ca 2 2 2
 2a  2b  2c  2ab  2bc  2ca  0 2 2 2 2 2 2
 a  2ab  b  b  2bc  c  c  2ca  a  0
 a b2 b c2 c  a2  0 2 2 2
Mà a  b  0; b  c  0; c  a  0 với mọi số a, b, c . 2 2 2
Suy ra a  b b  c c  a  0 
 ab2  0 
ab  0 a  b          
b  c2  0            b c 0 b c a b
c (điều phải chứng minh).          
c  a2  0 c a 0 c a    Câu 4. Cho A  BC vuông ở ,
A ( AB  AC) , đường cao AH , đường trung tuyến AM . Gọi E , F lần
lượt là hình chiếu vuông góc của H trên AB , AC . Trên tia đối của tia EH lấy
điểm P sao cho EP  EH , trên tia đối của tia FH lấy điểm Q sao cho FQ  FH .
a) Chứng minh ba điểm P , A , Q . thẳng hàng.
b) Chứng minh rằng tứ giác BPQC là hình thang vuông và BP  QC  BC .
c) Chứng minh AM vuông góc với EF
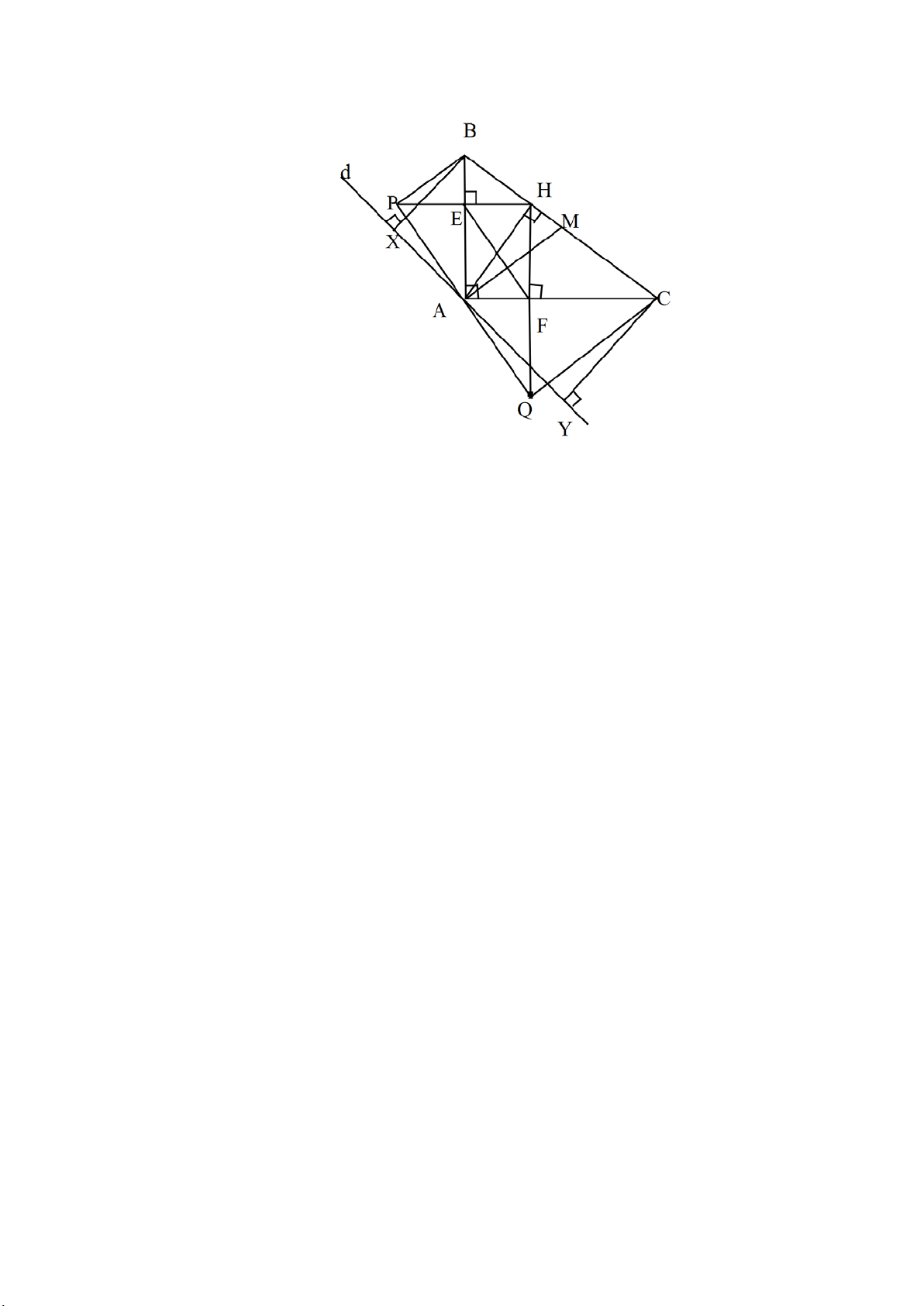
d) Gọi (d) là đường thẳng thay đổi, đi qua A , nhưng không cắt cạnh BC của tam giác ABC .
Gọi X , Y lần lượt là hình chiếu vuông góc của B , C trên (d) . Tìm vị trí của (d) để chu vi tứ
giác BXYC lớn nhất. Lời giải
a) Ta có P đối xứng với H qua E
 E là trung điểm của HP
mà AB vuông góc với HP
 AB là trung trực của HP
 H đối xứng với P qua AB   
AP  AH và góc HAE  PAE
Vì Q đối xứng với H qua F
 F là trung điểm của QH
mà AC vuông góc với QF
 AC là trung trực của QF
 H đối xứng với Q qua AC   
AQ  AH và HAF  QAF    
QAP  HAE  HAF  0 2  2BAC 180
 Ba điểm P , A , Q thẳng hàng. b) Xét A  QC và A  HC có
AQ  AH (cmt)  
HAF  QAF (cmt) AC chung  A  QC = A  HC (c.g.c)
 CQ  CH   0
;CQA  CHA  90  
Chứng minh tương tự ta có : BP  BH 0
; BPA  BHA  90
 BP QC  BH CH  BC
Xét tứ giác BPQC có BP  P ;
Q C Q  PQ  BP // CQ .  Mà 0 CQA  90
 BPQC là hình thang vuông. c) Xét QHP 
có EF là đường trung bình  EF // PQ Ta có : AH  AQ ( A  QC = A  HC )
AH  AP ( A  PB  A  HB )
 AP  AQ . Mà BM  MC
 Hình thang BCQP có AM là đường trung bình  AM // CQ
PQ  CQ  PQ  AM  EF  AM d) Ta có:
BX  AX 2   2 2 BX  AX  2 2  2AB
 BX  AX  AB 2
CY  AY2   2 2 CY  AY  2 2  2AC
 CY  AY  AC 2 Chu vi hình thang PBXYC
= BX + XY + CY + BC
= BX + AX + AY + CY + BC
≤ AB 2 + AC 2 + BC P
max = AB 2 + AC 2 + BC BXYC
 d là phân giác góc ngoài tại đỉnh A hay d vuông góc với phân giác  BAC . Câu 5.
a) ( Dành cho các lớp 8B, 8C, 8D, 8E )
Cho a , b , c là các số thực đôi một khác nhau thỏa mãn 3 3 3
a  b  c  3abc . Tính giá trị của
biểu thức M  a bb  cc  a abc
b) ( Dành riêng cho lớp 8A)
Với a , b là các số thực thỏa mãn 3 3
a  b 3ab  18 . Chứng minh rằng 9  a  b 1 Lời giải a) Ta có: 3 3 3
a  b  c  3abc   3 3 a  b  3
 c 3abc  0 3 2 2 3 3 2 2
 a 3a b 3ab b  c 3abc 3a b3ab  0
 a b3 3
 c 3ab(a b  c)  0   
 a b  c a b2 a b 2
c  c 3ab(a  b  c)  0    
 a b  c 2 2 2
a  2ab b acbc c 3ab  0  
 a b  c 2 2 2
a  b  c  ab  ac bc  0 1    
a  b  c a b2 b c2 c  a2  0   2  
a b c  0
 a bc 
TH1: a  b  c  0
 a b   ;
c b  c   ;
a c  a  b  . Khi đó M   c   a   b
  abc  abc   abc  0 .
TH2: a  b  c  M  2 .2 a .2
b c  abc  8abc  abc  9abc . b) Ta có 3 3
a  b 3ab  18 3 3
 a b 13ab  17
 a b3 3aba b13ab  17   
 a b   a b2 1
(a b) 1 3aba b   1  17    
 a b   2 2
1 a  b 1 ab  a b  17  0
 a b   2 2
1 a  b 1 ab  a b  0 1 2 2 2   mà 2 2
a  b 1 ab  a b 
ab a  1 b   1  0   2  
(dấu “=” không xảy ra vì
theo giả thiết a, b không thể đồng thời bằng 1)
 a b 1 0
 a b 1 3
Ta có: a  b 3aba  b   1  18 2 3 2
a b  0  3ab  a  b 4
 aba b   3 3
1  a  b2 a  b  
1 ( vì a  b 1 0 ) 4
Đặt a b  t 3 3 2
 18  t  t t   1 4 1 3 3 2
 t  t 18  0 4 4 1   3 2 t 3t   72  0 4 3 2
 t 3t  72  0 3 2
 t 72 3t 72 3  t 72
 t  5  9
 a b  9 .
Vậy 9  a b 1.
__________ THCS.TOANMATH.com __________
Document Outline

• de-thi-giua-hk1-toan-8-nam-2020-2021-truong-chuyen-ha-noi-amsterdam